有理函数不定积分的一个综合公式
不定积分求解运算法则

不定积分求解运算法则不定积分求解是微积分中的重要内容之一,它可以用来求解函数的原函数,为我们提供了求解定积分和解微分方程等问题的基础。
在求解不定积分时,我们需要掌握一些运算法则,这些法则可以帮助我们更加高效地求解不定积分。
一、基本积分法则基本积分法则主要包括线性性、积化和差化和常数乘积的法则。
1.线性性:若f(x)和g(x)是连续函数,k为常数,则有:∫(kf(x) + g(x))dx = k∫f(x)dx + ∫g(x)dx2.积化和差化:对于连续函数f(x)和g(x),有:∫(f(x) ± g(x))dx = ∫f(x)dx ± ∫g(x)dx3.常数乘积法则:对于连续函数f(x)和常数k,有:∫k f(x)dx = k∫f(x)dx二、换元积分法则换元积分法则也称为u-置换法,它是利用复合函数的求导和求逆的关系进行积分的一种方法。
1.一元换元法则:设u=g(x)是x的可导函数,f(u)是u的原函数,则有:∫f(g(x))g'(x)dx = ∫f(u)du2.多元换元法则:对于多元函数,设u=g(x,y)和v=h(x,y)是x,y的可导函数,f(u,v)是u,v的原函数,则有:∬f(g(x, y), h(x, y))(∂(g, h)/∂(x, y))dxdy = ∬f(u, v)dudv 三、分部积分法则分部积分法是利用求导的乘积法则进行积分的方法,可以将一个积分转化为两个因子相乘的形式,从而简化计算。
1.一元分部积分法则:设u=f(x)和v=g(x)是可导函数,f'(x)和g'(x)是它们的导数,则有:∫u v' dx = uv - ∫u'v dx2.多元分部积分法则:对于多元函数,设u=f(x,y)和v=g(x,y)是可导函数,f'(x,y)和g'(x,y)是它们的导数,则有:∫∫u ∂v/∂x dA = ∮uv dy - ∫∫∂u/∂y v dA四、有理函数分解积分法则有理函数分解积分法用于求解有理函数的不定积分,即把一个有理函数表示为几个基本函数的和的形式。
常用不定积分公式

常用不定积分公式1. 基本积分公式:对于n不等于-1的任意实数,有∫x^n dx = (x^(n+1))/(n+1) + C,其中C为常数。
2. 幂函数积分公式:∫a^x dx = (a^x)/ln(a) + C,其中a为大于0且不等于1的常数,C为常数。
3.基本三角函数积分公式:(1) ∫sin(x) dx = -cos(x) + C(2) ∫cos(x) dx = sin(x) + C(3) ∫sec^2(x) dx = tan(x) + C(4) ∫csc^2(x) dx = -cot(x) + C(5) ∫sec(x)tan(x) dx = sec(x) + C(6) ∫csc(x)cot(x) dx = -csc(x) + C4.基本指数函数积分公式:(1) ∫e^x dx = e^x + C(2) ∫a^x(ln(a)/a^x) dx = a^x + C,其中a为大于0且不等于1的常数,C为常数。
5.基本对数函数积分公式:(1) ∫1/x dx = ln,x, + C(2) ∫ln(x) dx = x(ln,x, - 1) + C6.基本双曲函数积分公式:(1) ∫sinh(x) dx = cosh(x) + C(2) ∫cosh(x) dx = sinh(x) + C(3) ∫sech^2(x) dx = tanh(x) + C(4) ∫csech^2(x) dx = -coth(x) + C(5) ∫sech(x)tanh(x) dx = -sech(x) + C(6) ∫csech(x)coth(x) dx = -csech(x) + C7. 部分积分法:对于两个可导函数u(x)和v(x),有∫u(x)v'(x) dx = u(x)v(x) - ∫v(x)u'(x) dx。
8. 代换法:对于一个可导函数u(g(x)),有∫u'(g(x))g'(x) dx =∫u'(u) du。
有理函数的不定积分

例5. 求
( x 2 x 2) (2 x 2) d x 解: 原式 2 2 ( x 2 x 2)
dx d( x 2 x 2) 2 2 2 ( x 1) 1 ( x 2 x 2)
2
2
1 C arctan(x 1) 2 x 2x 2
2
2
例11. 求 解: 为去掉被积函数分母中的根式, 取根指数 2, 3 的最小公倍数 6, 令 x t , 则有 5 1 2 6 t d t 原式 3 2 6 ( t t 1 ) dt 1 t t t
6
6
2 1t 3 1 ln 1 t t t 3 2
2
例3. 求 解: 原式
x 2x 3 2 d( x 1) 1 d( x 2 x 3) 3 2 2 x 2x 3 ( x 1) 2 ( 2 ) 2 3 x 1 1 2 arctan C ln x 2 x 3 2 2 2
1 ( 2 x 2) 3 2
例2. 求 解: 已知 1 1 4 2x 1 2 2 (1 2 x)(1 x ) 5 1 2 x 1 x 1 x 2
2 d(1 2 x) 1 d(1 x ) 1 dx 原式 2 2 5 5 1 2x 5 1 x 1 x 2 1 1 2 ln 1 2 x ln (1 x ) arctan x C 5 5 5
1 Bx C A 2 (1 2 x)(1 x ) 1 2 x 1 x 2
A(1 x 2 ) ( Bx C )(1 2 x) 2 (1 2 x)(1 x ) 2 1 A(1 x ) ( Bx C)(1 2x), 1 4 1 取x 得A , 取x 0得1 A C, C , 5 5 2 2 取x 1得1 2 A 3( B C), B
有理函数积分法

第21讲 理函数的不定积分一、有理函数的不定积分有理函数是指由两个多项式函数的商所表示的函数,其一般形式为mm mn n n xxx x x Q x P x R βββααα++++++==-- 110110)()()(, (1)其中,m 为n 非负整数,n ααα,,,10 与m βββ ,,10都是常数,且00≠α,00≠β. 若n m >,则称它为真分式;若n m ≤,则称它为假分式.由多项式的除法可知,假分式总能化为一个多项式与一个真分式之和.由于多项式的不定积分是容易求得的,因此只需研究真分式的不定积分,故设(1)为一有理真分式. 根据代数知识,有理真分式必定可以表示成若干个部分分式之和(称为部分分式分解).因而问题归结为求那些部分分式的不定积分.为此,先把怎样分解部分分式的步骤简述如下(可与例1对照着做): 第一步 对分母()x Q 在实系数内作标准分解: ()()()()()tt t s q p x q x p xa x a x x Q μμλλ++++--=21121121, (2)其中()t iji ,,2,1,1,0 ==μλβ均为自然数,而且.,,2,1,04;2211t j q p m j j si tj ji =-=+∑∑==μλ第二步 根据分母的各个因式分别写出与之相应的部分分式:对于每个形如()ka x -的因式,它所对应的部分分式是 ()();221kka x A a x A ax A -++-+-对每个形如()kq px x ++2的因式,它所对应的部分分式是()().22222211kkk q px xC x B q px xC x B qpx x C x B ++++++++++++把所有部分分式加起来,使之等于()x R .(至此,部分分式中的常数系数i i i C B A ,,尚为待定的.)第三步 确定待定系数:一般方法是将所有部分分式通分相加,所得分式的分母即为原分母()x Q ,而其分子亦应与原分子()x P 恒等.于是,按同幂项系数必定相等,得到一组关于待定系数的线性方程,这组方程的解就是需要确定的系数.例1 对()8425109422345234-+--+-++-=x x x x x x x x x x R 作部分分式分解解 按上述步骤依次执行如下:()=x Q 84252345-+--+x x x x x ()()().12222+-+-=x x x x部分分式分解的待定形式为()().122222210+-++++++-=x x C Bx x A x A x A x R (3)用()x Q 乘上式两边,得一恒等式()()1210942220234+-+≡-++-x x x A x x x x +()()()()()121222221+--++-+-x x x A x x x x A+()()()222+-+x x C Bx (4)然后使等式两边同幂项系数相等,得到线性方程组:⎪⎪⎪⎩⎪⎪⎪⎨⎧-=---=--+=+----=+++-=++常数项的系数,的系数,的系数,的系数 .1082449483442433123,22102122103210410C A A A x C B A A x C B A A A x C B A A A x B A A 求出它的解:1,1,1,2,1210=-=-===C B A A A ,并代人(3)式,这便完成了)(x R 的部分分式分解:.11)2(12221)(22+---+-++-=x x x x x x x R上述待定系数法有时可用较简便的方法去替代.例如可将x 的某些特定值(如0)(=x Q 的根)代人(4)式,以便得到一组较简单的方程,或直接求得某几个待定系数的值.对于上例,若分别用2=x 和2-=x 代人(4)式,立即求得1120-==A A 和,于是(4)式简化成为)1)(2)(2(161232134+-+-=-+-x x x x A x x x .)2)(2)((2+-++x x C Bx为继续求得C B A ,,1,还可用x 的三个简单值代人上式,如令1,1,0-=x ,相应得到⎪⎩⎪⎨⎧=+-=++=+.83,233,42111C B A C B A C A 由此易得1,1,21=-==C B A .这就同样确定了所有待定系数. 一旦完成了部分分式分解,最后求各个部分分式的不定积分.由以上讨论知道,任何有理真分式的不定积分都将归为求以下两种形式的不定积分:⎰-I ka x dx)()(;()⎰<-+++I I )04()(22q p dx q px x M Lx k.对于()I ,已知()()⎪⎩⎪⎨⎧>+--=+-=--⎰.1,11,1,ln )(1k C a x k k C a x a x dx k k对于()II ,只要作适当换元(令2p x t +=),便化为()⎰⎰++=+++dt rtNLt dx q px xMLx kk222)(⎰⎰+++=,)()(2222kkr t dt N dt r t t L (5)其中.2,422L p M N pq r-=-=.当1=k 时,(5)式右边两个不定积分分别为⎰++=+C r t dt rtt)ln(212222,.a r c t a n 122C rtr rtdt+=+⎰ (6) 当2≥k 时,(5)式右边第一个不定积分为C r t k dt r t tk k++-=+⎰-12222))(1(21)(.对于第二个不定积分,记 ,)(122⎰-+=k k r tdtI 可用分部积分法导出递推公式如下:dt r t t r t rI kk ⎰+-+=)()(1222222⎰+-=-dt r ttrI rkk )(11222212⎰⎪⎪⎭⎫ ⎝⎛+-+=--122212)(1)1(211k k r t td k r I r.)()1(2111122212⎥⎦⎤⎢⎣⎡-+-+=---k k k I r t tk r I r 经整理得到.)1(232))(1(2121222----++-=k k k I k r k r t k r tI (7)重复使用递推公式(7),最终归为计算1I ,这已由(6)式给出. 把所有这些局部结果代回(5)式,并令2p x t +=,就II )的计算.例2 求.)22(1222dx x xx ⎰+-+解:在本题中,由于被积函数的分母只有单一因式,因此,部分分式分解能被简化为222222)22()12()22()22(1+--++-=+-+x x x x x x x x .)22(12221222+--++-=x x x x x现分别计算部分分式的不定积分如下:.)1arctan(1)1()1(22122C x x x d x x dx +-=+--=+-⎰⎰dx x xx dx x xx ⎰⎰+-+-=+--2222)22(1)22()22(12++-+-=⎰222)22()22(x xx x d []⎰+--221)1()1(x x d.)1(221222⎰+++--=tdtx x由递推公式(7),求得其中⎰⎰+++=+121)1(2)1(2222tdtt t t dt .)1arctan(21)22(2122C x x x x +-++--=于是得到.)1a r c t a n (23)22(23)22(12222C x x x x dx x xx +-++--=+-+⎰二、三角函数有理式的不定积分⎰dx x x R )cos ,(sin 是三角函数有理式的不定积分。
有理函数的积分
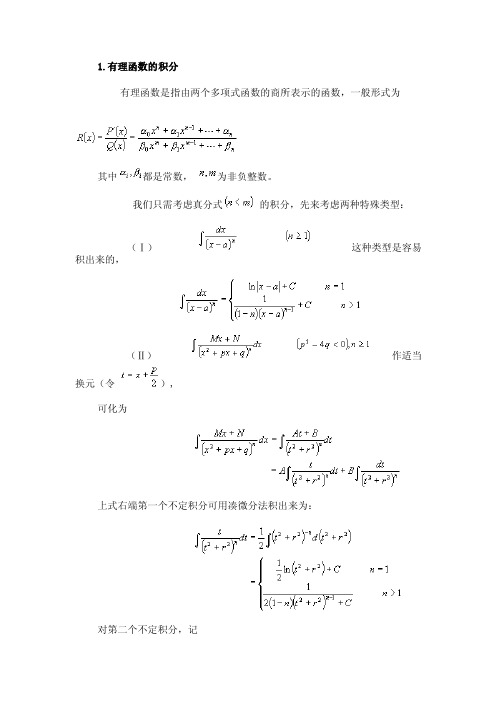
1.有理函数的积分有理函数是指由两个多项式函数的商所表示的函数,一般形式为其中都是常数,为非负整数。
我们只需考虑真分式的积分,先来考虑两种特殊类型:(Ⅰ)这种类型是容易积出来的,(Ⅱ)作适当换元(令),可化为上式右端第一个不定积分可用凑微分法积出来为:对第二个不定积分,记用分部积分法可导出递推公式:整理得重复使用递推公式,最终归结为计算而可积出来为这样就可完成对不定积分(Ⅱ)的计算。
对任一个有理函数而言,均可写成一个多项式与一个有理真分式的和,而多项式的积分问题已经解决,下面主要考虑有理真分式(不妨设)的积分问题。
为叙述简便,不妨设.其方法是将化成许多简单分式(即类型(Ⅰ)、(Ⅱ))的代数和然后逐项积分。
由于类型(Ⅰ)、(Ⅱ)总是可“积出来”的,从面有理函数总是可以“积出来”。
下面简述分解有理真分式()的步骤:第一步按代数学的结论,将分母分解成实系数的一次因式与二次因式的乘幂之积。
其中均为自然数。
第二步根据因式分解结构,写出的部分分式的待定形式:对于每个形如的因式,所对应的部分分式为对于每个形如的因式,所对应的部分分式为把各个因式所对应的部分分式加起来,就完成了对的部分分式分解。
第三步确定待定系数:通分后比较分子上的多次式的系数,得待定系数的线性方程组,由此解得待定系数的值。
例8.13 求2.三角函数有理式和积分由及常数经过有限次四则运算所得的函数称为关于的有理式(或三角函数有理式)。
用表示对于这种函数的不定积分我们总可通过代换,化为以为变量的有理函数的积分。
理由是,,,又,故从而上面的讨论说明:三角函数有理式也总是可以“积出来”的,但对具体问题而言,用上述方法往往计算量太大,因此,有时要考虑用其它简便方法。
(1)如果是的奇函数时,即则设即可。
例如求(1);(2).(2)如果是的奇函数时,即则设即可。
例如求.(3)如果是关于与的偶函数时,即则设即可。
例如求(1);(2).(4)请研究被积函数为(为自然数)时的情况。
不定积分方法总结

A(a cos x b sin x) B(a cos' x b sin' x) 来做。 a cos x b sin x
sin x cos x 或 cos x sin x
。再用待定系数
简单无理函数的积分
一般用第二类换元法中的那些变换形式。
1 5 2 3 t t t c 5 3 1 (8 4 x 2 3 x 4 ) 1 x 2 c 15
例4
求
1 dx x ( x 7 2)
解:令 x 1 dx 1 dt 2
t t
1 t 1 x( x7 2) dx 1 7 ( t 2 )dt ( ) 2 t
1 arctan( x 2 ) c 2
例5
求
1 1 e x dx
1 ex ex ex 1 e x dx (1 1 e x )dx 1 dx d (1 e x ) x ln(1 e x ) c x 1 e
解法一:
1 1 e x dx
2 a ( 1 sin 2 t) a costdt
a
2
cos2 tdt
1 cos 2t a2 a dt 2 2
a2 1dt 2
cos 2tdt
a2 a2 1 t ( sin 2t ) c 2 2 2
sin t cost
x a a2 x2 a x a2 x2 a2
f ( x)dx [ f [ g (t )]g ' (t )dt]
t g 1 ( x )
例1
数学分析8-383 有理函数和可化为有理函数的不定积分

作部分
分式分解.
前页 后页 返回
解 因为 Q( x) x5 x4 5x3 2x2 4x 8 ( x 2)( x 2)2( x2 x 1).
所以 R( x) A0 A1 A2 Bx C , x 2 x 2 ( x 2)2 x2 x 1
两边乘以 Q( x), 得到 2x4 x3 4x2 9x 10
上述部分分式中的待定系数 Ai , Bi , Ci .
前页 后页 返回
3. 确定待定系数的方法 把所有分式通分相加, 所得分式的分子与原分子
P(x) 应该相等. 根据两个多项式相等时同次项系数 必定相等的原则, 得到待定系数所满足的线性方程
组, 由此解出待定系数.
例1
对
R( x)
2x4 x3 4x2 9x 10 x5 x4 5x3 2x2 4x 8
2
2
dx
x
1 2
2
2
3
2
1 ln | x2 x 1 | 1 2 arctan 2x 1 C.
2
23
3
于是
I ln | x 2 | ln | x 2 | 1 1 ln | x2 x 1 | x2 2
1 arctan 2x 1 C.
3
3
前页 后页 返回
例3
Q( x) ( x a1 ) 1 ( x as ) s ( x2 p1x q1)1
s
t
其中 i , j N+ , 且 i 2 j m,
i 1
j1
( x2 pt x qt )t ,
pj2 4qj 0, j 1,2, ,t.
2. 根据分母各个因式分别写出与之相应的部分分
r 2 )k1
C.
记 Ik
不定积分公式总结

不定积分公式总结不定积分是微积分中的一项重要内容,它是定积分的逆运算。
在不定积分中,我们需要找到原函数,即原函数的导函数为被积函数。
在实际运算中,我们会使用一系列的公式和方法来求解不定积分。
以下是一些常用的不定积分公式总结。
1. 线性函数:对于形如 f(x) = ax + b 的线性函数,其不定积分为F(x) = (1/2)ax^2 + bx + C,其中 a、b 和 C 为常数。
2.幂函数:不定积分的幂函数公式为F(x)=(1/(n+1))x^(n+1)+C,其中n为实数且n≠-1、例如,对于x^3的不定积分,结果为F(x)=(1/4)x^4+C。
3. 指数函数:不定积分的指数函数公式为 F(x) = (1/a^x * ln,a,) + C,其中 a 为正实数且a ≠ 1、例如,对于 2^x 的不定积分,结果为 F(x) = (1/ln2)2^x + C。
4. 对数函数:不定积分的对数函数公式为 F(x) = x * (ln,x, - 1) + C。
5. 三角函数:不定积分的三角函数公式包括正弦函数、余弦函数、正切函数和余切函数等。
例如,正弦函数的不定积分为 F(x) = -cos(x) + C,余弦函数的不定积分为 F(x) = sin(x) + C。
6. 反三角函数:不定积分的反三角函数公式为 F(x) = arcsin(x) +C 或 F(x) = arccos(x) + C。
其中,arcsin(x) 表示 x 的反正弦函数。
7. 代换法:对于一些复杂的函数,我们可以通过代换来简化积分运算。
常用的代换方法包括令 u = g(x),然后求 du/dx,并将原函数中的x 替换为 u。
8.部分分式分解法:对于一些有理函数,我们可以将其进行部分分式分解,然后再分别求不定积分。
9. 分部积分法:分部积分法是一个用于简化一些积分的方法。
其公式为∫(u * dv) = uv - ∫(v * du)。
这个公式通过不断的选取 u 和dv 来进行迭代,从而简化复杂函数的积分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有理函数不定积分的一个综合公式
有理函数不定积分是数学中一个重要的概念,它是求解某些函数的积分的一种方法。
有理函数不定积分的一个综合公式是:
∫f(x)dx=f(x)ln|x|+C
其中,f(x)是一个有理函数,C是一个常数。
有理函数不定积分的一个综合公式可以用来求解有理函数的积分。
它可以用来求解一元函数的积分,也可以用来求解多元函数的积分。
有理函数不定积分的一个综合公式可以用来求解有理函数的积分,但是它也有一些局限性。
它只能用来求解有理函数的积分,而不能用来求解非有理函数的积分。
有理函数不定积分的一个综合公式是一个重要的数学概念,它可以用来求解有理函数的积分,但是它也有一些局限性。
因此,在使用有理函数不定积分的一个综合公式求解积分时,应该根据实际情况选择合适的方法。
