隐马尔可夫模型的多序列比对研究
利用马尔可夫模型进行基因序列分析的教程(五)

基因序列分析是生物信息学领域的重要研究内容之一。
利用马尔可夫模型进行基因序列分析可以帮助研究者理解基因的结构和功能,从而为疾病的治疗和预防提供重要的信息。
本文将介绍利用马尔可夫模型进行基因序列分析的基本原理和方法,希望读者能够通过本文了解基因序列分析的基本知识,并能够在实际研究中应用马尔可夫模型进行基因序列分析。
1. 马尔可夫模型简介马尔可夫模型是一种描述随机过程的数学模型,它具有“马尔可夫性质”,即未来的状态仅仅取决于当前的状态,与过去的状态无关。
在基因序列分析中,可以利用马尔可夫模型描述DNA序列中碱基的分布规律,从而推断基因的结构和功能。
2. 马尔可夫模型在基因序列分析中的应用在基因序列分析中,马尔可夫模型通常被用来预测DNA序列中的隐含Markov 模型和隐含马尔可夫模型,以及用在基因识别中。
通过对已知基因序列的训练,可以建立马尔可夫模型,然后利用该模型对未知的基因序列进行预测和分析。
3. 利用马尔可夫模型进行DNA序列的建模在利用马尔可夫模型进行基因序列分析时,首先需要对DNA序列进行建模。
通常情况下,可以将DNA序列中的碱基分为四类:A、C、G和T。
然后,可以利用马尔可夫模型描述碱基之间的转移概率。
以二阶马尔可夫模型为例,可以建立一个4*4的矩阵,表示从一个碱基转移到另一个碱基的概率。
4. 马尔可夫模型参数的估计在建立马尔可夫模型之后,需要对模型的参数进行估计。
参数估计的方法通常包括极大似然估计和贝叶斯估计。
通过对已知的训练数据进行统计分析,可以估计马尔可夫模型中的转移概率和初始状态概率。
5. 利用马尔可夫模型进行基因识别基因识别是基因序列分析的重要任务之一。
利用马尔可夫模型可以对DNA序列进行分析,从而识别其中的基因区域。
通过对DNA序列进行标记,可以利用马尔可夫模型进行概率推断,从而识别基因区域和非基因区域。
6. 马尔可夫模型在基因序列比对中的应用除了基因识别外,马尔可夫模型还可以应用于基因序列比对。
5隐马尔可夫模型简介
算法
评估问题:向前算法
定义向前变量 采用动态规划算法,复杂度O(N2T)
解码问题:韦特比(Viterbi)算法
采用动态规划算法,复杂度O(N2T)
学习问题:向前向后算法
EM算法的一个特例,带隐变量的最大似然估计
算法:向前算法(一)
P (O | λ ) = ∑ P (O, X | λ ) = ∑ P ( X | λ ) P (O | X , λ )
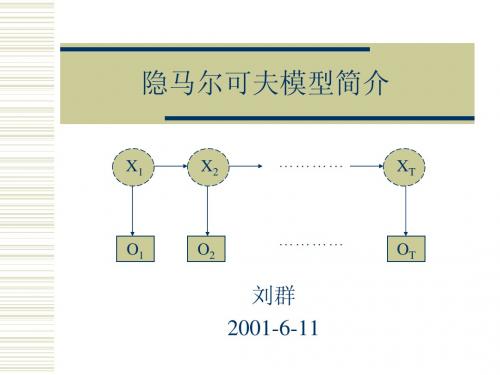
隐马尔可夫模型简介
X1 X2 ………… XT
O1
O2
…………
OT
刘群 2001-6-11
假设
对于一个随机事件,有一个观察值序列:O1,...,OT 该事件隐含着一个状态序列:X1,...,XT 假设1:马尔可夫假设(状态构成一阶马尔可夫链) p(Xi|Xi-1…X1) = p(Xi|Xi-1) 假设2:不动性假设(状态与具体时间无关) p(Xi+1|Xi) = p(Xj+1|Xj),对任意i,j成立 假设3:输出独立性假设(输出仅与当前状态有关) p(O1,...,OT | X1,...,XT) = Π p(Ot | Xt)
资源
Rabiner, L. R., A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition, Proceedings of the IEEE, vol. 77, no. 2, Feb. 1989, pgs 257 - 285. There is a lot of notation but verbose explanations accompany. 翁富良,王野翊,计算语言学导论,中国社会科学出版 社,1998 HTK:HMM Toolkit Hidden Markov Model (HMM) White Paper (GeneMatcher) ……
生物信息学中的计算方法和工具

生物信息学中的计算方法和工具生物信息学是生命科学中的一个重要领域,它研究如何从大量的生物数据中提取信息,以更好地理解生物学现象和生物学系统的运作规律。
在生物学的研究中,生物信息学可用于DNA、RNA、蛋白质等生物分子的序列分析,以及基因功能研究、治疗和预防疾病、新药开发等。
本文将重点介绍生物信息学领域中的计算方法和工具。
基本概念生物信息学中的计算方法和工具主要涉及以下方面:1. 序列比对:指将两段或多段序列进行对比,以确定它们的相似程度和差异点。
比对方法包括全局比对、局部比对和多序列比对等。
2. 基因预测:指对一个序列或一组序列进行分析,以确定其中是否存在基因序列和其位置、结构和功能等。
基因预测通常使用的方法包括基于序列或基于比对的方法。
3. 基因注释:指为已知或新发现的基因序列提供更多相关信息的过程。
根据序列相似性和功能分析,可以对其进行已知基因注释、预测基因注释、轨迹注释等。
4. 进化分析:研究生物种系的进化关系、起源和分化过程,主要方法包括序列比对、物种树和系统发育树分析等。
5. 蛋白质结构预测:指根据氨基酸序列对蛋白质结构进行模拟和预测的方法。
此外,还可以通过生物标记分析、三维结构分析、功能域分析等多种方法进行细化分析。
生物信息学计算方法和工具1. BLASTBLAST是生物信息学领域最常用的序列比对工具之一。
它可以通过比对数据库中所有已知序列,快速找出输入序列与之相似的序列,并提供序列相似度和信心度评估等信息。
2. HMMERHMMER是一种基于隐马尔可夫模型(HMM)的序列比对工具,主要用于蛋白质序列的域注释和拓扑域分析。
HMMER与BLAST相比,在序列的相对差异较大情况下,更具优势。
3. NCBI EntrezNCBI Entrez是一个基于网络的生物学检索系统,它允许通过NCBI中不同数据库与序列进行搜索。
4. ClustalWClustalW是一种多序列比对工具,它可以对两个或多个序列进行全局或局部比对,并产生序列的进化关系树。
三种分析蛋白结构域的方法

三种分析蛋白结构域的方法蛋白质是生命体内重要的功能分子,它们通过其特有的三维结构来实现其功能。
蛋白结构域是指蛋白质结构中具有独立功能和收缩性的区域。
分析蛋白结构域的方法对于理解蛋白的功能和机制有重要意义。
以下是三种常用的分析蛋白结构域的方法。
第一种方法是比对分析。
比对分析是通过比对已知结构域的蛋白质序列和结构与待研究蛋白质序列和结构进行对比,以此来鉴定待研究蛋白质中的结构域。
比对分析常用的工具有BLAST和HMMER等。
BLAST(基本局部序列比对工具)通过比对两个蛋白序列的共同片段来确定相似性,可以帮助确定蛋白质的结构域。
HMMER(隐含马尔可夫模型比对工具)则建立了一个隐含马尔可夫模型,将待研究的蛋白质序列与已知结构域的蛋白质序列进行比对,以此来确定结构域。
第二种方法是结构预测。
结构预测是通过计算机程序对蛋白质序列进行建模,以预测其三维结构。
常见的结构预测方法有基于比对的序列相似性建模、基于物理力学的方法和基于机器学习的方法等。
基于比对的序列相似性建模方法通过比对已知结构域的蛋白质序列与待研究蛋白质序列来构建模型,以此来预测待研究蛋白质的结构域。
基于物理力学的方法则基于分子力学和物理化学原理,通过计算机模拟来推测蛋白质的结构。
基于机器学习的方法则使用已知结构域的蛋白质数据来训练算法,以此来预测待研究蛋白质的结构域。
第三种方法是功能簇分析。
功能簇分析是通过聚类算法来将蛋白质分为不同的簇,以确定其中的结构域。
常见的聚类算法有层次聚类、基于密度的聚类和K均值聚类等。
层次聚类是将样本逐步合并成不同的簇,直到达到预定的停止条件。
基于密度的聚类则是根据样本的密度将其分为不同的簇。
K均值聚类是将样本分为K个不同的簇,使得簇内的样本之间的差异最小化。
通过功能簇分析可以鉴定出具有相似功能的蛋白质结构域。
综上所述,比对分析、结构预测和功能簇分析是常用的分析蛋白结构域的方法。
这些方法能够帮助鉴定蛋白质中的结构域,进而理解其功能和机制。
生物信息学中多序列比对算法的研究与改进

生物信息学中多序列比对算法的研究与改进生物信息学是研究生物学领域中的大规模生物数据的收集、存储、处理和分析的一门学科。
其中,多序列比对是生物信息学中一个重要的任务,可以帮助我们理解生物序列的相似性和差异性,从而揭示生物进化、功能和结构的信息。
本文将介绍多序列比对算法的基本原理、常用的方法和一些改进策略。
多序列比对的基本原理是将多个生物序列在一定的比对模型下进行比对,找到它们之间的共有特征和差异。
而这种比对过程是通过构建一个比对矩阵来完成的,该矩阵记录了每对序列之间的相似性得分。
常用的比对模型包括全局比对、局部比对和连续比对。
全局比对是将所有序列从头至尾进行比对,适合于序列相似性较高且较短的情况。
常用的算法有Needleman-Wunsch算法和Smith-Waterman算法。
Needleman-Wunsch算法使用了动态规划的思想,通过计算不同序列位置之间的得分矩阵,找到最优的比对方案。
Smith-Waterman算法是对Needleman-Wunsch算法的改进,它引入了负得分以处理局部比对的情况。
局部比对是将序列的某个片段与其他序列进行比对。
这种比对方法适用于序列相似性低或存在插入/缺失的情况。
常用的算法有BLAST、FASTA和PSI-BLAST。
BLAST算法使用了快速查找的技术,先找到一些高度相似的序列片段,再进行进一步的比对。
FASTA算法也是通过生成比对矩阵来找到相似片段,但它比BLAST更加灵敏。
PSI-BLAST算法将多次比对与序列数据库的搜索相结合,用于找到蛋白质序列中的保守和演化区域。
连续比对是将序列中的一个或多个连续子序列与其他序列进行比对。
这种比对方法可用于寻找序列中的结构域和功能区域。
常用的算法有HMMER和COBALT。
HMMER算法使用了隐马尔可夫模型和HMM-profile来比对序列中的结构域,具有较好的准确性和灵敏性。
COBALT算法是一种基于Conserved Domain Database (CDD) 的比对方法,通过利用数据库中的结构域信息来找到序列中的结构域。
多序列比对算法

多序列比对算法多序列比对算法是一种可用来比较多个相应序列之间的结构和功能差异的序列分析工具。
它可以被用来比较两个或多个序列,以发现它们之间的结构和功能差异。
多序列比对算法的核心思想是比较序列之间的相似性,搜索最适合的生物序列分析方法。
它是一种两个或多个生物分子序列之间的相似性分析和比较方法。
多序列比对算法具有广泛的应用,主要用于生物信息学中许多重要的问题,如深入了解功能性蛋白质、研究RNA结构和功能、设计药物靶点等。
它还可以用于挖掘基因的结构和功能,提升蛋白质的结构和功能,研究核酸、蛋白质和多种细胞的进化古迹,以及研究蛋白质的生物信息学。
多序列比对算法可以利用其卓越的识别能力找出两个或多个相互关联的序列中的相似片段。
许多多序列比对算法都基于概率模型,能够更准确地找出两个或多个序列之间有用的序列特征。
例如,多序列比对算法可以用于研究序列模式和相似性预测。
多序列比对算法可以应用于基因组定位,获得与序列相关的基因、转录因子和调控元件的功能和结构信息。
这种序列比对算法也可以用来预测基因在基因组中的位置,提供关于生物活性的结构信息,甚至可以用来挖掘复杂的信号转导网络中的基础关系。
此外,多序列比对算法可用于发现复杂对称结构,这对于研究生物体结构是非常有用的。
它也可以用于预测氨基酸序列或基因组中的结构和功能,它们是一种可以被用来预测基因表达状态和发挥作用的分子模型。
因此,多序列比对算法在生物序列分析领域占据了重要的地位。
多序列比对算法有很多种,如Smith-Waterman算法、Needleman-Wunsch算法、BLAST算法、Sequence Alignment算法、Clustal算法、HMM算法和全局模式填充法等,它们使用不同的功能来完成多序列比对任务。
Smith-Waterman算法是一种计算最长公共子字串的动态规划算法,可以找到最佳比对结果。
而Needleman-Wunsch算法是一种全局比对算法,该算法可以找到两个序列之间最佳比对结果,甚至可以是局部比对的变体。
隐马尔可夫模型(有例子-具体易懂)课件

定义前向变量为:
“在时间步t, 得到t之前的所有明符号序列, 且时间 步t的状态是Si”这一事件的概率, 记为 (t, i) = P(o1,…,ot, qt = Si|λ)
则
算法过程
HMM的网格结构
前向算法过程演示
t=1
t=2
t=3
t=4
t=5
t=T
t=6
t=7
问题 1 – 评估问题
给定
一个骰子掷出的点数记录
124552646214614613613666166466163661636616361651561511514612356234
问题
会出现这个点数记录的概率有多大? 求P(O|λ)
问题 2 – 解码问题
给定
一个骰子掷出的点数记录
124552646214614613613666166466163661636616361651561511514612356234
HMM的三个基本问题
令 λ = {π,A,B} 为给定HMM的参数, 令 O = O1,...,OT 为观察值序列,则有关于 隐马尔可夫模型(HMM)的三个基本问题: 1.评估问题: 对于给定模型,求某个观察值序列的概率P(O|λ) ; 2.解码问题: 对于给定模型和观察值序列,求可能性最大的状态序列maxQ{P(Q|O,λ)}; 3.学习问题: 对于给定的一个观察值序列O,调整参数λ,使得观察值出现的概率P(O|λ)最大。
5点
1/6
3/16
6点
1/6
3/8
公平骰子A与灌铅骰子B的区别:
时间
1
2
3
4
5
6
7
骰子
A
A
多序列比对

对于数目较少且较短的序列来说都不 切实际
多维的动态规划算法
Sequence 1
Sequence 2
分而治之方法
分而治之 (Divide and Conquer, DCA)方法 将MSA的空间复 杂度减小 DCA在线MSA
http://bioweb.pasteur.fr/seqanal/int erfaces/dca-simple.html
So in effect …
Sequence 1
Sequence 2
SP(Sum of Pairs)方法
为了找到最佳比对,并解决动态 规则算法的计算复杂问题, Carrillo & Lipman (1988)发明了 SP(Sum of Pairs)方法
进行所有序列间的双序列比对
基于双序列比对分数产生一个相邻连 接进化树(neighbor-join tree) 根据进化树提供的序列间关系按顺序 对序列进行比对 比对可以用以下两种方法: - slow/accurate - fast/approximate
CLUSTALW
******** CLUSTAL W (1.8) Multiple Sequence Alignments ******** 1.Sequence Input From Disc 2. Multiple Alignments 3. Profile / Structure Alignments 4. Phylogenetic trees S. Execute a system command H. HELP X. EXIT (leave program)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
PP(′(′ XX,|YY))-ΣX P(X|Y)ln
பைடு நூலகம்
PP((XX,|YY))=
ΣP(X|Y)ln X
PP(′(′ XX,|YY))+ΣX P(X|Y)ln
PP((XX,|YY))=
ΣP(X|Y)ln X
PP((′ XX,,YY))+ΣX P(X|Y)ln
ln PP((′ XX,,YY))≥0,则:
P(′ Y)≥P(Y)
(1)
证明 因为 P(′ X|Y)>0,P(X|Y)>0,P(′ X,Y)>0,P(X,Y)>0,
(f x)=lnx 在(0,+∞)有:lnx≤x-1,则:
ΣP(X|Y)ln X
PP((′ XX||YY))≤ΣX P(X|Y)[
PP((′ XX||YY))-1]=
400067,China 2.School of Computer Science & Information Engineering,Chongqing Technology and Business University,Chongqing 400067,China 3.Economics and Management Center,Chongqing Technology and Business University,Chongqing 400067,China E-mail:luozeju@
组,其中 Σ 是比对序列字母集,S={S1 ,S2 ,…,Sk }是比对序列的
集合,其中 S(i i=1,2,…,k)是以集合的形式代表一条序列,G=
(gij)是一个比对矩阵,其元素是 Σ 中的元素。
例如,若对 DNA,Σ={A,T,G,C,-(} 其中“-”表示空位或删
除状态),对 RNA,Σ={A,U,G,C,-},若针对蛋白质,Σ 是 20 种
摘 要:研究一种关于隐马尔可夫模型的多序列比对,利用值和特征序列的保守性,通过增加频率因子,改进传统隐马尔可夫模型 算法的不足。实验表明,新算法不但提高了模型的稳定性,而且应用于蛋白质家族识别,平均识别率比传统隐马尔可夫算法提高了 3.3 个百分点。 关键词:隐马尔可夫模型;多序列分析;蛋白质识别 DOI:10.3778/j.issn.1002-8331.2010.07.052 文章编号:1002-8331(2010)07-0171-04 文献标识码:A 中图分类号:TP391;TN957.52
对特征序列进行研究具有重要意义,首先,利用特征序列 可以对一个序列进行数据库搜索,以寻找它所在家族;其次,可 以比较不同家族的进化关系;另外,它是构建隐马尔可夫模型 的理论基础。如果所进行比对的序列是具有生物学进化意义的 相关序列家族,那么每条序列可以看成是这条特征序列经过插 入、删除、匹配而进化的结果。
由于 HMMS 模型能节省大量时间和空间,因而越来越引 起计算生物学的关注。隐马尔可夫理论最初是由 Baum 及他的
基金项目:国家“十一五”科技支撑计划重大项目资助(the National Great Project of Scientific and Technical Supporting Programs Funded by Ministry of Science & Technology of China During the 11th Five-year Plan. No.2006BAJ05A06);重庆市科委自然科学基金(No.2007BB2205); 重庆市科委重点攻关项目(No.2008AC0043)。
ΣP(′ X|Y)-ΣP(X|Y)=1-1=0
X
X
则ΣP X
(X|Y)ln
PP(′(XX||YY))=-
ΣP X
(X
|Y)ln
PP(′(XX||YY))≥0,因
ΣP(X|Y)=1,则 X
lnP(′ Y)-lnP(Y)=ΣP(X|Y)lnP(′ Y)-ΣP(X|Y)lnP(Y)=
X
X
ΣP(X|Y)ln X
Computer Engineering and Applications 计算机工程与应用
2010,46(7) 171
隐马尔可夫模型的多序列比对研究
罗泽举 1,2,宋丽红 3 LUO Ze-ju1,2,SONG Li-hong3
1.重庆工商大学 长江上游经济研究中心,重庆 400067 2.重庆工商大学 计算机科学与信息工程学院,重庆 400067 3.重庆工商大学 经济管理实验教学中心,重庆 400067 1.Research Center of the Economy of the Upper Reaches of Yangtze River,Chongqing Technology and Business University,Chongqing
图 1 一个有 5 条序列的多重序列比对矩阵 G
3 特征序列
序列的进化可以看成是一个特征序列经过若干代衍变的 结果,这个特征序列描绘了这个多重序列共同进化的本质特 征,算法的关键就是寻找和这个特征序列相同的匹配。这里利 用子序列(Subsequence)方法来描述特征序列,就是从多重序 列比对中找出每列出现字符最多的元素,例如图 1 的 S1 ,S2 , …,S5 的特征序列是:ATGTC。如果多重序列比对里每列元素中 出现字符一样多,则随机取其中一个元素。
个特征序列经过若干代衍变的结果[1]。 多重序列分析是一个非常困难的问题,涉及许多模型的选
择,Carillo 和 Lipman 引入了基于两两最优化比对分数的多重 序列比对方法,并得到了广泛应用,但是这种方法对于计算时 间和空间的耗费极大,被证明是 NP 难题[2]。许多研究者利用启 发式和近似算法改进了比对分数算法[3],包括 Feng 和 Doolittle 的 Clustal 算法,但这种算法是利用进化树思想先进行两两比 对,再根据相似性进行分组比对,直到最终得到比对结果,因此 其时间复杂度仍然很高[4]。由于一个基因家族的特征序列非常 保守,家族的进化可以认为是这个特征序列经过一系列插入、 替代、删除的结果,这个过程正好可以用隐马尔可夫模型 (Hidden Markov Models,HMMS)来描述。
同事于 60 年代末 70 年代初提出,并开始用于语音识别[5]。最早 用于计算生物学是于 80 年代末 90 年代初,目前已经用于 DNA 模型构建,蛋白质二级结构预测,基因预测,横跨膜蛋白 识别,其中应用最为普遍的是 Krogh 等人的基于 profile 家族 共同特征提取的蛋白质序列分析[6-7]。
4 隐马尔可夫模型 4.1 隐马尔可夫模型的定义
定义 2 模型 λ=(S,Σ,A,B,π)称为隐马尔可夫模型。其中 S={S1 ,S2 ,…,SN }为状态集合,Σ={O1 ,O2 ,…,OM }是观察符号或 观察向量的集合,A=(aij)为状态转移概率矩阵,记为 aij =P(qt+1 = Sj |qt =Si),1≤i,j≤N;B=(b(j k))表示在状态 Sj 时产生观察符号 vk ∈Σ 的离散概率值或连续概率密度矩阵。其中 b(j k)=P(vk |qt = Sj),1≤j≤N,1≤k≤M;π=(πj)是初始状态分布矩阵,πj =P(q1 = Sj),1≤j≤N,πj ≥0,Σπj =1。
lnP(O|λ)称为 L 值。
当用 HMM 模型进行识别时,首先用 EM 算法对参数 A,
B,π 进行重估,然后利用新参数来计算产生当前序列概率的对
数值(logarithm likelihood,L 值),再根据 L 值来识别对象所属
的类。设当前模型为 λ=(A,B,π),训练重估模型参数后的模型
*
上述定义中当观察符号 vk 是离散符号时,叫离散马尔可
夫模型;当 vk 是连续矢量时,叫连续马尔可夫模型,其关键参
数是 A,B,π,故模型一般简记为 λ=(A,B,π)。
定义 3(logarithm likelihood Value,L 值) 设由模型 λ 产生
观察序列 O 的概率为 P(O|λ),其自然对数值 L=logP(O|λ)=
提出一种基于隐马尔可夫模型的多序列比对算法,利用 L 值和特征序列的保守性,通过增加频率因子,改进传统隐马尔 可夫模型算法的不足。实验表明,用于蛋白质家族的识别,新算 法比传统算法的识别率提高了 3.3 个百分点。
2 多重序列比对的数学模型
定义 1 三元组 Ω=(Σ,S,G) 称为一个多重序列比对序列
1 引言
随着 21 世纪生命科学时代的来临,生命的进化已成为人 类研究的一个热点。为了探索进化的轨迹,就必须研究其家族 的同源性,而一个基因家族往往由若干条 DNA 序列组成,因此 只有弄清多个序列之间的相互关系,才能真正揭示基因家族的 进化特征。如果能知道蛋白质的结构信息,它将比序列信息更 适合解释实际发生的遗传事件,因为蛋白质结构除了提供序列 信息外,还描绘了分子间相互作用等。然而,遗憾的是,目前得 到的蛋白质三维结构数据非常有限,人们还无法弄清许许多多 的蛋白质结构,这就迫使人们不得不利用大量已知的一维序列 信息进行研究。多序列比对分析正是在这样的背景下产生的, 它提供了人们通过研究序列的相似性来探索同源性的重要方 法。通过多重序列比对,发现代表它们进化的特征序列(con- sensus sequence),于是基因家族成员的进化可以看成是由这
LUO Ze-ju,SONG Li-hong.Multiple sequence analysis of hidden Markov puter Engineering and Applications, 2010,46(7):171-174.
Abstract:A new multiple sequence alignment about Hidden Markov Models(HMMs) is researched,using the conservative feature of L value and consensus sequence,by increasing frequency factor,traditional HMMs learning algorithm is improved.Experiment indicates that not only the stability of the model is improved,but also a average improvement of 3.3% is achieved for protein family recognition by comparing the new algorithm with the traditional one. Key words:hidden markov models;multiple sequence analysis;protein recognition
