用excel解决整数规划问题
整数规划模型Excel求解的简化方法

整数规划模型Excel求解的简化方法作者:陈候炎徐玉娥陈其嶙来源:《科学与财富》2011年第12期[摘要] 整数规划是一类典型的线性规划问题。
对于这类问题,运筹学中已有解决的方法,但比较繁琐。
本文利用Excel软件的“规划求解”工具,对整数规划问题求解的模型建立和求解作了较详尽的论述。
[关键词] 整数规划问题 Excel 规划求解整数规划是线性规划中的一类典型问题,应用于解决生产实际的许多问题,有着广泛的应用前景。
对于这类问题,运筹学中已有解决方法,如分枝定界法、穷举法等,但很繁琐。
也有借助于Matlab、Mathematics和 Lingo等软件求解,但专业性太强。
相比之下,Excel功能强大,汉化水平高,菜单操作方便,拥有大量的函数、公式等,不需专门购买和安装。
为解决整数规划问题提供了一种很好的工具。
本文结合实例说明利用在Excel软件中“规划求解”工具,建立数学模型并求解整数规划问题。
1 “规划求解”工具Microsoft Excel的“规划求解”工具取自于Leon Lasdon和Allan Waren共同开发的非线性最优化代码。
“规划求解”是Execl中的一个加载宏。
1.1 安装“规划求解”加载宏是Excel的一个可选安装模块,在安装Microsoft Excel时,系统默认的安装方式不会安装宏程序,只有在选择“完全/定制安装”时才可选择安装这个模块。
如果采用“典型安装”,则“规划求解”工具没有安装,就必须重新启动Office安装程序并且选择Excel选项,在加载宏区段中选择“规划求解”,然后进行安装。
1.2 加载“规划求解”安装了“规划求解”之后,在“工具”菜单下可能仍然找不到“规划求解”,此时您可以选择“工具/加载宏”,在打开的“加载宏”对话框中选中“规划求解”复选框,确定后,就可以将“规划求解”命令添加到“工具”菜单栏中了。
2 整数规划的一般模型整数规划是线性规划的特殊情形,它的变量x仅取整数,其数学表达式有标准式、缩简形式、向量式、矩阵式等多种表现形式。
用excel解决整数规划问题
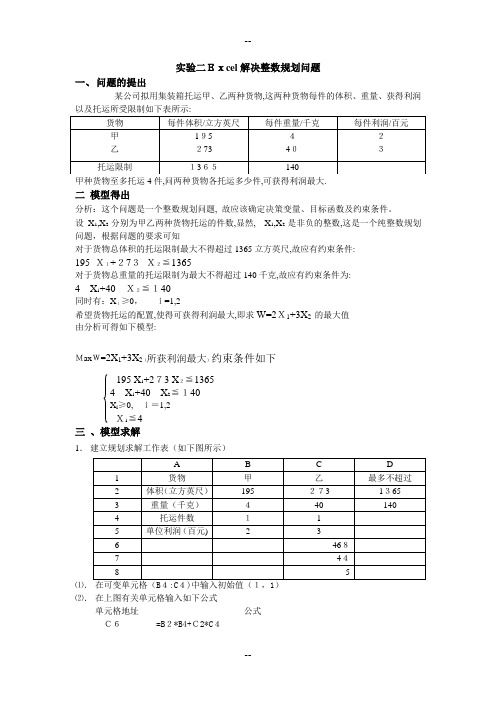
实验二Excel解决整数规划问题一、问题的提出某公司拟用集装箱托运甲、乙两种货物,这两种货物每件的体积、重量、获得利润以及托运所受限制如下表所示:二模型得出分析:这个问题是一个整数规划问题, 故应该确定决策变量、目标函数及约束条件。
设X1,X2分别为甲乙两种货物托运的件数,显然,X1,X2是非负的整数,这是一个纯整数规划问题,根据问题的要求可知对于货物总体积的托运限制最大不得超过1365立方英尺,故应有约束条件:195 X1+273X2≦1365对于货物总重量的托运限制为最大不得超过140千克,故应有约束条件为:4X1+40X2≦140同时有:Xi≥0,i=1,2希望货物托运的配置,使得可获得利润最大,即求W=2X1+3X2 的最大值由分析可得如下模型:MaxW=2X1+3X2 (所获利润最大)约束条件如下195 X1+273 X2≦13654X1+40X2≦140X i≥0, i=1,2X1≦4三、模型求解1.建立规划求解工作表(如下图所示)⑴.在可变单元格(B4:C4)中输入初始值(1,1)⑵.在上图有关单元格输入如下公式单元格地址公式C6 =B2*B4+C2*C4C7 =B3*B4+C3*C4C8 =B5*B4+C5*C4⑶.求最佳组合解:①.选取[工具]→[规划求解…]出现如下对话窗:②.在“设置目标单元格”窗口,输入C8。
③.选定“最大值”选项。
④.在可变单元格中输入B4:C4。
⑤.选取“添加”,出现“添加约束”窗口,在“添加约束”窗口输入:单元格引用位置运算符号约束值B4:C4 int单击“添加”,再输入以下约束条件:B4:C4 >= 0单击“添加”,再输入以下约束条件:B4 >= 4单击“添加”,再输入以下约束条件:C6 <= 1365单击“添加”,再输入以下约束条件:C7 <= 140,单击“确定”⑥在“规划求解参数”窗口,选择“求解。
”⑦选择“确定”,(计算结果如下表所示)⑧在“规划求解结果”对话框中选定保存“规划求解结果”,单击“确定”。
Excel Module 3 整数规划and0 1规划的应用

表1 公司生产数据(要求炼油厂满负荷运转)
炼油厂
年所需原油量
油田
R1 R2 R3 R4(新建)
100
F1
60
F2
80
F3
120 F4(进口)
SUM
360
(百万桶)
年原油产量
80 60 100 120
360
表2 从油田到炼油厂--原油运输成本数据
油田
R1
R2
R3 N1
F1
F2
F3 F4(进口) 炼油厂 需求量
例3 模型和Excel求解过程
目标函数:Max z=8x1+5x2+6x3+4x4 约束:
1.可用资金10 6*x1+3*x2+5*x3+2*x4<=10
2.互斥决策变量--至多只建1个仓库, x3+x4<=1(互斥决策变量的和<=1)
3.相依决策变量--建厂才建仓库, x1>=x3,x2>=x4
公寓楼 400 40 15
有限资源 2000 140
例3 选址(0-1规划应用)
A公司在L3地区有多个工厂和仓库,由于业务拓展的需要,管理层决定在 L1和L2地区建厂。需要决策的问题是在L1还是在L2建厂,或在2个地区都 建厂;并同时考虑至多建1个新仓库,如果建新仓库,该仓库应该与新建
厂在同一个地点。可用资金:10百万。
选址问题
中央财经大学 信息学院 吴靖
正确地使用方法, 并对结果做出恰当地解释。
§1 选址(运输)
例1 Site-Select Problem
一家石油公司,有油田并进口原油,有若干个炼油厂和配送中心,由于市场拓展的需要,公 司决定新建炼油厂,管理层需要为新炼油厂选址做出决策。决策的三个主要因素是: 1.从油田运送原油到所有炼油厂(含新建炼油厂)的运输成本; 2.从所有炼油厂(含新建炼油厂)到每一个配送中心的运输成本; 3.新炼油厂的运作成本。例如,劳动力成本、赋税、能源成本、保险成本等。
excel建模整数规划PPT课件

6.3.2 辅助0-1变量
第6章 整数规划
在例6.2中,每个0-1变量表示一个是非决策, 这些变量也称为0-1决策变量。除了这些0-1决 策变量,有时还引入其他一些0-1变量以帮助 建立模型。辅助0-1变量,是引入模型的附加 0-1变量,不代表一个是非决策,仅仅是为了 方便建立纯的或混合的0-1整数规划模型。
x
2
12
3
x
1
2 x2
18
s.t. x1 M y1
x
2
M y2
x1, x2 0 且 为 整 数
y1 ,
y2
0,1
RUC, School of Information ,Ye Xiang
6.3.2 辅助0-1变量
固定成本问题
在一般情况下,产品的成本是由固定成本和可变成 本两部分组成。固定成本是指在固定投入要素上的 支出,它不受产量影响,例如厂房和设备的租金、 贷款利息、管理费用等;可变成本是指在可变投入 要素上的支出,它是随着产量变化而变化的成本, 例如原材料费用、生产工人的工资、销售佣金等。
通常,变动成本和产量成正比,所以可以用下面的 表达式来代表某一产品的总成本
第6章 整数规划
实用运筹学 -运用Excel建模和求解
第6章 整数规划
RUC, School of Information ,Ye Xiang
本章内容要点
第6章 整数规划
整数规划的基本概念 整数规划问题的建模与应用
RUC, School of Information ,Ye Xiang
本章节内容
解:
(1)决策变量
设小型飞机与大型飞机的购买
用Excel求解数学规划

用Excel求解数学规划武汉大学水利水电学院万飚Excel是Microsoft Office办公软件中的一个组件,以其强大的电子表格处理功能备受广大用户的青睐。
由于Excel支持丰富的公式和函数,因而在一般财务计算、高级财务管理、财务分析、信息管理、管理决策、市场营销、工程管理,以及管理科学、经济学和统计学等领域都得到了广泛的应用。
一、关于规划求解“规划求解”是Microsoft Excel中的一个加载宏,借助它可以求解许多运筹学中的数学规划问题。
Excel的“规划求解”工具来自德克萨斯大学奥斯汀分校的Leon Lasdon和克里夫兰州立大学的Allan Waren共同开发的Generalized Reduced Gradient(GRG2)非线性最优化代码;线性规划和整数规划算法来自Frontline Systems公司的John Watson和Dan Fylstra 提供的有界变量单纯形法和分支定界法。
安装Office的时候,系统默认的安装方式不会安装该宏程序,需要用户自己选择安装。
安装方法为:从Excel菜单中选择“工具”→“加载宏”,打开如下对话框:选择其中的“规划求解”后单击“确定”按钮,会出现提示:“这项功能目前尚未安装,是否现在安装?”,选择“是”,系统要你插入Office的安装光盘,准备好后单击确定,很快就会安装完毕。
于是,你会发现在“工具”菜单下多出一个名为“规划求解”的子菜单,说明“规划求解”功能已经成功安装。
二、第一个线性规划问题例:求解以下线性规划问题:⎪⎪⎩⎪⎪⎨⎧≥≤≤≤++=0,124 16 48232 21212121x x x x x x x x z max 步骤:1.将模型中的目标函数和约束条件的系数输入到单元格中;为了使我们在操作过程中看得更清楚,可以附带输入相应的标识符,并给表格加上边框。
如下图所示:2.在E4单元格(目标值)输入“=SUMPRODUCT($C$3:$D$3,C4:D4)”;其中,SUMPRODUCT 函数的功能是将数组间对应的元素相乘,并返回乘积之和,即SUMPRODUCT($C$3:$D$3,C4:D4)=C3×C4+D3×D4;$C$3:$D$3表示这几个单元格为绝对引用。
EXCEL规划求解功能操作说明

E X C E L规划求解功能操作说明集团标准化办公室:[VV986T-J682P28-JP266L8-68PNN]Excel规划求解功能操作说明以Microsoft Excel2003为例,说明使用Excel的求解线性规划问题功能的使用方法。
一、加载规划求解功能1.点击【工具】按钮,在下拉菜单中选择【加载宏】功能。
2.在弹出的【可加载宏】选项卡中勾选【规划求解】,点击确定按钮。
此时,【工具】下拉菜单中增加规划求解功能,表示加载成功。
二、构造表格Excel表格并填入各项数据以教材18页【例题2-8】为例,构造表格如下:标题栏约束条件区目标函数区计算结果显示区1.录入约束条件系数约束条件(1)为5x 1+x 2-x 3+x 4=3,则在约束系数的第一行的x 1,x 2,x 3,x 4,x 5,限制条件,常数b 列下分别录入5,1,-1,1,0,=,3如下图所示。
约束系数区的第二行录入约束条件(2)的系数、限制符号及常数b ,即-10,6,2,0,1,=,2;约束系数区的第三行录入约束条件(3)(x1≥0)的系数、限制符号及常数b,即1,0,0,0,0,≥,0;约束系数区的第四行录入约束条件(4)(x2≥0)的系数、限制符号及常数b,即0,1,0,0,0,≥,0;约束系数区的第五行录入约束条件(5)(x3≥0)的系数、限制符号及常数b,即0,0,1,0,0,≥,0;约束系数区的第六行录入约束条件(6)(x4≥0)的系数、限制符号及常数b,即0,0,0,1,0,≥,0;约束系数区的第七行录入约束条件(7)(x5≥0)的系数、限制符号及常数b,即0,0,0,0,1,≥,0。
如下图所示。
2.录入目标函数系数目标函数为maxZ=4x1-2x2-x3,则在目标函数的x1,x2,x3,x4,x5列下分别录入4,-2,-1,0,0,如下图所示。
3. 录入约束条件的计算公式双击约束条件(1)行的“总和”单元格,录入以下内容:“=B3*B12+C3*C12+D3*D12+E3*E12+F3*F12”说明:录入的内容即是约束条件(1)的计算公式,其中“B3*B12”代表5x1; “C3*C12”代表1x2;“D3*D12”代表-1x3;“E3*E12”代表1x4;“F3*F12”代表0x5。
规划求解——整数规划实例(《物流成本管理》P105例3-9)

1、Excel2010规划求解初次使用的加载方式:文件/选项/加载项/管理“Excel加载项”,
2、添加约束时单击“Int”,约束值将显示为整数;单击“Bin”,则显示为二进制。
3、数据输入是对“目标函数”右一个单元格和“约束”下几个单元格进行表示,其他均属于说明性标签
4、规划求解可用于求解线性规划、整数规划、运输问题、指派问题、最短路径问题及最大流问题等。
cel加载项”,转到/勾选“Excel加载项”,确定;然后在主界面选项卡“数据”可以找到“规划求解”为二进制。
表示,其他均属于说明性标签,便于理解。
路径问题及最大流问题等。
找到“规划求解”。
用Excel软件求解规划问题的方法

用Excel 软件求解规划的方法Microsoft Excel 软件是当今十分流行的功能强大操作方便的软件。
在Microsoft Excel 软件中,具有规划求解功能。
如图1,在工具菜单下,一般有“规划求解”项,若未有,则应先运行“加载宏”项目把其安装上。
图1 图21 一般线性规划的求解现在让我们以下面的模型为例,介绍如何利用Microsoft Excel 软件求解线性规划模型的操作方法。
首先,打开Microsoft Excel 的一个工作簿,把模型的约束系数矩阵置于A1至B4范围,约束常数置于D1至D4范围,而利润系数则置于A5至B5范围。
选择A7至B7范围作可变单元(即这两个格相当于变量X1与X2),并输入初值0。
然后,在单元格C1处输入“=A1*A7+B1*B7”,即第一个约束不等式的左边;同理,在单元格C2处输入“=A2*A7+B2*B7”,即第二个约束不等式的左边;对C3与C4也同样处理。
最后,以单元格C5作目标单元格,输入“=A5*A7+B5*B7”。
如图2。
接下来,按下主菜单的工具处,再在下拉菜单处选择“规划求解”,则弹出窗口如图3。
⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥≤+≤≤≤0x 0,x x x x x x 4+x s.t. x +x =f max 21112121222700050122700075.182700025.56270000155.75.2图3 图4在“设置目标单元格”处输入“C5”,然后选“最大值”,再在“可变单元格”处输入“A7:B7”,在“约束”处按一下“添加”按钮,又弹出如图4的窗口。
在此,我们要添加5个约束:“C1 <= D1”、“C2 <= D2”、“C3 <= D3”、“C4 <= D4”、“A7:B7 >= 0”。
对第一个约束,在“单元格引用位置”处输入“C1”,在中间下拉框选择“<=”, 再在“约束值”处输入“D1”。
然后按“添加”按钮,再类似地添加其它约束。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二Excel解决整数规划问题
一、问题的提出
某公司拟用集装箱托运甲、乙两种货物,这两种货物每件的体积、重量、获得利润以及托运所受限制如下表所示:
甲种货物至多托运4件,问两种货物各托运多少件,可获得利润最大.
二模型得出
分析:这个问题是一个整数规划问题, 故应该确定决策变量、目标函数及约束条件。
设X1,X2分别为甲乙两种货物托运的件数,显然, X1,X2是非负的整数,这是一个纯整数规划问题,根据问题的要求可知
对于货物总体积的托运限制最大不得超过1365立方英尺,故应有约束条件:
195 X1+273 X2≦1365
对于货物总重量的托运限制为最大不得超过140千克,故应有约束条件为:
4 X1+40 X2≦140
同时有:X i≥0, i=1,2
希望货物托运的配置,使得可获得利润最大,即求W=2X1+3X2 的最大值
由分析可得如下模型:
MaxW=2X1+3X2 (所获利润最大)约束条件如下
195 X1+273 X2≦1365
4 X1+40 X2≦140
X i≥0, i=1,2
X1≦4
三、模型求解
1.建立规划求解工作表(如下图所示)
⑴.在可变单元格(B4:C4)中输入初始值(1,1)
⑵.在上图有关单元格输入如下公式
单元格地址公式
C6 =B2*B4+C2*C4
C7 =B3*B4+C3*C4
C8 =B5*B4+C5*C4
⑶.求最佳组合解:
①.选取[工具]→[规划求解…]出现如下对话窗:
②.在“设置目标单元格”窗口,输入C8。
③.选定“最大值”选项。
④.在可变单元格中输入B4:C4。
⑤.选取“添加”,出现“添加约束”窗口,在“添加约束”窗口输入:
单元格引用位置运算符号约束值
B4:C4 int
单击“添加”,再输入以下约束条件:
B4:C4 >= 0
单击“添加”,再输入以下约束条件:
B4 >= 4
单击“添加”,再输入以下约束条件:
C6 <= 1365
单击“添加”,再输入以下约束条件:
C7 <= 140,单击“确定”
⑥在“规划求解参数”窗口,选择“求解。
”
⑦选择“确定”,(计算结果如下表所示)
⑧在“规划求解结果”对话框中选定保存“规划求解结果”,单击“确定”。
于是我们就得到如下运算结果报告
四、报告分析
表1 Microsoft Excel 9.0 运算结果报告
目标函数的初值:当变量X=(1,1)时目标函数的值。
目标函数的终值:经过运算后的目标函数的最优值。
此表说明函数的最优值为14。
表2 可变单元格式
从此表看出我们的最优解(终值)为(4,2)。
Welcome To Download !!!
欢迎您的下载,资料仅供参考!。
