第十章含耦合电感的电路习题解答.doc
10章 含有耦合电感的电路

jω L2 (支路 支路3)L ± 同侧取 同侧取“ 支路 3=±M(同侧取“+”,异 异
R2
侧取“ 侧取“-”) (支路 1’=L1 m M,M前所取符 支路1)L 支路 , 前所取符 号与L 号与 3中的相反 (支路 2’=L2 m M,M前所取 支路2)L 支路 , 前所取 符号与L 符号与 3中的相反
反相串联无互感等效电路
R1 u1 u M L1 R1 L1-M u1 R2 u2 L2 u R2 L2-M u2
Z = Z1 + Z 2 = R1 + R2 + jω ( L1 + L2 − 2 M )
R1
L1 u1
2、顺向串联 、 每一耦合电感支路的阻抗为: 每一耦合电感支路的阻抗为:
Z1 = R1 + jω ( L1 + M )
两个耦合线圈的磁通链可表示为: 两个耦合线圈的磁通链可表示为:
ψ 1 = ψ 11 ± ψ 12
= L1i1±Mi2
ψ 2 = ±ψ 21 + ψ 22
= ±Mi1+L2i2 上式表明, 上式表明 , 耦合线圈中的磁通链与施感电流 线性关系 关系, 成 线性 关系 , 是各施感电流独立产生的磁通链叠 加的结果。 加的结果。
di di u2 = R2i + ( L2 −M ) dt dt di = R2i + ( L2 − M ) dt
无互感等效电路
R1 u1 u M L1 R1 L1-M u1 R2 u2 L2 u R2 L2-M u2
di u = u1 + u 2 = ( R1 + R2 )i + ( L1 + L2 − 2 M ) dt
L1 N1 L2 N2
电路分析基础第五版第10章

二、互感消去法(等效去耦法)
消去互感,变为无互感的电路计算,从而简化 电路的计算。
1、受控源替代去耦法
jM
I1
I2
+ +
U1
jL1
jL2
U2
I1
+
jL1
U1
jM I 2
I2
+
jL2
U
2
jM I 1
U1 jL1 I1 jMI2
U2 jL2 I2 jMI1
d2i dt
i 2 u 2
2
相量形式:
1
i1
U1 jL1 I1 jMI2
u1
U2 jL2 I2 jMI1
注意:
i 2 u 2
2
•互感元件的自感恒为正;
•互感元件的互感有正有负,与线圈的具体绕法及 两线圈的相互位置有关。
当每个电感元件中的自感磁链与互感磁链是互相 加强时(自感磁链与互感磁链同向),互感为正; 反之为负。(说法不同,正确理解)
+
U
L反L1L22M
等效电感不能为负值,
因此:L反0, M12(L1L2)
3、并联耦合电感的去耦等效
(1)同侧并联:同名端分别相联。
I
+
jM
U
jL1
jL2
I +
U
j L同
L同
L1L2 M2 L1 L2 2M
因为 L同 0 所以 L1L2M20
第十章含有耦合电感的电路-精选文档

d di u L dt dt
+
u _
在此电感元件中,磁链Ψ和感 应电压u均由流经本电感元件的电 流所产生,此磁链感应电压分别称 为自感磁链和自感电压。
2、互感:如图所示表示两个耦合电感,电流i1在线 圈1和2中产生的磁通分别为Φ11和Φ21,则Φ21≤Φ11。 这种一个线圈的磁通交链于另一线圈的现象,称为 磁耦合。电流i1称为施感电流。Φ11称为线圈1的自感 磁通,Φ21称为耦合磁通或互感磁通。如果线圈2的 匝数为N2,并假设互感磁通Φ21与线圈2的每一匝都 交链,则互感磁链为Ψ21=N2Φ21。
§10-1 互感
耦合电感:耦合元件,储能元件,记忆元件。
一、耦合电感:为互感线圈的理想化电路模型
1 、自感:对于线性非时变电感元件,当电流的 参考方向与磁通的参考方向符合右螺旋定则时, 磁链Ψ与电流I满足Ψ=Li,L为与时间无关的正实 常数。
根据电磁感应定律和线圈的绕向,若电压的参考 正极性指向参考负极性的方向与产生它的磁通的参 考方向符合右螺旋定则时,也就是在电压和电流关 联参考方向下,则
输入阻抗Z为
Z Z Z ( 8 j 4 ) 8 . 94 26 . 57 1 2
为: 50 0 V 令U ,解得 I
50 0 I U / Z A 5 . 59 26 . 57 A 8 . 94 26 . 57
第十章 含有耦合电感的电路
内容提要
本章主要介绍耦合电感中的磁耦合 现象、互感和耦合因数、耦合电感的同 名端和耦合电感的磁通链方程、电压电 流关系;还介绍含有耦合电感电路的分 析计算及空心变压器、理想变压器的初 步概念。
§10-1 互感 §10-2 含有耦合电感电路的计算 §10-3 空心变压器
电路原理第十章含耦合电感电路

•
•
•
•
U R1 I1 +j L1 I1 -j M I 2
•
•
•
•
U R 2 I 2 +j L2 I 2 -j M I1
•
•
•
I I1 I2
根据前面的电路图,列写方程:
U (R1 jL1)I1 jMI2 Z1I1 ZM I2
U (R2 jL2 )I2 jMI1 Z2I2 ZM I1
Ψ21 Ψ22
Ψ11 Ψ12
Ψ21 Ψ22
i1 a + u1
i2
-b
c+
u2
d
i1 *a + u1 -b
i2 c + u2 -d *
(a)
(b)
说明耦合线圈的伏安关系用图
Ψ1=Ψ11 +Ψ12 Ψ2=Ψ22 +Ψ21
Ψ1=Ψ11 -Ψ12 Ψ2=Ψ22 -Ψ21
11
21
N1 i1
N2
+ u11 – + u21 –
同名端与两个线圈的绕向和相对位置有关。
11
s
0
N1 i1 * •
+ u11 –
N2
N3
*
•
+ u21 – – u31 +
i
1*
*2
1•*
2
3
1'
2'
1'
2'*
3' •
两个以上线圈彼此耦合时,同名端应一对一对加以标记。 如果每个电感都有电流时,每个电感的磁通链等于自感磁 通链和所有互感磁通链的代数和。
通链Ψ22 。22 部分或全部与线圈1相链,产生线圈2对线圈
邱关源《电路》配套题库-课后习题(含有耦合电感的电路)【圣才出品】
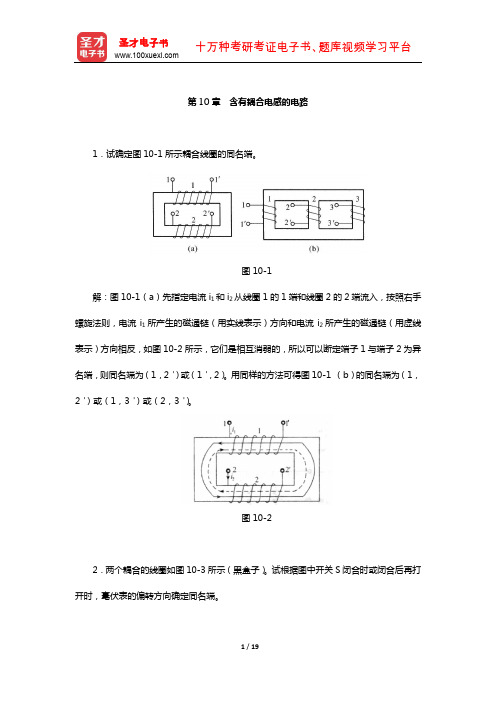
第10章含有耦合电感的电路1.试确定图10-1所示耦合线圈的同名端。
图10-1解:图10-1(a)先指定电流i1和i2从线圈1的1端和线圈2的2端流入,按照右手螺旋法则,电流i1所产生的磁通链(用实线表示)方向和电流i2所产生的磁通链(用虚线表示)方向相反,如图10-2所示,它们是相互消弱的,所以可以断定端子1与端子2为异名端,则同名端为(1,2')或(1',2)。
用同样的方法可得图10-1 (b)的同名端为(1,2')或(1,3')或(2,3')。
图10-22.两个耦合的线圈如图10-3所示(黑盒子)。
试根据图中开关S闭合时或闭合后再打开时,毫伏表的偏转方向确定同名端。
图10-3解:根据右手螺旋法可知,线圈的同名端为(1,2)。
当开关S闭合时,线圈1中随时间增大的电流i从电源正极流入线圈端子1,这时毫伏表的高电位与端子1为同名端;当开关S闭合后再打开时,电流i减小,毫伏表的低电位端与端子1为同名端。
3.若有电流i1=2+5cos(10t+30°)A,i2=10A,各从图10-4(a)所示线圈的1端和2端流入,并设线圈1的电感=6H,线圈2的电感=3H,互感为M=4H。
试求:(1)各线圈的磁通链;(2)端电压和;(3)耦合因数k。
解:(1)(1,2)为异名端,两个线圈的磁通是相互消弱的,所以(2)根据电压和磁通的关系得:(3)耦合因数为:k==0.943。
4.如图10-5所示电路中(1)=8H,=2H,M=2H;(2)=8H,=2H,M=4H;(3)==M=4H。
试求以上三种情况从端子1-1′看进去的等效电感。
图10-5解:(a)=M+(L1-M)//(L2-M)当L1=8H,L2=2H,M=2H时,=2H;当L1=8H,L2=2H,M=4H时,=0H;当L1=L2=M=4H时,=4H。
(b)=-M+(L1+M)//(L2+M)当L1=8H,L2=2H,M=2H时,=0.857H;当L1=8H,L2=2H,M=4H时,=0H;当L1=L2=M=4H时,=0H。
第十章含耦合电感的电路

r R
E
(a)
r R
E
(b)
直接连接
P
I
2
R
E R
r
2
R
8
6 100
2
8
25mW
用匝比为n = 3的变压器耦合
扬声器的反射阻抗
R'
N1 N2
2
R
300 100
i1 * N1
n :1
i2
பைடு நூலகம்
+
N2
u2
*
-
实际变压器与理想变压器近似的条件
变压器原、副边线圈自电感 :L1、L2 耦合电感 : M k L1L2 近似条件: k M 1 L1、L2很大
L1L2
n n1 n2
例题
一个理想变压器的额定值是2400V/120V,9.6kVA且 在次级有50匝。计算:(a)匝数比,(b)初级的匝 数,(c)初级绕组和次级绕组的额定电流值。
原、副边匝比: 初级匝数:
n V1 2400 20 V2 120
n1 n 50 2050 1000 匝
初级绕组和次级绕组的额定电流值
I1
9600 V1
9600 2400
4A
I2
9600 V2
9600 120
80A
例题
求负载的端电压 U 2。
副边电压、电流关系。 配合电阻元件等,可模拟实际变压器
电路习题第十章

第十章 含有耦合电感的电路习题一、填空题1.电路如图1-1所示,已知负载R L =100Ω时可获得最大功率,则R o =( )2.图1-2所示理想变压器,若此时R L 可以获得最大功率,则变比n 为( )3. 图1-3电路,求输入电阻R ab =( )图1-1 图1-2 图1-34. 如图1-4所示单口网络的开路电压和等效电阻为( )V 和( )Ω8Ω3:1a b 2:1图1-4 图1-55.如图1-5所示电路的等效电阻Rab=( )。
二、计算题。
1.图1所示电路,V )cos(210t u s ω=,R 1=10 Ω,R 2=40 Ω, L 1=L 2=0.1mH , M=0.02mH , C 1=C 2=0.01µF ,ω=106rad/s 。
列出回路电流方程并求电流1i 和2i图12.图2所示,已知R=1Ω, ωL 1=2Ω, ωL 2=32Ω, 耦合系数k = 1,Ω=32C 1ω,求 1I •、2U •。
图23.图3示电路,电路原已稳定,t = 0时开关S 由1转向2,求t >0时的电容电流)(t i c 。
图34.图4示,已知正弦电源电压U=200V ,R=500Ω,L=5H ,L1=2H ,M=1H ,L2=0.5H , C=200μF ,电流表的读数为零:求:(1)电源的角频率ω;(2)各支路的电流;(3)电路的P 、Q 、S 、功率因数图45.求图5所示,负载Z L 是:C L =1F 元件,求单口网络的输入阻抗Zab 。
1Ωa b 2Ωj2Ωj1Ωω=1rad/s Zj1Ω图56.图6所示电路中R=50Ω,L 1=70mH ,L 2=25mH ,M=25mH ,C=1uF ,正弦电压5000U V =∠,ω=104rad/s 。
画出此电路的去耦等效图,并求各支路电流(相量形式)。
Rj ωL 1j ωL 2U +1I 2I I j ωM图67.电路如图7,已知u s = 20.2 cos(5t + 45°)V ,画出此电路的去耦等效电路图,分析计算负载Z 取何值时可获得最大功率?并计算最大功率max P 。
第10章含有耦合电感的电路例题
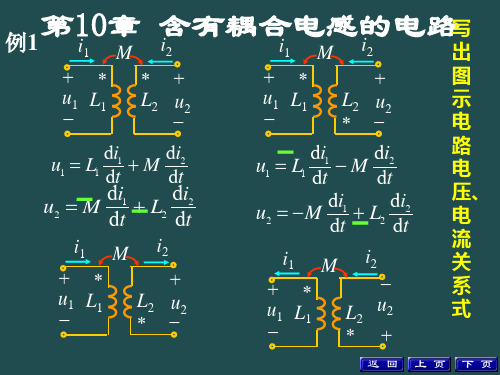
I1
R1
j(L1
S
L3
2M )31
U0c jM12I1 jM 23I1 jM I 31` 1 jL3I1
j(L3 M12 M 23 M 31)U S R1 j(L1 L3 2M 31)
返回 上页 下页
•
解2 作出去耦等效电路,(一对一对消):
1/j C1 j M 1/j C2
+
**
U S –
R1
j
L1
j L2
R2
11
解1
L1 L2 M 20 Z22 R2 j(
100
Z11
L2
1
C2
100
C1
R1 j(
L1 C2 1C1
)
10
) R2
返回 上页 下页
•
应用原边等效电路
1150 j146
14.850 V
20 j1130.4
(M )2 1462 j18.85
Z11 20 j1130.4
I2
j18.5
U OC 42.08
j18.85
0.3530
A
返回 上页 下页
•
例10 全耦合电路如图,求初级端ab的等效阻抗。
求 : I1 , I2.
I1 R1 j M R2
解1
应用原边 等效电路
+
U S
j L*1
*j
I2
L2
RL
Z11 R1 jωL1
–
20 j1130.4Ω
Z22 R2 RL jωL2 42.08 j18.85 Ω
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十章(含耦合电感的电路)习题解答
一、选择题
1.图10—1所示电路的等效电感=eq L A 。
A.8H ; B.7H ; C.15H ; D.11H
解:由图示电路可得 121 d d 2d d )
63(u t i t i =++, 0d d 4d 221=+t
i
t i d
从以上两式中消去
t
i d d 2
得t i u d d 811=,由此可见
8=eq L H
2.图10—2所示电路中,V )cos(18t u s ω=,则=2i B A 。
A.)cos(2t ω; B.)cos(6t ω; C.)cos(6t ω-; D.0
解:图中理想变压器的副边处于短路,副边电压为0。
根据理想变压器原副边电压的关系可知原边的电压也为0,因此,有
A )cos(29
)
cos(18 1t t i ω=ω=
再由理想变压器原副边电流的关系n
i i
121= (注意此处电流2i 的参考方向)得
A )cos(612t ni i ω==
因此,该题应选B 。
3.将图10─3(a )所示电路化为图10—3(b )所示的等效去耦电路,取哪一组符号取决于 C 。
A.1L 、2L 中电流同时流入还是流出节点0;
B.1L 、2L 中一个电流流入0,另一个电流流出节点0 ;
C.1L 、2L 的同名端相对于0点是在同侧还是在异侧,且与电流参考方向无关;
D.1L 、2L 的同名端相对于0点是在同侧还是在异侧,且与电流参考方向有关。
解:耦合电感去耦后电路中的M 前面是取“+”还是取“–”,完全取决于耦合电感的同名端是在同侧还是在异侧,而与两个电感中电流的参考方向没有任何关系。
因此,此题选C 。
4.图10—4所示电路中,=i Z B 。
A .Ω2j ; B.Ωj1; C.Ωj3; D.Ωj8
解:将图10—4去耦后的等效电路如图10—4(a ),由图10—4(a )得
j1 j6
j6j6
j6j2Ω=+⨯+
-=i Z
因此,该题选B。
5.在图10—5所示电路中,=i Z D 。
A .Ωj8; B.Ωj6; C.Ωj12; D.Ωj4
解:图中的耦合电感反向串联,其等效阻抗为
j4j22j4j4j 2j j 21Ω=⨯-+=ω⨯-ω+ω=M L L Z i
所以此题选D 。
6.互感系数M 与下列哪个因素无关 D
A .两线圈形状和结构; B.两线圈几何位置; C.空间煤质; D.两线圈电压电流参考方向 7.理想变压器主要特性不包括 C
A .变换电压; B.变换电流; C.变换功率; D.变换阻抗 8.对于图10-6所示电路中,下列电压、电流的关系叙述中,正确的是:D
A.
121211
22,di di di di u L M u M L dt dt dt dt
=--=--; B.12121122,di di di di u L M u M L dt dt dt dt
=-=-+; C .121211
22,di di di di
u L M u M
L dt dt
dt dt
=+=--; 图1-6 D. 121211
22,di di di di
u L M u M L dt dt dt dt
=+=+ 9.如果图10-7(b )是图10-7(a )的去耦等效电路,则图10-7(b )中的1Z 等于:C
A. j M ω-;
B. j M ω; C . ()1j L M ω-;
D. ()1j L M ω+。
图10-7(a ) 图10-7(b )
10.在应用等效电路法分析空心变压器时,若原边阻抗为11Z ,副边阻抗为22Z ,互感阻抗为j M ω。
则副边对原边的引入阻抗l Z 等于:B A.22
j M Z ω+; B.
()2
22
M Z ω; C .11
j M Z ω+; D.
()2
11
M Z ω
二、填空题
1.电路如图10─6所示,41=L mH ,92=L mH ,3=M mH ,当S 打开时,=eq L mH 7;
当S 闭合时,=eq L mH 3。
图10-8 图10-8(a )
解:当S 打开时,两个具有磁耦合的电感反向串联,其等效电感为
7221=-+=M L L L eq mH ;
当S 闭合时,将互感消去可得 图10—8(a )所示的电路。
由图10—8(a )得其等效电感为
mH 3)
(221=-+-+
-=M
L M M L M M L L eq
2.在图10─9所示电路中(02=i 时),=u t
i M L s
d d )
(1+。
图10-9 图10-9(a )
解:消去图10—9中的互感得其等效电路如图10—9(a )所示。
由图10—9(a )可得
t
i
M L t i M L u d d )(d d )
(2211+++=
由于2i 等于0,s s i i i i =+=21,所以
t
i M L u s
d d )
(1+= 3.在图10─10所示电路中,谐振频率15.1590=f H Z 。
图10-10
解:6
010
20)01.0202.001.0(21
-⨯⨯⨯++π=
f = 159.15 Hz
4.在图10─11所示电路中,若 )cos(24t i s ω=A ,Ω=10R ,Ω+=j3)4(1Z ,
Ω+=j4)3(2Z ,电压表内阻无穷大,则电压表读数为20V 。
图10-11 图10-11(a )
解:对图10—11的电路进行等效变换,得其相量模型如图10—11(a )。
图中的 0/400=s
U V 。
电压表的内阻为无限大,那么02=I 。
根据理想变压器原副边电流相量的关系可知01=I ,即s
U U =1。
而 0120/202
121===s U U U V 所以电压表的读数为20V 。
5.在图10─12所示电路中,j2)2(-=i Z Ω。
图10-12
解:Ω-=-+
=)2j 2()8j 4(4
1
1i Z 三.计算题
1.在图10─13所示电路中,已知220=s U V ,Ω+= j4)3(Z ,求Z 消耗的平均功率。
图10-13
解:从原边向副边看进去的阻抗为
Ω+=⨯= j400)300(102
Z Z i
以电源电压相量为参考相量,即 00/220=s
U V ,于是 0113.53/44.0j400
300220-=+==i s Z U I A
Z 消耗的平均功率为
W 8.58)13.53cos(44.0220cos 0
1=⨯=ϕ=I U P S
2. 在图10─14所示正弦交流电路中,已知rad/S 100=ω,01
0/4=I A ,求s U 。
图10-14 图10-14(a )
解:消去图10—14中的互感可得图10—14(a ),由图14—(a )可得
V 90/8.368.36j 0/4)3
j 2j 3j 2j 8j (00==⨯+⨯+=s
U 3.在图10─15所示正弦交流电路中,已知 ) (cos 22t u s =V ,求电流i 。
图10-15 图10-15(a ) 解:图10—15所示电路去耦后的电路如图10—15(a )。
由于s u 的角频率为/s rad 1,所以图中两段电感电容串联电路均发生谐振,整个电路等效于一个Ω2电阻。
于是
A )cos(22
t u i s
==
4.在图10─16所示正弦稳态电路中,Ω=40R , Ω=ω60L , Ω=ω20M ,
Ω=ω401
1
C , Ω=ω2012
C , 00/80=S U V ,求电流1I 及2I 。
图10-16 图10-16 (a ) 图10-16 (b )
解:将图10—16的电路去耦后,等效于图10—16(a )所示的电路(注:图中所有阻抗的单位均为Ω),图10—16(a )可进一步等效为图10—16(b )。
从图10—16(b )可见电路发生了并联
谐振,电感、电容两端的电压均为2/s U ,参考方向和1
I 的参考方向相同。
因此,有 A 1 j 40
j 0/40 ,A 1 j 40j 0/400
201-===-=I I
5.欲使图10─17所示电路处于串联谐振状态,电源电压)(t u 的角频率ω应为多少?
图10-17 图10-17(a )
解:将图10—17去耦后,电路等效变换为图10—17(a )所示的电路。
则
s /rad 100010
1116
=⨯==
ω-LC
6. 图10-18所示电路处于正弦稳态,求:1∙
I 、2∙
I 、2∙
U 。
()1212122224104880
0.5245A 0.250A 0.250A 20V
j I j I j I j I I I U I ⎧-=∠︒
⎪⎨-++=⎪⎩∠-︒∠︒⨯∠︒∠︒解之得:==又 =8=8=。
