2011中考总复习数学教材过关训练:一次函数
2011中考函数及其图象专题测试题及答案

(函数及其图象)(试卷满分 150 分,考试时间 120 分钟)一、选择题(本题共10 小题,每小题4 分,满分40分)每一个小题都给出代号为A,B,C,D的四个结论,其中只有一个是正确的,把正确结论的代号写在题后的括号内.每一小题:选对得4分,不选、选错或选出的代号超过一个的(不论是否写在括号内)一律得0分。
1.已知反比例函数 y= a-2x 的图象在第二、四象限,则a 的取值范围是( )。
A .a ≤2B .a ≥2C .a <2D .a >22.若 ab >0,bc<0,则直线y=-a b x -c b不通过( )。
A .第一象限 B 第二象限 C .第三象限 D .第四象限3.若二次函数y=x2-2x+c 图象的顶点在x 轴上,则c 等于( )。
A .-1B .1C .21 D .2 4.已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的解析式为( )。
A .y=-x-2B .y=-x-6C .y=-x+10D .y=-x-15.已知一次函数y= kx+b 的图象经过第一、二、四象限,则反比例函数y= kb x的图象大致为( )。
6.二次函数y=x2-4x+3的图象交x 轴于A 、B 两点,交y 轴于点C ,则△ABC 的面积为A .1B .3C .4D .67.已知一次函数y=kx+b 的图象如图所示,当x <0时,y 的取值范围是( )。
A .y >0B .y <0C .-2<y <0D .y <-28.如图是二次函数y=ax2+bx+c 的图象,则点(a+b ,ac)在( )。
A .第一象限B .第二象限C .第三象限D .第四象限x yO??.二次函数c bx axy ++=2(0≠a①a c >;④b ??a c >,其中正确的个数是( )。
A . 0个 B . 1个 C . 2个D . 3个A O DC EF x y B10.如图,正方形OABC ADEF ,的顶点A D C ,,在坐标轴上,点F 在AB上,点B E ,在函数1(0)y x x=>的图象上,则点E 的坐标是( )A.⎝⎭ B.⎝⎭C.⎝⎭ D.⎝⎭二、填空题(本题共 4 小题,每小题 5 分,满分 20 分)11.已知y 与(2x+1)成反比例,且当x=1时,y=2,那么当x=-1时,y=_________。
2011全国中考数学真题解析120考点汇编 一次函数与反比例函数的综合应用1
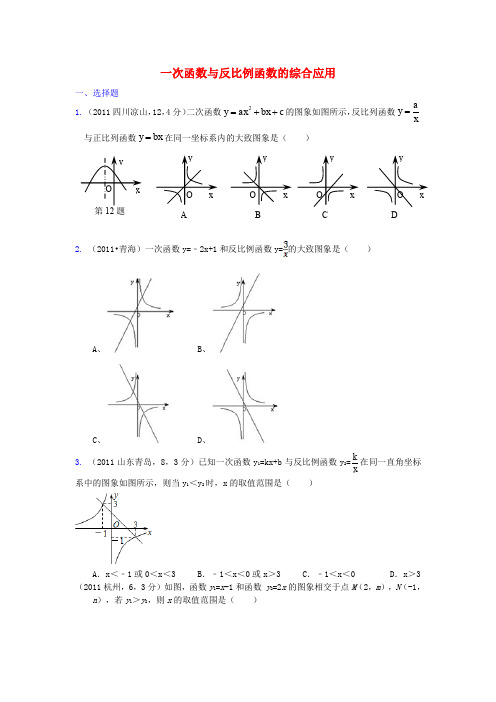
一次函数与反比例函数的综合应用一、选择题1. (2011四川凉山,12,4分)二次函数2y ax bx c =++的图象如图所示,反比列函数ay x=与正比列函数y bx =在同一坐标系内的大致图象是( )2. (2011•青海)一次函数y=﹣2x+1和反比例函数y=的大致图象是( )A 、B 、C 、D 、3. (2011山东青岛,8,3分)已知一次函数y 1=kx+b 与反比例函数y 2=kx在同一直角坐标系中的图象如图所示,则当y 1<y 2时,x 的取值范围是( )A .x <﹣1或0<x <3B .﹣1<x <0或x >3C .﹣1<x <0D .x >3 (2011杭州,6,3分)如图,函数y 1=x -1和函数 y 2=2x 的图象相交于点M (2,m ),N (-1,n ),若y 1>y 2,则x 的取值范围是( )ABDCA .x <-1或0<x <2B .x <-1或x >2C .-1<x <0或0<x <2D .-1<x <0或x >24.(2011浙江台州,9,4分)如图,双曲线y =mx与直线y =kx +b 交于点M .N ,并且点M 的坐标为(1,3),点N 的纵坐标为﹣1.根据图象信息可得关于x 的方程mx=kx +b 的解为( )A .﹣3,1B .﹣3,3C .﹣1,1D .﹣1,35. (2011•丹东,6,3分)反比例函数y=xk的图象如图所示,则一次函数y=kx+k 的图象大致是( )A 、B 、C 、D 、6.(2011•宜昌,15,3分)如图,直线y=x+2与双曲线y=3m x在第二象限有两个交点,那么m 的取值范围在数轴上表示为( )A 、B 、C 、D 、7. (2011贵州毕节,9,3分)一次函数)0(≠+=k k kx y 和反比例函数)0(≠=k xky 在同一直角坐标系中的图象大致是( )8. (2011•贵阳10,分)如图,反比例函数y 1=xk 1和正比例函数y 2=k 2x 的图象交于A (﹣1,﹣3)、B (1,3)两点,若xk 1>k 2x ,则x 的取值范围是( )A 、﹣1<x <0B 、﹣1<x <110.(2011广西百色,10,4分)二次函数的图象如图,则反比例函数y =﹣x与一次函数y =bx +c 的图象在同一坐标系内的图象大致是( )A .B .C .D .11. (2011•恩施州5,3分)一次函数y 1=k 1x+b 和反比例函数y 2=xk 2(k 1∙k 2≠0)的图象如图所示,若y 1>y 2,则x 的取值范围是( )A 、﹣2<x <0或x >1B 、﹣2<x <113. (2011陕西,8,3分)如图,过y 轴正半轴上的任意一点P ,作x 轴的平行线,分别与反比例函数xy xy 24=-=和的图象交于点A 和点B ,若点C 是x 轴上任意一点,连接AC 、BC ,则△ABC 的面积为 ( )A.3 B.4 C.5 D.6 二、填空题1.(2011江苏南京,15,2分)设函数y=2x与y=x﹣1的图象的交点坐标为(a,B),则11a b-的值为﹣12.2.(2011江苏苏州,18,3分)如图,已知点A,3),AB丄x轴,垂足为B,连接OA,反比例函数kyx=(k>0)的图象与线段OA、AB分别交于点C、D.若AB=3BD,以点C为圆心,CA的54倍的长为半径作圆,则该圆与x轴的位置关系是__________(填”相离”,“相切”或“相交“).3.(2011湖北荆州,16,3分)如图,双曲线 y=2x (x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得AB′C,B′点落在OA上,则四边形OABC的面积是.4.(2011广西崇左,8,2分)若一次函数的图象经过反比例函数xy 4-=图象上的两点(1,m )和(n ,2),则这个一次函数的解析式是 .5.(2011湖北黄石,15,3分)若一次函数y=kx+1的图象与反比例函数xy 1=的图象没有公共点,则实数k 的取值范围是.6.(2011成都,25,4分)在平面直角坐标系xOy 中,已知反比例函数xky 2=(0≠k )满足:当x <0时,y 随x 的增大而减小.若该反比例函数的图象与直线k x y 3+-=都经过点P ,且7=OP ,则实数K=.7.(2011•包头,18,3分)如图,已知A (﹣1,m )与B (2,m+33)是反比例函数y=的图象上的两个点,点C 是直线AB 与x 轴的交点,则点C 的坐标是 .8. (2011浙江宁波,18,3)正方形的A 1B 1P 1P 2顶点P 1、P 2在反比例函数y =x2(x >0)的图象上,顶点A 1、B 1分别在x 轴、y 轴的正半轴上,再在其右侧作正方形P 2P 3A 2B 2,顶点P 3在反比例函数y =x 2(x >0)的图象上,顶点A 2在x 轴的正半轴上,则点P 3的坐标为( , ).9. (2011浙江衢州,15,4分)在直角坐标系中,有如图所示的Rt△ABO ,AB ⊥x 轴于点B ,斜边AO =10,si n ∠AOB =35,反比例函数(0)ky k x=>的图象经过AO 的中点C ,且与AB 交于点D ,则点D 的坐标为( , ).10.(2011浙江丽水,16,4分)如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为kyx=.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O´B´.(1)当点O´与点A重合时,点P的坐标是(,);(2)设P(t,0),当O´B´与双曲线有交点时,t的取值范围是.2.(2011四川广安,24,8分)如图6所示,直线l1的方程为y=-x+l,直线l2的方程为y=x+5,且两直线相交于点P,过点P的双曲线kyx=与直线l1的另一交点为Q(3,M).(1)求双曲线的解析式.(2)根据图象直接写出不等式kx>-x+l的解集.3.(2011•南通)如图,直线l经过点A(1,0),且与双曲线y=mx(x>0)交于点B(2,1),过点P(p,p-1)(p>1)作x轴的平行线分别交曲线y=mx(x>0)和y=-mx(x<0)于M,N两点.(1)求m的值及直线l的解析式;(2)若点P 在直线y =2上,求证:△PMB ∽△PNA ;(3)是否存在实数p ,使得S △AMN =4S △APM ?若存在,请求出所有满足条件的p 的值;若不存在,请说明理由.4. (2011•宁夏,24,8分)在Rt△ABC 中,∠C=90°,∠A=30°,BC=2.若将此直角三角形的一条直角边BC 或AC 与x 轴重合,使点A 或点B 刚好在反比例函数xy 6=(x >0)的图象上时,设△ABC 在第一象限部分的面积分别记做S 1、S 2(如图1、图2所示)D 是斜边与y 轴的交点,通过计算比较S 1、S 2的大小.5. (2011山西,20,7分)如图,在平面直角坐标系中,一次函数y =k x +b 的图象分别交x 轴、y 轴于A 、B 两点,与反比例函数xmy =的图象交于C 、D 两点,DE ⊥x 轴于点E ,已知C 点的坐标是(6,-1),DE =3.(1)求反比例函数与一次函数的解析式.(2)根据图象直接回答:当x 为何值时,一次函数的值大于反比例函数的值?6.(2011天津,20, 分)已知一次函数y 1=x +b (b 为常数)的图象与反比例函数2k y x=(k 为常数,且k ≠0 )的图象相交于点P (3,1). (I )求这两个函数的解析式:(II )当x >3时,试判断y 1与y 2的大小,并说明理由.7. (2011重庆綦江,23,10分)如图,已知A (4,a ),B (-2,-4)是一次函数y=kx +b 的图象和反比例函数y =-xm的图象的交点.(1)求反比例函数和一次函数的解祈式.(2)求△A0B 的面积. 8. (2011重庆市,23,10分)如图, 在平面直角坐标系中,一次函数y kx b =+(k ≠0)的图象与反比例函数xmy =(m ≠0)的图象相交于A 、B 两点. 求:(1)根据图象写出A 、B 两点的坐标并分别求出反比例函数和一次函数的解析式; (2)根据图象写出:当x 为何值时,一次函数值大于反比例函数值.9.(2010重庆,22,10分)如图,在平面直角坐标系x 0y 中,一次函数y =kx +b (k ≠0)的图象与反比例函数my x(m ≠0)的图象交于二、四象限内的A 、B 两点,与x 轴交于C 点,点B 的坐标为(6,n ).线段OA =5,E 为x 轴上一点,且sin ∠AOE =45.(1)求该反比例函数和一次函数的解析式; (2)求△AOC 的面积.10. (2011湖北潜江,21,8分)如图,已知直线AB 与x 轴交于点C ,与双曲线y =xk 交于A (3,320)、B (—5,a )两点.AD ⊥x 轴于点D ,BE ∥x 轴且与y 轴交于点E . (1)求点B 的坐标及直线AB 的解析式; (2)判断四边形CBED 的形状,并说明理由.11. (2011•贵港)如图所示,反比例函数y=的图象与一次函数y=kx ﹣3的图象在第一象限内相交于点A (4,m ).(1)求m 的值及一次函数的解析式;(2)若直线x=2与反比例和一次函数的图象分别交于点B 、C ,求线段BC 的长.22题图12.(2011•柳州)如图,直线y=kx+k(k≠0)与双曲线y=在第一象限内相交于点M,与x轴交于点A.(1)求m的取值范围和点A的坐标;(2)若点B的坐标为(3,0),AM=5,S△ABM=8,求双曲线的函数表达式.13.(2011•安顺)如图,已知反比例函数的图象经过第二象限内的点A(﹣1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数的图象上另一点C(n,一2).(1)求直线y=ax+b的解析式;(2)设直线y=ax+b与x轴交于点M,求AM的长.14.(2011黑龙江大庆,23,7分)如图所示,制作一种产品的同时,需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系,已知该材料在加热前的温度为l5℃,加热5分钟使材料温度达到60℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时问x成反比例函数关系.(1)分别求出该材料加热和停止加热过程中y 与x 的函数关系(要写出x 的取值范);(2)根据工艺要求,在材料温度不低于30℃的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理所用的时间为多少分钟?15. 2011山东菏泽,17,10分)(1)已知一次函数y =x +2与反比例函数k y=x,其中一次函数y =x +2的图象经过点P (k ,5).①试确定反比例函数的表达式;②若点Q 是上述一次函数与反比例函数图象在第三象限的交点,求点Q 的坐标.16. (2011•临沂,24,10分)如图,一次函数y=kx+b 与反比例函数y=m x 的图象相较于A (2,3),B (﹣3,n )两点.(1)求一次函数与反比例函数的解析式;(2)根据所给条件,请直接写出不等式kx+b >m x的解集; (3)过点B 作BC⊥x 轴,垂足为C ,求S △ABC .17. (2011泰安,26,10分)如图,一次函数y =k 1x +b 的图象经过A (0,-2),B (1,0)两点,与反比例函数xk y 2 的图象在第一象限内的交点为M ,若△OBM 的面积为2. (1)求一次函数和反比例函数的表达式;(2)在x 轴上是否存在点P ,使AM ⊥MP ?若存在,求出点P 的坐标;若不存在,说明理由.18. (2011山东烟台,22,8分) 如图,已知反比例函数11k y x=(k 1>0)与一次函数2221(0)y k x k =+≠相交于A 、B 两点,AC ⊥x 轴于点C . 若△OAC 的面积为1,且tan∠AOC =2 .(1)求出反比例函数与一次函数的解析式;(2)请直接写出B 点的坐标,并指出当x 为何值时,反比例函数y 1的值大于一次函数y 2的值?19. (2011•山西)如图,在平面直角坐标系中,一次函数y=kx+b 的图象分别交x 轴、y 轴于A 、B 两点,与反比例函数m y x=的图象交于C 、D 两点,DE⊥x 轴于点E .已知C 点的坐标是(6,﹣1),DE =3.(1)求反比例函数与一次函数的解析式.(2)根据图象直接回答:当x 为何值时,一次函数的值大于反比例函数的值?20.(2011四川达州,18,6分)给出下列命题:命题1:直线y =x 与双曲线1y x=有一个交点是(1,1);命题2:直线y =8x 与双曲线2y x =有一个交点是(12,4); 命题3:直线y =27x 与双曲线3y x =有一个交点是(13,9); 命题4:直线y =64x 与双曲线4y x =有一个交点是(14,16); …(1)请你阅读、观察上面命题,猜想出命题n (n 为正整数);(2)请验证你猜想的命题n 是真命题.21. (2011四川广安,24,8分)如图6所示,直线l 1的方程为y =-x +l ,直线l 2的方程为y =x +5,且两直线相交于点P ,过点P 的双曲线k y x=与直线l 1的另一交点为Q (3,M ).(1)求双曲线的解析式.(2)根据图象直接写出不等式k x>-x +l 的解集.22. (2011四川泸州,24,7分)如图,已知函数y = x6(x >0)的图象与一次函数y =kx +b 的图象交于点A (1,m ),B (n ,2)两点.(1)求一次函数的解析式;(2)将一次函数y =kx +b 的图象沿x 轴负方向平移a (a >0)个单位长度得到新图象,求这个新图象与函数 y =x6 (x >0)的图象只有一个交点M 时a 的值及交点M 的坐标.24. (2011四川攀枝花,20)如图,已知反比例函数y=x (m 是常数,m≠0),一次函数y=ax+b (a 、b 为常数,a≠0),其中一次函数与x 轴,y 轴的交点分别是A (﹣4,0),B (0,2).(1)求一次函数的关系式;(2)反比例函数图象上有一点P 满足:①PA⊥x 轴;②PO=17(O 为坐标原点),求反比例函数的关系式;(3)求点P 关于原点的对称点Q 的坐标,判断点Q 是否在该反比例函数的图象上.25.(2011四川雅安,23,10分)如图,过y 轴上点A 的一次函数与反比例函数相交于B 、D 两点,B (﹣2,3),BC⊥x 轴于C ,四边形OABC 面积为4.(1)求反比例函数和一次函数的解析式;(2)求点D 的坐标;(3)当x 在什么取值范围内,一次函数的值大于反比例函数的值.(直接写出结果)26. (2011四川雅安23,10分)如图,过y 轴上点A 的一次函数与反比例函数相交于B .D 两点,)3,2(-B ,轴x BC ⊥于C ,四边形OABC 面积为4。
中考数学复习专题综合过关检测—一次函数(含解析)

中考数学复习专题综合过关检测—一次函数(含解析)(考试时间:90分钟,试卷满分:100分)一、选择题(本题共10小题,每小题3分,共30分)。
1.(2023秋•铜陵期中)下列函数①y=πx,②y=﹣2x+3,③,④,⑤y=x2﹣1中,是一次函数的有()A.1个B.2个C.3个D.4个【答案】C【解答】解:①y=πx,是一次函数,符合题意;②y=﹣2x+3,是一次函数,符合题意;③,x的次数不为1,不是一次函数,不符合题意;④,是一次函数,符合题意;⑤y=x2﹣1x的次数不为1,不是一次函数,不符合题意;即一次函数有①②④,共3个,故选:C.2.(2023•长沙模拟)已知一次函数y=ax﹣4的函数值y随x的增大而减小,则该函数的图象大致是()A.B.C.D.【答案】B【解答】解:∵一次函数y=ax﹣4的函数值y随x的增大而减小,∴a<0,∵b=﹣4<0,∴y=ax﹣4经过第二、三、四象限,故选:B.3.(2022秋•大东区校级期末)将一次函数y=﹣2x的图象沿y轴向下平移4个单位长度后,所得图象的函数表达式为()A.y=﹣2(x﹣4)B.y=﹣2x+4C.y=﹣2(x+4)D.y=﹣2x﹣4【答案】D【解答】解:由上加下减”的原则可知,将一次函数y=﹣2x的图象沿y轴向下平移4个单位长度后,所得图象的函数表达式为:y=﹣2x﹣4.故选:D.4.(2022秋•碑林区期末)一次函数y=kx+b图象经过(1,1),(2,﹣4),则k与b的值为()A.B.C.D.【答案】C【解答】解:把(1,1),(2,﹣4)代入一次函数y=kx+b,得,解得:.故选:C.5.(2023春•乾安县期末)已知A(﹣,y1)、B(﹣,y2)、C(1,y3)是一次函数y=﹣3x+b的图象上三点,则y1,y2,y3的大小关系是()A.y1<y2<y3B.y2<y1<y3C.y3<y1<y2D.y3<y2<y1【答案】C【解答】解:∵A(﹣,y1)、B(﹣,y2)、C(1,y3)是一次函数y=﹣3x+b的图象上三点,∴y1=1+b,y2=+b,y3=﹣3+b.∵﹣3+b<1+b<+b,∴y3<y1<y2.故选:C.6.(2023•灞桥区校级二模)若一次函数y=(m﹣1)x+m﹣2的图象不经过第二象限,则m的取值范围是()A.m>1B.m<2C.1<m<2D.1<m≤2【答案】D【解答】解:∵一次函数y=(m﹣1)x+m﹣2的图象不经过第二象限,∴m﹣1>0且m﹣2≤0,解得1<m≤2,故选:D.7.(2023春•开福区校级期末)对于函数y=﹣2x+4,说法正确的是()A.点A(1,3)在这个函数图象上B.y随着x的增大而增大C.它的图象必过一、三象限D.当x>2时,y<0【答案】D【解答】解:A.当x=1时,y=﹣2×1+4=2,2≠3,∴点(1,3)不在这个函数图象上,选项A不符合题意;B.∵k=﹣2<0,∴y随x的增大而减小,选项B不符合题意;C.∵k=﹣2<0,b=4>0,∴一次函数y=﹣2x+4的图象经过第一、二、四象限,选项C不符合题意;D.当x>2时,y<﹣2×2+4=0,选项D符合题意.故选:D.8.(2023•南岗区校级二模)在全民健身越野比赛中,乙选手匀速跑完全程,甲选手1.5小时后的速度为每小时10千米,甲、乙两选手的行程y(千米)随时间z(时)变化的图象(全程)如图所示.下列说法:①起跑后半小时内甲的速度为每小时16千米;②第1小时两人都跑了10千米;③两人都跑了20千米;④乙比甲晚到0.3小时.其中正确的个数有()A.1个B.2个C.3个D.4个【答案】C【解答】解:①起跑后半小时内甲的速度为8÷0.5=16千米/小时,故①正确;②根据函数图象的交点坐标,可得第1小时两人都跑了10千米,故②正确;③根据甲1小时跑10km,可得2小时跑20km,故两人都跑了20千米,故③正确;④根据0.5~1.5小时内,甲半小时跑2km,可得1小时跑4km,故1.5小时跑了12km,剩余的8km需要的时间为8÷10=0.8小时,根据1.5+0.8﹣2=0.3,可得甲比乙晚到0.3小时,故④错误.故选:C.9.(2023秋•合肥期中)如图,已知一次函数y=ax+b和y=kx的图象相交于点P,则根据图象可得二元一次方程组的解是()A.B.C.D.【答案】D【解答】解:如图所示:根据图中信息可得二元一次方程组的解是:.故选:D.10.(2023春•盖州市期末)如图,直线y=x+2与y轴相交于点A0,过点A0作x轴的平行线交直线y=0.5x+1于点B1,过点B1作y轴的平行线交直线y=x+2于点A1,再过点A1作x轴的平行线交直线y=0.5x+1于点B2,过点B2作y轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1,A2,A3,…,与直线y=0.5x+1上的点B1,B2,B3,…,则A8B9的长为()A.64B.128C.256D.512【答案】D【解答】解:对于直线y=x+2,令x=0,求出y=2,即A0(0,2),∵A0B1∥x轴,∴B1的纵坐标为2,将y=2代入y=0.5x+1中得:x=2,即B1(2,2),∴A0B1=2=21,∵A1B1∥y轴,∴A1的横坐标为2,将x=2代入直线y=x+2中得:y=4,即A1(2,4),∴A1与B2的纵坐标为4,将y=4代入y=0.5x+1中得:x=6,即B2(4,6),∴A1B2=4=22,同理A2B3=8=23,…,A n﹣1B n=2n,则A8B9的长为29=512.故选:D.二、填空题(本题共6题,每小题2分,共12分)。
2011中学考试数学真题解析汇报48_一次函数与反比例函数地综合应用(含问题详解)

一次函数与反比例函数的综合应用
一、选择题
1.(2011凉山,12,4分)二次函数 的图象如图所示,反比列函数 与正比列函数 在同一坐标系的大致图象是( )
2.(2011•)一次函数y=﹣2x+1和反比例函数y=的大致图象是( )
A、B、
C、D、
3.(2011,8,3分)已知一次函数y1=kx+b与反比例函数y2= 在同一直角坐标系中的图象如图所示,则当y1<y2时,x的取值围是( )
A、﹣2<x<0或x>1B、﹣2<x<1
C、x<﹣2或x>1D、x<﹣2或0<x<1
考点:反比例函数与一次函数的交点问题。
专题:数形结合。
分析:根据图象可以知道一次函数y1=k1x+b和反比例函数y2= (k1∙k2≠0)的图象的交点的横坐标,若y1>y2,则根据图象可以确定x的取值围.
解答:解:如图,依题意得一次函数y1=k1x+b和反比例函数y2= (k1∙k2≠0)的图象的交点的横坐标分别为x=﹣2或x=1,
考点:直线与圆的位置关系;反比例函数图象上点的坐标特征.
分析:根据D点的坐标为( ,1),得出反比例函数 解析式,再根据A点坐标得出AO直线解析式,进而得出两图象的交点坐标,进而得出AC的长度,再利用直线与圆的位置关系得出答案.
解答:解:∵已知点A的坐标为( ,3),AB=3BD,
∴AB=3,BD=1,
A.3 B.4 C.5 D.6
考点:反比例函数综合题。
专题:计算题。
分析:先设P(0,b),由直线APB∥x轴,则A,B两点的纵坐标都为b,而A,B分别在反比例函数 的图象上,可得到A点坐标为(﹣,b),B点坐标为(,b),从而求出AB的长,然后根据三角形的面积公式计算即可.
2011中考数学一次函数的应用_复习课件(共52)第14课时

►
一次函数的应用
考点一 用一次函数解决实际问题 在解答一次函数的应用题时,应从给定的信息 中抽象出一次函数关系,理清哪个是自变量, 哪个是自变量的函数,再利用一次函数的图象 与性质求解,同时要注意自变量的取值范围. 一次函数y=kx+b(k≠0)的自变量x的范围是全体实 数.图象是直线,因此没有最大值与最小值.但由 实际问题得到的一次函数解析式,自变量的取值范 围一般受到限制,则图象为线段和射线,根据函数 图象的性质,就存在最大值和最小值.
第14课时
一次函数的应用
► 类型之二 利用一次函数解决收费问题 命题角度: 1.利用一次函数解决个税收取问题 2.利用一次函数解决水,电,煤气等资源收费问题
例3 [2010· 南平] 我国西南五省市的部分地区发生严重旱灾, 为鼓励节约用水,某市自来水公司采取分段收费标准,如图 反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系. (1)小明家五月份用水8吨,应交水费________元; (2)按上述分段收费标准,小明家三、四月份分别交水费26元 和18元,问四月份比三月份节约用水多少吨?
第14课时
一次函数的应用
例2 [2010· 西安] 某蒜薹(tá i)生产基地喜获丰收,收获蒜薹 200吨,经市场调查,可采用批发、零售、冷库储藏后销 售三种方式,并且按这三种方式销售,计划每吨平均售价 及成本如下表:若经过一段时间,蒜薹按计划全部售出获 得的总利润为y(元),蒜薹零售x(吨),且零售量是批发量 的. (1)求y与x之间的函数关系式; (2)由于受条件限制,经冷库储藏售出的蒜薹最多80吨,求该 生产基地按计划全部售完蒜薹获得的最大利润.
第14课时
► 类型之三
一次函数的应用
利用一次函数解决其他生活实际问题
2011年-2018年河北省中考一次函数汇编

2011-2018河北省中考一次函数汇编(2011)11.如图4,在长形中截取两个相同的圆作为圆柱的上、下底面,剩余的矩形作为圆住的侧面,刚好能组合成圆住.设矩形的长和宽分别为y 和x ,则y 与x 的函数图象大致是(2011)24.(本小题满分9分)已知A 、B 两地的路程为240千米,某经销商每天都要用汽车或火车将x 吨保鲜品一次性由A 地运往B 地,受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.现在有货运收费项目及收费标准表,行驶路程S (千米)与行驶时间t (时)的函数图象(如图13中①),上周货运量折线统计图(如图13中②)等信息如下:⑴汽车的速度为__________千米/时, 火车的速度为_________千米/时;设每天用汽车和火车运输的总费用分别为y 汽(元)和y 火(元),分别求y 汽、y 火与x 的函数关系式(不必写出x 的取值范围)及x 为何值时y 汽>y 火;(总费用=运输费+冷藏费+固定费用)(2012改编)22.(本小题满分8分)如图12,四边形ABCD 是平行四边形,点A (1,0),B (3,1),C (3,3),点P 是一次函数y =kx +3-3k (k ≠0)的图象的一个点.(2)通过计算,说明一次函数y =kx +3-3k (k ≠0)的图象一定过点C ;(1、3问使用到反比例函数,所以去掉了)图12(2013)16.如图9,梯形ABCD 中,AB ∥DC ,DE ⊥AB ,CF ⊥AB ,且AE = EF = FB = 5,DE = 12动点P 从点A 出发,沿折线AD -DC -CB 以每秒1个单位 长的速度运动到点B 停止.设运动时间为t 秒,y = S △EPF , 则y 与t 的函数图象大致是(2013)23.如图15,A (0,1),M (3,2),N (4,4).动点P 从点A 出发,沿轴以每秒1个单位长的速度向上移动,且过点P 的直线l :y =-x +b 也随之移动,设移动时间为t 秒.(1)当t =3时,求l 的解析式;(2)若点M ,N 位于l 的异侧,确定t 的取值范围;(3)直接写出t 为何值时,点M 关于l 的对称点落在坐标轴上.(2015)14.如图6,直线332:--=x y l 与直线a y =(a 为常数)的交点在第四象限,则a 可能在( ) A.21<<a B.02<<-a图6C.23-≤≤-aD.410-<<-a(2015)23(本小题满分10分)水平放置的容器内原有210毫米高的水,如图12,将若干个球逐一放入该容器中,每放入一个大球水面就上升4毫米,每放入一个小球水面就上升3毫米,假定放入容器中的所有球完全浸没水中且水不溢出,设水面高为y 毫米.(1)只放入大球,且个数为x 大,求y 与x 大的函数关系式(不必写出x 大的范围);(2)仅放入6个大球后,开始放入小球,且小球个数为x 小. ①求y 与x 小的函数关系式(不必写出x 小的范围); ②限定水面高不超过260毫米,最多能放入几个小球?(2016)5.若00<≠b k ,,则b kx y +=的图象可能是 ( )(2016)24.本小题满分10分)某商店通过调低价格的方式促销n 个不同的玩具,调整后的单价y (元)与调整前的单价x (元)满足一次函数关系,如下表:⑴求y 与x 的函数关系式,并确定x 的取值范围;⑵某个玩具调整前单价是108元,顾客购买这个玩具省了多少钱? ⑶这n 个玩具调整前、后的平均单价分别为x ,y ,猜想x 与y 的关系式,图12并写出推导过程.(2017)24.(本小题满分10分)如图16,直角坐标系xOy 中,A(0,5),直线x =-5与x 轴交于点D ,直线83983--=x y 与x 轴及直线x =-5分别交于点C ,E.点B ,E 关于x 轴对称,连接AB.(1)求点C ,E 的坐标及直线AB 的解析式; (2)设面积的和CDE ABDO S S S ∆=+四边形,求S 的值;(3)在求(2)中S 时,嘉琪有个想法:“将△CDE 沿x 轴翻折到△CDB 的位置,而△CDB 与四边形ABDO 拼接后可看成△AOC ,这样求S 便转化为直接求△AOC 的面积不更快捷吗?”但大家经反复验算,发现S S AOC ≠Δ,请通过计算解释他的想法错在哪里.(2018)24.(本小题满分10分)如图14,直角坐标系xOy 中,一次函数521+-=x y 的图象1l 分别与x ,y 轴交于A ,B 两点,正比例函数的图象2l 与1l 交于点C(m ,4).(1)求m 的值及2l 的解析式; (2)求BOC AOC S S ∆∆-的值;(3)一次函数1+=kx y 的图象为3l ,且1l ,2l ,3l 不能围成三角形,直接写出k 的值.图16答案: 11.A24. 解: ⑴ 60,100. ⑵依题意,得240=2402520060y x x ⨯+⨯+汽. =500200y x +汽.240=240 1.652280100y x x ⨯+⨯+火. =3962280y x +火.若y 汽 >y 火,得500200x +>3962280x +, ∴x >20.2216.A图142114.D5.B(2017)(2018)。
2011中考数学真题解析48_一次函数与反比例函数的综合应用(含答案)
全国中考真题解析一次函数与反比例函数的综合应用一、选择题1. (2011四川凉山,12,4分)二次函数2y ax bx c =++的图象如图所示,反比列函数ay x=与正比列函数y bx =在同一坐标系内的大致图象是( )2. (2011•青海)一次函数y=﹣2x+1和反比例函数y=的大致图象是( )A 、B 、C 、D 、3. (2011山东青岛,8,3分)已知一次函数y 1=kx+b 与反比例函数y 2=kx在同一直角坐标系中的图象如图所示,则当y 1<y 2时,x 的取值范围是( )A .x <﹣1或0<x <3B .﹣1<x <0或x >3C .﹣1<x <0D .x >3(2011杭州,6,3分)如图,函数y 1=x -1和函数 y 2=2x 的图象相交于点M (2,m ),N (-1,n ),若y 1>y 2,则x 的取值范围是( )O xy O yxAO yxBO yxDO yxCA .x <-1或0<x<2 B .x <-1或x >2 C .-1<x <0或0<x <2 D .-1<x <0或x >24.(2011浙江台州,9,4分)如图,双曲线y =mx与直线y =kx +b 交于点M .N ,并且点M 的坐标为(1,3),点N 的纵坐标为﹣1.根据图象信息可得关于x 的方程mx=kx +b 的解为( )A .﹣3,1B .﹣3,3C .﹣1,1D .﹣1,35. (2011•丹东,6,3分)反比例函数y=xk的图象如图所示,则一次函数y=kx+k 的图象大致是( )Oyxxy OOy xxyOOyxA 、B 、C 、D 、6. (2011•宜昌,15,3分)如图,直线y=x+2与双曲线y=3m x在第二象限有两个交点,那么m 的取值范围在数轴上表示为( )考点:反比例函数与一次函数的交点问题;在数轴上表示不等式的解集。
A 、B 、C 、D 、7. (2011贵州毕节,9,3分)一次函数)0(≠+=k k kx y 和反比例函数)0(≠=k xky 在同一直角坐标系中的图象大致是( )8. (2011•贵阳10,分)如图,反比例函数y 1=xk 1和正比例函数y 2=k 2x 的图象交于A (﹣1,﹣3)、B (1,3)两点,若xk 1>k 2x ,则x 的取值范围是( )A 、﹣1<x <0B 、﹣1<x <1C 、x <﹣1或0<x <1D 、﹣1<x <0或x >1考点:反比例函数与一次函数的交点问题。
中考数学专项复习《一次函数》练习题及答案
中考数学专项复习《一次函数》练习题及答案一、单选题1.如图,在一次函数y=﹣x+10的图象上取一点P,作PA⊥x轴,PB⊥y轴,垂足为B,且矩形PBOA的面积为9,则这样的点P个数共有()A.1个B.2个C.3个D.4个2.在同一坐标系内,函数y=kx2和y=kx+2(k≠0)的图象大致如图()A.B.C.D.3.有甲、乙两个不同的水箱,容量分别为a升和b升,且已各装了一些水.若将甲中的水全倒入乙箱之后,乙箱还可以继续装20升水才会满;若将乙箱中的水倒入甲箱,装满甲箱后,乙箱里还剩10升水,则a,b之间的数量关系是()A.b=a+15B.b=a+20C.b=a+30D.b=a+404.关于一次函数y=5x-3的描述,下列说法正确的是()A.图象经过第一、二、三象限B.向下平移3个单位长度,可得到y=5xC.y随x的增大而增大D.图象经过点(-3,0)5.已知函数y=kx(k≠0)的大致图象如图所示,则函数y=kx-k的图象大致是()A.B.C.D.6.防汛期间,下表记录了某水库16h内水位的变化情况,其中x表示时间(单位:h),y表示水位高度(单位:m),当x=8h时,达到警戒水位,开始开闸放水,此时,y与xx/h012810121416y/m1414.5151814.412119)A.第1小时B.第10小时C.第14小时D.第16小时7.若点P(2,4)在正比例函数y=kx的图象上,则下列各点在此函数图象上的是()A.(−3,4)B.(−2,−4)C.(0.5,4)D.(1,5)8.已知直线y=kx+b(k≠0)与x轴的交点在x轴的正半轴,下列结论:①k>0,b>0;②k>0,b<0;③k<0,b>0;④k<0,b<0.其中正确的结论的个数是()A.1B.2C.3D.49.下列y关于x的函数中是正比例函数的为()A.y=x2B.y=2x C.y=x2D.y=x+1210.如图,一次函数y=kx+b与y=﹣x+4的图象相交于点P(m,1),则关于x、y的二元一次方程组{y=kx+by=−x+4的解是()A .{x =3y =1B .{x =2.6y =1C .{x =2y =1D .{x =1y =111.关于函数y=ax 2和函数y=ax+a (a≠0)在同一坐标系中的图象,A ,B ,C ,D 四位同学各画了一种,你认为可能画对的图象是( )A .B .C .D .12.已知一次函数y=kx ﹣k 与反比例函数 y =k x在同一直角坐标系中的大致图象是( )A .B .C .D .二、填空题13.如图,直线y =kx −3与x 轴、y 轴分别交于点B 与点A ,OB =13OA ,点C 是直线AB 上的一点,且位于第二象限,当⊥OBC 的面积为3时,点C 的坐标为 .14.如图,直线y=kx+b(k>0)与x轴的交点为(﹣2,0),则关于x的不等式kx+b<0的解集是.15.若直线y=kx+b平行直线y=3x+4,且过点(1,﹣2),则直线的关系式为.16.若函数y=−x+3与y=2x+b的图象相交于x轴上的一点,则b的值为.17.在平面直角坐标系中将直线y=x+2沿着y轴向下平移3个单位长度,平移后的直线所对应的函数解析式为.18.某自行车存车处在星期日的存车为4000辆次,其中变速车存车费是每辆一次0.3元,普通车存车费是每辆一次0.2元,若普通车存车数为x辆次,存车总收入y(元)与x的函数关系式是.三、综合题19.作出函数y=2x+6的图象并回答:(1)x取何值时,y=0;(2)x取何值时,y>0?(3)x取何值时,y<0?20.某家电集团公司研制生产的新家电,前期投资200万元,每生产一台这种新家电,后期还需投资0.3万元,已知每台新家电售价为0.5万元.设总投资为P万元,总利润为Q万元(总利润=总产值-总投资),新家电总产量为x台.(假设可按售价全部卖出)(1)试用x的代数式表示P和Q;(2)当总产量达到900台时,该公司能否盈利?(3)当总产量达到多少台时,该公司开始盈利?21.如图所示,已知二次函数y1=−x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,与y轴的交点为点C.(1)求m的值;(2)若经过点B的一次函数y2=kx+b平分⊥ABC的面积.求k、b的值.22.阅读下列材料:实验数据显示,一般成人喝250毫升低度白酒后,其血液中酒精含量(毫克/百毫升)随时间的增加逐步增高达到峰值,之后血液中酒精含量随时间的增加逐渐降低.小带根据相关数据和学习函数的经验,对血液中酒精含量随时间变化的规律进行了探究,发现血液中酒精含量y是时间x的函数,其中y表示血液中酒精含量(毫克/百毫升),x表示饮酒后的时间(小时).下表记录了6小时内11个时间点血液中酒精含量y(毫克/百毫升)随饮酒后的时间x(小时)(x >0)的变化情况.下面是小带的探究过程,请补充完整:(1)如图,在平面直角坐标系xOy中以上表中各对数值为坐标描点,图中已给出部分点,请你描出剩余的点,画出血液中酒精含量y随时间x变化的函数图象;(2)观察表中数据及图象可发现此函数图象在直线x=32两侧可以用不同的函数表达式表示,请你任选其中一部分写出表达式;(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:30在家喝完250毫升低度白酒,第二天早上7:00能否驾车去上班?请说明理由.23.在平面直角坐标系xOy中直线l1:y1=kx+b与直线y=2x平行,且经过点(1,0).(1)求直线l1的解析式;(2)已知直线l2:y2=mx+1,过点p(n,0)作x轴的垂线,与直线l1交于点M,与直线l2交于点N.结合图象回答:①若m=1,当点M在点N的上方时,直接写出n的取值范围;②若对任意的n>2,都有点M在点N的上方,直接写出m的取值范围.24.如图,已知直线y=﹣2x+12分别与Y轴,X轴交于A,B两点,点M在Y轴上,以点M为圆心的⊥M与直线AB相切于点D,连接MD.(1)求证:⊥ADM⊥⊥AOB;(2)如果⊥M的半径为2 √5,请写出点M的坐标,并写出以(﹣52,292)为顶点,且过点M的抛物线的解析式;(3)在(2)条件下,试问在此抛物线上是否存在点P使以P、A、M三点为顶点的三角形与⊥AOB相似?如果存在,请求出所有符合条件的点P的坐标;如果不存在,请说明理由.参考答案1.【答案】D2.【答案】D3.【答案】C4.【答案】C5.【答案】A6.【答案】C7.【答案】B8.【答案】B9.【答案】C10.【答案】A11.【答案】D12.【答案】B13.【答案】(−3,6)14.【答案】x<﹣215.【答案】y=3x﹣316.【答案】-617.【答案】y=x-118.【答案】y=-0.1x+120019.【答案】(1)解答: 由图象得:x=-3时,y=0;(2)解答:y=2x+6>0,解x>-3当x>-3时,y>0;(3)解答:y=2x+6<0,解x<-3当x<-3时,y<0.20.【答案】(1)解:P=200+0.3x,Q=0.5x-(200+0.3x)=0.2 x-200.(2)解:当x=900时即当总产量达到900台时,没有盈利,亏了20万元.(3)解:当Q >0时,开始盈利,即0.2x −200>0,解得x >1000 当总产量超过1000台时,公司开始盈利.21.【答案】(1)解:∵ 二次函数y 1=−x 2+2x +m 的图象与x 轴的一个交点为A (3,0)∴0=−9+6+m ∴ m=3; (2)解:如图∵一次函数y 2=kx +b 平分⊥ABC 的面积 ∴一次函数y 2=kx +b 平分线段AC ∴ 一次函数y 2=kx +b 经过AC 的中点E ∵m=3∴−x 2+2x +3=0时,解得x 1=−1 x 2=3 ∴ 点B 的坐标为B (-1,0) 当x =0时,y =3∴ 点C 的坐标为C (0,3) ∴ 点E 的坐标为E (32,32)∵ 一次函数y 2=kx +b 经过点B ∴{0=−k +b32=32k +b 解得:{k =35b =3522.【答案】(1)解:图象如图所示.(2)解:y=-200x2+400x(0≤x≤ 32)或y=225x(x> 32)(3)解:不能.理由如下:把y=20代入反比例函数y=225x得x=11.25.∵晚上20:30经过11.25小时为第二天早上7:45∴第二天早上7:45以后才可以驾车上路∴第二天早上7:00不能驾车去上班23.【答案】(1)解:∵直线l1:y1=kx+b与直线y=2x平行∴k=2把点(1,0)代入直线y=2x+b中得到0=2+b解得b=−2∴直线l1的解析式为y=2x−2;(2)解:如图①若m=1,则直线l2:y2=x+1联立{y=x+1y=2x−2解得{x=3y=4由图象可知当n>3时,点M在点N的上方;②把x=2代入y=2x−2求得y=2把x=2,y=2代入y=mx+1得解得m=1 2∴若对任意的n>2,都有点M在点N的上方,m的取值范围是m⩽12.24.【答案】(1)证明:∵AB是⊥M切线,D是切点∴MD⊥AB.∴⊥MDA=⊥AOB=90°又⊥MAD=⊥BAO∴⊥ADM⊥⊥AOB(2)解:设M(0,m)由直线y=2x+12得,OA=12,OB=6则AM=12﹣m,而DM=2 √5在Rt⊥AOB中AB= √OA2+OB2= √122+62=6 √5∵⊥ADM⊥⊥AOB∴AMDM=ABOB即2√5= 6√56,解得m=2∴M(0,2)设顶点为(﹣52,292)的抛物线解析式为y=a(x+52)2+ 292将M点坐标代入,得a(0+ 52)2+ 292=2解得a=﹣2所以,抛物线解析式为y=﹣2(x+ 52)2+ 292(3)解:存在.①当顶点M为直角顶点时,M、P两点关于抛物线对称轴x=﹣52轴对称此时MP=5,AM=12﹣2=10,AM:MP=2:1,符合题意∴P(﹣5,2);②当顶点A为直角顶点时,P点纵坐标为12,代入抛物线解析式,得﹣2(x+ 52)2+ 292=12解得x=﹣52± √52,此时AP=﹣52± √52,AM=10,不符合题意;③当顶点P为直角顶点时,则由相似三角形的性质可知,P(n,﹣2n+2 )或(2n,﹣n+2)若P(n,2n+2),则﹣2n﹣12n=10,解得n=﹣4,当x=﹣4,y=﹣2(﹣4+52)2+292=10,﹣2n+2=10,符合题意若P(2n,﹣n+2),则﹣n﹣4n=10,解得n=﹣2,而当x=2n=﹣4时,y=﹣2(﹣4+ 52)2+292=10,﹣n+2=4,不符合题意所以,符合条件的P点坐标为(5,2),(4,10).。
中考数学复习----《一次函数之定义、图像与性质》知识点总结与专项练习题(含答案解析)
中考数学复习----《一次函数之定义、图像与性质》知识点总结与专项练习题(含答案解析)知识点总结1. 一次函数的定义:一般地,形如()0≠+=k b k b kx y 是常数且,的函数叫做一次函数。
2. 一次函数的图像:是不经过原点的一条直线。
3. 一次函数的图像与性质:一次函数与x 轴的交点坐标公式为:⎪⎭⎫ ⎝⎛−0 ,k b;与y 轴的交点坐标公式为:()b ,0。
专项练习题1.(2022•沈阳)在平面直角坐标系中,一次函数y =﹣x +1的图像是( )A .B .C .D .【分析】依据一次函数y =x +1的图像经过点(0,1)和(1,0),即可得到一次函数y =﹣x +1的图像经过一、二、四象限.【解答】解:一次函数y =﹣x +1中,令x =0,则y =1;令y =0,则x =1, ∴一次函数y =﹣x +1的图像经过点(0,1)和(1,0), ∴一次函数y =﹣x +1的图像经过一、二、四象限, 故选:C .2.(2022•安徽)在同一平面直角坐标系中,一次函数y =ax +a 2与y =a 2x +a 的图像可能是( )A .B .C .D .【分析】利用一次函数的性质进行判断.【解答】解:∵y=ax+a2与y=a2x+a,∴x=1时,两函数的值都是a2+a,∴两直线的交点的横坐标为1,若a>0,则一次函数y=ax+a2与y=a2x+a都是增函数,且都交y轴的正半轴,图像都经过第一、二、三象限;若a<0,则一次函数y=ax+a2经过第一、二、四象限,y=a2x+a经过第一、三、四象限,且两直线的交点的横坐标为1;故选:D.3.(2022•辽宁)如图,在同一平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2的图像分别为直线l1和直线l2,下列结论正确的是()A.k1•k2<0B.k1+k2<0C.b1﹣b2<0D.b1•b2<0【分析】根据一次函数y=k1x+b1与y=k2x+b2的图像位置,可得k1>0,b1>0,k2>0,b2<0,然后逐一判断即可解答.【解答】解:∵一次函数y=k1x+b1的图像过一、二、三象限,∴k1>0,b1>0,∵一次函数y=k2x+b2的图像过一、三、四象限,∴k2>0,b2<0,∴A、k1•k2>0,故A不符合题意;B、k1+k2>0,故B不符合题意;C、b1﹣b2>0,故C不符合题意;D、b1•b2<0,故D符合题意;故选:D.4.(2022•六盘水)如图是一次函数y=kx+b的图像,下列说法正确的是()A.y随x增大而增大B.图像经过第三象限C.当x≥0时,y≤b D.当x<0时,y<0【分析】根据一次函数的图像和性质进行判断即可.【解答】解:由图像得:图像过一、二、四象限,则k<0,b>0,当k<0时,y随x的增大而减小,故A、B错误,由图像得:与y轴的交点为(0,b),所以当x≥0时,从图像看,y≤b,故C正确,符合题意;当x<0时,y>b>0,故D错误.故选:C.5.(2022•兰州)若一次函数y=2x+1的图像经过点(﹣3,y1),(4,y2),则y1与y2的大小关系是()A.y1<y2B.y1>y2C.y1≤y2D.y1≥y2【分析】先根据一次函数的解析式判断出函数的增减性,再根据﹣3<4即可得出结论.【解答】解:∵一次函数y=2x+1中,k=2>0,∴y随着x的增大而增大.∵点(﹣3,y1)和(4,y2)是一次函数y=2x+1图像上的两个点,﹣3<4,∴y1<y2.故选:A.6.(2022•凉山州)一次函数y=3x+b(b≥0)的图像一定不经过()A.第一象限B.第二象限C.第三象限D.第四象限【分析】根据一次函数的图像与系数的关系即可得出结论.【解答】解:∵函数y=3x+b(b≥0)中,k=3>0,b≥0,∴当b=0时,此函数的图像经过一、三象限,不经过第四象限;当b>0时,此函数的图像经过一、二、三象限,不经过第四象限.则一定不经过第四象限.故选:D.7.(2022•济宁)已知直线y1=x﹣1与y2=kx+b相交于点(2,1).请写出一个b值(写出一个即可),使x>2时,y1>y2.【分析】由题意可知,当b>﹣1时满足题意,故b可以取0.【解答】解:直线y1=x﹣1与y2=kx+b相交于点(2,1).∵x>2时,y1>y2.∴b>﹣1,故b可以取0,故答案为:0(答案不唯一).8.(2022•上海)已知直线y=kx+b过第一象限且函数值随着x的增大而减小,请列举出来这样的一条直线:.【分析】根据一次函数的性质,写出符合条件的函数关系式即可.【解答】解:∵直线y=kx+b过第一象限且函数值随着x的增大而减小,∴k<0,b>0,∴符合条件的函数关系式可以为:y=﹣x+1(答案不唯一).故答案为:y=﹣x+1(答案不唯一).9.(2022•无锡)请写出一个函数的表达式,使其图像分别与x轴的负半轴、y轴的正半轴相交:.【分析】设函数的解析式为y=kx+b(k≠0),再根据一次函数的图像分别与x轴的负半轴、y轴的正半轴相交可知k>0,b>0,写出符合此条件的函数解析式即可.【解答】解:设一次函数的解析式为y=kx+b(k≠0),∵一次函数的图像分别与x轴的负半轴、y轴的正半轴相交,∴k>0,b>0,∴符合条件的函数解析式可以为:y=x+1(答案不唯一).故答案为:y=x+1(答案不唯一).10.(2022•湘潭)请写出一个y随x增大而增大的一次函数表达式.【分析】根据y随着x的增大而增大时,比例系数k>0即可确定一次函数的表达式.【解答】解:在y=kx+b中,若k>0,则y随x增大而增大,∴只需写出一个k>0的一次函数表达式即可,比如:y=x﹣2,故答案为:y=x﹣2(答案不唯一).11.(2022•宿迁)甲、乙两位同学各给出某函数的一个特征,甲:“函数值y随自变量x增大而减小”;乙:“函数图像经过点(0,2)”,请你写出一个同时满足这两个特征的函数,其表达式是.【分析】根据甲、乙两位同学给出的函数特征可判断出该函数为一次函数,再利用一次函数的性质,可得出k<0,b=2,取k=﹣1即可得出结论.【解答】解:∵函数值y随自变量x增大而减小,且该函数图像经过点(0,2),∴该函数为一次函数.设一次函数的表达式为y=kx+b(k≠0),则k<0,b=2.取k=﹣1,此时一次函数的表达式为y=﹣x+2.故答案为:y=﹣x+2(答案不唯一).12.(2022•甘肃)若一次函数y=kx﹣2的函数值y随着自变量x值的增大而增大,则k=(写出一个满足条件的值).【分析】根据函数值y随着自变量x值的增大而增大得到k>0,写出一个正数即可.【解答】解:∵函数值y随着自变量x值的增大而增大,∴k>0,∴k=2(答案不唯一).故答案为:2(答案不唯一).13.(2022•柳州)如图,直线y1=x+3分别与x轴、y轴交于点A和点C,直线y2=﹣x+3分别与x轴、y轴交于点B和点C,点P(m,2)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为()A.1B.2C.4D.6【分析】由于P的纵坐标为2,故点P在直线y=2上,要求符合题意的m值,则P点为直线y=2与题目中两直线的交点,此时m存在最大值与最小值,故可求得.【解答】解:∵点P(m,2)是△ABC内部(包括边上)的一点,∴点P 在直线y =2上,如图所示,当P 为直线y =2与直线y 2的交点时,m 取最大值, 当P 为直线y =2与直线y 1的交点时,m 取最小值, ∵y 2=﹣x +3中令y =2,则x =1, y 1=x +3中令y =2,则x =﹣1, ∴m 的最大值为1,m 的最小值为﹣1.则m 的最大值与最小值之差为:1﹣(﹣1)=2. 故选:B .14.(2022•遵义)若一次函数y =(k +3)x ﹣1的函数值y 随x 的增大而减小,则k 值可能是( ) A .2B .23C .﹣21 D .﹣4【分析】根据一次项系数小于0时,一次函数的函数值y 随x 的增大而减小列出不等式求解即可.【解答】解:∵一次函数y =(k +3)x ﹣1的函数值y 随着x 的增大而减小, ∴k +3<0, 解得k <﹣3.所以k 的值可以是﹣4, 故选:D .15.(2022•包头)在一次函数y =﹣5ax +b (a ≠0)中,y 的值随x 值的增大而增大,且ab >0,则点A (a ,b )在( ) A .第四象限B .第三象限C .第二象限D .第一象限【分析】根据一次函数的增减性,确定自变量x 的系数﹣5a 的符号,再根据ab >0,确定b 的符号,从而确定点A (a ,b )所在的象限.【解答】解:∵在一次函数y =﹣5ax +b 中,y 随x 的增大而增大, ∴﹣5a >0,∴a <0. ∵ab >0, ∴a ,b 同号, ∴b <0.∴点A (a ,b )在第三象限. 故选:B .16.(2022•眉山)一次函数y =(2m ﹣1)x +2的值随x 的增大而增大,则点P (﹣m ,m )所在象限为( ) A .第一象限B .第二象限C .第三象限D .第四象限【分析】根据一次函数的性质求出m 的范围,再根据每个象限点的坐标特征判断P 点所处的象限即可.【解答】解:∵一次函数y =(2m ﹣1)x +2的值随x 的增大而增大, ∴2m ﹣1>0, 解得:m >,∴P (﹣m ,m )在第二象限, 故选:B .17.(2022•天津)若一次函数y =x +b (b 是常数)的图像经过第一、二、三象限,则b 的值可以是 (写出一个即可).【分析】根据一次函数的图像可知b >0即可.【解答】解:∵一次函数y =x +b (b 是常数)的图像经过第一、二、三象限, ∴b >0, 可取b =1,故答案为:1.(答案不唯一,满足b >0即可) 18.(2022•邵阳)在直角坐标系中,已知点A (23,m ),点B (27,n )是直线y =kx +b(k <0)上的两点,则m ,n 的大小关系是( ) A .m <nB .m >nC .m ≥nD .m ≤n【分析】根据k <0可知函数y 随着x 增大而减小,再根>即可比较m 和n 的大小.【解答】解:点A (,m ),点B (,n )是直线y =kx +b 上的两点,且k <0,∴一次函数y 随着x 增大而减小, ∵>,∴m <n , 故选:A .19.(2022•株洲)在平面直角坐标系中,一次函数y =5x +1的图像与y 轴的交点的坐标为( ) A .(0,﹣1)B .(﹣51,0) C .(51,0) D .(0,1)【分析】一次函数的图像与y 轴的交点的横坐标是0,当x =0时,y =1,从而得出答案. 【解答】解:∵当x =0时,y =1,∴一次函数y =5x +1的图像与y 轴的交点的坐标为(0,1), 故选:D .20.(2022•绍兴)已知(x 1,y 1),(x 2,y 2),(x 3,y 3)为直线y =﹣2x +3上的三个点,且x 1<x 2<x 3,则以下判断正确的是( ) A .若x 1x 2>0,则y 1y 3>0 B .若x 1x 3<0,则y 1y 2>0C .若x 2x 3>0,则y 1y 3>0D .若x 2x 3<0,则y 1y 2>0【分析】根据一次函数的性质和各个选项中的条件,可以判断是否正确,从而可以解答本题.【解答】解:∵直线y =﹣2x +3,∴y 随x 的增大而减小,当y =0时,x =1.5,∵(x 1,y 1),(x 2,y 2),(x 3,y 3)为直线y =﹣2x +3上的三个点,且x 1<x 2<x 3, ∴若x 1x 2>0,则x 1,x 2同号,但不能确定y 1y 3的正负,故选项A 不符合题意; 若x 1x 3<0,则x 1,x 3异号,但不能确定y 1y 2的正负,故选项B 不符合题意; 若x 2x 3>0,则x 2,x 3同号,但不能确定y 1y 3的正负,故选项C 不符合题意;若x 2x 3<0,则x 2,x 3异号,则x 1,x 2同时为负,故y 1,y 2同时为正,故y 1y 2>0,故选项D 符合题意; 故选:D .21.(2022•盘锦)点A (x 1,y 1),B (x 2,y 2)在一次函数y =(a ﹣2)x +1的图像上,当x 1>x 2时,y 1<y 2,则a 的取值范围是 . 【分析】根据一次函数的性质,建立不等式计算即可.【解答】解:∵当x1>x2时,y1<y2,∴a﹣2<0,∴a<2,故答案为:a<2.22.(2022•永州)已知一次函数y=x+1的图像经过点(m,2),则m=.【分析】由一次函数y=x+1的图像经过点(m,2),利用一次函数图像上点的坐标特征可得出2=m+1,解之即可求出m的值.【解答】解:∵一次函数y=x+1的图像经过点(m,2),∴2=m+1,∴m=1.故答案为:1.。
2011年全国中考数学模拟汇编15一次函数(正比例函数)的图像与性质(2份)
第15题图16.一次函数的应用A 组一 选择题1. (2011杭州市余杭中考模拟) 某饮料公司的饮料车间先将散装饮料灌装成瓶装饮料,再将瓶装饮料装箱出车间,该车 间有灌装、装箱生产线共26条, 每条灌装、装箱生产线的生产流量分别如图1、2所示. 某日8:00~11:00,车间内的生产线全部投入生产,图3表示该时段内未装箱的瓶装饮料存量变化情况,则灌装生产线有 条.【答案】 142. (2011浙江新昌县模拟)连降6天大雨,某水库的蓄水量随时间的增加而直线上升.若该水库的蓄水量V (万米3)与降雨的时间t (天)的关系如图 所示,则下列说法正确的是A.降雨后,蓄水量每天减少5万米3B.降雨后,蓄水量每天增加5万米3C.降雨开始时,蓄水量为20万米3D.降雨第6天,蓄水量增加40万米3 【答案】B二 填空题1.(2011浙江舟山市模拟)小高从家门口骑车去单位上班,先走平路到达点A ,再走上坡路到达点B ,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是 ▲ 分钟。
【答案】 15分钟2.(南京市江宁区2011年中考一模)中国已经进入一个老龄化社会,“老人”是一个模糊概念,•有人想用“老人系数”来表示一个人的老年化程度,其中一个人的“老人系数”与年龄的关系如图所(第15题)t/天V/万米350403020165432100第6题图老人系数示,按照这样的规定,一个年龄为70岁的人,他的“老人系数”为▲ .答案:0.5三解答题1. (2011杭州市进化一中模拟)(本小题满分10分)甲乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留一小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为60km/h,两车间距离y(km)与乙车行驶时间x(h)之间的函数图象如下.(1)将图中()填上适当的值,并求甲车从A到B的速度.(2)求从甲车返回到与乙车相遇过程中y与x的函数关系式,自变量取值范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011中考总复习数学教材过关训练:一次函数
一、填空题
1.函数y=42x中,自变量x的取值范围是__________________.
答案:x≠4
提示:要使分式有意义,则分母不等于0,即x-4≠0.
2.一次函数y=kx+b,当k<0时,y随x的增大而__________________.
答案:减小
提示:根据一次函数的性质,k<0时,y随x的增大而减小.
3.若正比例函数的图象经过点(2,-3),则其图象经过第____________象限.
答案:二、四
提示:k=-23<0,y随x的增大而减小,过原点,过第二、四象限.
4.若函数y=kx-1的图象经过点(-1,5),则k的值是___________________.
答案:-6
提示:图象经过点(-1,5),即将x=-1时,y=5代入.
5.△ABC中,∠B=∠A=α,则∠C与α的关系式为______________.
答案:∠C=180°-2α
提示:三角形内角和定理.
6.(2010黑龙江中考)点A为直线y=-2x+2上的一点,点A到两坐标轴的距离相等,则点A的坐标为
______________.
答案:(2,-2)或(32,32)
提示:点A到两坐标轴的距离相等,即|y|=|x|,可转化成y=-x或y=x,则有-x=-2x+2或x=-2x+2,解得x=2
或x=32.
二、选择题
7.函数y=3x中,自变量x的取值范围是
A.x>3 B.x≥3
C.x>-3 D.x≥-3
答案:B
提示:要使根式有意义,则被开方数大于或等于0.
8.已知函数y=kx,且k<0,图象过点(-1,y1)、(-2,y2),则y1与y2的大小关系为
A.y1=y2 B.y1
C.y1>y2 D.无法确定
答案:B
提示:k<0,y随x的增大而减小.-1>-2,则y1<y2.
9.(2010江苏苏州中考)已知一次函数y=kx-k,若y随x的增大而减小,则该函数的图象经过___________象限.
A.一、二、三 B.一、二、四
C.二、三、四 D.一、三、四
答案:B
提示:y随x的增大而减小,则k<0,自左向右呈下降趋势,b=-k>0,图象交y轴于正半轴,因此直线
经过一、二、四象限.
10.(2010江苏苏州中考)将直线y=2x向上平移两个单位,所得直线是
A.y=2x+2 B.y=2x-2 C.y=2(x-2) D.y=2(x+2)
答案:A
提示:直线y=2x向上平移两个单位,即横坐标相同,纵坐标+2,y=2x+2.
三、解答题
11.已知一次函数的图象经过点(1,-4)和点(2,5),
(1)求一次函数的关系式;
(2)画出函数图象.
(1)答案:y=9x-13;
提示:已知两点求关系式用待定系数法,可先设y=kx+b,当x=1时y=-4,x=2时y=5.代入转化成方程组
k+b=-4,2k+b=5,解得k=9,b=-13.
(2)
12.在某地,人们发现某种蟋蟀1分钟所叫次数与当地温度之间近似为一次函数关系.下面是蟋蟀所叫次数与
温度变化情况对照表:
蟋蟀所叫次数 … 84 98 119 …
温度(℃) …
15 17 20
…
(1)根据表中数据确定该一次函数的关系式;
(2)如果蟋蟀1分钟叫了57次,那么该地当时的温度大约为多少摄氏度?
(1)答案:y=7x-21.
提示:用待定系数法,是一次函数可设y=kx+b,当y=84时,x=15;y=119时,x=20.代入转化成方程组
15k+b=84,20k+b=119,解得k=7,b=-21.
(2)答案:温度大约是11摄氏度.
提示:当y=57时,代入函数式求出x≈11.
13.某公司在甲、乙两座仓库分别有农用车12辆和6辆,现需要调往A县10辆,调往B县8辆,已知从甲座仓
库调运1辆农用车到A县和B县运费分别为40元和80元,从乙仓库调运一辆农用车到A县和B县费用为
30元和50元.设从乙仓库调往A县农用车x辆,
(1)求总运费y关于x的函数关系.
(2)要求总运费不超过900元,共有几种调运方案?选出总运费最低的调运方案,最低运费是多少元?
(1)答案:y=20x+860.
提示:从乙仓库调往A县农用车x辆,则乙仓库调往B县农用车(6-x)辆,甲仓库调往A县农用车(10-x)
辆,甲仓库调往B县农用车12-(10-x)辆,即x+2辆,所需总运费y=30x+50(6-x)+ 40(10-x)+80(x+2)=20x+860.
(2)答案:20x+860≤900,解得0≤x≤2,有三种方案,当x=0时,运费最低,最低运费为860元.
提示:这里y随x的增大而增大,即x越大,y越大,x越小,y越小,当x取最小值时,运费最低.
14.某图书超市开展两种方式的租书业务:
一种是使用会员卡(需交卡钱),另一种是使用租书卡(不交卡钱).使用这两种卡租书,租书费用y(元)与租书时
间x(天)之间的关系如图所示(租书费用=卡钱+租金).根据图8-1所提供的信息回答下列问题:
图8-1
(1)根据实际情境,找出图象存在的问题.
(2)L1、L2分别表示哪种租书业务的图象?
(3)两种租书方式每天租书的收费分别是多少元?
(4)分别写出用租书卡和会员卡租书的费用y(元)与租书时间x(天)之间的函数关系式.
(5)若两种租书卡的使用期限均为一年,则在这一年中如何选取这两种租书方式比较划算?
(1)答案:实际问题中图象只取第一象限内及坐标轴的射线L1、L2.
提示:注意数学问题与实际问题的不同和数学解释实际问题的合理性.
(2)答案:L1、L2分别表示使用租书卡,使用会员卡.
提示:租书卡不交卡钱,图象经过原点.
(3)答案:使用租书卡每天收费0.5元,使用会员卡每天收费0.3元.
提示:使用租书卡每天收费50÷100=0.5,使用会员卡每天收费(50-20)÷100=0.3.
(4)答案:L1:y=0.5x,L2:y=0.3x+20.
提示:使用租书卡每天收费0.5元,x天费用为0.5x;使用会员卡每天收费0.3元,x天费用为0.3x,再加
卡费20元.
(5)答案:100天以内用租书卡划算,100天以外用会员卡划算.
提示:当y1=y2时,x=100,即使用100天两种卡都一样;100天以内租书卡的图象在会员卡下面,说明用租
书卡便宜;100天以外会员卡的图象在租书卡的下面,说明会员卡划算.
