九年级数学一元二次方程(带答案解析)
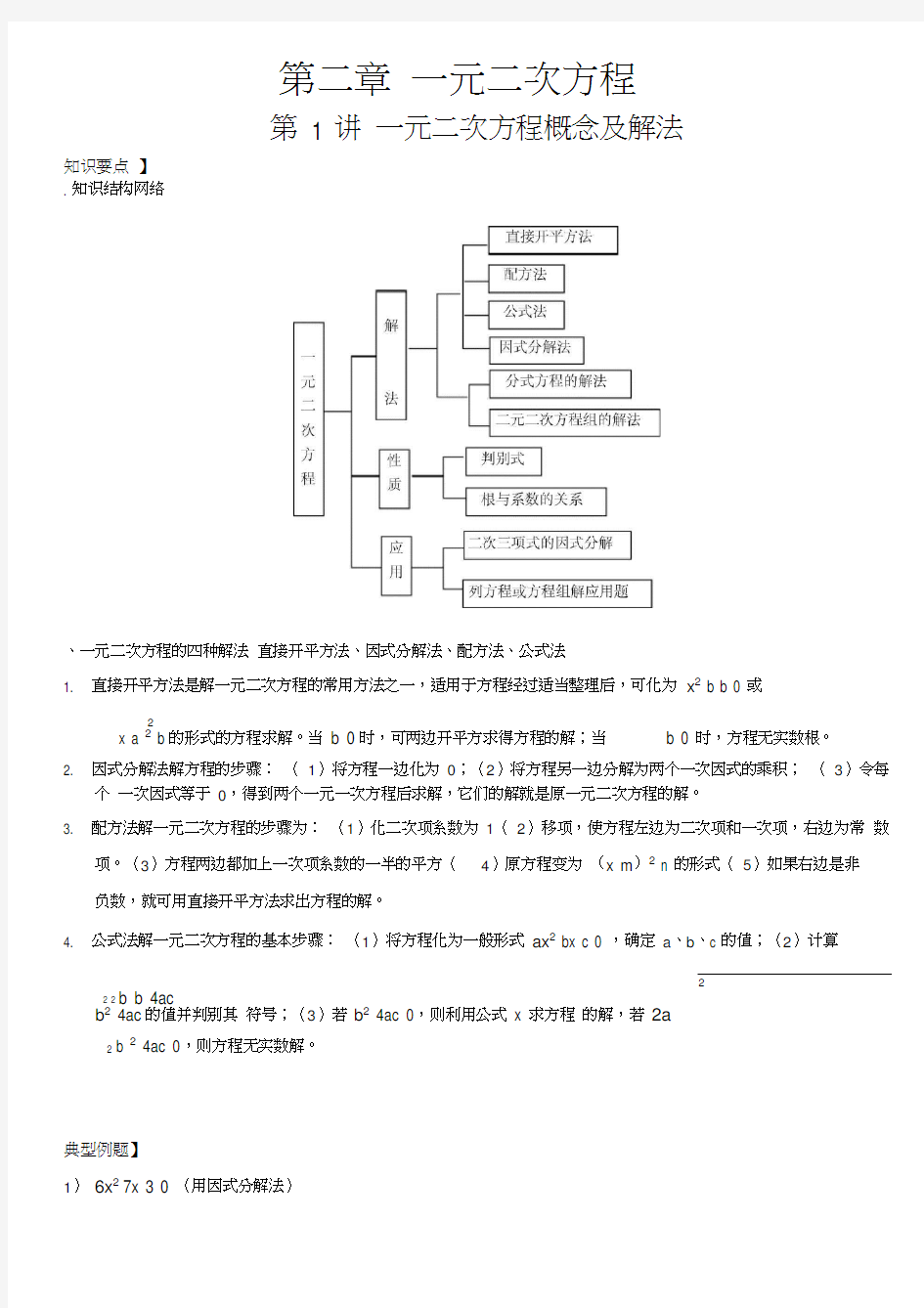

第二章一元二次方程
第 1 讲一元二次方程概念及解法
知识要点】
. 知识结构网络
、一元二次方程的四种解法直接开平方法、因式分解法、配方法、公式法
1. 直接开平方法是解一元二次方程的常用方法之一,适用于方程经过适当整理后,可化为x2 b b 0 或
2
x a 2 b的形式的方程求解。当b 0时,可两边开平方求得方程的解;当 b 0 时,方程无实数根。
2. 因式分解法解方程的步骤:(1)将方程一边化为0;(2)将方程另一边分解为两个一次因式的乘积;(3)令每
个一次因式等于0,得到两个一元一次方程后求解,它们的解就是原一元二次方程的解。
3. 配方法解一元二次方程的步骤为:(1)化二次项系数为1(2)移项,使方程左边为二次项和一次项,右边为常数
项。(3)方程两边都加上一次项系数的一半的平方(4)原方程变为(x m)2 n 的形式(5)如果右边是非负数,就可用直接开平方法求出方程的解。
4. 公式法解一元二次方程的基本步骤:(1)将方程化为一般形式ax2 bx c 0 ,确定a、b、c 的值;(2)计算
2
2 2 b b 4ac
b2 4ac的值并判别其符号;(3)若b2 4ac 0,则利用公式x 求方程的解,若2a
b 2 4a
c 0,则方程无实数解。
2
典型例题】
1)6x27x 3 0 (用因式分解法)
30
解:(3x 1)( 2x 3) 0
,x 2
经典练习】
、直接开方法
二、配方法注: (1) 2x 2
2x 30 0
二、公式法
1. 用求根公式法解下列方程
2
(1)x 2 2x 2 0;
∴ 3x 1 0或 2x
2)3x 2
4x 1(用公式
法)
解: 3x 2
4x 4)2
3×(
1) 28 0
x 1
3) 2x 2 解: x 2 x 2 (x ∴x ∴ x 1
28 2 × 3
( 4)
27
3 ,x 2
2x 30
27
3
用配方法)
2 x
2 22
4) 3 2,
15 ( 42
) 2
4
121 8
11 4
15
( 42
)2
x 2 5
2 2
1) (x 1)2 (1 2x)2
2)(x
a ) 2 b
x 1
2 2) 3x 2
4x 1
解:
2
(2) 2y2 8y 1 0 ;
解:
21
(3) 2x2 3x 0 ;
8
解:
(4) 3y2 2y 1;
解:
(5) 2x2 5x 1 0;
解:
2
(6) x2 2 5x 3 0 ;
解:
2
(7) 3x2 4x 5 0 ;
解:(7) 方程无实数根;
(8) 2x2 4 3x 2 2 0 ;
解:
2
(9) 0.02x2 0.03x 0.35;
解:(9) 先在方程两边同乘以100,化为整数系数,再代入求根公式,
(10) (1 2 3)x x2 3(1 3)
解:。
三、因式分解
1. 用因式分解法解下列各方程:
2
(1)x2-5x-24=0;
解:;
(2)12x2+x-6=0;
解:;
2
(3)x2-4x-165=0
解:;
2
(4)2x2-23x+56=0;
解:(2x 7)(x 8) 0,x1 7,x2 8;
2
(5)9x224x 16 4x 12;
解:
(6)3(x 3) 3(3 x)2;
解:
(7)x2( 3 2)x 6 0 解:;
(8)(x 2)2 5x 10 6;
2
解:(x -2)2-5(x -2)+6=0,(x-2-2)(x -2-3)=0,x1=4,x2=5;(9)t(t +3)=28;
2
解:(9)t2+3t -28=0,(t +7)(t -4)=0,t1=-7,t2=4;(10)(x +1)(x +3)=15。
2 解:x
+4x+3=15,(x +6)(x -2)=0,x1=-6,x2=2
2. 用因式分解法解下列方程:
2
(1)(y-1)2+2y(y -1)=0;解:;
22
(2)(3x+2)2=4(x -3)2;
解:[( 3x 2) 2(x 3)][(3x2)2(x3)] 0
(5x4)( x 8) 0,x 14
5,
x28
(3)
22
9(2x +3) 2-4(2x -5)2=0;
解:[3(2x +3) +2(2x -5)][3(2x+3)
-
2(2x-5)]=0,
(10x 1)( 2x 19) 0,x11
10
,
x219
2
(4)
2
(2y +1) 2+3(2y +1)+2=0。
解:[(2y +1) +1][(2y +1)+2]
=
0,
三、综合练习
1. 下列方程中,有两个相等实数根的方程是( B )
A. 7x 2-x-1=0
B. 9x 2=4(3x -1)
C.
2
x 2 7x 15 0
3 2 2 D. x x 1 0 22
2. 若 a ,b ,c 互不相等,则方程 (a + b + c )x +2(a + b + c )x + 3= 0( C ) A. 有两个相等的实数根 B. 有两个不相等的实数根 C.
没有实数根
D. 根的情况不确定
解析:
2
因为△= 4(a + b +222
12(a 2+ b 2+ c 2
) 2 2 2
=4( -2a 2-2b 2-2c 2+2ab +2ac +2bc )
222
=- 4[(a -b ) +(b -c ) +(c -a ) ] <0
3. 若方程 m 2x 2 (2m 3)x 1 0的两个实根的倒数和是 S ,求: S 的取值围。
S 3
2
3
S 且S ≠ 3 。
2
4. 已知关于 x 的方程 x 2+(2m +1)x + (m - 2) 2= 0。 m 取什么值时, (1)方程有两个不相等的实数根?
(2)方程有两个相等的实数根? (3)方程没有实数根?
解析: △= (2m +1)2-4(m -2) 2=5(4m -3) 。
(1)当 ,即 时,原方程有两个不相等的实数根; ( 2)当 时,原方程有两个相等的实数根; (3)当
时,原方程没有实数根。
5. 已知关于 x 的方程 x 2 2(k 1)x k 2 2k 1 0 ①
(1)求证:对于任意实数 k ,方程①总有两个不相等的实数根。
实数根。
分析: 本题是二次方程与不等式的综合题,即利用方程有两个实根, 表示 m ,借助 m 的取值围就可求出 S 的取值围。
2m 3
解: 设方程的两个实根为 x 1,x 2,
则x 1
x 2
, x x
2 , 1 2 m
∵方程有两个实根
∴ (2m 3)2
4m 2
且
m
2
≠0
∴ m 3
且 m ≠ 0 4
2m 3
11
∵S
x 1
x 2
x 1 x m 2
2m 3
x 1x 2
1
0 ,求出 m 的取值围,再用 S 的代数
式
1
2
m
S 3
2
3
4且
≠0
2)如果 a 是关于 y 的方程 y 2 (x 1
x 2 2k )y (x 1 k )(x 2 k )
0 ②的根, 其中 x 1,x 2 为方程①的两个
2
m
2
求:代数式 (1
a
)÷ 4
· a 1
的值。 a a 1 a 1 a
分析: 第( 1 )题直接运用根的判别式即可得到结论,第( 2 )题首先利用根与系数关系可将方程②化成
2
2 2
y 2 2y 1 0,再利用根的定义得到 a 2
2a 1,将代数式化简后,把 a 2 2a 1整体代入即可求出代数
式的值。
(1)证明:
2 2 2 2
∵ 4(k 1)2 4(k 2 2k 1) 4k 2 8k 4 4k 2 8k 4 8 0
∴对于任意实数 k ,方程①总有两个不相等的实数根。
3与
a 2,c 2 时, m 4 是否成立,并说明理由;
∴ x 1 x 2 2(k 1),x 1x 2
k 2
2k 1
∴ x 1 x 2 2k
2(k 1)
2k
2
(x 1 k )( x 2
k ) x 1x 2
k ( x 1
x 2) k 2
k 2 2k
1 2k (k
1) k
2
1
∴方程② 为 y 2 2y 1 0
∵a 是方程②的根,
2
∴ a 2a
1 0
∴ a ≠ 0, a 2
1 ≠ 0,a 2
2a 1
1a ÷
4 ·a 2 1
∴ ( )
a a 1 a 1a
2
a 1 a 2
a 1·a 2 1
(a
1 a
2 )( a 2
1) a (a 1) · 4 ·
a
4a 2
[a 1 (2a
1)]( 2a 1
1) ( a ·) 2a
1
4a 2
4a 2
2
2)解: ∵x 1,x 2是方程①的两个实数
根
注: 第( 2)问中的整体代换在恒等变形中有广泛的应用。
6. 已知关于 x 的一元二次方程 ax 2
解: (1)
当a
1,c 3时,原方程化为 x 2 2x 3
0,则 x 1
1,x 2
3
∴
m
[1 (
3)] 2 16 4
即m 4成立
当a 2,c
2
时,
原方程化为 2x 2 4x
20
由
42
4 × 2 ×
2 0 ,可设方程的两根分别为 x 1,x 2
则
x 1
2
x 2
2
,
x 1x 2
2)若对于任意一个非零的实
数 a ,
m
4 总成立,数 c 及 m 的
值。
2ax c 0 的两个实数根之差的平方为 m 1)试分别判断当 a 1, c
2
1.关于x的一元二次方程(a c)x 2 bx ac
0有两个相等的实数根,那么以a、b、c 为三边长的三角形是
∴m
22
(x1 x2 ) (x1 x2) 4x1x2 4 2 2 4
即m4不成立
(2
)
设原方程两个实数根是x1,x2
则x1
c x 2 2,x 1x2
a
m (x1 x 2)2 (x1x2)2 4x1x 24 4c a
∵对于任意一个非零的实数
4c
a,都有4
a
4
∴ c 0
当c 0时,4a20
∴ c 0,m 4
第 2 讲根的判别式
【知识要点】
1. 根的判别式:
关于x 的一元二次方程ax2bx c 0(a≠ 0)
b24ac
当0 时,方程有两个不相等的实根
当0 时,方程有两个相等的实根
当0 时,方程无实根
【典型例题】
1. a ,b,c 是三角形的三条边,
求证:关于x 的方程b2x2+(b 2+ c 2-a2)x +c2=0 没有实数根
分析:此题需证出△< 0。已知条件中a,b,c 是三角形的三边,所以有a>0,b> 0,c>0。还应注意有一个隐含关系“任意两边之和大于第三边” ,“任意两边之差小于第三边” 。
证明:因为△=(b2+c2-a2)2-4b2c2
2 2 2 2 2 2
=[(b 2+ c 2-a2)+2bc][(b 2+c2-a2)-2bc]
2 2 2 2
=[(b +c)2-a2][(b -c)2-a2]
=(b +c +a)(b +c-a)(b - c +a)(b -c-a)。
(要判断这个乘积是不是负的,应审查每个因式的正、负)
因为b+c>a,即b+c-a>0,
同理b-c+a> 0,又c+a>b,即b-c-a< 0。
又a+b+c>0,所以△=(b +c+a)(b +c-a)(b - c +a)(b -c-a)<0。所以,原方程没有实数根。
经典习题】
4
()
A. 以 a 为斜边的直角三角形
B. 以 c 为斜边的直角三角形
C. 以 b 为底边的等腰三角形
D.
以 c 为底边的等腰三角形
1
2. 已知关于 x 的一元二次方程 x 2 (k 1)x k 2 1 0
4
(1)k 取什么值时,方程有两个实数根。 (2)如果方程的两个实数根 x 1,x 2满足 |x 1| x 2,求 k 的值。 解:(1)
[ (k 1)] 2 4( 1
k 2 1) 2k 3 0
4
33
解得 k ,∴ 当 k
时,方程有两个实数根
22
(2)∵| x 1 | x 2 ,分两种情况
0,∴
由根与系数关系,
∴k
∴ (x 1 x 2)2
2
x 1x 2
11
[ (2k
1)] 2 2(k 2
2) 11 4k 2 4k 1
2k 2
4
11
2k 2
4k
6 0
k 2
2k 3 0
(k
3)( k 1) 0
11
2
x 12
2
x
22 ①当 x 1
0时,得 x 1 x 2 ,∴方程有两个相等的实数根。
2, ②当 x
0时, x 2
x 1,∴ x 1 x 2 0
∴k
1,由(1)知k
3
, 2,
矛盾 ∴k
1舍去
3. 已知方程 x 2 (2k
1)x
k 2
2 0 的两根的平方和为 11,求 k 的值。
解: 设方程的两根为 x 1,x 2
则有 x 1
x 2
(2k
1), x 1x 2 k 2 2
4
∴ k 1
3, k 2 1 ∵
( 2k 1)2
4(k 2 2)
4k
9
∴当k 3时, 0,舍去 当k 1时, 0。 注: 用根与系数关系后,要计算判别式检验是否有实根。 4.含有绝对值的一元二次方程 (1). 方程 x|x| -8|x| -4=0 的实数根的个数是(
) A. 1 B. 2 C. 3 D. 4 解: 显然 x =0 不是方程的根。 当 x <0 时,x |x |- 8|x |-4<0。 ∴x < 0 的任何实数不可能是方程的根。 当 x >0 时,方程为 x 2- 8x -4=0。 此方程两根之积为- 4< 0,可见两根为一正一负。又因 故负根舍去。所以方程只有一个实数根。应选 A 。 2). 求方程 x 2-|2x -1| - 4=0的实数根。
1
解: 令 2x 1 0得 x
2
x >0,
显然 x 2不是方程的解
当x
1
时
, 2
方程是 x 2 (2x
1) 4
2
即x 2
2x 3 0,解得 x
3或x
1
=- 1 舍去, ∴ x =3
当x
1
时, 2
方程是 x 2 (1
2x ) 4
即x 2 2x 5 0,解得 x 1 ± 6
x
1 6 舍去,∴ x
16
故方程的实数根是 x 1 3,x 2 16
。
1
5. a , b ,c ,d 为有理数,先规定一种新的运
算:
ac
bd
ad bc ,那么 (21 x) 4x 5 =18时, x=
6. 已知 x 1,x 2 是方程 x 2 4x 19 0的两根,求代数式
3
x 1
35x 2 1 的值。
7. (, 19,10 分)已知关于 x 的一元二次方程 ax 2 bx 1 0(a
0) 有两个相等的实数
根,求
ab 2
(a
2) 2 b 2
值。
分析】由于这个方程有两个相等的实数根,因此⊿=b2 4a 0,可得出a、b 之间的关系,然后
将
ab
2 (a 2)2b24
a,
化简后,用含b 的代数式表示a,即可求出这个分式的
值.
答案】解:∵ 2 ax bx 1 0(a 0)有两个相等的实数根,
2
∴⊿=b2 4ac 0 ,即b
24a 0 .全品中考网
(a
ab
2
2) 2b24
ab
2
a
2
4a 4 b24
ab
2
2
a
4a b
2
ab
2
2
a
22
0,∴ ab22 b2 4
a
2
a
8. (中考)若关于x 的一元二次方
程
x2 2(2 k)x k 2 12 0 有实数根1)数k 的取值
围;
设t k,求t 的最小值.
3)解:(1)∵一元二次方程x
2
2(2 k)x k 2 12 0有实数根4)0,
1)求2)设
(6)解得k 2 .?????????(7)
(3
)
由根与系数的关系
得:(8)∴t
42k42
,
k k k
(9)∵k2,∴
24 k
20,(10
)442 k
2,
(11
)
即t的最小值为
-
4.
已知关于
x 的
一元二次方程x2 = 2( 1-
m
)
即4(2 k)2 4(k 2 12) 0 ,
5)
m的取值
围;
9. (中考)
x -m2的两实数根为x1,
x2.
[ 2(2 k)] 4 2k ,6分
7分
10 分
y = x1 + x2,当y 取得最小值时,求相应m的值,并求出最小
值.
答案】(1)将原方程整理为x2 + 2(m-1)x + m2 = 0 .
原方程有两个实数根,
△= [ 2 (m-1)2-4m2 =-8m + 4 ≥0,得m≤1.
2
2 2
2)∵ x1,x2为x2 + 2(m-1)x + m2 = 0 的两根,
1∴ y = x1 + x2 = -2m + 2 ,且m≤.
2 1 因而y 随m的增大而减小,故当m = 1时,取得极小值1.
2
10. (中考)关于x 的一元二次方程x2 x p 1 0有两实数根x1、x2.
(1)求p的取值围;( 4 分)
(2)若[2 x1(1 x1)][ 2 x2(1 x2)] 9,求p的值.(6分)
答案】解:( 1)由题意得:
( 1) 2 4(p 1) 0. ????2 分
5
解得:p ????4 分4
(2)由[2 x1(1 x1)][2 x2(1 x2)] 9得,
22
(2 x1x12 )( 2 x2x22) 9. ????6 分
x1,x2 是方程x2 x p 1 0的两实数根x12 x1p 1 0,x22 x2p 1 0,
22
x1 x1 p 1,x2 x2 p 1.
(2 p 1)(2 p 1) 9,即(p 1)2 9. ????8 分
p 2,或p 4. ????9 分
5
p , 所求p 的值为p 4. ????10分4
说明:1.可利用x1x21,得x11x2,
x2 1 x1 代入原求值式中求解;
11. (中考)已知关于x 的方程x2 2(k 3)x k2 4k 1 0.(1)若这个方程有实数根,求k 的取值
围;
(2)若这个方程有一个根为1,求k 的值;22
(3)若以方程x2 2(k 3)x k 2 4k 1 0的两个根为横坐标、纵坐标的点恰在反比例函数y m的图
象上,求满足条件的m的最小值.
x
【答案】解: (1)由题意得△= 2 k 3 2 4 k2 4k 1 ≥0
化简得2k 10≥0,解得k≤5.
(2)将1代入方程,整理得k2 6k 6 0 ,解这个方程得k1 3 3 ,k2 3 3.
(3)设方程x2 2(k 3)x k2 4k 1 0的两个根为x1,x2,
根据题意得m x1x2 .又由一元二次方程根与系数的关系得x1x2 k2 4k 1,
22
那么 m k 2 4k 1 k 2 2
5 ,所以,当 k =2 时 m 取得最小值- 5
a 1
解得: k
4 .················································· 7分
第 3 讲 根与系数的关系
知识要点 】 1. 根与系数关系
关于 x 的一元二次方程 ax 2
bx c 0(a ≠ 0)
当
0时,有
x 1
x 2
bc
,
x 1x 2
aa
推论 1 : 如果方程 x 2 px q 0 的两个实数根是 x 1 , x 2,那么 x 1
x 2
p,x 1x 2
q.
推论 2 : 以x 1,x 2为根的 一元
次方程(二次项系数为 1)是: x 2
(x 1
x 2 )
x x 1 x 2
典型例题】
1. 已知方程 x 2 3xm 0 的两个实根中,其中一个是另一个的 2 倍,求 m 的值。 解: 设方程的一个根
为 x ,另一根 2x
x 2x
3
1
由根系关系知
2
x
·2x m
2
2
x
1
解得: 2
m 1
12. (中考) 已知关
于
x 的一元二次方程 x 2 6x k 2 0( k 为常数).
(1)求证:方程有两个不相等的实数根;
(2)设 x 1, x 2为方程的两个实数根,且
x 1
2x 2 14 ,试求出方程的两个实数根和 k 的
值. 【答案】 解:( 1)
b 2 4a
c ( 6)2
4 1(
k 2) 36 4k 2 0,·············
···· 2 分
因此方程有两个不相等的实数根 3分 ( 2)Q x 1 b6
x 2
6 ,
2
a 1
4分
又
Q x 1 2x 2 14 ,
解方程组 x 1 x 2 6, x 1 2x 2 14,
解
得:
x
1
2,
·····················
x 2 8.
5分
方法一:将 x 1
2 代入原方程得: ( 2)2
6 ( 2) k 2 0 ,···············
· 6 分
解得: k
4 .
7分
c k
方法二:将 x 1和x 2代入 x 1x 2 ,得: 2 8 ,······················6 分
m1
2. 已知方程3x27x30的两根x1、x2 (x1 x2)不解方程,求x1x2和x12 x22的值。
2
解: 由题设条件 x 2
x 1 x 2
x 1 x 2
x 1x 2 1
2
x 1 x 2
4x
1 x
2
13
x 12 x 2
2
经典习题】 . 选择题。 1. 已知 x A. 2 , -1 2. 已知方程 A. 4 3. 若方程 A. 4. 若方程 A. C. 5. A. 6.
A. C.
x 1 x 2
x 2
7
2
3 39 3
x 1 x 2
3是关
于
3x 2
x 2
x
2
,
方程 x 2
x 1 px
px
B.
5
,
x 2 x x 2 x
2 x 1x 2
x 2
7 13
x 的一元 次方程 B. -1 , 2
4 xm 1
B. -4
B. 2p 2
k1 x 2 2kx 3
C. -2 , 1
0的两根互为相反数,
则
C. 1
D. -1
0 的一个根,则 k
D. 1 ,-2 m 的值是
(
根分别为( )
0有两负根,
则
k 的取值围是(
k0
C. k 1
4
D. 0 k 1
4
0 的两根中,只有一个是
0 ,
B. p 0, q 0
D. 不能确定
那么(
0的大根与小根之差等于
(
C. 1
为根的,且二次项系数为
B. x 2 D. x 2
D. 2p 2 1
1 的一元二次方程是
(
x1 x1
9.
7. 8.
9. 10. 11. 填空题。
关于 x 的一元二次方程
已知一元二次方程 ax 2
已知方程 x 2
mx 已知
是方程 x 2
x 2 已知 2 2
13, 1 2m
1 x m
2 0 的两根互为倒数,则 m =
bx 0 两根比 2:3,则 a ,b ,c 之间的关系
是
0的两根 x 1、x 2 ,且 x 1 2 x 2
5x 20
三 . 解答题。
2 12. 已知方程 2x 2 3x 70 的两根 13. 设 x 1、x 2 是方程 x 2 试题答案】 . 选择题。 1. A 2. B 填空题。
2 9 ,则 m
7.
的两根,不解方程可
得:
2 ,则以
11
33
为根的一元二次方程是
,求作以 2 、 2 为两根的方程。 2m 1 x m 2 0 的两个实根,且两实根的倒数和等于 3. D 4. B 5. C 3,试求 m 的
值。 6. B
22
2 m 1 4m 2 0 2 m1 1 m
2 m 1 m1
8. 设
x 1 2t , x 2 3t ,则 5t
6t 2
b
a c a
6b 2 25ac
x 1 x 2 m
1
x 1x 2 mm 4
1 2
3
x 1 2 x 2 2 9
10.
11.
m m 4 2m 5
3
m2 2m 150
5或m
5时,
由此
22
3 原方程
△<
5 25
24
185
8
1
23
8
6或
所求方程x2
三. 解答题。
13
13
5或
,
故舍
去,
25
13
33
2454 41
2
13
22
5x
12
0或2
x23x 2
3
12. 解: 由题意
7
2
2
即
22
3
9 2
22
2 2 2
5
2
2
9 7
2 2
8
故所求方程是 x 2
9
x 8 0,即 2x 2
9x 160 2
由 1 :4m 1 0
1 m
4
由
4 :x 1 x 2 3x 1x 2 2m 1 3m 2
2
3m 2
2m 1 0 m 1 3m 1 0 1 m 1 1, m 2
3
11
m 2 不符合题意, m 舍去 2
3 4 m1
第 4 讲 一元二次方程的应用
【知识要点 】
1. 列一元二次方程解实际问题的步骤:
( 1) 设:设好未知数,根据实际问题,可直接设未知数,也可间接设未知数,不要漏泄单位。 ( 2) 列:根据题意,利用所蕴含的相等关系列出一元二次方程,注意等号两边的单位要一致。 ( 3) 解:解所列的一元二次方程。
( 4) 验:检验所列方程的解是否符合实际问题情境,将不符合题意的方程的解舍去。 ( 5) 答:根据题意,写出答案。
【典型例题】
1. 某农户种植花生,原来种植的花生的亩产量为 200kg ,出油率为 50%(即每 100kg 花生可加工成花生油 50kg ),现在
2m 1 2 4m 2 0
x 1
x 2 2m 1
13. 解:
2
x 1x 2
m 1
1
3
x 1
x 2
1 2 3 4
1 种植新品种花生后,每亩收获的花生可加工成花生油132kg,其中花生出油率的增长率是亩产量的增长率的1,求:
2 新品种花生亩产量的增长率。
解:设新品种花生亩产量的增长率为x ,
1 则有200(1 x )·50%·(1 x) 132
2
解得x1 0.2,x2 3. 2(不合题意,舍去)
答:新品种花生亩产量的增长率是20%。
注:对于增长率问题,解这类问题的公式是a(1 x)n b ,其中,a是原来的量,x是平均增长率,n是增长的次数, b 为增长的量。
2. 某商场销售一批名牌衬衫,平均每天可售出20 件,每件赢利40 元,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价 1 元,商场平均每天可多售出 2 件。
求:( 1)若商场平均每天要赢利1200 元,每件衬衫应降价多少元?
( 2)每件衬衫降价多少元时,商场平均每天赢利最多?
解: ( 1)设每件衬衫应降价x 元,则有
(40x)(20 2x)1200
30x2000
2 x
解得x110,x220
根据题意,取x=20,∴每件衬衫应降低20 元。
(2)商场每天赢利
(40 x)( 20 2x)
2
800 60x 2x 2
2(x 15)21250
当x 15 时,商场赢利最多,共1250 元∴每件衬衫降价15 元时,商场平均每天获利最多。
【经典习题】
1. 一个两位数,十位数字与个位数字之和是5,把这个数的个位数字与十位数字对调位置后,所得的新两位数与原来
的两位数的乘积为736,求原来的两位数。
2.一次会议上,每两个参加会议的人都相互握了一次手,有人统计一共握了66 次手。这次会议到会的有多少人?
3.某水果批发商场经销一种高档水果,如果每千克赢利10 元,每天可售出500 千克。经市场调查发现,在进货价格
不变的情况下,若每千克涨价 1 元,日销售量将减少20 千克。现该商场要保证每天赢利6000 元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
【模拟试题】
(一)填空题
2
1. 一元二次方程(3x 2)(2x 1) 2x 2 化为一般式后, a ______________________ ,b ____________ ,c ___________
2. 若方程x2x m有两个实数根,则m的值是____________ 。
3. 关于x 的一元二次方程kx26x 1 0 有两个不相等的实数根,则k 的取值围是______________ 。
4. 关于x 的一元二次方程2x2x m 0 的一个根是1,另一个根是______________ ,m= __________ 。
5. 若x1、x2是方程2x24x 3 0的两个根,则(x1 1)(x2 1) = _____________________ 。
2 2 1 1
6. 已知两不等实数a、b 满足条件2a2 7a 1 0,2b2 7b 1 0,则 1 1_____________________________
ab
7. 已知a、b 是方程x22x 7 0的两个实数根,则a23b24b ___________________ 。
(二)解下列方程
1. (2x 1)216 0
2
2. x28x 9 0
3. (x 1)22(1 x)
4. x25x 2 0
5. x(x 7) 60
(三)解答题
2m
1. 已知关于x 的方程x 2 (m 2)x 3 0
2
①求证无论m取什么实数值,这个方程总有两个不相同的实数根
②若这个方程的两个实数根x1 、x2满足2x1 x2 m 2,求m的值
2. 已知关于x 的方程x22mx 3m 0的两个实数根是x1、x2,且(x1 x2)2 16,如果关于x 的另一个方程x22mx 6m 9 0 的两个实数根都在x1和x2之间,求m的值。
第一次课后作业
经典练习】
1. 已知x=-1 是关于x 的方程2x2 ax 3a 0 的一个根,则a=
2
2. 若方程(m1)x m 12mx3 0 是关于x 的一元二次方程,求m的值。
2
3. 若(m 1)x m2 15x 3 0是关于x 的一元二次方程,则m= 。a2b2
4. 已知a≠0,a≠b,x=1 是方程ax2 bx 10 0的一个解,则的值是
2a 2b
5. 关于x 的一元二次方程(m 2)x2 3m2x m2 4 0 有一根为0,求2m2 4m 3的值。
2008
6.已知m是方程x2 2008x 1 0 的一个不为零的根,求m2 2007m 2的值。m21
7. 已知关于x 的方程2x2 kx 1 0的一个根与方程2x 14 的根相等。
1x
(1) 求k 的值.(2) 求方程2x2 kx 1 0的另一个根.
8.已知x=1 是一元二次方程x2 mx n 0的一个根,则m2 2mn n2的值为
9.已知方程x2 bx a 0 有一个根是-a ( a≠ 0),则下列代数式的值恒为常数的是( )
A.ab B. a C.a+b D.a-b
b
第二次课后作业
1. 用配方法解方程:2x2 7x 4 0.
2. 将二次三项式2x2 4x 6进行配方,正确的结果是( )
A. 2(x 1)2 4
B. 2(x 1)2 4
C. 2(x 2)2 2
D. 2(x 2) 2 2
3. 求证:不论m取何值,2m2 4m 9 的值都不小于7.
