相控阵天线方向图推导及仿真
相控阵天线相位中心的时域全波仿真

[ ] en+1/2
=
en−1/ 2
+
Δt
M
−1 ε
C~ M−μ1bn
+
jnS
bn+1 = bn − Δt C en+1/ 2
在满足 Courant-Friedrichs-Levy (CFL)稳定
性 条 件 Δt ≤
εμ
⎜⎛ ⎝
1 Δx
⎟⎞ 2 ⎠
+
⎜⎜⎝⎛
1 Δy
⎟⎟⎠⎞ 2
+
⎜⎛ ⎝
1 Δz
⎟⎞ 2 ⎠
相控阵天线相位中心的时域全波仿真
王红丽 张敏
(同济大学 电子信息与工程学院)
摘要:采用有限积分技术对有源相控阵进行全波时域仿真,计算其相中心等远场特性。同
时,在 CST 微波工作室®中利用后处理命令对天线阵进行仿真,当天线阵在较小的角度范围
内进行扫描时,全波仿真和后处理合成所得结果都很准确。在较大的扫描角时,采用后处理
坐标变换前
坐标变换后
图 3 625 单元天线阵的 3D 方向图
对于 625 单元有源相控阵,其单元天线 的主瓣方向为+Z 方向,相位中心为(-1.04, -1.55,4.33),均方差为 1.09。当主瓣方向 旋转到 30 度位置时,坐标变换前后所得 3 维方向图如图 3 所示。而且,坐标变换前计 算 所 得 相 位 中 心 为 ( 929.70 , -315.95 , -9559.35),均方差 Sigma 的值为 27575.40, 该相位中心是以 Z 轴范围内的电场分量为基 准进行计算的,因而并不是我们需要的主瓣 范围内的相位中心。坐标变换后计算所得的 原坐标系下的相位中心为(14.31,13.32, 34.34),均方差 Sigma 的值为 11.45。可见, 在相控阵的相位中心计算过程中,坐标变换 是非常必要的,而且坐标的变换并不改变其 他的远场信息。
相控阵雷达天线方向图仿真研究

2008 年第 1 期 中国雷达 China Radar
37
图 3 d/λ = 0. 5 时的天线方向图 图 4 d/λ = 1 时的天线方向图
参考文献
[ 1 ] 张社欣 ,李文臣 ,郭新海. 密度加权相控阵天线方向图仿真 [J ] . 舰船电子对抗 ,2006 ,29 (4)
(ψ- φ) 。按等比级数求和并运用尤拉公式 ,式(1) 化简为
E (θ)
=
E
si n [
N 2
(ψ -
φ)
]
ej[
N2
1
(ψ-
φ)
]
si n [
1 2
(ψ -
φ)
]
由式 (1) 容易看出 ,当φ = ψ时 , 各分量同相相加 , 场强
幅值最大 ,其值为
| E(θ) | max = N E
场强幅值最大时的归一化方向性函数为
φ = 0 时 , 也就是各阵元等幅同相馈电时 , 由式 (2) 可 知 ,若θ = 0 ,有 F(θ) = 1 ,即方向图最大值在阵列法线 方向 。当φ ≠0 时 , 则方向图最大值方向 (波束指向) 就 要偏移 ,偏移角θ0 由移相器相移量φ决定 。θ0 =θ时 ,应 有 F(θ0 ) = 1 ,由式 (2) 可知应满足
位为基准 ,则
N- 1
∑ E(θ) = E ejk (ψ-φ)
(1)
k=0
式中 :ψ = λ2πd sinθ———由于波程差引起的相邻阵元辐
射场的相位差 ; φ———相邻阵元激励电流相位差 ; kψ———波程差引起的 Ek 对 E0 的相位引前 ; kφ———激励电流相位差引起的 Ek 对 E0 的相位迟后。 任一阵元辐射场与前一阵元辐射场之间的相位差为
有源相控阵天线结构仿真分析

第37卷第1期2020年1月机㊀㊀电㊀㊀工㊀㊀程JournalofMechanical&ElectricalEngineeringVol.37No.1Jan.2020收稿日期:2019-05-26基金项目:国家自然科学基金资助项目(51490664)作者简介:顾叶青(1979-)ꎬ男ꎬ江苏苏州人ꎬ研究员级高级工程师ꎬ主要从事有源相控阵雷达天线结构设计方面的研究ꎮE ̄mail:13913365261@139.comDOI:10.3969/j.issn.1001-4551.2020.01.011有源相控阵天线结构仿真分析∗顾叶青ꎬ孙为民ꎬ余㊀觉(南京电子技术研究所ꎬ江苏南京210039)摘要:针对当前有源相控阵天线设计过程中亟需进行合理的结构力学仿真ꎬ以确保天线的环境适应性要求㊁精度以及刚强度性能的问题ꎬ分别对天线结构力学仿真㊁有限元模型修正和结构优化分析过程进行了分析ꎮ结合舰载㊁机载㊁车载㊁星载等不同雷达天线结构的特点ꎬ阐述了未来雷达天线结构力学仿真的重点在于强冲击㊁振动疲劳㊁动态载荷等作用下的天线刚强度分析ꎬ以及天线系统功能一体化优化设计ꎻ利用两个工程设计案例ꎬ讨论了有限元模型修正以及结构尺寸优化在有源相控阵天线结构设计中的应用效果ꎮ研究结果表明:对有限元模型进行适当的修正ꎬ可显著提高相控阵天线力学仿真的精度ꎻ通过对天线结构进行尺寸优化ꎬ能够在确保天线力学性能的前提下实现轻量化ꎮ关键词:有源相控阵天线ꎻ结构力学仿真ꎻ模型修正ꎻ结构优化中图分类号:TH114ꎻO342㊀㊀㊀㊀文献标识码:A文章编号:1001-4551(2020)01-0059-05StructuresimulationfortheactivephasedarrayantennaGUYe ̄qingꎬSUNWei ̄minꎬYUJue(NanjingResearchInstituteofElectronicTechnologyꎬNanjing210039ꎬChina)Abstract:Aimingatthisproblemthatreasonablemechanicssimulationhasbeendevelopedasanessentialapproachinthedesignofstructureofactivephasedarrayantennatomeettherequirementsofenvironmentaladaptabilityꎬaccuracyandperformanceꎬtheprocessesofstructuralsimulationꎬfiniteelementmodelcorrectionꎬandstructuraloptimizationfortheantennawererespectivelyreviewed.Thestructurecharacteris ̄ticsofshipborneꎬairborneꎬvehicle ̄borneꎬspaceborneꎬandmissile ̄borneantennaswerealldiscussed.Itwaspointedoutthatthefuturefo ̄cuseslieinthemechanicalanalysesandstructurallyintegrateddesignoftheantennaunderstrongimpactꎬvibrationfatigueanddynamicload ̄ing.Twoengineeringexampleswerepresentedinordertointroducetheapplicationeffectsoffiniteelementmodelcorrectionandsizeoptimi ̄zationintheengineeringdesignoftheactivephasedarrayantenna.Theresultsindicatethatthefiniteelementmodelcorrectioncanimprovetheaccuracyofmechanicssimulationofthephasedarrayantennasignificantlyꎬandthesizeoptimizationcanhelptoachievelighterantennastructurewithequalmechanicalperformance.Keywords:activephasedarrayantennaꎻstructuralsimulationꎻmodelcorrectionꎻstructuraloptimization0㊀引㊀言随着现代信息战争需求和科技的不断发展ꎬ有源相控阵体制在可靠性㊁隐身性㊁抗干扰能力和多目标攻击能力等方面均有大幅度提升ꎬ已成为现代雷达产品的主流ꎮ有源相控阵天线已越来越多地应用于陆基㊁海基㊁空基㊁以及天基雷达中ꎮ有源相控阵天线内部安装有T/R组件㊁子阵组件㊁馈电网络㊁电源等大量电子设备ꎬ与一般反射面天线相比ꎬ其天线结构除承受风载㊁冰雪㊁自重等载荷ꎬ还必须要能够承受安装在其内部的电子设备的重量ꎮ这些设备的重量往往是天线结构自重的数倍ꎬ约占天线阵面总重的2/3ꎮ因此ꎬ这些都对天线结构的刚强度(尤其是动载荷作用下的刚强度)提出了更高的要求[1 ̄2]ꎮ由于现代有源相控阵天线结构和功能日趋复杂ꎬ成本㊁研制周期等限制条件均会对天线整体结构的试验产生制约ꎮ针对这一问题ꎬ利用以有限元理论为基础的力学仿真技术ꎬ模拟理论模型和大型试验模型已经成为主流的科研手段ꎮ本文将对有源相控阵天线的结构力学仿真㊁有限元模型修正以及结构优化分析过程进行综合评述ꎬ最后针对两个工程案例进行具体讨论ꎮ1㊀天线结构力学仿真分析1.1㊀天线结构仿真的主要内容天线结构的力学仿真计算步骤主要包括:(1)结构模型化(创建天线结构的几何模型以及划分有限元网格)ꎻ(2)施加边界条件(施加约束条件㊁施加载荷条件)ꎻ(3)设置天线结构的材料特性及定义单元属性ꎻ(4)设置分析参数并提交分析ꎻ(5)计算结果的处理等ꎮ天线结构力学仿真的类型主要有: (1)静力学仿真分析ꎮ通过常规的静力计算对天线结构的静态强度进行校核ꎻ(2)动力学仿真分析ꎮ研究时变/频变载荷对天线结构整体或部件力学性能的影响ꎬ分析过程中需考虑阻尼㊁惯性等效应的作用ꎻ(3)屈曲分析ꎮ研究天线结构在特定载荷下的稳定性ꎬ确定天线结构失稳的临界载荷等问题[3]ꎮ对各类天线结构力学性能有限元建模㊁仿真过程进行归纳ꎬ天线结构力学仿真应遵循的准则有: (1)天线结构件的取舍不应改变原有真实受力状况下的传力路径ꎻ(2)单元的选取要能够代表天线结构中相应部位的真实应力状态ꎻ(3)有限元网格的剖分应适应应力梯度的变化ꎬ以保证数值解的收敛ꎻ(4)元素的连接处理应反映节点位移的真实情况(连续或不连续)ꎻ(5)相关元素的参数选取应保证天线结构的刚度等效ꎻ(6)边界约束条件的处理应符合天线结构的真实支撑状态ꎻ(7)质量的堆聚应满足质量㊁质心㊁惯性矩及惯性积的等效要求ꎻ(8)当量阻尼计算应符合能量等价要求ꎻ(9)天线结构中载荷的简化不应跨越主要受力构件ꎮ1.2㊀典型天线结构力学仿真特点典型天线阵面力学仿真图如图1所示ꎮ不同使用环境条件下的雷达产品ꎬ其承受的环境载荷形式各不相同ꎬ进行天线结构力学仿真的侧重点也有所不同ꎬ具体如下:图1㊀典型天线阵面力学仿真(1)舰载有源相控阵天线必须要承受舰上武器系统发射㊁轮机组及水下冲击等引起的振动冲击载荷ꎮ为了避免舰载天线结构发生共振破坏ꎬ要求整个天线阵面装舰后ꎬ其固有频率避开舰体外部干扰力的频率[4]ꎮ同时ꎬ对于舰载相控阵天线ꎬ强冲击环境条件是天线仿真校核的重点ꎻ(2)由于飞机上振动工况居多ꎬ机载雷达天线结构在仿真设计中ꎬ通常要进行动力学分析ꎬ以给出产品在振动载荷作用下的加速度响应和应力响应[5]ꎮ但是ꎬ对于机载雷达天线在振动载荷作用下的疲劳破坏形式㊁破坏机理以及振动疲劳寿命评估ꎬ还需进一步重点关注ꎻ(3)对于车载高机动有源相控阵天线ꎬ在结构力学仿真过程中ꎬ通常需进行风载荷作用下的强度校核ꎮ其中ꎬ天线阵面的风压分布由经验公式获得[6]ꎬ利用有限元软件可仿真计算出天线阵面的应力分布ꎮ但是ꎬ在风载荷动态脉动以及雷达天线转动条件下ꎬ天线阵面的风压分布会发生持续变化ꎬ导致天线阵面根部支耳㊁车体撑腿等连接关键区出现应力幅ꎬ可能导致雷达系统产生结构疲劳ꎮ因此ꎬ动态风载荷仿真是未来车载天线设计校核的重点ꎮ此外ꎬ星载㊁弹载有源相控阵天线ꎬ其体积和重量往往都有严格限制ꎬ天线结构力学仿真是关键环节ꎮ通常有源相控阵天线受内部设备布局的限制ꎬ无法通06 机㊀㊀电㊀㊀工㊀㊀程第37卷过直接增加天线结构厚度的方法提高天线结构的刚强度ꎮ一个较好的解决方法是巧妙合理地利用阵面内大量的电子设备结构ꎬ通过功能结构一体化设计ꎬ将离散结构设计为连续的阵面骨架受力结构ꎬ从而减轻重量ꎬ增加天线阵面整体或局部的刚强度[7]ꎮ可利用的电功能件包括T/R组件㊁电源组件㊁子阵㊁射频馈线网络㊁走线层等ꎻ结构功能件包括冷却水道管网㊁各种形式的导轨结构以及各种走线支架等ꎮ通过天线系统功能结构一体化设计优化和系统仿真技术ꎬ可以减轻天线重量ꎮ2㊀天线结构有限元模型修正2.1㊀模型修正基本理论在对天线结构进行有限元建模分析的过程中ꎬ不仅要对实际天线结构系统进行离散化ꎬ还需要对天线结构的几何特征㊁边界约束条件等作力学上的等效简化ꎮ当结构的形状或受力情况复杂时ꎬ等效简化所得的仿真结果可能与实际结果存在明显差异ꎮ此外ꎬ不同的简化方式往往也会造成完全不同的仿真结果ꎮ因此ꎬ为了提高有限元仿真的精度ꎬ增强仿真结果与真实结果的逼近程度ꎬ有必要对有限元模型进行修正分析[8]ꎮ有限元模型修正是以实际结构试验或工作的响应为目标ꎬ以有限元模型的各种力学特征为修正对象ꎬ以合理的修正理论及修正算法为基础和手段ꎬ以一定的收敛准则为判别标准的系统工程ꎮ有限元模型的物理和力学特征主要包括材料参数㊁连接方式㊁加载方式㊁边界条件和阻尼模式等ꎮ有限元模型修正理论包括有限元误差理论㊁修正变量及其敏感度分析理论ꎬ以及目标函数构建方法ꎮ误差是有限元模型修正的前提ꎬ其主要包括3类: (1)对连续的工程结构进行离散化ꎬ可产生阶次误差ꎬ其随着阶次提高而降低ꎻ(2)建模过程中ꎬ对实际结构进行简化所产生的结构误差ꎮ例如ꎬ在有限元模型中ꎬ忽略圆角导致模型的质量㊁刚度矩阵与实际存在差异ꎻ(3)对非线性的材料属性或边界条件进行常量化或线性化ꎬ导致参数误差[9]ꎮ为了减小误差ꎬ通常选取结构的设计参数ꎬ如密度㊁弹性模量㊁截面积㊁惯性矩等作为修正变量ꎬ对有限元模型进行改进ꎮ在修正过程中ꎬ预先对修正变量进行敏感度分析ꎬ遴选出对结构响应影响较为关键的变量ꎬ可减小计算分析的工作量ꎮ假设结构的响应输出F满足:F=f(p)ꎬp=[p1ꎬp2 pn](1)式中:p n个设计参数组成的向量矩阵ꎻp0 设计参数的初始设计值ꎮ则设计参数对输出响应的敏感度系数矩阵为:S=∂f∂pp=p0(2)目标函数是描述有限元模型静动特性与试验模型相应特性相关程度的表达式ꎮ有限元模型修正的目标ꎬ就是通过对修正变量进行设计改进ꎬ从而使目标函数的值趋于最小ꎬ实现有限元模型与试验模型的响应吻合ꎮ有限元模型修正流程图如图2所示ꎮ图2㊀有限元模型修正流程图2.2㊀模型修正案例某星载天线子阵面结构如图3所示ꎮ图3㊀某星载天线子阵面结构其尺寸为700mmˑ400mmˑ60mmꎬ主要由辐射单元层㊁复合材料框架层和有源模块层组成ꎮ其中ꎬ复材框架层为天线主受力构件ꎬ辐射单元与有源模块分别安装于框架两侧ꎮ天线子阵面的安装边界条件为左右对称ꎬ共10个螺栓连接点ꎮ为了确保天线电性能的实现ꎬ本文对阵面结构在动态载荷下的刚强度进行仿真ꎮ利用Hypermesh软件ꎬ建立子阵面有限元模型(图3)ꎮ复合材料蜂窝夹芯板采用壳单元建立ꎬ芯层采用体单元和壳单元共同建立ꎮ蜂窝板和天线单元间有电路板ꎬ采用体单元建立ꎮ安装于蜂窝板上的有源模块ꎬ采用壳单元建立ꎮ利用PATRAN和NASTRAN软件ꎬ对结构进行z方向的频响分析ꎬ并依次记录下激振频率分别为10Hz㊁20Hz 80Hz条件下ꎬ结构上某测点的加速度响应值ꎮ进一步ꎬ笔者在子阵面冲击试验台中ꎬ利用加速度传感器ꎬ实测激振频率在10Hz~80Hz条件下该测点的加速度响应ꎮ测点加速度仿真值与试验值对比如表1所示ꎮ16第1期顾叶青ꎬ等:有源相控阵天线结构仿真分析表1㊀测点加速度仿真值与试验值对比频率/Hz加速度试验值/(mm s-2)加速度仿真值/(mm s-2)模型修正前模型修正后相对偏差/(%)模型修正前模型修正后1041227.2841181.6641227.650.1110.0012062455.7162170.6962457.950.4560.00430169161.17167326.2169174.401.0850.00840191229.77187209.8191255.102.1020.01350229134.98220555.8229178.303.7440.01960300961.44281107.9301028.206.5970.02270472897.19413869.5472963.8012.4820.014801174143.38867267.31173886.0026.1360.022㊀㊀从表1可以看出:仿真与试验测试结果之间存在较为明显的差异ꎬ且随着激励频率的提高ꎬ仿真值与试验值的差距急剧增大ꎬ两者之间的相对偏差最大达到26.136%ꎮ为了提高有限元仿真的精度ꎬ本文对有限元模型进行修正ꎮ定义有限元模型修正的目标函数为ꎬ仿真及试验结果在各个频率点下测点加速度的均方差ꎮ实际分析中ꎬ共选取8个测点ꎬ目标函数如下:Y=18ð8i=11jð8j=1aeiꎬj-asiꎬjaeiꎬjæèçöø÷2ð8j=11j(3)式中:i 测点编号ꎻj 频率点编号ꎻaeiꎬj 测点i在j频率下的加速度试验值ꎻasiꎬj 测点i在j频率下的加速度仿真值ꎮ通过分析ꎬ本文选取了蜂窝材料属性ꎬ以及螺栓刚度分量等81个参数作为初始修正变量ꎮ进一步ꎬ在敏感度分析的基础上ꎬ将修正变量的个数缩减到35个ꎮ被忽略的变量主要包括螺栓的侧向抗压刚度㊁抗弯刚度以及剪切刚度ꎮ将修正后的模型再次进行运算ꎬ可得到测点在不同激励频率下的加速度响应(如表1所示)ꎮ显然ꎬ此时修正模型与试验模型的响应效果吻合度非常好ꎬ仿真值与试验值的相对偏差最大不超过0.022%ꎮ可见ꎬ相比模型修正前ꎬ有限元仿真的精度提升达1188倍ꎮ3㊀天线结构优化分析3.1㊀结构优化基本理论理想的雷达天线结构设计ꎬ需满足刚强度指标ꎬ符合结构轻薄化㊁成本低廉㊁可靠性好等优点ꎮ随着有限元法和数学规划理论的发展ꎬ使人们不仅有了强大的结构分析工具软件ꎬ还有了一套系统的优化设计方法[10]ꎮ从设计对象和变量的特点来看ꎬ结构优化设计可分为3个层次:(1)尺寸优化ꎮ是在确定的形状下ꎬ对构件的截面㊁性质等进行优化ꎬ其设计变量通常为截面尺寸㊁截面积㊁惯性矩等ꎻ(2)形状优化ꎮ主要用来确定结构的边界或内部的几何形状ꎬ达到改善结构的受力状况和应力分布ꎬ降低局部区域应力集中的目的ꎻ(3)拓扑优化ꎮ一般旨在寻求结构刚度在设计空间最佳的分布形式ꎬ或结构最佳的传力形式ꎮ工程中的大多数优化问题属于带约束条件的非线性数学规划问题ꎮ非线性规划问题的求解方法大致分为3类:(1)可行方向法ꎮ从可行点出发ꎬ每次迭代都沿着下降的方向进行搜索ꎬ从而求出目标函数值下降的新可行点ꎻ(2)罚函数法ꎮ根据约束函数和目标函数ꎬ构造具有惩罚效果的目标函数序列ꎬ从而将约束问题转化为无约束问题ꎬ逐渐逼近优化问题的最优解ꎻ(3)基于序列近似的思想ꎬ可将原目标函数的求解转化为对序列子问题的优化求解ꎮ例如ꎬ对目标函数进行二次泰勒展开ꎬ并将约束条件线性化ꎬ将原非线性数学规划问题转化为二次规划问题ꎮ近年来ꎬ通过模拟生物行为或自然现象ꎬ形成了一系列具有自组织性㊁自适应性的智能优化算法ꎬ如遗传算法㊁模拟退火算法㊁蚁群算法和粒子群算法等ꎬ为求解复杂的工程优化设计问题提供了新的技术手段ꎮ3.2㊀结构优化案例本文结合某工程实例进行具体详细的说明ꎮ某天线系统骨架结构如图4所示ꎮ图4㊀某天线系统骨架结构图4中ꎬ该天线要求在保证雷达阵面精度的情况下ꎬ使天线阵面尽量实现轻量化ꎬ需要对天线结构进行26 机㊀㊀电㊀㊀工㊀㊀程第37卷尺寸优化ꎮ因此ꎬ建立该天线结构的有限元模型ꎮ优化设计的主要目标为天线舱骨架的重量ꎮ优化的约束条件为ꎬ天线阵面在25m/s风速的正风载荷作用下ꎬ不考虑结构自重ꎬ阵面最大变形量ɤ8mmꎮ定义优化模型的各个要素如下:(1)设计变量为每层天线舱骨架钢梁的截面尺寸ꎬ梁宽Wꎬ梁高H和厚度T(T=t1=t2)ꎬ截面梁有12个品种ꎬ共36个设计变量ꎬ变量的优化范围为其初始值的ʃ60%ꎻ(2)目标函数为天线舱骨架重量(Weight)ꎻ(3)设计约束条件为天线阵面在目标正风载荷作用下的最大容许变形量(8mm)ꎮ通过仿真分析ꎬ本文得到前18个敏感度影响因子如图5所示ꎮ图5㊀前18个敏感度影响因子天线阵面重量迭代优化过程如图6所示ꎮ图6㊀天线阵面重量迭代优化过程根据最终结果可知:优化后骨架重量为320tꎬ相对初始状态减重达到120tꎬ结构重量减轻了27.3%ꎬ结构优化效果显著ꎮ4㊀结束语本文对有源相控阵天线的结构力学仿真㊁有限元模型修正ꎬ以及结构优化分析过程进行了综合评述ꎻ针对不同形式的雷达产品ꎬ分别阐述了其进行力学结构仿真的特点ꎬ和需要重点关注的问题ꎮ具体有:(1)舰载雷达天线结构仿真ꎮ未来的研究重点在于强冲击环境下的力学性能校核ꎻ(2)机载天线力学仿真ꎮ需要重点关注振动载荷作用下的疲劳仿真ꎻ(3)考虑到车载天线的服役环境ꎬ其力学仿真应当主要关注动态风载荷条件下的强度校核ꎻ(4)受制于体积和重量的约束ꎬ星载和弹载雷达结构仿真未来的关注点则在于系统功能结构一体化优化设计ꎮ最后ꎬ本文针对两个工程案例进行了详细讨论ꎬ利用有限元模型修正ꎬ使某星载天线子阵面结构仿真的精度最高提升达1188倍ꎻ而通过对某地面雷达天线做尺寸优化ꎬ可使其在确保刚强度性能的条件下ꎬ结构减重达27.3%ꎮ参考文献(References):[1]㊀唐宝富ꎬ钟剑锋ꎬ顾叶青.有源相控阵雷达天线结构设计[M].西安:西安电子科技大学出版社ꎬ2016.[2]㊀杨㊀静ꎬ王志海.某车载雷达天线骨架结构优化设计[J].电子机械工程ꎬ2015ꎬ31(2):52 ̄58.[3]㊀龙㊀凯ꎬ贾长治ꎬ李宝峰.Patran2010与Nastran2010有限元分析从入门到精通[M].北京:机械工业出版社ꎬ2011.[4]㊀方㊀同ꎬ薛㊀璞.振动理论及应用[M].西安:西北工业大学出版社ꎬ1998.[5]㊀郭先松ꎬ孔令兵ꎬ刘小飞.机载预警雷达天线发展趋势及关键技术[J].现代雷达ꎬ2015ꎬ37(12):19 ̄24.[6]㊀王春圆.巨型射电望远镜风荷载特性的数值模拟研究[D].哈尔滨:哈尔滨工业大学机电工程学院ꎬ2012.[7]㊀曾天俊.军民两用雷达天线薄壁件关键制造技术路径研究[J].机电信息ꎬ2015(36):112 ̄114.[8]㊀杨玉霞ꎬ李艳钰.基于贝叶斯方法的收割机发动机盖有限元模型修正[J].农业化研究ꎬ2019(9):250 ̄260.[9]㊀张㊀欣ꎬ于㊀澜ꎬ张㊀淼.数学规划法在有限元模型修正中的应用[J].长春工程学院学报ꎬ2018ꎬ19(4):119 ̄124.[10]㊀胡㊀峰ꎬ王志海.基于优化驱动法的雷达天线结构设计与仿真优化[J].机械工程与自动化ꎬ2015(3):40 ̄42[编辑:程㊀浩]本文引用格式:顾叶青ꎬ孙为民ꎬ余㊀觉.有源相控阵天线结构仿真分析[J].机电工程ꎬ2020ꎬ37(1):59-63.GUYe ̄qingꎬSUNWei ̄minꎬYUJue.Structuresimulationfortheactivephasedarrayantenna[J].JournalofMechanical&ElectricalEngineeringꎬ2020ꎬ37(1):59-63.«机电工程»杂志:http://www.meem.com.cn36 第1期顾叶青ꎬ等:有源相控阵天线结构仿真分析。
相控阵天线的相位方向图研究

对天线的相位方向图的研究较少 [4]。在成像雷达领域,特别 是复杂模式下的雷达成像,相位方向图对高精度成像的作用 就显现出来。
网络通信与安全紫金山实验室作为江苏省市政府重点 打造的科研单位,承担着 B5G/6G 关键技术的研发工作。其 中超低成本 CMOS 工艺毫米波芯片、大规模相控阵天线设 计是重点研发方向之一。本文以一维相控阵天线为例,研 究了相控阵天线的扫描、发射波束展宽与接收波束展宽三 种天线的基本工作模式下的相位方向图。发射波束展宽采 用相位对称加权的方式实现;而接收波束展宽则通过幅度 对称加权实现。研究发现不同模式下,相控阵天线的相位 方向图规律不同,而对特别关注的主波束范围内,呈现出 不同的特性。
摘 要:文章从相控阵天线的基本理论出发,分析了相控阵天线在扫描、发射展宽、接收展宽三种情况下的相位方向图特
性。首先根据理论分析指出选择天线单元相位中心平面的几何中心作为相控阵天线相位方向图的参考基点在工程上最为合理,然
后分析了阵面在扫描以及接收幅度对称加权情况下,远场相对呈矩形波状,并且在天线的主波束范围内相位相等;而在发射相位
当波束进行扫描时,φn=0;当进行相位加权时,φn ≠ 0;an 为各辐射单元的幅相特性,若 an 均相等时,表示不进行加权; an 不相等时,进行了加权。
该函数是天线阵列远场幅度与相位特性的表征,不同的
天线单元形式具有不同的单元方向函数。对一定规模的阵列
天线,天线的波束宽度远小于天线单元的波束宽度,天线单
M/2](不失一般性,认为 M 为奇数,若 M 为偶数,则范围
为 [-(M-1)/2,(M-1)/2]),此时,远场方向性函数为:
(( ( )=
-
(( -
)) ))
天线线列阵方向图
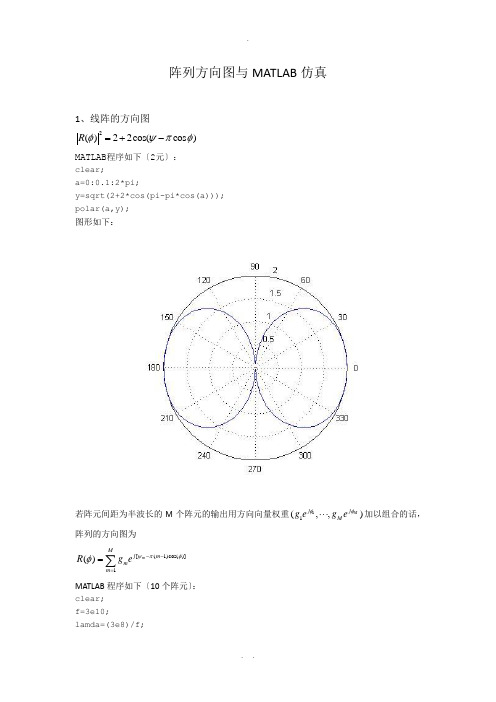
阵列方向图与MATLAB 仿真1、线阵的方向图2()22cos(cos )R φψπφ=+-MATLAB 程序如下〔2元〕:clear;a=0:0.1:2*pi;y=sqrt(2+2*cos(pi-pi*cos(a)));polar(a,y); 图形如下:若阵元间距为半波长的M 个阵元的输出用方向向量权重11(,,)M j j M g eg e φφ⋅⋅⋅加以组合的话,阵列的方向图为 [(1)cos()]1()m Mj m m m R g e ψπφφ--==∑MATLAB 程序如下〔10个阵元〕:clear;f=3e10;lamda=(3e8)/f;beta=2.*pi/lamda;n=10;t=0:0.01:2*pi;d=lamda/4;W=beta.*d.*cos(t);z1=((n/2).*W)-n/2*beta* d;z2=((1/2).*W)-1/2*beta* d;F1=sin(z1)./(n.*sin(z2));iK1=abs(F1) ;polar(t,K1);方向图如下:2、圆阵方向图程序如下:clc;clear all;close all;M = 16; % 行阵元数k = 0.8090; % k = r/lambdaDOA_theta = 90; % 方位角DOA_fi = 0; % 俯仰角% 形成方位角为theta,俯仰角位fi的波束的权值m = [0 : M-1];w = exp(-j*2*pi*k*cos(2*pi*m'/M-DOA_theta*pi/180)*cos(DOA_fi*pi/180));% w = exp(-j*2*pi*k*(cos(2*pi*m'/M)*cos(DOA_theta*pi/180)*cos(DOA_fi*pi/180)+sin(2*pi*m'/M)*si n(DOA_fi*pi/180))); % 竖直放置% w = chebwin(M, 20) .* w; % 行加切比雪夫权% 绘制水平面放置的均匀圆阵的方向图theta = linspace(0,180,360);fi = linspace(0,90,180);for i_theta = 1 : length(theta)for i_fi = 1 : length(fi)a = exp(-j*2*pi*k*cos(2*pi*m'/M-theta(i_theta)*pi/180)*cos(fi(i_fi)*pi/180));%a=exp(-j*2*pi*k*(cos(2*pi*m'/M)*cos(theta(i_theta)*pi/180)*cos(fi(i_fi)*pi/180)+sin(2*pi*m'/ M)*sin(fi(i_fi)*pi/180))); % 竖直放置Y(i_theta,i_fi) = w'*a;endendY= abs(Y); Y = Y/max(max(Y));Y = 20*log10(Y);% Y = (Y+20) .* ((Y+20)>0) - 20; % 切图Z = Y + 20;Z = Z .* (Z > 0);Y = Z - 20;figure; mesh(fi, theta, Y); view([66, 33]);title('水平放置时的均匀圆阵方向图');% title('竖面放置时的均匀圆阵方向图'); % 竖直放置axis([0 90 0 180 -20 0]);xlabel('俯仰角/(\circ)'); ylabel('方位角/(\circ)'); zlabel('P/dB');figure; contour(fi, theta, Y);方向图如下:3、平面阵方向图:clc;clear all;close all;Row_N = 16; % 行阵元数Col_N = 16; % 列阵元数k = 0.5; % k = d/lambdaDOA_theta = 90; % 方位角DOA_fi = 0; % 俯仰角% 形成方位角为theta,俯仰角位fi的波束的权值Row_n = [0 : Row_N-1]; Col_n = [0 : Col_N-1];W_Row = exp(-j*2*pi*k*Row_n'*cos(DOA_theta*pi/180)*cos(DOA_fi*pi/180)); W_Col = exp(-j*2*pi*k*Col_n'*sin(DOA_theta*pi/180)*cos(DOA_fi*pi/180)); % W_Col = exp(-j*2*pi*k*Col_n'*sin(DOA_fi*pi/180)); % 竖直放置W_Row = chebwin(Row_N, 20) .* W_Row; % 行加切比雪夫权W_Col = chebwin(Col_N, 30) .* W_Col; % 列加切比雪夫权W = kron(W_Row, W_Col); % 合成的权值N*N x 1% 绘制水平面放置的平面阵的方向图theta = linspace(0,180,180);fi = linspace(0,90,90);for i_theta = 1 : length(theta)for i_fi = 1 : length(fi)row_temp = exp(-j*2*pi*k*Row_n'*cos(theta(i_theta)*pi/180)*cos(fi(i_fi)*pi/180)); % 行导向矢量N x 1col_temp = exp(-j*2*pi*k*Col_n'*sin(theta(i_theta)*pi/180)*cos(fi(i_fi)*pi/180)); % 列导向矢量N x 1% col_temp = exp(-j*2*pi*k*Col_n'*sin(fi(i_fi)*pi/180)); % 竖直放置Y(i_theta,i_fi) = W'*kron(row_temp, col_temp); % 合成的导向矢量N*N x 1 endendY= abs(Y); Y = Y/max(max(Y));Y = 20*log10(Y);Y = (Y+60) .* ((Y+60)>0) - 60; % 切图% Z = Y + 60;% Z = Z .* (Z > 0);% Y = Z - 60;figure; mesh(fi, theta, Y); view([66, 33]);title('水平面放置时的面阵方向图');axis([0 90 0 180 -60 0]);xlabel('俯仰角/(\circ)'); ylabel('方位角(\circ)'); zlabel('P/dB');figure; contour(fi, theta, Y);方向图如下:4、CAPON方法波束形成MATLAB程序如下〔阵元16,信号源3,快拍数1024〕:clear alli=sqrt(-1);j=i;M=16;%均匀线阵列数目P=3;%信号源数目f0=10;f1=50;f2=100;%信号频率nn=1024;%快拍数angle1=-15;angle2=15;angle3=30;%the signal angleth=[angle1;angle2;angle3]';SN1=10;SN2=10;SN3=10;%信噪比sn=[SN1;SN2;SN3];degrad=pi/180;tt=0:.001:1024;x0=exp(-j*2*pi*f0*tt);%3个信号x0、x1、x2x1=exp(-j*2*pi*f1*tt); %x2=exp(-j*2*pi*f2*tt); %t=1:nn;S=[x0(t);x1(t);x2(t)];nr=randn(M,nn);ni=randn(M,nn);u=nr+j*ni;%复高斯白噪声Ps=S*S'./nn;%信号能量ps=diag(Ps);refp=2*10.^(sn/10);tmp=sqrt(refp./ps);S2=diag(tmp)*S;%加入噪声tmp=-j*pi*sin(th*degrad);tmp2=[0:M-1]';a2=tmp2*tmp;A=exp(a2);X=A*S2+.1*u;%接收到的信号Rxx=X*X'./nn;%相关矩阵invRxx=inv(Rxx);%搜寻信号th2=[-90:90]';tmp=-j*pi*sin(th2'*degrad);tmp2=[0:M-1]';a2=tmp2*tmp;A2=exp(a2);den=A2'*invRxx*A2;doa=1./den;semilogy(th2,doa,'r');title('spectrum'); xlabel('angle'); ylabel('spectrum'); axis([-90 90 1e1 1e5]); grid;。
舰载相控阵雷达建模与仿真

2 8
方位角 锥伸舟 海 明窗瘁 列天蛙方 向圉
了天象方向图和滤波误 差。
J 由于 K a l ma n滤波算法的增益系数是动态得到,
可 实 时 估 计 目标 的滤 波 信 息 和 预测 信 息 ,将 此 结果输 出。
5 o 七 ’ 。
l
. . .
.
假设 阵元数 4 0 * 4 0 ,方位和俯仰维扫描 范
围均是 ( 一 2 O 。 , 2 0 。 ) ,天线 中 心指 向 为 ( 0 。 , 0 。 ) 。 载频 f c = l e 9 Hz 。 如图 l ,分 别 加 了 矩 形 窗 和 海 明 窗 ,看 出
f p u b l i c : / / 基 本 函数
嚣 &
上进行雷达模块建模和仿真则是对实 际系统进
行部分理论 研究的有效手段 。本文使用 V i s u a l S t u d i o 2 0 0 5平 台 则 能 生 成 模 块 的 动 态 链 接 库
MO DE L( ) ;/ / 构造 函数,对 模块进
行 初 始 化 v o i d i n i t i a l ( ) ;/ / 初 始 化 函数 ,读 取 初 始 化 参 数 v o i d八 l n ( ) ; / / 运 行 函 数 ,完 成 组 件 的 运 行 工作
DL L文件 ,仿真速度快 、兼容性好 。
2 舰 载 相 控 阵模 型
.
。 f T ■ r 下 I
I l _ . 1 t 跚 f I 『 l 1 n _ _
・
1 .
h
平面相控阵天线方向图测量中的栅瓣问题仿真与分析研究

(1)
其中 f (θ , ϕ ) 称为单元天线的方向函数,即元因子,虽然天线阵中各个阵元之间存在互耦, 每个天线元的电流分布必然受到其他天线元的影响, 靠近边缘的阵元所受的影响与阵中心所 受的影响必然不同,不过,这些影响都比较小,通常认为阵中所有天线元具有相同的方向函 数,即 f (θ , ϕ ) = 1 。 F (θ , ϕ ) 称为阵因子,它与阵中各天线元的位置、激励电流幅度和相位 有关。因此,在阵列天线中,方向性主要由阵因子来决定。在平面相控阵天线中,有:
ϕ
2
3
...
N-1
N
y
x
dx
dy
图 1 矩形平面相控阵天线
N −1
对于 xoz 平面, ϕ = 0 ,于是 f ay (θ , ϕ = 0) =
M −1
∑Ae
n n =0
jnα y
为常数,平面阵因子为
f a (θ , 0) = ∑ Am e jm ( kd x sinθ +α x ) = f ax (θ )
�
(c) d x = d y = 2.5λ
图 2 扫描角度为 ±20 时 8 × 8 均匀激励面阵波束扫描方向图 由仿真结果图 2 可知,在阵元间距 d x = d y = 0.5λ、1.5λ、2.5λ 的情况下,通过控制 扫描角度,可以清晰地看到在 ±20 扫描范围内,波束唯一并且指向目标方向,并没有出现 栅瓣。 在 其 余 条 件 不 变 化 的 情 况 下 , 扩 大 扫 描 范 围 , 控 制 电 扫 描 为
1
的幅度为 I n ,步进相位为 α y ,从而形成矩形栅格的平面阵。其中第 (m, n ) 号阵元的电流幅 度为 I mn 。根据方向图乘积定理,天线阵的方向函数 D (θ , ϕ ) 可以表示成单元天线的方向函 数 f (θ , ϕ ) 和阵因子 F (θ , ϕ ) 的乘积:
理解相控阵天线的方向图

理解相控阵天线的方向图考虑一维阵列天线,由一排间隔很近的发射单元组成,每个阵元在所有方向上发射一个振幅、相位和频率相同的波。
为了测量这些波在不同方位角下的总强度,我们把一个场强探测器放在足够远的地方,使得从探测器到所有发射单元的视线几乎平行。
从阵列垂直平分线上的一个点开始,我们将场强探测器沿固定半径的弧线从阵列中心移动。
在任何一点上,场强取决于接收波的相对相位,而相对相位又取决于发射单元之间的距离差。
如果我们从阵列的一端画一条垂直于视线到探测器的直线(AB),那么这些差异就能很好地显示出来。
这条线与阵列的夹角等于探测器的方位角θ。
现在,如果θ为零,并且探测器远离阵列,则探测器到所有发射器的距离基本上是相同的。
这些波是同相位的,它们的场强叠加成一个很大的值。
但是,如果θ大于零,那么探测器到发射单元的距离就会逐渐增大。
因此,接收波的相位都略有不同,场强之和没有θ为零时那么大。
随着方位角的增大,距离差增大。
最终达到了一个点,如探测器至第一发射器(第1号)的距离与至中心发射器(第7号)距离之差为半波长。
那么,1号接收波与7号接收波相互抵消。
从2号和8号收到的波也是如此。
以此类推,从所有发射器接收到的波强度之和为零。
探测器已经到达了天线辐射强度总和为零的方位角。
如果θ进一步增加,阵列末端发射器的波将不再完全抵消,并且之和会增加。
当探测器到阵列首末两端的距离之差为1.5个波长时,会达到另一个峰值。
3到10发射单元发出的波依然对消,但两头发射器发出的波,1和2以及11和12,相加能够产生一个可观的结果。
探测器的位置位于阵列第一旁瓣的中心。
如果θ进一步增加,发生对消的部分就会增加,并且重复上述过程。
场强与方位角的关系如图所示,可由下列方程表示。
其中E是场强,x与θ成正比。
这被称为sinx/x或sinc函数。
实际上,x=π(L/λ)sinθ。
其中是波长。
所以只有当θ值比较小时,x与θ成正比。
随着θ的增加,逐渐小于θ,导致高阶旁瓣的幅度逐渐减小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相控阵天线方向推导及仿真
1、推导线阵天线方向图公式
一个接收线阵,由等间距为d 的N 个各向同性单元组成,那么在θ方向,相
邻单元接收信号的相位差为Ф=2πd
λsinθ,线阵排列情况如图1所示。
图1 线阵排列示意图
因为天线辐射方向图可以由天线上各种各样电流源辐射的单独贡献进行矢
量叠加而得出,故各单元电压和为:
E a =sin (ωt )+sin (ωt +ϕ)+sin (ωt +2ϕ)+⋯+sin[ωt +(N −1)ϕ]
将等式两边同时乘以2sin(ϕ
2),根据积化和差、和差化积等相关数学公式,可得到如下公式:
2sin (ϕ2)E a =cos (ωt −ϕ2)−cos (ωt +ϕ2)+cos (ωt +ϕ2)−cos (ωt −32
ϕ)
+⋯+cos (ωt +2N −32ϕ)−cos(ωt +2N −1
2ϕ)
整理得,2sin (ϕ
2)E a =cos (ωt −ϕ
2)−cos (ωt +
2N−12
ϕ)
=2sin(ωt +
N −12ϕ)sin(N
2
ϕ) 最终得到场强方向图,E a =sin[ωt +(N −1)ϕ2⁄]sin(Nϕ2⁄)
sin(ϕ2⁄)
平方归一化后,得到辐射方向图(阵列因子):
|G a (θ)|=sin 2[Nπ(d
λ)sinθ]
N 2sin 2[π(d
λ
)sinθ]
上式中,当(d
λ)sinθ=0,±1,±2,···±n 时|G a (θ)|取得相等的最大值,但是我们
只期望看到(d
λ)sinθ=0的情况,取其他值产生的栅瓣是我们所不想见到的,为避免这种情况,特令d <λ。
前面的公式中认定主瓣指向为0°,当主瓣指向θ0方向时,则各向同性单元
线阵的归一化辐射方向图为:
G (θ)=sin 2[Nπ(d
λ)(sinθ−sinθ0)]
N 2sin 2[π(d λ
)(sinθ−sinθ0)]
此时,由于−2≤sin (θ)−sin (θ0)≤2,故防止产生栅瓣的条件为d <λ2⁄。
当来波方向与主瓣指向相近时sinθ−sinθ0很小,有:
sin 2[π(d λ)(sinθ−sinθ0)]≈[π(d
λ
)(sinθ−sinθ0)]2
这时的辐射方向图是sin 2μμ2⁄的形式,式中μ=(d
λ)(sinθ−sinθ0),当μ=±0.443π时,天线方向图被衰减到最大值的一半,又因为sinθ−sinθ0项可以写成
sinθ−sinθ0=sin (θ−θ0)cos (θ0)−[1−cos (θ−θ0)]sin (θ−θ0)
当θ0很小时,方程右边第二项可以忽略,所以sinθ−sinθ0≈sin (θ−
θ0)cos (θ0)。
最终我们可以得到天线的半功率波束宽度为θB ≈0.886λ
Ndcosθ0
(rad )。
2、电子扫描阵列天线方向图仿真
·1、不同参数情况下的栅瓣现象及分析
由前面的分析可知,归一化后的天线方向图可以表示为:
G a (θ)=
sin 2(Nπd
λ
(sin θ−sin θ0))
N 2sin 2(πd
λ
(sin θ−sin θ0))
其中d 表示天线长度, N 表示天线阵元个数,λ表示信号波长。
当πd
λ(sin θ−sin θ0)=0,±1,±2,⋯,±n,⋯n ≥1,n ∈Z 时,G a (θ)的分子、分母均为0,由洛毕达法则可知,当sin θ−sin θ0=±n λ
d 时,G a (θ)取最大值1,其中sin θ−sin θ0=0,即θ=θ0时,是主瓣,sin θ−sin θ0=±n λ
d 的解对应的是
栅瓣。
所以为了防止栅瓣的出现,必须要求波长和天线长度满足:
d<d max=
λ
max sinθ−sinθ0
当d≥d max时,会出现栅瓣,假设栅瓣对应的角度为θg,则
sinθg−sinθ0=±n λd
即
θg=arcsin(sinθ0±n λd )
θg的具体求法参见“arcsin.m”
为了对不同参数情况下的栅瓣现象进行分析,本实验主要包括:
·1 固定θ0,λ,改变d,观察并记录栅瓣出现的位置,并对试验结果做出分析。
·2 固定d,λ,改变θ0,观察并记录栅瓣出现的位置,并对试验结果做出分析。
·3 固定θ0,d,改变λ,观察并记录栅瓣出现的位置,并对试验结果做出分析。
·4 仿真并解释频率色散与扫描限制。
1.假设θ0=0,λ=0.5,则d max=0.5,下图给出了d取不同值时的情况:
由上图可以看出,在θ0=0,λ=0.5,d max=0.5的条件下,当d<d max时,只有主瓣,没有栅瓣,是我们想要的结果;当d>d max时,出现栅瓣,且栅瓣个数随着d的增加而增加。
假设θ0=30。
,λ=0.5,则d max=0.33333,下图给出了d取不同值时的情况:
由上图可以看出,在θ0=30。
,λ=0.5,d max=0.33的条件下,当d<d max时,只有主瓣,没有栅瓣,是我们想要的结果;当d>d max时,出现栅瓣,且栅瓣个数随着d的增加而增加。
2.假设d=0.5,λ=0.5,下图给出了θ0取不同值时的情况:
由上图可以看出,在d=0.5,λ=0.5的条件下,当θ0取不同值时,d max=0.33会发生变化,进而会影响栅瓣的数量和位置。
栅瓣会随着θ0的变大而出现。
3.假设d=0.5,θ0=30°,下图给出了λ取不同值时的情况:
由上图可以看出,在d=0.5,θ0=30°的条件下,当λ取不同值时,d max= 0.33会发生变化,进而会影响栅瓣的数量和位置。
栅瓣会随着λ的变大而消失。
下表列出了在λ=0.5的条件下,不同θ0和d对应的主瓣、栅瓣角度:
由以上仿真可以知道,只有天线孔径d<d max时,才不会出现栅瓣,而d max 并不是一层不变的,它与信号频率和天线扫描角度有关。
1,2,3代码参考“AntennaPattern.m”
4.阵列天线能够工作的基础是:由于扫描方向而引入的时间误差能够被相位误差代替(窄带假设)。
之所以有上面的替代是因为电路中实现精确可变的时间延迟要比相位延迟难得多,通常电路中是通过移相器产生相位延迟,进而对接收信号进行相位补偿。
相位器与来波频率无关,即对所有频率的来波信号都会产生相同的相位延迟φ,由
φ=2πd
λ
sinθ0
可知,如果希望天线扫描θ1,按照λ1设计时,有
φ1=2πd
λ1
sinθ1
按照λ2设计时,有
φ2=2πd
λ1
sinθ1’=
2πd
λ2
sinθ1
而雷达总会有一定带宽,经过同一个移相器后,最高频f1和最低频f2就会产生一个误差θ1−θ1’。
下面分别分析θ0和∆λ的影响。
4.1 固定∆λ,d,分析θ0的影响:
由上图可以看出,随着θ0的增大,误差在不断变大。
4.2 固定θ0,d,分析∆λ的影响:
由上图可以看出,随着∆λ的增大,误差在不断变大。
4 代码参考“AntennaPattern2.m”
·2、主瓣宽度和功率增益随扫描角变化情况。
根据前面得理论分析,天线的半功率波束宽度为:
0.886cos B Nd λθθ≈ 其中,N 为天线阵元个数,d 为单元间距,0θ为扫描角度。
当0θ很大时,这个表达式是无效的,并且阵列的性能会变得很差,而且随着波束从侧射开始扫描,互藕影响也会相应增加,因此,我们在这儿讨论的时候,扫描角度被限制在60±。
在没有栅瓣的情况下(/2d λ=)进行仿真并改变0θ的值,
得到主瓣宽度和
功率增益随扫描角度变化的曲线,实验结果如下图:
从图中可以看出,实际仿真结果与理论分析结果一致,随着扫描角的增大,主瓣宽度会相应的增大,相应的后果是天线增益会随扫描角度的增大而减小。
代码参考“Effect.m ”
01020304050602530
35
40
45
天线方向图主瓣宽度随扫描角度的变化
扫描角度/°主瓣宽度/°0102030405060-16-15
-14-13
-12
天线增益随扫描角度的变化
扫描角度/°天线增益(d B )。
