学而思小学六年级奥数电子版教材
小学奥数知识点梳理【完整版】

学而思小学奥数知识点梳理学而思教材编写组 侍春雷前言小学奥数知识点梳理,对于学而思的小学奥数大纲建设尤其必要,不过,对于知识点的概括很可能出现以偏概全挂一漏万的现象,为此,本人参考了单尊主编的《小学数学奥林匹克》、中国少年报社主编的《华杯赛教材》、《华杯赛集训指南》以及学而思的《寒假班系列教材》和华罗庚学校的教材共五套教材,力图打破原有体系,重新整合划分,构建十七块体系(其第十七为解题方法汇集,可补充相应杂题),原则上简明扼要,努力刻画小学奥数知识的主树干。
概述一、 计算1. 四则混合运算繁分数⑴ 运算顺序⑵ 分数、小数混合运算技巧一般而言:① 加减运算中,能化成有限小数的统一以小数形式;② 乘除运算中,统一以分数形式。
⑶带分数与假分数的互化⑷繁分数的化简2. 简便计算⑴凑整思想⑵基准数思想⑶裂项与拆分⑷提取公因数⑸商不变性质⑹改变运算顺序① 运算定律的综合运用② 连减的性质③ 连除的性质④ 同级运算移项的性质⑤ 增减括号的性质⑥ 变式提取公因数形如:1212......(......)n n a b a b a b a a a b ÷±÷±±÷=±±±÷3. 估算求某式的整数部分:扩缩法4. 比较大小① 通分a. 通分母b. 通分子② 跟“中介”比③ 利用倒数性质 若111a b c>>,则c>b>a.。
形如:312123m m m n n n >>,则312123n n n m m m <<。
5. 定义新运算6. 特殊数列求和运用相关公式:①()21321+=++n n n ②()()612121222++=+++n n n n ③()21n a n n n n =+=+ ④()()412121222333+=++=+++n n n n ⑤131171001⨯⨯⨯=⨯=abc abc abcabc⑥()()b a b a b a -+=-22 ⑦1+2+3+4…(n-1)+n+(n-1)+…4+3+2+1=n 2二、 数论1. 奇偶性问题奇±奇=偶 奇×奇=奇奇±偶=奇 奇×偶=偶偶±偶=偶 偶×偶=偶2. 位值原则 形如:abc =100a+10b+c4. 整除性质① 如果c|a 、c|b ,那么c|(a ±b)。
学而思奥数大白本

学而思奥数大白本1. 简介学而思奥数大白本是一套专为学生学习奥林匹克数学而设计的教材。
它以培养学生的逻辑思维、创造力和问题解决能力为目标,通过系统的课程设置和丰富的习题训练,帮助学生全面提高数学素养。
2. 教材特点2.1 全面详细学而思奥数大白本涵盖了中小学阶段的各个年级,从初级到高级,内容全面且详细。
每个年级的教材都按照教育部最新课程标准进行编写,包括了必修知识和拓展内容。
无论是基础知识还是应用题,都有详细的讲解和例题演示,帮助学生理解掌握。
2.2 深入浅出教材在讲解中注重深入浅出,将抽象概念用简单易懂的方式呈现给学生。
通过具体实例、图表和逻辑推理等方法,帮助学生建立起对数学概念和原理的直观认识。
教材还提供了丰富的思维导图和彩色插图,使学习过程更加生动有趣。
2.3 强调应用能力学而思奥数大白本注重培养学生的应用能力。
教材中设计了大量的实际问题和拓展题,涉及到科学、工程、经济等不同领域。
通过解决这些问题,学生可以将所学的数学知识应用到实际生活中,提高问题解决的能力和创造性思维。
2.4 系统训练教材中提供了丰富的习题和练习册,帮助学生系统地巩固所学知识。
习题分为基础题、拓展题和综合题三个难度级别,涵盖了各个章节的重点内容。
每个章节后都有详细的答案解析,方便学生自我检测和纠正错误。
3. 教材结构3.1 年级划分学而思奥数大白本按照中小学阶段的年级进行划分,包括小学一年级到初中三年级和高中一年级到三年级。
每个年级都有相应的教材和练习册。
3.2 章节设置每个年级的教材都按照章节进行划分,每个章节涵盖了一个或多个相关的数学知识点。
教材中的内容由浅入深,逐步展开,帮助学生建立起扎实的数学基础。
3.3 习题设计每个章节后都有相应的习题和练习册。
习题分为基础题、拓展题和综合题三个难度级别,以满足不同层次学生的需求。
习题设计既注重基本技能的训练,也注重思维能力和创造力的培养。
4. 学而思奥数大白本与奥林匹克数学学而思奥数大白本作为一套专业教材,与奥林匹克数学有着密切联系。
学而思数学六年级 第2讲几何一-直线形面积练习题---答案
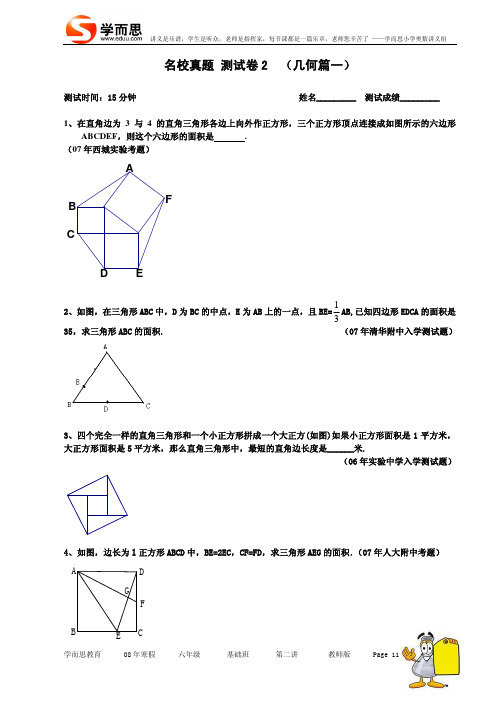
名校真题 测试卷2 (几何篇一)测试时间:15分钟 姓名_________ 测试成绩_________1、在直角边为3与4的直角三角形各边上向外作正方形,三个正方形顶点连接成如图所示的六边形ABCDEF ,则这个六边形的面积是 . (07年西城实验考题)FEDCB A2、如图,在三角形ABC 中,D 为BC 的中点,E 为AB 上的一点,且BE=13AB,已知四边形EDCA 的面积是35,求三角形ABC 的面积. (07年清华附中入学测试题)3、四个完全一样的直角三角形和一个小正方形拼成一个大正方(如图)如果小正方形面积是1平方米,大正方形面积是5平方米,那么直角三角形中,最短的直角边长度是______米.(06年实验中学入学测试题)4、如图,边长为l 正方形ABCD 中,BE=2EC,CF=FD,求三角形AEG 的面积.(07年人大附中考题)GFED CBA5、如图,长方形ABCD 中,AB=8,BC=10,E 是BA 延长线上一点,CE 交AD 于F,△AEF 比△CDF 的面积大40,求AE 的长. (07年四中分班考试题)F ED CB A附答案】 图:总面积=三个正方形+中间三角形+CD 边三角形+AB 边=32+42+52【 1. 【解】如三角形+EF 边三角形+12×3×4+12×3×4+12×3×4+12×3×4=742. 【解】根据定理:ABC BED ΔΔ=3211××=61,所以四边形ACDE 的面积就是6-1=5份,这样三角形35÷5×6=42.. 【解】小正方形面积是1平方米,大正方形面积是5平方米,所以外边四个为. 【解】连接EF.因为BE=2EC,CF=FD,所以S △DEF =(C3面积和是5-1=4,所以每个三角形的面积是1,这个图形是“弦形”,所以长直角边和短直角边差就是中间正方形的边长,所以求出短边长就是1. (请注意),先外补4个同样的小直角三角形,得到一个大正方形,其边长两直角边的和,根据两直角边的和是3(通过补完后大图的面积求得) 又根据两直角边的差是1(根据最中间的小正方形的面积求得) 所以,根据和差关系,求出长边为2, 短边为1. 421×31×21)S 正方形ABCD =121S GF ED CBA 正方形ABCD .因为S △AED =21S 正方形ABCD ,根据燕尾定理,AG:GF=21:121=6,所以S △AGE =6S △GEF =76S △AEF .因为S △ABE =31S 正方形ABCD ,S △ADF =41S 正方形ABCD , S△CEF=121S 正方形ABCD ,所以S △AEF =1-31-41-121=31,所以S △AGE =76×31=72,三角形AEG 的面积是72.. 【解】(法一)△AEF 比△CDF 的面积大40,所以三角形AED 的面积比三角形DEC 大40,而两个三面积等于长方形ABCD 面积的一半,所以△CDE 的面积为40,三角形△AED 为40+40=80,5角形的高是一样的都等于10,所以三角形AED 的底比三角形DEC 的底长40×2÷10=8,即AE 的长为8+8=16(法二)△CDE 的而△AED 的高已知为10,所以△AED 的底AE 长16.第二讲 小升初专项训练 几何篇(一)一、小升初考试热点及命题方向随着小升初考察难度的增加,几何问题变越来越难,一方面,几何问题仍是中学考察的重点,各学校更题).尤其重、2008年考点预测2008年的小升初考试将继续以大题形式考查几何,命题的热点在于等积变换和燕尾定理在求解三角形、主要常用数学方法运用首先我们来讨论一下和三角形面积有关的问题,大家都知道,三角形的面积喜欢几何思维好的学生,这样更有利于小学和初中的衔接;另一方面几何问题由于类型众多,很多知识点需要提前学,这就加快了学生知识的综合运用,而这恰恰是重点中学学校所期望的.几何问题是小升初考试的重要内容,分值一般在12-14分(包含1道大题和2道左右的小要的就是平面图形中的面积计算,几何从内容方面,可以简单的分为直线形面积(三角形四边形为主),圆的面积以及二者的综合.其中直线形面积近年来考的比较多,值得我们重点学习. 从解题方法上来看,有割补法,代数法等,有的题目还会用到有关包含与排除的知识.二面积里的运用.同时还需要重点关注在长方形和平行四边形框架内运用边长比等于相似比的定理,请老师重点补充沙漏原理的讲解.三 1. 等积变换:在三角形中的=12×底×高,面积之比等于对应高的比 和三角形面积比有关的题目中它们都能发挥巨2. 用燕尾定理,求线段比:于同一点O, 上述定理给出了一个新的转化面积比与线段比的手段,因此我们有 【结论1】等底的三角形【结论2】等高的三角形面积之比等于对应底的比这2个结论看起来很显然,可大家小看它们,在许多大的作用,因为它们把三角形的面积比转化为了线段的比.运A OE DF C B 在三角形ABC 中,AD,BE,CF 相交那么S △ABO :S △ACO =BD:DC因为△ABO 和△ACO 的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用.3.平行线分线段定理(即利用求面积来间接求出线段的比例关系) 同学们应该对下图所示的图形非常熟悉了.相交线段AD 和AE 被平行线段BC 和DE 所截,得到的三角形ABC 和ADE 形状完全相似.所谓“形状完全相似”的含义是:两个三角形的对应角相等,对应边成比例.体现在右图中, 就是AB:AD=BC:DE=AC:CE=三角形ABC 的高:三角形ADE 的高.这种关系称为“相似”,同学们上了中学将会深入学习.相似三角形对应边的比例关系在解几何问题的时候非常有用,要多加练习.EDCB ACBEDA在实际运用的时候,相似的三角形往往作为图形的一部分,有时还要经过翻转、平移等变化(如右下4. 利用“中间桥梁”联系两块图形的面积关系角形的面积,就相对比较简单了,在解题过程中5. 差不变原理的运用面积,可以给两个图形都加上一个相同的图形,化不规则为规则,然后再作比6. 其他方法类型中几何题目的考点以面积为主,但不排除出现以线段和角度为考点的题目,只、典型例题解析三角形中的运用 例1】(★★)如图,四边形ABCD 中,AC 和BD 相交于O 点,三角形ADO 的面积=5,三角形DOC 的面图),往往不易看出相似关系.如(右下图)AB 平行于DE,有比例式AB:DE=AC:CE=BC:CD,三角形ABC 与三角形DEC 也是相似三角形.下图形状要牢记并且要熟练掌握比例式. 比较两个四边形的面积的大小很难,但比较三将难以处理的四边形化作三角形来处理,把三角形作为“中间桥梁”建立两组图形之间的数量关系, 题目处理起来就容易了. 比较不规则几何图形较,数量关系就清晰了,这种方法的实质是算术中的差不变原理. 虽然小升初考试要在解题过程中,将难以处理的量通过几何变化,化成我们熟悉的数量关系.题目即可迎刃而解.四【典型例题解析】1 等积变化在【积=4,三角形AOB 的面积=15,求三角形BOC 的面积是多少?ABCDO【解】:S △ADO =5,S △DOC =4根据结论2,△ADO 与△DOC 同高所以面积比等于底的比,即AO:OC=5:4同理S △AOB :S △BOC =AO:OC=5:4,因为S △AOB =15所以S △BOC =12.【总结】从这个题目我们可以发现,题目的条件和结论都是三角形的面积比,我们在解题过程中借助结拓展】S △AOD ×S △BOC =S △COD ×S △AOB ,也适用于任意四边形. 练习】如下图,某公园的外轮廓是四边形ABCD,被对角线AC、BD 分成四个部分,△AOB 面积为1平论2,先把面积比转化成线段比,再把线段比用结论2转化成面积比,解决了问题.事实上,这2次转化的过程就相当于在条件和结论中搭了一座“桥梁”,请同学们体会一下.【【方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园陆地的面积是6.92平方千米,求人工湖的面积是多少平方千米?(空白部分为陆地,阴影部分为水面.)例2】(★★★)如图,ABCD 是一长方形纸片,把它的左下角沿虚线EC 折叠过去成右图,AE 恰好AD 是的【41,三角形CDE 面积是27,三角形AHE 面积是3,三角形BCG 面积是16,问三角形DGH(阴影)的面积是多少?27EDCBA B解】S ACE =27÷3=9,S ABCE =27+9+9=45,S 阴=27-(45-3-16)=1. 2 燕尾定理在三角形中的运用 例(★★★)在△ABC 中【【3】DC BD =2:1, EC AE =1:3,求OEOB=? DCE OBA【分析】题目求的是边的比值,我们可以通过分别求出每条边的值再作比值,也可以通过三角形的面积比来做桥梁,但题目没告诉我们边的长度,所以方法二是我们要首选的方法.本题的图形一看就知道是燕尾定理的基本图,但2个燕尾似乎少了一个,因此应该补全,所以第一步我们要连接OC.【解】连接OCDCAE OB因为AE:EC=1:3 (条件),所以AOECOES S ΔΔ=1:3 若设AOE S x Δ=,则3COE S x Δ=,所以, 根据燕尾定理4AOC S x Δ=2:1AOB AOC S BD S DC ΔΔ==,所以8AOB S x Δ=,所以88:1AOB AOE S BO xOE S xΔΔ===.【例4】(★★★)三角形ABC 中,C 是直角,已知AC=2,CD=2,CB=3,AM=BM,那么三角形AMN(阴影部分)的面积为多少?ABD ABD C C【解】因为缺少尾巴,所以连接BN 如下,的面积为3×2÷2=3这样我们可以根据燕尾定理很容易发现ABC ΔACN Δ:ANB Δ=CD:BD=2:1;同理CBN Δ:ACN Δ=BM:AM=1:1;设面积为1份,则AMN ΔMNB Δ的面积也是1份,所以ANB Δ得面积就是1+1=2份,而:1,所以ACN Δ:ANB Δ=CD:BD=2ACN Δ得面积就是4份:;CBN ΔACN Δ=BM:AM=1:1,所以CBN 也是Δ4份,这样ABC Δ的面积总共分成4+4+1+1=103×份,所以阴影面积为1=10310.【例5】(★★★)如图,三角形A 的面积形CD BC 是16,D 是AC 的中点,E 是BD 的中点,那四边EF 的面积是多少?【解】连接DF.因为E 是BD 的中点,所以S △FBE =S △FDE ,S △ABE =S △ADE ,所以S △ABF =S △ADF .因为D 是AC 中点,所以S △ADF =S △CDF ,所以S △ABF =S △ADF =S △CDF .因为三角形ABC 的面积是16,所以S △CDF =316,S △ABD =8,S △AED =4,所以S △FDE =316-4=34,所以四边形CDEF 的面积是16+4=20【例6】如图,平行四边形ABCD【解】S △BCD =1+4+4+6=16,S △OCD 4和6.求:(1)求△OCF =21S 以S △OCF =8-4=4,所以,=ΔΔCEG OEG S S 所而S △OCE = S △OCB - S △OBE =8-6=2,所以,21EG CG CE ====63GF GO EB 所以S △GCE =322=×.31在三角形中的运用正方形ABCD ,M 为AD 边上的中点,求图中的阴影部分面积.3平行线分线段定理【例7】(★★★)如右图,单位【解1】(平行线分线段定理)两块阴影部分的面积相等,AM GM BC GB ==21,所以GM =32,而三角形GB ABG和三角形AMB 同底,所以S △BAG =32S △ABM =32×1×12=61×21,又因为三角形BAM 和三角形CAM 同底等高,所以阴影面积为61×2=31.【解2】(燕尾定理运用)四边形AMCB 的面积为(0.5+1)×1÷2=43,根据燕尾定理在梯形中的运用,知道::: =A :BC :AM×BC:AM×BC=AMG ΔBCG ΔBAG ΔCMG ΔM 22212⎛⎞⎜⎟⎝⎠:1:221:21=1:4:2:份,所以面积为2;所以四边形AMCB 的面积分成1+4+2+2=9份,阴影面积占43×224122++++=314. 【解3】(等积变化运用)如右图,连结DG,有:S △ACM =S △BAM (同底等高), AC 又S △AGM =S △GDM (等底同高)又S △BAG =S △ADG (△BAG 与△ADG 关于对称) 因此,11AGM D S S ΔΔ==22AG ABG S Δ 2AGB ABM S S ΔΔ=3 又1111222ABM S AM AB Δ=⋅⋅=⋅⋅=14所以,2211AGB ABM S S ΔΔ==×=所以,3346123阴影AGB S S Δ=×=.是平行四边形,面积为72平方厘米,BC 的中点.则积为多少平方厘米?【例8】(★★★★)如图,ABCD E,F 分别为边AB,图形中阴影部分的面【解1】由AE:CD=1:2,CF:AD=1:2,得到对角线被DE 和DF 分为三等分. 以得到空白部分是DEBF 面积的2/3.空白部分面积为72÷2÷3×2=24平方厘米72-24=48平方厘米.理”的运用.连接BD,OE,OF 这样我们可以发现S1的面积是整个四边形的可【解2】出现梯形时可以考虑一下”燕尾定14,即14S2:S4=份×72=18(平方厘米),在梯形AEOD 中,AD=2×OE,这样我们运用”燕尾定理”得:S5:S3:1:4:2:2,把面积分成9份,求出阴影面积占5份,同理可以求出梯形DCFO 中阴影也占5,所以阴影面积=(72-18) ×59=30,总阴影面积为30+18=48(平方厘米).4利用“中间桥梁”联系两块图形的面积关系【例9】(★★)如图,正方形ABCD 的边长是4厘米,CG=3厘米,矩形DEFG 的长DG 为5厘米,求它DE 等于多少厘米?的宽GF EHD C BA G【解】:连结AG,自A 作FECBAH 垂直于DG 于H,在△ADG 中,AD=4,DC=4(AD 上的高). ∴S △AGD =4×4÷2=8,又DG=5, ∴S △AGD =AH×DG÷2,∴AH=8×2÷5=3.2(厘米), ∴DE=3.2(厘米).5 差不变原理的运用【例10】(★★★)左下图所示的DA ABCD 的边BC 长10cm,直角三角形BCE 的直角边EC 长8cm,已知两块阴影部分的面积和比△EFG 的面积大10cm 2,求CF 的长. 两块阴影部分的面积和比△EFG 的面积大10,两部分分别加上四边形BCFG,这样四边形ABCD三角形BEC 的面积大10cm2CE【解】:的面积比S △B =12底是10cm,所以高是5cm. ×10×8=40 所以四边形ABCD 的面积是50cm 2.6 其他常考题型 【例11】(★★)下图中,五角星的五个顶角的度数和是多少?OEOEDCBADB AC:连接AB(见右图),AC 交BE 于点O.因为∠AOB=∠COD,所以∠OAB+∠OBA=∠OCE+∠OEC.由此角星五个顶角之和等于三角形ABD 的三个内角之和,是180度. 【课外知识】春秋战国时代,一位父亲和他的儿子出征打战.父亲已做了将军,儿子还只是马前卒.又一阵号角吹响,战鼓雷鸣了,父亲庄严地托起一个箭囊,其中插着一只箭.父亲郑重对儿子说:“这是家袭宝箭,配带身边,力量无穷,但千万不可抽出来.”那是一个极其精美的箭囊,厚牛皮打制,镶着幽幽泛光的铜边儿,再看露出的箭尾.一眼便能认定用上等的孔雀羽毛制作.儿子喜上眉梢,贪婪地推想箭杆、箭头的模样,耳旁仿佛嗖嗖地箭声掠过,敌方的主帅应声折马而毙.果然,配带宝箭的儿子英勇非凡,所向披靡.当鸣金收兵的号角吹响时,儿子再也禁不住得胜的豪气,完全背弃了父亲的叮嘱,强烈的欲望驱赶着他呼一声就拔出宝箭,试图看个究竟.骤然间他惊呆了.一拂开蒙蒙的硝烟,父亲拣起那柄断箭,沉重地啐一口道:“不相信自己的意志,永远也做不成将军.”托在一只宝箭上,多么愚蠢,而当一个人把生命的核心与把柄交给别人,又多么危险!比如把在儿女身上;把幸福寄托在丈夫身上;把生活保障寄托在单位身上……己才是一只箭,若要它坚韧,若要它锋利,若要它百步穿杨,百发百中,磨砺它,拯救它的都【解】推知,五只断箭,箭囊里装着一只折断的箭.我一直刳着只断箭打仗呢!儿子吓出了一身冷汗,仿佛顷刻间失去支柱的房子,轰然意志坍塌了.结果不言自明,儿子惨死于乱军之中.把胜败寄希望寄托温馨提示:自只能是自己.练习题在三角形ABC 的各边上,分别取AD、BE、CF 各等于AB、BC、CA 长的三分之一,如果三角形DEF 的积为2平方厘米,求三角形ABC 的面积是多少?1、面答案:6平方厘米.2、在图中,四边形ABCD 的对角线AC 与BD 交F=CE,BG=DE,于点E,且A 当四边形ABCD 的面积为25平方厘米时,三角形EFG的面积是多少?答案:25平方厘米.如图,正方形ABCD 的面积是120平方厘米,E 是AB 的中点,F 是BC3、的中点,四边形BGHF 的面积是________平方厘米.E F GB HCD A EB C来源:02年小学数学奥林匹克试题 使BK=CD. 三角形EHK 与三角形DHC 成比例,DC:=2:3,所以DH:HK=2:3,由于三角形DEK 的面积=90平方厘米,所以EHK 的面积=90÷【解】:延长EB 到K,EK 3三角形5形EHK 的面积-三角形=54平方厘米,所以四边形EBFH 的面积=三角BKF 的面积=24平方厘米.同理,EB:DC=1:2,所以BG:GD=1:2,所以三角形EBG 的面积=13×三角形EBD 的面积=10平方厘米,所以,四边形BHGF 的面积是24-10=14平方厘米.4、直线CF 与平行四边形ABCD 的AB 边相交于E 点,如果三角形BEF 的面积为6平方厘米,求三角形ADE的面积是多少?答案:6平方厘米.5、(★★★)如图,正方形ABCD 的边长是4厘米,CG=3厘米,矩形DEF 宽DE 等于多少厘米?G 的长DG 为5厘米,求它的G F E HG F ED A DCB A B C【解】:连结AG,自A 作AH 垂直于DG 于H,在△ADG 中,AD=4,DC=4(AD 上的高).∴S △AGD =4×4÷2=8(平方厘米),又DG=5(厘米), ∴S △AGD =AH×DG÷2,米),∴DE=AH=3.2(厘米).∴AH=8×2÷5=3.2(厘。
奥数教材推荐

奥数教材推荐小学奥数教辅书可以分为三类:教材;习题集;竞赛试题汇编。
下面分别进行介绍。
(一)教材类1、《明心数学资优教程》刘嘉编著,湖北教育出版社出版《明心数学资优教程》是目前最好的小学奥数教材,由武汉的明心资优教育(武汉的一家培训机构)的刘嘉老师主编,计划出版八卷四册,现已出版了3册:第二卷上(2007年)、第三卷上(2007年)、第四卷上(又分第1、2分册)(2008年),所以实际上是已经出了4本。
《明心数学资优教程》这套书最大优点有:① 每一讲前面的数学经纬都非常的生动有趣而且富有知识性;②每一道例题的解答过程都非常详细,很适合家长用来辅导学生及学生自学,另外对于新老师的教学其实也有指导帮助的作用。
而且有些例题后面都有关于例题的知识背景的介绍(这样的往往是数学史上著名的问题),还有例题不同的表达形式(相当于变式),可起到举一反三的作用;③每一讲后面的练习题有些是与前面的例题相对应的,这样学生在做练习题时可以回想前面的例题的解题思路,既是对前面例题的回顾又是对练习题的启发(实际上大部分奥数教材都是这样做的,比如后面要介绍的仁华学校数学课本及《奥数教程》等,当然学而思讲义也是如此)。
《明心数学资优教程》最大的缺点就是——出得太慢了~说是要出八卷,到目前为止还只出了三卷四本。
2、《仁华学校奥林匹克数学课本》中国大百科全书出版社,一至六年级都有仁华学校出的课本,因了仁华的江湖地位,自然是值得重视的。
这套书知识面覆盖的很全,小学奥数需要掌握的知识里面都会讲到,题目难度比较适中,有基础题,也有中等题,难题相对少一些。
仁华学校这套书可以说是中规中矩,但六年级那册比较有特色,讲了许多别的书不太重视的内容,比如小数中的进位制、以及用了四讲来讲棋盘上的数学,都是很值得一看的。
3、《小学奥数总复习教程》学而思编著的第一本书,电子工业出版社汇聚了学而思众多奥数名师和教研高手编著而成的,主要是为六年级面临小升初的孩子们准备的,脱胎于学而思讲义却又不同于学而思讲义,每道例题后面都有初级点拨、深度提示和全解过程,其中前两部分都是对于解题思路的提示,对于学生做题富有启发性。
小学六年级奥数教学ppt课件:

再次,作系统的训练。在讲课的时候, 我经常对同学们讲:“奥数,只看不练,等于 白干”。学奥数,就像学自行车,你的理论知 识再好,没有足量的练习,你还是不能真正 掌握奥数。
像速算、巧算的题目,这样题目几乎每 次考试都会出现,但是这样题目同学得分情 况十分不好!!究其原因:一是没有对这类题目 很好的总结学习,二是没有对这类题目系统 的训练。
比如说,三四年级中的“假设法”、“对应 法”、“画图法”等等,在五六年级中的分数应 用题、行程问题、工作问题中运用;在五、六年级 的教材上,大量出现小学奥数里的知识,比如五、 六年级的“解决问题的策略”、可能性”等等, 解决思路相同但会加进新学到的知识,如分数、 比例、负数、图形等等。
五六年级,是关键的两年,这两年一定要全 力以赴,如果你在三四年级已经打好了基础,相 信五六年级的压力就非常小了。相反,估计你就 要加把劲了。五六年级如果从头一点点的学,估 计是没有太多的时间了,这个时候老师会根据你 的情况,给你来一个个性化的辅导方案,只要你 肯下功夫,相信,也能后来者居上!
其次,改掉自己的坏习惯。奥数学习好的学 生,特别是男生,都有马虎的毛病,他们不怕题目 多难,而是怕题目简单。
二、奥数学习不扎实的同学。
更多的同学,或者说是大多数同学的状况是这 样的:他们四年级或五年级才开始学习奥数,有的 甚至是六年级暑假刚开始学,我们称这样的同学是 半路出家的学生;
有的同学是从三年级开始学的奥数,但是学 了2年,只是听课,没有做过系统的训练,甚至是没 有做过训练,有的同学家长就跟我抱怨说:以前, 他们的孩子在某某学校学习奥数,学校的老师不负 责任--只是讲课,不留作业--这样学过来的学生, 我们只能说他听过奥数课,但并没有真正学到奥数。 那一下三种情况:
一、奥数学的很扎实
小学奥数(学而思讲义)

【分析】 设11112005200620072008a +++=,则 114420082004a ´<<´,所求数1111110111219+++ 的整数部分是几? [分析] 11111111111110101112191010101010>==++++++ 111 1.91111111110101112191919191919<==++++++ 即1<原式<1.9,所以原式的整数部分是1. (第四届2试试题)若11111a =,1111111b =,111111111c =,则a ,b ,c 中最大的是________,最小的是________.【分析】 此题比较方法很多,方法之一倒数法:111011a =,1110111b =,11101111c =,111a b c>>,即a b c <<(第六届2试试题)(10.120.23)(0.120.230.34)(10.120.230.34)(0.120.23)++´++-+++´+=______.【分析】 换元的思想即“打包”,令0.120.23a =+,0.120.230.34b =++,原式(1)(1)a b b a =+´-+´b a =-=0.34(第六届五年级2试试题)计算下面的算式(7.88 6.77 5.66++)´(9.3110.9810++)-(7.88 6.77 5.6610+++)´(9.3110.98+) [分析] 换元的思想即“打包”,令7.88 6.77 5.66a =++,9.3110.98b =+,则原式a =´(10b +)-(10a +)b ´=(10ab a +)-(10ab b +)101010ab a ab b =+--=´(a b -) 10=´(7.88 6.77 5.669.3110.98++--)100.020.2=´=(第五届2试试题)111112005200620072008+++的整数部分是 以20081200450250144a =>>= 所以整数部分是501(第三届华杯赛复赛试题)(祖冲之杯数学邀请赛)如果222221333331,222223333334A B ==,那么A 和B 中较大的数是 .[分析] 222221666663666662333331222223666669666668333334A B ==>==, 即A 大(希望杯培训题)计算:11111111112345678910612203042567290110+++++++++= 【分析】 原式11112310612110=++++++++1115523341011=++++´´´ 1155211=+-已知三位数abc 如上,三位数abc 与它的反序数cba 的和能否等于999?如果和等于989,这样的三位数有 个.【分析】 否,十位29b ¹;和等于989,4b =,a 、c 的情况有1+8、2+7、3+6、4+5、5+4、6+3、7+2、8+1这7种。
六年级数学奥数讲义练习第11讲假设法解题(二)(全国通用版,含答案)
六年级数学奥数讲义练习第11讲假设法解题(二)(全国通用版,含答案)一、知识要点已知甲是乙的几分之几,又知甲与乙各改变一定的数量后两者之间新的倍数关系,要求甲、乙两个数是多少,这样的应用题称为变倍问题。
应用题中的变倍问题,有两数同增、两数同减、一增一减等各种情况。
虽然其中的数量关系比较复杂,但解答时的关键仍是确定哪个量为单位“1”,然后通过假设,找出变化前后的相差数相当于单位“1”的几分之几,从而求出单位“1”的量,其他要求的量就迎刃而解了。
二、精讲精练【例题1】两根铁丝,第一根长度是第二根的3倍,两根各用去6米,第一根剩下的长度是第二根剩下的长度的5倍,第二根原来有多少米?【思路导航】假设第一根用去6×3=18米,那么第一根剩下的长度仍是第二根剩下长度的3倍,而事实上第一根比假设的少用去(6×3-6)=12米,也就多剩下第二根剩下的长度的(5-3)=2倍。
(6×3-3)÷(5-3)+6=12(米)答:第二根原来有12米。
练习1:1、丁晓原有书的本数是王阳的5倍,若两人同时各借出5本给其他同学,则丁晓书的本数是王阳的10倍,两人原来各有书多少本?2、在植树劳动中,光明中学植树的棵数是光明小学的3倍,如果中学增加450棵,小学增加400棵,则中学是小学的2倍。
求中、小学原来各植树多少棵?3、两堆煤,第一堆是第二堆的2倍,第一堆用去8吨,第二堆用去11吨,第一堆剩下的重量是第二堆的4倍。
求第二堆煤原来是多少吨?【答案】1.丁晓有45本书,王阳有9本书。
2.中学原来植树1050棵,小学原来植树350棵。
3.18吨【例题2】王明平时积蓄下来的零花钱比陈刚的3倍多6.40元,若两个人各买了一本4.40元的故事书后,王明的钱就是陈刚的8倍,陈刚原来有零花钱多少元?【思路导航】假设仍然保持王明的钱比陈刚的3倍多6.40元,则王明要相应地花去4.40×3 =13.20元,但王明只花去了4.40元,比13.20元少13.20-4.40=8.80元,那么王明买书后的钱比陈刚买书后的钱的3倍多6.40+8.80=15.20元,而题中已告诉:买书后王明的钱是陈刚的8倍,所以,15.20元就对应着陈刚花钱后剩下钱的8-3=5倍。
小学六年级奥数课件:最值问题共25页PPT
60、生活的道路一旦选定,就要勇敢地 走到底 ,题
61、辍学如磨刀之石,不见其损,日 有所亏 。 62、奇文共欣赞,疑义相与析。
63、暧暧远人村,依依墟里烟,狗吠 深巷中 ,鸡鸣 桑树颠 。 64、一生复能几,倏如流电惊。 65、少无适俗韵,性本爱丘山。
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
学而思小学数学视频
[3021-4] 小学数学 数论专题 精讲—— 整数分拆 (三年级 、四年 级)[ 刘晓宇CS4讲全] [3022-6] 小学奥数 八大必考 之数论专 题精讲: 数的整除 (四、五 年级数论 3级)[ 刘晓宇VS6讲全] [3023-2] 小学数学 数论专题 精讲—— 质数、合 数、约数 定理(四 年级、五 年级)[ 刘晓宇VS2讲全] [3024-4] 小学奥数 数论专题 精讲—— 因数与倍 数(五年 级、六年 级)[ 谷运增BS4讲全]
[104158]2014三 年级小机 灵初赛真 题与高频 考点VIP 全能班 [吴桐CS8讲全] [1062324]小学 奥数数论 专题精讲 之无懈 [1610]三 升四暑期 数学竞赛 班(兰 海)+三 年级奥数 系统复习 班 金颖 (缺30-45 讲) [166116]2010 年秋季六 年级数学 竞赛班 [刘阳NS16讲 全] [178416]四升 五暑期数 学超常班 [杨秀情 C-S16讲 全] [1889-8] 三年级奥 数必考知 识点系统 复习全能 班上
[3029-4] 小学奥数 八大必考 之数论专 题精讲: 数论综合 之整除与 余数(五 、六年级 数论8级 上)[BS4讲全] [3030-2] 小学奥数 数论专题 精讲—— 数论综合 之数论应 用(五年 级、六年 级)[ 谷运增BS2讲全] [3036-2] 小学奥数 八大必考 之行程专 题精讲: 火车过桥 (四、五 年级行程 3级上) [谷运增 V-S2讲 全] [3037-2] 小学奥数 八大必考 之行程专 题精讲: 多次相遇 (四、五 年级行程 3级下) [谷运增 V-S2讲 全]
[360120]2011 暑期五升 六奥数竞 赛班 [谷 运增共20 讲全] [谷运增 N-S20讲 全] [3656-6] 小学超难 奥数题— 数论专题 (五年级 、六年 级) [3681-2] 世界趣题 与奥数思 维(四年 级、五年 级、六年 级)[谷 运增V-S2 讲全] [37358]2012迎 春杯三年 级初赛 VIP全能 班 [刘 阳C-S8讲 全] [37458]2012寒 假二年级 奥数强化 班[史乐 X-S8讲 全] [3746]28 90-2012 寒假二年 级奥数竞 赛班
学而思6年级暑假数学培训目录
学而思6年级暑假数学培训目录
第一训:突破加减竖式
第二卅巧填算符初步
第三讲剪拼幽形
第四讲图文代换
第五讲巧移物体
第六讲左右畸开发3(逻辑推理)
第七讲期末测评
二年级寒假班
第一讲认识倍
第二讲带余除法初步
第三讲有趣的自然数串
第四讲分割图像
第五讲枚涨洼的妙刖第六讲鸡兔同笼初步
第七讲期末测评
三年级寒假班
第一讲角度初识
第二讲速算与巧算之四则运算第三讲字母表示数
第四讲和差倍
第五讲倒退与蚓示
第六讲方阵
第七讲期末测评。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 测试1·计算篇 1. 计算128)288122411681120180148124181(
2. )1119171()131111917151()1311119171()111917151( 3. 计算:2004×2003-2003×2002+2002×2001-2001×2000+…+2×1= 4.有一列数:……第2008个数是________ . 5.看规律13 = 12,13 + 23 = 32,13 + 23 + 33 = 62 ……,试求63 + 73 + … + 143 2
第1讲 小升初专项训练·计算 四五年级经典难题回顾 例1 求下列算式计算结果的各位数字之和:2576666666200562006个个
例2 求数1911211111011的整数部分是几? 小升初重点题型精讲 例1 595491474371353251 .
例2 )19956.15.019954.01993(22.550276951922.510939519 例3 )25118100412200811()25138100432200831( . 巩固 计算:416024340143214016940146 . 3
例4 计算:10199507535323112222 . 拓展 计算:10981943273215 . 例5 12+23+34+45+56+67+78+89+910= . 巩固:23+34+45+…+100101= . 拓展 计算:123+234+345+…+91011= . 例6 [2007 –(8.58.5-1.51.5)÷10]÷160-0.3= . 巩固 计算:53×57 – 47×43 = . 例7 计算:11×19 + 12×18 + 13×17 + 14×16 = . 4
拓展 计算:1×99 + 2×98 + 3×97 + … + 49×51 = . 例8 计算:1×99 + 2×97 + 3×95 + … + 50×1 = .
家庭作业 1. 797291585381373172 .
2. )5246.5(402323153236 . 3. )2231966913200711()2237966973200771( .
4. 计算:119951199511993119931717151513132222222222 . 5. 计算:11×29 + 12×28 + … + 19×21 = . 5
名校真题 1. 如图,AD = DB, AE = EF = FC,已知阴影部分面积为5平方厘米,△ABC的面积是_________平方厘米.
2. 如图,ABCD与AEFG均为正方形,三角形ABH的面积为6平方厘米,图中阴影部分的面积为_________.
3. 如图,长方形ABCD的面积是36,E是AD的三等分点,AE = 2ED,则阴影部分的面积是 . 4. 如图,边长为1的正方形ABCD中,BE = 2EC,CF = FD,求三角形AEG的面积.
5. 如图,3个边长为3的正方形,甲的中心在乙的一个顶点上, 乙的中心在丙的一个顶点上,甲与丙不重叠,求甲、乙、丙叫 共覆盖的面积是 。 6
第2讲 小升初专项训练·几何一 四五年级经典难题回顾 例1 如右图所示,在长方形内画出一些直线,已知边上有三块 面积分别是13,35,49,那么图中阴影部分的面积是多少?
例2 如图,长方形ABCD中,BE:EC = 2:3,DF:FC = 1:2, 三角形DFG的面积为2平方厘米,求长方形ABCD的面积。
例3如图,已知正方形ABCD的边长为10厘米,E为AD中点, F为CE中点,G为BF中点,求三角形BDG的面积.
小升初重点题型精讲 例1如图,正方形的边长为10,四边形EFGH的面积为5, 那么阴影部分的面积是 .
例2 E、M分别为直角梯形ABCD两边上的点,且DO、CP、AIE彼此平行, 若AD = 5,BC=7,AE=5,EB = 3.求阴影部分的面积.
例3已知ABCD是平行四边形,BC:CE=3:2,三角形ODE的面积为6平方厘米.则阴影部分的面积是 平方厘米. 7
铺垫 右图中ABCD是梯形,ABED是平行四边形,已知三角形 面积如图所示(单位:平方厘米),阴影部分的面积是 平方厘米。
例4如图所示,BD、CF将长方形ABCD分成4块,△DEF的面积是4平方厘米,△CED的面积是6平方厘米.问:四边形ABEF的面积是多少平方厘米?
拓展 如图,长方形ABCD被CE、DF分成四块,已知其中3块 的面积分别为2、5、8平方厘米,那么余下的四边形OFBC的 面积为 平方厘米.
例5如图,三角形ABC的面积是16,D是AC的中点,E是BD 的中点,那四边形CDEF的面积是多少?
拓展 如右图,三角形ABC中,AF:FB=BD:DC= CE:AE=3:2, 且三角形ABC的面积是l,则三角形ABE的面积为 , 三角形AGE的面积为 ,三角形GHI的面积为 .
例6如图,边长为10的正方形中有一等宽的十字,其面积(阴 影部分)为36,则十字中央的小正方形面积为 .
例7如图,阴影部分四边形的外接图形是边长为10 cm的正方形, 则阴影部分四边形的面积是 cm2. 8
巩固 如图,如果长方形ABCD的面积是56平方厘米,那么四边 形MNPQ的面积是多少平方厘米?
例8三角形AEF的面积是17,DE、BF的长度分别为11、3. 求长方形ABCD的面积.
拓展 如图,长方形ABCD中,AB= 67,BC = 30.E、F分别 是AB、BC边上的两点,BE + BF = 49.那么,三角形DEF 面积的最小值是 。
家庭作业 1.如图,正方形的边长为12,阴影部分的面积为60, 那么四边形EFGH的面积是 。
2.如图所示,BD、CF将长方形ABCD分成4块,ADEF的面积 是5平方厘米,ACED的面积是10平方厘米,问:四边形 ABEF的面积是多少平方厘米?
3.在△ABC中,BD:DC=3:2,AE:EC=3:1,求OB:0E=?
4.三角形ABC中,C是直角,已知AC=2,CD=2,CB=3, AM=BM,那么三角形AMN(阴影部分)的面积为多少? 9
5.如图,阴影部分四边形的外接图形是边长为12 cm的 正方形,则阴影部分四边形的面积是多少?
名校真题 1. 已知三角形ABC是直角三角形,AC=4cm,BC=2cm,求阴影部分的面积.
2. 已知图中正方形的面积是20平方厘米,则图中里外两个圆的面积之 和是 .(л取3.14)
3. 奥运会的会徽是五环图,一个五环图是由 内圆直径为6厘米,外圆直径为8厘米的五个 环组成,其中两两相交的小曲边四边形(阴影 部分)的面积都相等,已知五个圆环盖住的面 积是了7.1平方厘米,求每个小曲边四边形的面积.(л=3.14 )
4. 如图,有一个边长是5的立方体,如果它的左上方截去一个边 分别是5,3,2的长方体,那么它的表面积减少了百分之 .
5. 选项中有4个立方体,其中是用左边图形折成的是( ) 10
第3讲 小升初专项训练·几何二 四五年级经典难题回顾 例1 如右图所示,直角三角形ABC的斜边AB长为10厘米, ∠ABC= 60°,此时BC长5厘米.以点B为中心,将△ABC 顺时针旋转120°,点A、C分别到达点E、D的位置.求AC 边扫过的图形即图中阴影部分的面积.(л取3)
例2 如图,ABCD是矩形,BC=6cm,AB=10cm,对角线 AC、BD相交O.E、F分别是AD与BC的中点,图中的 阴影部分以EF为轴旋转一周,则白色部分扫出的立体 图形的体积是多少立方厘米?(丌取j)
拓展 如图,ABCD是矩形,BC= 6cm,AB=10cm, 对角线AC、BD相交O.图中的阴影部分以CD为轴旋转一周,则阴影部分扫出的立体的体积是多少立方厘米?
小升初重点题型精讲 例1如图,等腰直角三角形ABC的腰为10厘米;以A为圆心, EF为圆弧,组成扇形AEF;阴影部分甲与乙的面积相等.求扇形 所在的圆的面积。 11
巩固 三角形ABC是直角三角形,阴影I的面积比阴影Ⅱ的面 积小25cm2,AB=8cm,求BC的长度.
例2在一个边长为2厘米的正方形内,分别以它的三条边为直径 向内作三个半圆,则图中阴影部分的面积为 平方厘米.
巩固 如图,正方形边长为1,正方形的4个顶点和4条边分 别为4个圆的圆心和半径,求阴影部分面积.(л取3114)
例3 如图所示,在半径,为4cm的图中有两条互相垂直的线段, 阴影部分面积爿与其它部分面积B之差(大减小)是 cm2
巩固 如图所示,长方形ABCD,长是8 cm,则阴影部分的面积 是 .(л=3.14)
例4如下图所示,曲线PRSQ和ROS是两个半圆,RS平行于PQ. 如果大半圆的半径是1米,那么阴影部分是多少平方米? (л取3.14)
巩固 在右图所示的正方形ABCD中,对角线AC长2厘米,
