2014-2015年上海市闵行区八年级上学期期中数学试卷及参考答案
2014-2015学年度第一学期期中八年级数学
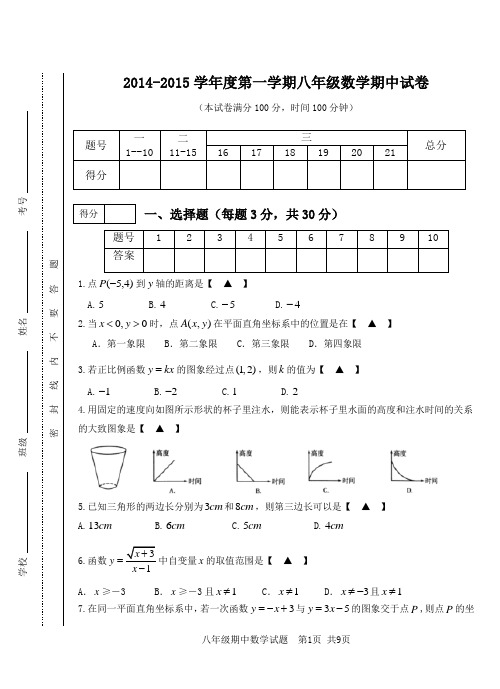
2014-2015学年度第一学期八年级数学期中试卷(本试卷满分100分,时间100分钟)题号 一 1--10 二11-15三总分 16 17 18 19 20 21 得分一、选择题(每题3分,共30分)题号 12345678910 答案1.点)4,5(-P 到y 轴的距离是【 ▲ 】A.5B.4C.5-D.4-2.当0,0><y x 时,点(,)A x y 在平面直角坐标系中的位置是在【 ▲ 】 A .第一象限 B .第二象限 C .第三象限 D .第四象限3.若正比例函数y kx =的图象经过点(1,2),则k 的值为【 ▲ 】 A.1- B.2- C.1 D.24.用固定的速度向如图所示形状的杯子里注水,则能表示杯子里水面的高度和注水时间的关系的大致图象是【 ▲ 】5.已知三角形的两边长分别为cm 3和cm 8,则第三边长可以是【 ▲ 】 A.cm 13 B.cm 6 C.cm 5D.cm 46.函数3x y +=中自变量x 的取值范围是【 ▲ 】 A .x ≥-3 B .x ≥-3且1x ≠ C .1x ≠ D .3x ≠-且1x ≠7.在同一平面直角坐标系中,若一次函数3y x =-+与35y x =-的图象交于点P ,则点P 的坐得分学校 班级 姓名 考号密封 线 内 不 要 答 题标为【 ▲ 】A.(1,4)-B.(1,2)-C.(2,1)-D.(2,1) 8.一次函数b kx y +=的图象如图所示,则不等式2>+b kx 的 解集为【 ▲ 】A.0>xB.0<xC.1-<xD.1->x9.一个三角形的两个内角分别是ο55和ο72,这个三角形的外角不可能是【 ▲ 】 A. 125° B.108° C.127° D.137°10.甲、乙两个同学从m 400环形跑道上的同一点出发,同时同向而行,甲的速度为s m /6,乙的速度为s m /4.设经过x (s )后,跑道上此两人间的较短部分的长度为y (m ),则y 与x (0≤x ≤300)之间函数关系可用图象表示为【 ▲ 】A. B. C. D.二、填空题(每题4分,共20分)11.如图,是某风景区几个主要景点示意图,根据图中信息可确定 九疑山的中心位置C 点的坐标为 .12.已知直线3-=x y 与22+=x y 的交点为)8,5(--,则方程组 的⎩⎨⎧=+-=--02203y x y x 解是 .13.直线a x y +-=2经过点),3(1y 和点),2(2y -,则1y 2y (填“>”、 “<”或“=”). 14.如果将函数x y 2=的图象向左平移m (0>m )个单位,正好等于将它向上平移n (0>n )个单位,则m 和n 之间的关系为 .15.某人用80元充值卡坐某种刷卡出租车,按行驶里程收费.km 3内收费8元,以后每超过km1得分第8题图第11题图加收5.1元.若此人第一次坐出租车(331)xkm x ≤≤,则充值卡中所余的费用y (元)与x ()km 之间的关系式是 . 三、解答题(共55分)16.(本小题7分)如图,A B C 、、三点的坐标分别为3,4()、1,2()、5,0(),将ABC ∆先向下平移四个单位得到'''A B C ∆,再将'''A B C ∆向左平移五个单位得到111A B C ∆.(1)请你在图上画出'''A B C ∆和111A B C ∆; (2)观察所画的图形写出'A 和1A 的坐标;(3)计算ABC ∆的面积.17.(本小题8分)综合与实践世界上大部分国家都使用摄氏温度()C o,但美国、英国等国家的天气预报仍然使用华氏温度()F o.两种计量之间有如下对应:(1(2)求出华氏0度时摄氏是多少度?(3)华氏温度的值与对应摄氏温度的值有相等的可能吗?如果有,请求出该值.xy –1–2–3–4–512345–1–2–3–4–512345O18.(本小题8分)如图,在ABC ∆中,AC AB =,AC 上的中线把三角形的周长分为cm 24和cm 30的两个部分,求三角形各边的长.19.(本小题10分) 已知2+y 与x 成正比例,且2-=x 时,0=y . (1)求y 与x 之间的函数关系式; (2)画出函数的图象;(3)设点P 在y 轴负半轴上,(2)中的图象与x 轴、y 轴分别交于B A 、两点,且4=∆ABP S ,求P 点的坐标.20.(本小题10分) 已知,如图,在ABC ∆中,角平分线BD 、CD 相交于点D , (1)若ο80=∠A ,求BDC ∠的度数; (2)若ο120=∠BDC ,求A ∠的度数;(3)若βα=∠=∠BDC A ,,试求α、β之间的数量关系.第20题图21. (本小题12分) 我市某企业利用机器生产一种科技产品,机器从早上八点开始工作,中午十二点停止.产品生产出来后,需要包装入库.通常的办法是,机器先工作一段时间,包装工人再开始包装.某次包装工人工作了一段时间后,因临近下班,又抽掉了一部分工人来帮忙,使包装入库的速度提高了一倍.如图是生产出来后待包装入库的产品数量y(件)与时间t(h)的函数关系的图象.根据图象解决以下问题:(1)机器每小时生产件产品;工人包装入库的速度是件/h;(2)求线段BC的解析式;(3)如果要保证生产的产品恰好在半天(4h)时全部包装入库,原有包装工人应该在机器开始工作后多长时间时开始包装?2014-2015学年度第一学期八年级数学期中测试参考答案一、选择题1---5:ABDCB 6----10:BDADC 二、填空题 11.(3,1) 12.⎩⎨⎧-=-=85y x 13.< 14.2m=n 15.5.765.1+-=x y三、解答题16.(1)图略………………2分(2)'A (3,0);1A (-2,0)………………4分 (3)42214221222144⨯⨯-⨯⨯-⨯⨯-⨯=∆ABC S ………………6分 6=………………7分 17.解:(1)是一次函数.………………1分设摄氏温度值为x ,华氏温度值为y ,令y=kx+b321050b k b =⎧⎨+=⎩解得9,325k b == 9325y x =+………………4分 (2)当y=0时,93205x +=,解得1609x =-,即华氏0度时,摄氏是1609-.…………6分 (3)依题意得9325y x y x⎧=+⎪⎨⎪=⎩ 解得40y x ==-即华氏温度的值与摄氏温度的值在-40时相等.………………8分 18.解:设AB=AC=2x ,则AD=CD=x ,(1)当AB +AD=30,BC +CD=24时,有2x +x=30, ∴x=10,………………2分 2x=20,BC=24-10=14,三边分别为:20cm ,20cm ,14cm .………………4分(2)当AB +AD=24,BC +CD=30,有2x +x=24∴x=8,………………6分BC=30-8=22,三边分别为:16cm ,16cm ,22cm .………………8分19.解:(1)∵y+2与x 成正比例,∴设y+2=kx (k 是常数,且k ≠0)∵当x=-2时,y=0. ∴0+2=k ·(-2),∴k =-1. ∴函数关系式为x+2=-x , 即y=-x-2.………………3分 (2)列表;x 0 -2 y-2描点、连线,图象如图所示.………………6分 (3)函数y=-x-2分别交x 轴、y 轴于A ,B 两点, ∴A (-2,0),B (0,-2). ∵S △ABP =21·|BP|·|OA|=4, ∴|BP|=428||8==OA . ∴点P 与点B 的距离为4. 又∵B 点坐标为(0,-2),且P 在y 轴负半轴上, ∴P 点坐标为(0,-6).………………10分 20.(1)∵∠A=80°,∴∠ABC+∠ACD=180°-80°=100° ∵BD 、CD 是角平分线 ∴∠DBC+∠DCB=οο5010021)(21=⨯=∠+∠ACB ABC ∴∠BDC=180°-∠DBC-∠DCB=180°-50°=130°;………………3分 (2)当∠BDC=120°,∴∠DBC+∠DCB=180°-120°=60° ∵BD 、CD 是角平分线∴οο120602)(2=⨯=∠+∠=∠+∠DCB DBC ACB ABC∴∠A=180°-(∠ABC+∠ACB)=180°-120°=60°;………………6分 (3)∵∠A=α,∴∠ABC+∠ACB=180°-α ∵BD 、CD 是角平分线 ∴∠DBC+∠DCB=)180(21)(21α-⨯=∠+∠οACB ABC ∴∠BDC=180°-(∠DBC+∠DCB)=180°-αα2190)180(21+=-οο ∴︒+=9021αβ………………10分 21.(1)150,250………………4分(2)由包装速度提高一倍可知,最后阶段包装速度为500件/时,100÷500=0.2,所以点C 的坐标为(4.2,0),………………6分设y=kt+b ,则41004.20k b k b +=⎧⎨+=⎩,解得500,2100k b =-= 5002100y t =-+………………8分(3)设机器开始工作后t 小时,包装工人开始包装,则 150×4=250(4-t ) 解得t=1.6即原有工人应该在机器开始工作1.6小时后开始包装.………………12分。
2014-2015学年八年级上学期期中联考数学试题(含答案)

2014-2015学年八年级上学期期中联考数学试题(含答案)(时间:100分钟,满分:100分)一、选择题(每题3分,共30分)1、下面各组线段中,能组成三角形的是( )A .5,11,6B .8,8,16C .10,5,4D .6,9,14 2、下列命题中:⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等.其中真命题的个数有( )A.3个B.2个C.1个D.0个 3、一个多边形内角和是10800,则这个多边形的边数为 ( ) A 、 6 B 、 7 C 、 8 D 、 9 4、等腰三角形的一个角是50,则它的底角是( ) A. 50 B. 50或65 C 、80 D 、65 5、和点P (2,5-)关于x 轴对称的点是( )A (-2,5-)B (2,5-)C (2,5)D (-2,5) 6、已知直角三角形中30°角所对的直角边为2 cm ,则斜边的长为( ). A .2 cm B .4 cm C .6 cm D .8 cm7、如图,已知12=∠∠,AC AD =,增加下列条件:①AB AE =;②BC ED =;③C D =∠∠;④B E =∠∠.其中能使ABC AED △≌△的条件有( ) A.4个 B.3个C.2个 D.个8、如图,先将正方形纸片对折,折痕为MN ,再把B 点折叠在折痕MN 上,折痕为AE ,点B 在MN 上的对应点为H ,沿AH 和DH 剪下,这样剪得的三角形中 ( ) A .AD DH AH ≠= B .AD DH AH == C .DH AD AH ≠= D .AD DH AH ≠≠9、如图,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 内部时,∠A 与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )A .∠A=∠1+∠2B .2∠A=∠1+∠2C .3∠A=2∠1+∠2D .3∠A=2(∠1+∠2)10、把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.在自然界和日常生活中,大量地存在这种图形变换(如图1).结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图2)的对应点所具有的性质是( ) A .对应点连线与对称轴垂直 B .对应点连线被对称轴平分 C .对应点连线被对称轴垂直平分 D .对应点连线互相平行 二、填空题(每题3分,共24分)11、为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条这样做的道理是_________ ______。
初中数学八年级2014—2015第一学期期中学业水平测试卷附参考答案

2014—2015 第一学期初二数学期中学业水平测试、选一选,牛刀初试露锋芒!(每小题3分,共42分)1.下列图形中,轴对称图形的个数是()A. 4个2 .下列说法正确的是()A .三角形的角平分线是射线。
B.三角形三条高都在三角形内。
C. 三角形的三条角平分线有可能在三角形内,也可能在三角形外。
D. 三角形三条中线相交于一点。
3 .两根木棒长分别为5cm和7cm,要选择第三根,将它们钉成一个三角形,?如果第三根木棒长为偶数, 则组成方法有b5E2RGbCAPA. 3种B. 4种C. 5种D. 6种4. 下列各组条件中,不能判定△AB4A A/B/C/的一组是()/ / / / / //—”//A、/ A=Z A,/B=Z B ,AB= A BB、/ A=Z A , AB= A B , AC=A C/ / / J / / / / / / /C、/ A=/ A , AB= A B , BC= B CD、AB= A B , AC=A C ,BC= B C5. 如图,已知△ ABC的六个元素,则下面甲、乙、丙三个三角形中和△ ABC全等的图形是(D.只有丙6.如图1,将长方形ABCD纸片沿对角线BD折叠,使点C落在C •处,BC交AD于丘,若• DBC =22.5 °,贝恠不添加任何辅助线的情况下, 则图中45的角(虚线也视为角的边)的个数是()A. 5个E 22.12.如图5,△ ABC 的三边 AB 、BC CA 长分别是 20、30、40,其三条 角平分线将△ ABC 分为三个三角形,则 S A ABO : S A BCO:CAO 等于( )A . 1 : 1 : 1B . 1 : 2 : 3C . 2 : 3 : 4D . 3 : 4 : 513.如图6, 一圆柱高8cm,底面半径2cm,—只蚂蚁从点A 爬到点B 处吃食,要爬行的最短路程 (二 取 3)是() DXDiTa9E3dA.20cm;B.10cm;C.14cm;D. 无法确定.7•如图2,有一张直角三角形纸片,两直角边 △ ABC 折叠,使点B 与点A 重合,折痕为DE 为( )A. 10 cm B . 12cmC8、若等腰三角形的腰长为10,底边长为12,A 、6B 、7C 、8AC=5cm BC=10cm则厶ACD 的周长盒命 图2 E.15cmD . 20cm则底边上的高为()D 、99.如图3,小明把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事 的办法是()p1EanqFDPwA.带①去B.带②去C.带③去D.带①和②去10、下列条件中,不能确定三角形是直角三角形的是(A.三角形中有两个角是互为余角; B.三角形三个内角之比为3 : 2 : 1; C.三角形的三边之比为3 : 2 : 1 ; D.三角形中有两个内角的差等于第三个内角 11.把两个都有一个锐角为30°的一样大小的直角三角形拼成如图 4所示的图形,两条直角边在同一直线上.则图中等腰三角形有( )个. A. 1个B . 2个C.3 个D.4 个F C D图4图5A图614.如图7所示,已知△ ABC和厶BDE都是等边三角形。
2014-2015学年度上八年数学期中试卷

2014——2015学年度第一学期八年级数学期中试卷一、填空题(每题3 分,共30分)1、如图ABC 中,AD 是BC 上的中线,BE 是ABD 中AD 边上的中线,若ABC 的面积是24,则ABE 的面积是________。
2、在等腰△ABC 中,如果两边长分别为6cm 、10cm ,则这个等腰三角形的周长为________.3、如图,CD 、CE 分别是△ABC 的高和角平分线,∠A =30°,∠B =60°,则∠DCE = .4、如图,∠1=_____.5、一个多边形的内角和为540°,则这个多边形的边数是_____________。
6、若一个多边形的每一个外角都等于45°,则这个多边形是___________边形.7、如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3= .8、如图,正方形的边长为4 cm ,则图中阴影部分的面积为 cm 2。
9、如图,在△ABC 中,∠ACB=90°,BE 平分∠ABC ,ED ⊥AB 于D .如果∠A=30°,AE=6cm ,那么CE 等于10、如图,一块四边形绿化园地,四角都做有半径为R 的圆形喷水池,则这四个喷水池占去二、选择题(每题3 分,共30 分)11、以下各组线段为边,能组成三角形的是( )A .1cm ,2cm ,4cmB .8cm ,6cm ,4cmC .12cm ,5cm ,6cmD .2cm ,3cm ,6cm 12、下面四个图形中,线段BE 是⊿ABC 的高的图是( )A B C D13、如图,将一副三角板叠放在一起,使直角的顶点重合于O ,则∠AOC+∠DOB=( ) A 、900B 、1200C 、1600D 、18014、三角形一个外角小于与它相邻的内角,这个三角形是( )A .直角三角形B .锐角三角形C .钝角三角形D .属于哪一类不能确定15、如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3等于 ( ) A .30° B .50° C .20° D .40°16、已知△ABC ≌△A ′B ′C ′,且△ABC 的周长为20,AB =8,BC =5,那么A ′C ′等于( ) A .5 B .6 C .7 D .817、如图,在△ABC 与△DEF 中,已有条件AB =DE ,还需添加两个条件才能使△ABC ≌△DEF ,不能添加的一组条件是( )1题图 3题图 4题图 7题图8题图 9题图 10题图13题图15题图 17题图A.∠B=∠E,BC=EF B. BC=EF,AC=DF C. ∠A=∠D,∠B=∠E D. ∠A=∠D,BC=EF 18、将一张矩形的纸对折,然后用笔尖在上面扎出“B”,再把它铺平,你可见到A B C D19、下列图形中,轴对称图形的个数是()A.4个 B.3个 C.2个 D.1个20、已知点P(1,)与Q (,2)关于x 轴成轴对称,则的值为()A.-1 B.1 C.-3 D. 3三、作图题(本题8分)21.按要求作图(不写作法,但要保留作图痕迹)如图,已知直线l和其外两点A,B, (1)试在图甲的直线l上找点C,使AC+BC得值最小;(2)试在图乙的直线l上找点D ,使得值最小。
上海2014-2015学年八年级上学期期中考试数学试题

田家炳中学2014-2015学年第一学期八年级数学期中测试一、选择题:(每小题3分,共18分)1. 下列方程是关于x 的一元二次方程的是( ) A .20ax bx c ++= B.2560k x k ++= C. 21320x x x++= D.()223210k x x +++= 2、用配方法解下列方程时,配方有错误的是( )A. 22990x x --=化为()21100x -= B.2890x x ++=化为()2425x +=C.22740t t --=化为1681472=⎪⎭⎫ ⎝⎛-t D.23420y y --=化为910322=⎪⎭⎫ ⎝⎛-y3、若函数2(26)(1)y m x m x =++-是正比例函数,则m 的值是( ) A 、m =-3 B 、m =1 C 、m =3 C 、m >-34、若y 与-3x 成反比例,x 与z4成正比例,则y 是z 的( ) A. 正比例函数 B 、反比例函数 C 、一次函数 D 、不能确定52,那么它的长y cm 与宽x cm 之间的函数关系用图象表示大致()AB C D6、∆ABC 中, 90=∠C ,AC=1,AB=2,点O 是AB 的中点,直线l 是线段AO 的垂直平分线,那么下列命题中,错误的是( )A.直线l 不经过点CB.点C 在直线l 上C.直线l 与AC 边相交D.直线l 与BC 边相交 二、填空题:(每小题2分,共28分)7. 关于x 的一元二次方程22(1)230m x x m m +++--=的一个根为x=0,则m 的值为__________ 8. 若关于x 的方程kx 2 -2x -1=0有两个不相等的实数根,则k 的取值范围是___________ 9. 方程x x =+2)32(的解是10. 我市某企业为节约用水,自建污水净化站,7月份净化污水3000吨,9月份增加到3630吨,则这两个月净化污水量的平均每月增加的百分率为 .11. 若12,x x 是方程x 2 -6x+k -1=0的两个根,且242221=+x x ,则k 的值为______________12. 函数1y x =-中自变量x 的取值范围是 。
2014-2015学年上海市闵行区九年级上学期期中数学试卷与解析

2014-2015学年上海市闵行区九年级(上)期中数学试卷一、选择题(本大题共6题,每题3分,满分18分)1.(3分)下列图形一定是相似图形的是()A.两个矩形B.两个正方形C.两个直角三角形 D.两个等腰三角形2.(3分)已知Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中正确的是()A.sinA=B.cosA=C.tanA=D.cotA=3.(3分)如果两个三角形相似,其中一个三角形的两个内角分别为82°、53°,那么另一个三角形中最小的内角为()A.82°B.53°C.45°D.不能确定4.(3分)如图:在△ABC中,点D、E分别在AB、AC上,根据下列给定的条件,不能判断DE与BC平行的是()A.B.C.D.5.(3分)如果线段b是线段a,c的比例中项,a:c=4:9,那么下列结论中正确的是()A.a:b=4:9 B.b:c=2:3 C.a:b=3:2 D.b:c=3:26.(3分)如图:已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列三角形中与△BDF一定相似的是()A.△BAC B.△BEC C.△BAE D.△BFA二、填空题(本大题共12题,每题2分,满分24分)7.(2分)已知:x:y=2:3,则(x+y):y=.8.(2分)如果在比例尺为1:1 000 000的地图上,A、B两地的图上距离是3.5厘米,那么A、B两地的实际距离是千米.9.(2分)已知两个相似三角形的相似比是4:9,那么它们对应的角平分线之比是.10.(2分)已知在△ABC中,AD是中线,G是重心,如果GD=3cm,那么AG= cm.11.(2分)已知点D是线段AB的黄金分割点(AD>BD),如果AB=2,那么AD 的长为.(结果保留根号)12.(2分)已知向量与方向相反,长度为5,则用来表示为:.13.(2分)如图,在△ABC中,D,E分别是AB,AC的中点,那么△ADE与四边形DBCE的面积之比是.14.(2分)如图,AD∥BC∥EF,AE:AB=2:3,DF=8,则FC=.15.(2分)在Rt△ABC中,∠C=90°,BC=3,,那么AB=.16.(2分)已知在△ABC中,AB=AC=5cm,BC=5,那么∠A=度.17.(2分)如图,四边形ABCD中,AC与BD交于点O,若BD=3DO,当OC:OA的值为时,则有AB∥DC.18.(2分)如图,已知平行四边形ABCD的面积等于12,AB=6,点P是AB上一点,PQ∥AD交BD于点Q,当AP:BP=1:5时,四边形PBCQ的面积是.三、解答题(第19-22题每题7分;第23-24题每题9分;第25题12分,共58分)19.(7分)计算:2sin260°﹣tan45°+cos30°•cot60°.20.(7分)已知两个不平行的向量、,求作:.(不要求写作法)21.(7分)如图,在Rt△ABC中,∠C=90°,AC=3,tanB=.(1)求BC的长;(2)求cosA的值.22.(7分)如图,已知在△ABC中,AD是BC边的中线,AE=EF=CF,BE与AD 交于点G,求DF:GB的值.23.(9分)已知:如图,在△ABC中,点D为边BC上的点,=,∠BAD=∠CAE.(1)求证:△BAC∽△DAE;(2)当∠BAC=90°时,求证:EC⊥BC.24.(9分)正方形ABCD中,AB=8,点P是CD上的一点,CE⊥BP垂足为E,EF ⊥AE与边BC交于点F(1)求证:△FCE∽△ABE;(2)当△ABE的周长是△FCE周长2倍时,求CP的长.25.(12分)如图1,已知正方形ABCD边长为1,点Q为BC延长线上的一个动点,QA与CD、BD分别交于点P、E.(1)当CQ=时,求的值;(2)如图2,如果对角线AC与BD相交于点O,联结QO,交CD于点F,设CQ=x,S△EOQ=y,求y关于x的函数关系式,并求出x的取值范围;(3)在(2)的条件下,△DEP能否与△DBQ相似,若能请求出x的值,若不能请说明理由.2014-2015学年上海市闵行区九年级(上)期中数学试卷参考答案与试题解析一、选择题(本大题共6题,每题3分,满分18分)1.(3分)下列图形一定是相似图形的是()A.两个矩形B.两个正方形C.两个直角三角形 D.两个等腰三角形【解答】解:A、两个矩形,对应角相等,对应边不一定成比例,故不符合题意;B、两个正方形,形状相同,大小不一定相同,符合相似性定义,故符合题意;C、两个直角三角形,只有一个直角相同,锐角不一定相等,故不符合题意;D、两个等腰三角形顶角不一定相等,故不符合题意.故选:B.2.(3分)已知Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中正确的是()A.sinA=B.cosA=C.tanA=D.cotA=【解答】解:如图:由勾股定理得:AB===,所以sinA===,cosA===,tanA==,cotA==,所以只有选项D正确,选项A、B、C都错误.故选:D.3.(3分)如果两个三角形相似,其中一个三角形的两个内角分别为82°、53°,那么另一个三角形中最小的内角为()A.82°B.53°C.45°D.不能确定【解答】解:∵一个三角形的两个内角分别为82°、53°,∴另一个内角=180°﹣82°﹣53°=45°.∵两个三角形相似,∴另一个三角形中最小的内角为45°.故选:C.4.(3分)如图:在△ABC中,点D、E分别在AB、AC上,根据下列给定的条件,不能判断DE与BC平行的是()A.B.C.D.【解答】解:∵,∴DE∥BC,A不合题意;∵,∴DE∥BC,B不合题意;∵,∴DE∥BC,C不合题意;,不能判断DE与BC平行,D符合题意;故选:D.5.(3分)如果线段b是线段a,c的比例中项,a:c=4:9,那么下列结论中正确的是()A.a:b=4:9 B.b:c=2:3 C.a:b=3:2 D.b:c=3:2【解答】解:∵a:c=4:9,∴9a=4c,∴a=c,c=a.∵线段b是线段a,c的比例中项,∴a:b=b:c,即b2=ac=c2=a2,∴b=c=a,∴a:b=c:c=2:3,∴b:c=a:b=2:3,故选:B.6.(3分)如图:已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列三角形中与△BDF一定相似的是()A.△BAC B.△BEC C.△BAE D.△BFA【解答】证明:∵BE平分∠ABC,∴∠ABE=∠CBE,∵∠BAD=∠C,∴△BFA∽△BEC,∴∠BFA=∠BEC,∴∠BFD=∠BEA,∵∠ABE=∠CBE,∴△BDF∽△BAE.故选:C.二、填空题(本大题共12题,每题2分,满分24分)7.(2分)已知:x:y=2:3,则(x+y):y=.【解答】解:∵=,∴=+1=+1=.故答案为:.8.(2分)如果在比例尺为1:1 000 000的地图上,A、B两地的图上距离是3.5厘米,那么A、B两地的实际距离是35千米.【解答】解:设A、B两地的实际距离是x厘米,∵比例尺为1:1 000 000,A、B两地的图上距离是3.5厘米,∴=,解得:x=3500000,∵3500000厘米=35千米,∴A、B两地的实际距离是35千米.故答案为:35.9.(2分)已知两个相似三角形的相似比是4:9,那么它们对应的角平分线之比是4:9.【解答】解:∵两个相似三角形的相似比是4:9,∴它们对应的角平分线之比是4:9.故答案为:4:9.10.(2分)已知在△ABC中,AD是中线,G是重心,如果GD=3cm,那么AG= 6cm.【解答】解:∵G是△ABC的重心,且AD是中线,∴AG=2GD=6cm.11.(2分)已知点D是线段AB的黄金分割点(AD>BD),如果AB=2,那么AD的长为.(结果保留根号)【解答】解:由于D为线段AB=8cm的黄金分割点,且AD>BD,则AD=2×=﹣1.故本题答案为:﹣1.12.(2分)已知向量与方向相反,长度为5,则用来表示为:=﹣且||=||=5.【解答】解:∵与方向相反,长度为5,∴=﹣且||=||=5.故答案为:=﹣且||=||=5.13.(2分)如图,在△ABC中,D,E分别是AB,AC的中点,那么△ADE与四边形DBCE的面积之比是1:3.【解答】解:∵D,E分别是AB,AC的中点∴DE∥BC∴△ADE∽△ABC,∴AD:AB=1:2∴△ADE与△ABC的面积之比为1:4∴△ADE与四边形DBCE的面积之比是1:3.故答案为:1:3.14.(2分)如图,AD∥BC∥EF,AE:AB=2:3,DF=8,则FC=4.【解答】解:∵AD∥BC∥EF,AE:AB=2:3,∴=,即,解得:DC=12,∴FC=DC﹣DF=12﹣8=4;故答案为:4.15.(2分)在Rt△ABC中,∠C=90°,BC=3,,那么AB=15.【解答】解:如图:∵=,BC=3,∴AB=5BC=15,故答案为:15.16.(2分)已知在△ABC中,AB=AC=5cm,BC=5,那么∠A=120度.【解答】解:作AD⊥BC于D,∵AB=AC=5cm,底边BC=5cm,∴AD是∠A的平分线,BD=DC=BC=,∴Sin∠BAD==,∴∠BAD=60°,∴∠BAC=120°.故答案为:120.17.(2分)如图,四边形ABCD中,AC与BD交于点O,若BD=3DO,当OC:OA的值为时,则有AB∥DC.【解答】当OC:OA的值为时,则有AB∥DC,证明:∵BD=3DO,∴BO=2D0,∴,∵,∴,∵∠COD=∠AOB,∴△COD∽△AOB,∴∠DCA=∠BAC,AB∥DC,故答案为.18.(2分)如图,已知平行四边形ABCD的面积等于12,AB=6,点P是AB上一点,PQ∥AD交BD于点Q,当AP:BP=1:5时,四边形PBCQ的面积是.【解答】解:∵平行四边形ABCD的面积等于12,∴S=S△BCD=S平行四边形ABCD=6,△ABD∵PQ∥AD,∴△BPQ∽△ABD,DQ:BQ=AP:BP=1:5∴=()2,∵AP:BP=1:5,∴=,过D作DE⊥AB于E,QF⊥PB于F,∵AB=6,∴DE=2,AP=1,PB=5,∴QF=,∴S△PBQ=××5=,∵PQ∥AD,∴DQ:BQ=AP:BP=1:5,∴BQ:BD=5:6,∴S△BCQ=S△BCD=5,∴四边形PBCQ的面积=S△PBQ +S△BCQ=,故答案为:.三、解答题(第19-22题每题7分;第23-24题每题9分;第25题12分,共58分)19.(7分)计算:2sin260°﹣tan45°+cos30°•cot60°.【解答】解:原式=2×()2﹣1+×=﹣1+=1.20.(7分)已知两个不平行的向量、,求作:.(不要求写作法)【解答】解:=+3﹣4+=2﹣.如图:∵=2,=,∴=﹣=2﹣.则即为所求.21.(7分)如图,在Rt△ABC中,∠C=90°,AC=3,tanB=.(1)求BC的长;(2)求cosA的值.【解答】解:(1)∵∠C=90°,AC=3,tanB=,∴tanB===,∴BC=6;(2)∵AC=3,BC=6,∴AB==3,∴cosA===.22.(7分)如图,已知在△ABC中,AD是BC边的中线,AE=EF=CF,BE与AD 交于点G,求DF:GB的值.【解答】解:∵AD是BC边的中线,∴BD=CD,∵AE=EF=CF,∴DF是△BCE的中位线,∴DF∥BE,DF=BE,∴GE:DF=AE:AF=1:2,∴DF:GB=2:3.23.(9分)已知:如图,在△ABC中,点D为边BC上的点,=,∠BAD=∠CAE.(1)求证:△BAC∽△DAE;(2)当∠BAC=90°时,求证:EC⊥BC.【解答】(1)证明:∵∠BAD=∠CAE,∴∠BAD+∠DAC=∠DAC+∠CAE,即∠DAE,∵=,∴=,∴△BAC∽△DAE;(2)解:∵△BAC∽△DAE,∴∠B=∠ACE,∵∠BAC=90°,∴∠B+∠ACB=90°,∴∠ACB+∠ACB=90°,即∠BCE=90°,∴EC⊥BC.24.(9分)正方形ABCD中,AB=8,点P是CD上的一点,CE⊥BP垂足为E,EF⊥AE与边BC交于点F(1)求证:△FCE∽△ABE;(2)当△ABE的周长是△FCE周长2倍时,求CP的长.【解答】(1)证明:∵CE⊥BP,EF⊥AE,∴∠AEB+∠BEF=∠BEF+∠FEC,∴∠AEB=∠FEC,正方形ABCD中,∵∠ABC=∠BCD=90°,∴∠EPC+∠ECP=∠BCE+∠ECP=90°,∴∠ECF=∠BPC,∵AB∥CD,∴∠ABE=∠BPC,∴∠ABE=∠ECF,∴△ABE∽△CEF;(2)∵△ABE∽△CEF,△ABE的周长是△FCE周长2倍,∴,∵∠CBE=∠ECP,∠BEC=∠CEP,∴△CPE∽△BCE,∴=,∵BC=AB=8,∴CP=4.25.(12分)如图1,已知正方形ABCD边长为1,点Q为BC延长线上的一个动点,QA与CD、BD分别交于点P、E.(1)当CQ=时,求的值;(2)如图2,如果对角线AC与BD相交于点O,联结QO,交CD于点F,设CQ=x,S△EOQ=y,求y关于x的函数关系式,并求出x的取值范围;(3)在(2)的条件下,△DEP能否与△DBQ相似,若能请求出x的值,若不能请说明理由.【解答】解:(1)∵CQ=,∴BQ=BC+CQ=1+=,∵AD∥BQ,∴==,∴=;(2)作QH⊥BD,垂足为点H,∵ABCD是正方形,∴∠DBQ=45°,在Rt△BQH中,QH=BQsin∠DBQ=(1+x),∵AD∥BQ,∴=,∵BD=,∴DE=,∵OD=BD=,∴OE=OD﹣DE=﹣=,∴y=OE•QH=×(1+x)×=(x>0);(3)∵四边形ABCD是正方形,∴∠EDP=∠DBQ=45°,若∠DEP=∠BDQ,则△DEP∽△BDQ,∵∠DEP=∠DBQ+∠AQC,∠BDQ=∠BDC+∠1,∴∠AQC=∠1=∠2,在△DAP和△CQD中,,∴△DAP≌△CQD(ASA),∴DP=CQ=x,∴PC=1﹣x,∵△ADP∽△QCP,∴=,∴=,解得:x1=,x2=(舍去),∴x的值是.。
2014-2015学年上海市闵行区九校联考八年级(下)期中数学试卷
2014-2015学年上海市闵行区九校联考八年级(下)期中数学试卷显示答案一、选择题(每题3分,满分18分)1.下列函数中,是一次函数的是( )A .y =1x+1 B .y=-2x C .y=x 2+2 D .y=kx+b(k 、b 是常数)2.下列关于x 的方程中,有实数根的是( )A .x 2+2x+3=0B .x 3+2=0C .x x-1=1x-1D .x-2+3=03.下列方程组中,属于二元二次方程组的为( )A . ⎩⎨⎧x +y =0x -y =2B . ⎩⎨⎧1x + 2y ==-4C . ⎩⎨⎧x + y =1x +y =1D . ⎩⎨⎧3x =2xy =4 4.一次函数y=kx+b 的图象如图所示,当y >4时,x 的取值范围是( )A .x <0B .x >0C .x <2D .x >25.某农场开挖一条长480米的渠道,开工后每天比原计划多挖20米,结果提前4天完成任务,若设原计划每天挖x 米,那么下列方程中正确的是( )A .480x-20- 480x =4B .480x - 480x+4=20C .480x - 480x+20=4D .480x-4- 480x=20 6.李庄与张庄两地之间的距离是100千米,若汽车以平均每小时80千米的速度从李庄开往张庄,则汽车距张庄的路程y (千米)与行驶时间x (小时)之间的函数关系式是( )A .y=80x-100B .y=-80x-100C .y=80x+100D .y=-80x+100二、填空题(每题2分,满分24分)7.一次函数y=x-5在y 轴上的截距是________.8.直线y=12x-1与x 轴的交点坐标是________ .9.如图,将直线OA 向下平移2个单位,得到一个一次函数的图象,那么这个一次函数的解析式是________.10.如果y=-x+m 不经过第一象限,那么实数m 的取值范围是________.11.若点A ()7,y 1、点B ()5,y 2是直线y =- 12x+b(b 为常数)上的点,则y 1,y 2大小关系是________.12.二项方程12x 5-16=0的实数根是________.13.关于x 的方程m(x+2)=3(m≠0)的解为________.14.在解方程3x x-1+ 2x-2x +3=0时,如果设x x-1=y ,则原方程可化为关于y 的一元二次方程的一般形式是________.15.把二元二次方程x 2-5xy+6y 2=0化成两个一次方程,那么这两个一次方程是________.16.如果一个多边形的每一个外角都等于72°,则该多边形的内角和等于________ 度.17.如果x=3是方程x x-3=2- k 3-x的增根,那么k 的值为________ .18.已知直线y=kx+b 与坐标轴围成的三角形面积是6,且经过(3,0),则这条直线的解析式为________.三、计算题(每题6分,满分24分)19.解方程:2x+1-1=11-x. 20.解方程:6-2 x-3=x .21.解方程组: ⎩⎨⎧x 2-9y 2=15x +3y =5. 22.解方程组: ⎩⎨⎧4x +y + 6x -y==1.四、解答题:(满分24分,其中23题7分;24题8分;25题9分)23.已知一次函数图象经过点M(4,3)且平行于直线y=- 34x+3(1)求这个函数的解析式;(2)所求得的一次函数的图象与坐标轴围成的三角形面积.24.甲、乙两家便利店到批发站采购一批饮料,共25箱,由于两店所处的地理位置不同,因此甲店的销售价格比乙店的销售价格每箱多10元.当两店将所进的饮料全部售完后,甲店的营业额为1000元,比乙店少350元,求甲乙两店各进货多少箱饮料?25.一个水槽有进水管和出水管各一个,进水管每分钟进水m升,出水管每分钟出水n升,水槽在开始5分钟内只进水不出水,随后15分钟内既进水又出水,得到时间x(分)与水量y(升)之间的关系如图所示:(1)求m、n的值;(2)如果在20分钟之后只出水不进水,单位时间进、出水量不变,求这段时间内y 关于x的函数解析式及定义域,并画出图象.五、解答题(共1小题,满分10分)26.如图①所示,直线L:y=mx+5m与x轴负半轴、y轴正半轴分别交于A、B两点.(1)当OA=OB时,请确定直线L的解析式.(2)在(1)的条件下,如图②所示,设Q为AB延长线上一点,作直线OQ,过点A、B两点分别作AM⊥OQ于点M,BN⊥OQ于点N,若AM=4,BN=3,求MN的长.(3)如图③,当m取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为边,点B为直角顶点,在第一、二象限内作等腰直角三角形OBF和等腰直角三角形ABE,联结EF交y轴于点P,.问:当点B在y轴正半轴上运动时,试猜想PB的长是否为定值,若是,请求出其值;若不是,请说明理由.纠错/评论点击显示评论解析质量:好中差提交。
2014--2015学年八年级上数学期中测试卷含答案R
《二元一次方程组》提高测试姓名 班级 学号(一)填空题(每空2分,共28分):1.已知(a -2)x -by |a |-1=5是关于x 、y 的二元一次方程,则a =______,b =_____. 2.若|2a +3b -7|与(2a +5b -1)2互为相反数,则a =______,b =______. 4.2x -3y =4x -y =5的解为_______________.5.已知⎩⎨⎧==12y x -是方程组⎩⎨⎧=++=-274123ny x y mx 的解,则m 2-n 2的值为_________.6.若满足方程组⎩⎨⎧=-+=-6)12(423y k kx y x 的x 、y 的值相等,则k =_______. 7.已知2a =3b =4c ,且a +b -c =121,则a =_______,b =_______,c =_______. 8.解方程组⎪⎩⎪⎨⎧=+=+=+634323x z z y y x ,得x =______,y =______,z =______.(二)选择题(每小题2分,共16分):9.若方程组⎩⎨⎧=++=-10)1(232y k kx y x 的解互为相反数,则k 的值为…………………( )(A )8 (B )9 (C )10 (D )1110.若⎩⎨⎧-==20y x ,⎪⎩⎪⎨⎧==311y x 都是关于x 、y 的方程|a |x +by =6的解,则a +b 的值为( ) (A )4 (B )-10 (C )4或-10 (D )-4或10 11.关于x ,y 的二元一次方程ax +b =y 的两个解是⎩⎨⎧-==11y x ,⎩⎨⎧==12y x ,则这个二元一次方程是……………………( )(A )y =2x +3 (B )y =2x -3(C )y =2x +1 (D )y =-2x +112.由方程组⎩⎨⎧=+-=+-0432032z y x z y x 可得,x ∶y ∶z 是………………………………( )(A )1∶2∶1 (B )1∶(-2)∶(-1)(C )1∶(-2)∶1 (D )1∶2∶(-1) 13.如果⎩⎨⎧=-=21y x 是方程组⎩⎨⎧=-=+1cy bx by ax 的解,那么,下列各式中成立的是…( )(A )a +4c =2 (B )4a +c =2 (C )a +4c +2=0 (D )4a +c +2=014.关于x 、y 的二元一次方程组⎩⎨⎧=+=-2312y mx y x 没有解时,m 的值是…………( )(A )-6 (B )-6 (C )1 (D )015.若方程组⎪⎩⎪⎨⎧=+=+52243y bax y x 与⎪⎩⎪⎨⎧=-=-5243y x by x a 有相同的解,则a 、b 的值为( ) (A )2,3 (B )3,2 (C )2,-1 (D )-1,216.若2a +5b +4z =0,3a +b -7z =0,则a +b -c 的值是……………………( )(A )0 (B )1 (C )2 (D )-1(三)解方程组(每小题4分,共16分):17.⎪⎪⎩⎪⎪⎨⎧=+=-+.022325232y x y y x 18.⎪⎩⎪⎨⎧⨯=++=-8001005.8%60%10)503(5)150(2y x y x19.⎪⎩⎪⎨⎧=++-=+--.6)(2)(3152y x y x yx y x 20.⎪⎩⎪⎨⎧=---=+-=+-.441454y x z x z y z y x《二元一次方程组》提高测试姓名班级学号(四)解答题(每小题5分,共20分):21.已知⎩⎨⎧=+-=-+25434zyxzyx,xyz≠0,求222223yxzxyx+++的值.22.甲、乙两人解方程组⎩⎨⎧=+-=-514byaxbyx,甲因看错a,解得⎩⎨⎧==32yx,乙将其中一个方程的b写成了它的相反数,解得⎩⎨⎧-=-=21yx,求a、b的值.23.已知满足方程2 x-3 y=m-4与3 x+4 y=m+5的x,y也满足方程2x+3y=3m-8,求m的值.24.当x=1,3,-2时,代数式ax2+bx+c的值分别为2,0,20,求:(1)a、b、c的值;(2)当x=-2时,ax2+bx+c的值.(五)列方程组解应用题(第1题6分,其余各7分,共20分):25.有一个三位整数,将左边的数字移到右边,则比原来的数小45;又知百位上的数的9倍比由十位上的数与个位上的数组成的两位数小3.求原来的数.⎩⎨⎧=++=-+.y x xy y x 391045100 26.某人买了4 000元融资券,一种是一年期,年利率为9%,另一种是两年期,年利率是12%,分别在一年和两年到期时取出,共得利息780元.两种融资券各买了多少?27.汽车从A 地开往B 地,如果在原计划时间的前一半时间每小时驶40千米,而后一半时间由每小时行驶50千米,可按时到达.但汽车以每小时40千米的速度行至离AB 中点还差40千米时发生故障,停车半小时后,又以每小时55千米的速度前进,结果仍按时到达B 地.求AB 两地的距离及原计划行驶的时间.《二元一次方程组》提高测试 答案(一)填空题(每空2分,共28分):1.已知(a -2)x -by |a |-1=5是关于x 、y 的二元一次方程,则a =______,b =_____. 【提示】要满足“二元”“一次”两个条件,必须a -2≠0,且b ≠0,及| a |-1=1. 【答案】a =-2,b ≠0.2.若|2a +3b -7|与(2a +5b -1)2互为相反数,则a =______,b =______. 【提示】由“互为相反数”,得|2a +3 b -7|+(2a +5b -1)2=0,再解方程组⎩⎨⎧=-+=-+01520732b a b a 【答案】a =8,b =-3.3.二元一次方程3x +2y =15的正整数解为_______________. 【提示】将方程化为y =2315x-,由y >0、x >0易知x 比0大但比5小,且x 、y 均为整数.【答案】⎩⎨⎧==61y x ,⎩⎨⎧==.33y x4.2x -3y =4x -y =5的解为_______________.【提示】解方程组⎩⎨⎧=-=-54532y x y x .【答案】⎩⎨⎧-==.11y x 5.已知⎩⎨⎧==12y x -是方程组⎩⎨⎧=++=-274123ny x y mx 的解,则m 2-n 2的值为_________.【提示】把⎩⎨⎧==12y x -代入方程组,求m ,n 的值.【答案】-438.6.若满足方程组⎩⎨⎧=-+=-6)12(423y k kx y x 的x 、y 的值相等,则k =_______.【提示】作y =x 的代换,先求出x 、y 的值.【答案】k =65. 7.已知2a =3b =4c ,且a +b -c =121,则a =_______,b =_______,c =_______. 【提示】即作方程组⎪⎪⎩⎪⎪⎨⎧=-+==121432c b a cb a ,故可设a =2 k ,b =3 k ,c = 4 k ,代入另一个方程求k 的值. 【答案】a =61,b =41,c =31.【点评】设“比例系数”是解有关数量比的问题的常用方法.8.解方程组⎪⎩⎪⎨⎧=+=+=+634323x z z y y x ,得x =______,y =______,z =______.【提示】根据方程组的特征,可将三个方程左、右两边分别相加,得2 x +3 y +z =6,再与3 y +z =4相减,可得x .【答案】x =1,y =31,z =3. (二)选择题(每小题2分,共16分):9.若方程组⎩⎨⎧=++=-10)1(232y k kx y x 的解互为相反数,则k 的值为…………………( )(A )8 (B )9 (C )10 (D )11【提示】将y =-x 代入方程2 x -y =3,得x =1,y =-1,再代入含字母k 的方程求解.【答案】D .10.若⎩⎨⎧-==20y x ,⎪⎩⎪⎨⎧==311y x 都是关于x 、y 的方程|a |x +by =6的解,则a +b 的值为( ) (A )4 (B )-10 (C )4或-10 (D )-4或10 【提示】将x 、y 对应值代入,得关于| a |,b 的方程组⎪⎩⎪⎨⎧=+=-.631||62b a b 【答案】C .【点评】解有关绝对值的方程,要分类讨论.11.关于x ,y 的二元一次方程ax +b =y 的两个解是⎩⎨⎧-==11y x ,⎩⎨⎧==12y x ,则这个二元一次方程是……………………( )(A )y =2x +3 (B )y =2x -3 (C )y =2x +1 (D )y =-2x +1【提示】将x 、y 的两对数值代入ax +b =y ,求得关于a 、b 的方程组,求得a 、b 再代入已知方程. 【答案】B .【点评】通过列方程组求待定字母系数是常用的解题方法.12.由方程组⎩⎨⎧=+-=+-0432032z y x z y x 可得,x ∶y ∶z 是………………………………( )(A )1∶2∶1 (B )1∶(-2)∶(-1)(C )1∶(-2)∶1 (D )1∶2∶(-1)【提示】解方程组时,可用一个未知数的代数式表示另外两个未知数,再根据比例的性质求解. 【答案】A .【点评】当方程组未知数的个数多于方程的个数时,把其中一个未知数看作已知常数来解方程组,是可行的方法.13.如果⎩⎨⎧=-=21y x 是方程组⎩⎨⎧=-=+10cy bx by ax 的解,那么,下列各式中成立的是…( ) (A )a +4c =2 (B )4a +c =2 (C )a +4c +2=0 (D )4a +c +2=0 【提示】将⎩⎨⎧=-=21y x 代入方程组,消去b ,可得关于a 、c 的等式.【答案】C .14.关于x 、y 的二元一次方程组⎩⎨⎧=+=-2312y mx y x 没有解时,m 的值是…………( )(A )-6 (B )-6 (C )1 (D )0【提示】只要满足m ∶2=3∶(-1)的条件,求m 的值. 【答案】B . 【点评】对于方程组⎩⎨⎧=+=+222111c y b x a c y b x a ,仅当21a a =21b b ≠21c c时方程组无解.15.若方程组⎪⎩⎪⎨⎧=+=+52243y bax y x 与⎪⎩⎪⎨⎧=-=-5243y x by x a有相同的解,则a 、b 的值为( ) (A )2,3 (B )3,2 (C )2,-1 (D )-1,2【提示】由题意,有“相同的解”,可得方程组⎩⎨⎧=-=+52243y x y x ,解之并代入方程组⎪⎪⎩⎪⎪⎨⎧=-=-4352by x a y b ax ,求a 、b . 【答案】B . 【点评】对方程组“解”的含义的正确理解是建立可解方程组的关键. 16.若2a +5b +4z =0,3a +b -7z =0,则a +b -c 的值是……………………( )(A )0 (B )1 (C )2 (D )-1【提示】把c 看作已知数,解方程组⎩⎨⎧=-+=++0730452c b a c b a 用关于c 的代数式表示a 、b ,再代入a +b -c .【答案】A .【点评】本题还可采用整体代换(即把a +b -c 看作一个整体)的求解方法. (三)解方程组(每小题4分,共16分):17.⎪⎪⎩⎪⎪⎨⎧=+=-+.022325232y x y y x【提示】将方程组化为一般形式,再求解.【答案】⎪⎩⎪⎨⎧-==.232y x18.⎪⎩⎪⎨⎧⨯=++=-8001005.8%60%10)503(5)150(2y x y x 【提示】将方程组化为整系数方程的一般形式,再用加减法消元. 【答案】⎩⎨⎧==.30500y x19.⎪⎩⎪⎨⎧=++-=+--.6)(2)(3152y x y x yx y x 【提示】用换元法,设x -y =A ,x +y =B ,解关于A 、B 的方程组⎪⎩⎪⎨⎧=+=-623152B A BA , 进而求得x ,y .【答案】⎩⎨⎧-==.11y x20.⎪⎩⎪⎨⎧=---=+-=+-.441454y x z x z y z y x 【提示】 将三个方程左,右两边分别相加,得4x -4y +4z =8,故 x -y +z =2 ④,把④分别与第一、二个方程联立,然后用加、减消元法即可求得x 、z的值.【答案】⎪⎪⎪⎩⎪⎪⎪⎨⎧=-==.15451z y x(四)解答题(每小题5分,共20分):21.已知⎩⎨⎧=+-=-+0254034z y x z y x ,xyz ≠0,求222223y x zxy x +++的值. 【提示】把z 看作已知数,用z 的代数式表示x 、y ,可求得x ∶y ∶z =1∶2∶3.设x =k ,y =2 k ,z =3 k ,代入代数式.【答案】516. 【点评】本题考查了方程组解法的灵活运用及比例的性质.若采用分别消去三个元可得方程21 y -14 z =0,21 x -7 z =0,14 x -7 y =0,仍不能由此求得x 、y 、z 的确定解,因为这三个方程不是互相独立的.22.甲、乙两人解方程组⎩⎨⎧=+-=-514by ax by x ,甲因看错a ,解得⎩⎨⎧==32y x ,乙将其中一个方程的b 写成了它的相反数,解得⎩⎨⎧-=-=21y x ,求a 、b 的值.【提示】可从题意的反面入手,即没看错什么入手.如甲看错a ,即没看错b ,所求得的解应满足4 x -by =-1;而乙写错了一个方程中的b ,则要分析才能确定,经判断是将第二方程中的b 写错. 【答案】a =1,b =3.23.已知满足方程2 x -3 y =m -4与3 x +4 y =m +5的x ,y 也满足方程2x +3y =3m -8,求m 的值.【提示】由题意可先解方程组⎩⎨⎧-=+-=-8332432m y x m y x 用m 的代数式表示x ,y再代入3 x +4 y =m +5. 【答案】m =5.24.当x =1,3,-2时,代数式ax 2+bx +c 的值分别为2,0,20,求:(1)a 、b 、c 的值;(2)当x =-2时,ax 2+bx +c 的值.【提示】由题得关于a 、b 、c 的三元一次方程组,求出a 、b 、c 再代入这个代数式. 【答案】a =1,b =-5,c =6;20.【点评】本例若不设第一问,原则上也应在求出a 、b 、c 后先写出这个代数式,再利用它求值.用待定系数法求a 、b 、c ,是解这类问题常用的方法.(五)列方程组解应用题(第1题6分,其余各7分,共20分):25.有一个三位整数,将左边的数字移到右边,则比原来的数小45;又知百位上的数的9倍比由十位上的数与个位上的数组成的两位数小3.求原来的数. 【提示】设百位上的数为x ,由十位上的数与个位上的数组成的两位数为y ,根据题意,得⎩⎨⎧=++=-+.y x xy y x 391045100 【答案】x =4,y =39,三位数是439.【点评】本例分别设十位上的数和个位上的数为不同的未知数,无论从列方程组还是解方程组都更加简捷易行.26.某人买了4 000元融资券,一种是一年期,年利率为9%,另一种是两年期,年利率是12%,分别在一年和两年到期时取出,共得利息780元.两种融资券各买了多少?【提示】若设一年期、二年期的融资券各买x 元,y 元,由题意,得⎪⎩⎪⎨⎧=⋅+=+78010012210090004y x y x【答案】x =1 200,y =2 800.【点评】本题列方程组时,易将二年期的融资券的利息误认为是10012y 元,应弄清题设给出的是年利率,故几年到期的利息应该乘几.27.汽车从A 地开往B 地,如果在原计划时间的前一半时间每小时驶40千米,而后一半时间由每小时行驶50千米,可按时到达.但汽车以每小时40千米的速度行至离AB 中点还差40千米时发生故障,停车半小时后,又以每小时55千米的速度前进,结果仍按时到达B 地.求AB 两地的距离及原计划行驶的时间. 【提示】设原计划用x 小时,AB 两地距离的一半为y 千米, 根据题意,得⎪⎪⎩⎪⎪⎨⎧-=++-=⋅+⋅21554040402250240x y y y x x 【答案】x =8,2y =360.【点评】 与本例中设AB 两地距离的一半为y 千米一样,也可设原计划的一半时间为x 小时.恰当地设未知数,可以使列方程组和解方程组都更加简便.。
2014-2015八年级第一学期期中试卷(含答案)
ACB D E 人教版2014-2015学年度第一学期八年级数学期中考试试卷(含参考答案)一、选择题:(本题满分24分,每小题3分)在下列各题的四个备选答案中,只有一个是正确的,请把你认为正确的答案的字母代号填在题后的括号内。
......... 1.下列各组线段能组成一个三角形的是( ).(A)5cm ,8cm ,12cm (B)2cm ,3cm ,6cm (C)3cm ,3cm ,6cm (D)4cm ,7cm ,11cm 2.下列图案是轴对称图形的有( )。
A.(1)(2)B.(1)(3)C.(1)(4)D.(2)(3)(1) (2) (3) (4)3.下列几种说法:①全等三角形的对应边相等;②面积相等的两个三角形全等;③周长相等的两个三角形全等;④全等的两个三角形一定重合。
其中正确的是( )。
A. ①② B. ②③ C. ③④ D. ①④ 4.已知直角三角形中30°角所对的直角边为2㎝,则斜边的长为( )。
A. 2 ㎝B. 4 ㎝C. 6 ㎝D. 8㎝ 5.点M (1,2)关于y 轴对称的点的坐标为 ( )。
A.(—1,2)B.(-1,-2)C. (1,-2)D. (2,-1) 6.如图,∠B=∠D=90°,CB=CD ,∠1=40°,则∠2=( )。
A .40° B. 45° C. 60° D. 50°7. 如图所示,在△ABC 中,已知点D,E,F 分别为边BC,AD,CE 的中点,且S △ABC=4cm 2,则阴影部分的面积等于( )A.2cm 2B.1cm 2C.12cm 2D.1 4 cm 28.已知等腰三角形一个内角是70°,则另外两个内角的度数是( )A.55°, 55°B.70°, 40°C.55°, 55°或70°, 40°D.以上都不对 二 、填空题:(本题满分24分,每小题3分)9.一扇窗户打开后,用窗钩可将其固定,这里运用的几何原理为 。
2014-2015学年上海市闵行区九校联考八年级(上)期末数学试卷
2014-2015学年上海市闵行区九校联考八年级(上)期末数学试卷一、选择题(每题3分,共18分)1.(3分)下列各组代数式中,互为有理化因式的是()A.+1与1﹣B.+y与﹣﹣y C.2﹣与﹣2 D.与x 2.(3分)关于x的方程x2+kx﹣1=0的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.只有一个实数根 D.没有实数根3.(3分)分别以下列各组线段为边的三角形中不是直角三角形的是()A.10,24,26 B.15,20,25 C.8,10,12 D.1,,4.(3分)已知,在△ABC中,CD是中线,CD=AB,那么下列判断错误的是()A.∠DAC=∠DCA B.∠DBC=∠DCB C.∠ACB=90°D.∠A=30°5.(3分)下列说法中正确的是()A.每个命题都有逆命题B.每个定理都有逆定理C.真命题的逆命题是真命题D.假命题的逆命题是假命题6.(3分)如图,在矩形ABCD中,AB=1,BC=2,动点E从点C出发,以每秒1个单位的速度沿路线C→D→A作匀速运动,点E到达A点运动停止,那么△BEC 的面积y与点E运动的时间x秒之间的函数图象大致是()A.B. C. D.二、填空题(每题2分,共24分)7.(2分)化简:=.8.(2分)计算:(2+3)(2﹣3)=.9.(2分)方程(x+1)2=3x+3的根是.10.(2分)在实数范围内分解因式2x2﹣3xy﹣4y2=.11.(2分)一件商品原价每件1000元,连续两次降价后每件810元,若每次降价的百分率相同,那么每次降价的百分率是.12.(2分)A(﹣1,3)在正比例函数y=kx图象上,则y随着x的增大而.13.(2分)已知函数f(x)=,那么f(﹣1)=.14.(2分)函数y=的定义域是.15.(2分)直角坐标平面内两点P(4,﹣3)、Q(2,﹣1)距离是.16.(2分)如图,矩形内有两个相邻的正方形,面积分别为4和2,那么阴影部分的面积是.17.(2分)在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足是E,则AE:BE=.18.(2分)点E、F分别在一张长方形纸条ABCD的边AD、BC上,将这张纸条沿着直线EF对折后如图,BF与DE交于点G,如果∠BGD=30°,长方形纸条的宽AB=2cm,那么这张纸条对折后的重叠部分的面积S△GEF=cm2.三、简答题(第19、20每题5分,第21、22、23每题6分,满分28分)19.(5分)计算:(+2+(﹣)0+÷.20.(5分)解方程:+=x.21.(6分)已知正比例函数y=k1x(k1≠0)的图象经过A(2,﹣4)、B(m,2)两点.(1)求m的值;(2)如果点B在反比例函数(k2≠0)的图象上,求反比例函数的解析式.22.(6分)有两段长度相等的河渠挖掘任务,分别交给甲、乙两个工程队同时进行挖掘.如图是反映所挖河渠长度y(米)与挖掘时间x(时)之间关系的部分图象.请解答下列问题:(1)乙队开挖到30米时,用了小时;开挖6小时时,甲队比乙队多挖了米;(2)甲队在0≤x≤6的时段内,y与x之间的函数关系式是;(3)如果甲队施工速度不变,乙队在开挖6小时后,施工速度应为每小时米,才能与甲队同时完成110米的挖掘任务.23.(6分)已知:如图,AD∥BC,DB平分∠ADC,CE平分∠BCD,交AB于点E,BD于点O.求证:点O到EB与ED的距离相等.四、(第24题6分,第25、26题每题7分,满分20分)24.(6分)如图1,在边长为20cm和15cm的长方形纸片中剪去一个一边长为xcm的小长方形后,将图中的阴影部分Ⅰ剪下,恰好能与原纸片拼成一个面积为264cm2的长方形(如图2).问x的长是多少?25.(7分)已知:如图,在△ABC中,BD⊥AC,D为垂足,E是AB的中点,EF ∥BC,交AC于点F,∠A=2∠C.求证:DE=AB.26.(7分)如图,在平面直角坐标系中,直线AB分别与x轴正半轴交于点A、B,OA=3,OB=,将△AOB沿直线AB翻折,点O的对应点C恰好落在双曲线y=(k>0)上.(1)求k的值;(2)如果将△ABC绕AC的中点旋转180°得到△PCA.①请直接写出点P的坐标;②判断点P是否在双曲线y=上,并说明理由.五、(本题满分10分)27.(10分)在Rt△ABC中,∠C=90°,∠B=30°,AB=10,点D是射线CB上的一个动点,△ADE是等边三角形,点F是AB的中点,联结EF.(1)如图,当点D在线段CB上时,①求证:△AEF≌△ADC;②联结BE,设线段CD=x,线段BE=y,求y关于x的函数解析式及定义域;(2)当∠DAB=15°时,求△ADE的面积.2014-2015学年上海市闵行区九校联考八年级(上)期末数学试卷参考答案一、选择题(每题3分,共18分)1.A;2.A;3.C;4.D;5.A;6.D;二、填空题(每题2分,共24分)7.;8.2;9.x=﹣1或x=2;10.(x+y)(x+y),;11.10%;12.减小;13.2+;14.x≤;15.2;16.2 ﹣2.;17.1:3;18.4;三、简答题(第19、20每题5分,第21、22、23每题6分,满分28分)19.;20.;21.;22.2;10;y=10x(0≤x≤6);12;23.;四、(第24题6分,第25、26题每题7分,满分20分)24.;25.;26.;五、(本题满分10分)27.;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014-2015学年上海市闵行区八年级(上)期中数学试卷一、填空题(每小题2分,共28分)1.(2.00分)化简:=.2.(2.00分)写出的一个有理化因式.3.(2.00分)=•成立的条件为.4.(2.00分)化简:+1=.5.(2.00分)若最简根式与是同类根式,则2a+b=.6.(2.00分)在实数范围内因式分解:y4+5y2﹣14=.7.(2.00分)已知关于x的一元二次方程x2+x+m﹣1=0有实数根,则m的取值范围是.8.(2.00分)已知a<﹣4,化简﹣|2﹣a|=.9.(2.00分)某公司一月份的产值为70万元,二、三月份的平均增长率都为x,三月份的产值比二月份产值多10万元,则可列方程为.10.(2.00分)若﹣﹣6=0,则+=.11.(2.00分)如图,已知OC是∠AOB的平分线,DC∥OB,那么△DOC一定是三角形(填按边分类的所属类型).12.(2.00分)把“同角的补角相等”改为如果…,那么…的形式:.13.(2.00分)如图,已知AB=CD,要使△ABC≌△DCB成立,还需填加一个条件,那么这个条件可是:.14.(2.00分)在△DEF中,DE=DF,EG为DF边上的高,∠DEG=70°,则∠EDF=.二、选择题(每小题3分,共12分)15.(3.00分)下列二次根式中,属于同类二次根式的是()A.与B.与C.与D.与16.(3.00分)化简(a>0),下列结果正确的是()A.b B.b C.﹣b D.﹣b17.(3.00分)下列命题中,真命题的个数是()(1)等腰三角形两腰上的高相等;(2)在空间中,垂直于同一直线的两条直线平行;(3)两条直线被第三条直线所截,内错角相等;(4)一个角的两边与另一个角的两边分别平行,则这两个角相等.A.1 B.2 C.3 D.418.(3.00分)等腰三角形的一边长为4,另两边长是关于x的方程x2﹣20x+m=0的两个实数根,则m的值为()A.64 B.100 C.48 D.64或100三、简答题(19、20、21、22、24每题4分,23题8分共28分)19.(4.00分)计算:6﹣﹣(4﹣).20.(4.00分)计算:×(﹣2)÷.21.(4.00分)已知:x=,y=,求的值.22.(4.00分)解不等式:(x﹣1)>2(x+1)﹣3.23.(8.00分)用适当的方法解方程:(1)(1﹣x)2﹣2(x﹣1)﹣35=0;(2)x2+4x﹣2=0.24.(4.00分)用配方法解方程:3x2+4x﹣2=0.四、解答题:(每题8分,共16分)25.(8.00分)已知:关于x的一元二次方程(m﹣1)x2﹣2mx+m+3=0.(1)当m为何值时,方程无实数根;(2)当m为何值时,方程有两实数根.26.(8.00分)有一面积为150㎡的长方形养鸡场,一边靠墙(墙长17米),墙对面设一个2米宽的门,另三边(门除外)用竹篱笆围成,篱笆总长33米,求养鸡场的长和宽各多少米?五、综合题(每题8分,共16分)27.(8.00分)求证:等腰三角形底边中线上任意一点到两腰的距离相等.(1)根据题意画出图形,并写出已知和求证;(2)证明结论.28.(8.00分)某机械租赁公司有同一型号设备40套.经过一段时间的经营发现:当每套设备的月租金为270元时,恰好全部出租.在此基础上,当每套设备的月租金每提高10元时,这种设备就少出租一套,且未租出的一套设备每月需要支出费用20元.(1)设每套设备的月租金为x(元),用含x的代数式表示未租出的设备数(套)以及所有未租设备(套)的支出费用;(2)租赁公司的月收益能否达到11140元?如果能则此时应该出租多少套设备?每套的月租金是多少元?如果不能则请说明理由.2014-2015学年上海市闵行区八年级(上)期中数学试卷参考答案与试题解析一、填空题(每小题2分,共28分)1.(2.00分)化简:=.【解答】解:==.故答案为:.2.(2.00分)写出的一个有理化因式.【解答】解:写出的一个有理化因式.故答案为:.3.(2.00分)=•成立的条件为﹣1≤x≤1.【解答】解:∵=•成立,∴1﹣x2≥0,1+x≥0,1﹣x≥0,∴﹣1≤x≤1,故答案为:﹣1≤x≤1.4.(2.00分)化简:+1=1.【解答】解:∵二次根式有意义,﹣a2≥0∴a=0,∴+1=0+1=1,故答案为:1.5.(2.00分)若最简根式与是同类根式,则2a+b=3.【解答】解:∵最简根式与是同类根式,∴2a﹣4=2,3a+b=a﹣b,解得a=3,b=﹣3,∴2a+b=2×3﹣3=3,故答案为:3.6.(2.00分)在实数范围内因式分解:y4+5y2﹣14=(y+)(y﹣)(y2+7).【解答】解:原式=(y2﹣2)(y2+7)=(y+)(y﹣)(y2+7).故答案为:(y+)(y﹣)(y2+7).7.(2.00分)已知关于x的一元二次方程x2+x+m﹣1=0有实数根,则m的取值范围是.【解答】解:∵关于x的一元二次方程x2+x+m﹣1=0有实数根,∴△≥0,即1﹣4(m﹣1)≥0,∴m≤.故答案为:m≤.8.(2.00分)已知a<﹣4,化简﹣|2﹣a|=﹣5.【解答】解:∵a<﹣4,∴﹣|2﹣a|=﹣(a+3)﹣(2﹣a)=﹣a﹣3﹣2+a=﹣5.故答案为:﹣5.9.(2.00分)某公司一月份的产值为70万元,二、三月份的平均增长率都为x,三月份的产值比二月份产值多10万元,则可列方程为70(1+x)2=70(1+x)+10.【解答】解:设每月产值增长的百分率是x.由题意得:70(1+x)2=70(1+x)+10,故答案为:70(1+x)2=70(1+x)+10.10.(2.00分)若﹣﹣6=0,则+=3.【解答】解:令+=t,则原式变为t2﹣t﹣6=0,解得t1=3,t2=﹣2,∵+≥0,∴+=3.故答案为:3.11.(2.00分)如图,已知OC是∠AOB的平分线,DC∥OB,那么△DOC一定是等腰三角形(填按边分类的所属类型).【解答】解:∵DC∥OB,∴∠DCO=∠BOC,又OC是∠AOB的平分线,∴∠DOC=∠BOC=∠DCO,∴△DOC一定是等腰三角形.故答案为:等腰.12.(2.00分)把“同角的补角相等”改为如果…,那么…的形式:如果两个角都是同一个角的补角,那么这两个角相等.【解答】解:“同角的补角相等”改为如果…,那么…的形式:如果两个角都是同一个角的补角,那么这两个角相等.故答案为如果两个角都是同一个角的补角,那么这两个角相等.13.(2.00分)如图,已知AB=CD,要使△ABC≌△DCB成立,还需填加一个条件,那么这个条件可是:AC=BD.【解答】证明:在△ABC和△DCB中,,∴△ABC≌△DCB(SSS).14.(2.00分)在△DEF中,DE=DF,EG为DF边上的高,∠DEG=70°,则∠EDF= 20°或160°.【解答】解:如图1,当∠DEG=70°时,∠EDF=90°﹣∠DEG=90°﹣70°=20°;如图2,当∠DEG=70°时,∠GDE=90°﹣∠DEG=20°,则∠EDF=180°﹣∠GDE=180°﹣20°=60°,故答案为:20°或160°.二、选择题(每小题3分,共12分)15.(3.00分)下列二次根式中,属于同类二次根式的是()A.与B.与C.与D.与【解答】解:A、与,不是同类二次根式,B、=与,不是同类二次根式,C、=3与=,是同类二次根式,D、=2与=2,不是同类二次根式,故选:C.16.(3.00分)化简(a>0),下列结果正确的是()A.b B.b C.﹣b D.﹣b【解答】解:∵a>0,ab3>0,∴b>0,∴=b.故选:B.17.(3.00分)下列命题中,真命题的个数是()(1)等腰三角形两腰上的高相等;(2)在空间中,垂直于同一直线的两条直线平行;(3)两条直线被第三条直线所截,内错角相等;(4)一个角的两边与另一个角的两边分别平行,则这两个角相等.A.1 B.2 C.3 D.4【解答】解:(1)等腰三角形两腰上的高相等,故(1)说法正确,故(1)是真命题;(2)不在同一个平面内,垂直于同一条直线的两条直线一面,故(2)说法错误,故(2)是假命题;(3)两条直线不平行,内错角不相等,故(3)说法错误,故(3)是假命题;(4)一个角的两边与另一个角的两边分别平行,则这两个角相等或互补,故(4)说法错误,故(4)是假命题;故选:A.18.(3.00分)等腰三角形的一边长为4,另两边长是关于x的方程x2﹣20x+m=0的两个实数根,则m的值为()A.64 B.100 C.48 D.64或100【解答】解:∵一个等腰三角形的一边长为4,另两边长是关于x的方程x2﹣20x+m=0的两根,①当腰长为4时,把x=4代入原方程得16﹣80+m=0,∴m=64,∴原方程变为:x2﹣20x+64=0,设方程的另一个根为x,则4+x=20,∴x=16,∵4+4<16∴不能构成三角形;②当底边为4时,那么x的方程x2﹣20x+m=0的两根是相等的,∴△=(﹣20)2﹣4m=0,∴m=100,∴方程变为x2﹣20x+100=0,∴方程的两根相等为x1=x2=10,∴三角形的周长为4+2×10=24.综上,m的值是100,故选:B.三、简答题(19、20、21、22、24每题4分,23题8分共28分)19.(4.00分)计算:6﹣﹣(4﹣).【解答】解:原式=3﹣﹣+4=2+.20.(4.00分)计算:×(﹣2)÷.【解答】解:×(﹣2)÷=×(﹣2)×=﹣=﹣=﹣.21.(4.00分)已知:x=,y=,求的值.【解答】解:∵x=,y=,∴x+y=3,xy==1,∴===2.22.(4.00分)解不等式:(x﹣1)>2(x+1)﹣3.【解答】解:去括号得:x﹣>2x﹣,移项、合并同类项得:(﹣2)x>﹣,∵﹣2<0,∴x<,整理得:x<﹣5﹣.23.(8.00分)用适当的方法解方程:(1)(1﹣x)2﹣2(x﹣1)﹣35=0;(2)x2+4x﹣2=0.【解答】解:(1)(x﹣1)2﹣2(x﹣1)﹣35=0;因式分解得(x﹣1﹣7)(x﹣1+5)=0x﹣8=0或x+4=0解得x1=8,x2=﹣4;(2)x2+4x=2,x2+4x+4=6(x+2)2=6x+2=±,x=±﹣2,x1=﹣2,x2=﹣﹣2.24.(4.00分)用配方法解方程:3x2+4x﹣2=0.【解答】解:由原方程,得x2+x=,x2+x+()2=+()2,(x+)2=,x+=±,解得x1=,x2=.四、解答题:(每题8分,共16分)25.(8.00分)已知:关于x的一元二次方程(m﹣1)x2﹣2mx+m+3=0.(1)当m为何值时,方程无实数根;(2)当m为何值时,方程有两实数根.【解答】解:方程的判别式为△=(﹣2m)2﹣4(m﹣1)(m+3)=4m2﹣(4m2+8m ﹣12)=12﹣8m,又方程为一元二次方程,可知m﹣1≠0,即m≠1,(1)当方程无实数根时,则有△<0,即12﹣8m<0,解得m>,所以当m>时,方程无实数根;(2)当方程有两实数根时,则有△≥0,即12﹣8m≥0,解得m≤,且m≠1,所以当m≤且m≠1时方程有两实数根.26.(8.00分)有一面积为150㎡的长方形养鸡场,一边靠墙(墙长17米),墙对面设一个2米宽的门,另三边(门除外)用竹篱笆围成,篱笆总长33米,求养鸡场的长和宽各多少米?【解答】解:设鸡场的长为x,因为篱笆总长为33米,由图可知宽为:米,则根据题意列方程为:x×=150,解得:x1=15,x2=20(大于墙长,舍去).宽为:10米.所以鸡场的长为15米,宽为10米.五、综合题(每题8分,共16分)27.(8.00分)求证:等腰三角形底边中线上任意一点到两腰的距离相等.(1)根据题意画出图形,并写出已知和求证;(2)证明结论.【解答】解:(1)已知:在△ABC中,AB=AC,AD为BC边上的中线,P为AD 上的任一点,PE⊥AB,PF⊥AC,求证:PE=PF;(2)证明:∵AB=AC,AD为BC边上的中线,∴AD平分∠BAC,∵PE⊥AB,PF⊥AC,∴PE=PF.28.(8.00分)某机械租赁公司有同一型号设备40套.经过一段时间的经营发现:当每套设备的月租金为270元时,恰好全部出租.在此基础上,当每套设备的月租金每提高10元时,这种设备就少出租一套,且未租出的一套设备每月需要支出费用20元.(1)设每套设备的月租金为x(元),用含x的代数式表示未租出的设备数(套)以及所有未租设备(套)的支出费用;(2)租赁公司的月收益能否达到11140元?如果能则此时应该出租多少套设备?每套的月租金是多少元?如果不能则请说明理由.【解答】解:(1)未租出的设备为,套,所有未出租设备支出的费用为20×=(2x﹣540)元;(2)x×[40﹣(x﹣270)÷10]﹣20×[(x﹣270)÷10]=11140,x2﹣650x+106000=0,△=b2﹣4ac=﹣1500<0,故租赁公司的月收益不能达到11140元.赠送初中数学几何模型【模型五】垂直弦模型:图形特征:运用举例:1.已知A、B、C、D是⊙O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.O DAB CEAOD CB2.如图,已知四边形ABCD 内接于⊙O ,对角线AC ⊥BD 于P ,设⊙O 的半径是2。
