高中数学必修二立体几何线面平行专题练习(含答案)
高中人版B版数学必修二练习:1.2.2 第1课时 平行直线 直线与平面平行 Word版含答案

1.2.2 空间中的平行关系第一课时平行直线直线与平面平行1.下列命题正确的是( D )(A)若直线l上有无数点不在平面α内,则l∥α(B)若直线l与平面α平行,则直线l与α内任一条直线平行(C)如果两条平行线中的一条与平面α平行,则另一条也与α平行(D)若直线l与平面α平行,则直线l与平面α无公共点解析:A.直线l与α相交,l上有无数点不在平面α内,故A不正确;C.当另一条直线在平面α内时,不平行,故C不正确;B显然不正确,因为除平行外,还有异面,所以选D.2.如图所示,在空间四边形ABCD中,E,F分别是AB,AD上的点,且AE∶EB=AF∶FD=1∶4,又H,G分别是BC,CD的中点,则( D )(A)BD∥平面EFGH,且四边形EFGH是矩形(B)HG∥平面ABD,且四边形EFGH是菱形(C)HE∥平面ADC,且四边形EFGH是梯形(D)EF∥平面BCD,且四边形EFGH是梯形解析:由AE∶EB=AF∶FD=1∶4知,EF BD,由H,G为BC,CD中点知HG BD,故EF∥HG且EF≠HG,所以四边形EFGH为梯形,又因为EF⊄平面BCD,HG⊂平面BCD,所以EF∥平面BCD.3.已知在三棱锥A BCD中,M,N分别为AB,CD的中点,则下列结论正确的是( D )(A)MN≥(AC+BD)(B)MN≤(AC+BD)(C)MN=(AC+BD)(D)MN<(AC+BD)解析:设BC中点为P,连接MP,PN.在△MPN中,MN<MP+PN,所以MN<(AC+BD),故选D.4.已知△ABC,△DBC分别在平面α,β内,E∈AB,F∈AC,M∈DB,N∈DC,且EF∥MN,则EF与BC的位置关系是( A )(A)平行(B)相交或平行(C)平行或异面(D)平行或异面或相交解析:因为EF∥MN,EF⊄平面BCD,MN⊂平面BCD,所以EF∥平面BCD,又EF⊂平面ABC,且平面ABC∩平面BCD=BC,所以EF∥BC,故选A.5.设m,n为平面α外的两条直线,给出下面三个论断:①m∥n,②m∥α,③n∥α,以其中两个作为条件,另一个作为结论,构成一个命题,写出你认为正确的命题: .解析:由m,n为平面α外的直线,且m∥n可得:若m∥α,则n∥α,或若n∥α则m∥α.答案:①②⇒③(或①③⇒②)6.如图,四棱锥P ABCD的底面ABCD是平行四边形,E,F分别是棱AD,PC 的中点.证明:EF∥平面PAB.证明:如图,取PB的中点M,连接MF,AM.因为F为PC的中点,故MF∥BC且MF=BC.由已知有BC∥AD,BC=AD.又由于E为AD的中点,因而MF∥AE且MF=AE,故四边形AMFE为平行四边形,所以EF∥AM.又AM⊂平面PAB,而EF⊄平面PAB,所以EF∥平面PAB.7.(2017·全国Ⅰ卷)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( A )解析:如图O为正方形CDBE的两条对角线的交点,从而O为BC的中点,在△ACB中,OQ为中位线,所以OQ∥AB,OQ∩平面MNQ=Q,所以,AB与平面MNQ相交,而不是平行,故选A.8.下列四个命题:①直线a∥直线b,则a平行于经过b的任何平面;②若直线a∥平面α,那么a与α内无数条直线平行;③若直线a,b都平行于平面α,则a∥b;④若直线a∥b,a∥平面α,则b∥α.其中正确的命题个数为( A )(A)1 (B)2 (C)3 (D)4解析:①不正确,因为a有可能在经过直线b的平面内;②正确;③不正确,因为a,b可以平行、相交,也可以异面;④不正确,有可能b⊂α,故选A.9.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是.(写出所有符合要求的图形序号)解析:①如图a,连MN,则平面MNP扩展与正方体的各面相交得截面图MNPQ,再连接QN,则AB∥QN,所以AB∥平面MNP;②不能得出;③能,如图b.连接EC,则EC∥MP,AB∥EC,所以AB∥MP,从而可得AB∥平面MNP;④如图c,连接ND,MC,即为平面MNP扩展后的截面图,将直线AB平移到ED,则ED∥AB,而ED与平面MNP相交,即AB与平面MNP相交.答案:①③10.如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.求证:GF∥平面ADE.证明:如图,取AE的中点H,连接HG,HD,又G是BE的中点,所以GH∥AB,且GH=AB.又F是CD的中点,所以DF=CD.由四边形ABCD是矩形得,AB∥CD,AB=CD,所以GH∥DF,且GH=DF,从而四边形HGFD是平行四边形,所以GF∥DH.又DH⊂平面ADE,GF⊄平面ADE,所以GF∥平面ADE.11.如图,四棱锥P ABCD中,底面ABCD为矩形,E为PD的中点.(1)证明:PB∥平面AEC;(2)若平面APD∩平面PBC=直线l.证明:l∥BC.证明:(1)连接BD交AC于点O,连结EO.因为四边形ABCD为矩形,所以O为BD的中点. 又E为PD的中点,所以EO∥PB.又EO⊂平面AEC,PB⊄平面AEC,所以PB∥平面AEC.(2)因为四边形ABCD为矩形,所以BC∥AD,又BC⊄平面APD,AD⊂平面APD,所以BC∥平面APD,又BC⊂平面PBC,平面APD∩平面PBC=l,所以l∥BC.。
立体几何线面平行垂直、面面平行垂直专题练习(高三党必做)

立体几何线面平行垂直、面面平行垂直专题一、解答题(本大题共27小题,共324.0分)1.如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明:MN∥平面PAB;(2)求直线AN与平面PMN所成角的正弦值.2.如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=AD,∠BAD=∠ABC=90°,E是PD的中点.BC=12(1)证明:直线CE∥平面PAB;(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.3.如图,在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∠BAC=90°,AC=AB=AA1,E是BC的中点.(1)求证:AE⊥B1C;(2)求异面直线AE与A1C所成的角的大小;(3)若G为C1C中点,求二面角C-AG-E的正切值.4.如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=√6,AP=4AF.(Ⅰ)求证:PO⊥底面ABCD;(Ⅱ)求直线CP与平面BDF所成角的大小;(Ⅲ)在线段PB上是否存在一点M,使得CM∥平面BDF如果存在,求BM的值,如果不存在,请说明理BP由.5.如图,在直三棱柱ABC-A1B l C1中,AC=BC=√2,∠ACB=90°.AA1=2,D为AB的中点.(Ⅰ)求证:AC⊥BC1;(Ⅱ)求证:AC1∥平面B1CD:(Ⅲ)求异面直线AC1与B1C所成角的余弦值.6.如图,正三棱柱ABC-A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.(1)求异面直线BP与AC1所成角的余弦值;(2)求直线CC1与平面AQC1所成角的正弦值.7.如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=√6,AB=4.(1)求证:M为PB的中点;(2)求二面角B-PD-A的大小;(3)求直线MC与平面BDP所成角的正弦值.8.如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设AP=1,AD=√3,三棱锥P-ABD的体积V=√3,求A到平面PBC的距4离.9.如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.(Ⅰ)证明:BE⊥DC;(Ⅱ)求直线BE与平面PBD所成角的正弦值;(Ⅲ)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.10.如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.(Ⅰ)证明:CE∥平面PAB;(Ⅱ)求直线CE与平面PBC所成角的正弦值.11.如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点,N是CE的中点.(I)求证:EM⊥AD;(II)求证:MN∥平面ADE;(III)求点A到平面BCE的距离.12.已知几何体ABCDEF中,AB∥CD,AD⊥DC,EA⊥平面ABCD,FC∥EA,AB=AD=EA=1,CD=CF=2.(Ⅰ)求证:平面EBD⊥平面BCF;(Ⅱ)求点B到平面ECD的距离.13.如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD=2,E、F分别为CD、PB的中点.(1)求证:EF∥平面PAD;(2)求证:平面AEF⊥平面PAB;(3)设AB=√2AD,求直线AC与平面AEF所成角θ的正弦值.14.如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠ADC=45∘,AD=AC=2,O为AC的中点,PO⊥平面ABCD且PO=6,M为BD的中点.(1)证明:AD⊥平面PAC;(2)求直线AM与平面ABCD所成角的正切值.15.如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=√2,点D为A1C1的中点.(I)求证:BC1∥平面AB1D;(II)求证:A1C⊥平面AB1D;(Ⅲ)求异面直线AD与BC1所成角的大小.16.如图,P-ABD和Q-BCD为两个全等的正棱锥,且A,B,C,D四点共面,其中AB=1,∠APB=90°.(Ⅰ)求证:BD⊥平面APQ;(Ⅱ)求直线PB与平面PDQ所成角的正弦值.17.如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥底面ABC,AB=BC=2,∠ACB=30°,∠C1CB=60°,BC1⊥A1C,E为AC的中点,侧棱CC1=2.(1)求证:A1C⊥平面C1EB;(2)求直线CC1与平面ABC所成角的余弦值.18.如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,AB=6,BC=2√3,AC=2√6,D为线段AB上的点,且AD=2DB,PD⊥AC.(1)求证:PD⊥平面ABC;,求点B到平面PAC的距离.(2)若∠PAB=π419.如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,△ABC为正三角形,D是BC边的中点,AA1=AB=1.(1)求证:平面ADB1⊥平面BB1C1C;(2)求点B到平面ADB1的距离.20.如图,在三棱锥P-ABC中,点D,E,F分别为棱PC,AC,AB的中点,已知PA⊥平面ABC,AB⊥BC,且AB=BC.(1)求证:平面BED⊥平面PAC;(2)求二面角F-DE-B的大小;(3)若PA=6,DF=5,求PC与平面PAB所成角的正切值.21.如图,在四棱锥P—ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2√2.(1)证明PA∥平面BDE;(2)证明AC⊥平面PBD;(3)求直线BC与平面PBD所成的角的正切值.22.如图所示,在四棱台ABCD-A1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为菱形,∠BAD=120°,AB=AA1=2A1B1=2.(Ⅰ)若M为CD中点,求证:AM⊥平面AA1B1B;(Ⅱ)求直线DD1与平面A1BD所成角的正弦值.=√2.23.如图,在直三棱柱ABC−A1B1C1中,∠ACB=90°,E为A1C1的中点,CC1C1E(Ⅰ)证明:CE⊥平面AB1C1;(Ⅱ)若AA1=√6,∠BAC=30°,求点E到平面AB1C的距离.24.如图,在四棱锥E-ABCD中,底面ABCD是边长为√2的正方形,平面AEC⊥平面CDE,∠AEC=90°,F为DE中点,且DE=1.(Ⅰ)求证:BE∥平面ACF;(Ⅱ)求证:CD⊥DE;(Ⅲ)求FC与平面ABCD所成角的正弦值.25.已知:平行四边形ABCD中,∠DAB=45°,AB=√2AD=2√2,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=√2,M为线段BC的中点.(1)求证:直线MF∥平面BED;(2)求证:平面BED⊥平面EAD;(3)求直线BF与平面BED所成角的正弦值.26.如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=√2,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AC=√2,AB=BC=1,E为AD中点.(Ⅰ)求证:PE⊥平面ABCD;(Ⅱ)求异面直线PB与CD所成角的余弦值;(Ⅲ)求平面PAB与平面PCD所成的二面角.27.如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.(1)证明:AB1⊥平面A1B1C1;(2)求直线AC1与平面ABB1所成的角的正弦值.答案和解析1.【答案】(1)证明:法一、如图,取PB 中点G ,连接AG ,NG ,∵N 为PC 的中点, ∴NG ∥BC ,且NG =12BC ,又AM =23AD =2,BC =4,且AD ∥BC , ∴AM ∥BC ,且AM =12BC ,则NG ∥AM ,且NG =AM ,∴四边形AMNG 为平行四边形,则NM ∥AG , ∵AG ⊂平面PAB ,NM ⊄平面PAB , ∴MN ∥平面PAB ; 法二、在△PAC 中,过N 作NE ⊥AC ,垂足为E ,连接ME , 在△ABC 中,由已知AB =AC =3,BC =4,得cos ∠ACB =42+32−322×4×3=23,∵AD ∥BC ,∴cos ∠EAM =23,则sin ∠EAM =√53,在△EAM 中,∵AM =23AD =2,AE =12AC =32,由余弦定理得:EM =√AE 2+AM 2−2AE ⋅AM ⋅cos∠EAM =√94+4−2×32×2×23=32,∴cos ∠AEM =(32)2+(32)2−42×32×32=19,而在△ABC 中,cos ∠BAC =32+32−422×3×3=19,∴cos ∠AEM =cos ∠BAC ,即∠AEM =∠BAC , ∴AB ∥EM ,则EM ∥平面PAB .由PA ⊥底面ABCD ,得PA ⊥AC ,又NE ⊥AC , ∴NE ∥PA ,则NE ∥平面PAB . ∵NE ∩EM =E ,∴平面NEM ∥平面PAB ,则MN ∥平面PAB ;(2)解:在△AMC 中,由AM =2,AC =3,cos ∠MAC =23,得CM 2=AC 2+AM 2-2AC •AM •cos ∠MAC =9+4−2×3×2×23=5.∴AM 2+MC 2=AC 2,则AM ⊥MC , ∵PA ⊥底面ABCD ,PA ⊂平面PAD ,∴平面ABCD ⊥平面PAD ,且平面ABCD ∩平面PAD =AD , ∴CM ⊥平面PAD ,则平面PNM ⊥平面PAD .在平面PAD 内,过A 作AF ⊥PM ,交PM 于F ,连接NF ,则∠ANF 为直线AN 与平面PMN 所成角.在Rt△PAC中,由N是PC的中点,得AN=12PC=12√PA2+PC2=52,在Rt△PAM中,由PA•AM=PM•AF,得AF=PA⋅AMPM =√42+22=4√55,∴sin∠ANF=AFAN =4√5552=8√525.∴直线AN与平面PMN所成角的正弦值为8√525.【解析】本题考查直线与平面平行的判定,考查直线与平面所成角的求法,考查数学转化思想方法,考查了空间想象能力和计算能力,是中档题.(1)法一、取PB中点G,连接AG,NG,由三角形的中位线定理可得NG∥BC,且NG=12BC,再由已知得AM∥BC,且AM=12BC,得到NG∥AM,且NG=AM,说明四边形AMNG为平行四边形,可得NM∥AG,由线面平行的判定得到MN∥平面PAB;法二、证明MN∥平面PAB,转化为证明平面NEM∥平面PAB,在△PAC中,过N作NE⊥AC,垂足为E,连接ME,由已知PA⊥底面ABCD,可得PA∥NE,通过求解直角三角形得到ME∥AB,由面面平行的判定可得平面NEM∥平面PAB,则结论得证;(2)由勾股定理得CM⊥AD,进一步得到平面PNM⊥平面PAD,在平面PAD内,过A作AF⊥PM,交PM于F,连接NF,则∠ANF为直线AN与平面PMN所成角.然后求解直角三角形可得直线AN与平面PMN所成角的正弦值.2.【答案】(1)证明:取PA的中点F,连接EF,BF,因为E是PD的中点,所以EF∥AD,EF=12AD,AB=BC=12AD,∠BAD=∠ABC=90°,∴BC∥AD,EF∥BC,EF=BC,∴四边形BCEF是平行四边形,可得CE∥BF,BF⊂平面PAB,CE⊄平面PAB,∴直线CE∥平面PAB;(2)解:如图所示,取AD中点O,连接PO,CO,由于△PAD为正三角形,则PO⊥AD,因为侧面PAD为等边三角形且垂直于底面ABCD,平面PAD∩平面ABCD=AD,所以PO⊥平面ABCD,所以PO⊥CO. 因为AO=AB=BC=12AD,且∠BAD=∠ABC= 90∘,所以四边形ABCO是矩形,所以CO⊥AD,以O为原点,OC为x轴,OD为y轴,OP为z轴建立空间直角坐标系,不妨设AB=BC=12AD=1,则OA=OD=AB=CO=1.又因为△POC为直角三角形,|OC|=√33|OP|,所以∠PCO=60∘.作MN⊥CO,垂足为N,连接BN,因为PO ⊥CO ,所以MN //PO ,且PO ⊥平面ABCD ,所以MN ⊥平面ABCD ,所以∠MBN 即为直线BM 与平面ABCD 所成的角, 设CN =t ,因为∠PCO =60∘,所以MN =√3t ,BN =√BC 2+CN 2=√t 2+1. 因为∠MBN =45∘,所以MN =BN ,即√3t =√t 2+1,解得t =√22,所以ON =1−√22,MN =√62,所以A (0,−1,0),B (1,−1,0),M (1−√22,0,√62),D (0,1,0),则AB ⃗⃗⃗⃗⃗ =(1,0,0),AD⃗⃗⃗⃗⃗⃗ =(0,2,0),AM ⃗⃗⃗⃗⃗⃗ =(1−√22,1,√62). 设平面MAB 和平面DAB 的法向量分别为n 1⃗⃗⃗⃗ =(x 1,y 1,z 1),n 2⃗⃗⃗⃗ =(x 2,y 2,z 2), 则{AB ⃗⃗⃗⃗⃗ ·n 1⃗⃗⃗⃗ =0AM ⃗⃗⃗⃗⃗⃗ ·n 1⃗⃗⃗⃗ =0,即{x 1=0(1−√22)x 1+y 1+√62z 1=0, 可取z 1=−2,则n 1⃗⃗⃗⃗ =(0,√6,−2), 同理可得n 2⃗⃗⃗⃗ =(0,0,1),所以.因为二面角M -AB -D 是锐角,所以其余弦值为√105.【解析】本题考查直线与平面平行的判定定理的应用,空间向量求二面角夹角,考查空间想象能力以及计算能力,属于中档题.(1)取PA 的中点F ,连接EF ,BF ,通过证明CE ∥BF ,利用直线与平面平行的判定定理证明即可.(2)取AD 中点O ,连接PO ,CO ,作MN ⊥CO ,垂足为N ,以O 为原点,OC 为x 轴,OD 为y 轴,OP 为z 轴建立空间直角坐标系,即可求出二面角M -AB -D 的余弦值.3.【答案】证明:(1)因为BB 1⊥面ABC ,AE ⊂面ABC ,所以AE ⊥BB 1,由AB =AC ,E 为BC 的中点得到AE ⊥BC , ∵BC ∩BB 1=B ,BC 、BB 1⊂面BB 1C 1C , ∴AE ⊥面BB 1C 1C ,,∴AE ⊥B 1C ;解:(2)取B 1C 1的中点E 1,连A 1E 1,E 1C ,则AE ∥A 1E 1, ∴∠E 1A 1C 是异面直线AE 与A 1C 所成的角, 设AC =AB =AA 1=2,则由∠BAC =90°, 可得A 1E 1=AE =√2,A 1C =2√2,E 1C 1=EC =12BC =√2,∴E 1C =√E 1C 12+C 1C 2=√6,∵在△E 1A 1C 中,cos ∠E 1A 1C =2+8−62⋅√2⋅2√2=12, 所以异面直线AE 与A 1C 所成的角为π3;(3)连接AG ,设P 是AC 的中点,过点P 作PQ ⊥AG 于Q ,连EP ,EQ ,则EP ⊥AC ,又∵平面ABC ⊥平面ACC 1A 1,平面ABC ∩平面ACC 1A 1=AC ∴EP ⊥平面ACC 1A 1, 而PQ ⊥AG ∴EQ ⊥AG .∴∠PQE 是二面角C -AG -E 的平面角, 由(2)假设知:EP =1,AP =1, Rt △ACG ∽Rt △AQP ,PQ =CG·AP AG=1√5,故tan ∠PQE =PEPQ =√5,所以二面角C -AG -E 的平面角正切值是√5.【解析】本题考查异面直线的夹角,线线垂直的判定,属于中档题,熟练掌握线面垂直,线线垂直与面面垂直之间的转化及异面直线夹角及二面角的定义,是解答本题的关键,属于较难题.(1)由BB 1⊥面ABC 及线面垂直的性质可得AE ⊥BB 1,由AC =AB ,E 是BC 的中点,及等腰三角形三线合一,可得AE ⊥BC ,结合线面垂直的判定定理可证得AE ⊥面BB 1C 1C ,进而由线面垂直的性质得到AE ⊥B 1C ;(2)取B 1C 1的中点E 1,连A 1E 1,E 1C ,根据异面直线夹角定义可得,∠E 1A 1C 是异面直线A 与A 1C 所成的角,设AC =AB =AA 1=2,解三角形E 1A 1C 可得答案. (3)连接AG ,设P 是AC 的中点,过点P 作PQ ⊥AG 于Q ,连EP ,EQ ,则EP ⊥AC ,由直三棱锥的侧面与底面垂直,结合面面垂直的性质定理,可得EP ⊥平面ACC 1A 1,进而由二面角的定义可得∠PQE 是二面角C -AG -E 的平面角.4.【答案】(Ⅰ)证明:因为底面ABCD 是菱形,AC ∩BD =O ,所以O 为AC ,BD 中点.-------------------------------------(1分)又因为PA =PC ,PB =PD ,所以PO ⊥AC ,PO ⊥BD ,---------------------------------------(3分)所以PO ⊥底面ABCD .----------------------------------------(4分)(Ⅱ)解:由底面ABCD 是菱形可得AC ⊥BD , 又由(Ⅰ)可知PO ⊥AC ,PO ⊥BD .如图,以O 为原点建立空间直角坐标系O -xyz .由△PAC 是边长为2的等边三角形,PB =PD =√6,可得PO =√3,OB =OD =√3.所以A(1,0,0),C(−1,0,0),B(0,√3,0),P(0,0,√3).---------------------------------------(5分)所以CP ⃗⃗⃗⃗⃗ =(1,0,√3),AP ⃗⃗⃗⃗⃗ =(−1,0,√3). 由已知可得OF ⃗⃗⃗⃗⃗ =OA⃗⃗⃗⃗⃗ +14AP ⃗⃗⃗⃗⃗ =(34,0,√34)-----------------------------------------(6分) 设平面BDF 的法向量为n −=(x ,y ,z ),则{√3y =034x +√34z =0令x =1,则z =−√3,所以n ⃗ =(1,0,-√3).----------------------------------------(8分) 因为cos <CP ⃗⃗⃗⃗⃗ ,n ⃗ >=CP ⃗⃗⃗⃗⃗ ⋅n ⃗⃗|CP ⃗⃗⃗⃗⃗ ||n ⃗⃗ |=-12,----------------------------------------(9分) 所以直线CP 与平面BDF 所成角的正弦值为12,所以直线CP 与平面BDF 所成角的大小为30°.-----------------------------------------(10分)(Ⅲ)解:设BMBP =λ(0≤λ≤1),则CM ⃗⃗⃗⃗⃗⃗ =CB ⃗⃗⃗⃗⃗ +BM ⃗⃗⃗⃗⃗⃗ =CB ⃗⃗⃗⃗⃗ +λBP ⃗⃗⃗⃗⃗ =(1,√3(1−λ),√3λ).---------------------------------(11分)若使CM ∥平面BDF ,需且仅需CM −⋅n ⃗ =0且CM ⊄平面BDF ,---------------------(12分) 解得λ=13∈[0,1],----------------------------------------(13分) 所以在线段PB 上存在一点M ,使得CM ∥平面BDF . 此时BM BP =13.-----------------------------------(14分)【解析】(Ⅰ)证明PO ⊥底面ABCD ,只需证明PO ⊥AC ,PO ⊥BD ;(Ⅱ)建立空间直角坐标系,求出直线CP 的方向向量,平面BDF 的法向量,利用向量的夹角公式可求直线CP 与平面BDF 所成角的大小;(Ⅲ)设BMBP =λ(0≤λ≤1),若使CM ∥平面BDF ,需且仅需CM −⋅n ⃗ =0且CM ⊄平面BDF ,即可得出结论.本题考查线面垂直,考查线面平行,考查线面角,考查向量知识的运用,正确求出向量的坐标是关键.5.【答案】解:(I )证明:∵CC 1⊥平面ABC ,AC ⊂平面ABC ,∠ACB =90°, ∴CC 1⊥AC ,AC ⊥BC ,又BC ∩CC 1=C ,∴AC ⊥平面BCC 1,BC 1⊂平面BCC 1, ∴AC ⊥BC 1.(II )证明:如图,设CB 1∩C 1B =E ,连接DE , ∵D 为AB 的中点,E 为C 1B 的中点,∴DE ∥AC 1, ∵DE ⊂平面B 1CD ,AC 1⊄平面B 1CD , ∴AC 1∥平面B 1CD .(III )解:由DE ∥AC 1,∠CED 为AC 1与B 1C 所成的角,在△CDE 中,DE =12AC 1=12√AC 2+CC 12=√62, CE =12B 1C =12√BC 2+BB 12=√62,CD =12AB =12√AC 2+BC 2=1,cos ∠CED =CE 2+DE 2−CD 22×CE×DE=32+32−12×√62×√62=23,∴异面直线AC 1与B 1C 所成角的余弦值为23.【解析】本题考查线线垂直的判定、线面平行的判定、异面直线及其所成的角. (I )先证线面垂直,再由线面垂直证明线线垂直即可; (II )作平行线,由线线平行证明线面平行即可;(III )先证明∠CED 为异面直线所成的角,再在三角形中利用余弦定理计算即可. 6.【答案】解:如图,在正三棱柱ABC -A 1B 1C 1中, 设AC ,A 1C 1的中点分别为O ,O 1, 则,OB ⊥OC ,OO 1⊥OC ,OO 1⊥OB ,故以{OB ⃗⃗⃗⃗⃗⃗ ,OC ⃗⃗⃗⃗⃗ ,OO 1⃗⃗⃗⃗⃗⃗⃗⃗ }为基底, 建立空间直角坐标系O -xyz ,∵AB =AA 1=2,A (0,-1,0),B (√3,0,0), C (0,1,0),A 1(0,-1,2),B 1(√3,0,2),C 1(0,1,2).(1)点P 为A 1B 1的中点.∴P(√32,−12,2),∴BP ⃗⃗⃗⃗⃗ =(−√32,−12,2),AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2,2). |cos <BP ⃗⃗⃗⃗⃗ ,AC 1⃗⃗⃗⃗⃗⃗⃗ >|=|BP ⃗⃗⃗⃗⃗ ⋅AC 1⃗⃗⃗⃗⃗⃗⃗⃗||BP ⃗⃗⃗⃗⃗ |⋅|AC 1⃗⃗⃗⃗⃗⃗⃗⃗ |=|−1+4|√5×2√2=3√1020.∴异面直线BP 与AC 1所成角的余弦值为:3√1020; (2)∵Q 为BC 的中点.∴Q (√32,12,0)∴AQ ⃗⃗⃗⃗⃗ =(√32,32,0),AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2,2),CC 1⃗⃗⃗⃗⃗⃗⃗ =(0,0,2),设平面AQC 1的一个法向量为n⃗ =(x ,y ,z ), 由{AQ ⃗⃗⃗⃗⃗ ·n ⃗ =√32x +32y =0AC 1⃗⃗⃗⃗⃗⃗⃗ ·n⃗ =2y +2z =0,可取n⃗ =(√3,-1,1), 设直线CC 1与平面AQC 1所成角的正弦值为θ, sinθ=|cos|=|CC 1⃗⃗⃗⃗⃗⃗⃗ ⋅n ⃗ ||CC 1⃗⃗⃗⃗⃗⃗⃗ |⋅|n⃗ |=2√5×2=√55, ∴直线CC 1与平面AQC 1所成角的正弦值为√55.【解析】本题考查了向量法求空间角,属于中档题.设AC ,A 1C 1的中点分别为O ,O 1,以{OB ⃗⃗⃗⃗⃗⃗ ,OC ⃗⃗⃗⃗⃗ ,OO 1⃗⃗⃗⃗⃗⃗⃗⃗ }为基底,建立空间直角坐标系O -xyz ,(1)由|cos <BP ⃗⃗⃗⃗⃗ ,AC 1⃗⃗⃗⃗⃗⃗⃗ >|=|BP ⃗⃗⃗⃗⃗⃗ ⋅AC 1⃗⃗⃗⃗⃗⃗⃗⃗||BP ⃗⃗⃗⃗⃗⃗ |⋅|AC 1⃗⃗⃗⃗⃗⃗⃗⃗ |可得异面直线BP 与AC 1所成角的余弦值;(2)求得平面AQC 1的一个法向量为n⃗ ,设直线CC 1与平面AQC 1所成角的正弦值为θ,可得sinθ=|cos <CC 1⃗⃗⃗⃗⃗⃗⃗ ,n⃗ >|=|CC 1⃗⃗⃗⃗⃗⃗⃗ ⋅n ⃗⃗ ||CC 1⃗⃗⃗⃗⃗⃗⃗ |⋅|n ⃗⃗ |,即可得直线CC 1与平面AQC 1所成角的正弦值.7.【答案】(1)证明:如图,设AC ∩BD =O ,∵ABCD 为正方形,∴O 为BD 的中点,连接OM ,∵PD ∥平面MAC ,PD ⊂平面PBD ,平面PBD ∩平面AMC =OM , ∴PD ∥OM ,则BOBD =BM BP,即M 为PB 的中点;(2)解:取AD 中点G , ∵PA =PD ,∴PG ⊥AD ,∵平面PAD ⊥平面ABCD ,且平面PAD ∩平面ABCD =AD , ∴PG ⊥平面ABCD ,则PG ⊥AD ,连接OG ,则PG ⊥OG ,由G 是AD 的中点,O 是AC 的中点,可得OG ∥DC ,则OG ⊥AD .以G 为坐标原点,分别以GD 、GO 、GP 所在直线为x 、y 、z 轴距离空间直角坐标系, 由PA =PD =√6,AB =4,得D (2,0,0),A (-2,0,0),P (0,0,√2),C (2,4,0),B (-2,4,0),M (-1,2,√22),DP ⃗⃗⃗⃗⃗ =(−2,0,√2),DB⃗⃗⃗⃗⃗⃗ =(−4,4,0). 设平面PBD 的一个法向量为m ⃗⃗⃗ =(x ,y ,z),则由{m ⃗⃗⃗ ⋅DP ⃗⃗⃗⃗⃗ =0m⃗⃗⃗ ⋅DB ⃗⃗⃗⃗⃗⃗ =0,得{−2x +√2z =0−4x +4y =0,取z =√2,得m ⃗⃗⃗ =(1,1,√2). 取平面PAD 的一个法向量为n ⃗ =(0,1,0).∴cos <m ⃗⃗⃗ ,n ⃗ >=m ⃗⃗⃗ ⋅n ⃗⃗ |m ⃗⃗⃗ ||n ⃗⃗ |=12×1=12. ∴二面角B -PD -A 的大小为60°;(3)解:CM ⃗⃗⃗⃗⃗⃗ =(−3,−2,√22),平面BDP 的一个法向量为m ⃗⃗⃗ =(1,1,√2).∴直线MC 与平面BDP 所成角的正弦值为|cos <CM ⃗⃗⃗⃗⃗⃗ ,m ⃗⃗⃗ >|=|CM ⃗⃗⃗⃗⃗⃗⋅m ⃗⃗⃗|CM ⃗⃗⃗⃗⃗⃗ ||m ⃗⃗⃗ ||=|−2√9+4+12×1|=2√69.【解析】本题考查线面角与面面角的求法,训练了利用空间向量求空间角,属中档题.(1)设AC ∩BD =O ,则O 为BD 的中点,连接OM ,利用线面平行的性质证明OM ∥PD ,再由平行线截线段成比例可得M 为PB 的中点;(2)取AD 中点G ,可得PG ⊥AD ,再由面面垂直的性质可得PG ⊥平面ABCD ,则PG ⊥AD ,连接OG ,则PG ⊥OG ,再证明OG ⊥AD .以G 为坐标原点,分别以GD 、GO 、GP 所在直线为x 、y 、z 轴距离空间直角坐标系,求出平面PBD 与平面PAD 的一个法向量,由两法向量所成角的大小可得二面角B -PD -A 的大小;(3)求出CM⃗⃗⃗⃗⃗⃗ 的坐标,由CM ⃗⃗⃗⃗⃗⃗ 与平面PBD 的法向量所成角的余弦值的绝对值可得直线MC 与平面BDP 所成角的正弦值.8.【答案】解:(Ⅰ)证明:设BD 与AC 的交点为O ,连结EO , ∵ABCD 是矩形, ∴O 为BD 的中点 ∵E 为PD 的中点, ∴EO ∥PB .EO ⊂平面AEC ,PB ⊄平面AEC ∴PB ∥平面AEC ;(Ⅱ)∵AP =1,AD =√3,三棱锥P -ABD 的体积V =√34,∴V =16PA ⋅AB ⋅AD =√36AB =√34,∴AB =32,PB =√1+(32)2=√132.作AH ⊥PB 交PB 于H , 由题意可知BC ⊥平面PAB , ∴BC ⊥AH ,故AH ⊥平面PBC .又在三角形PAB 中,由射影定理可得:AH =PA⋅AB PB=3√1313A 到平面PBC 的距离3√1313.【解析】本题考查直线与平面垂直,点到平面的距离的求法,考查空间想象能力以及计算能力.(Ⅰ)设BD 与AC 的交点为O ,连结EO ,通过直线与平面平行的判定定理证明PB ∥平面AEC ;(Ⅱ)通过AP =1,AD =√3,三棱锥P -ABD 的体积V =√34,求出AB ,作AH ⊥PB 角PB于H ,说明AH 就是A 到平面PBC 的距离.通过解三角形求解即可. 9.【答案】证明:(I )∵PA ⊥底面ABCD ,AD ⊥AB , 以A 为坐标原点,建立如图所示的空间直角坐标系,∵AD =DC =AP =2,AB =1,点E 为棱PC 的中点. ∴B (1,0,0),C (2,2,0),D (0,2,0), P (0,0,2),E (1,1,1)∴BE⃗⃗⃗⃗⃗ =(0,1,1),DC ⃗⃗⃗⃗⃗ =(2,0,0) ∵BE ⃗⃗⃗⃗⃗ •DC ⃗⃗⃗⃗⃗ =0, ∴BE ⊥DC ;(Ⅱ)∵BD ⃗⃗⃗⃗⃗⃗ =(-1,2,0),PB ⃗⃗⃗⃗⃗ =(1,0,-2),设平面PBD 的法向量m⃗⃗⃗ =(x ,y ,z ), 由{m ⃗⃗⃗ ⋅BD ⃗⃗⃗⃗⃗⃗ =0m⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗ =0,得{−x +2y =0x −2z =0, 令y =1,则m⃗⃗⃗ =(2,1,1), 则直线BE 与平面PBD 所成角θ满足: sinθ=m⃗⃗⃗ ⋅BE ⃗⃗⃗⃗⃗⃗ |m ⃗⃗⃗ |⋅|BE ⃗⃗⃗⃗⃗⃗ |=2√6×√2=√33, 故直线BE 与平面PBD 所成角的正弦值为√33.(Ⅲ)∵BC⃗⃗⃗⃗⃗ =(1,2,0),CP ⃗⃗⃗⃗⃗ =(-2,-2,2),AC ⃗⃗⃗⃗⃗ =(2,2,0), 由F 点在棱PC 上,设CF⃗⃗⃗⃗⃗ =λCP ⃗⃗⃗⃗⃗ =(-2λ,-2λ,2λ)(0≤λ≤1), 故BF ⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ +CF⃗⃗⃗⃗⃗ =(1-2λ,2-2λ,2λ)(0≤λ≤1), 由BF ⊥AC ,得BF ⃗⃗⃗⃗⃗ •AC ⃗⃗⃗⃗⃗ =2(1-2λ)+2(2-2λ)=0, 解得λ=34,即BF ⃗⃗⃗⃗⃗ =(-12,12,32), 设平面FBA 的法向量为n ⃗ =(a ,b ,c ), 由{n ⃗ ⋅AB ⃗⃗⃗⃗⃗ =0n ⃗ ⋅BF ⃗⃗⃗⃗⃗ =0,得{a =0−12a +12b +32c =0令c =1,则n⃗ =(0,-3,1), 取平面ABP 的法向量i =(0,1,0), 则二面角F -AB -P 的平面角α满足: cosα=|i ⋅n ⃗⃗ ||i|⋅|n ⃗⃗ |=3√10=3√1010,故二面角F -AB -P 的余弦值为:3√1010【解析】本题考查的知识点是空间二面角的平面角,建立空间直角坐标系,将二面角问题转化为向量夹角问题,是解答的关键.(I )以A 为坐标原点,建立空间直角坐标系,求出BE ,DC 的方向向量,根据BE ⃗⃗⃗⃗⃗ •DC ⃗⃗⃗⃗⃗ =0,可得BE ⊥DC ;(II )求出平面PBD 的一个法向量,代入向量夹角公式,可得直线BE 与平面PBD 所成角的正弦值;(Ⅲ)根据BF ⊥AC ,求出向量BF ⃗⃗⃗⃗⃗ 的坐标,进而求出平面FAB 和平面ABP 的法向量,代入向量夹角公式,可得二面角F -AB -P 的余弦值. 10.【答案】证明:(Ⅰ)取AD 的中点F ,连接EF ,CF ,∵E 为PD 的中点,∴EF ∥PA ,EF ∥平面PAB ,在四边形ABCD 中,BC ∥AD ,AD =2DC =2CB ,F 为中点,∴四边形CBAF 为平行四边形,故CF ∥AB ,CF ∥平面PAB ,∵CF ∩EF =F ,EF ∥平面PAB ,CF ∥平面PAB , ∴平面EFC ∥平面ABP , ∵EC ⊂平面EFC , ∴EC ∥平面PAB .解:(Ⅱ)连接BF ,过F 作FM ⊥PB 于M ,连接PF , ∵PA =PD ,∴PF ⊥AD ,∵DF ∥BC ,DF =BC ,CD ⊥AD ,∴四边形BCDF 为矩形,∴BF ⊥AD , 又AD ∥BC ,故PF ⊥BC ,BF ⊥BC ,又BF ∩PF =F ,BF 、PF ⊂平面PBF ,BC ⊄平面PBF , ∴BC ⊥平面PBF ,∴BC ⊥PB ,设DC =CB =1,由PC =AD =2DC =2CB ,得AD =PC =2, ∴PB =√PC 2−BC 2=√4−1=√3, BF =PF =1,∴MF =√12−(√32)2=12,又BC ⊥平面PBF ,∴BC ⊥MF ,又PB ∩BC =B ,PB 、BC ⊂平面PBC ,MF ⊄平面PBC , ∴MF ⊥平面PBC ,即点F 到平面PBC 的距离为12,∵MF =12,D 到平面PBC 的距离应该和MF 平行且相等,均为12, E 为PD 中点,E 到平面PBC 的垂足也为所在线段的中点,即中位线, ∴E 到平面PBC 的距离为14,在△PCD 中,PC =2,CD =1,PD =√2,,故由余弦定理得CE =√2, 设直线CE 与平面PBC 所成角为θ,则sinθ=14CE=√28.【解析】本题考查线面平行的证明,考查线面角的正弦值的求法,考查空间中线线、能力,考查数形结合思想、化归与转化思想,属于中档题.(Ⅰ)取AD的中点F,连结EF,CF,推导出EF∥PA,CF∥AB,从而平面EFC∥平面ABP,由此能证明EC∥平面PAB.(Ⅱ)连结BF,过F作FM⊥PB于M,连结PF,推导出四边形BCDF为矩形,从而BF⊥AD,进而AD⊥平面PBF,由AD∥BC,得BC⊥PB,再求出BC⊥MF,由此能求出sinθ.11.【答案】证明:(Ⅰ)∵EA=EB,M是AB的中点,∴EM⊥AB,∵平面ABE⊥平面ABCD,平面ABE∩平面ABCD=AB,EM⊂平面ABE,∴EM⊥平面ABCD,∵AD⊂平面ABCD,∴EM⊥AD;(Ⅱ)取DE的中点F,连接AF,NF,∵N是CE的中点,∴NF=//12CD,∵M是AB的中点,∴AM=//12CD,∴NF=//AM,∴四边形AMNF是平行四边形,∴MN∥AF,∵MN⊄平面ADE,AF⊂平面ADE,∴MN∥平面ADE;解:(III)设点A到平面BCE的距离为d,由(I)知ME⊥平面ABC,BC=BE=2,MC=ME=√3,则CE=√6,BN=√BE2−EN2=√102,∴S△BCE=12CE⋅BN=√152,S△ABC=12BA×BC×sin60°=√3,∵V A-BCE=V E-ABC,即13S△BCE×d=13S△ABC×ME,解得d=2√155,故点A到平面BCE的距离为2√155.【解析】本题考查线线垂直、线面平行的证明,考查点到平面的距离的求法,涉及到力、数据处理能力,考查数形结合思想,是中档题.(Ⅰ)推导出EM ⊥AB ,从而EM ⊥平面ABCD ,由此能证明EM ⊥AD ;(Ⅱ)取DE 的中点F ,连接AF ,NF ,推导出四边形AMNF 是平行四边形,从而MN ∥AF ,由此能证明MN ∥平面ADE ;(III )设点A 到平面BCE 的距离为d ,由V A -BCE =V E -ABC ,能求出点A 到平面BCE 的距离.12.【答案】(I )证明:∵AB ∥CD ,AD ⊥DC ,AB =AD =1,CD =2,∴BD =BC =√2, ∴BD 2+BC 2=CD 2, ∴BD ⊥BC ,∵EA ⊥平面ABCD ,BD ⊂平面ABCD , ∴EA ⊥BD ,∵EA ∥FC , ∴FC ⊥BD ,又BC ⊂平面BCF ,FC ⊂平面BCF ,BC ∩CF =C , ∴BD ⊥平面FBC , 又BD ⊂平面BDE ,∴平面BDE ⊥平面BCF .(II )解:过A 作AM ⊥DE ,垂足为M , ∵EA ⊥平面ABCD ,CD ⊂平面ABCD , ∴EA ⊥CD ,又CD ⊥AD ,EA ∩AD =A , ∴CD ⊥平面EAD ,又AM ⊂平面EAD , ∴AM ⊥CD ,又AM ⊥DE ,DE ∩CD =D , ∴AM ⊥平面CDE ,∵AD =AE =1,EA ⊥AD ,∴AM =√22,即A 到平面CDE 的距离为√22,∵AB ∥CD ,CD ⊂平面CDE ,AB ⊄平面CDE , ∴AB ∥平面CDE ,∴B 到平面CDE 的距离为√22.【解析】(I )先计算BD ,BC ,利用勾股定理的逆定理证明BD ⊥BC ,再利用EA ⊥平面ABCD 得出AE ⊥BD ,从而有CF ⊥BD ,故而推出BD ⊥平面FBC ,于是平面EBD ⊥平面BCF ;(II )证明AB ∥平面CDE ,于是B 到平面CDE 的距离等于A 到平面CDE 的距离,过A 作AM ⊥DE ,证明AM ⊥平面CDE ,于是AM 的长即为B 到平面CDE 的距离. 本题考查了线面垂直、面面垂直的判定与性质,空间距离的计算,属于中档题. 13.【答案】证明:方法一:(1)取PA 中点G ,连结DG 、FG . ∵F 是PB 的中点, ∴GF ∥AB 且GF =12AB ,又底面ABCD 为矩形,E 是DC 中点, ∴DE ∥AB 且DE =12AB∴GF ∥DE 且GF =DE ,∴EF ∥DG∵DG ⊂平面PAD ,EF ⊄平面PAD , ∴EF ∥平面PAD .(2)∵PD ⊥底面ABCD ,AB ⊂面ABCD ∴PD ⊥AB又底面ABCD 为矩形 ∴AD ⊥AB 又PD ∩AD =D ∴AB ⊥平面PAD ∵DG ⊂平面PAD ∴AB ⊥DG∵AD =PD ,G 为AP 中点 ∴DG ⊥AP又AB ∩AP =A , ∴DG ⊥平面PAB又由(1)知EF ∥DG ∴EF ⊥平面PAB ,又EF ⊂面AEF ∴平面AEF ⊥平面PAB .证法二:(1)以D 为坐标原点,DA 、DC 、DP 所在直线分别为x 轴、y 轴、z 轴,建立如图所示空间直角坐标系.设AB =a . ∵AD =PD =2,∴A (2,0,0),B (2,a ,0),C (0,a ,0),P (0,0,2), ∵E 、F 分别为CD ,PB 的中点 ∴E (0,a2,0),F (1,a2,0).∴EF ⃗⃗⃗⃗⃗ =(1,0,1), ∵DP ⃗⃗⃗⃗⃗ +DA ⃗⃗⃗⃗⃗ =(0,0,2)+(2,0,0)=(2,0,2), ∴EF ⃗⃗⃗⃗⃗ =12(DP ⃗⃗⃗⃗⃗ +DA ⃗⃗⃗⃗⃗ )=12DP ⃗⃗⃗⃗⃗ +12DA ⃗⃗⃗⃗⃗ , 故EF ⃗⃗⃗⃗⃗ 、DP ⃗⃗⃗⃗⃗ 、DA ⃗⃗⃗⃗⃗ 共面, 又EF ⊄平面PAD ∴EF ∥平面PAD .(2)由(1)知EF ⃗⃗⃗⃗⃗ =(1,0,1),AB ⃗⃗⃗⃗⃗ =(0,a ,0),AP⃗⃗⃗⃗⃗ =(−2,0,2). ∴EF ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ =0,EF ⃗⃗⃗⃗⃗ •AP ⃗⃗⃗⃗⃗ =-2+0+2=0, ∴EF ⃗⃗⃗⃗⃗ ⊥AB ⃗⃗⃗⃗⃗ ,EF ⃗⃗⃗⃗⃗ ⊥AP ⃗⃗⃗⃗⃗ , 又AB ∩AP =A ,∴EF ⊥平面PAB , 又EF ⊂平面AEF ,∴平面AEF ⊥平面PAB , (3)AB =2√2由(1)知,∴AE ⃗⃗⃗⃗⃗ =(-2,√2,0),EF⃗⃗⃗⃗⃗ =(1,0,1)设平面AEF 的法向量n ⃗ =(x ,y ,z),则{n⃗ ⋅AE ⃗⃗⃗⃗⃗ =0n ⃗ ⋅EF ⃗⃗⃗⃗⃗ =0即−2x +√2y =0令x =1,则y =√2,z =-1, ∴n⃗ =(1,√2,-1), 又AC⃗⃗⃗⃗⃗ =(-2,2√2,0), ∴cos <AC⃗⃗⃗⃗⃗ ,n ⃗ >=−2+4+02√12=√36, ∴sinθ=|cos <AC⃗⃗⃗⃗⃗ ,n ⃗ >|=√36.【解析】方法一;(1)取PA 中点G ,连结DG 、FG ,要证明EF ∥平面PAD ,我们可以证明EF 与平面PAD 中的直线AD 平行,根据E 、F 分别是PB 、PC 的中点,利用中位线定理结合线面平行的判定定理,即可得到答案. (2)根据线面垂直的和面面垂直的判断定理即可证明.方法二:(1)求出直线EF 所在的向量,得到EF ⃗⃗⃗⃗⃗ =12(DP ⃗⃗⃗⃗⃗ +DA ⃗⃗⃗⃗⃗ )=12DP ⃗⃗⃗⃗⃗ +12DA ⃗⃗⃗⃗⃗ ,即可证明EF ∥平面PAD .(2)再求出平面内两条相交直线所在的向量,然后利用向量的数量积为0,根据线面垂直的判定定理得到线面垂直,即可证明平面AEF ⊥平面PAB(3)求出平面的法向量以及直线所在的向量,再利用向量的有关运算求出两个向量的夹角,进而转化为线面角,即可解决问题.本题考查了本题考查的知识点是直线与平面平行的判定,面面垂直,直线与平面所成的角,解决此类问题的关键是熟练掌握几何体的结构特征,进而得到空间中点、线、面的位置关系,利于建立空间之间坐标系,利用向量的有关知识解决空间角与空间距离以及线面的位置关系等问题,属于中档题.14.【答案】解:(1)证明:∵PO ⊥平面ABCD ,且AD ⊂平面ABCD , ∴PO ⊥AD , ∵∠ADC =45°且AD =AC =2, ∴∠ACD =45°, ∴∠DAC =90°, ∴AD ⊥AC ,∵AC ⊂平面PAC ,PO ⊂平面PAC ,且AC ∩PO =O , ∴由直线和平面垂直的判定定理知AD ⊥平面PAC . (2)解:取DO 中点N ,连接MN ,AN , 由PO ⊥平面ABCD ,得MN ⊥平面ABCD , ∴∠MAN 是直线AM 与平面ABCD 所成的角, ∵M 为PD 的中点, ∴MN ∥PO ,且MN =12PO =3, AN =12DO =√52,在Rt △ANM 中,tan ∠MAN =MNAN =3√52=6√55, 即直线AM 与平面ABCD 所成角的正切值为6√55.【解析】(1)由PO ⊥平面ABCD ,得PO ⊥AD ,由∠ADC =45°,AD =AC ,得AD ⊥AC ,从而证明AD ⊥平面PAC .(2)取DO 中点N ,连接MN ,AN ,由M 为PD 的中点,知MN ∥PO ,由PO ⊥平面出直线AM 与平面ABCD 所成角的正切值.本题考查直线与平面垂直的证明,考查直线与平面所成角的正切值的求法.解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题. 15.【答案】证明:(I )在三棱柱ABC -A 1B 1C 1中,连接A 1B ,交AB 1于O 点,连接OD∵在△A 1BC 1中,A 1D =DC 1,A 1O =OB , ∴OD ∥BC 1,又∵OD ⊂平面AB 1D ,BC 1⊄平面AB 1D ; ∴BC 1∥平面AB 1D ;(II )在三棱柱ABC -A 1B 1C 1中,A 1A ⊥平面A 1B 1C 1; ∵B 1D ⊂平面A 1B 1C 1; ∴A 1A ⊥B 1D在△A 1B 1C 1中,D 为A 1C 1的中点 ∴B 1D ⊥A 1C 1又∵A 1A ∩A 1C 1=A 1,A 1A ,A 1C 1⊂平面AA 1C 1C , ∴B 1D ⊥平面AA 1C 1C , 又∵A 1C ⊂平面AA 1C 1C , ∴B 1D ⊥A 1C又∵A 1D AA 1=AA1AC =√22∴∠DA 1A =∠A 1AC =90°∴△DA 1A ∽△A 1AC ,∠ADA 1=∠CA 1A∵∠DA 1C +∠CA 1A =90° ∴∠DA 1C +∠ADA 1=90°∴A 1C ⊥AD又∵B 1D ∩AD =D ,B 1D ,AD ⊂平面AB 1D ; ∴A 1C ⊥平面AB 1D ;解:(III )由(I )得,OD ∥BC 1, 故AD 与BC 1所成的角即为∠ADO在△ADO 中,AD =√3,OD =12BC 1=√62,AO =12A 1B =√62,∵AD 2=OD 2+AO 2,OD =AO∴△ADO 为等腰直角三角形故∠ADO =45°即异面直线AD 与BC 1所成角等于45°【解析】(I )连接A 1B ,交AB 1于O 点,连接OD ,由平行四边形性质及三角形中位线定理可得OD ∥BC 1,进而由线面平行的判定定理得到BC 1∥平面AB 1D ;(II )由直棱柱的几何特征可得A 1A ⊥B 1D ,由等边三角形三线合一可得B 1D ⊥A 1C 1,进而由线面垂直的判定定理得到B 1D ⊥平面AA 1C 1C ,再由三角形相似得到A 1C ⊥AD 后,可证得A 1C ⊥平面AB 1D .(III )由(I )中OD ∥BC 1,可得异面直线AD 与BC 1所成角即∠ADO ,解△ADO 可得答案.本题考查的知识点是直线与平面垂直的判定,异面直线及其所成的角,直线与平面平行的判定,(I )的关键是证得OD ∥BC 1,(II )的关键是熟练掌握线面垂直与线线垂直之间的转化,(III )的关键是得到异面直线AD 与BC 1所成角即∠ADO .16.【答案】(Ⅰ)证明:由P -ABD ,Q -BCD 是相同正三棱锥,且∠APB =90°,分别过P 、Q 作PE ⊥平面ABD ,QF ⊥平面BCD ,垂足分别为E 、F ,则E 、F 分别为底面正三角形ABD 与BCD 的中心. 连接EF 交BD 于G ,则G 为BD 的中点,连接PG 、QG ,则PG ⊥BD ,QG ⊥BD ,又PG ∩QG =G ,∴BD ⊥平面PQG ,则BD ⊥PQ , 再由正三棱锥的性质可得PA ⊥BD , 又PQ ∩PA =P ,∴BD ⊥平面APQ ;(Ⅱ)∵正三棱锥的底面边长为1,且∠APB =90°,∴PQ =EF =2EG =2×13AG =2×13×√32=√33, PE =√(√22)2−(√33)2=√66,则V B−PQD =13×12×√33×√66×1=√236.△PDQ 底边PQ 上的高为√(√22)2−(√36)2=√156,∴S △PDQ =12×√33×√156=√512.设B 到平面PQD 的距离为h ,则13×√512ℎ=√236,得h =√105.∴直线PB 与平面PDQ 所成角的正弦值为√105√22=2√55.【解析】(Ⅰ)由题意分别过P 、Q 作PE ⊥平面ABD ,QF ⊥平面BCD ,可得E 、F 分别为底面正三角形ABD 与BCD 的中心.连接EF 交BD 于G ,可得PG ⊥BD ,QG ⊥BD ,由线面垂直的判定及性质可得BD ⊥PQ ,再由正三棱锥的性质可得PA ⊥BD ,则BD ⊥平面APQ ;(Ⅱ)由已知求得PQ ,PE 的长,求得四面体B -PQD 的体积,利用等积法求出B 到平面PQD 的距离,则直线PB 与平面PDQ 所成角的正弦值可求.本题考查直线与平面所成的角,考查线面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题. 17.【答案】(1)证明:如图:∵AB =BC ,E 为AC 的中点,∴BE ⊥AC ,∵平面A 1ACC 1⊥平面ABC ,平面A 1ACC 1∩平面ABC =AC , ∴BE ⊥平面A 1ACC 1,∵A 1C ⊂平面A 1ACC 1,∴BE ⊥A 1C .(2)解:∵面A1ACC1⊥面ABC,∴C1在面ABC上的射影H在AC上,∴∠C1CA为直线C1C与面ABC所成的角.过H作HM⊥BC于M,连C1M,在Rt△C1CM中,CM=CC1cos∠C1CM=2cos60°=1.在Rt△CMH中,CH=CMcos∠ACB =2√33.∴在Rt△C1CH中,cos∠C1CH=CHCC1=23√32=√33.∴直线C1C与面ABC所成的角的余弦值为√33.【解析】(1)证明BE⊥平面A1ACC1,可得BE⊥A1C,即可证明:A1C⊥平面C1EB;(2)判断∠C1CA为直线C1C与面ABC所成的角.过H作HM⊥BC于M,连C1M,即可求直线CC1与平面ABC所成角的余弦值.本题考查线面垂直的判定与性质,考查线面角,考查学生分析解决问题的能力,属于中档题.18.【答案】证明:(1)连接CD,据题知AD=4,BD=2,∵AC2+BC2=AB2,∴∠ACB=90°,∴cos∠ABC=2√36=√33,∴CD2=4+12−2×2×2√3cos∠ABC=8,∴CD=2√2,∴CD2+AD2=AC2,∴CD⊥AB,又∵平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,CD⊂平面ABC,∴CD⊥平面PAB,∵PD⊂平面PAB,∴CD⊥PD,∵PD⊥AC,CD∩AC=C,CD、AC⊂平面ABC,∴PD⊥平面ABC.解:(2)∵∠PAB=π4,∴PD=AD=4,∴PA=4√2,在Rt△PCD中,PC=√PD2+CD2=2√6,∴△PAC是等腰三角形,∴S△PAC=8√2,设点B到平面PAC的距离为d,由V B-PAC=V P-ABC,得13S△PAC×d=13S△ABC×PD,∴d==3,故点B到平面PAC的距离为3.【解析】本题考查线面垂直的证明,考查点到平面的距离的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.(1)连接CD,推导出CD⊥AB,CD⊥PD,由此能证明PD⊥平面ABC.(2)设点B到平面PAC的距离为d,由V B-PAC=V P-ABC,能求出点B到平面PAC的距离.19.【答案】解:(1)证明:∵ABC-A1B1C1中,A1A⊥平面ABC,又BB 1⊂平面BB 1C 1C , ∴平面BB 1C 1C ⊥平面ABC ,∵△ABC 为正三角形,D 为BC 的中点, ∴AD ⊥BC ,又平面BB 1C 1C ∩平面ABC =BC , ∴AD ⊥平面BB 1C 1C , 又AD ⊂平面ADB 1,∴平面ADB 1⊥平面BB 1C 1C ;(2)由(1)可得△ADB 1为直角三角形, 又AD =√32,B 1D =√52,∴S △ADB 1=12×AD ×B 1D =√158,又S △ADB =12S △ABC =√38,设点B 到平面ADB 1的距离为d , 则V B−ADB 1=V B 1−ADB , ∴13S △ADB 1⋅d =13S △ADB ⋅BB 1, ∴点B 到平面ADB 1的距离d =S △ADB ⋅BB 1S △ADB 1=√3√15=√55.【解析】本题考查面面垂直的证明,考查点到平面的距离的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.(1)推导出BB 1⊥平面ABC ,从而平面BB 1C 1C ⊥平面ABC ,推导出AD ⊥BC ,从而AD ⊥平面BB 1C 1C ,由此能证明平面ADB 1⊥平面BB 1C 1C ;(2)设点B 到平面ADB 1的距离为d ,由V B−ADB 1=V B 1−ADB ,能求出点B 到平面ADB 1的距离.20.【答案】证明:(1)∵PA ⊥平面ABC ,BE ⊂平面ABC , ∴PA ⊥BE .∵AB =BC ,E 为AC 的中点, ∴BE ⊥AC ,又PA ⊂平面PAC ,AC ⊂平面PAC ,PA ∩AC =A , ∴BE ⊥平面PAC ,又BE ⊂平面BED , ∴平面BED ⊥平面PAC .(2)∵D ,E 是PC ,AC 的中点, ∴DE ∥PA ,又PA ⊥平面ABC ,∴DE ⊥平面ABC ,∵EF ⊂平面ABC ,BE ⊂平面ABC , ∴DE ⊥EF ,DE ⊥BE .∴∠FEB 为二面角F -DE -B 的平面角.∵E ,F 分别是AC ,AB 的中点,AB =AC , ∴EF =12BC =12AB =BF ,EF ∥BC .又AB ⊥BC ,∴BF ⊥EF ,∴△BEF 为等腰直角三角形,∴∠FEB =45°. ∴二面角F -DE -B 为45°.∴PA⊥BC,又BC⊥AB,PA⊂平面PAB,AB⊂平面PAB,PA∩AB=A,∴BC⊥平面PAB.∴∠CPB为直线PC与平面PAB所成的角.∵PA=6,∴DE=12PA=3,又DF=5,∴EF=√DF2−DE2=4.∴AB=BC=8.∴PB=√PA2+AB2=10.∴tan∠CPB=BCPB =4 5.【解析】(1)通过证明BE⊥平面PAC得出平面BED⊥平面PAC;(2)由DE∥PA得出DE⊥平面ABC,故DE⊥EF,DE⊥BE,于是∠FEB为所求二面角的平面角,根据△BEF为等腰直角三角形得出二面角的度数;(3)证明BC⊥平面PAB得出∠CPB为所求角,利用勾股定理得出BC,PB,即可得出tan∠CPB.本题考查了线面垂直,面面垂直的判定,空间角的计算,做出空间角是解题关键,属于中档题.21.【答案】解:(1)证明:设AC∩BD=H,连接EH,在△ADC中,因为AD=CD,且DB平分∠ADC,所以H为AC的中点,又有题设,E为PC的中点,故EH∥PA,又HE⊂平面BDE,PA⊄平面BDE,所以PA∥平面BDE(2)证明:因为PD⊥平面ABCD,AC⊂平面ABCD,所以PD⊥AC由(1)知,BD⊥AC,PD∩BD=D,故AC⊥平面PBD(3)由AC⊥平面PBD可知,BH为BC在平面PBD内的射影,所以∠CBH为直线与平面PBD所成的角.由AD⊥CD,AD=CD=1,DB=2√2,可得DH=CH=√22,BH=3√22在Rt△BHC中,tan∠CBH=CHBH =13,所以直线BC与平面PBD所成的角的正切值为13.【解析】(1)欲证PA∥平面BDE,根据直线与平面平行的判定定理可知只需证PA与平面BDE内一直线平行,设AC∩BD=H,连接EH,根据中位线定理可知EH∥PA,而又HE⊂平面BDE,PA⊄平面BDE,满足定理所需条件;(2)欲证AC⊥平面PBD,根据直线与平面垂直的判定定理可知只需证AC与平面PBD内两相交直线垂直,而PD⊥AC,BD⊥AC,PD∩BD=D,满足定理所需条件;(3)由AC⊥平面PBD可知,BH为BC在平面PBD内的射影,则∠CBH为直线与平面PBD所成的角,在Rt△BHC中,求出此角即可.本小题主要考查直线与平面平行.直线和平面垂直.直线和平面所成的角等基础知识,考查空间想象能力、运算能力和推理能力.。
高中数学必修二 8 5 空间直线、平面的平行(精练)(含答案)

8.5 空间直线、平面的平行(精练)【题组一 线线平行】1.(2021·全国·高一课时练习)如图,在三棱锥A -BCD 中,E ,F ,G ,H 分别是边AC ,CD ,BD ,AB 的中点,且AD =BC ,那么四边形EFGH 是( )A .平行四边形B .矩形C .菱形D .正方形【答案】C【解析】因为,H G 分别是,BA BD 的中点,所以//HG AD ,且1=2HG AD ,同理//EF AD ,且1=2EF AD ,//HE BC ,且1=2HE BC ,//GF BC ,且1=2GF BC ,又=AD BC ,可得四边形EFGH 为菱形.故选:C.2.(2021·全国·高一课时练习)如果两直线a ∥b ,且a ∥α,则b 与α的位置关系是( ) A .相交 B .b ∥αC .b ⊂αD .b ∥α或b ⊂α【答案】D【解析】由a ∥b ,且a ∥α,结合线面平行的判定定理,知b 与α平行或b ⊂α.故选:D3.(2021·全国·高一课时练习)如图,在三棱柱ABC-A 1B 1C 1中,E ,F 分别是AB ,AC 上的点,且AE ∶EB=AF ∶FC ,则EF 与B 1C 1的位置关系是_____.【答案】平行【解析】在△ABC 中,AE ∶EB=AF ∶FC ,∴EF ∥BC ,三棱柱ABC-A 1B 1C 1中,有BC ∥B 1C 1,∴EF ∥B 1C 1.故答案为:平行4.(2021·全国·高一课时练习)如图是正方体的表面展开图,E ,F ,G ,H 分别是棱的中点,则EF 与GH 在原正方体中的位置关系为______.【答案】平行【解析】由题意,将正方体的表面展开图还原构造成正方体,如图所示: 分别取AB ,AA 1的中点Q ,P ,连接EP ,FQ ,PQ ,A 1B , 由正方体的结构特征可得EF ∥PQ ,又因为点Q ,P ,H ,G 分别是AB ,AA 1,A 1B 1,BB 1的中点,故PQ ∥A 1B ,HG ∥A 1B , 故PQ ∥HG ,所以EF ∥GH . 故答案为:平行5.(2021·广东东莞·高一期中)如图,点P ,Q ,R ,S 分别在正方体的四条棱上,且是所在棱的中点,则直线PQ 与RS 是平行直线的图是________(填序号).【答案】①②【解析】根据正方体的结构特征,可得①②中RS 与PQ 均是平行直线,④中RS 和PQ 是相交直线,③中RS 和PQ 是是异面直线.故答案为:①②.6.(2021·全国·高一课时练习)如图,在三棱柱111ABC A B C -中,,E F 分别是,AB AC 上的点,且::AE EB AF FC =,则EF 与11B C 的位置关系是______.【答案】平行 【解析】在ABC 中,::,//AE EB AF FC EF BC =∴.又.11//BC B C ,所以11//EF B C .故答案为:平行.7.(2021·全国·高一课时练习)如图,△ABC 和△A'B'C'的对应顶点的连线AA',BB',CC'交于同一点O ,且2'''3AO BO CO OA OB OC ===.(1)求证:A'B'∥AB ,A'C'∥AC ,B'C'∥BC ; (2)求'''ABC A B C S S的值.【答案】(1)证明见解析;(2)49.【解析】(1)∵AA'∩BB'=O 且2''3AO BO A O B O ==, ∴AB ∥A'B',同理,AC ∥A'C',BC ∥B'C'.(2)∵A'B'∥AB ,A'C'∥AC ,由图知:AB 和A'B',AC 和A'C'方向相反,∴∠BAC=∠B'A'C',同理,∠ABC=∠A'B'C',∠ACB=∠A'C'B',∴△ABC ∽△A'B'C', ∴2'''3AB AO A B OA ==,∴2'''2439ABC A B C SS⎛⎫== ⎪⎝⎭. 8(2021·全国·高一课时练习)已知E ,F ,G ,H 为空间四边形ABCD 的边AB ,BC ,CD ,DA 上的点,若12AE AH AB AD ==,13CFCGCB CD == 证明:四边形EFGH 为梯形. 【答案】证明见解析【解析】证明:如图,在ABD中,因为12AE AHAB AD==,所以EH∥BD且EH=12BD.在BCD中,因为13CF CGCB CD==,所以FG∥BD且FG=13BD,所以EH∥FG且EH>FG,所以四边形EFGH为梯形.9.(2021·全国·高一课时练习)如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.(1)求证:四边形BB1M1M为平行四边形;(2)求证:∠BMC=∠B1M1C1.【答案】(1)证明详见解析;(2)证明详见解析.【解析】(1)在正方形ADD1A1中,M、M1分别为AD、A1D1的中点,∴MM1∥AA1,MM1=AA1.又∵AA1∥BB1,AA1=BB1,∴MM1∥BB1,且MM1=BB1,∴四边形BB1M1M为平行四边形.(2)法一:由(1)知四边形BB1M1M为平行四边形,∴B1M1∥BM.同理可得四边形CC1M1M为平行四边形,∴C1M1∥CM.由平面几何知识可知,∠BMC和∠B1M1C1都是锐角.∴∠BMC=∠B1M1C1.法二:由(1)知四边形BB1M1M为平行四边形,∴B1M1=BM.同理可得四边形CC1M1M为平行四边形,∴C1M1=CM.又∵B1C1=BC,∴△BCM≌△B1C1M1.∴∠BMC=∠B1M1C1.【题组二线面平行】1.(2021·全国·高一课时练习)如图,点A,B,C,M,N为正方体的顶点或所在棱的中点,则下列各图中,不满足直线//MN平面ABC的是( )A .B .C .D .【答案】D【解析】对于A ,由正方体的性质可得////MN EF AC ,可得直线//MN 平面ABC ,能满足;对于B ,作出完整的截面ADBCEF ,由正方体的性质可得MN //AD ,可得直线MN //平面ABC ,能满足;对于C ,作出完整的截面ABCD ,由正方体的性质可得MN //BD ,可得直线MN //平面ABC ,能满足;对于D,作出完整的截面,如下图ABNMHC,可得MN在平面ABC内,不能得出平行,不能满足.故选:D.2 .(2021·福建长汀·高一期中)(多选)如图所示,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点,给出以下结论,其中正确的是( )A.OM∥PD B.OM∥平面PACC.OM∥平面PDA D.OM∥平面PBA【答案】AC【解析】因为矩形对角线的交点为O,所以O是BD的中点,∴为△PBD的中位线,又M为PB的中点,OM∴,//OM PD又OM⊄平面PAD,PD⊂平面PAD,所以OM∥平面PDA,故AC正确;OM与平面PAC有公共点O,与平面PBA有公共点M,故BD错误.故选:AC.3.(2021·吉林·长春市第八中学高一期中)(多选)下列四个正方体图形中,A,B为正方体的两个顶点,M、AB平面MNP的图形是( )N、P分别为其所在棱的中点,不能得出//A.B.C.D.【答案】BC【解析】对于A:连接AC,如图①所示.由MN∥AC,NP∥BC,MN∩NP=N,AC∩BC=C,可知平面MNP∥平面ACB,所以AB∥平面MNP.故不选A;对于B:连接BC交MP于D,连接DN,如图②所示由于N是AC的中点,D不是BC的中点,所以在平面ABC内AB 与DN相交,所以直线AB与平面MNP相交,故选B;对于C:连接CD,如图③所示则AB∥CD,而CD与PN相交,即CD与平面MNP相交,所以直线AB与平面MNP相交,故选C;对于D:连接CD,如图④所示.则AB∥CD∥NP,由线面平行的判定定理可知AB∥平面MNP综上所述,不能得出AB∥平面MNP的图形是B和C.故选:BC4.(2021·全国·高一课时练习)下列四个正方体图形中,,A B 为正方体的两个顶点,,,M N P 分别为其所在棱的中点,能得出//AB 平面MNP 的图形的序号是________.【答案】①④【解析】在①中:如图:因为,,M N P 分别为其所在棱的中点,所以//MN AC ,//NP BC , 因为MN ⊄面ABC ,AC ⊂面ABC ,所以//MN 面ABC ,同理可得//PN 面ABC , 因为MN NP N ⋂=,所以面//ABC 面MNP ,因为AB面ABC ,所以//AB 平面MNP ,故①成立;在②中,若下底面中心为O ,连接NO ,可得//NO AB ,NO ⋂面MNP N =,所以AB 与平面MNP 不平行,故②不成立;在③中:如图:平面PMN 即为平面PNBC ,因为AB ⋂面PNBC B =,所以AB 与面MNP 不平行,故③不成立;在④中:如图://AC BD 且AC BD =,所以四边形ACDB 是平行四边形,可得//AB CD ,因为//NP CD ,所以//AB NP ,因为AB ⊄面MNP ,NP ⊂面MNP , 所以所以//AB 平面MNP ,故④成立.故答案为:①④.5.(2021·全国·高一课时练习)已知正三棱柱ABC ﹣A 1B 1C 1的边长均为E ,F 分别是线段AC 1和BB 1的中点.(1)求证:EF //平面ABC ; (2)求三棱锥C ﹣ABE 的体积. 【答案】(1)证明见解析;(2)3.【解析】(1)证明:取AC 的中点为G ,连结GE ,GB , 在△ACC 1中,EG 为中位线,所以EG //CC 1,112EG CC =,又因为CC 1//BB 1,CC 1=BB 1,F 为BB 1的中点, 所以EG //BF ,EG =BF ,所以四边形EFBG 为平行四边形,所以EF //GB ,又EF ⊄平面ABC ,GB ⊂平面ABC , 所以EF //平面ABC . (2)因为E 为AC 1的中点,所以E 到底面ABC 的距离是C 1到底面ABC 的距离的一半,即三棱锥E ﹣ABC 的高h =12CC 1又△ABC 的面积为2S ==所以133C ABE E ABC V V --==⨯.6.(2021·全国·高一课时练习)如图,正方形ABCD 和四边形ACEF 所在平面相交.//EF AC ,AB =1EF =.求证://AF 平面BDE .【答案】证明见解析【解析】设AC ,BD 交于点G ,连接EG ,因为四边形ABCD 是正方形,AB =所以BC =2AC =,112AG AC ==, 又因为1EF =,所以EF AG =,又//EF AC ,所以四边形AGEF 为平行四边形.所以AF //EG .又因为AF ⊄平面BDE ,EG ⊂平面BDE ,所以//AF 平面BDE .7.(2021·全国·高一课时练习)如图,ABC 是正三角形,AE 和CD 都垂直于平面ABC ,且2AE AB a ==,CD a =,F 是BE 的中点,求证://DF 平面ABC .【答案】证明见解析【解析】证明:取AB 的中点G ,连接FG ,CG ,可得//FG AE ,12FG AE =.因为CD ⊥平面ABC ,AE ⊥平面ABC ,所以//CD AE . 又因为12CD AE =.所以//FG CD ,FG CD =.所以四边形CDFG 是平行四边形,所以//DF CG . 又因为CG ⊂平面ABC ,DF ⊄平面ABC ,所以//DF 平面ABC .8.(2021·全国·高一课时练习)如图所示,已知正方形ABCD 和正方形ABEF 所在的平面相交于AB ,点M 、N 分别在AC 和BF 上,且AM FN =.求证;//MN 平面BCE .【答案】证明见解析.【解析】如图所示,连接AN 并延长交BE 的延长线于G ,连接CG .∵//AF BG ,∴AN FN NG NB=,又,AM FN AC FB ==,∴MC NB =, ∴FN AM NB MC=,∴AN AM NG MC =, ∴//NM CG .∵CG ⊂平面CBE ,NM ⊄平面CBE ,∴//MN 平面BCE .9.(2021·黑龙江齐齐哈尔·高一期末)如图,在四棱锥P ABCD -中,平面PBC ⊥平面ABCD ,90PBC ∠=︒,//AD BC ,90ABC ∠=︒,222AB AD ===,E 为PC 的中点.(1)证明://DE 平面APB ;(2)若2BP =,求三棱锥E DBP -的体积.【答案】(1)证明见解析;(2)13. 【解析】(1)取PB 中点F ,连接FE ,FA ,∵E 是CP 的中点,∴//EF CB ,12EF CB , ∵//AD BC ,90ABC ∠=︒,∴90DAB ∠=︒,∵1AD AB ==,∴BD 45ADB ∠=︒,则45DBC ∠=︒,又∵CD =,∴90CDB ∠=︒,可得2CB =,∴//AD CB ,12AD CB =,∴//EF AD ,EF AD =,得四边形ADEF 为平行四边形,∴//DE AF ,又DE ⊄平面ABP ,AF ⊂平面ABP ,∴//DE 平面APB ;(2)取BC 中点O ,连接DO ,∴⊥DO CB ,∵平面PBC ⊥平面ABCD ,平面PBC 平面ABCD CB =,∴DO ⊥平面PBC ,则DO 为三棱锥D EBP -的高,又∵2BC BP ==,∴BE CP ⊥,得12BE CP =∴1111111332323E DBP D EBP EBP V V DO S DO BE EP --⎛⎫⎛==⋅=⨯⨯⨯=⨯⨯= ⎪ ⎝⎭⎝△. 故三棱锥E DBP -的体积为13. 10.(2021·广西·钦州市第四中学高一月考)如图,在直三棱柱ABC ﹣A 1B 1C 1中,AB ⊥BC ,AA 1=AC =2,BC =1,E ,F 分别是A 1C 1,BC 的中点.(1)求证:C 1F //平面ABE ;(2)求三棱锥A ﹣BCE 的体积.【答案】(1)证明见解析;【解析】(1)证明:取AB 的中点G ,连接EG ,FG ,∵E ,F ,G 分别是A 1C 1,BC ,AB 的中点,∴FG //AC ,且FG =12AC ,EC 1=12A 1C 1,∵AC //A 1C 1且AC =A 1C 1,∴GF //EC 1且GF =EC 1,∴四边形FGEC 1为平行四边形,得C 1F //EG ,又∵EG ⊂平面ABE ,C 1F ⊄平面ABE ,∴C 1F //平面ABE ;(2)∵AA 1=AC =2,BC =1,AB ⊥BC ,∴AB .∴三棱锥A ﹣BEC 的体积V =V A ﹣BEC =V E ﹣ABC =113ABC S AA ⋅=111232⨯⨯=11(2021·广西·钦州市第四中学高一月考)如图,在五面体ABCDEF 中,四边形ABCD 是直角梯形,∠BAD =90°,BC //AD ,AB =AF =BC =12AD =1,AF ⊥平面ABCD ,N ,G 分别为DF ,CD 的中点.(1)求证:NC //平面FAB ;(2)求三棱锥E ﹣ACG 的体积.【答案】(1)证明见解析;(2)16. 【解析】(1)取AD 的中点M ,连接NM ,CM ,在△ADF 中,∵N 是FD 的中点,M 是AD 的中点,∴//NM FA ,由于NM ⊄平面FAB ,FA ⊂平面FAB ,所以//NM 平面FAB .在梯形ABCD 中,BC //AD ,AD =2BC ,M 是AD 的中点,∴BC =AM ,BC //AM ,可得四边形ABCM 为平行四边形,则CM //AB ,由于CM ⊄平面FAB ,AB 平面FAB ,所以//CM 平面FAB .∵CM ∩NM =M ,∴平面NMC //平面FAB ,又NC ⊂平面NMC ,∴NC //平面FAB ;(2)∵BC //AD ,AD ⊂平面ADEF ,BC ⊄平面ADEF ,∴BC //平面ADEF ,∵BC ⊂平面BCEF ,平面BCEF ∩平面ADEF =EF ,∴BC //EF ,又BC ⊂平面ABCD ,EF ⊄平面ABCD ,∴EF //平面ABCD ,连接FC ,FG ,则V E ﹣ACG =V F ﹣ACG .∵四边形ABCD 是直角梯形,∠BAD =90°,BC //AD ,AB =AF =BC =12AD =1,∴CD =AC ACD =90°,CG ,又AF ⊥平面ABCD ,∴1132E ACG V CG AC AF -=⨯⨯⨯=1111326⨯=.故三棱锥E ﹣ACG 的体积为16.12.(2021·山西·太原市第五十六中学校高一月考)如图,在正方体1111ABCD A B C D -中,E ,F ,P ,Q 分别是棱AB ,AD ,1DD ,1BB 的中点.求证:1//BC 平面EFPQ .【答案】证明见解析.【解析】在正方体1111ABCD A B C D -中,连接1AD ,因为11AB C D =且11//AB C D ,所以四边形11ABC D 是平行四边形,可得11//AD BC ,因为F ,P 分别是AD 、1DD 的中点,所以1//FP AD ,所以1//BC FP ,又FP ⊂平面EFPQ ,且1BC ⊄平面EFPQ , 所以直线1//BC 平面EFPQ .13.(2021·重庆第二外国语学校高一月考)如图,正三棱柱111ABC A B C -中,14AA =,ABC 的边长为6,,D E 分别为棱1,AC CC 的中点.(1)1AB //平面1BDC ;(2)求异面直线DE 与1AB 所成角的余弦值.【答案】(1)证明见解析;(2)1726【解析】(1)如图所示:连接1B C 与1BC 交于点O ,连接DO ,因为D 分别为棱AC 的中点.所以1//AB OD ,又1AB ⊄平面1BDC ,OD ⊂平面1BDC ,所以1AB //平面1BDC ;(2)由(1)知:1//AB OD ,所以EDO ∠是异面直线DE 与1AB 所成的角,连接OE ,在DEC Rt △中,DE =在1Rt BC C △中,1BC =因为三棱柱是正三棱柱,所以BD ⊥平面11A ACC ,则1BD DC ⊥,在1Rt BDC △中,112DO BC == 又3EO =,所以由余弦定理得: 222cos 2DE DO EO EDO DE DO+-∠=⋅, 22231726+-=,所以异面直线DE 与1AB 所成角的余弦值是1726. 14(2021·重庆市育才中学高一期中)如图,在四棱锥P ABCD -中,底面ABCD 是矩形,PD ⊥平面ABCD , 4AD PD ==,点Q 是PC 的中点.(1)求证:PA //平面BDQ ; (2)在线段AB 上是否存在点F ,使直线PF 与平面PAD 所成的角为30°?若存在,求出AF 的长,若不存在,请说明理由?【答案】(1)见解析;(2)存在,AF =【解析】(1)连结AC ,交BD 于O ,如图所示,底面ABCD 是矩形,因此O 为AC 中点,且点Q 是PC 的中点//PA QO ∴又PA ⊄平面BDQ ,QO ⊆平面BDQ PA ∴//平面BDQ (2)PD ⊥平面ABCD ,AB ⊆平面ABCD PD AB ∴⊥又AD AB ⊥,,,PD AD D PD AD =⊆平面PAD AB ∴⊥平面PAD∴直线PF 与平面PAD 所成的角即为30APF ︒∠=AF AP ∴==因此存在点F ,使直线PF 与平面PAD 所成的角为30°,此 时AF =15.(2021·江苏如皋·高一月考)如图,在多面体ABCDE 中,60ABD ∠=︒,2BD AB =,AB CD ⊥,(1)//AB DE ,且2DE AB =,点M 为EC 的中点,求证://AM 平面BCD ;(2)若BCD △是边长为2的等边三角形,BA =N 在线段CD 上,且2DN CN =,求BN 与平面ACD 所成角的大小;【答案】(1)证明见解析;(2)30.【解析】(1)如图,取线段CD 的中点F ,连接BF ,MF在CDE △中,点M 为EC 的中点,点F 为线段CD 的中点//MF DE ∴,且12MF DE = 又//AB DE ,且2DE AB =,//AB MF ∴,AB MF =∴四边形ABFM 为平行四边形//AM BF ∴AM ⊄平面BCD ,BF ⊂平面BCD //AM ∴平面BCD(2)在ABD △中,2BD AB =,60ABD ∠=︒90BAD ∴∠=︒即AB AD ⊥ 又AB CD ⊥,AD CD D =,AD 、CD ⊂平面ACD AB ∴⊥平面ACD BNA ∴∠即为BN 与平面ACD 所成的角在BCN △中,2BC =,23CN =,由余弦定理得:BN ==又在直角三角形ABN 中,BA =BN =,AN ==cos AN BNA BN ∠== ∴BN 与平面ACD 所成角的大小为30.16(2021·山西省长治市第二中学校高一月考)如图:在四棱锥P ABCD -中,AB ∥CD ,3AB CD =,点E 是PC 上的一点,(1)若//BE 平面PAD ,求PEEC的值. (2)若平面ABE 将四棱锥分成体积相等的两部分,求PEEC的值. 【答案】(1)12;(2)2.【解析】(1)过点E 做//EF CD 交PD F 于,连接AF ,AB //CD ,CD //EF ,//BE 平面PAD ,平面PAD 平面ABEF AF =,ABEF ∴是平行四边形,13EF AB CD ==12PE EC ∴= (2)过点E 做//EF CD 交PD F 于,连接AF BF 、设PE PC,λ=则PAF PADSS=λ,2PEF PCDS S=λ13344P ABD P ABCD P BCD P ABCD CD AB,V V ,V V ----=∴==2P ABEF P ABF P BEF B APF B PEF P BAD P BCD V V V V V V V -------=+=+=+λλ231442P ABCD P ABCD P ABCD V V V ---=+=λλ,化简得:2320λλ+-=,解得:23λ=或1λ=-(舍去),2PEEC∴=.17.(2021·河北·深州长江中学高一期中)如图,正四棱锥,4,2S ABCD SA AB -==,E 为SC 中点.(1)求证://SA 平面BDE ; (2)求四棱锥S ABCD -的体积;【答案】(1)证明见解析;. 【解析】(1)连接AC ,交BD 于点O ,连接OE .因为四棱锥S ABCD -为正四棱锥,所以四边形ABCD 为正方形,即O 为AC 中点, 因为E 为SC 中点,所以OE 为SAC 的中位线,所以//OE SA , 因为OE ⊂平面BDE ,SA ⊄平面BDE ,//SA 平面BDE . (2)连接SO ,如图所示:在正四棱锥S ABCD -中,SO ⊥平面ABCD ,即棱锥的高为SO ,在Rt SOB 中,SO ==211233S ABCD ABCD V SO S -=⋅=18.(2021·江苏·金陵中学高一期中)如图,在四棱锥O -ABCD 中,底面ABCD 是边长为1的菱形,∠ABC =4π,OA ⊥平面ABCD ,OA =2,M 为OA 的中点,N 为BC 的中点.(1)画出平面AMN 与平面OCD 的交线(保留作图痕迹,不需写出作法); (2)证明:直线MN //平面OCD ; (3)求异面直线AB 与MD 所成角的大小. 【答案】(1)图形见解析;(2)证明见解析;(3)3π. 【解析】(1) 延长AN ,CD ,两直线相交于点E ,OE .为平面AMN 与平面OCD 的交线;(2)延长AN ,CD ,两直线相交于点E ,由已知12NC AD =,NC AD ,∴ N 为AE 的中点,又M 为AO 的中点,∴ MN ∥OE , 又OE ⊂ 平面OCD ,MN ⊄平面OCD ,∴ MN ∥平面OCD ;(3)∵ AB ∥CD ,∴ 异面直线AB 与MD 所成角为CMD ∠或其补角,∵ 底面ABCD 是边长为1的菱形,∠ABC =4π,∴ AC =1CD =,又OA ⊥平面ABCD ,OA =2,M 为OA 的中点,∴ MD =MC ∴ 1cos 2CMD ∠==, ∴ =3CMD π∠,∴ 异面直线AB 与MD 所成角的大小为3π. 【题组三 面面平行】1.(2021·全国·高一课时练习)如图,E ,F ,G ,H 分别是正方体ABCD A 1B 1C 1D 1的棱BC ,CC 1,C 1D 1,AA 1的中点.求证:(1)EG //平面BB 1D 1D ; (2)平面BDF //平面B 1D 1H .【答案】(1)证明见解析;(2)证明见解析.【解析】(1)如图,取B 1D 1的中点O ,连接GO ,OB ,因为OG =12B 1C 1,BE =12B 1C 1,所以BE =OG ,且11////BE B C OG 所以四边形BEGO 为平行四边形,故OB //EG , 因为OB ⊂平面BB 1D 1D ,EG ⊄平面BB 1D 1D ,所以EG //平面BB 1D 1D .(2)由于1111//,BB DD BB DD =所以四边形11BB D D 为平行四边形所以BD //B 1D 1. 连接HB ,D 1F ,1,HD BF 取P 为1DD 中点,连结,AP PF因此////,AB CD PF AB CD PF ==因此四边形ABFP 为平行四边形,故有//AP BF 又11//,AH PD AH PD =因此四边形1AHD P 为平行四边形,故有1//AP HD 故HD 1//BF .又B 1D 1∩HD 1=D 1,BD ∩BF =B ,所以平面BDF //平面B 1D 1H .2.(2021·浙江·台州市路桥区东方理想学校高一月考)如图,在四棱锥P ABCD -中,四边形ABCD 为平行四边形,E ,F 分别为BC ,PC 的中点,ACBD O =.求证:(1)//OF 平面APD ; (2)平面//OEF 平面APB .【答案】(1)证明见解析;(2)证明见解析.【解析】(1)ABCD O ⇒为AC 中点,又F 为PC 中点,∴//OF PA ,PA ⊂平面PAD ,OF ⊄平面PAD ,∴//OF 平面PAD ; (2)∵E ,F 分别为BC ,PC 的中点,∴//EF PB ,PB ⊂平面APB ,EF ⊄平面APB ∴//EF 平面APB ,同理可证://OE 平面APB 又OEEF E =,∴平面//OEF 平面APB3.(2021·安徽·合肥艺术中学 高一期中)如图,在多面体ABCDEF 中,ABCD 是正方形,BF ⊥平面,ABCD DE ⊥平面ABCD ,,BF DE M =为棱AE 的中点.(1)证明:平面//BMD 平面EFC ;(2)若2AB BF ==,求三棱锥A CEF -的体积.【答案】(1)证明见解析;(2)43.【解析】(1)设AC 与BD 交于点N ,则N 为AC 的中点,//.MN EC ∴MN ∴⊄平面,EFC EC ⊂平面,//EFC MN ∴平面.EFCBF ⊥平面,ABCD DE ⊥平面,//ABCD BF DE ∴, ,BF DE BDEF =∴为平行四边形,//.BD EF ∴BD ⊄平面,EFC EF ⊂平面,//EFC BD ∴平面.EFC ,MN BD N ⋂=∴平面BDM //平面EFC ;(2)连接,EN FN .在正方形ABCD 中,AC BD ⊥,BF ⊥平面,.ABCD BF AC ∴⊥BF BD B ⋂=,AC ∴⊥平面BDEF ,且垂足为N , 11142223323A CEF NEFV AC S-∴=⋅⋅=⨯⨯⨯⨯= ∴三棱锥A CEF -的体积为43. 4.(2021·广东实验中学高一期中)已知正方体1111ABCD A B C D -中,P 、Q 分别为对角线BD 、1CD 上的点,且123CQ BP QD PD ==.(1)求证//PQ 平面11A D DA ; (2)若R 是CD 上的点,当CRCD的值为多少时,能使平面//PQR 平面11B C CB ?请给出证明. 【答案】(1)证明见解析;(2)25CR CD =,证明见解析. 【解析】(1)证明:连结CP 并延长与DA 的延长线交于M 点, 因为四边形ABCD 为正方形,所以//BC AD ,故PBC PDM ∽,所以23CP BP PM PD ==, 又因为123CQ BP QD PD ==,所以123CQ CP QD PM ==,所以1//PQ MD . 又1MD ⊂平面11A D DA ,PQ ⊄平面11A D DA ,故//PQ 平面11A D DA ; (2)当25CR CD =时,能使平面//PQR 平面11B C CB ,证明:因为25CR CD =,即有23CR RD =,故123CQ CR QD RD ==,所以1//QR DD , 又∵11//DD CC ,∴//QR CC ,又1CC ⊂平面11B C CB ,QR ⊄平面11B C CB , 所以//QR 平面11A D DA , 由23CR BPRD PD==,得//PR BC ,BC ⊂平面11B C CB ,PR ⊄平面11B C CB ,所以//PR 平面11B C CB ,又PRRQ R =,所以平面//PQR 平面11B C CB .5.(2021·浙江·嘉兴市第五高级中学高一期中)如图所示,已知点P 是平行四边形ABCD 所在平面外一点,,N K 分别为,PC PA 的中点,平面PBC 平面APD l =.(1)求证://l BC ;(2)直线PB 上是否存在点H ,使得平面//KNH 平面ABCD ,并加以证明.【答案】(1)证明见解析;(2)当H 为PB 中点时,平面//KNH 平面ABCD ,证明见解析. 【解析】(1)因为四边形ABCD 是平行四边形,所以//BC AD ,因为AD ⊂平面PAD ,BC ⊄平面PAD ,所以//BC 平面PAD , 又因为平面PAD 平面PBC l =,BC ⊂平面PBC ,所以//BC l . (2)当H 为PB 中点时,平面//KNH 平面ABCD . 证明如下:取PB 的中点H ,连接KH ,NH ,KN , 因为,N K 分别为,PC PA 的中点,所以//NH BC ,//KH AB ,又NH ⊄平面ABCD ,BC ⊂平面ABCD ,所以//NH 平面ABCD ,同理可证//KH 平面ABCD . 又因为KH ⊂平面KNH ,NH ⊂平面KNH ,KH NH H ⋂=, 所以平面//KNH 平面ABCD .6.(2021·福建浦城·高一期中)如图所示,在三棱柱111ABC A B C -中,E 、F 、G 、H 分别是AB ,AC ,11A B ,11A C 的中点,求证:(1)//GH 平面1A EF ,(2)平面1//A EF 平面BCHG .【答案】(1)证明见解析;(2)证明见解析.【解析】证明:(1)因为G ,H 分别是11A B ,11A C 的中点,所以GH 是111A B C △的中位线,则11//GH B C , 因为E ,F 分别是11A B ,11A C 的中点,所以EF 是ABC 的中位线,则//EF BC ,又因为11//B C BC ,所以//EF GH ,EF ⊂平面1A EF ,GH ⊂/平面1A EF ,所以//GH 平面1A EF , (2)由G ,E 分别为11A B ,AB 的中点,11//A B AB ,所以1//AG EB ,1AG EB =,所以1A EBG 是平行四边形,所以1//A E GB . 1A E ⊂平面1A EF ,BG ⊂/平面1A EF ,所以//BG 平面1A EF ,又BG ⊂平面BCHG ,GH ⊂平面BCHG ,且BG GH G =,所以平面1//A EF 平面BCHG .7.(2021·江苏·无锡市堰桥高级中学高一期中)如图,在四棱柱1111ABCD A B C D -中,点M 是线段11B D 上的一个动点,E ,F 分别是BC ,CM 的中点.(1)求证://EF 平面11BDD B ;(2)设G 为棱CD 上的一点,问:当G 在什么位置时,平面//GEF 平面11BDD B ? 【答案】(1)证明见解析;(2)G 是DC 中点.【解析】(1)在四棱柱1111ABCD A B C D -中,连接BM ,如图,因E ,F 分别是BC ,CM 的中点,则有//EF BM ,又EF ⊄平面11BDD B ,BM ⊂平面11BDD B , 所以//EF 平面11BDD B ;(2)G 是DC 中点,使得平面//GEF 平面11BDD B ,理由如下: 取CD 的中点G ,连接EG ,FG ,而E 是BC 的中点,于是得//EG BD , 而EG ⊄平面11BDD B ,BD ⊂平面11BDD B ,从而得//EG 平面11BDD B ,由(1)知//EF 平面11BDD B ,EF EG E =,且,EF EG ⊂平面GEF ,因此有平面//GEF 平面11BDD B ,所以当G 是DC 的中点时,平面//GEF 平面11BDD B .8.(2021·全国·高一课时练习)如图,在正方体1111ABCD A B C D -中,S 是11B D 的中点,E ,F ,G 分别是BC ,DC ,SC 的中点,求证:(1)直线//EG 平面11BDD B ; (2)平面//EFG 平面11BDD B .【答案】(1)证明见解析:(2)证明见解析: 【解析】(1)如图所示,连接SB ,在SBC △中,G 是SC 中点,E 是BC 中点,所以//EG SB , 且SB ⊂平面11BDD B ,EG ⊄平面11BDD B , 所以//EG 平面11BDD B(2)在BCD △中,E ,F 分别为BC ,DC 的中点,所以//EF BD , 且BD ⊂平面11BDD B ,EF ⊄平面11BDD B ,所以//EF 平面11BDD B ; 由(1)得://EG 平面11BDD B ,且因为EG EF E =,,EG EF ⊂平面EFG ,所以平面//EFG 平面11BDD B9.(2021·吉林·长春市第二十九中学高一期中)如图所示,在三棱柱111ABC A B C -中,E ,F ,G ,H 分别是AB ,AC ,1111,A B AC 的中点.(1)求证://GH 平面ABC ; (2)求证:平面1EFA //平面BCHG . 【答案】(1)证明见解析;(2)证明见解析. 【解析】(1)在三棱柱111ABC A B C -中,因为G ,H 分别是11A B ,11A C 的中点, 所以11//GH B C ,又因为11//BC B C ,所以//GH BC .因为GH ⊄平面ABC ,BC ⊂平面ABC ,所以//GH 面ABC ; (2)因为E ,F 分别是AB ,AC 的中点,所以//EF BC . 又因为在三棱柱111ABC A B C -中,G 为11A B 的中点,所以1//AG EB ,1AG EB =,即四边形1A EBG 为平行四边形.所以1//A E BG . 因为//EF BC ,EF ⊄平面BCHG ,BC ⊂平面BCHG ,所以//EF 平面BCHG , 因为1//A E BG ,1A E ⊄平面BCHG ,BG ⊂平面BCHG ,所以1//A E 平面BCHG , 又因为1,EF A E ⊂平面1A EF ,且1EFA E E =,所以平面1//A EF 平面BCHG .10.(2021·江苏省镇江中学高一月考)如图,在三棱柱111ABC A B C -中,底面ABC 是正三角形,1AA ⊥平面ABC ,已知2AB =D 是11A B 的中点,E 、F 、G 分别是AC ,BC ,CD 的中点.(1)求FG 与1BB 所成角的大小; (2)求证:平面//EFG 平面11ABB A 【答案】(1)30; (2)证明见解析.【解析】(1)连接DB ,因为,G F 分别是,DC BC 的中点,所以//GF BD , 所以异面直线FG 与1BB 所成角即为直线DB 与1BB 所成的角, 在直角1DB B中,由111,DB BB =111tan DB DBB BB ∠==, 所以130DBB ∠=.(2)由(1)知//GF BD ,BD ⊂平面11ABB A GF ⊄,平面ABB 1A 1,所以//GF 平面11ABB A , 因为E 是AC 的中点,所以//EF AB , 因为AB平面11ABB A ,且EF ⊄平面11ABB A ,所以//EF 平面11ABB A ,又因为EF FG F ⋂=,且,EF FG ⊂平面EFG , 所以平面//EFG 平面11ABB A .【题组四 判断及性质定理的辨析】1.(2021·山西太原·高一期末)对于两个不同的平面α,β和三条不同的直线a ,b ,c .有以下几个命题: ①若//a b ,//b c ,则//a c ;②若//a α,//b α,则//a b ;③若//a b ,//b α,则//a α; ④若//a α,//a β,则//αβ;⑤若//a α,//αβ,则//a β. 则其中所有错误的命题是( ) A .③④⑤ B .②④⑤C .②③④D .②③④⑤【答案】D【解析】解:因为//a b ,//b c ,根据空间中直线平行的传递性,得//a c ,故①正确; 因为//a α,//b α,所以直线,a b 平行,异面,相交均有可能,故②错误; 若//a b ,//b α,则//a α或a α⊂,故③错误; 若//a α,//a β,则平面,αβ平行或相交,故④错误; 若//a α,//αβ,则//a β或a β⊂,故⑤错误. 所以错误的命题是②③④⑤. 故选:D.2 .(2021·全国·高一课时练习)(多选)已知,a b 表示两条直线,,,αβγ表示三个不重合的平面,给出下列命题,正确的是( )A .若,a b αγβγ==,且//a b ,则//αβB .若,a b 相交,且都在,αβ外,//,//,//,//a b a b ααββ,则//αβC .若//,//a b αβ,且//a b ,则//αβD .若,//,a a b αβαβ⊂=,则//a b 【答案】BD 【解析】A :若,a b αγβγ==,且//a b ,则,αβ可能相交、平行,错误;B :若,a b 相交,且都在,αβ外,//,//,//,//a b a b ααββ,由面面平行的判定可得//αβ,正确;C :若//,//a b αβ,且//a b ,则,αβ可能相交、平行,错误;D :若,//,a a b αβαβ⊂=,由线面平行的性质定理得//a b ,正确. 故选:BD3.(2021·辽宁·大连市第一中学高一月考)已知m ,n ,p 是三条不同的直线,α,β,γ是三个不同的平面,有下列命题:①//////m nm p p n ⎧⇒⎨⎩;②若//m α,//m β,则//αβ; ③m α⊂,//n α,则//m n ;④直线//m α,直线//n α,那么//m n ; ⑤若//m α,βn//,//m n ,则//αβ;⑥若//αγ,//βγ,则//αβ. 其中正确的说法为______(填序号) 【答案】①⑥【解析】对于①,根据平行的性质有:////m n p n ⎧⎨⎩,即//m p ,故①正确;对于②,由//,//,m m αβ得//αβ或,αβ相交,故②错误; 对于③,由,//,m n αα⊂得//m n ,或,m n 异面,故③错误;对于④,由直线//m α,直线//n α,可得//m n ,m n ,异面,m n ,相交,故④错误; 对于⑤,由//,//,m n αβ//m n ,得//αβ或αβ,相交,故⑤错误; 对于⑥,若////αγβγ,,由面面平行的传递性得//αβ,故⑥正确, 故答案为:①⑥.【题组五 平行的综合运用】1.(2021·广西·玉林市育才中学高一月考).如图,正方体1111ABCD A B C D -的棱长为2, E 是棱AB 的中点, F 是侧面11AA D D 内一点,若//EF 平面11BB D D ,则EF 的长度的范围为__________.【答案】【解析】如图所示:分别取11,AD A D 的中点M ,N ,连接EM ,EN ,MN , 因为E 为AB 的中点,所以//EM BD ,又EM ⊄平面11BB D D ,BD ⊂平面11BB D D , 所以//EM 平面11BB D D , 同理//MN 平面11BB D D , 又MN EM M ⋂=,所以平面//EMN 平面11BB D D ,又F 是侧面11AA D D 内一点,且//EF 平面11BB D D , 所以点F 的轨迹为线段MN ,故EF 的最小值为EM =最大值为EN =所以EF 的长度的范围为,故答案为:2.(2021·江苏省镇江中学高一月考)如图所示,正方体1111ABCD A B C D -棱长为3,M 、N 分别是下底面的棱11A B ,11B C 的中点,P 是上底面的棱AD 上的一点,1AP =,过P ,M 、N 的平面交上底面于PQ ,Q 在CD 上,则PQ =________.【答案】【解析】因为平面//ABCD 平面1111D C B A , 平面ABCD ∩平面PQNM PQ =, 平面1111D C B A ∩平面PQNM MN =, 所以//MN PQ ,又因为//MN AC , 所以//PQ AC . 又因为1AP =,所以23PD DQ PQ AD CD AC ===,所以2233PQ AC ==⨯=故答案为: 3.(2021·安徽安庆·高一期末)在棱长为4的正方体1111ABCD A B C D -中,点P 是棱AB 的中点,过点A 作与截面1PB C 平行的截面,则所得截面的面积为____________.【答案】【解析】取CD 、A 1B 1的中点M 、N ,连结C 1M 、MA 、AN 、NC 1∵C 1N//PC ,B 1P ∥AN ,B 1P ∩CP =P ,C 1N ∩AN =N ,∴平面C 1MAN //平面PCB 1∴平面C 1MAN 就是过点A 与界面1PCB 平行的截面由图可知,平面1C MAN为菱形,且AM AN ===正方体中,1AC ==根据余弦定理,22211111cos 2?5AN NC AC ANC AN NC +-∠==-,且()10πANC ∠∈,1sin ANC ∴∠==所以截面的面积1112?sin 2S AN NC ANC =⨯∠==故答案为:4.(2021·福建南平·高一期末)如图,在棱长为2的正方体1111ABCD A B C D -中,E ,F ,G ,H 分别为11A D ,11A B ,1BB ,11B C 的中点,点P 为线段1CC 上的动点,且1(01)CPCC λλ=≤≤.(1)是否存在λ使得//HP 平面EFG ,若存在,求出λ的值并给出证明过程;若不存在,请说明理由; (2)画出平面EFG 截该正方体所得的截面,并求出此截面的面积.【答案】(1)存在,1=2λ,证明见解析;(2)画图见解析;【解析】(1)当1=2λ时,//HP 平面EFG .取11C D 中点K ,连接HK ,PK ,11B D ,则//HK 11B D ,//EF 11B D , 如图所示:故//HK EF ,又HK ⊄平面EFG ,EF ⊂平面EFG ,//HK ∴平面EFG ,同理,//PK 平面EFG , 又HK=PK K ,HK PK ⊂,平面HPK ,故平面//HPK 平面EFG ,HP ⊂平面HPK ,//HP ∴平面EFG ;(2)平面EFG 截正方体1111ABCD A B C D -的截面为正六边形EFGRSRT , 如图所示:又正方体1111ABCD A B C D -的棱长为2,故正六边形EFGRSRT ,∴截面面积为:26=5.(2021·广东·珠海市第二中学高一期中)已知正方体1111ABCD A B C D -中的棱长为2,1O 是11A C 中点.(1)求证:平面11//AO D 平面1DBC ;(2)设1BB 的中点为M ,过A 、M 、1C 作一截面,交1DD 于点N ,求截面1AMC N 的面积.【答案】(1)证明见解析;(2)【解析】(1)如图,连接AC ,BD ,若AC BD O =,连接1OC ,由11//AA CC ,11AA CC =,可得四边形11AAC C 为平行四边形, ∴11//AC A C ,又11C O AO =,∴四边形11AOC O 为平行四边形,即11//AO C O ,而1AO ⊄平面1DBC ,1C O ⊂平面1DBC , 1//AO ∴平面1DBC ,同理,11ABC D 是平行四边形,即11//AD BC ,而1AD ⊄平面1DBC ,1BC ⊂平面1DBC , ∴1//AD 平面1DBC ,而11AO AD A ⋂=,∴平面11//AO D 平面1DBC .(2)连接AM ,1C M ,平面1AMC 与平面11AA D D 交于AN , 由平面11//AA D D 平面11BB C C ,且平面1AMC 平面111BB C C C M =,平面1AMC 平面11AA D D AN =, 1//C M AN ∴,同理有1//AM C N ,即四边形1AMC N 为平行四边形, 在Rt ABM 与11Rt C B M 中,易知1AM C M =,即四边形1AMC N 为菱形,故N 为1DD 的中点. ∵正方体1111ABCD A B C D -的棱长为2,MN ∴1AC∴截面面积12S =⨯。
高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)
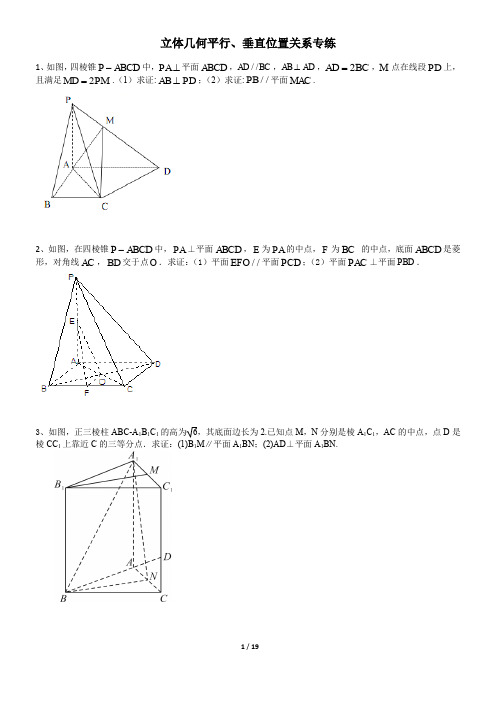
立体几何平行、垂直位置关系专练1、如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .2、如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD .3、如图,正三棱柱ABC-A 1B 1C 1的高为6,其底面边长为2.已知点M ,N 分别是棱A 1C 1,AC 的中点,点D 是棱CC 1上靠近C 的三等分点.求证:(1)B 1M ∥平面A 1BN ;(2)AD ⊥平面A 1BN.4、如图,等边三角形ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点.(1)证明:CM⊥DE;(2)在边AC上找一点N,使CD∥平面BEN.5、如图,矩形ABCD所在平面与三角形ABE所在平面互相垂直,AE=AB,M,N,H分别为DE,AB,BE 的中点.求证:(1)MN∥平面BEC;(2)AH⊥CE.6、如图,在三棱台ABCDEF中,CF⊥平面DEF,AB⊥BC.(1)设平面ACE∩平面DEF=a,求证:DF∥a;(2)若EF=CF=2BC,试问在线段BE上是否存在点G,使得平面DFG⊥平面CDE?若存在请确定点G的位置;若不存在,请说明理由.7、在三棱锥S ABC -中,平面SAB ⊥平面SBC ,AB BC ⊥,AS AB =,过A 作AF SB ⊥,垂足为F ,点E ,G 分别是棱SA ,SC 的中点.(1)求证:平面EFG ∥平面ABC .(2)求证:BC SA ⊥.8、如图,在直三棱柱111ABC A B C -中,AB BC ⊥,点D 为棱1C C 的中点,1AC 与1A D 交于点E ,1BC 与1B D 交于点F ,连结EF .求证:(1)//AB EF ;(2)平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A 1B 1∥平面DEC 1;(2)BE ⊥C 1E .点,平面PAB ⊥底面ABCD ,90PAB ∠= .求证:(1)//PB 平面AEC ;(2)平面PAC ⊥平面ABCD .11、2.(2020·江苏省镇江高三二模)如图,三棱锥P ABC -中,点D ,E 分别为AB ,BC 的中点,且平面PDE ⊥平面ABC .()1求证://AC 平面PDE ;()2若2PD AC ==,PE =PBC ⊥平面ABC .12、(2020·江苏省建湖高级中学高三月考)如图,在四面体ABCD 中,,90AD BD ABC =∠= ,点,E F 分别为棱,AB AC 上的点,点G 为棱AD 的中点,且平面//EFG 平面BCD .(1)求证:12EF BC =;(2)求证:平面EFD ⊥平面ABC .点,PA ⊥平面ABCD .(1)求证://PB 平面AEC ;(2)若四边形ABCD 是矩形且PA AD =,求证:AE ⊥平面PCD .14、(2020·江苏省高三二模)如图,在三棱柱111ABC A B C -中,侧面11ABB A ⊥底面ABC ,AB AC ⊥,E ,F 分别是棱AB ,BC 的中点.求证:(1)11AC ∥平面1B EF ;(2)1AC B E ⊥.15、(2020·江苏省连云港高三)如图,在四棱锥P ABCD -中,底面ABCD 为矩形,平面PAD ⊥平面ABCD ,PA PD ⊥,PA PD =,E 、F 分别为AD 、PB 的中点.(Ⅰ)求证:PE BC ⊥;(Ⅱ)求证:平面PAB ⊥平面PCD ;(Ⅲ)求证://EF 平面PCD .16、(2020·江苏省苏州高三)如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A1B 1∥平面DEC 1;(2)BE ⊥C 1E .17、(2020·江苏省通州高三)如图,在三棱柱111ABC A B C -中,侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点.(1)求证: 平面ABE ⊥平面11B BCC ;(2)求证:1C F ∥平面ABE ;18、(2020·江苏省高三三模)如图,三棱柱111ABC A B C -中,1BC B C =,O 为四边形11ACC A 对角线交点,F 为棱1BB 的中点,且AF ⊥平面11BCC B .(1)证明://OF 平面ABC ;(2)证明:四边形11ACC A 为矩形.参考答案1.如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .【解析】(1)∵四棱锥P ABCD -中,PA ⊥平面ABCD ,AB 平面ABCD , ∴AB PA ⊥,又AB AD ⊥,,PA AD ⊂平面PAD ,PA AD A ⋂=, ∴AB ⊥面PAD .PD ⊂面PAD ,∴AB PD ⊥. (2)连结BD AC O ⋂=,连结MO , ∵//AD BC ,2AD BC =,2DO BO ∴=,∵在PBD ∆中,2DM MP =,2DO BO =∴//PB MO , 又PB ⊄面MAC ,MO ⊂面MAC ,∴//PB 面MAC .2.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD . 【详解】(1)因为在ΔPAC 中,E 为PA 的中点,O 为AC 的中点, 所以//EO PC又EO ⊄平面PCD ,PC ⊂平面PCD , 所以//EO 平面PCD同理可证,//FO 平面PCD ,又EO FO O = ,EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD .(2)因为PA ⊥平面ABCD ,BD ⊂平面ABCD , 所以PA BD ⊥因为底面ABCD 是菱形,所以AC BD ⊥,又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。
2017-2018学年高中数学必修二 练习:2-2 直线、平面平行的判定及其性质 2-2-3 含答案 精品

第二章 2.2 2.2.3A级基础巩固一、选择题1.正方体ABCD-A1B1C1D1中,截面BA1C1与直线AC的位置关系是导学号 09024417( A )A.AC∥截面BA1C1B.AC与截面BA1C1相交C.AC在截面BA1C1内D.以上答案都错误[解析] ∵AC∥A1C1,又∵AC⊄面BA1C1,∴AC∥面BA1C1.2.如右图所示的三棱柱ABC-A1B1C1中,过A1B1的平面与平面ABC交于直线DE,则DE与AB的位置关系是导学号 09024418( B )A.异面B.平行C.相交D.以上均有可能[解析] ∵A1B1∥AB,AB⊂平面ABC,A1B1⊄平面ABC,∴A1B1∥平面ABC.又A1B1⊂平面A1B1ED,平面A1B1ED∩平面ABC=DE,∴DE∥A1B1.又AB∥A1B1,∴DE∥AB.3.下列命题正确的是导学号 09024419( D )A.若直线a∥平面α,直线b∥平面α,则直线a∥直线bB.若直线a∥平面α,直线a与直线b相交,则直线b与平面α相交C.若直线a∥平面α,直线a∥直线b,则直线b∥平面αD.若直线a∥平面α,则直线a与平面α内任意一条直线都无公共点[解析] A中,直线a与直线b也可能异面、相交,所以不正确;B中,直线b也可能与平面α平行,所以不正确;C 中,直线b 也可能在平面α内,所以不正确;根据直线与平面平行的定义知D 正确,故选D .4.如图,在三棱柱ABC -A 1B 1C 1中,AM =2MA 1,BN =2NB 1,过MN 作一平面交底面三角形ABC 的边BC 、AC 于点E 、F ,则导学号 09024420( B )A .MF ∥NEB .四边形MNEF 为梯形C .四边形MNEF 为平行四边形D .A 1B 1∥NE[解析] ∵在▱AA 1B 1B 中,AM =2MA 1,BN =2NB 1,∴AM 綊BN ,∴MN 綊AB .又MN ⊄平面ABC ,AB ⊂平面ABC ,∴MN ∥平面ABC .又MN ⊂平面MNEF ,平面MNEF ∩平面ABC =EF ,∴MN ∥EF ,∴EF ∥AB ,显然在△ABC 中EF ≠AB ,∴EF ≠MN ,∴四边形MNEF 为梯形.故选B .5.如右图所示,在空间四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 上的点,EH ∥FG ,则EH 与BD 的位置关系是导学号 09024421( A )A .平行B .相交C .异面D .不确定[解析] ∵EH ∥FG ,FG ⊂平面BCD ,EH ⊄平面BCD , ∴EH ∥平面BCD .∵EH ⊂平面ABD ,平面ABD ∩平面BCD =BD , ∴EH ∥BD .6.已知正方体AC 1的棱长为1,点P 是面AA 1D 1D 的中心,点Q 是面A 1B 1C 1D 1的对角线B 1D 1上一点,且PQ ∥平面AA 1B 1B ,则线段PQ 的长为导学号 09024422( C )A .1B . 2C .22D .32[解析] 由PQ ∥平面AA 1BB 知PQ ∥AB 1,又P 为AO 1的中点,∴PQ =12AB 1=22.二、填空题7.如图,a ∥α,A 是α的另一侧的点,B 、C 、D ∈a ,线段AB 、AC 、AD 分别交平面α于E 、F 、G ,若BD =4,CF =4,AF =5,则EG =__209__.导学号 09024423[解析] ∵a ∥α,α∩平面ABD =EG ,∴a ∥EG ,即BD ∥EG , ∴EG BD =AF AF +FC ,则EG =AF ·BD AF +FC =5×45+4=209. 8.(2016·扬州高二检测)在正方体ABCD -A 1B 1C 1D 1中,若过A ,C ,B 1三点的平面与底面A 1B 1C 1D 1的交线为l ,则l 与A 1C 1的位置关系是__l ∥A 1C 1__.导学号 09024424[解析] ∵平面ABCD ∥平面A 1B 1C 1D 1,AC ⊂平面ABCD ,∴AC ∥平面A 1B 1C 1D 1.又平面ACB 1经过直线AC 与平面A 1B 1C 1D 1相交于直线l , ∴AC ∥l . 三、解答题9.如图,在正方体ABCD -A 1B 1C 1D 1中,E 、F 分别是棱AA 1和BB 1的中点,过EF 的平面EFGH 分别交BC 和AD 于点G 、H ,求证:AB ∥GH .导学号 09024425[解析] ∵E 、F 分别是AA 1和BB 1的中点,∴EF ∥AB . 又AB ⊄平面EFGH ,EF ⊂平面EFGH , ∴AB ∥平面EFGH . 又AB ⊂平面ABCD ,平面ABCD ∩平面EFGH =GH ,∴AB ∥GH .10.四棱锥P -ABCD 的底面ABCD 是梯形,AB ∥CD ,且AB =23CD .试问在PC 上能否找到一点E ,使得BE ∥平面PAD ?若能,请确定E 点的位置,并给出证明;若不能,请说明理由.导学号 09024426[解析] 在PC 上取点E ,使CE PE =12,则BE ∥平面PAD .证明如下:延长DA 和CB 交于点F ,连接PF . 梯形ABCD 中,AB ∥CD ,AB =23CD .∴AB CD =BF FC =23, ∴BC BF =12. 又CE PE =12,∴△PFC 中,CE PE =BC BF, ∴BE ∥PF ,而BE ⊄平面PAD ,PF ⊂平面PAD . ∴BE ∥平面PAD .B 级 素养提升一、选择题1.a 、b 是两条异面直线,下列结论正确的是导学号 09024427( D ) A .过不在a 、b 上的任一点,可作一个平面与a 、b 平行 B .过不在a 、b 上的任一点,可作一条直线与a 、b 相交 C .过不在a 、b 上的任一点,可作一条直线与a 、b 都平行 D .过a 可以并且只可以作一个平面与b 平行[解析] A 错,若点与a 所确定的平面与b 平行时,就不能使这个平面与a 平行了. B 错,若点与a 所确定的平面与b 平行时,就不能作一条直线与a ,b 相交. C 错,假如这样的直线存在,根据公理4就可有a ∥b ,这与a ,b 异面矛盾.D 正确,在a 上任取一点A ,过A 点作直线c ∥b ,则c 与a 确定一个平面与b 平行,这个平面是唯一的.2.过平面α外的直线l ,作一组平面与α相交,如果所得的交线为a 、b 、c 、…,那么这些交线的位置关系为导学号 09024428( D )A .都平行B .都相交且一定交于同一点C .都相交但不一定交于同一点D .都平行或交于同一点[解析] 若l ∥平面α,则交线都平行; 若l ∩平面α=A ,则交线都交于同一点A .3.如图,在三棱锥S -ABC 中,E 、F 分别是SB 、SC 上的点,且EF ∥平面ABC ,则导学号 09024429( B )A .EF 与BC 相交B .EF ∥BC C .EF 与BC 异面D .以上均有可能[解析] ∵EF ⊂平面SBC ,EF ∥平面ABC ,平面SBC ∩平面ABC =BC ,∴EF ∥BC . 4.不同直线m 、n 和不同平面α、β,给出下列命题: ①⎭⎪⎬⎪⎫α∥βm ⊂α⇒m ∥β;②⎭⎪⎬⎪⎫m ∥n m ∥β⇒n ∥β;③⎭⎪⎬⎪⎫m ⊂αn ⊂β⇒m 、n 异面.其中假命题有导学号 09024431( C ) A .0个B .1个C .2个D .3个[解析] ∵α∥β,∴α与β没有公共点. 又∵m ⊂α,∴m 与β没有公共点, ∴m ∥β,故①正确,②③错误.二、填空题5.已知A 、B 、C 、D 四点不共面,且AB ∥平面α,CD ∥α,AC ∩α=E ,AD ∩α=F ,BD ∩α=H ,BC ∩α=G ,则四边形EFHG 是__平行__四边形.导学号 09024432[解析] ∵AB ∥α,平面ABD ∩α=FH ,平面ABC ∩α=EG ,∴AB ∥FH ,AB ∥EG ,∴FH ∥EG ,同理EF ∥GH ,∴四边形EFHG 是平行四边形.6.(2016·成都高二检测)长方体ABCD -A 1B 1C 1D 1的底面ABCD 是正方形,其侧面展开图是边长为8的正方形.E ,F 分别是侧棱AA 1、CC 1上的动点,AE +CF =8.P 在棱AA 1上,且AP =2,若EF ∥平面PBD ,则CF =__2__.导学号 09024433[解析] 连接AC 交BD 于O ,连接PO .因为EF ∥平面PBD ,EF ⊂平面EACF ,平面EACF ∩平面PBD =PO ,所以EF ∥PO ,在PA 1上截取PQ =AP =2,连接QC ,则QC ∥PO ,所以EF ∥QC ,所以EFCQ 为平行四边形,则CF =EQ ,又因为AE +CF =8,AE +A 1E =8,所以A 1E =CF =EQ =12A 1Q =2,从而CF =2.C 级 能力拔高1.如图所示,一平面与空间四边形对角线AC 、BD 都平行,且交空间四边形边AB 、BC 、CD 、DA 分别于E 、F 、G 、H .导学号 09024434(1)求证:EFGH 为平行四边形; (2)若AC =BD ,EFGH 能否为菱形?(3)若AC =BD =a ,求证:平行四边形EFGH 周长为定值.[解析] (1)∵AC ∥平面EFGH ,平面ACD ∩平面EFGH =GH ,且AC ⊂面ACD , ∴AC ∥GH ,同理可证,AC ∥EF ,BD ∥EH ,BD ∥FG . ∴EF ∥GH ,EH ∥FG .∴四边形EFGH 为平行四边形. (2)设AC =BD =a ,EH =x ,GH =y ,AH HD =m n. ∵GH ∥AC ,∴GH ︰AC =DH ︰DA =DH ︰(DH +HA ). 即:y ︰a =n ︰(m +n ),∴y =nm +na . 同理可得:x =EH =mm +na . ∴当AC =BD 时,若m =n 即AH =HD 时,则EH =GH ,四边形EFGH 为菱形. (3)设EH =x ,GH =y ,H 为AD 上一点且AH ︰HD =m ︰n .∵EH ∥BD ,∴EH BD =AHAD.即x a =m m +n ,∴x =mm +na .同理:y =nm +n a ,∴周长=2(x +y )=2a (定值).2.如图,在三棱柱ABC -A 1B 1C 1中,点E 、F 分别是棱CC 1、BB 1上的点,点M 是线段AC 上的动点,EC =2FB =2,若MB ∥平面AEF ,试判断点M 在何位置.导学号 09024435[解析] 若MB ∥平面AEF ,过F 、B 、M 作平面FBMN 交AE 于N ,连接MN 、NF .因为BF ∥平面AA 1C 1C ,BF ⊂平面FBMN ,平面FBMN ∩平面AA 1C 1C =MN ,所以BF ∥MN .又MB ∥平面AEF ,MB ⊂平面FBMN ,平面FBMN ∩平面AEF =FN ,所以MB ∥FN ,所以BFNM 是平行四边形,所以MN ∥BF ,MN =BF =1. 而EC ∥FB ,EC =2FB =2, 所以MN ∥EC ,MN =12EC =1,故MN 是△ACE 的中位线.所以M 是AC 的中点时,MB ∥平面AEF .。
高一必修2立体几何--平行与垂直关系强化练习(含答案)

高一数学必修二空间中平行与垂直关系强化练习1. 空间中,垂直于同一直线的两条直线( )A.平行 B .相交 C .异面 D .以上均有可能2. 已知互不相同的直线l,m,n 与平面, ,则下列叙述错误的是()A.若m //l ,n// l ,则m// n B .若m // ,n// ,则m// nC.若m ,m, 则 D .若m , ,则m// 或m3. 下列说法正确的是( )A. 如果一条直线与一个平面内的无数条直线平行,则这条直线与这个平面平行B. 两个平面相交于唯一的公共点C.如果一条直线与一个平面有两个不同的公共点,则它们必有无数个公共点D.平面外的一条直线必与该平面内无数条直线平行4. 如图,ABCD﹣A1B1C1D1 为正方体,下面结论错误的是()A.BD∥平面CB1D1B.AC1⊥B1CC.AC1⊥平面CB1D1D.直线CC1 与平面CB1D1 所成的角为45°5. 如图,四棱锥V ABCD 中,底面ABCD 是边长为2 的正方形,其他四个侧面都是侧棱长为 5 的等腰三角形,则二面角V AB C 的大小()A.30 B .45 C .60 D .1206.下列四个结论:⑴两条直线都和同一个平面平行,则这两条直线平行。
⑵两条直线没有公共点,则这两条直线平行。
⑶两条直线都和第三条直线垂直,则这两条直线平行。
⑷一条直线和一个平面内无数条直线没有公共点,则这条直线和这个平面平行。
其中正确的个数为()A.0 B .1 C .2 D .37. 在四面体ABCD中,已知棱AC 的长为 2 ,其余各棱长都为1,则二面角 A CD B 的余弦值为()A.12B .13C .33D .236.在三棱柱A BC A B C 中,各棱都相等,侧棱垂直底面,点 D 是侧面BB1C1C 的中心,1 1 1则AD 与平面BB1C1C 所成角的大小是.7.直二面角-l -的棱l 上有一点A,在平面, 内各有一条射线AB,AC 都与l 成45 ,AB , AC ,则BAC 。
人教A版高中数学必修第二册课后习题 第8章 立体几何初步 8.5.2 直线与平面平行
8.5.2 直线与平面平行课后训练巩固提升A.若a∥α,b⊂α,则a∥bB.若a∥α,b∥α,则a∥bC.若a∥b,b⊂α,则a∥αD.若a∥b,a∥α,则b∥α或b⊂α2.在梯形ABCD中,AB∥CD,AB⊂平面α,CD⊄平面α,则直线CD与平面α内的直线的位置关系只能是( )A.平行B.平行或异面C.平行或相交D.异面或相交,CD∥α,则平面α内的直线与CD可能平行,也可能异面.3.已知E,F,G,H分别是四面体A-BCD的棱AB,BC,CD,DA的中点,则四面体的六条棱所在直线中与平面EFGH平行的条数是( )A.0B.1C.2D.3,由线面平行的判定定理可知BD∥平面EFGH,AC∥平面EFGH.4.(多选题)在正方体ABCD-A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,则下列结论正确的是( )A.FG∥平面AA1D1DB.EF∥平面BC1D1C.FG∥平面BC1D1D.EG∥平面AA1D1DABCD-A1B1C1D1中,因为F,G分别是B1C1,BB1的中点,所以FG ∥BC1.连接AD1(图略),因为BC1∥AD1,所以FG∥AD1.因为FG⊄平面AA1D1D,AD1⊂平面AA1D1D,所以FG∥平面AA1D1D,故A正确;连接A1C1(图略),因为EF∥A1C1,A1C1与平面BC1D1相交,所以EF与平面BC1D1相交,故B错误;因为FG∥BC1,且FG⊄平面BC1D1,BC1⊂平面BC1D1,所以FG∥平面BC1D1,故C正确;因为EG与AA1相交,且EG在平面AA1D1D外,所以EG与平面AA1D1D相交,故D错误.5.如图,在长方体ABCD-A'B'C'D'中,(1)与CD平行的平面是;(2)与CC'平行的平面是;(3)与BC平行的平面是.平面A'C',平面AB'(2)平面AB',平面AD'(3)平面A'C',平面AD'6.如图所示,平面α过正方体ABCD-A1B1C1D1的三个顶点B,D,A1,且α与底面A1B1C1D1的交线为l,则l与B1D1的位置关系是.DD 1∥BB 1,DD 1=BB 1,所以四边形BDD 1B 1是平行四边形,所以BD ∥B 1D 1.又B 1D 1⊂平面A 1B 1C 1D 1,BD ⊄平面A 1B 1C 1D 1, 所以BD ∥平面A 1B 1C 1D 1. 又BD ⊂α,α∩平面A 1B 1C 1D 1=l, 所以l ∥BD.所以l ∥B 1D 1.7.在棱长为a 的正方体ABCD-A 1B 1C 1D 1中,M,N 分别是棱A 1B 1,B 1C 1的中点,P 是棱AD 上一点,AP=a3,过点P,M,N 的平面与棱CD 交于点Q,则PQ= .AC,A 1C 1.∵M,N 分别是棱A 1B 1,B 1C 1的中点,∴MN ∥A 1C 1. 又知A 1C 1∥AC,∴MN ∥AC,又知MN ⊄平面ABCD,AC ⊂平面ABCD,∴MN ∥平面ABCD.又MN ⊂平面PMN,平面PMN∩平面ABCD=PQ, ∴MN ∥PQ.又知AP=a3,∴DP=DQ=23a,故PQ=2√23a.8.一个以A1B1C1为底面的三棱柱被一平面所截得到的几何体如图所示,截面为ABC.已知AA1=4,BB1=2,CC1=3.设O是AB的中点,证明:OC∥平面A1B1C1.O作OD∥AA1交A1B1于点D,连接C1D,则OD∥BB1∥CC1.(AA1+BB1)=3=CC1.所以OD CC1.所以四边形因为O是AB的中点,所以OD=12ODC1C是平行四边形.所以OC∥C1D.又因为C1D⊂平面A1B1C1,且OC⊄平面A1B1C1,所以OC∥平面A1B1C1.9.如图,在△ABC所在平面外有一点P,M,N分别是PC和AC上的点,过MN 作平面平行于BC,画出这个平面与其他各面的交线,并说明画法.N在平面ABC内作NE∥BC交AB于点E,过点M在平面PBC内作MF∥BC交PB于点F,连接EF,则平面MNEF为所求,其中MN,NE,EF,MF分别为平面MNEF与各面的交线,如图所示.说明画法如下:因为BC∥NE,BC⊄平面MNEF,NE⊂平面MNEF,所以BC∥平面MNEF.。
立体几何中线面平行的经典方法经典题(附详细解答)
FGGABCDECA BDEFDEB 1A 1C 1CM高中立体几何证明平行的专题(基本方法)立体几何中证明线面平行或面面平行都可转化为线线平行,而证明线线平行一般有以下的一些方法:(1)通过“平移”。
(2)利用三角形中位线的性质。
(3)利用平行四边形的性质。
(4)利用对应线段成比例。
(5)利用面面平行,等等。
(1) 通过“平移”再利用平行四边形的性质1.如图,四棱锥P -ABCD 的底面是平行四边形,点E 、F 分别为棱AB 、PD 的中点.求证:AF ∥平面PCE ;分析:取PC 的中点G ,连EG.,FG ,则易证AEGF 是平行四边形2、如图,已知直角梯形ABCD 中,AB ∥CD ,AB ⊥BC ,AB =1,BC =2,CD =1+3,过A 作AE ⊥CD ,垂足为E ,G 、F 分别为AD 、CE 的中点,现将△ADE 沿AE 折叠,使得DE ⊥EC.(Ⅰ)求证:BC ⊥面CDE ;(Ⅱ)求证:FG ∥面BCD ;分析:取DB 的中点H ,连GH,HC 则易证FGHC 是平行四边形3、已知直三棱柱ABC -A 1B 1C 1中,D, E, F 分别为AA 1, CC 1, AB 的中点,M 为BE 的中点, AC ⊥BE. 求证:(Ⅰ)C 1D ⊥BC ;(Ⅱ)C 1D ∥平面B 1FM.分析:连EA ,易证C 1EAD 是平行四边形,于是MF//EAE FBACDP(第1题图)4、如图所示, 四棱锥P ABCD 底面是直角梯形,,,AD CD AD BA CD=2AB, E 为PC 的中点,证明: //EB PAD 平面;分析::取PD 的中点F ,连EF,AF 则易证ABEF 是平行四边形(2) 利用三角形中位线的性质5、如图,已知E 、F 、G 、M 分别是四面体的棱AD 、CD 、BD 、BC 的中点,求证:AM ∥平面EFG 。
分析:连MD 交GF 于H ,易证EH 是△AMD 的中位线6、如图,ABCD 是正方形,O 是正方形的中心,E 是PC的中点。
高中数学人教A版必修2立体几何--线面平行的判定与性质同步检测(WORD文档有答案)
高中数学人教A 版必修2立体几何--线面平行的判定与性质同步检测班级 学号 姓名[基础练习]1.下列命题正确的是 ( )A 一直线与平面平行,则它与平面内任一直线平行B 一直线与平面平行,则平面内有且只有一个直线与已知直线平行C 一直线与平面平行,则平面内有无数直线与已知直线平行,它们在平面内彼此平行D 一直线与平面平行,则平面内任意直线都与已知直线异面2.若直线l 与平面α的一条平行线平行,则l 和α的位置关系是 ( )A α⊂lB α//lC αα//l l 或⊂D 相交和αl3.若直线a 在平面α内,直线a,b 是异面直线,则直线b 和α平面的位置关系是 ( )A .相交B 。
平行C 。
相交或平行D 。
相交且垂直4.下列各命题:(1) 经过两条平行直线中一条直线的平面必平行于另一条直线;(2) 若一条直线平行于两相交平面,则这条直线和交线平行;(3) 空间四边形中三条边的中点所确定平面和这个空间四边形的两条对角线都平行。
其中假命题的个数为 ( )A 0B 1C 2D 35.E 、F 、G 分别是四面体ABCD 的棱BC 、CD 、DA 的中点,则此四面体中与过E 、F 、G 的截面平行的棱的条数是A .0B 1C 2 D36.直线与平面平行的充要条件是A .直线与平面内的一条直线平行B 。
直线与平面内的两条直线不相交C .直线与平面内的任一直线都不相交D 。
直线与平行内的无数条直线平行7.若直线上有两点P 、Q 到平面α的距离相等,则直线l 与平面α的位置关系是 ( )A 平行B 相交C 平行或相交D 或平行、或相交、或在内8.a,b 为两异面直线,下列结论正确的是 ( )A 过不在a,b 上的任何一点,可作一个平面与a,b 都平行B 过不在a,b 上的任一点,可作一直线与a,b 都相交C 过不在a,b 上任一点,可作一直线与a,b 都平行D 过a 可以并且只可以作一个平面与b 平行9.判断下列命题是否正确:(1)过平面外一点可作无数条直线与这个平面平行 ( )(2)若直线α⊄l ,则l 不可能与α内无数条直线相交 ( )(3)若直线l 与平面α不平行,则l 与α内任一直线都不平行 ( )(4)经过两条平行线中一条直线的平面平行于另一条直线 ( )(5)若平面α内有一条直线和直线l 异面,则α⊄l ( )10.过直线外一点和这条直线平行的平面有 个。
人教A版必修二立体几何线面平行习题
线面平行习题1. 如图,在四棱锥P ABCD -中, / / A B C D .求证:CD ∥平面ABE .2. 如图,在四棱锥P ABCD -中,底面是棱长为1的菱形,M 是PB 的中点.求证:PD //平面ACM .3. 如图, 在正三棱柱111ABC A B C -中,点D 是AB 的中点.求证:1//BC 平面1A CD .4. 如图,在三棱柱ABC –A 1B 1C 1中,D 为AC 的中点,O 为四边形B 1C 1CB 的对角线的交点.求证:OD ∥平面A 1ABB 1.5. 如图,在长方体ABCD -1111D C B A 中,面1BMD N 与棱1CC ,1AA 分别交于点M ,N ,且M ,N 均为中点.求证:AC ∥平面1BMD N .6. 如图,在四棱锥P ABCD -中,//AD BC ,且2PA PD ==,222AD BC ==,PA CD ⊥,点E 在PC 上,且2PE EC =.求证:直线PA ∥平面BDE .7. 如图,四棱锥S ABCD -的底面ABCD 为直角梯形,//AB CD ,AB BC ⊥,22AB BC CD ==.若点M 是棱AB 的中点,求证://BC 平面SDM .8. ★如图,在三棱柱111ABC A B C -中,D 为11A B 的中点.证明:1//CA 平1BDC .9. ★如图,在三棱柱111ABC A B C -中,各个侧面均是边长为2的正方形,D 为线段AC 的中点.求证:直线1AB ∥平面1BC D .10. ★在长方体1111ABCD A B C D -中,底面ABCD 是边长为2的正方形,E 是AB 的中点,F 是1BB 的中点.求证://EF 平面11A DC .11. ★如图所示,在四棱锥C ABED -中,四边形ABED 是正方形,点,G F 分别是线段,EC BD 的中点. 求证://GF ABC 平面12. ★如图,在直三棱柱ABC -111A B C 中,E 是棱1CC 的中点,F是AB 的中点.求证:CF ∥平面1AB E .13. ★如图,在三棱柱111ABC A B C -中,ABC △是边长为4的正三角形,侧面11BB C C 是矩形,,D E 分别是线段11,BB AC 的中点. 求证:DE 平面ABC .14. ★如图,在四棱锥P ABCD -中,四边形ABCD 为矩形,,E F 分别为,PC BD 的中点.证明://EF 平面PAD .15. ★如图,在直三棱柱111ABC A B C -中,AB AC =,P 为1AA 的中点,Q 为BC 的中点. 求证://PQ 平面11A BC .16. ★如图,在多面体ABCDEF 中,四边形ABCD 是菱形,3ABC π∠=,四边形ABEF 是直角梯形,2FAB π∠=,AF BE ,22AF AB BE ===.证明:CE平面ADF .17. 在三棱锥P ABC -中,H 为PA 的中点,,M N 分别为棱,PA PB 上的点,且3PN NB =,MN 平面HBC ,求:PM PA 的值.18. 如图,正方形ABCD 的边长是13,平面ABCD 外一点P 到正方形各顶点的距离都是13,,M N 分别是,PA BD 上的点,且::PM MA BN ND =.求证:直线MN 平面PBC .19. 如图,正方体1111ABCD A B C D -中,点N 在BD 上,点M 在1B C 上,且CM DN =.求证:MN 面11AA BB。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线面平行问题一.选择题(共12小题)1.如果直线a∥平面α,那么直线a与平面α内的()A.一条直线不相交B.两条直线不相交C.无数条直线不相交D.任意一条直线不相交2.A,b,c为三条不重合的直线,α,β,γ为三个不重合平面,现给出六个命题①⇒a∥b ②⇒a∥b ③⇒α∥β④⇒α∥β ⑤⇒α∥a ⑥⇒α∥a其中正确的命题是()A.①②③B.①④⑤C.①④D.①③④3.下列说法正确的是()A.三点确定一个平面B.一条直线和一个点确定一个平面C.梯形一定是平面图形D.过平面外一点只有一条直线与该平面平行4.能保证直线与平面平行的条件是()A.直线与平面内的一条直线平行B.直线与平面内的某条直线不相交C.直线与平面内的无数条直线平行D.直线与平面内的所有直线不相交5.如图,各棱长均为1的正三棱柱ABC﹣A1B1C1,M,N分别为线段A1B,B1C上的动点,且MN∥平面ACC1A1,则这样的MN有()A.1条B.2条C.3条D.无数条6.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是()A.B. C. D.7.在正方体ABCD﹣A1B1C1D1中,E为DD1的中点,则下列直线中与平面ACE平行的是()A.BA1B.BD1C.BC1D.BB18.在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE:EB=AF:FD=1:4,又H,G 分别是BC,CD的中点,则()A.BD∥平面EFG,且四边形EFGH是平行四边形B.EF∥平面BCD,且四边形EFGH是梯形C.HG∥平面ABD,且四边形EFGH是平行四边形D.EH∥平面ADC,且四边形EFGH是梯形9.在三棱锥S﹣ABC中,E,F分别为SB,SC上的点,且EF∥面ABC,则()A.EF与BC相交B.EF∥BC C.EF与BC异面D.以上均有可能10.如图是某几何体的平面展开图,其中四边形ABCD为正方形,E,F分别为PA,PD的中点.在此几何体中,以下结论一定成立的是()A.直线BE∥PFB.B.直线EF∥平面PBCC.平面BCE⊥平面PADD.D.直线PB与DC所成角为60°11.平面α与△ABC的两边AB,AC分别交于点D,E,且AD:DB=AE:EC,如图,则BC与α的位置关系是()A.异面B.相交C.平行或相交D.平行12.如图,矩形ABCD中,AB=2AD,E是边AB的中点,将△ADE沿DE翻折成△A1DE,若M 为线段A1C的中点,则在翻折过程中,有下列四个命题:①存在某个位置,使MB∥平面A1DE;②点M在某个球面上运动;③存在某个位置使DE⊥A1C;④BM的长是定值,其中正确的结论是()A.①②③B.①②④C.①③④D.②③④二.解答题(共18小题)13.如图,四棱锥P﹣ABCD中,底面ABCD为菱形,PA⊥平面ABCD,BD交AC于点E,F是线段PC中点,G为线段EC中点.(Ⅰ)求证:FG∥平面PBD;(Ⅱ)求证:BD⊥FG.14.如图所示,PD垂直于正方形ABCD所在的平面,AB=2,PC与平面ABCD所成角是45°.F 是AD的中点,M是PC的中点,求证.DM∥平面PFB.15.如图,在四棱锥S﹣ABCD中,底面ABCD为菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.(1)求证:PQ∥平面SAD;(2)若SA=AB=2,求三棱锥S﹣ABC的体积.16.三棱柱ABC﹣A1B1C1中,若D为BB1上一点,M为AB的中点,N为BC的中点.求证:MN∥平面A1C1D.17.如图,在三棱锥P﹣ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.(1)求证:DE∥平面PBC;(2)求证:AB⊥PE;(3)求三棱锥P﹣BEC的体积.18.已知三棱柱ABC﹣A1B1C1的侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,M,N分别是A1B1,BC的中点.(Ⅰ)证明:MN∥平面ACC1A1;(II)求二面角M﹣AN﹣B的余弦值.19.如图所示,在直三棱柱ABC﹣A1B1C1中,CA=CB,点M,N分别是AB,A1B1的中点.(1)求证:BN∥平面A1MC;(2)若A1M⊥AB1,求证:AB1⊥A1C.20.如图,在四棱锥P﹣ABCD中,底面ABCD为等腰梯形,AD∥BC,,E,F分别为线段AD,PB的中点.(1)证明:PD∥平面CEF;(2)若PE⊥平面ABCD,PE=AB=2,求四面体P﹣DEF的体积.21.如图,矩形ABCD所在平面与三角形ABE所在平面互相垂直,AE=AB,M,N,H分别为DE,AB,BE的中点.(1)求证:MN∥平面BEC;(2)求证:AH⊥CE.22.如图,在直三棱柱ABC﹣A1B1C1中,AC=AA1=2,D为棱CC1的中点AB1∩A1B=O.(1)证明:C1O∥平面ABD;(2)已知AC⊥BC,△ABD的面积为,E为线段A1B上一点,且三棱锥C﹣ABE的体积为,求.23.如图,在三棱锥P﹣ABC中,PB⊥BC,AC⊥BC,点E,F,G分别为AB,BC,PC,的中点(1)求证:PB∥平面EFG;(2)求证:BC⊥EG.24.如图,在几何体ABC﹣A1B1C1中,点A1,B1,C1在平面ABC内的正投影分别为A,B,C,且AB⊥BC,AA1=BB1=4,AB=BC=CC1=2,E为AB1中点,(Ⅰ)求证;CE∥平面A1B1C1,(Ⅱ)求证:求二面角B1﹣AC1﹣C的大小.25.如图所示,在三棱柱ABC﹣A1B1C1中,底面ABC为等边三角形,AB=2,∠A1AB=∠A1AC=60°,M,N分別为AB,A1C1的中点.(1)证明:MN∥平面BCC1B1;(2)若MN=,求三棱柱ABC﹣A1B1C1的侧面积.26.如图,四棱柱ABCD﹣A1B1C1D1的底面为菱形,∠BAD=120°,AB=2,E,F为CD,AA1中点.(1)求证:DF∥平面B1AE;(2)若AA1⊥底面ABCD,且直线AD1与平面B1AE所成线面角的正弦值为,求AA1的长.27.如图,在直三棱柱ABC﹣A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,BC1∩B1C=E.求证:(Ⅰ)DE∥平面AA1C1C;(Ⅱ)BC1⊥AB1.28.四边形ABCD是正方形,O是正方形的中心,PO⊥平面ABCD,E是PC的中点.(1)求证:PA∥平面BDE;(2)求证:BD⊥PC.29.如图所示,在直四棱柱ABCD﹣A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.(1)求证:B1D1∥平面A1BD;(2)求证:MD⊥AC.30.如图所示,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2.(1)求证:AC∥平面BEF;(2)求四面体BDEF的体积.参考答案一.选择题(共12小题)1.解:根据线面平行的定义可知直线与平面无交点∵直线a∥平面α,∴直线a与平面α没有公共点从而直线a与平面α内任意一直线都没有公共点,则不相交故选:D.2.解:根据平行公理可知①正确;根据面面平行的判定定理可知④正确;对于②错在a、b可能相交或异面.对于③错在α与β可能相交,对于⑤⑥错在a可能在α内.故选:C.3.解:∵不在一条直线上的三点确定一个平面,三点在一条直线上时不能确定平面∴A不正确;∵点在直线上时,不能确定平面,∴B不正确;∵梯形有两条边平行,两条平行线确定一个平面,梯形的两腰也在平面内,∴C正确;∵过平面外一点与平面平行的平面内,过该点的直线都符合条件,∴D不正确.故选:C.4.解:A不正确,因为由直线与平面内的一条直线平行,不能推出直线与平面平行,直线有可能在平面内.B不正确,因为由直线与平面内的某条直线不相交,不能推出直线与平面平行,直线有可能在平面内,也可能和平面相交.C不正确,因为由直线与平面内的无数条直线平行,不能推出直线与平面平行,直线有可能在平面内.D正确,因为由直线与平面内的所有直线不相交,依据直线和平面平行的定义可得直线与平面平行.故选:D.5.解:如图,任取线段A1B上一点M,过M作MH∥AA1,交AB于H,过H作HG∥AC交BC于G,过G作CC1的平行线,与CB1一定有交点N,且MN∥平面ACC1A1,则这样的MN有无数个.故选:D.6.解:对于选项B,由于AB∥MQ,结合线面平行判定定理可知B不满足题意;对于选项C,由于AB∥MQ,结合线面平行判定定理可知C不满足题意;对于选项D,由于AB∥NQ,结合线面平行判定定理可知D不满足题意;所以选项A满足题意,故选:A.7.解:连结BD1,AC、BD,设AC∩BD=O,连结OE,∵在正方体ABCD﹣A1B1C1D1中,E为DD1的中点,∴O是BD中点,∴OE∥BD1,∵OE⊂平面ACE,BD1⊄平面ACE,∴BD1∥平面ACE.故选:B.8.解:如图,由条件知,EF∥BD,,GH∥BD,且;∴EF∥HG,且;∴四边形EFGH为梯形;EF∥BD,EF⊄平面BCD,BD⊂平面BCD;∴EF∥平面BCD;若EH∥平面ADC,则EH∥FG,显然EH不平行FG;∴EH不平行平面ADC;∴选项B正确.故选:B.9.证明:如图∵E,F分别为SB,SC上的点,且EF∥面ABC,又∵EF⊂平面SBC,平面SBC∩平面ABC=BC,∴EF∥BC.故选:B.10.解:如图所示,连接EF,BE∥PF显然不正确,是异面直线;∵E、F分别为PA、PD的中点,∴EF∥AD,∵AD∥BC,∴EF∥BC,∴直线EF∥平面PBC,选项B正确;EF∥BC,∵EF⊄平面PBC,BC⊂平面PBC,④由于不能推出线面垂直,故平面BCE⊥平面PAD不成立.选项C不正确;直线PB与DC所成角就是PB与AB所成角,不确定为60°,选项D不正确;故选:B.11.证明:∵AD:DB=AE:EC,∴DE∥BC,∵DE⊂平面α,BC⊄平面α,∴BC∥平面α.故选:D.12.解:对于①:取CD中点F,连接MF,BF,则MF∥DA1,BF∥DE,∴平面MBF∥平面A1DE,∴MB∥平面A1DE,故①正确对于②:∵B是定点,∴M是在以B为球心,MB为半径的球上,故②正确,对于③:若③成立,则由DE⊥CE,可得DE⊥面A1EC∴DE⊥A1E,而这与DA1⊥A1E矛盾,故③错误.对于④:由∠A1DE=∠MFB,MF=A1D=定值,FB=DE=定值,由余弦定理可得MB2=MF2+FB2﹣2MF•FB•cos∠MFB,所以MB是定值,故④正确.故正确的命题有:①②④,故选:B.二.解答题(共18小题)13.证明:(Ⅰ)连接PE,G、F为EC和PC的中点,∴FG∥PE,FG⊄平面PBD,PE⊂平面PBD,∴FG∥平面PBD…(6分)(Ⅱ)∵菱形ABCD,∴BD⊥AC,又PA⊥面ABCD,BD⊂平面ABCD,∴BD⊥PA,∵PA⊂平面PAC,AC⊂平面PAC,且PA∩AC=A,∴BD⊥平面PAC,FG⊂平面PAC,∴BD⊥FG…(14分)14.证明:∵PD垂直于正方形ABCD所在的平面,AB=2,PC与平面ABCD所成角是45°.F是AD的中点,M是PC的中点,∴以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,D(0,0,0),M(0,1,1),P(0,0,2),F(1,0,0),B(2,2,0),=(0,1,1),=(1,0,﹣2),=(2,2,﹣2),设平面PFB的法向量=(x,y,z),则,取z=1,得=(2,﹣1,1),∵=0,DM⊄平面PFB,∴DM∥平面PFB.15.证明:(1)取CD中点G,连结PG、QG,∵在四棱锥S﹣ABCD中,E,P,Q分别是棱AD,SC,AB的中点.∴PG∥SD,QG∥AD,∵PG∩QG=G,SD∩AD=D,∴平面PGQ∥平面SDA,∵PQ⊂平面PGQ,∴PQ∥平面SAD.(2)∵在四棱锥S﹣ABCD中,底面ABCD为菱形,∠BAD=60°,SA=SD,SA=AB=2,∴SE⊥AD,SE=,∵平面SAD⊥平面ABCD,平面SAD∩平面ABCD=AD,∴SE⊥平面ABC,∵S△ABC==,∴三棱锥S﹣ABC的体积V===1.16.证明:三棱柱ABC﹣A1B1C1中,M为AB的中点,N为BC的中点,∴MN∥AC,又AC∥A1C1,∴MN∥A1C1,又MN⊄面A1C1D,A1C1⊂面A1C1D,∴MN∥面A1C1D.17.证明:(1)∵D,E分别为AB,AC的中点,∴DE∥BC,又DE⊄平面PBC,BC⊂平面PBC,∴DE∥平面PBC.(2)连接PD,∵DE∥BC,又∠ABC=90°,∴DE⊥AB,又PA=PB,D为AB中点,∴PD⊥AB,又PD∩DE=D,PD⊂平面PDE,DE⊂平面PDE,∴AB⊥平面PDE,又PE⊂平面PDE,∴AB⊥PE.(3)∵平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PD⊥AB,PD⊂平面PAB,∴PD⊥平面ABC,∵△PAB是边长为2的等边三角形,∴PD=,∵E是AC的中点,∴.18.解:解法一:依条件可知AB、AC,AA1两两垂直,如图,以点A为原点建立空间直角坐标系A﹣xyz.根据条件容易求出如下各点坐标:A(0,0,0),B(0,2,0),C(﹣1,0,0),A1(0,0,2),B1(0,2,2),C1(﹣1,0,2),M(0,1,2),(I)证明:∵是平面ACCA1的一个法向量,且,所以又∵MN⊄平面ACC1A1,∴MN∥平面ACC1A1(II)设=(x,y,z)是平面AMN的法向量,因为,由得解得平面AMN的一个法向量=(4,2,﹣1)由已知,平面ABC的一个法向量为=(0,0,1)∴二面角M﹣AN﹣B的余弦值是解法二:(I)证明:设AC的中点为D,连接DN,A1D∵D,N分别是AC,BC的中点,∴又∵,∴,∴四边形A 1DNM是平行四边形∴A1D∥MN∵A1D⊂平面ACC1A1,MN⊄平面ACC1A1∴MN∥平面ACC1A1(II)如图,设AB的中点为H,连接MH,∴MH∥BB1∵BB1⊥底面ABC,∵BB1⊥AC,BB1⊥AB,∴MH⊥AC,MH⊥AB∴AB∩AC=A∴MH⊥底面ABC在平面ABC内,过点H做HG⊥AN,垂足为G连接MG,AN⊥HG,AN⊥MH,HG∩MH=H∴AN⊥平面MHG,则AN⊥MG∴∠MGH是二面角M﹣AN﹣B的平面角∵MH=BB1=2,由△AGH∽△BAC,得所以所以∴二面角M﹣AN﹣B的余弦值是19.证明:(1)因为ABC﹣A1B1C1是直三棱柱,所以AB∥A1B1,且AB=A1B1,又点M,N分别是AB、A1B1的中点,所以MB=A1N,且MB∥A1N.所以四边形A1NBM是平行四边形,从而A1M∥BN.又BN⊄平面A1MC,A1M⊂平面A1MC,所以BN∥平面A1MC;(2)因为ABC﹣A1B1C1是直三棱柱,所以AA1⊥底面ABC,而AA1⊂侧面ABB1A1,所以侧面ABB1A1⊥底面ABC.又CA=CB,且M是AB的中点,所以CM⊥AB.则由侧面ABB1A1⊥底面ABC,侧面ABB1A1∩底面ABC=AB,CM⊥AB,且CM⊂底面ABC,得CM⊥侧面ABB1A1.又AB1⊂侧面ABB1A1,所以AB1⊥CM.又AB1⊥A1M,A1M、MC平面A1MC,且A1M∩MC=M,所以AB1⊥平面A1MC.又A1C⊂平面A1MC,所以AB⊥A1C.20.(1)证明:连接BE、BD,BD交CE于点O,∵E为线段AD的中点,AD∥BC,,∴BC∥ED,∴四边形BCDE为平行四边形,∴O为BD的中点,又F是BP的中点,∴OF∥PD,又OF⊂平面CEF,PD⊄平面CEF,∴PD∥平面CEF;(2)解:由(1)知,四边形BCDE为平行四边形,∴BE∥CD,∵四边形ABCD为等腰梯形,AD∥BC,,∴AB=AE=BE,∴三角形ABE是等边三角形,∴,做BH⊥AD于H,则,∵PE⊥平面ABCD,PE⊂平面PAD,∴平面PAD⊥平面ABCD,又平面PAD∩平面ABCD=AD,BH⊥AD,BH⊂平面ABCD,∴BH⊥平面PAD,∴点B到平面PAD的距离为,又∵F为线段PB的中点,∴点F到平面PAD的距离等于点B到平面PAD的距离的一半,即,又,∴=.21.证明:(1)取CD中点F,连结NF、MF,∵矩形ABCD所在平面与三角形ABE所在平面互相垂直,M,N,H分别为DE,AB,BE的中点.∴NF∥BC,MF∥CE,∵NF∩MF=F,BC∥CE=C,NF、MF⊂平面MNF,BC、CE⊂平面BCE,∴平面BCE∥平面MNF,∵MN⊂平面MNF,∴MN∥平面BEC.(2)∵AE=AB,H为BE的中点,∴AH⊥BE.∵矩形ABCD所在平面与三角形ABE所在平面互相垂直,∴BC⊥平面ABE,∴BC⊥AH,∵BE∩BC=B,∴AH⊥平面BCE,∴AH⊥CE.22.证明:(1)取AB的中点F,连接OF,DF,∵侧面ABB1A1为平行四边形,∴O为AB1的中点,∴,又,∴,∴四边形OFDC1为平行四边形,则C1O∥DF.∵C1O⊄平面ABD,DF⊂平面ABD,∴C1O∥平面ABD.解:(2)过C作CH⊥AB于H,连接DH,∵DC⊥平面ABC,∴DC⊥AB.又CH∩CD=C,∴AB⊥平面CDH,∴AB⊥DH.设BC=x,则,,,∴△ABD的面积为,∴x=2.设E到平面ABC的距离为h,则,∴h=1,∴E与O重合,.23.证明:(1)∵点F,G分别为BC,PC,的中点,∴GF∥PB,∵PB⊄平面EFG,FG⊂平面EFG,∴PB∥平面EFG.(2)∵在三棱锥P﹣ABC中,PB⊥BC,AC⊥BC,点E,F,G分别为AB,BC,PC,的中点,∴EF∥AC,GF∥PB,∴EF⊥BC,GF⊥BC,∵EF∩FG=F,∴BC⊥平面EFG,∵EG⊂平面EFG,∴BC⊥EG.24.(Ⅰ)证明:∵点A1,B1,C1在平面ABC内的正投影分别为A,B,C,∴AA1∥BB1∥CC1,取A1B1中点F,连接EF,FC,则EF∥A1A,EF=A1A,∵AA14,CC1=2,∴CC1∥A1A,CC1=A1A,∴CC1∥EF,CC1=EF,∴四边形EFC1C为平行四边形,∴CE∥C1F,∵CE⊄平面A1B1C1,C1F⊂平面A1B1C1,∴CE∥平面A1B1C1;(Ⅱ)解:建立如图所示的坐标系,则A(2,0,0),C(0,2,0),B1(0,0,4),C1(0,2,2),∴=(﹣2,2,0),=(0,0,2),=(﹣2,0,4),=(0,2,﹣2).设平面ACC1的法向量为=(x,y,z),则,令x=1,则=(1,1,0).同理可得平面AB1C1的法向量为=(2,1,1),∴cos<,>==.由图可知二面角B1﹣AC1﹣C为钝角,∴二面角B1﹣AC1﹣C的大小为150°.25.证明:(1)如图,取BC中点P,连接MP,C1P.∵M为AB的中点,∴MP∥AC,且MP=AC.又AC∥A1C1,AC=A1C1,且NC1=,∴NC1∥MP,且NC1=MP.∴四边形MNC1P为平行四边形,∴NM∥PC1.又PC1⊂平面BCC1B1,MN⊄平面BCC1B1,∴MN∥平面BCC1B1.…………(4分)解:(2)如图,作BH⊥A1A,交AA1于H,连接CH.∵AC=AB,∠A1AB=∠A1AC,AH为公共边,∴△ABH≌△ACH,∴∠CHA=∠BHA.∴BH⊥AA1,⊥AA1.而BH∩CH=H,∴A1A⊥平面BCH,A1A⊥BC.又A1A∥C1C,∴C1C⊥BC.在直角△C1CP中,CP==1,C1P=MN=,∴C1C=.在直角△ABH中,BH=ABsin60°=.∴三棱柱ABC﹣A1B1C1的侧面积S=4×.……(12分)26.证明:(1)设G为AB1的中点,连EG,GF,因为FG,又DE,所以FG DE,所以四边形DEGF是平行四边形,所以DF∥EG又DF⊄平面B1AE,EG⊂平面B1AE,所以DF∥平面B1AE.解:(2)因为ABCD是菱形,且∠ABD=60°,所以△ABC是等边三角形取BC中点G,则AG⊥AD,因为AA1⊥平面ABCD,所以AA1⊥AG,AA1⊥AD建立如图的空间直角坐标系,令AA1=t(t>0),则A(0,0,0),,,D1(0,2,t),,,,设平面B1AE的一个法向量为,则且,取,设直线AD1与平面B1AE所成角为θ,则,解得t=2,故线段AA1的长为2.27.证明:(1)∵在直三棱柱ABC﹣A1B1C1中,BC1∩B1C=E,∴E是B1C的中点,∵AB1的中点为D,∴DE∥AC,∵AC⊂平面AA1C1C,DE⊄平面AA1C1C,∴DE∥平面AA1C1C.(2)∵在直三棱柱ABC﹣A1B1C1中,BC=CC1,∴BC1⊥B1C,AC⊥CC1,又AC⊥BC,BC∩CC1=C,∴AC⊥平面BCC1B1,∴AC⊥BC1,∵AC∩B1C=C,∴BC1⊥平面ACB1,∴BC1⊥AB1.28.证明:(1)连接AC,OE,则AC经过正方形中心点O,且O是AC的中点,又E是PC的中点,∴OE∥PA,又OE⊂平面BDE,PA⊄平面BDE,∴PA∥平面BDE.(2)∵PO⊥平面ABCD,BD⊂平面ABCD,∴PO⊥BD,四边形ABCD是正方形,∴BD⊥AC,又PO∩AC=O,PO⊂平面PAC,AC⊂平面PAC,∴BD⊥平面PAC,又PC⊂平面PAC,∴BD⊥PC.29.(1)证明:由直四棱柱,得BB1∥DD1,又∵BB1=DD1,∴BB1D1D是平行四边形,∴B1D1∥BD.而BD⊂平面A1BD,B1D1⊄平面A1BD,∴B1D1∥平面A1BD.(2)证明∵BB1⊥平面ABCD,AC⊂平面ABCD,∴BB1⊥AC.又∵BD⊥AC,且BD∩BB1=B,∴AC⊥平面BB1D.而MD⊂平面BB1D,∴MD⊥AC.30.证明:(1)设AC∩BD=O,取BE中点G,连接FG,OG,所以,OG∥DE,且OG=DE.因为AF∥DE,DE=2AF,所以AF∥OG,且OG=AF,从而四边形AFGO是平行四边形,FG∥OA.因为FG⊂平面BEF,AO⊄平面BEF,所以AO∥平面BEF,即AC∥平面BEF.…(6分)解:(2)因为平面ABCD⊥平面ADEF,AB⊥AD,所以AB⊥平面ADEF.因为AF∥DE,∠ADE=90°,DE=DA=2AF=2 所以△DEF的面积为S△DEF=×ED×AD=2,所以四面体BDEF的体积V=•S△DEF×AB=(12分)。
