物化第三章练习题+作业题资料
第五版物理化学第三章习题答案-图文

第五版物理化学第三章习题答案-图文以下是为大家整理的第五版物理化学第三章习题答案-图文的相关范文,本文关键词为第五,物理化学,第三章,习题,答案,图文,第三章,热力学,第,您可以从右上方搜索框检索更多相关文章,如果您觉得有用,请继续关注我们并推荐给您的好友,您可以在综合文库中查看更多范文。
第三章热力学第二定律3.1卡诺热机在(1)热机效率;(2)当向环境作功。
解:卡诺热机的效率为时,系统从高温热源吸收的热及向低温热源放出的热的高温热源和的低温热源间工作。
求根据定义3.2卡诺热机在(1)热机效率;(2)当从高温热源吸热解:(1)由卡诺循环的热机效率得出时,系统对环境作的功的高温热源和的低温热源间工作,求:及向低温热源放出的热(2)3.3卡诺热机在(1)热机效率;(2)当向低温热源放热解:(1)时,系统从高温热源吸热及对环境所作的功。
的高温热源和的低温热源间工作,求1(2)3.4试说明:在高温热源和低温热源间工作的不可逆热机与卡诺机联合操作时,若令卡诺热机得到的功wr等于不可逆热机作出的功-w。
假设不可逆热机的热机效率大于卡诺热机效率证:(反证法)设ηir>ηr不可逆热机从高温热源吸热则,向低温热源放热,对环境作功,其结果必然是有热量从低温热源流向高温热源,而违反势热力学第二定律的克劳修斯说法。
逆向卡诺热机从环境得功则从低温热源吸热向高温热源放热若使逆向卡诺热机向高温热源放出的热不可逆热机从高温热源吸收的热相等,即总的结果是:得自单一低温热源的热,变成了环境作功,违背了热力学第二定律的开尔文说法,同样也就违背了克劳修斯说法。
23.5高温热源温度低温热源,求此过程。
,低温热源温度,今有120KJ的热直接从高温热源传给解:将热源看作无限大,因此,传热过程对热源来说是可逆过程3.6不同的热机中作于情况下,当热机从高温热源吸热(1)可逆热机效率(2)不可逆热机效率(3)不可逆热机效率解:设热机向低温热源放热。
复旦 物理化学 第三章 习题答案

复旦物理化学第三章习题答案第三章习题解答1. 先求H 2O(g)→H 2O(l )J 8592p 3166ln RT G 1-==∆∆G 2=0∆G 3=V l(p ︒-3166)1)3166p (99710183=-⨯=∆G=∆G 1+∆G 2+∆G 3=–8590.9 J)l (O H G)g (O H )g (G )g (O 21)g (H 22mr22−−→−∆−−−−→−∆+∆r G ︒m (l )= ∆r G ︒m (g)+∆G=–228.57–8.59 =–237.16 kJ 2. 反应 C (s)+2H 2(g)=CH 4(g) ∆r G ︒m =–19397 J ⋅mol –1摩尔分数 0.8 0.1(1) T=1000K 时,097.0R 100019397exp RTGexp K mrp=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛∆-=156.08.01.0Q 2p ==Q ︒p >K ︒p 反应不会正向进行。
(2) 设压力为p ,当097.0p p 8.01.0Q 2p <⎪⎪⎭⎫ ⎝⎛= 时,即p>1.61p ︒时,反应才能进行。
3. SO 2Cl 2(g) + SO 2(g) → Cl 2(g) 反应前压力(kPa) 44.786 47.836 平衡时压力(kPa) x 44.786-x 47.836-x p 总=x+(44.786-x)+( 47.836-x)=86.096 kPa x=6.526 kPa39.2)325.101(526.6)526.6836.47)(526.6786.44()p (K K 1p p =--==-ν∆-4. H 2(g) + I 2(g) → 2HI(g) 开始(mol) 7.945.3平衡(mol) 2x 94.7- 2x 3.5- x ∆ν=01.502x 3.52x 94.7x K K 2x p=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-== x=9.478 mol (另一根x=19.30舍去)5. A(g) + B(g) → AB(g) 开始(mol) 1 1平衡(mol) 1-0.4 1-0.4 0.4 n 总=1.6 mol⎪⎪⎭⎫⎝⎛∆-=⎪⎪⎭⎫ ⎝⎛=ν∆RT G exp ppK K mr x p()⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛-R 3008368exp p p 6.1/6.06.1/4.012p=0.06206p ︒=6288 Pa 6. A(g) → B(g) 平衡压力 10p ︒ p ︒ 1.0101Kp==∆r G ︒m =–RTlnK ︒p =5708 J∆r G m (1)= ∆r G ︒m –RTlnQ ︒p(1)0J 398921lm 2985708>=+= 反应不会自发进行。
物理化学第三章课后答案完整版

物理化学第三章课后答案完整版第三章热⼒学第⼆定律3.1 卡诺热机在的⾼温热源和的低温热源间⼯作。
求(1)热机效率;(2)当向环境作功时,系统从⾼温热源吸收的热及向低温热源放出的热。
解:卡诺热机的效率为根据定义3.2 卡诺热机在的⾼温热源和的低温热源间⼯作,求:(1)热机效率;(2)当从⾼温热源吸热时,系统对环境作的功及向低温热源放出的热解:(1) 由卡诺循环的热机效率得出(2)3.3 卡诺热机在的⾼温热源和的低温热源间⼯作,求(1)热机效率;(2)当向低温热源放热时,系统从⾼温热源吸热及对环境所作的功。
解:(1)(2)3.4 试说明:在⾼温热源和低温热源间⼯作的不可逆热机与卡诺机联合操作时,若令卡诺热机得到的功r W 等于不可逆热机作出的功-W 。
假设不可逆热机的热机效率⼤于卡诺热机效率,其结果必然是有热量从低温热源流向⾼温热源,⽽违反势热⼒学第⼆定律的克劳修斯说法。
证:(反证法)设 r ir ηη>不可逆热机从⾼温热源吸热,向低温热源放热,对环境作功则逆向卡诺热机从环境得功从低温热源吸热向⾼温热源放热则若使逆向卡诺热机向⾼温热源放出的热不可逆热机从⾼温热源吸收的热相等,即总的结果是:得⾃单⼀低温热源的热,变成了环境作功,违背了热⼒学第⼆定律的开尔⽂说法,同样也就违背了克劳修斯说法。
3.5 ⾼温热源温度,低温热源温度,今有120KJ的热直接从⾼温热源传给低温热源,求此过程。
解:将热源看作⽆限⼤,因此,传热过程对热源来说是可逆过程3.6 不同的热机中作于的⾼温热源及的低温热源之间。
求下列三种情况下,当热机从⾼温热源吸热时,两热源的总熵变。
(1)可逆热机效率。
(2)不可逆热机效率。
(3)不可逆热机效率。
解:设热机向低温热源放热,根据热机效率的定义因此,上⾯三种过程的总熵变分别为。
3.7 已知⽔的⽐定压热容。
今有1 kg,10℃的⽔经下列三种不同过程加热成100 ℃的⽔,求过程的。
(1)系统与100℃的热源接触。
物理化学第三章 习题
返回
2013-7-28
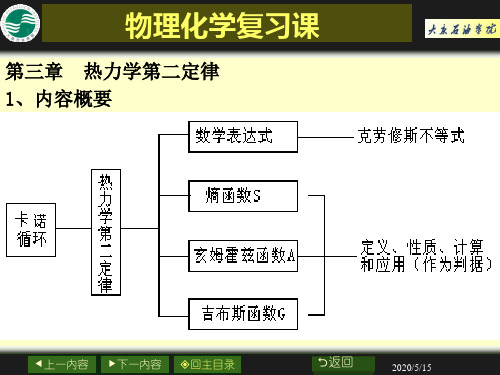
物理化学复习课
(8)某一化学反应的热效应除以反应温度T,即得此反应 得rSm。 解:不正确。化学反应的热效应rHm=QpQr。而rSm= Qr/T。所以rSmrHm/T。如果该反应的(rGm)T,p=0,则该 式成立。平衡时可逆。 T2 (9)在恒压下用酒精灯 S C p dT / T 加热某物质,该物质的熵变 T1 解:不正确。如该物质在加热过程中无相变化则该式成 立。否则不能成立。 (10)对于绝热系统,可用S0判断过程的方向和限度。
上一内容 下一内容 回主目录
A 九、证明题 试用热力学第二定律证明两条等温可逆线不会相交。 M
返回
2013-7-28
物理化学复习课
十、判断题 × 1、恒温过程的Q一定是零。 × 2、所有绝热过程的Q为零,sysS也必为零。 3、不可逆过程就是过程发生后,系统不能再复原的过 × 程 4、当热由系统传给环境时,系统的焓必减少。 5、一氧化碳的标准摩尔生成焓也是同温度下石墨的标 × 准摩尔燃烧焓。 6、实际气体绝热可逆过程的S一定为零,G不一定为 零。
)。
T , p ,nC
G D. n B
2、在298K.100kPa下将3mol O2(g),与4mol Ar(g)在一刚 性密闭容器内恒温混合,则此过程的( C ) A . W < 0 B. Δ U < 0 C. Δ S >0 D. Δ G > 0 3、 在一定温度范围内,某化学反应的⊿rHm与温度无关 ,那么该反应的⊿rSm随温度的升高而(C )。
解:不正确。若加上环境不对系统作功则设法成立。否则不能成立
上一内容 下一内容 回主目录
返回
(完整版)物理化学3-4章练习题

第三章 多组分系统热力学一.选择题:选择正确答案的编号,填在各题后的括号内:1.下面各个偏导式中,哪个是偏摩尔量( ) A.j n T p Bn ,,⎪⎪⎭⎫⎝⎛∂∂μ B.jn V S B n U ,,⎪⎪⎭⎫ ⎝⎛∂∂ C. jn T p B m n S ,,⎪⎪⎭⎫ ⎝⎛∂∂ D. j n T p B n V ,,⎪⎪⎭⎫ ⎝⎛∂∂ 2.下面各个偏导式中,哪个不是化学势( ) A. jn V S B n U ,,⎪⎪⎭⎫⎝⎛∂∂ B. jn p T Bn H ,,⎪⎪⎭⎫ ⎝⎛∂∂ C. jn p T Bn G ,,⎪⎪⎭⎫ ⎝⎛∂∂ D. jn V T Bn F ,,⎪⎪⎭⎫ ⎝⎛∂∂ 3.理想液态混合物中任一组分B,其偏摩尔量和摩尔量的关系为( )A. B H =*B m H , B. B V VBm *≠, C. B G =*B m G , D. B S =*B m S ,4.一定温度下,纯液体A 的饱和蒸汽压为pA*,化学势为*A μ,凝固点为*f T ,当A 中加入少量不挥发性溶质后,上述三个量p A,μA,Tf,它们的关系为( )A, p A*<pA*A μ<μA*f T <TfB. p A*>pA*A μ <μA*f T <TfC. p A*<pA*A μ<μA*f T >T fD.p A*>pA *A μ>μA*f T >Tf5.一定温度和压力下的乙醇水溶液中,若使乙醇的偏摩尔体积的变化dV>0.此时水的偏摩尔体积的变化dV水( )A. >0B.=0C. <0D.不能确定 6.对多组分体系中B 物质的偏摩尔量XB=Bj n p T Bn X ≠⎪⎪⎭⎫⎝⎛∂∂,,,下列叙述中不正确的是( ) A.X B是无限大量体系中B 物质每变化1 mol 时该体系容量性质X 的变化量B.X 为容量性质, XB也为容量性质C.XB不仅取决于T,p,而且取决于浓度D.X=X n B B ∑7.将固体NaCl 投放到水中, NaCl 逐渐溶解,最后达到饱和.开始溶解时溶液中的NaCl 的化学式为µ(a),饱和时溶液中NaCl 的化学势为µ(b),固体NaCl 的化学势为,则( ) A. µ(a)= µ(b)< µ(c) B. µ(a)= µ(b)> µ(c) C. µ(a)> µ(b)= µ(c) D. µ(a)<µ(b)= µ(c) 8.下列物理量中,( )既是偏摩尔量,又是化学势. A. Bj n p T Bn F ≠⎪⎪⎭⎫⎝⎛∂∂,, B. Bj n p S Bn H ≠⎪⎪⎭⎫ ⎝⎛∂∂,, C. Bj n p T Bn G ≠⎪⎪⎭⎫ ⎝⎛∂∂,, D. Bj n p S Bn U ≠⎪⎪⎭⎫ ⎝⎛∂∂,, 9.理想液态混合物的通性是( ) A 、 ΔV 混合=0 ΔH 混合=0 ΔS 混合>0 ΔG 混合<0 B 、 ΔV 混合=0 ΔH 混合=0 ΔS 混合>0 ΔG 混合=0 C 、 ΔV 混合> 0 ΔH 混合> 0 ΔS 混合>0 ΔG 混合<0 D 、 ΔV 混合=0 ΔH 混合=0 ΔS 混合=0 ΔG 混合=0 10.7、298K 时A 和B 两种气体在某一溶剂中溶解的亨利系数分别为kA 和kB ,且kA>kB ,则当A 和B 压力相同时,在该溶剂中溶解的量是 ( ) A 、 A 的量大于B 的量 B 、 A 的量小于B 的量 C 、 A 的量等于B 的量D 、 A 的量和B 的量无法比较11、313K 时纯液体A 的饱和蒸汽压是纯液体B 的21倍,A 和B 能形成理想液态混合物。
北京大学《物理化学》课后章节练习题第3章习题及答案

第三章 习题1. 在413.15K 时,纯C 6H 5Cl 和C 6H 5Br 的蒸气压分别为125.238kPa 和66.104kPa 。
假定两液体组成理想液体,若有一混合液,在413.15K 、101.325kPa 下沸腾,试求该溶液的组成,以及在此情况下,液面上蒸气的组成。
2. 液体A 与液体B 形成理想溶液。
在343.15K 时,1mol A 和2mol B 所成溶液的蒸气压为50.663kPa ,若在溶液中再加入3mol A ,则溶液的蒸气压增加到70.928kpa ,试求:(1)和。
*A p *B p (2)对第一种溶液,气相中A 、B 的摩尔分数各位若干?3. 若气体的状态方程为m (1)pV p RT β−=,求其逸度的表示式。
4. 液体A 和B 形成理想溶液。
现有一含有A 的物质的量分数为0.4的蒸气相,放在一个带活塞的气缸内,恒温下将蒸气慢慢压缩。
已知和分别为*A p *B p 0.4p θ×和1.2p θ×,计算:(a) 当液体开始凝聚出来时的蒸气总压。
(b) 该溶液在正常沸点b T 时的组成。
5. 在288.2K 、p θ时,某酒窖中存有10.0 m 3的酒,其中含乙醇96%(质量分数)。
今欲加水调制为含乙醇56%的酒,问(1)应加多少体积的水?(2)能得到多少立方米的含醇56%的酒已知该条件下水的密度999.1 kg.m -3,水和乙醇的偏摩尔体积分别为 乙醇的质量分数V H2O,m / (10-6 m 3.mol -1)V 乙醇,m / (10-6 m 3.mol -1)96%14.61 58.01 56%17.11 56.586. K 2SO 4在水溶液中的偏摩尔体积V 2,m 在298K 为V 2,m /m 3=3.228×10-5+1.821×10-5m 1/2/(mol·kg -1)1/2+2.2×10-8 m /(mol·kg -1)。
物理化学第三章习题答案

第三章热力学第二定律3.1 卡诺热机在的高温热源和的低温热源间工作;求1 热机效率;2 当向环境作功时,系统从高温热源吸收的热及向低温热源放出的热;解:卡诺热机的效率为根据定义3.2 卡诺热机在的高温热源和的低温热源间工作,求:1 热机效率;2 当从高温热源吸热时,系统对环境作的功及向低温热源放出的热解:1 由卡诺循环的热机效率得出23.3 卡诺热机在的高温热源和的低温热源间工作,求1热机效率;2当向低温热源放热时,系统从高温热源吸热及对环境所作的功;解: 123.4 试说明:在高温热源和低温热源间工作的不可逆热机与卡诺机联合操作时,若令卡诺热机得到的功r W 等于不可逆热机作出的功-W ;假设不可逆热机的热机效率大于卡诺热机效率,其结果必然是有热量从低温热源流向高温热源,而违反势热力学第二定律的克劳修斯说法;证: 反证法 设 r ir ηη>不可逆热机从高温热源吸热,向低温热源放热,对环境作功则逆向卡诺热机从环境得功从低温热源吸热向高温热源放热则若使逆向卡诺热机向高温热源放出的热不可逆热机从高温热源吸收的热相等,即总的结果是:得自单一低温热源的热,变成了环境作功,违背了热力学第二定律的开尔文说法,同样也就违背了克劳修斯说法;3.5 高温热源温度,低温热源温度,今有120KJ的热直接从高温热源传给低温热源,求此过程;解:将热源看作无限大,因此,传热过程对热源来说是可逆过程3.6 不同的热机中作于的高温热源及的低温热源之间;求下列三种情况下,当热机从高温热源吸热时,两热源的总熵变;1 可逆热机效率;2 不可逆热机效率;3 不可逆热机效率;解:设热机向低温热源放热,根据热机效率的定义因此,上面三种过程的总熵变分别为;3.7 已知水的比定压热容;今有1 kg,10℃的水经下列三种不同过程加热成100 ℃的水,求过程的;1系统与100℃的热源接触;2系统先与55℃的热源接触至热平衡,再与100℃的热源接触;3系统先与40℃,70℃的热源接触至热平衡,再与100℃的热源接触;解:熵为状态函数,在三种情况下系统的熵变相同在过程中系统所得到的热为热源所放出的热,因此3.8 已知氮N2, g的摩尔定压热容与温度的函数关系为将始态为300 K,100 kPa下1 mol的N2g置于1000 K的热源中,求下列过程1经恒压过程;2经恒容过程达到平衡态时的;解:1在恒压的情况下2在恒容情况下,将氮N2, g看作理想气体将代替上面各式中的,即可求得所需各量3.9 始态为,的某双原子理想气体1 mol,经下列不同途径变化到,的末态;求各步骤及途径的;1 恒温可逆膨胀;2先恒容冷却至使压力降至100 kPa,再恒压加热至;3 先绝热可逆膨胀到使压力降至100 kPa,再恒压加热至;解:1对理想气体恒温可逆膨胀,△U= 0,因此2先计算恒容冷却至使压力降至100 kPa,系统的温度T:3同理,先绝热可逆膨胀到使压力降至100 kPa时系统的温度T:根据理想气体绝热过程状态方程,各热力学量计算如下3.10 1mol理想气体在T=300K下,从始态100KPa 到下列各过程,求及;1 可逆膨胀到压力50Kpa;2 反抗恒定外压50Kpa,不可逆膨胀至平衡态;3 向真空自由膨胀至原体积的2倍3.11 某双原子理想气体从始态,经不同过程变化到下述状态,求各过程的解:1 过程1为PVT变化过程232.12 2 mol双原子理想气体从始态300 K,50 dm3,先恒容加热至400 K,再恒压加热至体积增大到100 dm3,求整个过程的;解:过程图示如下先求出末态的温度因此,3.13 4mol单原子理想气体从始态750K,150KPa,先恒容冷却使压力降至50KPa,再恒温可逆压缩至100KPa,求整个过程的解:ab3.14 3mol双原子理想气体从始态,先恒温可逆压缩使体积缩小至,再恒压加热至,求整个过程的及;解:ab3.15 5 mol单原子理想气体,从始态300 K,50 kPa先绝热可逆压缩至100 kPa,再恒压冷却至体积为85dm3的末态;求整个过程的Q,W,△U,△H及△S;3.16 始态300K,1MPa的单原子理想气体2mol,反抗0.2MPa的恒定外压绝热不可逆膨胀至平衡态;求过程的解:3.17 组成为的单原子气体A与双原子气体B的理想气体混合物共10 mol,从始态,绝热可逆压缩至的平衡态;求过程的;解:过程图示如下混合理想气体的绝热可逆状态方程推导如下容易得到3.18 单原子气体A与双原子气体B的理想气体混合物共8 mol,组成为,始态;今绝热反抗恒定外压不可逆膨胀至末态体积的平衡态;求过程的;解:过程图示如下先确定末态温度,绝热过程,因此3.19 常压下将100 g,27℃的水与200 g,72℃的水在绝热容器中混合,求最终水温t及过程的熵变;已知水的比定压热容;解:3.20 将温度均为300K,压力均为100KPa的100的的恒温恒压混合;求过程,假设和均可认为是理想气体;解:3.21 绝热恒容容器中有一绝热耐压隔板,隔板一侧为2mol的200K,的单原子理想气体A,另一侧为3mol的400K,100的双原子理想气体B;今将容器中的绝热隔板撤去,气体A与气体B混合达到平衡态,求过程的;解:A Bn=2mol n=3moln=2+3molT=200K T=400K T=V=V=V=∵绝热恒容 混合过程,Q = 0, W = 0 ∴△U = 00=40025×320023×20=4002002222)-)+-)-)+-T R T R T C n T C n B m ,V B A m ,V A ((((T 2 = 342.86K注:对理想气体,一种组分的存在不影响另外组分;即A 和B 的末态体积均为容器的体积;3.22 绝热恒容容器中有一绝热耐压隔板,隔板两侧均为N 2g;一侧容积50 dm 3,内有200 K 的N 2g 2 mol ;另一侧容积为75 dm 3, 内有500 K 的N 2g 4 mol ;N 2g 可认为理想气体;今将容器中的绝热隔板撤去,使系统达到平衡态;求过程的;解:过程图示如下同上题,末态温度T 确定如下经过第一步变化,两部分的体积和为即,除了隔板外,状态2与末态相同,因此注意21与22题的比较;3.23 甲醇在101.325KPa下的沸点正常沸点为,在此条件下的摩尔蒸发焓,求在上述温度、压力条件下,1Kg液态甲醇全部成为甲醇蒸汽时;解:3.24 常压下冰的熔点为0℃,比熔化焓,水的比定压热熔;在一绝热容器中有1 kg,25℃的水,现向容器中加入0.5 kg,0℃的冰,这是系统的始态;求系统达到平衡后,过程的;解:过程图示如下将过程看作恒压绝热过程;由于1 kg,25℃的水降温至0℃为只能导致克冰融化,因此3.25 常压下冰的熔点是,比熔化焓,水的比定压热熔,系统的始态为一绝热容器中1kg,的水及0.5kg 的冰,求系统达到平衡态后,过程的熵; 解:3.27 已知常压下冰的熔点为0℃,摩尔熔化焓,苯的熔点为5.5 1℃,摩尔熔化焓;液态水和固态苯的摩尔定压热容分别为及;今有两个用绝热层包围的容器,一容器中为0℃的8 mol H2Os与2 mol H2Ol成平衡,另一容器中为5.510℃的5 mol C6H6l与5 mol C6H6s成平衡;现将两容器接触,去掉两容器间的绝热层,使两容器达到新的平衡态;求过程的;解:粗略估算表明,5 mol C6H6l 完全凝固将使8 mol H2Os完全熔化,因此,过程图示如下总的过程为恒压绝热过程, ,3.28 将装有0.1 mol乙醚C2H52Ol的小玻璃瓶放入容积为10 dm3的恒容密闭的真空容器中,并在35.51℃的恒温槽中恒温;35.51℃为在101.325 kPa下乙醚的沸点;已知在此条件下乙醚的摩尔蒸发焓;今将小玻璃瓶打破,乙醚蒸发至平衡态;求1乙醚蒸气的压力;2过程的;解:将乙醚蒸气看作理想气体,由于恒温各状态函数的变化计算如下△H=△H1+△H2△S=△S1+△S2忽略液态乙醚的体积3.30.容积为20 dm3的密闭容器中共有2 mol H2O成气液平衡;已知80℃,100℃下水的饱和蒸气压分别为及,25 ℃水的摩尔蒸发焓;水和水蒸气在25 ~ 100 ℃间的平均定压摩尔热容分别为和;今将系统从80℃的平衡态恒容加热到100℃;求过程的;解:先估算100 ℃时,系统中是否存在液态水;设终态只存在水蒸气,其物质量为n, 则显然,只有一部分水蒸发,末态仍为气液平衡;因此有以下过程:设立如下途径第一步和第四步为可逆相变,第二步为液态水的恒温变压,第三步为液态水的恒压变温;先求80℃和100℃时水的摩尔蒸发热:3.31. O2g的摩尔定压热容与温度的函数关系为已知25 ℃下O2g的标准摩尔熵;求O2g 在100℃,50 kPa下的摩尔规定熵值;解:由公式3.32. 若参加化学反应的各物质的摩尔定压热容可表示为试推导化学反应的标准摩尔反应熵与温度T的函数关系式,并说明积分常数如何确定;解:对于标准摩尔反应熵,有式中3.33. 已知25℃时液态水的标准摩尔生成吉布斯函,水在25℃时的饱和蒸气压;求25℃时水蒸气的标准摩尔生成吉布斯函数; 解:恒温下3.34. 100℃的恒温槽中有一带有活塞的导热圆筒,筒中为2 mol N2g及装与小玻璃瓶中的3 mol H2Ol;环境的压力即系统的压力维持120 kPa不变;今将小玻璃瓶打碎,液态水蒸发至平衡态;求过程的;已知:水在100℃时的饱和蒸气压为,在此条件下水的摩尔蒸发焓;3.35. 已知100℃水的饱和蒸气压为101.325 kPa,此条件下水的摩尔蒸发焓;在置于100℃恒温槽中的容积为100 dm3的密闭容器中,有压力120 kPa的过饱和蒸气;此状态为亚稳态;今过饱和蒸气失稳,部分凝结成液态水达到热力学稳定的平衡态;求过程的;解:凝结蒸气的物质量为热力学各量计算如下3.36 已知在101.325 kPa下,水的沸点为100℃,其比蒸发焓;已知液态水和水蒸气在100~120℃范围内的平均比定压热容分别为:及;今有101.325 kPa下120℃的1 kg过热水变成同样温度、压力下的水蒸气;设计可逆途径,并按可逆途径分别求过程的及;解:设计可逆途径如下3.37 已知在100 kPa下水的凝固点为0℃,在-5 ℃,过冷水的比凝固焓,过冷水和冰的饱和蒸气压分别为,;今在100 kPa下,有-5℃ 1 kg的过冷水变为同样温度、压力下的冰,设计可逆途径,分别按可逆途径计算过程的及;解:设计可逆途径如下第二步、第四步为可逆相变,,第一步、第五步为凝聚相的恒温变压过程,,因此3.38 已知在-5℃,水和冰的密度分别为和;在-5℃,水和冰的相平衡压力为59.8 MPa;今有-℃C的1 kg水在100 kPa下凝固成同样温度下的冰,求过程的;假设,水和冰的密度不随压力改变;3.39 若在某温度范围内,一液体及其蒸气的摩尔定压热容均可表示成的形式,则液体的摩尔蒸发焓为其中,为积分常数; 试应用克劳修斯-克拉佩龙方程的微分式,推导出该温度范围内液体的饱和蒸气压p的对数ln p与热力学温度T 的函数关系式,积分常数为I;解:克—克方程为不定积分:3.40 化学反应如下:1利用附录中各物质的Sθm,△f Gθm数据,求上述反应在25℃时的△r Sθm,△r Gθm;2利用附录中各物质的△f Gθm数据,计算上述反应在25℃时的;325℃,若始态CH4g和H2g的分压均为150 kPa,末态COg和H2g的分压均为50 kPa,求反应的;解:3.41 已知化学反应中各物质的摩尔定压热容与温度间的函数关系为这个反应的标准摩尔反应熵与温度的关系为试用热力学基本方程推导出该反应的标准摩尔反应吉布斯函数与温度T的函数关系式;说明积分常数如何确定;解:根据方程热力学基本方程4.42 汞Hg在100 kPa下的熔点为-38.87℃,此时比融化焓;液态汞和固态汞的密度分别为和;求:1压力为10MPa下汞的熔点;2若要汞的熔点为-35℃,压力需增大之多少;解:根据Clapeyron方程,蒸气压与熔点间的关系为3.43 已知水在77℃时的饱和蒸气压为41.891 kPa;水在101.325 kPa下的正常沸点为100℃;求 1下面表示水的蒸气压与温度关系的方程式中的A和B值;2在此温度范围内水的摩尔蒸发焓;3在多大压力下水的沸点为105℃;解:1将两个点带入方程得2根据Clausius-Clapeyron方程33.44 水H2O和氯仿CHCl3在101.325 kPa下的正常沸点分别为100℃和61.5℃,摩尔蒸发焓分别为和;求两液体具有相同饱和蒸气压时的温度;解:根据Clausius-Clapeyron方程设它们具有相同蒸气压时的温度为T,则3.45 因同一温度下液体及其饱和蒸汽压的摩尔定压热容不同故液体的摩尔蒸发焓是温度的函数,试推导液体饱和蒸汽压与温度关系的克劳修斯——克拉佩龙方程的不定积分式;解:克—克方程不定积分得:3.46 求证:2 对理想气体证明:由H=fH,P可得对理想气体,3.50证明 1焦耳-汤姆逊系数2对理想气体证明:由H=fT,PdP PHdT T H dH T m p m m )()(∂∂+∂∂= m p Tm p m T m H C P HTH P H P T,)()()()(∂∂-=∂∂∂∂-=∂∂VdP TdS dH +=V PST P H T T +∂∂=∂∂∴)()(麦克斯韦关系式 P T T VP S )()(∂∂=∂∂- 代入上式V T TVP H P T +∂∂-=∂∂)()(T J mp m p mH C V T T V PT -=-∂∂-=∂∂μ,)()(2对于理想气体 p nRT V =pRT V m = p RT V p m =∂∂)(0,,=-=-=-mp m m m p mT J C V V C V T pRμ。
物理化学 答案 第三章_习题解答

Ο 在 298.15K 的 Δ r H m = −9.20kJ ⋅ mol −1 ,C2H5OH (1) 的标准摩尔燃烧焓为-1366.8kJ·mol 1, CH3COOH (1)
-
Ο 的为-874.54kJ·mol 1。试求 CH3COOC2H5(1)的标准摩尔生成焓 Δ f H m (298.15K) 。
-
解:根据题给数据,可设计下列过程:
Δr H m CH 2COOH (1) + C2 H 5OH (1) + 5O2 ( g ) ⎯⎯⎯ → CH 3COOC2 H 5 (1) + H 2O (1) + 5O2
Ο
Δ c H1
恒温 25℃ 4CO2(g)+5H2O(1)
Δc H 2
Ο Δ c H 2 = Δ c H1 − Δ r H m (298.15K ) Ο Ο Δ c H1 = Δ c H m (CH 3 COOH ,1, 298.15 K ) + Δ c H m (C2 HOH ,1, 298.15K )
(3) Δ r Η m = Δ f Η m (CH 3 OH ) − Δ f Η m (CH 4 ) −
Θ
Θ
Θ
1 Δ f ΗΘ m (O2 ) 2
= −238.7 − (−74.81) = −163.89 KJ ⋅ mol −1
Θ Θ Θ Δr Sm = Sm (CH 3 OH ) − S m (CH 4 ) −
= −393.51 − 74.81 − (−484.5) = −16.18 KJ ⋅ mol −1
Δ r C p ,m = C p ,m (CO2 ) + C p , m (CH 4 ) − C p ,m (CH 3COOH ) = 31.4 + 37.7 − 52.3 = 16.8 J ⋅ mol −1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题解析
例题5:由原料气环己烷开始,在230 ℃,101.325 kPa下进行如下脱
氢反应:C6H12 (g) 又知327 ℃时,
C6H6 (g)+H2 (g) 。测得平衡混合气中含氢气72%, f Gm (C6H12 , g) 200.25 kJ 。mol-1
f Gm (C6H6 , g) 129.7 kJ mol-1
9
例题解析
例10:已知反应Fe2O3(s) + 3CO(g)=2Fe(s) + 3CO2(g)在不同温度下的 KΘ如下: 温度t/℃ 100 250 1000
KΘ 1100 100 0.0721 在1120 ℃反应2CO2(g)=2CO(g) + O2(g) 的KΘ =1.4×10-12。今将Fe2O3 置于1120 ℃的容器内,问容器内氧的分压应该维持多大才可防止 Fe2O3还原成铁。
Ni(s)+
1 2
O2
(g)=NiO(s)
rGm (1000 K) 146.11 kJ mol-1
H
2
(g)+
1 2
O
2
(g)=H
2O(g)
rGm (1000 K) 191.08 kJ mol-1
解:1)明确问题;写出对应化学反应方程式。
3
例题解析
例题4:理想气体反应如下:3A(g)=B(g),在压力为101.325 kPa、 300.15 K下测得平衡时40% A(g)转化掉。在压力不变时,将温度提 高10 K,则 A(g)有41%转化掉。求上述反应的ΔrHmΘ及ΔrSmΘ。设 ΔrCp,m=0。 解:Van’t Hoff等压方程之定积分式。
例题解析
例题1:总压不变,加入惰性气体,化学平衡如何变?
Kn
B
n vB B,eq
K
Kn[
p总压
p
B
nB
]vB
1
例题解析
例题2:程p167-4.4.1
结论:b)组成没变,总压变,则平衡改变;但标准平衡常数没变。 c) 总压没变,加入惰性气体,则平衡改变;但标准平衡常数 没变。
2
例题解析
程p113 例3:将含水蒸气和氢气(摩尔分数分别为0.97和0.03)的气 体混合物加热到1000 K,此时该气体混合物能否与镍反应生成氧化 镍?已知:
求:(a)230 ℃时反应的标准平衡常数KΘ。(b)在230 ℃时,要 使反应平衡混合气中的氢气含量为66%时,需要多大的压力。(c) 若ΔrCp,m=0 ,求上述反应的ΔrHmΘ 。
5
例题解析
程p92 例6:钢铁在热处理炉中被二氧化碳氧化的反应为:
Fe(s)+CO2 (g)=FeO(s)+CO(g)
10
例题解析
例11:已知ZnO(s) +CO(g)=Zn(s) + CO2(g)为用蒸馏法炼锌的主要反 应,并知反应的ΔrGmΘ(T)为 ΔrGmΘ(T)= [199.85×103 + 7.322 T/ln(T/K) + 5.90×10-3(T/K)2 27.195×10-7 (T/K)3 - 179.8T/K] J·mol -1 求:(1) 1600 K时反应的平衡常数。 (2) 如在压力保持101325 Pa的条件下进行上述反应,求平衡时气体 的组成。
11
8
例题解析
例9:工业上用乙苯脱氢制苯乙烯的反应为 C6H5C2H5(g)=C6H5C2H3(g) + H2(g)。若反应在900 K下进行,其KΘ =1.51。试分别计算在下述情况下乙苯的平衡转化率。(a) 反应压力 为100 kPa;(b) 反应压力为10 kPa;(c) 反应压力为100 kPa,并加入 水蒸气使原料气中水蒸气与乙苯蒸气的物质的量之比为10:1。
ZnO(s)+2Ag(s)=Zn(s)+Ag2O(s), rHm 242.09 kJ mol-1
问增加温度时,有利于反应朝哪个方向进行。
定义:分解压:一定温度下化合物的分解反应达到平衡时,产生气 体的压力为该温度下该化合物的分解压。
解:1)明确反应为:NH4HS(s)=NH3(g)+ H2S(g)。在293.15 K下测得 平衡时系统的总压力为45.30 kPa。 求:(a) 分解反应在293.15 K下的KΘ;(b) 若容器体积为2.4 dm3,放 入的NH4HS(s)量为0.060 mol,达平衡时还余下固体的物质的量为多 少?(c) 若容器中原放有35.50 kPa的H2S(g),则放入大量的NH4HS(s) 固体并达平衡后,系统的总压力为多大?
已知在830 ℃时反应的标准平衡常数为2.4。问(1)当炉气中CO和 CO2的摩尔分数分别为0.6和0.4时钢铁是否被氧化?(2)若炉气成 分变为CO和CO2的摩尔分数分别为0.45和0.15时,其余为N2时,钢 铁发生什么变化? 解:判据选择和使用。
6
例题解析
程p113 例7:已知氧化银和氧化锌在温度1000 K时的分解压分别为 240 kPa和15.7 kPa。问在此温度下,(1)哪一种氧化物易分解? (2)若把纯锌和纯铁置于大气中,是否都易被氧化?(3)反应,
