轮胎稳态模型的分析综述_张向文 (2)

到的模型， 与试验结果较接近， 而经验模型公式简 单，便于计算和实际应用，但需要大量的试验数据。 由于试验条件限制和路面状况的多变性， 难以得到 所有路面状况和所有轮胎运动状态的试验数据。 因 此，经验模型只是根据有限的试验数据得到，模型外 推性不好，参数没有明确的物理意义。 4.1 多项式模型
多项式模型由 S.Germann 等人提出， 其利用简 单的多项式函数近似描述轮胎与路面摩擦系数和滑
Burckhardt 模型是 M.Burckhardt 提出的一种摩
擦系数 μ 与滑移率 s 的关系模型[43，44]：
μ（s）={c1[1-exp（-c2s）]-c3s}e-c4 v
（51）
式中，ci（i=1，…，4）随路面状况的变化而变化 ，可以 通 过 试 验 测 试 数 据 拟 合 得 到 ；e-c4v 反 映 速 度 变 化 引 起的摩擦系数变化。
0.8
0.4
0 0 0.2 0.4 0.6 0.8 1.0 sx
（a）随 纵 向 滑 移 率 的 变 化
2.0 1.6 1.2 μx
干沥青
湿沥青
干水泥
干鹅卵石
湿鹅卵石
雪
μy
冰
μx、μy
0.8
0.4
0 0 5 10 15 20 25 30 35 40 45 α/（°） （b）随 侧 偏 角 的 变 化
μ（s）=l1+l2s+l3lns+l4e-slns+l5e-s姨 s
（56）
其中，参数 li（i=1，…5）随路面状况的变化而变化，可
以根据试验测试数据拟合得到。 由于该模型采用线
性组合，各参数之间是线性关系，因此，参数的拟合
较容易。
由式（56）可以看出，通过调整参数 li（i=1，…5），
可以得到不同的摩擦系数，因此，利用式（56）可以拟
摩擦系数求解。但是，该修正模型仅在考虑单个轮胎时
可以实现线性化，若利用汽车的单轨模型或四轮模型，
多个轮胎摩擦系数与滑移率间的关系就无法转化为线
性形式，另外，该修正模型仅是趋近 Burckhardt 模型，
汽车技术
·综 述·
误差较大，参数较多，因此其适用范围有限，大部分
情况下还是采用公式（52）的 Burckhardt 模型进行轮
仿真不同速度下纵向摩擦系数、 侧向摩擦系数
随纵向滑移率和侧偏角的变化， 仿真参数 α=8°，sx= 0.2，其它参数与图 28 相同，结果如图 29 所示。
—2—
1.2
1.0 μy
μx
0.8
v=5 m/s v=10 m/s v=20 m/s v=30 m/s
μx、μy
0.6
0.4
0.2
0 0 0.2 0.4 0.6 0.8 1.0 sx
2012 年 第 4 期
—1—
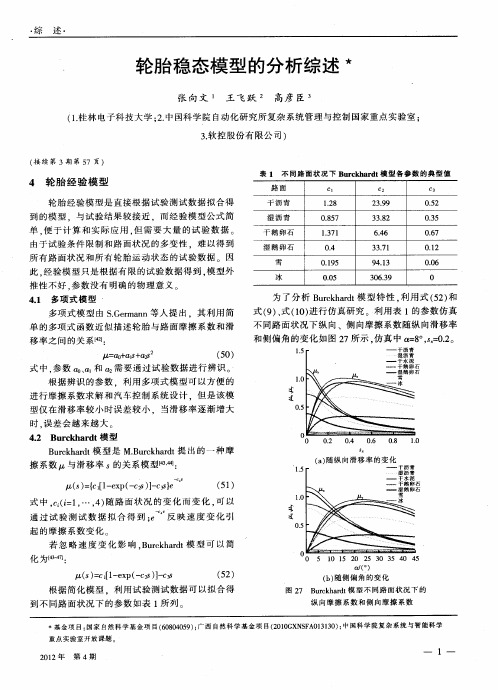
·综 述· 由图 27 可以看出，不同路面状况下纵向摩擦系
数和侧向摩擦系数不同， 因此 Burckhardt 模型可以 反映这二者在不同路面状况下的变化。
仿真得到不同侧偏角下纵向摩擦系数随纵向滑 移率的变化如图 28a 所示， 不同纵向滑移率下侧向 摩擦系数随侧偏角的变化如图 28b 所示， 仿真参数 c1=1.28，c2=23.99，c3=0.52，c4=0.01，v=10 m/s。
图 30 K-D 模型不同路面状况下的纵向摩擦系数
和侧向摩擦系数
2012 年 第 4 期
由图 30 可以看出，不同路面状况下的纵向摩擦
系数和侧向摩擦系数不同， 因此，K-D 模型可以反
映不同路面状况下纵向摩擦系数和侧向摩擦系数的
变化。
仿真得到不同侧偏角下纵向摩擦系数随纵向滑
移率的变化如图 31a 所示， 不同纵向滑移率下侧向
（a）随 纵 向 滑 移 率 的 变 化
1.2
v=5 m/s
1.0
μx
μy
v=10 m/s v=20 m/s v=30 m/s
0.8
μx、μy
0.6
0.4
0.2
0 0 5 10 15 20 25 30 35 40 45 α/（°） （b）随 侧 偏 角 的 变 化
图 29 Burckhardt 模型不同速度下的纵向摩擦系数
μx
1.2
α=5° α=10°
α=20°
1.0
α=30° α=40°
0.8
α=45°
0.6
0.4
0.2
0 0 0.2 0.4 0.6 0.8 1.0 sx
（a）随 纵 向 滑 移 率 的 变 化
1.2
sx=0.1 sx=0.2
sx=0.4
1.0
sx=0.6
sx=0.8
0.8
sx=0.9
μy
0.6
0.4
式中，参数 k1、k2、k3 随路面状况的变化而变化。
根据试验测试数据拟合得到不同路面状况下的
参数典型值如表 2 所列。
表 2 不同路面状况下 K-D 模型各参数的典型值
路面
k1
k2
干沥青
10.51
34.6
湿沥青
18.34
58.42
干鹅卵石
14.54
6.25
湿鹅卵石
58.23
51.01
雪
118.34
不同路面状况下纵向、 侧向摩擦系数随纵向滑移率
和侧偏角的变化如图 27 所示，仿真中 α=8°，sx=0.2。
1.5
μy 1.0
μx
干沥青 湿沥青 干水泥 干鹅卵石 湿鹅卵石 雪 冰
μx、μy
0.5
0 0
1.5 1.0
0.2 0.4 0.6 0.8 1.0 sx
（a）随 纵 向 滑 移 率 的 变 化
路面
c1
c2
c3
干沥青
1.28
23.99
0.52
湿沥青
0.857
33.82
0.35
干鹅卵石
1.371
6.46
0.67
湿鹅卵石
0.4
33.71
0.12
雪
0.195
94.13
0.06
冰
0.05
306.39
0
为了分析 Burckhardt 模型特性，利用式（52）和
式（9）、式（10）进行仿真研究。 利用表 1 的参数仿真
·综 述·
高彦臣 3 （1.桂 林 电 子 科 技 大 学 ；2.中 国 科 学 院 自 动 化 研 究 所 复 杂 系 统 管 理 与 控 制 国 家 重 点 实 验 室 ；
3.软控股份有限公司）
（接续第 3 期第 57 页）
4 轮胎经验模型
轮胎经验模型是直接根据试验测试数据拟合得
胎摩擦特性估计和汽车控制系统的设计与仿真。
4.3 K-D 模型
K-D 模 型 是 U.Kiencke 和 A.Daiβ 提 出 的 一 种
摩擦系数 μ 与滑移率 s 的关系模型， 是为了克服
Burckhardt 模型的强非线性而利用了分式多项式函 数[47]：
μ（s）=
k3s 1+k1s+k2s2
（55）
LC 模型是张向文和王飞跃根据试验测试数据， 在综合比较大量拟合函数基础上提出的一种基于摩
擦系数 μ 与滑移率 s 的线性组合 （Linear Combination）模型，它克服了 Burckhardt 模型和 K-D 模型的 非线性，利用指数函数、对数函数和幂函数的线性组
—3—
·综 述· 合描述摩擦系数与滑移率之间关系[5]：
摩擦系数随侧偏角的变化如图 31b 所示， 仿真参数
k1=10.51，k2=34.6，k3=25。
1.0
0.8
0.6
α=5° α=10° α=20° α=30° α=40° α=45°
μx
0.4
0.2
0 0 0.2 0.4 0.6 0.8 1.0 sx
（a）随 纵 向 滑 移 率 的 变 化
1.0
sx=0.1 sx=0.2
Burckhardt 模型多应用于描述轮胎的纵向摩擦 特性， 根据汽车的测量信息进行未知参数的估计和
摩擦系数的求解，用于汽车控制系统的设计和仿真。
由于 Burckhardt 模型存在非线性函数， 参数辨 识 比 较 复 杂 ， 为 了 实 现 线 性 化 ， 文 献 [45] 提 出 了 一 种
修正模型：
和侧向摩擦系数
由图 29 可以看出， 纵向摩擦系数和侧向摩擦系 数都随速度的增大而减小，根据文献[55]~文献[57]的结 果可以认为纵向摩擦系数、 侧向摩擦系数在纵向滑移
率、侧偏角较小时随速度的增大而增大，在纵向滑移率
和侧偏角较大时随速度的增大而减小。 因此，Burck-
hardt 模型可以反映纵向摩擦系数、侧向摩擦系数在纵 向滑移率、侧偏角较大情况下随速度的动态变化。
277.81
冰
536.07
1 010.8
假定参数 k3=25，其它参数采用表 2 数值，仿真 得到不同路面状况下纵向摩擦系数、侧向摩擦系数
随纵向滑移率和侧偏角的变化如图 30 所示， 仿真
参数 α=8°，sx=0.2。
2.0
1.6
1.2 μy
μx
干沥青 湿沥青 干水泥 干鹅卵石 湿鹅卵石 雪 冰
μx、μy
系数随侧偏角的增大而增大， 达到最大值后逐渐
下降；当纵向滑移率较大时，侧向摩擦系数随侧偏
角 的 增 大 逐 渐 增 大 。 这 与 文 献[53]~文 献[55]的 理
论 和 试 验 分 析 结 果 一 致 ， 因 此 ，Burckhardt 模 型 可
以反映纵向摩擦系数、 侧向摩擦系数随纵向滑移