汇总小学数学奥数题 周长、面积.ppt
巧求周长奥数题三年级

巧求周长奥数题三年级摘要:一、巧求周长奥数题背景介绍1.奥数题的概念和作用2.巧求周长题目的特点二、三年级巧求周长奥数题解析1.题目描述2.解题思路分析3.解题步骤详解三、巧求周长奥数题训练方法1.理解题意,分析题目类型2.掌握解题思路和方法3.多做练习,提高解题速度和准确度四、对学生的启示和建议1.培养数学兴趣和自信心2.养成良好的学习习惯和方法3.注重基础知识的学习和巩固正文:一、巧求周长奥数题背景介绍奥数,即奥林匹克数学竞赛,是一种针对中小学生的数学竞赛。
它旨在选拔和培养具有数学天赋和兴趣的学生,激发他们对数学的热爱和探索精神。
奥数题目涵盖了丰富的数学知识,包括几何、代数、组合、数论等多个领域。
巧求周长题是奥数题中的一种,主要考察学生对周长概念的理解和计算能力。
二、三年级巧求周长奥数题解析题目描述:一个正方形的周长是24 厘米,请问它的面积是多少平方厘米?解题思路分析:解决这道题的关键是让学生理解正方形周长和面积的关系。
正方形的周长等于4 个边长之和,而正方形的面积等于一个边长的平方。
因此,要求正方形的面积,只需要将周长除以4,然后求平方即可。
解题步骤详解:1.计算正方形的边长:周长24 厘米÷ 4 = 6 厘米2.计算正方形的面积:边长6 厘米× 6 厘米= 36 平方厘米所以,这个正方形的面积是36 平方厘米。
三、巧求周长奥数题训练方法1.理解题意,分析题目类型:首先要让学生理解题目的意思,明确需要解决的问题。
然后分析题目类型,找出解题的关键点。
2.掌握解题思路和方法:针对不同类型的题目,要让学生学会运用相应的解题思路和方法。
例如,对于巧求周长题,要让学生掌握正方形、长方形、圆等常见图形的周长计算方法。
3.多做练习,提高解题速度和准确度:通过大量的练习,让学生熟练掌握各种题型的解题方法,提高解题速度和准确度。
四、对学生的启示和建议1.培养数学兴趣和自信心:鼓励学生积极参与数学学习,发现数学的魅力,培养对数学的兴趣和自信心。
三年面积应用题奥数题

三年面积应用题奥数题题目1一块长方形菜地,长18米,宽12米,它的面积是多少平方米?如果在菜地四周围上篱笆,篱笆长多少米?答案:面积=18×12=216(平方米);周长=(18+12)×2=60(米)解析:长方形面积=长×宽,周长=(长+宽)×2。
题目2一个正方形花坛的边长是15米,这个花坛的面积是多少平方米?答案:15×15=225(平方米)解析:正方形面积=边长×边长。
题目3一块长方形手帕的长是20厘米,宽是15厘米,它的面积是多少平方厘米?答案:20×15=300(平方厘米)解析:长方形面积=长×宽。
题目4一间教室的长是9米,宽是6米,要铺上面积是3平方分米的地砖,需要多少块?答案:教室面积=9×6=54(平方米)=5400平方分米,5400÷3=1800(块)解析:先算出教室面积,单位换算后除以地砖面积。
题目5有一块长方形果园,长300米,宽200米,这块果园的面积是多少公顷?答案:300×200=60000(平方米)=6公顷解析:1公顷=10000平方米。
题目6一个长方形的面积是48平方分米,长是8分米,宽是多少分米?答案:48÷8=6(分米)解析:宽=面积÷长。
题目7一块正方形菜地的面积是144平方米,它的边长是多少米?答案:因为12×12=144,所以边长是12米。
解析:通过试算找到两个相同数字相乘等于面积。
题目8一张长方形纸,长28厘米,宽15厘米,从这张纸上剪下一个最大的正方形,正方形的面积是多少?剩下部分的面积是多少?答案:正方形面积=15×15=225(平方厘米),剩下部分面积=(28-15)×15=195(平方厘米)解析:剪下的最大正方形边长等于长方形的宽。
题目9一个长方形的周长是40厘米,长是12厘米,它的面积是多少平方厘米?答案:宽=(40÷2-12)=8(厘米),面积=12×8=96(平方厘米)解析:先根据周长求出宽,再算面积。
五年级奥数题:图形与面积含详细答案汇总

五年级奥数题:图形与面积一、填空题(共10小题,每小题3分,满分30分)1.(3分)如图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是_________厘米.2.(3分)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一小方格的面积是1.那么7,2,1三个数字所占的面积之和是_________.3.(3分) 如图中每一小方格的面积都是1平方厘米,那么用粗线围成的图形面积是_________平方厘米.4.(3分)(2014•长沙模拟)如图的两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是_________平方厘米.5.(3分)在△ABC中,BD=2DC,AE=BE,已知△ABC的面积是18平方厘米,则四边形AEDC的面积等于_________平方厘米.6.(3分)如图是边长为4厘米的正方形,AE=5厘米、OB是_________厘米.7.(3分)如图正方形ABCD的边长是4厘米,CG是3厘米,长方形DEFG的长DG是5厘米,那么它的宽DE是_________厘米.8.(3分)如图,一个矩形被分成10个小矩形,其中有6个小矩形的面积如图所示,那么这个大矩形的面积是_________.9.(3分)如图,正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是_________.10.(3分) 图中的长方形的长和宽分别是6厘米和4厘米,阴影部分的总面积是10平方厘米,四边形ABCD的面积是_________平方厘米.二、解答题(共4小题,满分0分)11.图中正六边形ABCDEF的面积是54.AP=2PF,CQ=2BQ,求阴影四边形CEPQ的面积.12.如图,涂阴影部分的小正六角星形面积是16平方厘米.问:大正六角星形面积是多少平方厘米.13.一个周长是56厘米的大长方形,按图中(1)与(2)所示意那样,划分为四个小长方形.在(1)中小长方形面积的比是:A:B=1:2,B:C=1:2.而在(2)中相应的比例是A':B’=1:3,B’:C’=1:3.又知,长方形D'的宽减去D的宽所得到的差,与D’的长减去在D的长所得到的差之比为1:3.求大长方形的面积.14.(2012•武汉模拟)如图,已知CD=5,DE=7,EF=15,FG=6,直线AB将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG的面积是_________.2010年五年级奥数题:图形与面积(B)参考答案与试题解析一、填空题(共10小题,每小题3分,满分30分)1.(3分)如图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是170厘米.考点:巧算周长.分析:要求该图形的周长,先求出每个小正方形的面积,根据正方形的面积公式,得出小正方形的边长,然后先算出该图形的外周的长,因为内、外的长相等,再乘2即可得出结论.解答:解:400÷16=25(平方厘米),因为5×5=25(平方厘米),所以每个小正方形的边长为5厘米,周长为:(5×4+5×4+5×3+5×2+5×3+5)×2,=85×2,=170(厘米);答:它的周长是170厘米.点评:此类题解答的关键是先求出每个小正方形的面积,根据正方形的面积公式,得出小正方形的边长,进而算出该图形的外周的长,因为内、外的长相等,再乘2即可得出结论.2.(3分)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一小方格的面积是1.那么7,2,1三个数字所占的面积之和是25.考点:组合图形的面积.分析:此题需要进行图形分解:“7"分成一个长方形、一个等腰直角三角形、一个平行四边形;“2"分成一个梯形、一个平行四边形、一个长方形;“1”分成一个梯形和两个长方形.然后进行图形转换,依据题目条件即可求出结果.解答:解:“7”所占的面积和=+3+4=,“2”所占的面积和=3+4+3=10,“1”所占的面积和=+7=,那么7,2,1三个数字所占的面积之和=++10=25.故答案为:25.点评:此题关键是进行图形分解和转换.3.(3分)如图中每一小方格的面积都是1平方厘米,那么用粗线围成的图形面积是6。
小学数学奥数测试题巧求周长_人教版

2019年小学奥数几何专题——巧求周长1.求图中所有线段的总长(单位:厘米)2.如图所示,一个大长方形被三条线段分成了四个小长方形,各条线段长度见图(单位:厘米).求:图中所有长方形的周长之和.3.如图,正方形的边长为4,被分割成如下12个小长方形,求这12个小长方形的所有周长之和.4.如右图,正方形ABCD的边长是6厘米,过正方形内的任意两点画直线,可把正方形分成9个小长方形。
这9个小长方形的周长之和是多少厘米?5.下图表示一块地,四周都用篱笆围起来,转弯处都是直角.已知西边篱笆长17米,南边篱笆长23米.四周篱笆长多少米?6.右图的周长是多少分米?7.计算右边图形的周长(单位:厘米)。
8.下图是一个锯齿状的零件,每一个锯齿的两条线段都长2厘米,求这个零件的周长.9.下图中标出的数表示每边长,单位是厘米.它的周长是多少厘米?10.右图是由七个长5厘米、宽3厘米的相同长方形经过竖放、横放而成的图形.求这个图形的周长?11.一个周长是20厘米的正方形,剪下一个周长是6厘米的正方形,剩下的图形的周长是多少?(写出所有可能的结果)12.求下图的周长.13.如下图是某校的平面图,已知线段a=120米,b=130米,c=70米,d=60米,l =250米.杨老师每天早晨绕学校跑3圈,问每天跑多少米?14.下面两张图中,周长较大的是哪一个?15.如下图,正方形操场边长100米,一只蚂蚁沿甲地走了一圈,另一只蚂蚁沿乙地走了一圈,谁走的路长?它们各走了多少米?16.求右图所示图形的周长(单位:分米)17.如图是一个机器零件的侧面图,图中每一条最短线段长5厘米,这个零件高30厘米,求这个零件侧面的周长是多少厘米?18.下图是一面砖墙的平面图,每块砖长20厘米,高8厘米,像图中那样一层、二层…一共摆十层,求摆好后这十层砖墙的周长是多少?19.右图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是多少厘米?20.下图是由边长为1厘米的11个正方形堆成的“土”字图形.试求出其周长.21.图⑴、图⑵都是由完全相同的正方形拼成的,并且图⑴的周长是22厘米,那么图⑵的周长是多少厘米?22.边长是15厘米的3个正方形拼成一个长方形,这个长方形的周长是多少?23.用一块长8分米,宽4分米的长方形纸板与两块边长4分米的正方形纸板拼成一个正方形.拼成的正方形的周长是多少分米?24.两个大小相同的正方形拼成了一个长方形,长方形的周长比原来的两个正方形周长的和减少了6厘米,原来一个正方形的周长是多少厘米?25.右图中的阴影部分BCGF是正方形,线段FH长18厘米,线段AC长24厘米,则长方形ADHE的周长是多少厘米?26.如图,在长方形ABCD中,EFGH是正方形.已知10cmHC=,求长AF=,7cm方形ABCD的周长.27.如右图所示,在一个正方形内画中、小两个正方形,使三个正方形具有公共顶点,这样大正方形被分割成了正方形区域甲,和L形区域乙和丙.甲的周长为4厘米,乙的边长是甲的周长的1.5倍,丙的周长是乙的周长的1.5倍,那么丙的周长为多少厘米?EF长多少厘米?第1页/共7页28.用若干个边长都是2厘米的平行四边形与三角形(如右图)拼接成一个大的平行四边形,已知大平行四边形的周长是244厘米,那么平行四边形和三角形各有多少个?29.用若干个边长都是2厘米的平行四边形与三角形(如右图)拼接成一个大的平行四边形,已知大平行四边形的周长是236厘米,那么平行四边形和三角形各有多少个?30.有9个小长方形,它们的长和宽分别相等,用这9个小长方形拼成的大长方形(如图)的面积是45平方厘米,求这个大长方形的周长.31.右图的长方形被分割成5个正方形,已知原长方形的面积为120平方厘米,求原长方形的长与宽.32.冯大叔给儿子做玩具用8个一样大的小长方形拼图,拼出了如图甲、乙的两种图案:图案甲是一个正方形,图案乙是一个大的长方形;图案甲的中间留下了边长是2cm的正方形小洞.求小长方形的长和宽?甲乙33.用同样的长方形条砖,在一个盆的周围砌成一个正方形边框,如右图所示.已知外面大正方形的周长是264厘米,里面小正方形的面积是900平方厘米,每块长方形条砖的长是多少厘米,宽是多少厘米?34.将若干个边长为1的正六边形(即单位六边形)拼接起来,得到一个拼接图形,如图:周长=6 周长=10 周长=12 周长=14那么,要拼接成周长等于18的拼接图形,需要多少个单位六边形?画出对应的一种图形.第1页/共7页参考答案1.48【解析】要注意到,题目所求的是图中所有线段的总长,而图中的线段,并不仅仅是A 、BC 、CD 、DE 四段,还包括AC 、BE 等等,因此不能简单地将图中标示的线段长度进行求和.同时应该注意到,;BE ,等等.因此,为了计算图中所有线段的总长,需要先计算AB 、BC 、CD 、DE 这四条线段分别被累加了几次.这里,可以按照每条线段分别是由几部分组成的加以讨论:由1段组成的线段共有4条,即AB 、BC 、CD 、DE ,而求和过程中AB 、BC 、CD 、DE 这四条线段各被累加了1次.类似地考虑到,由2段组成的线段共有3条,求和过程中AB 、DE 各被累加了1次,BC 、CD 各被累加了2次.由3段组成的线段共有2条,求和过程中AB 、DE 各被累加了1次,BC 、CD 各被累加了2次.由4段组成的线段只有AE ,其中AB 、BC 、CD 、DE 各被计算了1次.综上所述,AB 、DE 各被计算了4次,BC 、CD 各被计算了6次.因而图中所有线段的总长度为:2.136【解析】类似于上题,题目中所说的长方形,并不只包括最小的几个长方形,因此需要先求出每条线段在求和过程中被累加了多少次.因为没从大长方形的长上找到一条线段,就能对应地找到大长方形内的一个长方形,所以可以利用上一个问题的结论来解决这个问题.当然,要考虑到,每个长方形都有两条长和两条宽,因此计算过程中应该注意不要漏算.先考虑大长方形的长上各边:应用上一道题目的结论,每条边上长为4、3、1、2的线段分别被计算了4、6、6、4次.然后再考虑大长方形的宽:因为共有个长方形,所以长度为2的宽被计算了次. 故总周长可以用下式计算得到:.3.56【解析】4445256⨯+⨯⨯=.4.72【解析】从总体考虑,在求这9个小长方形的周长之和时,AB 、BC 、CD 、DA 这四条边被用了1次,其余四条虚线被用了2次,所以9个小长方形的周长之和是:6462472⨯+⨯⨯=(厘米)。
六年级圆的周长奥数题

六年级圆的周长奥数题一、基础题型1. 一个圆的半径是3厘米,它的周长是多少厘米?- 解析:根据圆的周长公式C = 2π r(其中C表示周长,π通常取3.14,r为半径)。
当r = 3厘米时,C=2×3.14×3 = 18.84厘米。
2. 已知圆的直径是8分米,求这个圆的周长。
- 解析:因为圆的周长C=π d(d是直径),当d = 8分米时,C = 3.14×8=25.12分米。
3. 一个圆的半径扩大到原来的2倍,它的周长扩大到原来的几倍?- 解析:设原来圆的半径为r,则原来的周长C_1 = 2π r。
半径扩大2倍后变为2r,此时周长C_2=2π×(2r) = 4π r。
C_2div C_1=(4π r)div(2π r)=2,所以它的周长扩大到原来的2倍。
4. 有一个圆形花坛,半径是5米,在它的周围铺一条宽1米的小路,求小路的外沿周长是多少米?- 解析:小路的外沿半径为5 + 1=6米。
根据圆的周长公式C = 2π r,当r = 6米时,C=2×3.14×6 = 37.68米。
5. 一个半圆的直径是10厘米,求这个半圆的弧长(周长的一半)。
- 解析:圆的周长C=π d,半圆的弧长为(1)/(2)π d。
当d = 10厘米时,弧长=(1)/(2)×3.14×10 = 15.7厘米。
二、组合图形中的圆周长问题6. 正方形的边长为10厘米,在正方形内画一个最大的圆,求这个圆的周长。
- 解析:正方形内最大的圆的直径等于正方形的边长,即d = 10厘米。
根据圆的周长公式C=π d,C = 3.14×10 = 30.4厘米。
7. 长方形的长是12厘米,宽是8厘米,在长方形内画一个最大的半圆,求这个半圆的弧长。
- 解析:因为长方形的长是12厘米,宽是8厘米,所以这个半圆的直径最大为12厘米。
半圆的弧长=(1)/(2)π d=(1)/(2)×3.14×12 = 18.84厘米。
六年级上册奥数题圆的面积

小学六年级奥数教材课程圆的周长和面积一条线段绕着它固定的一端在平面内旋转一周,它的另一端在平面内画出一条封闭的曲线,这条封闭的曲线就是圆。
画圆时,固定的一点叫做圆心,从圆心到圆上任意一点的线段叫做圆的半径,在同一个圆中,所有的半径都相等。
通过圆心,并且两端在圆上的线段叫做直径。
在同一个圆中,所有的直径都相等,且等于半径的2倍。
圆心决定圆的位置,半径决定圆的大小。
任意一个圆,它的周长除以直径的商总是一个固定的数,这个数叫圆周率。
如果用C 表示圆周的长度,d 表示这个圆的直径,r 表示它的半径,π表示圆周率,就有C dπ=或2C r。
π是一个无限不循环小数,π=3.14159265358979323846…。
圆的周长:C=2πr 或C=πd,圆的面积:S=πr 2。
圆的周长和面积计算的基本方法是仔细观察,发现特点,找出内在的联系,常常通过对图形的割补、旋转、平移、等积变形等方法加以解决。
需要精巧的构思和恰当的设计,把形象思维和抽象思维结合起来。
(本讲π均取 3.14)例1、上海外滩海关大钟钟面的直径是5.8米,钟面的面积是多少平方米?时针长2.7米,时针绕一圈时针尖端走过途径的长度是多少米?(得数保留一位小数)分析与解法:钟面的直径是5.8米这个条件是直接的,时针长指的是半径。
解:钟面的面积是:3.14×(5.8×2)2≈26.4(平方米)。
时针绕一圈时针尖端走过途径的长度是:2×3.14×2.7≈17.0(米)。
例2、如图所示,试比较大圆的面积与阴影部分的面积、大圆的周长与阴影部分的周长。
图图(1)分析与解法:本题有两问,一是比较阴影部分面积与大圆的面积;二是比较阴影部分周长与大圆的周长。
为了考虑问题方便,我们把图经过割补成图(1),在图(1)中更容易看出大圆与小圆阴影部分的关系。
学习目标总结重点AOB解:先比较大圆面积与阴影部分的面积。
设大圆半径为r,则小圆半径为r,大圆面积为S 1=πr 2。
图形奥数题
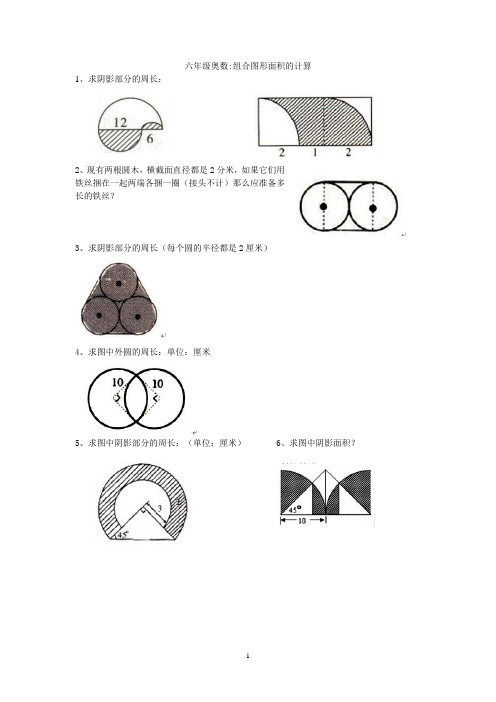
六年级奥数:组合图形面积的计算1、求阴影部分的周长:2、现有两根圆木,横截面直径都是2分米,如果它们用铁丝捆在一起两端各捆一圈(接头不计)那么应准备多长的铁丝?3、求阴影部分的周长(每个圆的半径都是2厘米)4、求图中外圆的周长:单位:厘米5、求图中阴影部分的周长:(单位:厘米)6、求图中阴影面积?7、已知阴影部分的面积是300平方厘米,求圆的面积。
8、图中阴影部分的面积是40平方厘米,求圆环的面积。
9、图中平行四边形的面积是100平方厘米,求阴影部分面积。
10、有一个半圆形零件,周长是20.56厘米,求这个半圆形零件的面积。
12、图中三角形ABC的边长为6厘米的正三角形,求阴影部分面积13、计算阴影部分面积。
(单位:厘米)14、求图中正方形面积与圆的面积之比15、图中圆的面积是942平方分米,那么正方形的面积是多少?如果正方形的面积是360平方厘米,那么圆的面积是多少?16、求图中阴影面积(单位:厘米) 17、求图中阴影面积(单位:厘米)18、求图中阴影面积(单位:厘米)19、如图,图中圆的直径AB是4厘米,平行四边形ABCD的面积是7平方厘米。
∠ABC=30º,求图中阴影面积(得数保留两位小数)20、如图:三角形ABC的面积是31.2平方厘米,圆的直径AC=6厘米,BD:DC=3:1,求图中阴影面积?21、在直角三角形ABC中,AB=6cm,BC=8cm,AB⊥BC。
分别是两条直角边的中点为圆心,以边长一半为半径画两个半圆交斜边与D,求图中的阴影面积?22、一个大圆内有3个大小不等的小圆(如图),这些小圆的圆心在大圆的同一直径上,连同大圆在内,每相邻的两个圆相切,已知大圆的周长是20厘米,求这2个小圆的周长之和是多少?23、大雪后的早晨,军军和爸爸踏着积雪,一前一后沿着一个圆形水池从同一起点朝同一方向跑步锻炼。
爸爸每步跑50CM,军军每步跑30CM,雪地上的脚印有时重合,跑完一圈,共留下1099个脚印。
小学数学奥数题 周长、面积培训资料共63页文档

39、勿问成功的秘诀为何,且尽全力做你应该做的事吧。——美华纳
ห้องสมุดไป่ตู้
40、学而不思则罔,思而不学则殆。——孔子
1、不要轻言放弃,否则对不起自己。
2、要冒一次险!整个生命就是一场冒险。走得最远的人,常是愿意 去做,并愿意去冒险的人。“稳妥”之船,从未能从岸边走远。-戴尔.卡耐基。
梦 境
3、人生就像一杯没有加糖的咖啡,喝起来是苦涩的,回味起来却有 久久不会退去的余香。
小学数学奥数题 周长、面积培训资料 4、守业的最好办法就是不断的发展。 5、当爱不能完美,我宁愿选择无悔,不管来生多么美丽,我不愿失 去今生对你的记忆,我不求天长地久的美景,我只要生生世世的轮 回里有你。
谢谢!
36、自己的鞋子,自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢,但是我从不后退。——亚伯拉罕·林肯
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
..。..
17
分析: 因为三角形EFD的面积比三角形 ABF的面积大6平方厘米,所以,三角形 BCE的面积比长方形ABCD的面积大6平方 厘米。三角形BCE的面积是6×4+6=30平 方厘米,EC的长则是30×2÷6=10厘米。 因此,ED的长是10-4=6厘米。
第9讲 周长、面积、体 积、表面积
梁碧湘
..。..
1
第一节 巧求周长
专题简析:
对于一些不规则的比较复杂的几何图形, 要求它们的周长,我们可以运用平移的方法, 把它转化为标准的长方形或正方形,然后再利 用周长公式进行计算。
将一个大长方形或正方形分割成若干个长方 形和正方形,那么图形周长就会增加几个长或 宽;反之,将若干个小长方形或正方形合成一 个大长方形或正方形,图形周长就会减少几个 长或宽。
是正方形,已知三角形AFH的面积是
7平方厘米。三角形CDH的面积是多少 平方厘米?
..。..
13
分析 : 设大正方形的边长是a,小正方
形的边长是b。
(1)梯形EFAD的面积是(a+b) ×b÷2,三角形EFC的面积也是 (a+b)×b÷2。所以,两者的面积 相等。
(2)因为三角形AFH的面积=梯形
底FD的长度。连接FC后就能得到一个三角 形EFC,用三角形EBC的面积减去三角形 FBC的面积就能得到三角形EFC的面积: 8×20÷2-8×8÷2=48平方厘米。 FD=48×2÷20=4.8厘米,所求梯形的面积 就是(4.8+8)×8÷2=51.2平方厘米。
..。..
16
例5 图中ABCD是长方形,长为6,宽为4,
..。..
23
例题4 : 在三角形ABC中,DC=2BD, CE=3AE,阴影部分的面积是20平方 厘米,求三角形ABC的面积。
..。..
24
分析
(1)因为CE=3AE,所以,三角形ADC的面 积是三角形ADE面积的4倍,是20×(1+3) =80平方厘为;
(2)又因为DC=2BD,所以,三角形ABD 的面积是三角形ADC面积的一半,是 80÷2=40平方厘米。因此,三角形ABC的 面积是80+40=120平方厘主。
..。..
2
例题1 : 下图是一个楼梯的侧面图,求此图 形的周长。
2米
3米
..。..
3
2米
3米
..。..
4
例题2 :下图是由6个边长2厘米的正方形拼 成的,这个图形的周长是多少厘米?
..。..
5
分析:这题我们可以用平移的方法将它转化 为一个长方形,如下图:
..。..
6
例题3 : 两个大小相同的正方形拼成一个 长方形后,周长比原来两个正方形周长的和减 少了6厘米。原来一个正方形的周长是多少厘?
叠组合。要正确解答组合图形的面积,应该注意以下 几点:
1,切实掌握有关简单图形的概念、公式,牢固建立空 间观念;
2,仔细观察,认真思考,看清所求图形是由哪几个基 本图形组合而成的;
3,适当采用增加辅助线等方法帮助解题;
4,采用割、补、分解、代换等方法,可将复杂问题变
得简单。
..。..
10
例1 : 一个等腰直角三角形,最长 的边是12厘米,这个三角形的面积 是多少平方厘米?
EFAD的面积-梯形EFHD的面积,而
三角形CDH的面积=三角形EFC的面积
-梯形EFHD的面积,所以,三角形
CDH的面积与三角形AFH的面积相等,
也是7平方厘米。 ..。..
14
例4 下图中正方形的边长为8厘米,CE为20 厘米,梯形BCDF的面积是多少平方厘米?
..。..
15
分析 :要求梯形的面积,关键是要求出上
三角形。已知两个三角形的面积(如图所示), 求另两个三角形的面积各是多少?(单位:
平方厘米)
..。..
22
分析:
1,因为三角形ABD与三角形ACD等底等高, 所以面积相等。因此,三角形ABO的面积 和三角形DOC的面积相等,也是6平方厘米。
2,因为三角形BOC的面积是三角形DOC面 积的2倍,所以BO的长度是OD的2倍,即 三角形ABO的面积也是三角形AOD的2倍。 所以,三角形AOD的面积是6÷2=3平方厘 米。
..。..
18
组合图形的面积(二)
专题简析: 在组合图形中,三角形的面积出现的机会很多,
解题时我们还可以记住下面三点: 1,两个三角形等底、等高,其面积相等; 2,两个三角形底相等,高成倍数关系,面积也
成倍数关系; 3,两个三角形高相等,底成倍数关系,面积也
成倍数关系。
..。..
19
例题2 下图中,边长为10和15的两个正方体 并放在一起,求三角形ABC(阴影部分)的 面积。
.36厘米的正方形 纸,剪成4个完全一样的小正方形纸片, 这4个小正方形周长的和比原来的正方 形周长增加了多少厘米?
..。..
8
..。..
9
第二节 组合图形的面积
第一专题简析:
组合图形是由两个或两个以上的简单的几何图形组合而 成的。组合的形式分为两种:一是拼合组合,二是重
..。..
20
分析 三角形ADC的面积是10×15÷2=75, 而三角形ABC的高是三角形BCD高的 15÷10=1.5倍,它们都以BC为边为底,所 以,三角形ABC的面积是三角形BCD的1.5 倍。阴影部分的面积是:7.5÷(1+1.5) ×1.5=45。
..。..
21
例题3 : 两条对角线把梯形ABCD分割成四个
..。..
25
复杂面积问题
专题简析:
解答有关“图形面积”问题时,应注意以下 几点:
1,细心观察,把握图形特点,合理地进行切 拼,从而使问题得以顺利地解决;
2,从整体上观察图形特征,掌握图形本质, 结合必要的分析推理和计算,使隐蔽的数 量关系明朗化。
..。..
26
例4:街心花园中一个正方形的花坛四 周有1米宽的水泥路,如果水泥路的总 面积是12平方米,中间花坛的面积是 多少平方米?
..。..
11
分析与解答 : 由于此三角形中只知道最长的 边是12厘米,所以,不能用三角形的面积公式 来计算它的面积。我们可以假设有4个这样的 三角形,且拼成了下图正方形。显然,这个正 方形的面积是12×12,那么,一个三角形的 面积就是12×12÷4=36平方厘米。
..。..
12
例3: 四边形ABCD和四边形DEFG都
