不同本构关系对混凝土受压截面承载力的对比分析
本构关系

④其它力学理论类模型。 (非弹性模型) 各类本构模型的理论基础、观点和方法迥异,表达形式多样, 简繁相差悬殊,适用范围和计算结果的差别大。很难确认一个 通用的混凝土本构模型,只能根据结构的特点、应力范围和精 度要求等加以适当选择。至今,实际工程中应用最明和使用方便的非线弹性 类本构模型。
1、各向同性本构模型
结构中的任何一点,共有6个独立的应力分量: 即正应力σ11、 σ22 、 σ33 剪应力τ12=τ21、 τ23=τ32 、 τ31=τ13 。 相应地也有6个应变分量: 为正应变ε11、 ε22 、 ε33 剪应变γ12=γ21、 γ23=γ32 、 γ31=γ13 假设材料的各方向同性、有相等的弹性常数,即可建立正应 力-正应变和剪应力-剪应变之间的关系如下:
所以,钢筋混凝土非线性本构关系的内容非常丰富,试验和 理论研究也有一定难度。经过各国研究人员的多年努力,本构 关系的研究已在宽广的领域内取得了大量成果,其中比较重要 和常用的本构关系有: ◆混凝土的单轴受压和受拉应力-应变关系;
◆混凝土的多轴强度(破坏准则)和应力-应变关系;
◆多种环境和受力条件下的混凝土应力-应变关系,包括受压 卸载和再加载,压拉反复加卸载,多次重复荷载(疲劳), 快速(毫秒或微秒级)加载和变形,高温(>l00oC)和低温 <0oC)状况下的加卸载,……;
4.8.2非线性分析中的各种本构关系
结构分析时,无论采用解析法和有限元法都要将整体结构离 散化、分解成各种计算单元。例如二、三维结构的解析法取为 二维或三维应力状态的点(微体),有限元法取为形状和尺寸 不同的块体;杆系结构可取为各杆件的截面、或其一段、或全 长;结构整体分析可取其局部,如高层建筑的一层作为基本计 算单元。因此,本构关系可建立在结构的不同层次和分析尺度 上.当然最基本的是材料一点的应力-应变关系,由此决定或推 导其他各种本构关系。 各种计算单元的本构关系一般是以标准条件下,即常温下短 时一次加载试验的测定值为基础确定的。当结构的环境和受力 条件有变化时,如反复加卸载、动载、荷载长期作用或高速冲 击作用、高温或低温状况、……等,混凝土的性能和本构关系随 之有不同程度的变化、必须进行相应修正,甚至重新建立专门 的本构关系。
混凝土承载力计算方法的比较分析

混凝土承载力计算方法的比较分析一、引言混凝土承载力计算是土木工程中非常重要的一项计算工作,它是评估结构安全性能的基础。
在土木工程中,混凝土承载力计算方法有多种,每种方法都有其独特的优点和适用范围。
本文将比较分析几种常见的混凝土承载力计算方法,以期为相关从业人员提供参考。
二、混凝土承载力计算方法比较1.极限状态设计法极限状态设计法是混凝土承载力计算方法中最常用的一种方法。
其计算原理是在计算承载力时考虑结构的强度、刚度和稳定性等因素,以满足建筑物在极限荷载作用下的安全性要求。
极限状态设计法的优点是计算方法简便、计算结果可靠,适用于大多数混凝土结构和荷载情况,但需要对荷载、强度和刚度等影响因素进行合理的假设和分析。
2.变形控制设计法变形控制设计法是在计算混凝土承载力时,强调结构在荷载作用下的变形控制能力,即以结构变形为设计控制要素的一种设计方法。
该方法的优点是可以有效地控制结构的变形,提高结构的抗震性能和耐久性,适用于抗震要求较高的建筑物和桥梁等工程。
但该方法需要考虑结构的刚度和变形限制等因素,计算方法相对较复杂。
3.极限状态限制设计法极限状态限制设计法是在极限状态设计法的基础上,增加了结构变形的限制条件,以确保结构在极限荷载作用下的安全性和稳定性。
该方法的优点是可以有效地控制结构的变形,提高抗震性能和耐久性,适用于抗震要求较高的建筑物和桥梁等工程。
但该方法计算过程较为复杂,需要考虑多个变形限制条件,容易出现误差。
4.弹塑性分析法弹塑性分析法是一种以结构弹塑性为基础的计算方法,其计算过程包括弹性分析和塑性分析两个阶段。
该方法的优点是可以考虑结构在荷载作用下的变形和破坏过程,具有较高的精度和可靠性,适用于复杂结构和特殊荷载情况。
但该方法计算过程较为繁琐,需要考虑多个影响因素,计算成本较高。
5.极限承载能力设计法极限承载能力设计法是一种以结构极限承载能力为基础的计算方法,其计算过程包括承载力计算和极限状态检验两个阶段。
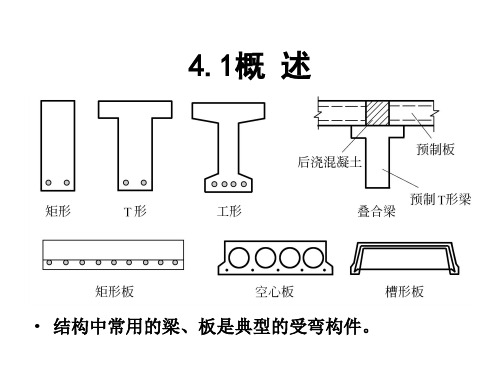
混凝土受弯构件正截面承载力计算
r As f y As a1 fcbx x a1 fc
bh0 bh0 f y bh0 f y h0 f y
令
x
h0
则
r
a1 fc
fy
令b为 = r max时的相对受压区高度,即
rmax
b
a1
f
fc
y
= r max时的破坏形态为受压区边缘混凝土达到极限压
c fc e0 e ecu
n
2
1 60
(
fcu,k
50)
2.0
各系数查表4-3
e0 0.002 0.5( fcu,k 50)105 0.002
ecu 0.0033 0.5( fcu,k 50)105 0.0033
4.钢筋应力—应变关系的假定(本构关系)
Ese e e y fy e ey
4.3钢筋混凝土受弯构件正截面试验研究
一、受弯构件正截面破坏过程
受弯构件正截面破坏分为三个阶段 • 第一阶段:裂缝开裂前 • 第二阶段:从开裂到钢筋屈服 • 第三阶段:从钢筋屈服到梁破坏
(1)第I阶段
当荷载比较小时,混凝土基本处 于弹性阶段,截面上应力分布为三 角形,荷载-挠度曲线或弯矩-曲率 曲线基本接近直线。截面抗弯刚度 较大,挠度和截面曲率很小,钢筋 的应力也很小,且都于弯矩近似成 正比。
My
Mu
Failure”,破坏前
可吸收较大的应变
能。
0
f
2.超筋梁(Over reinforced)破坏
钢筋配置过多,将发生这种破坏。 破坏特征:破坏时钢筋没有达到屈服强度,破坏是由 于压区混凝土被压碎引起,没有明显预兆,为脆性破 坏。
钢筋混凝土结构的本构关系及有限元模式共3篇

钢筋混凝土结构的本构关系及有限元模式共3篇钢筋混凝土结构的本构关系及有限元模式1钢筋混凝土结构的本构关系及有限元模式钢筋混凝土是建筑结构中广泛使用的材料之一。
在结构设计与分析过程中,了解钢筋混凝土的本构关系和有限元模式是十分重要的。
本文将从理论和实践两个层面介绍钢筋混凝土结构的本构关系及有限元模式。
一、理论基础1.1 本构关系本构关系是描述材料应力和应变之间关系的数学模型。
对于钢筋混凝土结构来说,其本构关系可以分为弹性和塑性两个阶段。
如图1所示,该曲线表现了材料的应变和应力之间的关系。
在开始阶段,钢筋混凝土材料表现出弹性行为,即在一定范围内,应变和应力呈线性关系,在这个范围内,应力的变化只取决于外力的变化。
当荷载增加时,材料进入塑性阶段,即出现残余变形,弹性不再适用。
此时,应变和应力的关系呈现非线性态势,应力会逐渐增大,直至材料失效。
图1 钢筋混凝土的本构关系曲线1.2 有限元分析有限元分析是一种近似解微分方程的数值分析方法。
该方法将问题分解成一个有限数量的小区域,在每个小区域内建立数学模型,通过连接小区域,组成总体的数学模型。
对于钢筋混凝土结构的有限元分析,可以采用三维有限元模型或二维\轴对称有限元模型等。
二、实践操作2.1 有限元模型的建立在进行有限元分析前,需要建立合适的有限元模型。
在钢筋混凝土结构的有限元分析中,通常采用ABAQUS、ANSYS软件进行模拟。
有限元模型的建立需要考虑结构的几何形状、材料特性、加载条件等,在模型建立的过程中需要进行模型分析和后处理,如应力监测、应变监测、变形量分析等。
2.2 本构关系的采用在建立有限元模型时需要设置材料弹性模量、泊松比、破坏应力等本构关系参数,这些参数可以通过试验数据和经验公式进行估算。
同时,基于实际结构的材料本身的特性和结构内力状态等影响因素,还需要考虑材料的非线性效应,包括弹塑性分析和的动力分析等。
三、应用现状在实际的建筑结构设计和分析中,钢筋混凝土结构的有限元分析被广泛采用,可以帮助工程师更加准确地预测材料的行为,并定位结构的破坏点及应急防御措施。
3种不同钢管混凝土本构关系模型研究

Research on three stress2stra in rela tion sh ips of concrete2f illed steel tube
WU W enp ing1 , HUAN G B ingsheng2 , FAN J ianhui2
(1. J iangsu Huning Steel M echanism Company L im ited, Yixing 214231, China; 2. College of Civil Engineering, Nanjing University of Technology, Nanjing 210009, China) Abstract: Three uniaxial stress2strain relationship s of concrete filled steel tube by Han linhai, Susantha and Saenz are introduced. According to the different concrete strength, p late radius2to2thickness (w idth2to2thickness) ratio, the uniaxial stress2strain relationship s of concrete2filled circular ( square) steel tube are analyzed and compared. The results show that steel tube p rovide a good confining effect to concrete when the radius2to2thickness (w idth2to2thickness) ratio is small, that is to say the concrete strength imp rove larger; the ductility and peak value of Saenz model show better than other models. Obviously, the confining effect to concrete of circular steel tube
不同本构模型的计算方法对地基承载力影响的研究

1 s i n e
上面的屈服准则是一种经过修正 的Mi s e s 屈服准则 ,它考虑 了静水应力
分量 的影 响 , 静水 应 力越 高 , 则 屈 服强 度 越 大 。 材 料 常数 的表 达式 如 下 :
即
p 。 : 4 3 ( 3
一
s i n e )
1 2 s i n 2  ̄  ̄
c
( 8)
对基 坑 围护 采用 同样 因素下 的计算 , 可得 到 如下计 算 结果
司
拐点。
, j j
从 上 图看 出粘 聚 力 c 和 内摩 擦 角 及 开 挖 深 度 对 地 基 承 载 力 有 很 大
主
3 . 对 比与 分析
( 4
、
O-
+
:
—
2 C c o s  ̄
( 0 J 4 )
s
材 料 的屈 服参 数 定 义为 :
。 : 4 3 ( 3
一
在单向压缩情况下ol =《 , o 2 = =0, 由式( 2 ) 得
2C c o s  ̄ b
d .: —
—
s i n e )
这 就是 根 据 Mo h r c o u l o m b 屈 服 准则 计算 出的 结果 , 作 者 力 求 在相 同 因素 下 进 行两 种 弹 塑性 模 型 的 对 比 与分 析 , 但 计 算结 果 仍 有 较 大 出入 ,分析 其 原 因 , 作 者 认 为 ,一 是 Mo h r ( 下转 g4 2 2  ̄)
在 对道 路进 行摊 铺 施工 措施 展 开之 前 , 其 车辆 自身 务必 要 保持 与 道 路 的 互相 平 行 , 同时 , 在摊 铺 机旁 边 还应 当有 清 洁工 和跟 车人 员 守候 待命 。 在 这一
混凝土抗压强度与抗剪强度的对比研究
混凝土抗压强度与抗剪强度的对比研究概述混凝土是一种广泛应用于建筑领域的材料。
其强度是评估混凝土质量的重要指标。
混凝土的抗压强度和抗剪强度是两个重要的强度参数。
本文将对混凝土抗压强度和抗剪强度进行对比研究,探讨它们之间的关系和差异。
混凝土抗压强度混凝土抗压强度是指混凝土在承受压力时的最大抵抗力。
它是评估混凝土质量的主要指标之一。
混凝土抗压强度受多种因素影响,包括混凝土配合比、水灰比、骨料种类和粒径等。
混凝土抗压强度的测试通常采用圆柱体试验。
在测试中,混凝土样品被放置在试验机中,施加压力,直至样品破裂。
测试结果以单位面积的压力值表示。
混凝土抗剪强度混凝土抗剪强度是指混凝土在承受剪切力时的最大抵抗力。
它是评估混凝土在承受横向力时的能力的主要指标之一。
混凝土抗剪强度受多种因素影响,包括混凝土配合比、水灰比、骨料种类和粒径等。
混凝土抗剪强度的测试通常采用剪切试验。
在测试中,混凝土样品被放置在试验机中,施加剪切力,直至样品破裂。
测试结果以单位面积的剪切力值表示。
混凝土抗压强度与抗剪强度的对比研究混凝土抗压强度和抗剪强度之间存在一定的关系和差异。
下面将从以下四个方面进行对比研究。
1. 影响因素混凝土抗压强度和抗剪强度受到的影响因素有很多相同之处,如混凝土配合比、水灰比、骨料种类和粒径等。
但是,混凝土抗剪强度还受到剪切面积的大小和形状的影响。
2. 测试方法混凝土抗压强度和抗剪强度的测试方法不同。
抗压强度的测试采用圆柱体试验,而抗剪强度的测试采用剪切试验。
由于测试方法的不同,两种强度参数的测试结果也不同。
3. 结果表示混凝土抗压强度的测试结果以单位面积的压力值表示,而抗剪强度的测试结果以单位面积的剪切力值表示。
由于测试结果的表示方式不同,两种强度参数的数值也不同。
4. 实际应用混凝土抗压强度和抗剪强度在实际应用中有不同的作用。
抗压强度是评估混凝土的承载能力和抗震能力的主要指标之一,而抗剪强度则是评估混凝土在承受横向力时的能力的主要指标之一。
混凝土的动力本构关系和破坏准则
混凝土的动力本构关系和破坏准则
混凝土是广泛应用于建筑和土木工程中的一种材料,其具有较高的强度、耐久性和施工方便等优点。
在研究混凝土力学性能时,混凝土的动力本构关系和破坏准则是一个重要的研究内容。
混凝土的动力本构关系是指混凝土在外力作用下的应力-应变关系。
在力学原理下,混凝土的的力学性质可以用应力应变曲线来表示。
混凝土在受到拉伸力时呈现出弹性行为,随着拉伸应力的增大,在达到一定应力时会出现应变加大的非线性行为,而在应力进一步增加时,会发生断裂。
而在受到压力时,混凝土呈现出弹性行为,并在达到最大强度后发生压缩破坏。
混凝土的动力本构关系可以用材料力学模型来描述。
目前常用的混凝土本构模型有弹性模型、塑性模型和强度与裂缝模型。
弹性模型是一种最简单的模型,它假设混凝土在受力时呈现出线弹性行为,并可以根据杨氏模量和泊松比来计算混凝土的应力和应变关系。
附加的弹塑性本构模型可以模拟混凝土的非线性行为,例如模拟混凝土在受力后出现的裂缝发展和非均匀变形等。
混凝土的破坏准则是指混凝土在应力达到一定临界值时发生破坏的判据。
破坏准则可以分为强度准则和能量准则两种类型。
强度准则是指在达到一定应力时,混凝土产生破坏。
常见的破坏准则有最大正应力准则、最大剪应力准则等。
能量准则是基于变形能或位能的原理,用来描述混凝土破坏的稳定性和可靠性。
常见的能量准则有极大能量释放准则、变形能准则等。
总结起来,混凝土的动态本构关系和破坏准则对于混凝土结构的设计和分析至关重要。
不同的本构模型和破坏准则可以更准确地描述混凝土的力学行为和破坏模式,帮助提高混凝土结构的设计和施工质量。
钢筋混凝土柱的受压承载力研究
钢筋混凝土柱的受压承载力研究一、引言钢筋混凝土柱是建筑结构中最常用的承重构件之一,其受压承载力是保证结构安全稳定的重要参数。
因此,对钢筋混凝土柱的受压承载力进行研究具有重要的理论和实用价值。
二、受力分析钢筋混凝土柱受力分析涉及到材料力学、结构力学等多个学科的知识,其中最基本的是静力学的知识。
在受力分析中,首先需要确定钢筋混凝土柱的截面形状、尺寸和材料性质等参数,并分析柱子受到的荷载类型和大小。
然后,根据静力平衡原理和材料力学的基本原理,建立柱子的受力模型,并计算柱子的受力状态。
在受力分析中,还需要考虑到一些特殊情况,比如柱子可能出现的屈曲、裂缝等问题,这些问题对柱子的受压承载力具有重要的影响。
三、影响受压承载力的因素钢筋混凝土柱的受压承载力受到多个因素的影响,主要包括以下几个方面:1.柱子的截面形状和尺寸:柱子的截面形状和尺寸对其受压承载力具有很大的影响。
一般来说,柱子的截面越大,其受压承载力也越大。
此外,柱子的截面形状也会影响其受压承载力,圆形截面的柱子比矩形截面的柱子具有更好的受压承载能力。
2.混凝土的强度:混凝土的强度是影响柱子受压承载力的重要因素之一。
混凝土的强度越高,其受压承载力也越大。
3.钢筋的强度和数量:钢筋是增强混凝土抗拉强度的重要材料,对柱子的受压承载力也有很大的影响。
一般来说,钢筋的强度越高,数量越多,柱子的受压承载力也越大。
4.柱子的长细比:柱子的长细比是指柱子的长度与截面尺寸之比。
当柱子的长细比超过一定值时,柱子容易出现屈曲,从而降低了其受压承载力。
5.荷载类型和大小:荷载类型和大小对柱子的受压承载力也有很大的影响。
不同类型的荷载对柱子的承载能力有不同的要求,而荷载大小也会影响柱子的受压承载力。
四、受压承载力的计算方法钢筋混凝土柱的受压承载力可以采用不同的计算方法,常用的有以下几种:1.按规范计算:根据国家规范中的公式和方法进行计算,是一种比较常用的方法。
2.试验方法:通过试验研究柱子的承载能力,可以得到柱子受压承载力的实际值。
混凝土构件的塑性承载能力研究
混凝土构件的塑性承载能力研究一、研究背景混凝土结构作为建筑中常用的结构形式,具有良好的耐久性、稳定性和承载能力,在建筑领域得到广泛应用。
其承载能力的研究一直是结构工程领域的热点问题,其中混凝土构件的塑性承载能力是其中的重要部分。
因此,对混凝土构件的塑性承载能力进行系统研究,对于提高混凝土结构的安全性和经济性,具有重要意义。
二、混凝土构件的塑性承载能力1. 塑性极限塑性极限是指混凝土结构在受到外力作用时,经过一定的变形后,出现塑性破坏的最大承载能力。
混凝土构件的塑性极限与材料的本构关系、受力状态等因素有关。
2. 塑性强度塑性强度是指混凝土构件在达到塑性极限前的最大承载能力。
其计算方法可以采用材料力学中的极限分析法或弹塑性分析法。
3. 塑性变形能力塑性变形能力是指混凝土构件在达到塑性极限后,仍能够继续变形并承载一定的荷载能力。
其计算方法可以采用极限分析法或弹塑性分析法。
三、混凝土构件塑性承载能力的影响因素1. 混凝土的强度和本构关系混凝土的强度和本构关系对混凝土构件的塑性承载能力有较大影响。
一般情况下,混凝土的强度越高,塑性承载能力越大。
2. 断面形状和受力状态混凝土构件的断面形状和受力状态对其塑性承载能力也有很大的影响。
对于同一种混凝土,不同形状和不同受力状态的构件,其塑性承载能力也是不同的。
3. 钢筋的配筋形式和数量钢筋的配筋形式和数量对混凝土构件的塑性承载能力也有很大的影响。
一般情况下,钢筋的配筋越合理,其塑性承载能力也越大。
4. 加强措施加强措施是指在混凝土构件中添加加强材料或钢筋等措施。
这些措施可以有效提高混凝土构件的塑性承载能力。
四、混凝土构件塑性承载能力的计算方法1. 极限分析法极限分析法是一种基于极限状态设计理论的计算方法。
该方法通过对混凝土构件的受力状态进行分析,确定其最不利的受力状态,然后计算其承载能力。
该方法计算简便,但不考虑结构的变形和塑性变形能力等因素。
2. 弹塑性分析法弹塑性分析法是一种基于弹塑性理论的计算方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
总第280期 交通科技 Serial No. 2802017 1 Transportation Science &* Technology No. 1 Feb. 2017
DOI 10. 3963/j. issn. 1671-7570. 2017. 01. 038
不同本构关系对混凝土受压截面承载力的对比分析严琼建(武汉理工大学交通学院武汉430063)
摘要讨论了混凝土不同应力-应变关系的简化模型下,其受压截面承载力的区别。对典型化本 构模型、美国E. Hognestad模型、清华大学过镇海教授模型3种不同的本构关系模型分别在相对 应的3种规范下的等效计算进行对比分析并得出结论。结果显示,以典型化本构模型按我国《混 凝土结构设计规范KGB50010 — 2010)计算得到的承载力相对安全。关键词本构关系模型等效矩形承载能力
作为建筑领域应用最广泛的材料,混凝土的 力学性质主要取决于各个组成成分材料的性质、 各组成成分配合比例,以及其之间的相互作用等 因素,同时还取决于混凝土的生产工艺和使用时 周围的环境等诸多因素混凝土压弯构件受压截面受力分析主要取决 于受压区混凝土的本构关系,以及应力分布的简 化,而混凝土本构关系曲线非线性特性较强,为了 让计算变得简单,人们提出了很多应力-应变关系 的简化模型。目前,用作混凝土本构关系理论依 据的力学原理数不胜数,概括起来可分为以下4 种情况:①线弹性理论;②非线性理论;③塑性理 论;④其他理论,包括内时理论、断裂力学和损伤 力学等理论依据也被作为理论依据来建立应力_ 应变关系模型[3]。我国和欧洲混凝土协会采用的是典型化简化 模型,而美国通用的是由该国学者E. HognestacF 提出的简化模型,对此清华大学教授过镇海[5]也提 出一种简化模型,下文将作为对照一并讨论。通过 3种不同本构模型得到的应力分布的等效参数,在 此基础之上,选取《混凝土结构设计规范》 (GB50010 — 2010)和欧洲混凝土协会规范2种不同 规范所使用的典型化模型、美国E. Hognestad模型 建议规范所使用的模型和过镇海模型3种本构关 系模型分别进行对比分析,并得出结论。1压应力等效的基本假定1.1平截面假定混凝土构件主要以受压为主,在构件工作中,从荷载为〇开始到荷载不断增大至构件破坏为 止,这个工作过程中,混凝土各截面应变均能较好 符合平截面假定。那么对于受拉区来说,在裂缝 产生后,该处钢筋和相邻的混凝土接触处发生了 一定的相对滑移,因此,在这些裂缝产生的平面, 平截面假定是不完全符合的,但是不考虑单个截 面的应变,而是考虑其平均应变,综合前人研究可 以发现,这些裂缝处平均应变也能够较好符合平 截面假定。也就是说,平截面假定在这些区域也 是适用的[6]。1.2不考虑混凝土的抗拉强度
在压应力等效过程中,如果混凝土出现裂缝, 此时,受拉区的混凝土已失去抗拉能力停止工作, 失去抗拉能力,即使有一^小部分位于中和轴附近 的混凝土仍然承担着抗拉任务,因其抗拉力较小, 在计算中不予考虑[7]。1. 3材料应力应变物理关系
1.3.1钢筋应力-应变曲线
钢筋的本构关系一般采用理想弹塑性模型, 见图1。对于一般钢筋,斜线段为弹性阶段,最高 点对应的应力值为屈服强度ay,相应的应变为屈 服应变e y,斜线段的斜率表示钢筋弹性模量£ s, 直线段为塑性阶段,对应的最大应变为强化段开 始的应变ek[8]。
收稿日期:2016-11-03图1钢筋应力-应变曲线图2017年第1期严琼建:不同本构关系对混凝土受压截面承载力的对比分析129
其表达式为{〇s = (0 ^ £s ^ £y)1 C7s f5"y (S s £ y )1.3.2混凝土应力-应变曲线1)典型化模型。其本构关系曲线模式图见 图2。其表达式为〇〇(〇<£<£〇)— (7〇 (e〇 ^ ^ ecu )表达式中参数根据不同规范取值不同,2种规 范的差别将直接导致混凝土承载能力的不同。其/cu,k —50中,我国规范规定^60>£〇—0. 002 +〇• 5X (/cu,k — 50) X 10-5,eu = 0• 003 3 — 0• 5 X (/cu,k — 50) X10-5;欧洲规范规定 w = l. 4 + 23. 4X’90 — /cu,k、4 ,£〇 = [2 + 0. 085 X (;/cu,k-50)°-53 ] X ^90 —/cu,k100102. 6 + 35XC-100X10 —2)美国E. Hognestad模型。其本构关系曲 线模式图见图3。(7〇C7 = C7〇 ( 1 — 〇. 15(〇<£<£〇)(e〇 ^ ^ £cu)— e〇 /3)过镇海模型。其本构关系曲线见图4。其表达式为£ \ / £
〇〇\i-1) +e!
(〇<£<£〇)(£〇<£< £cu)以上3式中:分别为混凝土的应力与应 变;a。为最大抗压强度(一般取为混凝土抗压强 度设计值)。
2受压区混凝土承载力的计算2.1受压区的矩形等效在对混凝土受弯构件的受压区域正截面承载 力Mu进行计算的过程中,需要清楚地知道破坏 时混凝土的压应力分布情况,尤其是受压区混凝 土的压应力合力C及其作用位置%,见图5。
a)梁截面b)应变分布c)实际应 d)应力
力分布 分_图5受压区等效矩形图 2.2等效方法及结果
由平截面假定很容易得到混凝土受压区高度 •^二以。,同样,也可得到£八。=3^。,以及> = £。色、/^。根据上述矩形截面来推导破坏时受压 区混凝土的压应力合力C及其合力作用位置义 的表达式,下面将以第一种本构关系模型为例来 进行计算。受压区混凝土的应力-应变模型曲线分为2 段,计算时要对2段表达式分别积分,然后求和。 得出压应力合力C表示如下。Cj(e)bdy
po
J 0由上述可知e/po
fec/!〇
C =(7〇b
JL
.y〇
+ ddy + I (j〇 bAy’」 心0
^ i rech〇 )
办 + dy =1、
u。>
(J〇Sch〇b\^l ——合力作用点:
£〇
^CU ,
[\ho
y〇
cF(e)dydy
~C
e<2130严琼建:不同本构关系对混凝土受压截面承载力的对比分析2017年第1期
显而易见,在求应力合力C和合力作用点位 置&时相当麻烦,给后续计算带来了很大困难。 为了简化计算,在前人研究的基础上,用等效矩形 的方法可以使之变得简单。所谓等效矩形,即保 持原有压应力合力大小及其作用位置不变,用简 单易算的矩形混凝土压应力图来等效实际的混凝 土压应力分布图,见图6S等效后的压应力图则 由量纲的量参数和y确定为矩 形压应力图的应力与受压区混凝土最大压应力 ^的比值。在将难于计算的压应力等效成矩形 后,计算将变得非常简单,再求值中,只需要计算 量纲的量参数s在规范中,不同型号的混凝土均 有其对应的量纲的量参数,故查阅其值即可使用。
图6等效矩形压应力分布 则可得合力C和合力作用点位置&分别 (C = ya〇bx = ya〇b^x% = (Jo ^ch〇
根据等代原则:保持压应力C不变,合力作 用位置也保持不变,则根据上式求解含有未知数 和7的联立方程,可得到
以上是关于典型化模型等效矩形的讨论,接 下来讨论美国E. Hognestad模型和过镇海模型 对受压区混凝土应力分布图形的等效。对于美国E. Hognestad模型,其本构关系曲 线的下降段为直线段,计算过程与上述模型相似, 也需要分开积分求得压应力合力,即c=rvbdy +
〇01 一 0. 15^cu
(y〇b\^0
(2、 V31& )
[%ho(y〇b\
bcjdh,
1-0. 15e — e〇
^cu)^y
,37 31e〇、4〇 120ec,
yc =Sch〇 —'
a(e)bydy
~C
6A)同理可求得
57-7(^) +3^V£cu / £cu
111-31^cu
114-68 ^ + 141^-£cu \£cu
111 - 33^cu
1 /37 31 £〇 \
对于过镇海模型,相对较为复杂,其本构关系 曲线下降段为有理式,取£ = 0. 002,混凝土极限 应变£ = 0,003 8,可得C =bdy +
I%%I (Jo
--1 +-^ a / s
〇
L y〇
(JL]
\y〇 >+ (j〇 6
[%ho
s/0, 002~dy
0. 15!0. 002
1
0. 002
e
0. 823 Ab (7〇^ch〇yc = 0. 442 2«fc/z〇
引入和y,得ip= 0. 883 4
[y = 0.931 0
2.3承载力计算在受压弯的混凝土构件中,将受压截面的压 应力计算简化等效矩形之后,钢筋混凝土受压弯 时正截面承载力计算公式为Mu = CK yc = 0. 5y(j〇b[]2^c2hQ2
在对混凝土正截面承载能力计算后,针对以 上3种规范进行对比,结果见表1。
