模型预测控制快速求解算法
《模型预测控制算法研究及其在水泥回转窑中的应用》

《模型预测控制算法研究及其在水泥回转窑中的应用》篇一一、引言随着工业自动化和智能化的快速发展,模型预测控制(MPC)算法作为一种先进的控制技术,已在众多工业领域得到了广泛应用。
本文将详细研究模型预测控制算法的原理及其在水泥回转窑中的应用,以探讨其在实际生产中的优化效果。
二、模型预测控制算法研究1. 模型预测控制算法原理模型预测控制(MPC)是一种基于数学模型的先进控制方法,它通过对系统未来的行为进行预测,从而实现对系统的优化控制。
MPC算法主要包括预测模型、参考轨迹、滚动优化和反馈校正四个部分。
(1)预测模型:用于描述系统未来的动态行为,通常为线性时不变系统或非线性系统模型。
(2)参考轨迹:设定了系统期望的轨迹,用于指导系统的优化控制。
(3)滚动优化:在每个控制周期内,根据当前的状态和预测模型,计算出一个最优控制序列,以使系统的性能指标达到最优。
(4)反馈校正:根据实际系统的反馈信息,对预测模型进行校正,以提高预测的准确性。
2. 模型预测控制算法的特点模型预测控制算法具有以下特点:可处理约束问题、具有显式的控制策略、可适应时变系统和非线性系统等。
此外,MPC算法还可以与多种优化算法相结合,如线性规划、非线性规划等,以满足不同系统的需求。
三、水泥回转窑工艺及控制难题水泥回转窑是水泥生产过程中的关键设备,其工艺复杂、运行环境恶劣。
在生产过程中,需要控制的关键参数包括温度、压力、转速等。
然而,由于回转窑内物料流动的复杂性、热工过程的非线性以及外部干扰等因素的影响,使得回转窑的控制成为一个难题。
传统的控制方法往往难以满足生产要求,需要研究更先进的控制技术。
四、模型预测控制算法在水泥回转窑中的应用针对水泥回转窑的控制难题,本文将研究模型预测控制算法在水泥回转窑中的应用。
具体包括以下几个方面:1. 建立回转窑的数学模型:根据回转窑的工艺流程和实际运行数据,建立回转窑的数学模型,为MPC算法的应用提供基础。
2. 设计MPC控制器:根据回转窑的数学模型和实际控制要求,设计合适的MPC控制器,实现对回转窑的优化控制。
8讲 预测控制主要算法

令此误差最小,即令 e(P)=0,得最优控制律:
u(k ) a P [ y s (k ) y (k ) ( g P i g i )u(k i )]
1 i 1 N
(2-12)
g i 为系统第 P 步的阶跃响应值。这就是单值预测控 其中 a P i 1
P
制算法,对 SISO 系统, a P 为标量;对 MIMO 系统,在输入输出 维数均为 m 时, a P 为 m×m 阵,这时计算可得到一定的简化。
1. 模型预测 DMC 中的预测模型是用被控对象的单位阶跃响应来描述的。 当在系统的输入端加上一控制增量后,在各采样时刻 t T 、 2T 、…、 NT 分别可在系统的输出端测得一系列采样值,它们可 用动态系数 a1、a2、…、aN 来表示,这种用动态系数和输入量来 描述各个采样时刻的系统输出和输入关系的过程特性,就是被控 对象的非参数数学模型。
(2-7)
3. 最优控制 通常采用下述二次型指标函数:
J k E T QE U (k )T RU(k )
J k 为得到最优解,令 U 0 ,得:
U (k ) (G1 QG1 R) 1 G1 Q[Ys (k 1) G2U (k 1) He(k )]
T T
(2-8)
U (k ) [u(k ) u(k M 1)
U (k 1) [u(k 1) u(k 1 N )]T
g1 g g1 2 G1 g g M M 1 g P g P 1
0 g2 g g 1 G2 3 P M 1 g P 1 g i i 1 PM
6. 闭环系统特性 对式(2-11)作 Z 变换:
mpc控制算法

mpc控制算法模型预测控制(MPC)是一种可以用来控制复杂过程的算法。
它可以根据设定的控制参数来实时地调整过程参数,从而最大限度地达到控制系统预期的输出目标。
MPC算法是一种智能控制系统,它综合考虑影响现实系统的动态变化参数,而不仅仅是考虑其瞬时量。
MPC控制算法是一种能够预测未来状态的控制方法,它可以根据不同的模型参数和控制策略,模拟出影响系统性能的多种变量,并可以在这些变量的影响下实时调整系统状态,从而达到系统性能最优化的目的。
MPC控制算法是一种智能控制,其中包括优化技术(像线性规划)、数学建模、系统参数调节等多种技术。
MPC控制算法既可以应用于离散系统,也可以应用于持续系统。
它以模型预测为基础,通过计算来预测和控制系统的输出,从而达到最佳控制系统性能的目的。
MPC控制算法的主要步骤包括:建立模型、分析调节器的特性,定义控制变量;其次,根据前面步骤构建模型,并通过数值求解来测试模型准确性;最后,根据求解结果,调整调节器参数,实现系统的控制目标。
MPC控制算法的应用领域很广,主要包括机械系统控制、电力系统控制、运距控制、航迹跟踪控制、位置跟踪控制、多机协调控制、空间结构控制等。
例如,MPC控制算法可以用于电力系统的有功功率调节;也可以用于航迹跟踪控制,实现无人机根据预设路径自动跟踪;还可以应用于多机协调、空间结构控制等领域,从而达到最大效果。
由于MPC控制算法可以模拟不同的过程参数,实时调整系统状态,因此具有杰出的优势。
首先,MPC控制算法有效的降低了模型的不确定性,使得模型的性能更稳定;其次,MPC控制算法可以有效地处理参数模糊性和运算误差;第三,MPC控制算法具有良好的自动调节能力,可以有效地抵抗环境和过程中的变化;最后,MPC控制算法可以控制复杂并发过程,有效地实现最优化控制。
可以看出,MPC控制算法在智能控制领域具有重要的作用。
它无需过多的参数设置,能够根据不断变化的状态实现自动调节,而且可以有效地降低参数不确定性,有效地抵抗外部和过程变化,实现性能最优化。
汽车轨迹跟踪模型预测控制的加速求解方法
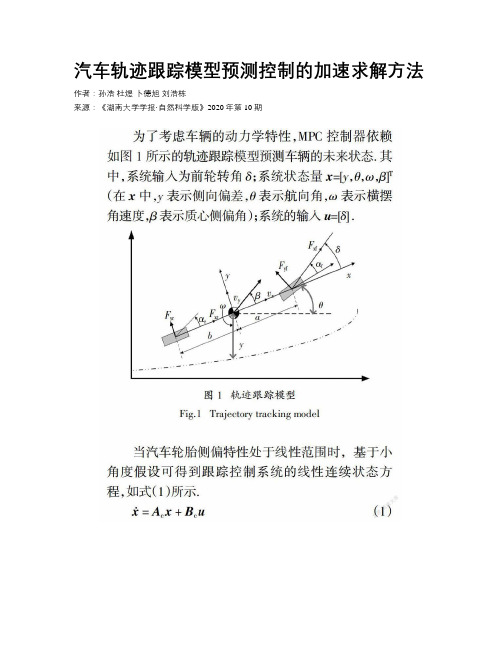
汽车轨迹跟踪模型预测控制的加速求解方法作者:孙浩杜煜卜德旭刘浩栋来源:《湖南大学学报·自然科学版》2020年第10期摘要:针对汽车轨迹跟踪模型预测控制求解中存在的规模较大、求解效率较低的问题,提出一种基于时域分解的加速计算方法提高求解效率. 首先引入全局一致性变量,将模型预测控制中邻接控制周期的时域耦合约束转化为全局一致性约束,实现时域解耦;随后在交叉方向乘子法框架下推导了时域分解后优化问题的分块更新方法,并设计了分块更新数值求解问题的停止准则,从而将大规模优化问题转化为小规模子问题;最后搭建了Simulink-CarSim平台进行了算法的仿真验证. 仿真结果表明,在求解精度不变的情况下,求解耗时下降24.21%,从而实现模型预测控制问题的加速求解.关键词:模型预测控制;自动驾驶汽车;轨迹跟踪;交叉方向乘子法;时域分解中图分类号:U461.99 文献标志码:AAccelerated Solution Method for Vehicle TrajectoryTracking Based on Model Predictive ControlSUN Hao1,2,DU Yu1,2†,BU Dexu3,LIU Haodong1,2(1. Beijing Key Laboratory of Information Service Engineering,Beijing Union University,Beijing 100101,China;2. College of Robotics,Beijing Union University,Beijing 100027,China;3. College of Traffic and Transportation Engineering,Central South University,Changsha 410076,China)Abstract:To solve the problems of large scale and low efficiency in the solution of intelligent vehicle trajectory tracking algorithm based on model predictive control,this paper proposes a time-domain splitting method to accelerate the calculation. First,global consistency variables are introduced to transform the time-domain coupling constraints of the adjacent control cycles into global consistency constraints,thus to achieve time-domain decoupling. Then,under the framework of Alternating Direction Method of Multipliers,the block updating method of optimization problem after time domain splitting is derived,and the stop criterion of block updating numerical solution is designed. Therefore,the large-scale optimization problem is converted into several small-scale sub-problems. Finally,the Simulink-CarSim platform is set up and the algorithm is verified by simulation. The simulation results show that,under the same accuracy of the solution,the efficiency of solution is improved by 24.21% on average with the proposed method,achieving accelerated solution for vehicle trajectory tracking based on model predictive control.Key words:model predictive control; autonomous vehicles; path tracking; alternating direction method of multipliers; time splitting自動驾驶汽车是提高交通系统安全、效率、经济等性能的有效途径,而轨迹跟踪是实现智能驾驶的核心技术之一[1],其目标是在满足汽车复杂动力学约束、行驶安全性约束前提下,以较小的偏差、较高的舒适性跟踪所规划的轨迹[2]. 模型预测控制(ModelPredictive Control,MPC)最早被应用在成本不敏感的大型工程中(如化工产业),并被认为是当年最具影响力的现代控制算法之一[3]. MPC通过引入参考模型,对约束的处理直接简单,不仅能够有效处理被控模型特性、约束带来影响,还能够通过滚动求解优化问题找到当前的最优控制量[4].基于上述优点,MPC在汽车轨迹跟踪问题的研究中得到国内外研究者的广泛关注.求解MPC问题的主流思路是将其转化为二次规划(Quadratic Programming,QP)问题. 其中,无约束MPC求解相对简单. Xu等以跟踪误差为性能指标实现AGV的轨迹跟踪控制[5],Shen等则建立了综合考虑跟踪精度和舒适性的目标函数[6],也有研究将输入量的边界建模为目标函数中代价值,构成“软约束”,但其数学原问题仍是无约束二次规划. 无约束二次规划问题可通过梯度下降等方法直接求解,但其局限在于仅考虑车辆的运动及动力学约束,没有考虑运动过程中所受到的其它约束,局限性较强. 因此,约束MPC更具备实际意义. 如Bo等建立了基于动力学的增量模型,考虑了执行机构的动力学特性约束[7]; Cai等则通过4自由度车辆模型加入车辆运动的侧翻约束,提高车辆跟踪控制的安全性[8]. 约束MPC的数学原问题是约束QP问题(MPC-QP问题),需要通过数值优化方法计算求解. 求解约束二次规划问题主要采用主动集法、内点法等方法,迭代次数较多. Wang和Boyd的研究表明,对于状态维数为m、控制输入维数为n、求解时域为T的MPC问题,状态转移形式及控制输入形式的MPC-QP问题求解的时间复杂度分别为O([T(n+m)]3)和O([Tn]3)[9]. 综上,虽然MPC在轨迹跟踪问题研究中得到广泛关注,但MPC-QP问题存在规模大、求解所需的浮点运算多、求解效率低的缺点,制约了MPC的性能. 因此,提高轨迹跟踪MPC问题的求解效率具有重要的意义.针对上述问题,本文提出一种加速求解方法以提高求解效率. 该方法通过交叉方向乘子法(Alternating Direction Method of Multipliers,ADMM)实现汽车轨迹跟踪问题的时域分解,将集中大规模的优化问题转为分块小规模优化问题,从而降低汽车轨迹跟踪MPC问题的时间复杂度,实现求解加速.1 模型预测控制问题的时域分解1.1 问题建模为了考虑车辆的动力学特性,MPC控制器依赖如图1所示的轨迹跟踪模型预测车辆的未来状态. 其中,系统输入为前轮转角δ;系统状态量x=[y,θ,ω,β]T(在x中,y表示侧向偏差,θ表示航向角,ω表示横摆角速度,β表示质心侧偏角);系统的输入u=[δ] .当汽车轮胎侧偏特性处于线性范围时,基于小角度假设可得到跟踪控制系统的线性连续状态方程,如式(1)所示.式(1)中各矩阵如式(2)所示. 其中,k1、k2分别为二自由度模型中车辆前、后轮等效侧偏刚度;a、b分别为二自由度模型中车辆直线到前、后轴的距离.那么,可得线性离散时间系统的狀态空间模型,如式(3)所示.x(k+1) = Ad x(k) + Bd u(k)(3)且连续与离散系统矩阵转换关系如式(4)所示,其中Ts为离散系统的采样时间.不失一般性,假设当前时刻系统状态为x0,根据离散系统的状态方程(3),在预测时域N内系统的输入与系统状态之间的转移关系如图 2所示,其中x∈Rm,u∈Rn.设离散时刻t下系统的参考状态为rt,那么综合考虑跟踪精度、舒适性的优化目标函数J 可用式(5)表示. 式中Q∈Rm × m、R∈Rn × n分别为状态变量、输入变量的权重对角矩阵.在轨迹跟踪问题中,代价函数越小越好. 对式(5)进行展开,轨迹跟踪的MPC问题可转化为如式(6)所示的约束二次规划问题. 在目标函数中,省略了不影响极值求解的常数项. 在约束条件中,(6a)表示汽车的动力学约束,(6b)表示不同时刻下状态变量及控制变量的可行域约束. 可以看出,虽然目标函数J在时域上解耦,但由于约束条件(6a)的存在(即t周期的终止状态为t+1周期的初始状态),并不能在求解过程中实现问题的分块解耦计算.1.2 时域分解为了实现问题的时域解耦,本文引入全局一致性变量,将汽车动力学带来的时域耦合约束转为全局一致性约束,从而实现问题的分块求解. 图 3为ADMM时域分解示意图.首先,以控制周期为单位对状态变量、控制变量进行分块表达. 对于所关注预测时域内的N个控制周期,按照次序给予编号1到N. 对于每个控制周期,该周期初始状态量、输入状态量和输出状态量可分别用x(t)t表达,其中上角标(t)表示为变量所属的分块编号,且块内变量之间的关系由汽车动力学特性决定,如式(7)所示:而块间关系由时域耦合约束决定,满足式(8):为解耦式(8)所示的时域耦合约束,引入全局一致性变量[z][~] = (z0,z1,…,zN)T ,并使x与z之间满足如式(9)所示的关系,其中:(9a)表示分块(t)的输入变量与zt-1的一致性约束;(9b)表示分块(t)的输出变量与zt的一致性约束.因此,联合式(7)~式(9),问题(6)可重写为如式(10)所示形式. 此时,邻接块之间不存在直接关系,其耦合约束通过一致性变量间接表达,从而实现控制周期之间时域解耦.2 分块求解方法2.1 问题求解综上所述,本文已经构建了MPC问题的时域分解范式,本节的工作则是基于ADMM求解时域分解后的问题. ADMM的标准构型如式(11)所示.为了方便地将式(10)转换为ADMM标准构型,引入块变量:[x][~]t = (x(t)求解MPC问题的主流思路是将其转化为二次规划(Quadratic Programming,QP)问题.其中,无约束MPC求解相对简单. Xu等以跟踪误差为性能指标实现AGV的轨迹跟踪控制[5],Shen等则建立了综合考虑跟踪精度和舒适性的目标函数[6],也有研究将输入量的边界建模为目标函数中代价值,构成“软约束”,但其数学原问题仍是无约束二次规划. 无约束二次规划问题可通过梯度下降等方法直接求解,但其局限在于仅考虑车辆的运动及动力学约束,没有考虑运动过程中所受到的其它约束,局限性较强. 因此,约束MPC更具备实际意义. 如Bo等建立了基于动力学的增量模型,考虑了执行机构的动力学特性约束[7]; Cai等则通过4自由度车辆模型加入车辆运动的侧翻约束,提高车辆跟踪控制的安全性[8]. 约束MPC的数学原问题是约束QP问题(MPC-QP问题),需要通过数值优化方法计算求解. 求解约束二次规划问题主要采用主动集法、内点法等方法,迭代次数较多. Wang和Boyd的研究表明,对于状态维数为m、控制输入维数为n、求解时域为T的MPC问题,状态转移形式及控制输入形式的MPC-QP问题求解的时间复杂度分别为O([T(n+m)]3)和O([Tn]3)[9]. 综上,虽然MPC在轨迹跟踪问题研究中得到广泛关注,但MPC-QP问题存在规模大、求解所需的浮点运算多、求解效率低的缺点,制约了MPC的性能. 因此,提高轨迹跟踪MPC问题的求解效率具有重要的意义.针对上述问题,本文提出一种加速求解方法以提高求解效率. 该方法通过交叉方向乘子法(Alternating Direction Method of Multipliers,ADMM)实现汽车轨迹跟踪问题的时域分解,将集中大规模的优化问题转为分块小规模优化问题,从而降低汽车轨迹跟踪MPC问题的时间复杂度,实现求解加速.1 模型预测控制问题的时域分解1.1 问题建模为了考虑车辆的动力学特性,MPC控制器依赖如图1所示的轨迹跟踪模型预测车辆的未来状态. 其中,系统输入为前轮转角δ;系统状态量x=[y,θ,ω,β]T(在x中,y表示侧向偏差,θ表示航向角,ω表示横摆角速度,β表示质心侧偏角);系统的输入u=[δ] .当汽车轮胎侧偏特性处于线性范围时,基于小角度假设可得到跟踪控制系统的线性连续状态方程,如式(1)所示.式(1)中各矩阵如式(2)所示. 其中,k1、k2分别为二自由度模型中车辆前、后轮等效侧偏刚度;a、b分别为二自由度模型中车辆直线到前、后轴的距离.那么,可得线性离散时间系统的状态空间模型,如式(3)所示.x(k+1) = Ad x(k) + Bd u(k)(3)且连续与离散系统矩阵转换关系如式(4)所示,其中Ts为离散系统的采样时间.不失一般性,假设当前时刻系统状态为x0,根据离散系统的状态方程(3),在预测时域N内系统的输入与系统状态之间的转移关系如图 2所示,其中x∈Rm,u∈Rn.設离散时刻t下系统的参考状态为rt,那么综合考虑跟踪精度、舒适性的优化目标函数J 可用式(5)表示. 式中Q∈Rm × m、R∈Rn × n分别为状态变量、输入变量的权重对角矩阵.在轨迹跟踪问题中,代价函数越小越好. 对式(5)进行展开,轨迹跟踪的MPC问题可转化为如式(6)所示的约束二次规划问题. 在目标函数中,省略了不影响极值求解的常数项. 在约束条件中,(6a)表示汽车的动力学约束,(6b)表示不同时刻下状态变量及控制变量的可行域约束. 可以看出,虽然目标函数J在时域上解耦,但由于约束条件(6a)的存在(即t周期的终止状态为t+1周期的初始状态),并不能在求解过程中实现问题的分块解耦计算.1.2 时域分解为了实现问题的时域解耦,本文引入全局一致性变量,将汽车动力学带来的时域耦合约束转为全局一致性约束,从而实现问题的分块求解. 图 3为ADMM时域分解示意图.首先,以控制周期为单位对状态变量、控制变量进行分块表达. 对于所关注预测时域内的N个控制周期,按照次序给予编号1到N. 对于每个控制周期,该周期初始状态量、输入状态量和输出状态量可分别用x(t)t表达,其中上角标(t)表示为变量所属的分块编号,且块内变量之间的关系由汽车动力学特性决定,如式(7)所示:而块间关系由时域耦合约束决定,满足式(8):为解耦式(8)所示的时域耦合约束,引入全局一致性变量[z][~] = (z0,z1,…,zN)T ,并使x与z之间满足如式(9)所示的关系,其中:(9a)表示分块(t)的输入变量与zt-1的一致性约束;(9b)表示分块(t)的输出变量与zt的一致性约束.因此,联合式(7)~式(9),问题(6)可重写为如式(10)所示形式. 此时,邻接块之间不存在直接关系,其耦合约束通过一致性变量间接表达,从而实现控制周期之间时域解耦.2 分块求解方法2.1 问题求解综上所述,本文已经构建了MPC问题的时域分解范式,本节的工作则是基于ADMM求解时域分解后的问题. ADMM的标准构型如式(11)所示.为了方便地将式(10)转换为ADMM标准构型,引入块变量:[x][~]t = (x(t)求解MPC问题的主流思路是将其转化为二次规划(Quadratic Programming,QP)问题.其中,无约束MPC求解相对简单. Xu等以跟踪误差为性能指标实现AGV的轨迹跟踪控制[5],Shen等则建立了综合考虑跟踪精度和舒适性的目标函数[6],也有研究将输入量的边界建模为目标函数中代价值,构成“软约束”,但其数学原问题仍是无约束二次规划. 无约束二次规划问题可通过梯度下降等方法直接求解,但其局限在于仅考虑车辆的运动及动力学约束,没有考虑运动过程中所受到的其它约束,局限性较强. 因此,约束MPC更具备实际意义. 如Bo等建立了基于动力学的增量模型,考虑了执行机构的动力学特性约束[7]; Cai等则通过4自由度车辆模型加入车辆运动的侧翻约束,提高车辆跟踪控制的安全性[8]. 约束MPC的数学原问题是约束QP问题(MPC-QP问题),需要通过数值优化方法计算求解. 求解约束二次规划问题主要采用主动集法、内点法等方法,迭代次數较多. Wang和Boyd的研究表明,对于状态维数为m、控制输入维数为n、求解时域为T的MPC问题,状态转移形式及控制输入形式的MPC-QP问题求解的时间复杂度分别为O([T(n+m)]3)和O([Tn]3)[9]. 综上,虽然MPC在轨迹跟踪问题研究中得到广泛关注,但MPC-QP问题存在规模大、求解所需的浮点运算多、求解效率低的缺点,制约了MPC的性能. 因此,提高轨迹跟踪MPC问题的求解效率具有重要的意义.针对上述问题,本文提出一种加速求解方法以提高求解效率. 该方法通过交叉方向乘子法(Alternating Direction Method of Multipliers,ADMM)实现汽车轨迹跟踪问题的时域分解,将集中大规模的优化问题转为分块小规模优化问题,从而降低汽车轨迹跟踪MPC问题的时间复杂度,实现求解加速.1 模型预测控制问题的时域分解1.1 问题建模为了考虑车辆的动力学特性,MPC控制器依赖如图1所示的轨迹跟踪模型预测车辆的未来状态. 其中,系统输入为前轮转角δ;系统状态量x=[y,θ,ω,β]T(在x中,y表示侧向偏差,θ表示航向角,ω表示横摆角速度,β表示质心侧偏角);系统的输入u=[δ] .当汽车轮胎侧偏特性处于线性范围时,基于小角度假设可得到跟踪控制系统的线性连续状态方程,如式(1)所示.式(1)中各矩阵如式(2)所示. 其中,k1、k2分别为二自由度模型中车辆前、后轮等效侧偏刚度;a、b分别为二自由度模型中车辆直线到前、后轴的距离.那么,可得线性离散时间系统的状态空间模型,如式(3)所示.x(k+1) = Ad x(k) + Bd u(k)(3)且连续与离散系统矩阵转换关系如式(4)所示,其中Ts为离散系统的采样时间.不失一般性,假设当前时刻系统状态为x0,根据离散系统的状态方程(3),在预测时域N内系统的输入与系统状态之间的转移关系如图 2所示,其中x∈Rm,u∈Rn.设离散时刻t下系统的参考状态为rt,那么综合考虑跟踪精度、舒适性的优化目标函数J 可用式(5)表示. 式中Q∈Rm × m、R∈Rn × n分别为状态变量、输入变量的权重对角矩阵.在轨迹跟踪问题中,代价函数越小越好. 对式(5)进行展开,轨迹跟踪的MPC问题可转化为如式(6)所示的约束二次规划问题. 在目标函数中,省略了不影响极值求解的常数项. 在约束条件中,(6a)表示汽车的动力学约束,(6b)表示不同时刻下状态变量及控制变量的可行域约束. 可以看出,虽然目标函数J在时域上解耦,但由于约束条件(6a)的存在(即t周期的终止状态为t+1周期的初始状态),并不能在求解过程中实现问题的分块解耦计算.1.2 时域分解为了实现问题的时域解耦,本文引入全局一致性变量,将汽车动力学带来的时域耦合约束转为全局一致性约束,从而实现问题的分块求解. 图 3为ADMM时域分解示意图.首先,以控制周期为单位对状态变量、控制变量进行分块表达. 对于所关注预测时域内的N个控制周期,按照次序给予编号1到N. 对于每个控制周期,该周期初始状态量、输入状态量和输出状态量可分别用x(t)t表达,其中上角标(t)表示为变量所属的分块编号,且块内变量之间的关系由汽车动力学特性决定,如式(7)所示:而块间关系由时域耦合约束决定,满足式(8):为解耦式(8)所示的时域耦合约束,引入全局一致性变量[z][~] = (z0,z1,…,zN)T ,并使x与z之间满足如式(9)所示的关系,其中:(9a)表示分块(t)的输入变量与zt-1的一致性约束;(9b)表示分块(t)的输出变量与zt的一致性约束.因此,联合式(7)~式(9),问题(6)可重写为如式(10)所示形式. 此时,邻接块之间不存在直接关系,其耦合约束通过一致性变量间接表达,从而实现控制周期之间时域解耦.2 分块求解方法2.1 问题求解综上所述,本文已经构建了MPC问题的时域分解范式,本节的工作则是基于ADMM求解时域分解后的问题. ADMM的标准构型如式(11)所示.为了方便地将式(10)转换为ADMM标准构型,引入块变量:[x][~]t = (x(t)。
制导与控制系统中的模型预测控制算法研究

制导与控制系统中的模型预测控制算法研究模型预测控制(Model Predictive Control,MPC)是一种先进的控制方法,被广泛应用于制导与控制系统中。
它基于数学模型对系统进行预测,并根据预测结果实时调节控制输入,以达到优化性能的目标。
本文将介绍模型预测控制算法在制导与控制系统中的应用,并着重探讨其研究进展和优势。
首先,我们需要了解制导与控制系统中的模型预测控制算法的基本原理。
它的核心思想是通过预测系统未来的状态和输出,来计算最优的控制输入。
具体而言,MPC通过建立数学模型来描述系统动力学,并将模型纳入优化问题中。
通过求解优化问题,找到最佳的控制输入序列,以最大化系统性能。
然后,根据优化结果中的第一个控制输入,进行实时调节。
这样,反复迭代执行,就实现了对系统的动态控制。
模型预测控制算法在制导与控制系统中的应用非常广泛。
它可以应用于各种领域,如工业过程控制、机器人控制、交通系统控制等。
在工业过程控制中,模型预测控制算法可以对复杂的生产过程进行优化控制,提高生产效率和产品质量。
在机器人控制中,MPC可以对机器人的路径规划和运动控制进行优化,实现更精确、更高效的运动控制。
在交通系统控制中,MPC可以对交通信号灯的灯相序列进行优化,减少交通拥堵和交通事故发生的可能性。
与传统的控制方法相比,模型预测控制算法具有一些明显的优势。
首先,MPC 可以处理非线性系统和具有约束的系统。
传统的线性控制方法往往无法应对非线性系统的复杂性和动态性,而MPC通过建立非线性模型,并将约束条件纳入优化问题,能够更好地应对非线性系统的控制问题。
其次,MPC能够在实时性和性能之间找到平衡。
MPC通过预测系统的未来行为,可以在满足系统性能要求的同时,考虑控制输入的变化范围,提供实时性和性能的平衡。
此外,MPC具有较好的鲁棒性和适应性,可以应对外部扰动和参数变化的影响。
近年来,模型预测控制算法在制导与控制系统中的研究取得了一系列重要的进展。
mpc快速求解方法

mpc快速求解方法
MPC(Model Predictive Control)是一种基于预测的控制算法,用于优化具有约束条件的非线性系统。
由于其计算复杂度较高,因此需要采用快速求解方法来提高计算效率。
以下是几种常用的MPC快速求解方法:
1. 块坐标下降法(Block Coordinate Descent):将多维的MPC问题分解为多个一维子问题,逐个求解每个子问题,从而降低计算复杂度。
2. 内点法(Interior Point Method):将MPC问题转化为一个二次规划问题,并使用内点法进行求解。
相比于传统的线性规划方法,内点法可以更好地处理约束条件,并且具有更快的收敛速度。
3. 序列二次规划(Sequential Quadratic Programming,SQP):将MPC问题转化为一个二次规划问题,并使用SQP方法进行求解。
SQP方法通过迭代优化当前时刻的二次规划子问题来逐步推进整个问题的求解过程,具有较高的计算效率和精度。
4. 蒙特卡洛模拟(Monte Carlo Simulation):对于一些复杂的MPC问题,可以通过蒙特卡洛模拟来进行快速求解。
该方法利用随机采样的思想,通过多次模拟来逼近真实的最优解,具有较好的鲁棒性和适应性。
以上是常用的MPC快速求解方法,不同的方法适用于不同类型的MPC问题,选择合适的方法可以提高计算效率和精度。
控制工程中的模型预测控制算法

控制工程中的模型预测控制算法随着工业化和数字化的高速发展,涉及自动化控制的应用越来越广泛,越来越深入。
不论是在实践中还是理论研究中,控制工程一直是一个备受关注的领域。
控制工程是研究如何在自动化装置中运用控制理论和技术对生产和生活中的控制问题进行分析、设计和实现的学科。
而控制算法作为控制工程的核心,尤其是模型预测控制算法,已经成为现代自动化控制中的重要技术手段之一。
模型预测控制算法(MPC)是一种基于模型的控制策略,通过将过程变量的状态预测与控制相结合,并对未来一段时间内的控制变量作出预测,最后对预测与实际变量进行比对,调整控制变量以达到最优控制目标。
MPC拥有突出的优点,如对控制变量作出预测、处理非线性、处理多变量等,使其在化工、石油、电子、材料、制造等领域具有广泛的应用。
MPC的实现MPC的实现同样是一个需要重视的问题。
对于MPC,其优化算法决定了控制系统的性能。
因此,MPC的实现过程中一个重要的考虑因素就是如何求解优化问题。
求解MPC中的优化问题可以采用数学优化算法,如线性规划、二次规划或非线性规划等。
而MPC的关键问题就是如何带约束的最优控制问题与上述数学方法相结合。
针对这个问题,MPC前瞻控制算法提供了一种有效的解决方案。
MPC前瞻控制算法MPC前瞻控制算法(MPC-PR)将数学优化算法与基于约束的控制(MPC)相结合,可轻松地解决MPC的实现问题。
对于复杂的物理系统,MPC-PR综合了高级预测模型、状态估计技术、多模型预测和优化控制算法,实现了一系列复杂动态约束的精确解决。
通过MPC-PR算法(如下图)的分层分解、扩展线性化和非线性规划,可以得到合适的状态估计和最优控制输入。
在任何时间点,该控制策略都能够考虑各种限制条件,并且考虑外部干扰、控制过程和多求解器并行处理等传统算法无法处理的约束条件。
MPC在工业领域的应用MPC在化工、石油、电子、材料、制造等领域的广泛应用,使它已成为工业制造领域中的重要技术手段之一。
模型预测控制快速求解算法

模型预测控制快速求解算法模型预测控制(Model Predictive Control,MPC)是一种基于在线计算的控制优化算法,能够统一处理带约束的多参数优化控制问题。
当被控对象结构和环境相对复杂时,模型预测控制需选择较大的预测时域和控制时域,因此大大增加了在线求解的计算时间,同时降低了控制效果。
从现有的算法来看,模型预测控制通常只适用于采样时间较大、动态过程变化较慢的系统中。
因此,研究快速模型预测控制算法具有一定的理论意义和应用价值。
虽然MPC方法为适应当今复杂的工业环境已经发展出各种智能预测控制方法,在工业领域中也得到了一定应用,但是算法的理论分析和实际应用之间仍然存在着一定差距,尤其在多输入多输出系统、非线性特性及参数时变的系统和结果不确定的系统中。
预测控制方法发展至今,仍然存在一些问题,具体如下:①模型难以建立。
模型是预测控制方法的基础,因此建立的模型越精确,预测控制效果越好。
尽管模型辨识技术已经在预测控制方法的建模过程中得以应用,但是仍无法建立非常精确的系统模型。
②在线计算过程不够优化。
预测控制方法的一大特征是在线优化,即根据系统当前状态、性能指标和约束条件进行在线计算得到当前状态的控制律。
在在线优化过程中,当前的优化算法主要有线性规划、二次规划和非线性规划等。
在线性系统中,预测控制的在线计算过程大多数采用二次规划方法进行求解,但若被控对象的输入输出个数较多或预测时域较大时,该优化方法的在线计算效率也会无法满足系统快速性需求。
而在非线性系统中,在线优化过程通常采用序列二次优化算法,但该方法的在线计算成本相对较高且不能完全保证系统稳定,因此也需要不断改进。
③误差问题。
由于系统建模往往不够精确,且被控系统中往往存在各种干扰,预测控制方法的预测值和实际值之间一定会产生误差。
虽然建模误差可以通过补偿进行校正,干扰误差可以通过反馈进行校正,但是当系统更复杂时,上述两种校正结合起来也无法将误差控制在一定范围内。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模型预测控制快速求解算法模型预测控制(Model Predictive Control,MPC)是一种基于在线计算的控制优化算法,能够统一处理带约束的多参数优化控制问题。
当被控对象结构和环境相对复杂时,模型预测控制需选择较大的预测时域和控制时域,因此大大增加了在线求解的计算时间,同时降低了控制效果。
从现有的算法来看,模型预测控制通常只适用于采样时间较大、动态过程变化较慢的系统中。
因此,研究快速模型预测控制算法具有一定的理论意义和应用价值。
虽然MPC方法为适应当今复杂的工业环境已经发展出各种智能预测控制方法,在工业领域中也得到了一定应用,但是算法的理论分析和实际应用之间仍然存在着一定差距,尤其在多输入多输出系统、非线性特性及参数时变的系统和结果不确定的系统中。
预测控制方法发展至今,仍然存在一些问题,具体如下:①模型难以建立。
模型是预测控制方法的基础,因此建立的模型越精确,预测控制效果越好。
尽管模型辨识技术已经在预测控制方法的建模过程中得以应用,但是仍无法建立非常精确的系统模型。
②在线计算过程不够优化。
预测控制方法的一大特征是在线优化,即根据系统当前状态、性能指标和约束条件进行在线计算得到当前状态的控制律。
在在线优化过程中,当前的优化算法主要有线性规划、二次规划和非线性规划等。
在线性系统中,预测控制的在线计算过程大多数采用二次规划方法进行求解,但若被控对象的输入输出个数较多或预测时域较大时,该优化方法的在线计算效率也会无法满足系统快速性需求。
而在非线性系统中,在线优化过程通常采用序列二次优化算法,但该方法的在线计算成本相对较高且不能完全保证系统稳定,因此也需要不断改进。
③误差问题。
由于系统建模往往不够精确,且被控系统中往往存在各种干扰,预测控制方法的预测值和实际值之间一定会产生误差。
虽然建模误差可以通过补偿进行校正,干扰误差可以通过反馈进行校正,但是当系统更复杂时,上述两种校正结合起来也无法将误差控制在一定范围内。
模型预测控制区别于其它算法的最大特征是处理多变量多约束线性系统的能力,但随着被控对象的输入输出个数的增多,预测控制方法为保证控制输出的精确性,往往会选取较大的预测步长和控制步长,但这样会大大增加在线优化过程的计算量,从而需要更多的计算时间。
因此,预测控制方法只能适用于采样周期较大且动态变化过程较慢的系统中。
为使预测控制方法能在更多场合中应用,快速模型预测控制算法成为了一个新的研究方向。
3.1 国内外研究现状近年来人们对预测控制算法的不足有了越来越清晰的认识,为了将该算法应用到更多领域,越来越多的学者对其进行不断研究和改进。
阅读近些年国内外核心期刊的文献可知,人们对预测控制方法能够在更大更复杂的系统中应用寄予了很高期望,同时也在其不足方面做了很多探究和尝试,发展出了多种智能预测控制方法。
快速模型预测控制算法作为目前智能预测控制方法之一,其研究方向主要有以下几个方面:(1)显式模型预测控制(Explicit Model Predictive Control,EMPC)2002年Alberto Bemporad等学者[1]提出了显式模型预测控制,该方法在预测控制基础之上,在线性时不变系统优化求解过程中引入多参数二次规划理论,对系统的状态区域进行凸划分,根据最优控制问题计算得到状态分区上相应的控制律。
EMPC将模型预测控制的在线计算过程转化为离线和在线计算相结合的过程,大大减少了算法的在线计算时间,弥补了MPC方法反复在线计算的不足,EMPC也在电力电子[2]、电机控制[3]等领域得到了很好应用。
但随着被控对象问题规模(如输入、状态维数、约束等)的增大,EMPC算法在离线计算过程中所求的状态分区数会呈指数倍增加,而状态分区数的增加不仅会导致存储状态分区所需的存储空间增加,还会导致EMPC算法在线查找最优解所需的计算时间增加,因此该算法很难适用于状态约束较多(状态变量往往不超过5)、预测步长较大的复杂系统。
基于以上原因,许多学者提出用近似的显式模型预测控制方法[4,5]来代替精确的EMPC算法,即通过牺牲一定的控制精度来降低计算过程中的复杂度,从而简化整个求解过程。
如文献[6]提出了显式模型预测控制的多尺度近似方法,通过引入分段线性插入法和自适应分层函数近似法,运用重心插值理论对EMPC离线计算出的状态空间进行网格划分,得到近似的状态分区和近似控制律。
基于同样的思想,文献[7]提出了显式模型预测控制多胞体近似方法,主要利用双描述法对最优控制问题进行近似处理,再通过重心插值得到近似控制律。
文献[8]基于小波的多分辨率分析提出了近似EMPC,通过二次插值和网格划分得到低复杂度且可保证系统稳定的近似控制律。
上述文献提出的方法均能在误差允许的范围内保证系统的控制性能,在一定程度上解决了EMPC随着问题规模增大而带来的复杂度和存储空间增大的问题。
(2)模型预测控制的简化算法MPC算法采用的是在线滚动优化的控制策略,但随着工业模型和环境越来越复杂,其在线计算量越来越大,所以限制了MPC算法在动态变化较快系统中的应用。
为减少MPC在线优化求解的计算量,有学者考虑对参数进行优化,提出了预测控制的简化算法,如将参数分块化的blocking技术[9],其思想是将越远离当前时刻的控制输入越粗略计算,从而减少在线计算量。
在此基础上,又有学者提出了移动blocking方法,其核心是限制系统优化变量个数同时增大系统的有效输入步长[10]。
相较于blocking技术,文献[11]提出的简化方法主要把约束分为起作用约束集、不起作用约束集和不确定约束集,对不起作用的约束集进行忽略操作,对起作用约束集和不确定约束集进行优化计算,从而降低在线计算量,加快控制进程。
(3)改进的在线优化算法模型预测控制的核心是采用反复的迭代优化进行在线求解,选取适当的在线优化方法可以提高在线计算速度。
近年来,有学者试图对模型预测控制的标准形式做适当变形或者近似处理,继而降低预测控制方法的在线计算量。
如文献[12]提出了一种用扩展的牛顿拉夫逊(Newton-Raphson)方法来代替传统的二次规划方法,当问题规模增大时,不仅能够保证优化问题总是收敛,还可以有效解决MPC 在线计算量过大的问题。
文献[13]提出了将表存储和在线优化相结合的部分枚举法(Partial Enumeration,PE),对于规模较大的线性模型不仅有很好的控制效果,而且求解速度是传统MPC算法的5倍以上。
文献[14]提出了基于降精度求解准则的序列二次规划法,主要通过牺牲一定的精确度来降低在线优化所需的迭代次数,从而提高在线求解速度。
文献[15]提出了可用于预测控制在线优化过程的有效内点法,该内点法不仅可以减少代码量,而且可以使在线计算时间提高2-5倍。
3.2 理论基础3.2.1 凸集与凸函数首先给出凸优化理论中凸集、凸函数和仿射的定义。
凸集:假设C 为n 维实数空间n R 中的集合,若C 中任意两点之间的线段仍然在集合C 中,即对于任意12,x x C ∈且对任意实数[]0,1λ∈,都满足: 12(1)x x C λλ+-∈(3-1)则称集合C 为凸集,反之则为非凸集。
满足凸集的集合具有以下性质: (1)若集合1C 、2C 都是凸集则集合{}12121122|,,C C x x y y y C y C +==+∈∈也是凸集。
(2)两个或多个凸集的交集仍为凸集。
(3)空集也是凸集。
凸函数:设()f x 是定义在非空凸集n C R ∈上的函数,对于凸集C 中任意的1x 和2x 以及任意实数[]0,1λ∈均满足1212((1))()(1)()f x x f x f x λλλλ+-≤+- (3-2)则称()f x 为凸函数,反之则为非凸函数(或称凹函数)。
若对12x x ≠和任意实数[]0,1λ∈均满足1212((1))()(1)()f x x f x f x λλλλ+-<+- (3-3)则称()f x 为严格凸函数。
同样,根据凸函数的定义可以推导出凸函数的几个性质,具体如下:(1)若1(),,()m f x f x 是定义在凸集C 上的凸函数,则11()()m m f x f x αα++也是凸集C 上的凸函数,其中α为任意实数。
(2)若函数()f x 是定义在凸集C 上的凸函数,则对于任意实数α,函数()f x α也是凸集C 上的凸函数。
(3)若()g x 是单调递增的凸函数,()f x 也是凸函数,则复合函数[]()g f x 也是凸函数。
(4)若()f x 和()g x 都是定义在凸集C 中非单调递增的凸函数,则()()f x g x 也是定义在凸集C 中的凸函数。
仿射:对于集合C 中任意两点1x 和2x 且任意实数R λ∈,若满足12(1)x x C λλ+-∈ (3-4)则称集合C 是仿射的。
也就是说,通过集合n C R ⊆中任意两点的直线仍在集合C 中。
3.2.2 凸优化问题凸优化问题是指性能指标函数和不等式约束函数均为凸函数且由约束条件所得到的集合是凸集的最优化问题。
由于凸优化问题的局部最优解就是全局最优解,因此对于一个实际问题,如果能表示成凸优化问题,则意味着该问题可以得到彻底解决,对实际应用有着十分重要的意义。
凸优化问题有多种形式,其基本形式可表示为:min ().. ()0 1,, ()0 1,,i i f x s t g x i m h x i p ≤=== (3-5)其中()f x 为性能指标函数,()0i g x ≤为不等式约束条件,()0i h x =为等式约束条件,()0 1,,()0 1,,i i g x i m C x h x i p ≤=⎧⎫=⎨⎬≤=⎩⎭为可行域(也称可行集或约束集)。
如果上述问题中性能指标函数()f x 和不等式约束()i g x 都是仿射函数,则该问题又称线性规划问题(Linear Programming ,LP ),其形式可表示为:min .. T c x ds t Gx h Ax b +≤=(3-6)其中,m n p n G R A R ⨯⨯∈∈,对于线性规划问题而言,通常将性能指标函数中常数项d 忽略,因为其不影响最优解的集合。
该问题的几何解释可由图3.1表示,图中阴影多面体为可行域P ,若性能指标函数中T c x 为线性的,则其等位曲线是和c 正交的超平面(图中的虚线),点*x 对即为最优点。
图3.1 线性规划的几何解释如果性能指标函数()f x 是凸二次型且约束条件是仿射函数,则该问题又称二次规划问题(Quadratic Programming ,QP )。
对于二次规划问题,其标准形式可表示为: 1min2.. T T x Qx q x r s t Ax b Gx h ++=≤(3-7)其中,,,,,n n m n m p n p Q S q R A R b R G R h R ⨯⨯+∈∈∈∈∈∈。
