湖南省2018年高考对口招生考试数学真题
(完整版)2018年湖南省普通高中学业水平考试数学试题(20200814150428)
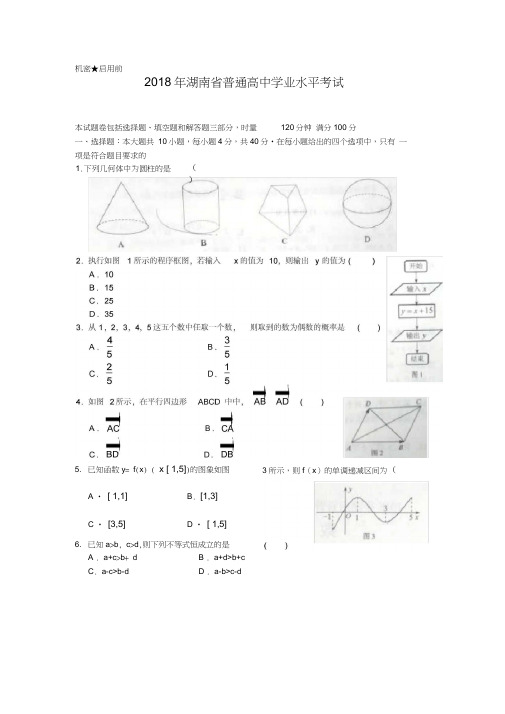
2018年湖南省普通高中学业水平考试本试题卷包括选择题、填空题和解答题三部分,时量 120分钟 满分100分一、选择题:本大题共 10小题,每小题4分,共40分•在每小题给出的四个选项中,只有 一项是符合题目要求的5. 已知函数y = f (x ) ( x [ 1,5])的图象如图A • [ 1,1]B . [1,3]C • [3,5]D • [ 1,5]6. 已知a >b , c >d ,则下列不等式恒成立的是A . a+c >b + dB . a+d>b+cC . a-c>b-dD . a-b>c-d机密★启用前1.下列几何体中为圆柱的是 ()3所示,则f (x )的单调递减区间为(7.为了得到函数y cos(x4)的图象象只需将 y cosx 的图象向左平移()1 A •丄个单位长度2 1C •丄个单位长度4B .—个单位长度2二、 填空题;本大题共 5小题,每小题4分,共20分, 11. 直线y x 3在y 轴上的截距为 ___________________ 。
12. ______________________ 比较大小:sin25 sin23 (填、”或 N ” 13.已知集合 A 1,2 , B 1,x .若 A 「|B2,则 x= _______ 。
14•某工厂甲、乙两个车间生产了同一种产品,数量分别为 60件、40件,现用分层抽样方法抽取一个容量为 n 的样本进行质量检测,已知从甲车间抽取了 6件产品,则n =。
x 215•设x , y 满足不等等式组y 2 ,贝U z = 2x — y 的最小值为 __________ 。
x y 2三、 解答题:本大题共 5小题,共40分,解答应写出文字说明、证明过程或演步 16. (本小题满分6分)函数 f(x) log 2(x1)的零点为(1 A .-Bi C .乜D . 122210.过点M (:2, 1)作圆 C : (x1)2 y 22的切线, 则切线条数为()A . 0B . 1C . 2D . 3在△ ABC 中, 已知 A = 30 ° B = 45 9.AC = •. 2,贝U BC =( )O4个单位长度7. 为了得到函数y cos(x 4)的图象象只需将y cosx的图象向左平移( )1已知函数f (x) x (x 0)x(1 )求f (1)的值(2)判断函数f (x)的奇偶性,并说明理由.(2)设函数f (x) 2,求f (x)的值域,17. (本小题满分8分)某学校为了解学生对食堂用餐的满意度,从全校在食堂用餐的 取100名学生对食堂用餐的满意度进行评分. 根据学生对食堂用餐满意度的评分,得到如图4所示的率分布直方图, (1) 求顺率分布直方图中 a 的值(2) 规定:学生对食堂用餐满意度的评分不低于80分为满意”试估计该校在食堂用 餐的3000名学生中 满意”的人数。
中职数学 2024年湖南省对口招生高考数学模拟试卷

2024年湖南省对口招生高考数学模拟试卷一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)A .∅B .{d }C .{a ,c }D .{b ,e }1.(4分)已知全集U ={a ,b ,c ,d ,e },集合N ={b ,d ,e },M ={a ,c ,d },则∁U (M ∪N )=( )A .{x |x <1}B .{x |x >4}C .{x |1<x <4}D .{x |x <1或x >4}2.(4分)不等式-x 2+5x -4>0的解集是( )A .6B .-4C .4或-6D .6或-43.(4分)已知点P (a ,2)到直线4x -3y +2=0的距离等于4,则a =( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.(4分)已知直线m 、n 和平面α,且n ⊆α,则“m ⊥α”是“m ⊥n ”的( )A .4B .4+4C .4D .4+45.(4分)设正四棱锥的底面边长和侧棱长都是2,则该四棱锥的表面积为( )M 3M 3M 5M 5A .2B .-2C .1D .-16.(4分)已知向量a =(-2,1),b =(4,3),c =(-1,λ).若(a +b )∥c ,则λ的值为( )→→→→→→A .(0,]B .[0,]C .(-∞,]D .[,+∞)7.(4分)已知函数f (x )=log a x (a >0且a ≠1)满足f (2)=-1,则不等式f (x )≥3的解集是( )18181818二、填空题(本大题共5个小题,每小题4分,共20分)A .10B .9C .8D .78.(4分)从某小学随机抽取100名学生,将他们的身高数据绘制成频率分布直方图如图所示,若要从身高在[120,130)、[130,140)、[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为( )A .f (-π)>f (-2)>-f (3)B .-f (3)>f (-π)>f (-2)C .f (-2)>-f (3)>f (-π)D .f (-π)>-f (3)>f (-2)9.(4分)已知f (x )是R 上的奇函数,且在区间[0,+∞)上是减函数,则f (-2),f (-π),-f (3)的大小关系是(A .函数y =sin 2x 的周期为πB .函数y =sinx 在区间(,)内是减函数C .函数y =sinx +cosx 的值域是[-2,2]D .函数y =sin 2x 的图像可由y =sin (2x -)的图像向左平移个单位得到10.(4分)下列命题中错误的是( )3π45π4π5π1011.(4分)已知sin (π+α)=-,α∈(,π),则sin 2α= .45π212.(4分)不等式|x -a |<2的解集为{x |-1<x <3},则实数a = .13.(4分)从7名运动员中选出4人参加校运会的4×100米接力赛,则甲、乙两人都不跑中间两棒的方法有 种.14.(4分)过点P (2,-1)作圆C :(x -1)2+(y -2)2=2的切线,切点为A 、B .则|PA |= .15.(4分)已知等差数列{a n }中a 1=13,且S 3=S 11,则S n 的最大值为 .三、解答题(本大题共7个小题,其中第21、22小题为选做题.满分50分.解答应写出文字说明、证明过程或演算步选做题:请考生在第21、22题中选择一题作答.若两题都做,则按所做的第21题计分.作答时,请写清题号.老师建科类做第21题,服务类做22题.16.(10分)已知点(4,2)在函数f (x )=的图象上.(1)求a 的值,并画出函数f (x )的图象;(2)求不等式f (x )<1的解集.{x +4,x ≤0x ,x >0log a 17.(10分)我校学生心理咨询中心服务电话的接通率为.21机2班的3名同学分别就某一问题在某天咨询该服务中心,只拨打一次电话,设X 表示他们中成功咨询的人数.求:(1)恰有2人成功咨询的概率;(2)随机变量X 的概率分布和数学期望、方差.3418.(10分)已知数列{a n }的前n 项和为S n ,且S n =2a n -3n (n ∈N +).(1)求a 1,a 2,a 3的值;(2)设b n =a n +3,证明数列{b n }为等比数列,并求通项公式a n .19.(10分)如图四棱锥P -ABCD 的底面是边长为2的菱形,且∠ABC =60°,PA =PC =2,PB =PD .(1)若O 是AC 与BD 的交点,证明:PO ⊥平面ABCD .(2)若点M 是PD 的中点,求异面直线AD 与CM 所成角的余弦值.20.(10分)已知椭圆C 的中心在坐标原点O ,焦点在x 轴上,离心率为,椭圆上一点P 到椭圆左右两焦点的距离之和为(1)求椭圆C 的标准方程;(2)已知直线l :y =x +m 与椭圆C 交于A 、B 两个不同的点,且弦AB 的中点恰好在圆+=上,求直线l 的方程.M 32x 2y 2172521.(10分)在平面四边形ABCD中,∠ADC=90°,∠A=45°,AB=2,BD=5.(1)求cos∠ADB;(2)若DC=2,求BC.M222.某公司计划在今年内同时出售变频空调机和智能洗衣机.由于这两种产品的市场需求量非常大,有多少就能销售多少,该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大.已知对这两种产品有直接限制的是资金和劳动力.通过调查,得到关于这两种产品的有关数据如表:资金(表中单位:百元)单位产品所需资金月资金供应量空调机洗衣机成本3020300劳动力:工资510110单位利润6试问:怎样确定两种货物的月供应量,才能使总利润达到最大,最大利润是多少?。
最新-2018年普通高等学校招生全国统一考试数学文试题

2018年普通高等学校招生全国统一考试数学文试题(湖南卷,解析版)【名师简评】湖南卷作为新课标改革以来第一年高考,试卷重点放在高中数学课程最基础、最核心的内容上,紧紧地围绕“双基”,对中学数学的核心内容和基本能力进行重点考查,特别是对高中数学的主干知识进行较为全面的考查。
整体试卷稳中求变,总体难度和计算量相比2018年的试卷来讲是稍稍降低。
试卷结构稳定,考点分布合理,叙述简洁,设问平稳体现了新课标数学的命题理念。
新增加知识的考查都比较简单。
试题有新意,对知识的理解程度、知识与能力综合运用要求较高,创新性的问题设置巧妙。
注重思维能力与应用意识的培养,把比较多的实际问题融合到试卷中.一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求的. 1. 复数21i-等于 A.1i + B. 1i - C. 1i -+ D. 1i --2. 下列命题中的假命题...是 A. ,lg 0x R x ∃∈= B. ,tan 1x R x ∃∈= C. 3,0x R x ∀∈> D. ,20x x R ∀∈>2.答案C【命题意图】本题考查了含有存在量词与全称量词的命题的真假判定。
【解析】当x=1时,lgx=0,即A 正确;当x=4π时,tanx=1,即B 正确;当x ≤0时,x 3>0不成立,即C 错误;对于任意的x ∈R ,都有2x>0,即D 正确;故选C ;3. 某商品销售量y (件)与销售价格x (元/件)负相关,则其回归方程可能是 A. 10200y x =-+ B. 10200y x =+ C. 10200y x =-- D. 10200y x =-3.答案A【命题意图】本题考查了线性回归方程及其实际应用问题。
【解析】由于某商品销售量y 与销售价格x 负相关,则b<0,排除选项B 和D ,而根据特殊值x=2,可以排除选项C ,故选A ;4. 极坐标方程cos ρθ=和参数方程1()2x t t y t =--⎧⎨=+⎩,为参数所表示的图形分别是A. 直线、直线B. 直线、圆C. 圆、圆D. 圆、直线5. 设抛物线28y x =上一点P 到y 轴的距离是4,则点P 到该抛物线焦点的距离是 A. 4 B. 6 C. 8 D. 125.答案B【命题意图】本题考查了抛物线的定义及其应用。
2018单独招生考试数学试卷(A)(1)

2018年单独招生《数学》试卷 第 1 页 共 2 页2018年单独招生考试《数学》试卷一.选择题:(本大题共10小题,每小题6分,共60分) (在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合A={a,b,c,d },B= {a,b,d }, 则=⋂B A ( )A .{a,b,c,d }B .{a,b,d }C .{c }D .φ2.下列函数是偶函数的是( )A .x 2y =B .x y sin =C .2x y =D .3x y =3.已知角045=θ,则=θtan ( )A .23 B .3 C .33D .1 4.数列2,4,, 8,16是( )A .等比数列B .等差数列C .常数列D .递减数列5.二次函数)0(2≠++=a c bx ax y 的图像是( ) A .直线 B .抛物线C . 双曲线D .椭圆6.直线52+-=x y 的斜率k 等于( ) A .-5B . 5C .-2D .27.圆922=+y x 的半径等于( )A .9B .29 C .23D .3 8.已知正方体的体积为64,则它的边长为( ) A .4 B .8 C . 16 D .329.3支篮球队之间进行比赛,每两队之间赛一场,共需安排( )场比赛 A .3 B .6 C . 9 D .2710.从1,2,3,4,5这五个数字中任取一个数,取出的数是偶数的概率为( )A .51B . 52C .53D .54二.填空题:(本大题共5小题,每小题6分,共30分)11.集合{}为自然数x x x ,3≤中共有 个元素。
12.函数23y -=x 的定义域为 13.在直角ABC ∆中,若345===BC AB AC ,,,则ABC ∆的面积等于14.已知一个函数)(x f y =为奇函数,若===-=y x y x 时则时1,21 15.底面半径为2cm ,高6cm 的圆柱体体积为三.判断题(本大题共5小题,每小题6分,共30分) (对的在题后括号内打√号,错的打×号)16. 任何一个数的三次方一定比它的二次方大。
湖南省 2022年普通高等学校对口招生考试数学试卷及参考答案

湖南省2022年普通高等学校对口招生考试数学试卷本试题卷包括选择题、填空题和解答题三部分,共5页。
时量120分钟。
满分120分。
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集U ={1,3,5,7},集合A ={3,5},则C U A =A.{1,7}B.{1,5}C.{3,7}D.{5,7}2.“(x +1)(x -3)=0”是“x =3”的A.充分不必要条件B.必要不充分条件C.充分且必要条件D.既不充分也不必要条件3.已知cos α=−31,且α∈(-π,0),则sin α=A.322-B.32 C.322 D.−324.下列函数中既是偶函数,又在区间(0,+∞)上单调递增的是A.y =cos xB.y =4xC.y =2x 2+1D.y =ln x5.已知sin 2x =a -1,则实数a 的取值范围是A.[-1,1]B.[0,1]C.[0,2]D.[-2,0]6.已知向量a =(2,-1),b =(-3,4),则a ·(2b -a )=A.-25B.-10C.10D.257.不等式|2x +5|>7的解集是A.(-6,1)B.(-∞,-6)∪(1,+∞)C.(-1,6)D.(-∞,-1)∪(6,+∞)8.已知a =0.90.9,b =0.91.8,c =1.80.9,则a ,b ,c 的大小关系是A.b <c <aB.a <c <bC.a <b <cD.b <a <c9.已知两条不同的直线m ,n 与平面α,则下列命题正确的是A.若m //α,n //α,则m //nB.若m ⊥n ,m//α,则n ⊥αC.若m ⊥n ,m ⊥α,则n ⊥αD.若m ⊥α,n ⊥α,则m //n10.已知点P 在直线l :x -y -6=0上,点Q 在圆O :x 2+y 2=2上,则|PQ |的最小值为A.24B.23C.22D.2二、填空题(本大题共5小题,每小题4分,共20分)11.在一次“党史”知识竞赛中,参加知识竞赛的10名学生的成绩如下表:成绩92959698人数1243则这10名学生的平均成绩是.12.经过点M (0,-2),且与直线x +y +1=0平行的直线方程为.13.若角α的终边经过点P (21,−23),则sin 2α=.14.如图,高为5cm,底面边长是3cm 的正四棱柱形工件,以它的两底面中心的连线为轴,钻出一个直径是2cm 的圆柱形孔,则剩余部分几何体的体积是____cm 3(圆周率π取3.14).(第14题)15.若数列{a n }满足a 1=1,且a n +1=2a n +1,则数列{a n }的通项公式a n =.三、解答题(本大题共7小题,其中第21,22小题为选做题,满分60分.解答应写出文字说明、证明过程或演算步骤)16.(本小题满分10分)已知函数f (x )=1+log 4(x +m ),f (1)=2.(1)求实数m 的值,并写出f (x )的定义域;(2)若f (x )<3,求x 的取值范围.、已知等差数列{a n}满足a1=1,a5-a3=4.(1)求a10;(2)设数列{a n}的前n项和为S n,问:S4,S8,S16是否成等比数列?请说明理由.18.(本小题满分10分)某班拟组织部分学生参观爱国主义教育基地.已知该班第一小组有5名男生与3名女生,从中任意选取3名学生去参观.(1)用ξ表示选取的3人中女生的人数,求ξ的分布列;(2)求选取的3人中,女生人数多于男生人数的概率.如图,在三棱锥P -ABC 中,PA ⊥平面ABC ,AB ⊥B C.(1)证明:平面PBC ⊥平面PAB ;(2)若AB =BC =2,直线PB 与平面ABC 所成的角为60°,求三棱锥P -ABC 的体积.(第19题)20.(本小题满分10分)已知双曲线C :12222=-by a x =1(a ,b >0)的离心率为26,左、右焦点分别为F 1,F 2,且|F 1F 2|=23(1)求双曲线C 的方程;(2)设直线y =x +3与双曲线C 相交于M ,N 两点,求MNF 2的面积.选做题:请考生在第21,22题中选择一题作答.如果两题都做,则按所做的第21题计分,作答时,请写清题号.21.(本小题满分10分)如图,点D为等边三角形ABC的边BC上一点,且BD=2DC,AD=7.(1)求CD的长;(2)求sin∠BAD的值.(第21题)22.(本小题满分10分)某工厂生产甲、乙两种电子产品,每生产一件甲产品需要A,B配件分别为4件和2件;每生产一件乙产品需要A,B配件分别为4件和6件.该厂每天可从配件厂最多获得A配件20件和B 配件18件,且生产一件甲产品的利润为4千元,生产一件乙产品的利润为5千元.问如何安排生产,才能使工厂每天利润最大?并求出利润的最大值.湖南省2022年普通高等学校对口招生考试数学试卷参考答案一、选择题1.A2.B3.A4.C5.C6.A7.B8.D9.D10.C二、填空题11.9612.02=++y x 13.23-14.29.315.12-n三、解答题16.解:(1))3(log 1)(32)1(log 1)1(44++=∴=⇒=++=x x f m m f 函数)(.3-)(303∞+->⇒>+,的定义域为即x f x x (2)1316316log 2)3(log )3(log 1)(444<⇒<+⇒=<+⇒++=x x x x x f )()(.133-3)(3-)(,的取值范围为时,的定义域为又x x f x f <∴∞+ 17.解:(1).19291924211035=⨯+=+=∴=⇒==-d a a d d a a (2)在等差数列{}n a 中.,,S 2562120116120161516211664228182887821816261464342141684164281116118114成等比数列S S S S S d a d a S d a d a S d a d a S ∴⋅==⨯+⨯=+=⨯⨯⨯+==⨯+⨯=+=⨯⨯⨯+==⨯+⨯=+=⨯⨯⨯+=18.解:(1)ξ可分别取0,1,2,3.561)3(5615)2(28155630)1(2855610)0(38333823153813253835==============C C P C C C P C C C P C C P ξξξξξ的分布列为ξ123P28528155615561(2)女生人数多于男生人数的概率为725615615)3()2(=+==+=ξξP P 19.解:(1)BCPA ABC⊥∴⊥平面P A PABPBC 平面平面平面则又⊥∴⊥=⋂⊥P ABBC AP A AB BC AB (2)60=∠∴⊥PBA ABC PB ABC P A 所成角即为与平面直线平面33432222131S 3132tan ABC -=⨯⨯⨯⨯===<⋅=h V PBA AB P A P AB ABC P 中,在直角三角形20.解:(1)3322F F 21=⇒==c c 12C 123226322222=-=-=-==⇒===y x a c b a a a c e 的方程为即双曲线(2)设M 、N 两点的坐标分别为()()2211,,,y x y x 3462421216)1(13032484)34(24)(183402834123222222122122121222=⨯⨯===-++-==⨯--=-++==-=+=++⇒⎪⎩⎪⎨⎧=-+=∆d MN S d F x x x x k MN x x x x x y x x y MNF 到直线的距离根据韦达定理可得21.解:(1)设AB 长为a ,则BD=a 32,DC=a 31在等边三角形ABC 中,131360cos 322)32(7cos 2222222===⇒⋅⋅-+=⇒⋅-+=︒a CD a a a a a BBD AB BD AB AD 则(2)在三角形ABD 中,根据正弦定理可得721sin sin sin sin =∠=∠⇒∠=∠AD B BD BAD B AD BAD BD 22.解:设生产甲产品为x 件,乙产品为y 件,公司获利为Z 元,则z =4000x +5000y由题意得:⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+⇒⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+009350018622044y x y x y x y x y x y x 如右图所示,当x =3,y =2时,Z max =4000×3+5000×2=22000(元)答:生产甲产品为3件,乙产品为2件时,公司获利最大为22000元.x+y=5yx x+3y=9o 、A (3,2)59534x+5y=0。
2024-2025年湖南省普通高等学校对口招生考试数学试题

湖南省2024年一般高等学校对口招生考试数 学 试 题一、选择题(在本题的每一小题的备选答案中,只有一个答案是正确的,请把你认为正确的选项填入题后的括号内。
多选不给分。
本大题共10小题,每小题5分,共50分)1、已知全集{,,,,,,}U a b c d e f g =,集合{,,}U a e f =,集合{,,,}U b d e f =,则()U M N =( )。
(A ){,}e f (B ){,}c g (C ){,,}a b d (D ){,,,,}a b c d g2、不等式250x ->的解集是( )。
(A )( (B )(,(5,)-∞+∞(B )(5,5)- (D )(,5)(5,)-∞-+∞3、已知cos 0.618α=,(0180)α<<,则α的近似值是( )。
(A )28.86 (B )38.17 (C )51.83 (D )63.144、下列命题错误的是( )。
(A )在复平面上,表示两个共轭复数的点关于实轴对称。
(B )复数1的三角形式是2(sin cos )33i ππ+。
(C )方程2160x +=在复数集内有两个根。
(D )复数1的模是2。
5、已知33212n n C C =,则n =( )。
(A )5 (B )6 (C )7 (D )86、已知向量(2,3),(1,5)a b =-=,则下列命题错误的是( )。
(A )2(0,3)a b += (B )3(7,4)a b -=-(C )||13a b += (D )13a b ⋅=7、过点(3,2),(4,5)P Q -的直线方程是( )。
(A )73230x y -+= (B )37230x y -+=(C )7370x y --= (D )3770x y --=8、已知椭圆2216251600x y +=上一点P 到椭圆一个焦点的距离为8,则P 到另一个焦点的距离为( )。
(A )6 (B )10 (C )12 (D )149、甲、乙、丙3同学投篮命中的概率依次为0.6,0.5,0.4,3人各投1次,则其中恰有2人投中的概率是( )。
湖南省近七年(2011-2017)对口高考数学试题分类
湖南省近七年(2011-2017)对口高考数学试题分类近七年湖南省普通高等学校对口招生考试的数学试题中,填空和选择题占据了很大比例。
以下是一些题目和解答:1.(2011.1)不等式(x-2)(x+1)≤0的解集是()A.(-1,2)B.(-∞,2) ∪ (2,+∞)C.[-1,2]D.(-∞,-1) ∪ [2,+∞]2.(2012.3)不等式2x-3>1的解集为()A.(1,2)B.(-∞,1) ∪ (2,+∞)C.(-∞,1)D.(2,+∞)3.(2013.7)不等式x^2-2x-3>0的解集为()A.(-3,1)B.(-∞,-3) ∪ (1,+∞)C.(-1,3)D.(-∞,-1) ∪ (3,+∞)4.(2014.7)若a<0,则关于x的不等式(x-3a)(x+2a)<0的解集为()A.{x|3a-2a} C.{x|-2a3a}5.(2015.8)不等式1-2x<3的解集为()A.{x|x-1} C.{x|-2<x<4} D.{x|-1<x<2}6.(2016.4)不等式2x+1>5的解集为()A.{x|x>2}B.{x|x2}7.(2016.13)若不等式x^2+x-c≤0的解集为{x-2≤x≤1},则c=5.8.(2017.7)不等式x-5x+6<0的解集为()A.{x|x3} C.{x|x3} D.{x|2<x<3}9.(2017.14)若关于x的不等式2x+b<3的解集为{x-3<x<5},则b=-1.1.(2011.2)方程x^2-px+q=0有解的充分必要条件是p^2-4q≥0.2.(2012.2)"x>3"是"x^2>9"的充分必要条件。
3.(2013.3)"x=2"是"(x-1)(x-2)=0"的充要条件。
湖南对口高考医学类真题
湖南对口高考医学类真题湖南对口高考医学类真题是指专门为湖南省招生的相关医学类职业考试。
考试本着特长培养、素质教育的宗旨,旨在选拔具有某些学科或综合能力的高水平人才。
该考试难度较高,内容涉及医学、生物学、化学、数学等多个学科。
以下是对湖南对口高考医学类真题的相关参考内容:1.医学类真题医学类真题的难度较高,涉及医学诊断、治疗、护理等多方面内容,考试时间为180分钟。
考试分为客观题和主观题两部分,主要考察考生在解决医疗、健康问题中的观察能力和应用能力。
参考内容包括:(1)医疗保健制度、医学伦理、法律等基础知识。
(2)医学经济学、管理学、心理学等相关知识。
(3)疾病的病因、诊断、治疗、预防等方面的知识。
(4)基础医学、临床医学、预防医学等多个学科的知识。
2.护理类真题护理类真题主要考察考生在临床护理操作、护理流程、疾病管理和根据医嘱执行护理等方面的技能和能力。
参考内容包括:(1)基础护理、专科护理、综合护理等多个方面的知识。
(2)护理常用设备、护理流程、卫生制度等相关知识。
(3)临床护理、病情观察、数据整理等相关技能。
(4)完成关于病情分析和护理计划等相关工作的知识和能力。
3.药学类真题药学类真题主要考察药物方面的相关知识和技能,包括药理学、药物制剂学、药理动力学、药物治疗学等方面的知识。
参考内容包括:(1)剂型设计、制剂生产和检测等相关知识。
(2)药物的分子结构、药理作用、药效学等相关知识。
(3)药物不良反应、药物相互作用等相关知识。
(4)各种药物的特点、适应症、给药途径等相关知识。
4.公共卫生类真题公共卫生类真题主要考察的是考生的公共卫生管理能力,包括公共卫生基础知识,卫生模式与方法,卫生规划与评估,卫生服务等方面的知识和实际应用能力。
参考内容包括:(1)基础公共卫生学,心理学,社会学等方面的知识。
(2)公共卫生管理的原则、流程与方法。
(3)解决卫生问题的实际应用能力,如进行人群筛查,疫情监测等。
2024年湖南对口高考数学试卷(含参考答案)
湖南省2024年普通高等学校对口招生考试数 学本试题卷包括选择题、填空题和解答题三部分,共5页。
时量120分钟,满分120分。
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合M={1,3,5},N={3,4,5,6},则=N MA.{3,5}B.{4,6}C.{1,4,6}D.{1,3,4,5,6 } 2.已知数列{a n }的通项公式为32+=n a n ,*∈N n ,若37=m a ,则=mA.15B.17C.20D.34 3.函数xx y 1+=的图像 A.关于原点对称 B.关于x 轴对称 C.关于y 轴对称 D.关于直线y=x 对称4.从7名学生中选派2名学生分别到甲、乙两地参加社会实践活动,则不同的选派方法共有A.14种B.21种C.42种D.49种 5.已知2log ,2,3.03.03.02===c b a ,则A.c b a <<B.a b c <<C.b c a <<D.b a c << 6.下列命题中,正确的是A.平行于同一个平面的两条直线必平行B.平行于同一个平面的两个平面必平行C.过平面外一点只可以作一条直线与这个平面平行D.过直线外一点只可以作一个平面与这条直线平行 7.“()()042=+-x x ”是“2=x ”的A.充分必要条件B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件 8.函数x x y cos sin 3+=取最大值时,x 的值可以为A.6π B.4π C.3π D.2π9.光线从点M(-3,3)射到点P(1,0)后被x 轴反射,则反射光线必经过的点是A.(3,5)B.(4,2)C.(4,4)D.(5,3)10.已知函数()x f y =在)[∞+,0上单调递增,且()()x f x f =-,则不等式()()31f x f <-的解集为A.()42,- B.()4,∞- C.()∞,4 D.()()∞+∞-,,42二、填空题(本大题共5小题,每小题4分,共20分)11.某学校为了解一年级120名男生和80名女生的身高情况,计划用分层抽样的方法抽取20名学生进行测量,则抽取的男生人数为 .12.已知向量()m a ,1=,()1,2=b ,且()b b a ⊥+,则实数=m .13.已知角α的顶点在坐标原点,始边与x 轴的非负半轴重合,终边上一点的坐标为⎪⎪⎭⎫⎝⎛-21,23,则α2sin . 14.已知函数()x x f ln =,若0>>b a ,且()()b f a f =,则=ab .15.已知点P 在圆01022=-+y y x 上运动,则点P 到直线0543=-+y x 的距离的最大值为 .三、解答题(本大题共7小题,其中第21,22小题为选做题。
2018中职生对口升学数学试题,真题
2018中职生对口升学数学试题本试卷分选择题和非选择题两部分,满分100分,考试时间为90分钟。
选择题注意事项:1.选择题答案必须填涂在答题卡上,写在试卷上的一律不计分。
2.答题前,考生必须将自己的姓名、准考证号、座位号、考试科目涂写在答题卡上。
3.考生须按规定正确涂卡,否则后果自负。
一、选择题(本大题共12小题,每小题3分,共36分)1.设全集U =R .集合A ={}{}()=≤=≤-B C A x x B x x U 则,0|,21|( ) A. [0, 3] B.(O, 3] C. [-1, 0) D. [-1, 0] 2.在等比数列{}n a 中, 已知===421,6,3a a a 则( ) A.12 B.18 C.24 D.48 3. lg 3 + lg 5 =( )A. lg 8B. lg 3·lg 5C. 15D. lg 15 4.下列函数为偶函数的是( )A.x y sin =B.)sin(x y +=πC.)sin(x y -=πD.)2sin(x y -=π5.下列函数在定义域内为增函数数的是( ) A.21x y = B.x y 21log =C.xy -=2D.xy 1=6.已知向量=⊥-=-=m b a m m b m a 则而且,),6,(),1,(( )A.-3B.2C.-3或2D.-2或3 7.已知x 3log =2则A.32=x B.32=x C.x =23D.23=x8.如果角α的终边过点P(-3.4).则=αcos ( ) A.53-B.53C.54-D.54 9.设直线m 平行于平面α,直线n 垂直于平面β,而且αβα⊄⊥n ,,则必有 A. m //n B.m ⊥n C. β⊥m D. n //α10.已知1916,2221=+y x F F 是椭圆的两焦点,过点1F 的直线交椭圆于A, B 两点,若=+=11,5BF AF AB 则A.16B.10C.10D.9非选择题注意事项:用蓝黑色钢笔或圆珠笔将答案直接写在试卷上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
病句辨析与修改(3)
页脚内容1
湖南省2018年普通高等学校对口招生考试
数学
本试题卷包括选择题、填空题和解答题三部分,共4页,时量120分钟,满分120分
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只
有一项是符合题目要求的)
1.已知集合A={1,2,3,4},B={3,4,5,6},则A∩B=( )
A.{1,2,3,4,5,6} B.{2,3,4}
C.{3,4} D.{1,2,5,6}
2. “92x”是“3x”的( )
A.充分必要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
3.函数xxy22的单调增区间是( )
A.(-∞,1] B. [1,+∞) C.(-∞,2] D.[0,+∞)
4.已知53cos, 且为第三象限角,则tan=( )
A.34 B.43 C.43 D.34
5.不等式112x的解集是( )
A.{0|xx} B.{1|xx}
C.{10|xx} D.{10|xxx或}
6.点M在直线01243yx上,O为坐标原点,则线段OM长度的最小值是
( )
A. 3 B. 4 C. 2512 D. 512
7.已知向量a,b满足7a,12b,42•ba,则向量a,b的夹角为( )
A. 30 B. 60° C. 120° D. 150°
8.下列命题中,错误..的是( )
A. 平行于同一个平面的两个平面平行
B. 平行于同一条直线的两个平面平行
病句辨析与修改(3)
页脚内容2
C. 一个平面与两个平行平面相交,交线平行
D. 一条直线与两个平行平面中的一个相交,则必与另一个相交
9.已知15sina,100sinb,200sinc,则cba,,的大小关系为( )
A. cba B. bca C. abc D. bac
10.过点(1,1)的直线与圆422yx相交于A,B两点,O为坐标原点,则OAB面积
的最大值为( )
A. 2 B. 4 C. 3 D. 23
二、填空题(本大题共5小题,每小题4分,共20分)
11. 某学校有900名学生,其中女生400名.按男女比例用分层抽样的方法,从该学校
学生中抽取一个容量为45的样本,则应抽取男生的人数为 .
12. 函bxxfcos)((b为常数)的部分图像如图所示,则b= .
13.6)1(x的展开式中
5
x
的系数为
(用数字作答)
14.已知向量
a=(1,2),b=(3,4),c=(11,16),且c=ax
+by,则yx .
15.如图,画一个边长为4的正方形,再将这个正方形各边的中点相连得到第2个正方
形,依次类推,这样一共画了10个正方形.则第10个正方形的面积为 .
病句辨析与修改(3)
页脚内容3
三、解答题(本大题共7小题,其中第21,22小题为选做题.满分60分,解答应写出
文字说明、证明过程或演算步骤)
16.(本小题满分10分)
已知数列{na}为等差数列,1a=1,3a=5,
(Ⅰ)求数列{na}的通项公式;
(Ⅱ)设数列{na}的前n项和为nS . 若nS=100,求n.
17.(本小题满分10分)
某种饮料共6瓶,其中有2瓶不合格,从中随机抽取2瓶检测.用 表示取出饮料
中不合格的瓶数.求
(Ⅰ)随机变量的分布列;
(Ⅱ)检测出有不合格饮料的概率.
病句辨析与修改(3)
页脚内容4
18.(本小题满分10分)
已知函数)3(log)(xxfa)1,0(aa且的图像过点(5,1)
(Ⅰ)求)(xf的解析式,并写出)(xf的定义域;
(Ⅱ)若1)(mf,求m的取值范围
19.(本小题满分10分)
如图,在三棱柱111CBAABC中,1AA⊥底面ABC,BCABAA1,
ABC90°,D为AC
的中点.
(I)证明:BD⊥平面CCAA11;
(Ⅱ)求直线1BA与平面CCAA11所成的角.
病句辨析与修改(3)
页脚内容5
20.(本小题满分10分)
已知椭圆:C12222byax(0ba)的焦点为1F(-1,0)、2F(1,0),点A(0,1)在椭圆C
上.
(I) 求椭圆C的方程;
(II) (Ⅱ)直线l过点1F且与1AF垂直,l与椭圆C相交于M,N两点,求MN的长.
选做题:请考生在第21,22题中选择一题作答.如果两题都做,则按所做的
第21题计分,作答时,请写清题号.
21.(本小题满分10分)
如图,在四边形ABCD中,6CDBC,4AB,BCD120°,
ABC75°,求四边形ABCD
的面积.
22. (本小题满分10分)
病句辨析与修改(3)
页脚内容6
某公司生产甲、乙两种产品均需用A,B两种原料.已知生产1吨每种产品所需
原料及每天原料的可用限额如表所示.如果生产1吨甲产品可获利润4万元,生产1吨
乙产品可获利润5万元.问:该公司如何规划生产,才能使公司每天获得的利润最大?
甲 乙 原料限额
A
(吨)
1 2 8
B
(吨)
3 2 12
