苏教版高中数学必修三练习:1.2.3循环结构 word版含答案
2019-2020学年高中数学必修三习题:第一章1.1-1.1.2第3课时循环结构、程序框图的画法 Word版含答案

第一章算法初步1.1 算法与程序框图1.1.2 程序框图与算法的基本逻辑结构第3课时循环结构、程序框图的画法A级基础巩固一、选择题1.下列关于循环结构的说法正确的是( )A.循环结构中,判断框内的条件是唯一的B.判断框中的条件成立时,要结束循环向下执行C.循环体中要对判断框中的条件变量有所改变才会使循环结构不会出现“死循环”D.循环结构就是无限循环的结构,执行程序时会永无止境地运行下去答案:C2.如图所示的程序框图表示的算法功能是( )A.计算小于100的奇数的连乘积B.计算从1开始的连续奇数的连乘积C.从1开始的连续奇数的连乘积,当乘积大于或等于100时,计算奇数的个数D.计算1×3×5×…×n≥100时的最小的n的值解析:循环一次时S=1×3,循环2次时,S=1×3×5,且S大于或等于100时输出i,故算法功能为D.答案:D3.如图所示的程序框图包含算法结构中的哪些结构?( )(1)条件结构(2)顺序结构(3)循环结构(4)无法确定A.(1)(2) B.(1)(3) C.(2)(3) D.(4)答案:A4.(2015·天津卷)阅读下面的程序框图,运行相应的程序,则输出i的值为( )A.2B.3C.4D.5解析:S=10,i=0,i=i+1=1,S=S-i=10-1=9,不满足S≤1,i=i+1=2,S=S-i=9-2=7,不满足S≤1,i=i+1=3,S=S-i=7-3=4,不满足S≤1,i=i+1=4,S=S-i=4-4=0,满足S≤1,输出i=4.答案:C5.在循环结构中,每次执行循环体前对控制循环的条件进行判断,当条件满足时执行循环体,不满足则停止,这样的循环结构是( )A.分支型循环B.直到型循环C.条件型循环D.当型循环答案:D二、填空题6.如图所示的程序框图,当输入x的值为5时,则其输出的结果是________.解析:因为x=5,x>0,所以x=5-3=2,x>0.所以x=2-3=-1.所以y=0.5-1=2.答案:27.(2015·安徽卷)执行如图所示的程序框图(算法流程图),输出的n为________.解析:各次循环中变量a,n的取值如下表所示:当a=1.416答案:48.执行如图所示的程序框图,若输出的a值大于2 015,那么判断框内的条件应为________.解析:第一次循环:k=1,a=1,满足条件,所以a=4×1+3=7,k=1+1=2.第二次循环:a=7<2 015,故继续循环,所以a=4×7+3=31,k=2+1=3.第三次循环:a =31<2 015,故继续循环,所以a =4×31+3=127,k =3+1=4. 第四次循环:a =127<2 015,故继续循环,所以a =4×127+3=511,k =4+1=5. 第五次循环:a =511<2 015,故继续循环,所以a =4×511+3=2 047,k =5+1=6. 由于a =2 047>2 015,故不符合条件,输出a 值.所以判断框内的条件是“k ≤5?”. 答案:k ≤5? 三、解答题9.画出计算1+12+13+…+110的值的程序框图. 解:程序框图如下图所示:10.如图所示的程序框图,(1)输入x =-1,n =3,则输出的数S 是多少? (2)该程序框图是什么型?试把它转化为另一种结构. 解:(1)当n =3时,i =3-1=2,满足i ≥0, 故S =6×(-1)+2+1=-3;执行i =i -1后i 的值为1,满足i ≥0, 故S =(-3)×(-1)+1+1=5;再执行i =i -1后i 的值为0,满足i ≥0, 故S =5×(-1)+0+1=-4;继续执行i =i -1后i 的值为-1,不满足i ≥0, 故输出S =-4.(2)原图是当型循环,改为直到型(如图):B级能力提升1.阅读下面的程序框图,运行相应的程序,输出S的值为( )A.15 B.105 C.245 D.945解析:初始:S=1,i=1;第一次:T=3,S=3,i=2;第二次:T=5,S=15,i=3;第三次:T=7,S=105,i=4,满足条件,退出循环,输出S的值为105.答案:B2.阅读如图所示的程序框图,运行相应的程序,则程序运行后输出的结果为________.解析:i=1,S=0.第一次循环:S =0+lg 13=-lg 3>-1,继续循环,i =3; 第二次循环:S =-lg 3+lg 35=-lg 5>-1,继续循环,i =5; 第三次循环:S =-lg 5+lg 57=-lg 7>-1,继续循环,i =7; 第四次循环:S =-lg 7+lg 79=-lg 9>-1,继续循环,i =9; 第五次循环:S =-lg 9+lg 911=-lg 11<-1,结束循环,输出i =9. 答案:93.某班共有学生50人,在一次数学测试中,要搜索出测试中及格(60分及以上)的成绩,试设计一个算法,并画出程序框图.解:算法如下: 第一步: i =1. 第二步,输入x .第三步,若x ≥60则输出. 第四步,i =i +1.第五步,判断i >50,是,结束;否则执行第二步. 程序框图如图所示:。
2020高中数学苏教版必修三 课下能力提升:(六) 循环语句-含答案

1.解析: s=6,n=5;s=11,n=4;s=15,n=3,退出循环,此时n=3.
答案: 3
2.解析:由条件i From 2 To 5知共循环4次.
第一次循环t←1×2=2,
第二次循环t←2×3=6,
第三次循环t←6×4=24,
第四次循环t←24×5=120.
故运行结果为120.
答案:120
End Do
PrintS
5.观察下列程序,该循环变量I共循环________次.
S←0
I←1
While S <60
S←S+I
I←I+1
End While
二、解答题
6.写出下列伪代码执行的结果.
7.试确定S=1+4+7+10+…中加到第几项时S≥300?写出伪代码.
8.给出某班50名学生的数学测试成绩,60分及60分以上的为及格,要求统计及格人数、及格人数的平均分、全班同学的平均分,画出流程图,并写出伪代码.
3.解析: 第一步:c=2,a=1,b=2;第二步:c=3,a=2,b=3;第三步:c=5,a=3,b=5.
答案:5
4.解析:依题意需计算10×9×8,该循环体共执行了三次,当完成S←S×8后应结束循环,因此在横线处应填8.
答案:8
5.解析: 由题意知该程序的作用是判断S=1+2+3+…+n≥60的最小整数n.
2.以下伪代码运行结果t=________.
t←1
ForiFrom 2 To 5
t←t×i
End For
Printt
3.根据以下伪代码,可知输出的结果b为________.
4.如果下列伪代码运行后输出的结果是720,则在横线处应填入的正整数为________.
高中数学苏教版必修三 能力提升习题:(三) 循环结构含答案
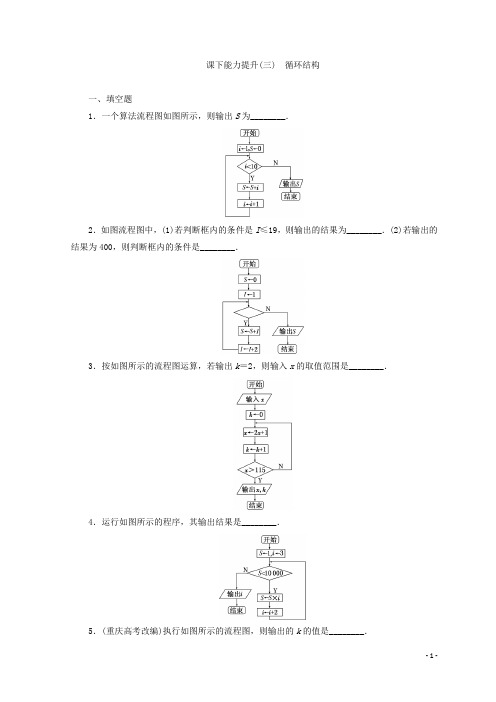
课下能力提升(三) 循环结构一、填空题1.一个算法流程图如图所示,则输出S为________.2.如图流程图中,(1)若判断框内的条件是I≤19,则输出的结果为________.(2)若输出的结果为400,则判断框内的条件是________.3.按如图所示的流程图运算,若输出k=2,则输入x的取值范围是________.4.运行如图所示的程序,其输出结果是________.5.(重庆高考改编)执行如图所示的流程图,则输出的k的值是________.二、解答题6.用循环结构写出计算11×3+12×4+13×5+…+1100×102的流程图.7.下列三图是为计算22+42+62+…+1002而绘制的算法流程图,根据流程图回答后面的问题:(1)其中正确的流程图有哪几个?错误的流程图有哪几个?错误的要指出错在哪里? (2)错误的流程图中,按该流程图所蕴含的算法,能执行到底吗?若能执行到底,最后输出的结果是什么?8.某高中男子田径队的50 m 赛跑成绩(单位:s)如下: 6.3,6.6,7.1,6.8,7.1,7.4,6.9,7.4,7.5,7.6,7.8, 6.4,6.5,6.4,6.5,6.7,7.0,6.9,6.4,7.1,7.0,7.2.设计一个算法,从这些成绩中搜索出成绩小于6.8 s 的队员,并画出流程图.答案1.解析:0+1+…+9=45.答案:452.解析:(1)S=1+3+5+…+19=100;(2)已知S=1+3+5+…+n=400,得n=39.即I≤39(或I<40或I<41).答案:(1)100 (2)I≤39(或I<40或I<41)3.解析:第一次运行x=2x+1,k=1,第二次运行x=2(2x+1)+1,k=2,此时输出x的值,则2x+1≤115且2(2x+1)+1>115,解得28<x≤57.答案:(28,57]4.解析:由题意知,流程图功能为1×3×5×…×i≥10 000,∴i=11,故输出的结果为i=11+2=13.答案:135.解析:利用循环结构相关知识直接运算求解.k=1,s=1+02=1;k=2,s=1+12=2;k=3,s=2+22=6;k=4,s=6+32=15;k=5,s=15+42=31>15.故输出k=5.答案:56.解:如图所示:7.解:(1)正确的流程图只有图③,图①有三处错误:第一处错误,第二个图框中i←42,应该是i←4,因为本流程图中的计数变量是i,不是i2,在22,42,…,1002中,指数都是2,而底数2,4,6,8,…,100是变化的,但前后两项的底数相差2,因此计数变量是顺加2.第二处错误,第三个图框中的内容错误,累加的是i2而不是i,故应改为p←p+i2.第三处错误,第四个图框中的内容,其中的指令i←i+1,应改为i←i+2,原因是底数前后两项相差2.图②所示的流程图中有一处错误,即判断框中的内容错误,应将框内的内容“i<100”改为“i≤100”或改为“i>100”且判断框下面的流程线上标注的Y和N互换.(2)图①虽然能进行到底,但执行的结果不是所期望的结果,按照这个流程图最终输出的结果是p=22+42+(42+1)+(42+2)+…+(42+84).图②虽然能进行到底,但最终输出的结果不是预期的结果而是22+42+62+…+982,少了1002.8.解:此男子田径队有22人,要解决该问题必须先对运动员进行编号.设第i个运动员编号为N i,成绩为G i,设计的算法如下:S1 i=1.S2 输入N i,G i.S3 如果G i<6.8,则输出N i,G i,并执行S4;否则,直接执行S4.S4 i=i+1.S5 如果i≤22,则返回S2;否则,算法结束.该算法的程序框图如图所示.。
高中数学 1.2.3循环结构导学案 苏教版必修3

正确的流程图序号为_________;
图③中,输出的结果为__________________________ (只须给出算式表达式).
你能用一个算法来表达上述过程吗?
你能猜想出循环结构的大致流程图吗?
【课堂研讨】
例1、写出求 值的一个算法.
例2、画出计算 值的一个算法的流程图.
例3、设计一个计算 个数的平均数的算法,并画出流程图.
【学后反思】
课题:1.2.3流程图——循环结构检测案
班级:姓名:学号:第学习小组
【课堂检测】
1.设计计算 值的一个算法,并画出流程图.
2.先分步写出计算 的一个算法,再画出流程图(使用循环结构).
3.用 代表第 个学生的学号, 代表第 个学生的成绩( ),上图表示了一个什么样的算法?
【课后巩固】
1.在算法中,需要重复执行同一操作的结构称为( )
A.顺序结构B.循环结构C.选择结构D.分支结构
2.写出计算 的一个算法,并画出流程图(使用循环结构).
课题:1.2.3流程图——循环结构
班级:姓名:学号:第学习小组
【学习目标】
1、理解循环结构的执行过程.
2、会用流程图表示循环结构.
【课前预习】
1.问题:
北京获得了 年的奥运会的主办权,你知道在申ห้องสมุดไป่ตู้奥运会的最后阶段时,国际奥委会是如何通过投票来决定主办权归属的吗?
对五个申报的城市进行表决的程序是:首先进行的第一轮投票,如果有哪一个城市得票超过半数,那么该城市将获得举办权,表决结束;如果所有的申报城市的票数都没有半数,则将得票最少的城市淘汰,然后重复上述过程,直到选出一个申办城市为止.
苏教版数学高一苏教版必修3知识导引1.2.3循环结构
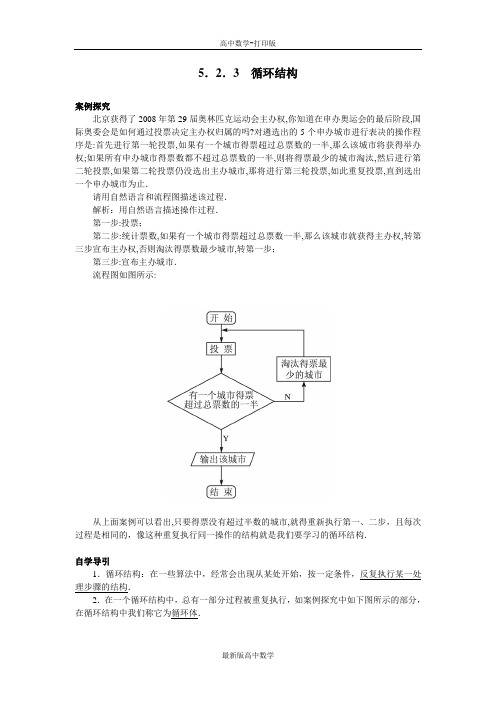
5.2.3循环结构案例探究北京获得了2008年第29届奥林匹克运动会主办权,你知道在申办奥运会的最后阶段,国际奥委会是如何通过投票决定主办权归属的吗?对遴选出的5个申办城市进行表决的操作程序是:首先进行第一轮投票,如果有一个城市得票超过总票数的一半,那么该城市将获得举办权;如果所有申办城市得票数都不超过总票数的一半,则将得票最少的城市淘汰,然后进行第二轮投票,如果第二轮投票仍没选出主办城市,那将进行第三轮投票,如此重复投票,直到选出一个申办城市为止.请用自然语言和流程图描述该过程.解析:用自然语言描述操作过程.第一步:投票;第二步:统计票数,如果有一个城市得票超过总票数一半,那么该城市就获得主办权,转第三步宣布主办权,否则淘汰得票数最少城市,转第一步;第三步:宣布主办城市.流程图如图所示:从上面案例可以看出,只要得票没有超过半数的城市,就得重新执行第一、二步,且每次过程是相同的,像这种重复执行同一操作的结构就是我们要学习的循环结构.自学导引1.循环结构:在一些算法中,经常会出现从某处开始,按一定条件,反复执行某一处理步骤的结构.2.在一个循环结构中,总有一部分过程被重复执行,如案例探究中如下图所示的部分,在循环结构中我们称它为循环体.3.循环结构在流程图中也是利用判断框表示,判断框内写上条件,两个出口分别对应着条件成立和条件不成立时执行的不同指令,其中一个要指向循环体,然后再从循环体回到判断框的入口处.它的基本结构形式有如下图所示的两种.其中上图(1)称为当型循环,当给定条件P成立时反复执行循环体,直到条件P不满足时,才停止循环,退出循环体;图(2)称为直到型循环,即先执行A块,再判断给定的条件P是否成立,若条件P不成立,则再执行循环体,直到条件P成立为止,才停止循环,退出循环体.4.简述三种基本逻辑结构特点.顺序结构:①顺序结构的语句与语句、框与框之间都是按从上到下的顺序;②顺序结构是最简单的算法结构,任何一个算法都离不开它;条件结构:①条件结构的语句与语句、框与框之间必须有一个环节是按条件的判断而进行的操作;②它包含一个判断框,当条件成立(或为“真”)时执行一个步骤,否则执行另一个步骤.循环结构:在一个循环结构中,总有一个处理过程要重复一系列的处理步骤若干次,而且每次的处理步骤完全相同.5.简述条件结构与循环结构的区别与联系.联系:它们都有一个或几个判断框,并且只有在进行判断后才可执行下一步.区别:条件结构中进行判断只进行一次,而循环结构中只要不满足条件就进行判断直到满足条件为止.疑难剖析一些算法中(如累加、累乘问题),若出现从某处开始按照一定的条件反复执行某一处理步骤的情况,需采用循环结构处理,关键要确定循环条件与循环体.一般来说,画出框图前,需确定三件事情:①确定循环变量和初始条件;②确定算法中反复执行的部分,即循环体;③确定循环的终止条件.【例1】画出求1×2×3×4×5×…×n的流程图.思路分析:这是一个累乘问题,重复进行了n-1次乘法,可以用循环结构描述,需引入累乘变量mul和计数变量i,这里mul与i每一次循环,它们的值都在改变,先用自然语言描述.解:算法:第一步:设mul的值为1;第二步:设i的值为2;第三步:如果i≤n执行第四步,否则转去执行第七步;第四步:计算mul乘i并将结果赋给mul;第五步:计算i加1并将结果赋给i;第六步:转去执行第三步;第七步:输出mul的值并结束算法.流程图如图:方法1:方法2:思维启示:(1)对于连乘积问题,其运算过程包含循环过程,于是可采用循环结构来描述算法.(2)本题中判断框起了一个控制作用,它决定了是继续执行循环体还是退出循环体.由于判断框中设置的循环条件不同,导致方法1是当型循环,方法2是直到型循环,可见当型循环和直到型循环是可以相互转化的.【例2】设计一个计算1+2+3+4+…+100的值的计算法,并画出流程图.思路分析:本题是一个累加问题,我们需要一个累加变量和一个计数变量,将累加变量初始值设为0,计数变量的值从1到100.解:算法:第一步:赋给累加变量sum初始值0,赋给计数变量i初始值1;第二步:若i>100,输出sum,否则执行第三、四步;第三步:计算sum=sum+i;第四步:i=i+1,并转到第二步.流程图如图:思维启示:(1)对于累加求和问题,往往包含循环运算的过程,可利用循环结构来设计算法.(2)运用循环结构描述算法时,关键是设置循环条件和循环体.【例3】给出以下10个数:5,9,80,43,95,73,28,17,60,36,要求把大于40的数找出来并输出.试画出该问题的算法流程图.思路分析:可以从第1个数开始与40比较大小,若该数大于40,就输出,小于或等于40,就直接再与下一个数比较大小,这样共需比较10次,可设计一个计数变量,用循环结构设计算法.解:流程图如图所示思维启示:本题的算法设计中既用了条件结构,也用了循环结构.条件结构用于判断输入的数是否大于40,循环结构用于控制输入的数的个数,这里用变量I作为计数变量.【例4】已知函数f(x)=x3-1,把区间[0,10]10等分,求函数在该区间的端点及各分点处的函数值,画出该算法的流程图.思路分析:把区间[0,10]10等分,每份长度均为1,9个分点处的值依次是1,2,3,…,9,这样连同两端点在内共有11个数:0,1,2,…,10,我们可以引入变量i,从0开始,每算一个函数值,i的值就加1,直到i=10为止.故可用一个循环结构设计算法.解:思维启示:对于这种有规律的重复计算问题,一般采用循环结构设计算法.【例5】给定两个正整数m,n(m≥n),求其最大公约数.写出算法,并画出流程图.解:算法如下;S1:输入两个正整数m,n;S2:取m除以n的余数,并用r保存;S3:若r=0,则n的当前值即为所求的最大公约数,转到步骤S5;否则执行步骤S4;S4:使m=n,n=r,转到步骤S2继续执行;S5:输出n,算法结束.流程图如图所示.拓展迁移【拓展点1】 画出计算1+21+31+41+…+n1值的一个算法流程图. 思路分析:从题目可以看出相加数的分子是不变的,而分母是有规律递增的,因此我们也可以引入累加变量sum 和计数变量i ,则sum=sum+i1这个式子是反复进行的.解:流程图如图所示:【拓展点2】 画出求21212121+++(共6个2)的值的算法的流程图.思路分析:这个式子实际上是求和,取倒数;再求和,取倒数,反复共需5次达到目的.第一个和为2+21;于是可用循环结构设计该算法. 解:流程图如图所示.【拓展点3】 画出求22222个n 的值的算法的流程图.思路分析:这个式子实际上是2乘以2,取其算术根;再乘以2,取其算术根,反复操作n-1次达到目的,于是可用循环结构设计该算法.解:该算法的流程图如图所示:思维启示:像这类有规律的重复运算问题,可以用循环结构设计算法,但要注意根据题目的运算规律设置循环体,根据运算的次数设置循环条件.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.2.3循环结构
【新知导读】
1.什么是循环结构?循环结构的基本框架是什么?
2.循环结构分为哪两类型?
3.对同一个问题,如果分别用当型循环和直到型循环来处理的话,两者判断的条件
相同吗?
【范例点睛】
例1.设计算法,输出1000以内能被3和5整除的所有正整数,画出算法流程
图。
思路点拨:这个问题很简单,凡是能被3和5整除的正整数都是15的倍数,由
于
1000=15×66+10,因此1000以内一共有66个这样的正整数。
易错辨析:此题既可以用当型循环又可以用直到型循环,但两者的判断的条件恰
好相反。
方法点评: 当一个算法中包含多次重复执行相同类型的操作时,应考虑使用循
环结构。
例2.设区间[0,1]是方程0)(xf的有解区间,画出用二分法算法求方程
0)(xf
在区间[0,1]上的一个近似解的流程图,要求精确度为.
思路点拨:对于给定的一元方程0)(xf,要求精确度为的近似解的算法如下:
1.确定有解区间)0)()((,bfafba
2.取],[ba的中点2ba.
3.计算函数)(xf在中点处的函数值)2(baf.
4.判断函数值)2(baf是否为0;
(1)如果为0,2bax就是方程的解,问题就得到了解决;
(2)如果函数值)2(baf不为0,则分下列两种情况:
①若0)2()(bafaf,则确定新的有解区间为)2,(baa;
②若0)2()(bafaf,则确定新的有解区间为),2(bba
5.判断新的有解区间的长度是否小于误差:
(1)如果新的有解区间长度大于误差,则在新的有解区间的基础上重复上述步骤;
(2)如果新的有解区间长度小于或等于误差,则取新的有解区间的中点为方程的
近似解.
在上述算法中:
(1)循环变量和初始条件
设两个变量ba,,分别表示有解区间的左端点和右端点,初始值分别为0和1.
(2)循环体
算法中反复执行的部分是判断函数值)2(baf是否为0:
①如果0)2(baf,输出2ba
②如果)2(baf不为0,则判断)2()(bafaf的符号:
ⅰ)如果0)2()(bafaf,2bab
ⅱ)如果0)2()(bafaf,2baa
(3)终止条件
①0)2(baf;
②ab
易错辨析:将终止条件ab当成循环体
方法点评:循环结构可以大大地简化算法的表述;循环变量在构造循环结构中发挥
了关键作用,本质上,这就是“函数的思想”。
【课外链接】
1.斐波拉契数列表示的是这样的一列数:0,1,1,2,3,5,…,后一项等于
前两项的和。设计一个算法流程图,输出这个数列的前50项。
思路点拨:设置50个变量:50321,,,,AAAA,表示斐波拉契数列的前50项。
如果设iiiAAA,,12分别表示数列中连续的三项,则21iiiAAA,由这个递推关
系式知道,只要已知这个数列的前两项,就能将后面所有的项都输出来。
方法点评:因为算法中,反复计算和输出的步骤都是一样的,因此,可以用循环
结构来描述这个算法。
【随堂演练】
1.右图给出的是计算0101614121的值的一个程序框图,
其中判断框内应填入的条件是( )
(A)i>100 (B)i≤100 (C)i>50 (D)i≤50
2.在算法中,需要重复执行同一操作的结构称为( )
A顺序结构 B.循环结构 C.选择结构
N
S←S+1/I I←I+2 输出S
结束
I←2
Y
开始
S←0
