MAJ超效率模型
【国家自然科学基金】_超效率数据包络分析_基金支持热词逐年推荐_【万方软件创新助手】_20140731
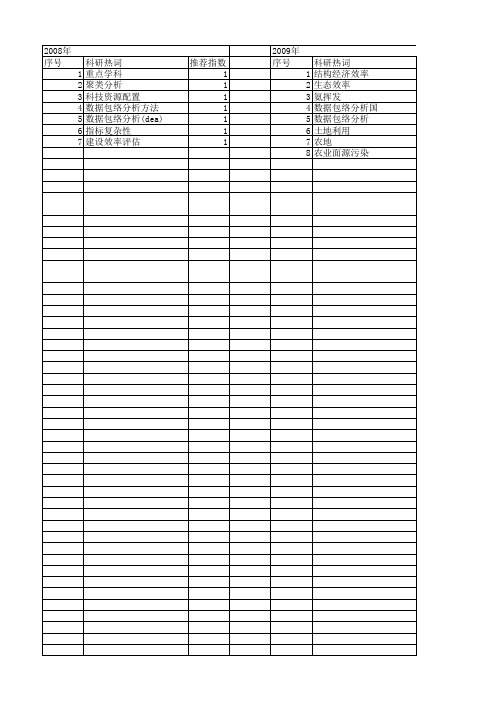
科研热词 重点学科 聚类分析 科技资源配置 数据包络分析方法 数据包络分析(dea) 指标复杂性 建设效率评估
推荐指数 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8
科研热词 结构经济效率 生态效率 氨挥发 数据包络分染
推荐指数 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9
科研热词 数据包络分析 过度投资 结构经济效率 效率评价 投入变量缺失系统 战略委员会 土地利用 决策分析 农地
推荐指数 3 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
2011年 科研热词 数据包络分析 超效率数据包络分析 超效率dea 超效率 视窗分析 绿色发展模式 组合评价 皖江城市带 生产效率 煤炭企业 梯级水电站群 投资效率 承接产业转移示范区 房地产业 发电效率指标 决策单元 农业投入产出效率 推荐指数 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年 序号 1 2 3 4 5
2014年 科研热词 标杆管理 数据包络分析法 效率 岗前平原工程模式区 农地整治 推荐指数 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
科研热词 推荐指数 超效率数据包络分析 2 超效率dea 2 装备 1 节能减排 1 立项评估 1 省际 1 电动汽车 1 熵权 1 旅游效率 1 方向性距离函数 1 敏感系数 1 改进的二进制粒子群优化算法 1 充电站规划 1 交通流量 1 交叉效率 1 m-l生产率指数 1
【国家自然科学基金】_变量替换_基金支持热词逐年推荐_【万方软件创新助手】_20140803
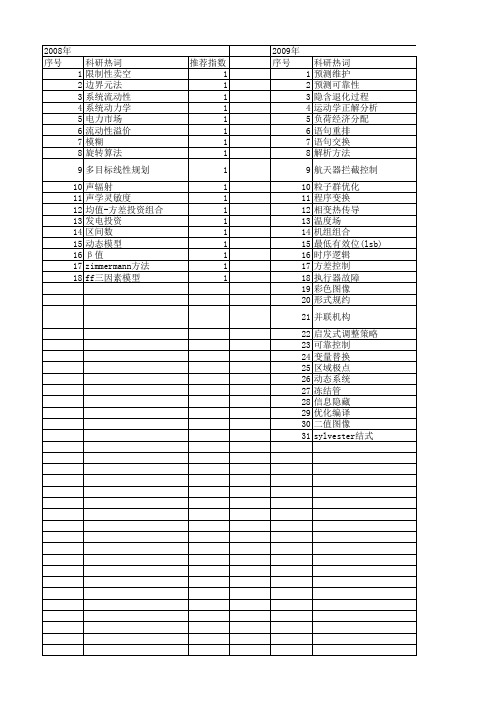
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
2011年 科研热词 推荐指数 道路友好性 2 改进天棚控制 2 平顺性 2 多轴重型货车 2 鸣唱 1 鲁棒h∞可靠控制 1 非线性系统 1 约束图 1 灰眉岩鹀(emberiza godlewskii) 1 混沌电路 1 流不敏感 1 有限时间稳定性 1 时变时滞 1 效鸣 1 指针分析 1 指向集 1 悬架系统 1 悬架 1 忆阻器 1 平衡点集 1 多lyapunov-krasovskii泛函 1 初始状态 1 切换系统 1 不确定性 1 andersen风格 1
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 性 隐含退化过程 运动学正解分析 负荷经济分配 语句重排 语句交换 解析方法 航天器拦截控制 粒子群优化 程序变换 相变热传导 温度场 机组组合 最低有效位(lsb) 时序逻辑 方差控制 执行器故障 彩色图像 形式规约 并联机构 启发式调整策略 可靠控制 变量替换 区域极点 动态系统 冻结管 信息隐藏 优化编译 二值图像 sylvester结式
超效率模型测算方法

超效率模型测算方法摘要:一、引言二、超效率模型概述1.模型定义2.模型应用领域三、超效率模型测算方法1.数据收集与处理2.模型构建与参数设置3.模型运算与结果分析四、模型案例分析1.案例背景2.案例应用3.案例成果五、模型在我国的实践与应用1.我国超效率模型的发展现状2.我国超效率模型的应用案例3.我国超效率模型的发展趋势六、总结与展望正文:一、引言随着科学技术的飞速发展和大数据时代的到来,各种模型和算法应运而生,为我们的工作和生活带来了极大的便利。
超效率模型作为一种先进的分析工具,已经在众多领域展现出强大的威力。
本文将从超效率模型的概述、测算方法、案例分析、在我国的实践与应用等方面进行全面解析,以期帮助读者更好地理解和应用这一模型。
二、超效率模型概述1.模型定义超效率模型(Super-Efficiency Model)是一种基于数据驱动的建模方法,通过挖掘数据中的潜在规律,对复杂系统进行高效、准确的分析和预测。
该模型具有较强的通用性,可以应用于各种领域,如企业管理、金融投资、科技创新等。
2.模型应用领域超效率模型在以下领域取得了显著成果:(1)企业管理:用于评价企业绩效、优化资源配置、制定战略决策等;(2)金融投资:用于评估投资项目、优化投资组合、预测市场走势等;(3)科技创新:用于评价创新能力、挖掘技术前沿、优化研发策略等。
三、超效率模型测算方法1.数据收集与处理超效率模型的测算首先需要收集大量的相关数据。
数据来源可以包括公开数据库、企业内部数据、专业调查等。
在收集数据后,需要对数据进行清洗、整理和预处理,以保证数据的质量和准确性。
2.模型构建与参数设置根据研究目的和数据特点,选择合适的数学模型和方法,如DEA、SFA、Malmquist指数等。
在模型构建过程中,要合理设置参数,以提高模型的拟合度和预测精度。
3.模型运算与结果分析将处理好的数据输入模型进行运算,得到各决策单元的效率值。
对结果进行分析,找出存在的问题,提出改进措施。
基于超效率SBM模型的城市节能环保产业效率评价及比较研究——以兰州市为例

市 (直辖市) 进行 区域 比较 。实证结果表 明,兰州市节能环保 产业效 率整体 呈现跨期 波动上 升趋 势 ,其 中技 术
Hale Waihona Puke 进 步对其贡献最 大,而纯技术 效率和规模 效率 未发 挥相 应作 用,产业组 织管理 水平有 待提 高 ,产 业结构有 望优
化 ;兰州市节能环保产业效 率在全 国居 中等水平 ,为 DEA非有效 ,在 从业人 员、清 洁能源利 用效率等 方面存在
以兰 州 市 为例
张雪梅 ,马鹏 琼
(兰州理工 大学经济 管理 学院 ,甘肃 兰州 730050)
摘 要 : 以 兰 州 市 为例 ,根 据 超 效 率 SBM 模 型 原 理 ,构 建 城 市 节 能 环 保 产 业 效 率评 价 指 标 体 系。 以 2007— 2015年
为评 价期间 ,首先利 用 Ma lmquist指数 对产业效率进行 动 态分 析及要 素分 解 ,然后在 全 国范 围内对 30个省会 城
solid waste a nd urban natural ecological construction.” T h ree wastes”tr eatment is still a focus of ef iciency impr ovement in
urban energy saving environmental protection industry.Finally,put f orward the countermeasure a n d suggestion according to the em pirica l conclusion. Key words: Supe r—eficiency SBM ;Malmquist index;energ y saving a n d envir onmenta l pr otection industr y ; ef i ciency e- va l Hation
MATLAB在超效率DEA模型中的应用_刘展

47 880 48 531 55 953
5 242
6 998
9 133 11 425
23.84
26.51
25.44
26.38
4 150.6 5 438.06 7 305.39 7 764.45
2010 26.21
89 653.71 1 798 1.31
25 149 55 010 16 539
27.69 9 901.52
假设有 n 个决策单元,它们的输入和输出数据分别为(xj, y)j (j=1,2,…,n),对于第 j(0 1芨j0芨n)个决策单元,SE-DEA 模型计算第 j0 个决策单元超效率值的评价表述式为[2]:
≥
m
s
Σ Σ ≥
≥≥minθ-ε( s-i + s+r),
≥ ≥
i=1
r=1
≥
≥
n
≥
≥≥s.t.
一、超效率 DEA 模型
超效率数据包络分析模型(Super Efficiency DEA,SE- DEA)是由 Andersen&Petersen 根据传统 DEA 模型所提出的 新模型。传统 DEA 模型如最基本的 C2R 模型对决策单元规 模有效性和技术有效性同时进行评价,BC2 模型用于专门评 价决策单元技术有效性,但 C2R 模型和 BC2 模型只能区别出 有效率与无效率的决策单元,无法进行比较和排序。超效率 DEA 模型与 C2R 模型的不同之处在于评价某个决策单元时 将其排除在决策单元集合之外,这样使得 C2R 模型中相对有 效的决策单元仍保持相对有效,同时不会改变在 C2R 模型中 相对无效决策单元在超效率 DEA 模型中的有效性,可以弥 补传统 DEA 模型的不足,计算出的效率值不再限制在 0 ̄1 的范围内,而是允许效率值超过 1,可以对各决策单元进行 比较和排序。模型如下:
基于SBM-DEA模型的碳排放效率研究——以中国主要城市群为例

基于SBM-DEA模型的碳排放效率研究——以中国主要城市
群为例
张晨旗;姜娟
【期刊名称】《生产力研究》
【年(卷),期】2024()5
【摘要】在“碳达峰”“碳中和”的背景下,基于我国六大城市群30座主要城市2015—2019年的相关数据,通过SBM模型测算其碳排放效率,并结合所在城市群具体分析。
结果表明:在国家相关政策的号召下,各主要城市能积极响应,努力实现经济水平与环境保护的协同、良性发展。
但城市与城市间、城市群之间还存在着明显的差距。
因此,要想进一步提高我国各城市及城市群的碳排放效率,应加强改造传统产业的绿色化升级;寻求并促进新的经济增长方式。
【总页数】5页(P35-39)
【作者】张晨旗;姜娟
【作者单位】南京邮电大学管理学院
【正文语种】中文
【中图分类】F124.5;F224.0
【相关文献】
1.基于三阶段SBM-DEA模型的中国区域碳排放效率研究
2.中国航空运输行业碳排放效率研究——基于非期望产出SBM-DEA模型
3.长江中游城市群碳效率时空演化特征——基于三阶段SBM-DEA模型
4.基于三阶段超效率SBM-DEA模型的
我国沿海五大城市群低碳物流效率研究5.碳排放约束下城镇建设用地效率研究——基于三阶段超效率SBM-DEA模型对京津冀地区的分析
因版权原因,仅展示原文概要,查看原文内容请购买。
基于超效率SBM-Malmquist模型的我国各地区高校技术创新国际化效率评价

拥有丰厚 的技 术创新 资源,技术创新 国际化效率 水平较 高;西南地 区投 入产 出数值较 小 ,但投入 产 出比仍 然较
高;东北三省效率值始终处 于较低水平 ,与其他地 区技 术创新 国际化水平存在 明显差距。通过 Malmquist指数分
析 ,各地 区高校 国际化 管理水平未处 于有效状 态。总体来看 ,研 发人 员技 术创新 能 力、国际化视 野需要进 一步
杨 博 ,曹 辉
(1.江苏大学发展 办,江苏镇 江 212000; 2.江苏大学教 育评估 中心 ,江苏镇 江 212000)
摘要 :从效率视 角,采 用非参数的数据 包络分析方法 ,基于 201l—20l5年我 国26个省 市面板数据 ,对我 国各地
区高校技 术创新 国际化 水平进行 评价研 究。通过超 效率 SBM模 型计 算发现 ,华 东、华 中、华 北地 区高校 众 多,
2018年第 16期
Science and Tec科hn技ol 管 理M研an究ag ement Research
2018 No.16
doi:10.3969/j.issn.1000—7695.2018.16.008
jm模型的均值函数

jm模型的均值函数JM模型是一种常用的混合效应模型,可以应用于右侧截尾和间断时间间隔数据(TRIC模型)。
其中,均值函数是JM模型中一个重要的组成部分。
本文将围绕JM模型的均值函数展开讨论,以帮助读者更好地了解该模型。
一、JM模型的基本概念JM模型是一种针对时间相关资料进行的混合效应模型,由Gill和Levy于1992年提出。
其核心思想是将观测时间分为若干个时间段,而各时间段内的观测数据被看作是独立的。
JM模型适用于时间相关的数据,可以很好地处理右侧截尾和间断时间间隔数据(TRIC模型)。
二、JM模型的均值函数1. 定义JM模型的均值函数是由混合效应模型中的固定效应和随机效应组成的,用于描述研究对象的基础性质和特征。
在JM模型中,固定效应被看作是与时间无关的,随机效应则反映了各个随机因素对数据的影响。
这两个效应的组合形成了JM模型的均值函数。
2. 公式JM模型的均值函数可以表示为:μ(t,xi)=μ0(t)+xi,其中μ(t,xi)是方程的均值函数,t是时间,xi是随机因素变量。
μ0(t)是固定效应,xi是随机效应。
3. 意义JM模型的均值函数描述了研究对象的基础性质和特征,包括对时间的依赖性和随机因素的影响。
具体来说,μ0(t)反映了固定效应对数据的影响,而xi则衡量了个体差异和其他随机因素的影响。
三、JM模型的应用领域JM模型适用于右侧截尾和间断时间间隔数据(TRIC模型),可以广泛应用于生命科学、医学、环境科学、社会科学等领域的数据分析。
例如,在生命科学中,JM模型可以用来分析肿瘤发生、生存分析等问题。
在社会科学中,JM模型可以应用于学术研究、市场调查等领域。
四、总结JM模型是一种常用的混合效应模型,其均值函数是模型中一个重要的组成部分。
均值函数描述了研究对象的基础性质和特征,包括对时间的依赖性和随机因素的影响。
JM模型适用于右侧截尾和间断时间间隔数据(TRIC模型),可以应用于生命科学、医学、环境科学、社会科学等领域的数据分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
262MEHRABIAN,ALIREZAEE AND JAHANSHAHLOO The paper unfolds as follows.Section2represents Andersen/Petersen’s model and presents the proposed model,both in the production possibility set(PPS).Section3presents an illustrative example.Section4presents an empirical investigation.A summary is given in Section5.2.Efficiency analysis by an alternative measureThere are n DMUs to be evaluated,each consumes varying amounts of m different inputs to produce s different outputs.In the model formulation,X p and Y p denote,respectively, the nonnegative vectors of input and output values for DMU p.Definition.The production possibility set(PPS)is the set{(X t,Y t)|the outputs Y t can be produced with the inputs X t}.The set of n DMUs of actual production possibility(X j,Y j),j=1,...,n is considered. Our focus is on the empirically defined production possibility set T with constant returns assumption that is specified by the following postulates:Postulate1(Ray Unboundedness).If(X t,Y t)∈T,then(λX t,λY t)∈T for allλ≥0. Postulate2(Convexity).If(X t,Y t)∈T and(X u,Y u)∈T,then(λX t+(1−λ)X u,λY t+(1−λ)Y u)∈T for allλ∈[0,1].Postulate3(Monotonicity).If(X t,Y t)∈T and X u≥X t,Y u≤Y t,then(X u,Y u)∈T. Postulate4(Inclusion of Observations).The observed(X j,Y j)∈T for all j=1,...,n. Postulate5(Minimum extrapolation).If a production possibility set T satisfies Postulates 1,2,3,and4,then T⊂T .The unique production possibility set with constant returns assumption determined by the above postulates is given by:T=(X t,Y t)|X t≥nj=1λj X j,Y t≤nj=1λj Y j,λj≥0for j=1,...,nFigure1represents a production possibility set,T,for the simplest case of single input and single output.For efficiency evaluation relative to the set T,we consider the following two mathe-matical programs:θ∗p=min a pη∗p=min w p+1subject to:subject to:(a p X p,Y p)∈T(X p+w p1,Y p)∈TThefirst program yields the measure of efficiency introduced by Charnes et al.[6].Hence, we call it the CCR-model.The second program is a new measure of efficiency that weA COMPLETE EFFICIENCY RANKING 263Figure 1.Production possibility set.introduce.For the set T above,these programs can be rewritten:θ∗p =min a p η∗p =min w p +1subject to:subject to:n j =1λj X j ≤a p X p ,nj =1λj X j ≤X p +w p 1,nj =1λj Y j ≥Y p ,n j =1λj Y j ≥Y p ,λj ≥0,j =1,...,n λj ≥0,j =1,...,n where 1is a vector of units.Note that the feasible solution of a p =1,λp =1,and λj =0,j =1,...,n ,j =p for the CCR-model implies that θ∗p ≤1and similarly the feasible solution of w p =0,λp =1,and λj =0,j =1,...,n ,j =p for the alternative formulation implies that η∗p ≤1.Also θ∗p ,η∗p ≥0,since for θ∗p or η∗p less than zero the corresponding input constraints will be inconsistent.Therefore θ∗p and η∗p lie between 0and 1.To rank the relative efficiency of DMUs with unit efficiency,Andersen and Petersen propose that evaluated unit be excluded from the mathematical program,leading to the264MEHRABIAN,ALIREZAEE AND JAHANSHAHLOO following programs depending on the unit p be evaluated:the AP-model the MAJ-modela∗p=min a p j∗p=min w p+1subject to:subject to:nj=1 j=p λj X j≤a p X p,nj=1j=pλj X j≤X p+w p1,nj=1 j=p λj Y j≥Y p,nj=1j=pλj Y j≥Y p,λj≥0,j=1,...,nλj≥0,j=1,...,nAlthough the optimal objective function values for the MAJ-model depend upon the units of measurement of input data,X j,j=1,...,n,unit independence is obtained by normalization1,that is,dividing input data by the maximum input(for each input).Note that for the case of full inefficiency,that is,when a DMU uses maximum inputs,for no production,both models provide zero scores,and for the case of full efficiency,both models provide not less than one scores.Hence,a∗p and j∗p lie between0and+∞.The following feasibility condition for the MAJ-model is readily verified. Proposition.(Necessary and sufficient condition for feasibility in the MAJ-model).The MAJ-model is feasible for evaluation of DMU p with output vector Y p≥0if and only if for each r,r=1,...,s,either y r p=0or there exists a DMU j,j=p,such that y r j=0. The hypothesis of the proposition is not sufficient for feasibility of the AP-model.Dula and Hichmen[10]presents a list of cases that leads to the infeasible problems.3.Illustrative exampleConsider the example given in Table1.There are5DMUs(A,B,C,D,and E)each consume two inputs to produce two outputs with constant returns assumption.We considerthree different instances of unit A,denoted A1,A2,and A3in Table1.DMU A1,DMU A2,parison test data.DMUs→A1A2A3B C D Einput1201510102input288854612output11111221output22221112A COMPLETE EFFICIENCY RANKING265Table2.Results.The CCR-model The AP-model The MAJ-modelDMU A1100%147%127.6%DMU A2100%infeasible131.0%DMU A3100%2000%130.9%and DMU A3are compared one at a time,with all other DMUs(B,C,D,and E)by theCCR-model,the AP-model,and the MAJ-model.Table2presents the results.The AP-model for evaluation of DMU A2leads to an infeasible problem because itsfirstinput is zero and for evaluation of DMU A3leads to a large score because of a relativelysmall value for itsfirst input.These difficulties can be removed by the MAJ-model.putational experienceIn Jahanshahloo and Alirezaee[11],the evaluation of teaching in the University for Teacher Education was considered.Teaching inputs were expressed in teacher hours and classified in terms of two inputs,professorial staff and instructors.Teaching outputs were expressed in student hours and classified in terms of two outputs,course enrollments in undergraduate and graduate studies.There are six efficient departments whose rankings appear in Table3.The AP-model is infeasible for Department of Women’s Physical,the9th DMU,and Institute of Mathematics,the19th DMU,which are indicated by asterisks.Note that these DMUs have zero inputs.Also,the Department of Theology and Islamic Culture,the2nd DMU,has an overestimation score in the AP-model because of relatively small input.The MAJ-model evaluates the9th and19th DMUs so that they have explicit ranking,and also the2nd DMU now has a more acceptable rank.For the other efficient DMUs,the two rankings are somewhat similar.Table3.Ranking the efficient units by the MAJ-model and the AP-model.EfficiencyDMUs The MAJ-model The AP-model19128%*5110%130%2109%174%15106%133%1105%115%9104%*266MEHRABIAN,ALIREZAEE AND JAHANSHAHLOO5.SummaryIn summary,the AP-model can,in practical application,lead to infeasible programs when some of the inputs vanish or large efficiency score when some of the inputs are small.The MAJ-model alleviates these problems.AcknowledgmentUseful comments from Professor C.van de Panne,the University of Calgary,Professor R.M.Thrall,Rice University,and the anonymous referees are gratefully acknowledged.Note1.Instead of scaling the input data in the MAJ-model,it is possible to change the input constraints to:nj=1 j=p λj x i j≤x i p+w p x iki,i=1,...,m,where x iki=maxj=1,...,nx i jReferences1.P.Andersen and N.C.Petersen,“A procedure for ranking efficient units in data envelopment analysis,”Department of Management,Working Paper No.11/1989,Odense University,Denmark,1989.2.P.Andersen and N.C.Petersen,“A procedure for ranking efficient units in data envelopment analysis,”Management Science,vol.39,pp.1261–1264,1993.3.R.D.Banker,A.Charnes,and W.W.Cooper,“Some models for estimating technical and scale inefficienciesin data envelopment analysis,”Management Science,vol.30,pp.1078–1092,1984.4.R.D.Banker and J.L.Gifford,“Relative Efficiency Analysis,”Unpublished manuscript(A1987versionappeared as a Working Paper,School of Urban and Public Affairs,Carnegie-Mellon University),1991.5.P.Bogetoft,“Incentive efficient production frontiers:An agency perspective on DEA,”Management Science,vol.40,pp.959–968,1994.6.A.Charnes,W.W.Cooper,and E.Rhodes,“Measuring the efficiency of decision making units,”EuropeanJournal of Operation Research,vol.2,pp.429–444,1978.7.A.Charnes,W.W.Cooper,and R.M.Thrall,“A structure for classifying and characterizing efficiency andinefficiency in data envelopment analysis,”The Journal of Productivity Analysis,vol.2,pp.197–237,1991.8.A.Charnes,S.Haag,P.Jaska,and J.Semple,“Sensitivity of efficiency classifications in the additive modelof data envelopment analysis,”International Journal of Systems Science,vol.23,pp.789–798,1992.9.M.L.Durchholz,“Large-scale data envelopment analysis models and related applications,”Ph.D.Thesis,Department of Computer Science and Engineering,Southern Methodist University,Dallas,TX75275,1994.10.J.H.Dula and B.L.Hickman,“Effects of excluding the column being scored from the DEA envelopment LPtechnology matrix,”The Journal of the Operational Research Society,vol.48,pp.1001–1012,1997.11.G.R.Jahanshahloo and M.R.Alirezaee,“Measuring the efficiency of academic units at the teacher traininguniversity,”in Proceeding of the26th Annual Iranian Mathematics Conference,1995,pp.167–171.12.R.G.Thompson,P.S.Dharmapala,and R.M.Thrall,“Importance for DEA of zeros in data,multipliers,andsolutions,”The Journal of Productivity Analysis,vol.4,pp.379–390,1993.13.R.M.Thrall,“Duality,Classification,and Slack in DEA,”Annals Operations Research,vol.66,pp.109–138,1996.。
