格点算面积
正方形格点面积公式

正方形格点面积公式一个正方形是一个具有四条边相等且四个角度都是直角(90度)的四边形。
一个正方形也是一个矩形,因为它满足矩形的定义:对角线相等且相互垂直。
格点是指二维平面上的一个点,其坐标值为整数。
例如,(0,0)、(1,2)和(-3,4)都是格点,而(0.5,0)、(1.3,2.8)和(-3,-1)则不是格点。
现在我们来推导正方形格点面积公式。
假设一个正方形的顶点坐标为(x1,y1),(x2,y2),(x3,y3)和(x4,y4)。
由于正方形的四条边相等,所以可以推导出以下关系:(x2-x1)=(y3-y2)=(x4-x3)=(y1-y4)=a(假设边长为a)由于一个正方形的对角线相等且相互垂直,所以可以推导出以下关系:(x2-x1)^2+(y2-y1)^2=(x3-x4)^2+(y3-y4)^2=2a^2解这组方程,我们得到:(x2-x1)^2+(y2-y1)^2=2a^2(x2-x1)^2+(y2-y1)^2+2(x2-x1)(y2-y1)=4a^2(将左边式子展开)(x2-x1+y2-y1)^2=4a^2(x2-x1+y2-y1)=2a所以,我们得到了正方形格点面积公式的一个关键点,即一个正方形的边长等于其两个对角顶点在同一水平线或垂直线上的格点数量的一半。
接下来,我们来证明正方形的面积等于其边长的平方。
假设正方形的边长为a,面积为A,我们需要证明A=a^2在正方形的格点内部,我们可以形成以格点为顶点的小正方形,以格点为顶点的小正方形的边长是正方形边长a的1/2或1/3或其他分数倍数。
这些小正方形的面积是a^2的一部分。
假设以a/2为边长的小正方形有N1个,以a/3为边长的小正方形有N2个,以a/4为边长的小正方形有N3个,以此类推。
因此,正方形的面积可以表示为:A=a^2+(a/2)^2+(a/3)^2+(a/4)^2+...=a^2(1+1/4+1/9+1/16+...)=a^2(1+1/2^2+1/3^2+1/4^2+...)我们可以使用数学知识证明这个级数的和为π^2/6、所以,我们得到:A=a^2(1+1/2^2+1/3^2+1/4^2+...)=a^2(π^2/6)=(a^2π^2)/6综上所述,我们得到正方形的格点面积公式:A=(a^2π^2)/6这就是正方形格点面积的公式。
格点多边形的面积计算

格点多边形的面积计算
格点多边形是指由若干个在平面上排列的格点构成的封闭图形。
计算格点多边形的面积可以使用格点计数法。
首先,我们需要找到格点多边形内部的所有整数坐标点。
这可以通过扫描整个多边形内部的每个格点来实现。
如果一个格点被多边形边界所覆盖,则该点为内部点;否则为外部点。
接下来,我们需要计算多边形和每个内部点之间的三角形面积。
可以通过计算每个三角形的底和高来实现。
三角形的底可以是一个格点到多边形的一个边界的垂线,而高是从该垂线下的格点到多边形另一条边的距离。
最后,将所有三角形的面积加起来即可得到格点多边形的面积。
需要注意的是,如果多边形边缘上有格点,则需要使用半格来计算面积。
也就是说,半个格点的面积应该被计算在多边形内部。
以上就是格点多边形的面积计算方法。
使用这种方法可以得到准确的结果,但需要花费较多的时间和计算量。
高斯小学奥数四年级下册含答案第04讲_格点图形面积计算
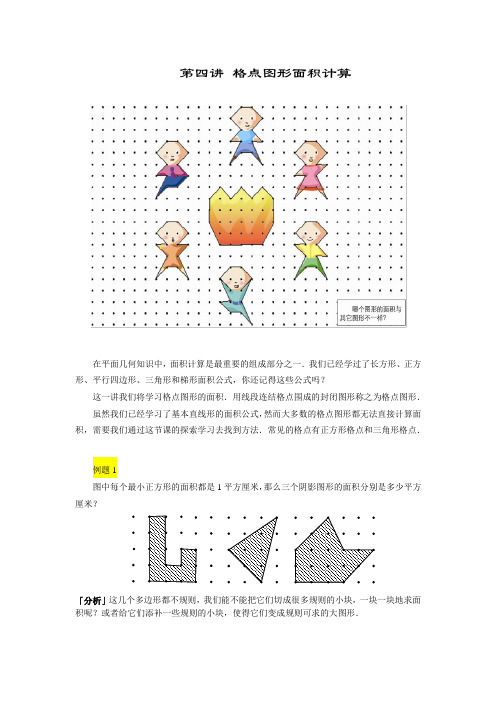
第四讲格点图形面积计算在平面几何知识中,面积计算是最重要的组成部分之一.我们已经学过了长方形、正方形、平行四边形、三角形和梯形面积公式,你还记得这些公式吗?这一讲我们将学习格点图形的面积.用线段连结格点围成的封闭图形称之为格点图形.虽然我们已经学习了基本直线形的面积公式,然而大多数的格点图形都无法直接计算面积,需要我们通过这节课的探索学习去找到方法.常见的格点有正方形格点和三角形格点.例题1图中每个最小正方形的面积都是1平方厘米,那么三个阴影图形的面积分别是多少平方厘米?「分析」这几个多边形都不规则,我们能不能把它们切成很多规则的小块,一块一块地求面积呢?或者给它们添补一些规则的小块,使得它们变成规则可求的大图形.练习1图中相邻两格点间的距离均为1厘米,那么阴影图形的面积分别是多少平方厘米?通过例1中的第1小题我们学会了将大块不规则图形“分割”成许多规则的图形,这种方法称为“分割法”;但是不一定每个图形都很容易分割,第2小题我们学会了把不好算的图形“添补”成规则的大图形,计算时用大图形的面积减去空白部分的面积,这种方法称为“添补法”.分割法,正所谓“大事化小”,把不规则的大图形化为规则的小图形.添补法则正好相反,是“以小见大”,把不规则图形周围添上规则的小图形,使总面积便于计算.使用割、补法的时候,一般应该从图形的顶点出发,尽量沿着格线划分,以便与小方格的面积找到联系或者利用垂直等性质.接下来我们用分割、添补的方法计算一下三角形格点图形的面积.例题2下图是一个三角形点阵,其中能连出的最小等边三角形的面积为1平方厘米.那么这五个图形的面积分别为多少平方厘米?「分析」前三个图是可以直接计算的,④、⑤是无法直接计算的,试着用分割、添补的方法解决吧!我们发现:如果一个三角形的两边都沿三角形格线方向,并且分别是最短线段的m 倍和n 倍,那么这个三角形的面积就是最小等边三角形面积的m n 倍.练习2下图是一个三角形点阵,其中能连出的最小等边三角形的面积为1平方厘米.那么这四个图形的面积分别为多少平方厘米?要计算格点图形的面积,我们只需要应用合适的方法,数一下要求的图形占了几个单位面积即可.当单位面积不为1时,我们就要格外小心了,千万不能在数完后再乘单位面积!对于复杂的格点图形,使用割补法一定能计算面积.但是割补法有时显得有些繁琐,有没有更简单明了的方法呢?那么我们接下来看一个简单快捷的方法.例如,我们要计算如下图的格点多边形的面积(假设最小的正方形面积是1).我们可以用割补的方法求出图形的面积,现在还有另一种方法,从格点数入手.围成阴影部分的边线,经过了一些格点.这些边界上的格点叫做边界格点,一共有12个;格点图形还完全盖住了一些格点,这些图形内部的格点叫做内部格点,一共有1个. 一般的,在最小正方形面积为1的正方形网格中,我们有:这样,按公式计算:122116÷+-=,我们就得出图中阴影部分的面积了.例题3 如图,相邻两格点间的距离均为1厘米,求阴影部分的面积?「分析」尝试着用格点图形面积公式计算一下把!先数数边界格点、内部格点分别有多少个呢?练习3如图,每一个最小正方形的面积都是2,阴影部分的面积是多少?类似地,在最小正三角形面积为1的三角形网格中,三角形格点图形也有面积计算公式:仔细比较这两个公式,可以发现:三角形格点的公式正好是正方形格点公式的2倍.大家想一下,为什么是这样呢?例题4如图,每个最小等边三角形的面积都是1平方厘米.阴影部分的面积是多少平方厘米?「分析」尝试着用格点图形面积公式计算一下把!先数数边界格点、内部格点分别有多少个呢?练习4如图,每个最小等边三角形的面积都是1平方厘米,阴影部分的面积是多少平方厘米?例题5如图,每一个最小正方形的面积都是3平方厘米.阴影部分的面积是多少平方厘米?「分析」试着比较分割法、添补法、公式法,这三个方法哪个更合适呢?例题6(1)左图中每个最小正三角形的面积是2平方厘米.阴影部分面积是多少平方厘米?(2)右图中每个最小正三角形的面积是4平方厘米.阴影部分面积是多少平方厘米?「分析」试着比较分割法、添补法、公式法,这三个方法哪个更合适呢?对于大部分格点图形而言,分割法和添补法都可以用来求面积.对于特殊的格点图形,如果不易分割,可以试试添补;如果不易添补,可以试试分割.如果用分割法和添补法都不易解决,那么格点公式就派上用场了!在使用格点公式时,有以下几点需要注意:(1)注意是正方形格点还是三角形格点;(2)按照顺序来数边界格点和内部格点;(3)用格点公式计算出来的不是面积,而是最小的正方形或正三角形的面积的倍数.看似这一讲的题目不是很难,怎么保证计算的准确性呢?如果你用分割法计算面积,不妨再用添补法验算一下.如果你用割补法计算面积,不妨再用格点公式算一算.用不同方法得到的都是同样的结果,基本上就不会出错了.课堂内外几何的起源古埃及人聚居在尼罗河附近,以在河边的农田耕作为生.可是尼罗河每隔一段时间会泛滥,河水涌上岸,把河边的农田淹没,冲毁农田的边界.所以,每次河水泛滥后,埃及人都要重新划分农田的范围和界限.埃及人在划分土地时,发现很多不同形状的农田,都可以分割为几块较细小的三角形农田,例:1块长方形农田2块大小相同的三角形农田1块梯形农田3块三角形农田这些不同形状的农田,其实就是不同的几何图形;把农田分割为几块较细小的农田,即是把几何图形分割.原来古埃及人是研究几何图形的先锋呢!作业1. 如图,每相邻两个格点的距离都是1,那么两个阴影图形的面积分别是________、________.2. 下图中三角形点阵所能连出的最小正三角形面积为1,图中两个图形的面积分别是________、________.3. 如图,最小正三角形的面积是4平方厘米,那么阴影部分的面积是________平方厘米.4. 右图中,每个最小正方形面积为2,则图中阴影部分的面积是________.5. 下图三角形点阵所能连出的最小正三角形面积为2,图形的面积是_________.第四讲 格点图形面积计算1. 例题1答案:7平方厘米;5平方厘米;11平方厘米详解:如图所示,用分割法、添补法.三个图形的面积分别是:4111127⨯+⨯+⨯=平方厘米; 4⨯⨯÷32⨯⨯÷2. 例题2答案:6;12;4;7;9详解:①:326⨯=平方厘米;②:4312⨯=平方厘米;③:224⨯=平方厘米;3. 例题3答案:6.5平方厘米 详解:内部格点:3个,边界格点:9个.面积=3921 6.5+÷-=平方厘米.4. 例题4答案:34平方厘米详解:内部格点:7个;边界格点:22个.面积:7222234⨯+-=平方厘米.5.例题5答案:19.5平方厘米;31.5平方厘米④: ⑤: 121212+17⨯+⨯+⨯= 或:441313137⨯-⨯-⨯-⨯= 2339⨯+= 或:441212139⨯-⨯-⨯-⨯=详解:可以分割、添补,也可以用公式法:(1)内部格点:4个;边界格点:7个.面积:()7241319.5÷+-⨯=平方厘米;(2)内部格点:8个;边界格点:7个.面积:()7281331.5÷+-⨯=平方厘米.6. 例题6答案:28平方厘米;56平方厘米详解:可以分割、添补,也可以用公式法:(1)内部格点:4个;边界格点:8个.面积:()4282228⨯+-⨯=平方厘米;(2)内部格点:3个;边界格点:10个.面积:()32102456⨯+-⨯=平方厘米.7. 练习1答案:3平方厘米;10平方厘米详解:如图,分别用分割法、添补法.8. 练习2答案:12;20;5;18 详解:①:3412⨯=平方厘米; ②:直接数,每层4个,共5层,4520⨯=9. 练习3答案:13 简答:内部格点:1个,边界格点:13个.面积=()11321213+÷-⨯=.10. 练习4答案:17平方厘米简答:内部格点:1个;边界格点:17个.面积:1217217⨯+-=平方厘米. ③: ④:1112125⨯+⨯+⨯= 122312818⨯+⨯+⨯+=11.作业1答案:6;6.5简答:可用分割或添补法完成.12.作业2答案:7;12简答:使用割补法分别计算.13.作业3答案:56简答:大正三角形的面积是254100⨯=平方厘米,利用添补法可得.14.作业4答案:29简答:综合利用分割法与添补法.也可以用正方形格点图形面积公式计算.注意每个最小正方形面积是2.15.作业5答案:44简答:综合利用分割法与添补法.也可以用三角形格点图形面积公式计算.注意每个最小正三角形面积是2.。
数格子估算面积与数格点估算面积———应用皮克定理在小学数学中进行估算
教材研究新课程NEW CURRICULUM《义务教育数学课程标准(2011年版)》对于估算有明确的要求,即“理解估算的意义”“会用方格纸估计不规则图形的面积”。
很多教师认为估算是在不要求精确计算的情况下使用的一种能快捷求出近似结果的计算方法,或者是检验精算结果是否正确的验算方法。
但是他们没有意识到,估算更重要的功能在于培养学生的数感、观察能力、空间想象能力和逻辑推理能力。
一、教材中对曲线图形面积的估算江苏教育出版社小学数学教材五年级上册第22页有这样一道例题:例11.下面是某自然保护区一个湖泊的平面图,如图1,(每个小方格表示1公顷)。
你能估计这个湖泊的面积大约是多少公顷吗?通过数格子来估算,55个整格,34个非整格,非整格的算半格,这个湖泊的面积大约是72公顷。
图1这个图形面积的准确值应该在55与89之间,上述估算方法不够精确,思维含量偏低,也较难引起学生的兴趣,有没有其他的估计方法呢?二、数格点估算面积1.数格点算面积的方法介绍通过阅读文献,我们认为,有一种数格点计算多边形面积的方法可以用来估算曲线图形的面积。
这种方法起源于格点多边形。
所谓格点多边形,就是说这个多边形的顶点全是格点,如图2:设S 为图2的面积,L 是边界上的格点数(组成格子的横竖线的交叉点正好在图形的边上),N 是内部格点数(交叉点在图形的内部),容易计算出图形面积是11。
如果联系到图形的L =6及N =9,还有L 2+N -1的关系式成立,这种方法是否具有一般性呢?2.数格点估算面积方法合理性的说明数格子的估计方法学生应该是可以理解的,但是数格点估算面积的方法有何依据呢?先以格点矩形为例。
看图3。
设图3矩形的长和宽分别为m 和n ,则面积S=mn 。
再来考虑这个矩形的边界格点数L ,L =2(m +1)+2(n -1);内部格点数N =(m -1)(n -1);而L 2+N -1=m +n +mn -m -n+1-1=mn ,所以关系式S =L 2+N -1对格点矩形是成立的。
格点与面积_小学奥数知道点详解

如下图,在一张由一组水平线和一组垂直线组成方格纸上,如果任意相邻平行线之间的距离都相等,我们就把这样两组平行线的交点称为格点(如下图中的红点),把图中相邻两个格点的距离看着一个单位长度,把每个小正方形的面积看作一个面积单位(如图中带阴影的方格)。
一个多边形的顶点如果全是格点,这个多边形就叫做格点多边形,本讲就,学习求格点多边形的面积问题。
这种格点多边形的面积计算起来很方便,一般有三种方法:①规则的格点多边形,可以运用多边形的面积公式求出面积;②一些简单而又特殊的格点多边形,可以通过数格子求出面积;③较复杂的不规则图形,一般用皮克公式计算。
其中数格子的方法比较原始,很少用。
任意格点多边形,只要数出多边形周界上的格点的个数及图内格点的个数,就可用下面的皮克公式算出面积:格点多边形面积=内格点个数 + 边格点数÷2-1这个公式是皮克(Pick)在1899年给出的,被称为“皮克定理”,这是一个实用而有趣的定理。
皮克定理的证明:将格点图中的每个点看作以这个点为圆心、以单位面积正方形的边长的一半为半径的圆。
格点多边形图内的点对应的圆的面积都是图形面积的一部分;而在多边形边界上的点对应的圆的面积只有一半属于这个多边形,且多边形每个角上的圆属于图内的面积都不到半个圆,少了其外角对应的扇形面积,因任意多边形的外角和是360度,正好是个整圆,所以周界上圆在图内的面积为:周界格点数÷2-1所以格点多边形面积为:图内格点个数+周界格点数÷2-1。
皮克定理的证明过程比较抽象,孩子难以理解。
本讲只要求孩子初步认识格点面积公式,掌握格点面积公式的应用,到初中还会进一步学习皮克定理。
例1:求下面各图形的面积。
【解析】:图①是个平行四边形,周界上有10个格点,图内有4个格点,根据格点面积公式,图①的面积为:4+10÷2-1=8;图②是个梯形,周界上有8个格点,图内有2个格点,根据格点面积公式,图②的面积为:2+8÷2-1=5;图③是个三角形,周界上有6个格点,图内有4个格点,根据格点面积公式,图③的面积为:4+6÷2-1=6;以上3个图形都是规则图形,但四年级学生还没有学过这3种图形的面积计算,不能用面积公式计算。
正方形格点面积公式

正方形格点面积公式
正方形格点面积公式是指一个正方形的面积可以用其边长的平方
除以2表示。
在计算正方形面积的过程中,我们可以使用不同的公式,例如正方形的面积可以使用边长乘以自身来计算,也可以使用对角线
的平方除以2来计算。
这些公式的计算方式都十分简单,但是在实际
应用中需要根据不同场景和需求灵活选择。
对于正方形格点面积,我们可以将其看作由若干个单位正方形组
成的图形。
每个单位正方形的面积为1,因此正方形格点面积所包含的单位正方形数量即为其面积的大小。
也就是说,一个边长为n的正方
形格点面积为n的平方。
此外,正方形格点面积公式在计算面积时还需要考虑格点的特殊
性质。
由于每个格点处都有一个坐标值,因此我们可以通过在坐标系
中标出正方形各个顶点的坐标值来计算正方形格点面积。
例如,当一
个正方形的顶点坐标分别为(x1,y1)、(x1,y2)、(x2,y2)和
(x2,y1)时,该正方形的面积可以用公式(x2 - x1)*(y2 - y1)
来计算。
总之,正方形格点面积公式简单易用,是计算正方形面积的常见
方法之一。
无论是在学习中还是在实际运用中,都具有一定的实用性
和价值。
正方形格点阵中多边形面积的计算公式
正方形格点阵中多边形面积的计算公式在正方形格点阵中,如果要计算多边形的面积,可以使用Pick定理或Shoelace定理两种方法。
1. Pick定理:Pick定理是一种用于计算多边形面积的简单而直观的方法,适用于多边形的顶点坐标都是整数的情况。
Pick定理的公式如下:面积=内部格点数+边上格点数/2-1其中,内部格点数表示多边形内部的格点数,边上格点数表示多边形边上的格点数。
假设我们有一个正方形格点阵,边长为a。
我们需要计算一个有n个顶点的多边形的面积。
首先,我们可以通过计算内部格点数和边上格点数来应用Pick定理。
内部格点数可以通过计算多边形内部的数量来获得。
画出多边形的边,可以看到多边形内部的格点数为S = a-2,即正方形的边长减去两个。
边上格点数可以通过计算多边形的边界格点数来获得。
每个边上有a个格点,因此多边形的边上格点数为n*a。
将这些值代入Pick 定理的公式,即可计算多边形的面积。
2. Shoelace定理:Shoelace定理是一种更普遍适用的方法,适用于多边形的顶点坐标可以是任意实数的情况。
Shoelace定理的公式如下:面积 = ,(x1*y2 + x2*y3 + ... + xn*y1) - (y1*x2 + y2*x3 + ... + yn*x1), / 2其中,(x1, y1), (x2, y2), ..., (xn, yn) 是多边形的顶点坐标,按逆时针方向排列。
假设我们有一个正方形格点阵,边长为a。
我们需要计算一个有n个顶点的多边形的面积。
首先,我们可以计算出多边形每个顶点的坐标。
对于正方形格点阵,每个格点的坐标可以表示为(i, j),其中i和j分别为行和列的索引。
我们可以将顶点坐标代入Shoelace定理的公式,从而计算多边形的面积。
需要注意的是,Shoelace定理的公式中的坐标需要按逆时针方向排列,以确保计算的结果为正。
综上所述,对于正方形格点阵中的多边形面积的计算,我们可以采用Pick定理或Shoelace定理两种方法。
格点多边形面积计算公式证明
格点多边形面积计算公式证明
格点多边形面积计算公式证明
几何学中,多边形面积计算问题一直以来颇受关注,格点多边形面积计算公式(Centroid Area Formula)也在相关概念中,占有关键的位置。
这个公式可以用
来有效的计算无论是几何图形的面积或者是多边形的面积。
本文将对这个公式的证明进行简要的说明。
格点多边形面积计算公式的证明依赖于一个基本的几何图形——无论是一个多
边形或者是一个圆形,都可以被用若干个无任何相似多边形拆分所替代。
对于任意一个多边形来说,它的面积就等于由这些相似多边形拆分出来子多边形总和。
此时,上述公式就可以用来计算拆分出来这些多边形的面积了。
就这个公式来说,它是通过矩形公式(Moment of Inertia Formula)和盒体
公式(Centroid Area Formula),将若干个多边形的面积叠加起来;首先利用盒
体公式,确定出多边形的质点,也就是多边形的重心,再利用矩形公式,确定这些多边形拆分出来的子多边形的面积总和。
具体而言,若多边形拆分出来有N个
(N>=3),且它们都有相同的弧度,则格点多边形面积计算公式如下:
面积= 52*Σi/N * sinθ/2 * Ri2
其中Σi/N 指的就是所计算的多边形的质点的值;sinθ/2指的是格点多边形
的圆心角的sin值;Ri2指的是所拆分出来的N个多边形的半径平方的读书。
通过上面的推导,我们可以得出格点多边形面积计算公式的证明,从而为计算
不同形状多边形面积提供了有效的方法。
毕克定理
巧用毕克定理妙解格点面积
上星期在上数学奥数的时候,发现其中的小狗图学生理解比较难,解题比较复杂。
所以我特意加了一节课,让学生对格点面积有个更清楚的认识,学会这类图形面积的计算。
在正方形的方格纸中.每个小方格的顶点叫做格点,这样就建立了一个方格网,方格网中任意两个相邻的交点间的距离均为一个单位.如果方格网中有一个多边形,它的每个顶点均为格点。
那么这个多边形叫做格点多边形。
这种格点多边形的面积计算我们使用毕克定理来计算很方便.
格点面积=内部格点数+周界格点数除以2再减1
注意点:一是毕克定理只对格点凸多边形适用,二是在数格点时要细心.。
第一讲格点与面积
第一讲格点与面积问
学习锦囊在一张纸上,先画出一些水平直线和一些竖直直线,并使任意两条相邻的平行线的距离都相等(通常规定是1个单位),这样在纸上就形成了一个方格网,其中的每个交点就叫做一个格点.在方格网中,以格点为顶点画出的多边形叫做格点多边形,例如,右图中的乡村小屋图形就是一个格点多边形.
回顾与反思这是等差数列问题的应用题。通过细心观察,深入分析,我们可以探索得出一些题目中隐含着一个等差数列,然后可以运用等差数列求和的公式求得结果。
基础练习
1. 12个同学聚会,如果见面时每个人都和其余的人握手一次,那么一共握手多少次?
2.小红看一本书,第一天看了3页,以后每天都比前一天多看2页,10天刚好看完,这本书总共多少页?
例42001年10月1日是星期一,那么,2002年1月1日是星期几?
一个星期是7天,因此7天为一个周期。10月1日是星期一,是第一个周期的第一天,再过7天即10月8日也是星期一。计算天数时为了方便,我们采用“算尾不算头”的方法,例如10月8日就用(8-1)÷7=1.没有余数说明8号仍是星期一。题中说从2001年10月1日到2002年1月1日,经过几天这才是这道题的关键。
2.777777+888888+999999的个位数字是几?
例33200被13除的余数是几?
3200表示200个3相乘,那么我们可以从1个3被13除,2个3被13除……,它们的余数中找到周期规律
31÷13=0……334÷13=6……3
