格点算面积
几何图形六年级

几何图形题型一:格点图形的面积计算(毕克定理) 1、正方形格点多边形的面积计算公式:(毕克定理)正方形格点多边形的面积=内点个数+界点个数÷2-1,如果用S 表示面积,N 表示图形内包含的格点数,L 表示图形周界上的格点数,那么,正方形格点面积可以表示为:S =N +12L -1。
2、三角形格点多边形及其面积计算公式每相邻三点成“∵”或“∴”,所形成的三角形都是等边三角形,规定它的面积为1,以这样的点为顶点画出的多边形为三角形格点多边形。
三角形格点多边形的面积计算公式:(毕克定理)三角形格点多边形的面积=(内点个数+界点个数÷2-1)×2,如果用S 表示面积,N 表示图形内包含的格点数,L 表示图形周界上的格点数,那么,三角形格点面积可以表示为:S =(N +12L -1)×2。
注意:1.毕克定理对任何格点图形都适用。
要区分面积是几个单位。
2.在数格点时要细心。
3.严格区分正方形格点多边形和三角形格点多边形。
正方形格点图形的面积[模型例题1.]如图是用橡皮筋在钉板上围成的一个三角形,计算它的面积是多少。
(每相邻两个小钉之间的距离都等于1个长度单位)分析 直接套用正方形格点多边形面积公式“正方形格点多边形的面积=内点个数+界点个数÷2-1”即可解答。
解:5+3÷2-1=5.5 答:三角形的面积为5.5。
[模型例题2.]如图所示,在边长为1厘米的正方形格点中,图形“”的面积是多少平方厘米?分析直接套用正方形格点多边形面积公式“正方形格点多边形的面积=内点个数+界点个数÷2-1”即可解答。
解:6+10÷2-1=10(平方厘米)答:图形“”的面积是10平方厘米。
三角形格点图形的面积[模型例题3.]下图中有28个点,其中每相邻的三点“∵”或“∴”所形成的三角形都是面积为1的等边三角形,试计算△ABC的面积。
分析直接套用三角形格点多边形面积公式“三角形格点多边形的面积=(内点个数+界点个数÷2-1)×2”即可解答。
四年级奥数专题 格点与面积(学生版)

学科培优数学“格点与面积”学生姓名授课日期教师姓名授课时长知识定位本讲知识点比较简单,首次引入面积这个概念,主要是培养学生对图形面积的感觉与认识。
【授课批注】在开始讲解面积这个概念之前可适当复习有关图形周长的概念,帮助学生区分周长和面积。
知识梳理格点图形的概念在一张纸上,先画出一些水平直线和一些竖直直线,并使任意两条相邻的平行线的距离都相等(通常规定是1个单位),这样在纸上就形成了一个方格网,其中的每个交点就叫做一个格点.在方格网中,以格点为顶点画出的多边形叫做格点多边形。
a)正方形格点正方形格点问题就是它的格点都是由两组互相垂直相交的平行线的交点构成的.每一个小方格都是一个小正方形b)三角形格点所谓三角形格点多边形是指:每相邻三点成“∵”或“∴”,所形成的三角形都是等边三角形.规定它的面积为1,以这样的点为顶点画出的多边形为三角形格点多边形.【授课批注】讲解格点图形概念的时候最好能借助诸如钉子板之类的道具,提高教学的形象性,更容易让学生理解,加深印象。
【重点难点解析】1.方形格点与三角形格点面积的特点2.格点图形的分割与拼补【竞赛考点挖掘】1.两种格点图形的基本面积计算2.格点图形面积的等量变形例题精讲【试题来源】【题目】判断下列图形哪些是格点多边形?【试题来源】【题目】如右图,计算各个格点多边形的面积.【试题来源】【题目】如右图(a),计算这个格点多边形的面积.【试题来源】【题目】右图是一个方格网,计算阴影部分的面积.【试题来源】【题目】分别计算右图中两个格点多边形的面积。
【试题来源】【题目】如图“乡村小屋”的面积是多少?【试题来源】【题目】第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一个小方格的面积是1,那么7、2、1三个数字所占的面积之和是多少?习题演练【试题来源】【题目】右图中每个小正方形的面积都是1,那么图中这只“狗”所占的面积是多少?【试题来源】【题目】用9个钉子钉成相互间隔为1厘米的正方阵(如右图).如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形,这样得到的三角形中,面积等于1平方厘米的三角形的个数有多少? 面积等于2平方厘米的三角形有多少个?【试题来源】【题目】在4×7的方格纸板上面有如阴影所示的“6”字,阴影边缘是线段或圆弧.问阴影面积占纸板面积的几分之几?【试题来源】【题目】右图是5×5的方格纸,小方格的面积是1平方厘米,小方格的顶点称为格点.请你在图上选7个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用直线连接后所围成的面积尽可能大.那么,所围图形的面积是______平方厘米.【试题来源】【题目】如图,每一个小方格的面积都是l平方厘米,那么用粗线围成的图形的面积是多少平方厘米?【试题来源】【题目】如图(a),有21个点,每相邻三个点成“∵”或“∴”,所形成的三角形都是等边三角形.计算三角形ABC的面积.【试题来源】【题目】如右图,每相邻三个点所形成的三角形都是面积为1的等边三角形,计算△ABC的面积.【试题来源】【题目】如右图,每相邻三个点所形成的三角形都是面积为1的正三角形,计算四边形ABCD 的面积.【试题来源】【题目】把大正三角形每边八等份,组成如右图所示的三角形网.如果大三角形的面积是128,求图中粗线所围成的三角形的面积.【试题来源】【题目】如图涂阴影部分的小正六角星形面积是16平方厘米,问:大正六角星形面积是多少平方厘米?【试题来源】【题目】如果下图中任意相邻的三个点构成的三角形面积都是2平方厘米.那么,三角形ABC 的面积是_____平方厘米【试题来源】【题目】把同一个三角形的三条边分别5等分、7等分(如图l图2),然后适当连接这些等分点,便得到了若干个面积相等的小三角形.已知图1中阴影部分面积是294平方分米,那么图2中阴影部分的面积是______平方分米.【试题来源】【题目】如图,如果每一个小三角形的面积是1平方厘米,那么四边形ABCD的面积是多少平方厘米?【试题来源】【题目】求下列各个格点多边形的面积【试题来源】【题目】右图是一个8 12面积单位的图形.求矩形内的箭形ABCDEFGH的面积.【试题来源】【题目】求下列格点多边形的面积(每相邻三个点“∵”或“∴”成面积为1的等边三角形).【试题来源】【题目】右图有12个点,相邻两个点之间的距离是1厘米,这些点可以连成多少个面积为2平方厘米的三角形?【试题来源】【题目】将图中的图形分割成面积相等的三块.。
格点法求面积的公式

面积计算公式:皮克公式:格点多边形面积=多边形一周的格点数÷2+多边形内部格点数-1
设格点多边形的面积为s,它各边上格点的个数和为x。
格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请写出s与x之间的关系式。
格点的起源
格点问题起源于以下两个问题的研究:
1、狄利克雷除数问题,即求x>1时D2(x)=区域{1≤u≤x,1≤v≤x,uv≤x}上的格点数。
1849年,狄利克雷证明了D2(x)=xlnx+(2ν一1)x+△(x),这里ν为欧拉常数,△(x)=O(x0.5)。
这一问题的目的是要求出使余项估计△(x)=O(x)成立的又的下确界θ0。
2、圆内格点问题,设x>1,A2(x)=圆内μ+ν≤x上的格点数。
高斯证明了A2(x)=πx+R(x),这里R(x)=O(x^1/2),求使余项估计R(x)=O(x)成立的λ的下确界α的问题,称之为圆内格点问题或高斯圆问题。
三角形格点面积求法

三角形格点面积求法在平面直角坐标系中,我们可以用格点来表示点的位置。
一个格点就是一个整数坐标点,例如(1,2)、(3,4)等等。
而一个三角形可以由三个不同的格点组成,我们可以通过这些格点来计算三角形的面积。
我们需要知道如何计算两个格点之间的距离。
假设有两个格点A(x1,y1)和B(x2,y2),它们之间的距离可以用勾股定理来计算:AB = √((x2-x1)² + (y2-y1)²)接下来,我们可以用海龙公式来计算三角形的面积。
假设三角形的三个顶点分别为A(x1,y1)、B(x2,y2)和C(x3,y3),则三角形的半周长可以用以下公式计算:s = (AB + AC + BC) / 2其中,AB、AC和BC分别为三角形的三条边的长度。
接下来,我们可以用以下公式来计算三角形的面积:S = √(s(s-AB)(s-AC)(s-BC))这个公式被称为海龙公式,它可以用来计算任意三角形的面积,不论是由格点组成的三角形还是由实数坐标点组成的三角形。
举个例子,假设有一个三角形,它的三个顶点分别为A(1,1)、B(3,2)和C(2,4)。
我们可以先计算出三条边的长度:AB = √((3-1)² + (2-1)²) = √5AC = √((2-1)² + (4-1)²) = √10BC = √((3-2)² + (2-4)²) = √5然后,我们可以计算出半周长:s = (AB + AC + BC) / 2 = (√5 + √10 + √5) / 2我们可以用海龙公式来计算三角形的面积:S = √(s(s-AB)(s-AC)(s-BC)) = √(s(s-AB)(s-AC)(s-BC)) = √(5/2 * 3/2 * 1/2 * 3/2) = 3/4因此,这个三角形的面积为3/4平方单位。
总结一下,我们可以用格点来表示三角形的顶点,然后用勾股定理来计算三角形的边长,最后用海龙公式来计算三角形的面积。
数格点算面积

图形序号 N
L
S
S与L的关 系
小组探究
满 足 条 件 N=2 的 格 点 多 边 形 中S、L之间的关系
活动三
画 几 个 满 足 条 件 N=2 的 格 点多边形 ,请填写表格:
图形序号 N
L
S
S与L的关 系
小组探究
满 足 条 件 N=3 的 格 点 多 边 形 中S、L之间的关系
活动四
画 几 个 满 足 条 件 N=3 的 格 点多边形 ,请填写表格:
图形序号 N
L
S
S与L的关 系
猜想归纳
N=0 N=1 N=2 N=3
S=1 L 1
2
S= 1 L+0
2
S=1 L 1
2
S=12 L 2
S=
1 L N 1 2
验证猜想
请你再画一个图形,验证所得
S=
1 L N 1 2
的正确性
L=15;LN==1177,,红S色=7多.5+边17形-1的=2S3.较5 大? LN==1177;;NN==1166,,S黄=色8.5多+边16形-1=的23S.5较大?
A
如果一个多边形的
E
顶点都在格点上,那么 B
这种多边形叫做格点多
C
DБайду номын сангаас
边形.
任务1
A
E
你会求图中格点多边
B
形的面积吗?请试一试!
C
D
方法提炼
B C
E D
补
B C
E D
割
有趣的是:
这种格点多边形的面积可以根据图形 内部及它的边上的格点的数目来计算, 算法十分简捷。
数格点 算面积

的正确性?
问题情境
L=15;L ,红色多边形的 S较大? N=17 =17 ,S=7.5+17-1=23.5 L S=8.5+16-1=23.5 N=17 =17; ;N N=16 =16, ,黄色多边形的 S较大?
活动小结
拓展研究
如果每相邻的四个点构成的小矩形的面积是 1,那么还 能用“皮克公式”来求多边形的面积吗?
0 0 0 0
3 4 5 6
0.5 1 1.5 2
1 S= 2 L-1
探究开始啦!
猜想归纳
N=0
N=1 N=2
N=3
S=
1 S= 2 L 1 1 S= L+0 2 1 S= L 1 2 1 S= 2 L 2
1 L N 1 2
验证猜想
你将如何验证归纳所得
S=
1 L N 1 2
☆ 1889 年发现了 S 、 L 、 N 三者数量关 系的“皮克公式”,并进行了证明,得 到“皮克定理”。
☆“皮克定理”被誉为有史以来“最重要 100 个数学定 理”之一。
活动任务
设格点多边形的面积为S,它的边上的格 点数为L,内部的格点数为N。
探究S与L、N之间的数量关系。
探究模拟
探究N=0的格点多边形中S与L之间的数量关系
拓展研究
如果每相邻的三个点构成的小等边三角形的面积是1 , 那么还能用“皮克公式”来求多边形的面积吗?
八年级数学实验课
数格点 算面积
连云港市新海实验中学 姜晓刚
预备知识
格点多边形的面积记为 S 格点多边形的边上的格点 的数量记为L 格点多边形的内部的格点 的数量记为NFra bibliotek问题情境
L=15;L=17,红色多边形的S较大?
格点多边形的面积计算

格点多边形的面积计算方法一:直接计算法直接计算法是最简单的计算格点多边形面积的方法,它基于平行坐标轴的直线与多边形相交的方法。
假设我们有一个以原点为起点的多边形,该多边形的边界由一系列的点组成,每个点的坐标都是整数。
我们可以将原点与多边形上的每个点分别与x轴和y轴构成的直线相交,得到一系列的交点,将这些交点连成一个新的多边形,它的面积就是我们要计算的格点多边形的面积。
具体的计算步骤如下:1.对于多边形中的每个顶点,分别将其与x轴和y轴构成的直线相交,并得到交点的坐标。
2.将这些交点按顺时针或逆时针的顺序依次连接起来,得到一个新的多边形。
3.使用新的多边形的顶点坐标计算其面积,可以使用多边形面积计算公式。
这种方法的优点是简单易懂,但是需要较多的计算步骤。
方法二:Shoelace公式Shoelace公式是一种通过顶点坐标计算多边形面积的方法,它适用于任意多边形的计算。
具体的计算步骤如下:1.将多边形的顶点按顺时针或逆时针的顺序依次标记为P1,P2,...,Pn。
2. 根据顶点的坐标,计算每一相邻顶点之间的乘积,即(x1y2+x2y3+...+xn-1yn+xny1)-(x2y1+x3y2+...+xnyn-1+x1y1)。
3.以绝对值的形式累加所有的乘积,得到的结果除以2即为多边形的面积。
例如,对于一个三角形ABC,顶点A的坐标为(x1,y1),顶点B的坐标为(x2,y2),顶点C的坐标为(x3,y3),则多边形的面积可以通过以下公式计算:(x1y2+x2y3+x3y1)-(x2y1+x3y2+x1y3)/2该方法的优点是计算步骤相对较少,适用于任意多边形。
方法三:Pick定理Pick定理是一种用于计算格点多边形面积的方法,它基于格点多边形的顶点和内部格点数量之间的关系。
具体的计算步骤如下:1.统计格点多边形内部的格点数量,其中格点的定义是坐标为整数的点,不包括多边形的边界上的点。
2.统计格点多边形边界上的格点数量,其中格点的定义是坐标为整数的点。
【详解】四年级下第04讲_格点图形面积计算
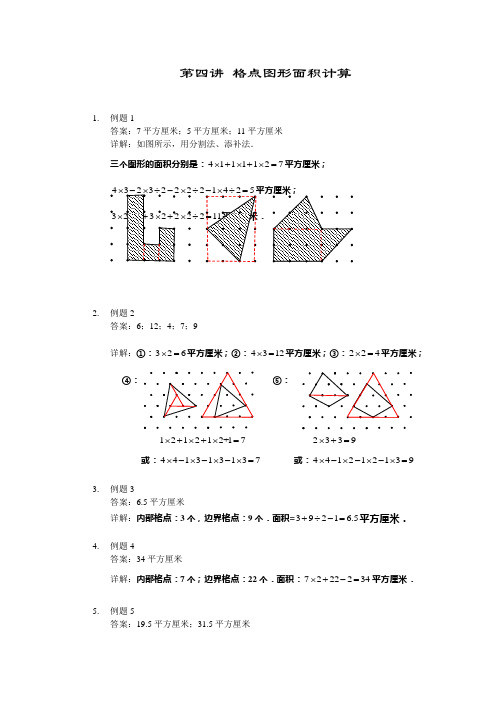
第四讲 格点图形面积计算1. 例题1答案:7平方厘米;5平方厘米;11平方厘米详解:如图所示,用分割法、添补法.三个图形的面积分别是:4111127⨯+⨯+⨯=平方厘米; 4⨯⨯÷32⨯⨯÷2. 例题2答案:6;12;4;7;9详解:①:326⨯=平方厘米;②:4312⨯=平方厘米;③:224⨯=平方厘米;3. 例题3答案:6.5平方厘米 详解:内部格点:3个,边界格点:9个.面积=3921 6.5+÷-=平方厘米.4. 例题4答案:34平方厘米详解:内部格点:7个;边界格点:22个.面积:7222234⨯+-=平方厘米.5.例题5答案:19.5平方厘米;31.5平方厘米④: ⑤: 121212+17⨯+⨯+⨯= 或:441313137⨯-⨯-⨯-⨯= 2339⨯+= 或:441212139⨯-⨯-⨯-⨯=详解:可以分割、添补,也可以用公式法:(1)内部格点:4个;边界格点:7个.面积:()7241319.5÷+-⨯=平方厘米;(2)内部格点:8个;边界格点:7个.面积:()7281331.5÷+-⨯=平方厘米.6. 例题6答案:28平方厘米;56平方厘米详解:可以分割、添补,也可以用公式法:(1)内部格点:4个;边界格点:8个.面积:()4282228⨯+-⨯=平方厘米;(2)内部格点:3个;边界格点:10个.面积:()32102456⨯+-⨯=平方厘米.7. 练习1答案:3平方厘米;10平方厘米详解:如图,分别用分割法、添补法.8. 练习2答案:12;20;5;18 详解:①:3412⨯=平方厘米; ②:直接数,每层4个,共5层,4520⨯=9. 练习3答案:13 简答:内部格点:1个,边界格点:13个.面积=()11321213+÷-⨯=.10. 练习4答案:17平方厘米简答:内部格点:1个;边界格点:17个.面积:1217217⨯+-=平方厘米. ③: ④:1112125⨯+⨯+⨯= 122312818⨯+⨯+⨯+=11.作业1答案:6;6.5简答:可用分割或添补法完成.12.作业2答案:7;12简答:使用割补法分别计算.13.作业3答案:56简答:大正三角形的面积是254100⨯=平方厘米,利用添补法可得.14.作业4答案:29简答:综合利用分割法与添补法.也可以用正方形格点图形面积公式计算.注意每个最小正方形面积是2.15.作业5答案:44简答:综合利用分割法与添补法.也可以用三角形格点图形面积公式计算.注意每个最小正三角形面积是2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S L2N 2
7
1
2
2
S L2 2
3
S L23 2
…
…
…
NL
S 值
当N等于0 时S与L之 间关系式
当N等 在N=0基础之 于0时S 上增加多少
值
现S与N、L 之间的关系
14
4 S L2
2
2
2
2
1
S L2N 2
24 6
2
S L2 2
2 2
2
S L2N 2
34 8
S L2
2
2
2
2
3
S L2N 2
…
N L S值 当N等于 当N等于 在N=0基础 现S与N、L
0时S与 0时S值 之上增加多 之间的关系
N之间关
少
系式
结论
1
6
6
S L2
4
2
2
2
2
6
8 S L2
4
2
2
2
3
6
10 2
S L2 2
4 2
…… …
…
1
S L2 1 2
2
S L22
S L2N 2
2
3
S L23
2
…
三、对比分析收获成果
第一阶段:课前准备 知识预备:格点多边形
格点多边形:方格网中的每个
交点叫做格点(如右图中的点A、 B、C、D、E…),每一个小方格
C
的边长是1个单位长度即是每个小
正方形的面积为1如右图阴影正方
形.
如果一个多边形的所有顶点
D
都在格点上,那么这个多边形叫做
格点多边形(如图中的多边形
ABCDE)
B A
E
二、课前回顾(个人展示)
第一阶段:课前准备
1.如右图,网格小正方形的边长
为1,
求△ABC的面积
A
分析:针对这个问题目前我们学过两种思 想方法:①分割思想,②拼凑思想
B
思考:网格点与三角形有几种位置
C
关系?
三种:在三角形外部、在三角形
边上以及在三角形内部。
由此我们知道与格点多边形有关的格点有两部分,一部分是边上的格点、还有就 是多边形内部的格点。接下来我们一起来探讨用与格点多边形有关的格点来计 算格点多边形的面积。
五、小结
1、过程小结: 经历了画图、列表、分析数据、寻找规律
的过程
2、 方法小结: 在“探求规律性问题”时,先明确变量,然后通
过固定某些变量的值来探求其余变量的变化规律,“以不变应 万变”帮助我们简化问题。
六、课后训练
1、课前回顾△ABC的面积用此公式怎么算?结果和我们之前的计算结果相同吗?
2、如下图,在边长为1的正方形网格中数格点算面积,看谁又快又准。
(5,3),(5,4)…(6,1),(6,2),(6,3),(6,4), …的格点多边
形
NL
13 23 33 ……
S值 当N等于 当N等于0时 在N=0基 现S与N、L
0时S值 S与L之间关 础之上增 之间的关系
系式
加多少
结论
3
1
2
2
S L2 2
1
S L 2 1 2
5
1
2
2
S L2 2
2
S L22 2
图一
图二
七、拓展研究
五、拓展研究 1、如图,如果每相邻的四个格点构成的长方形的面积为1, 那么还能用“皮克公式”来计算格点多边形的面积吗?
2、如图,如果每相邻的三个点构成的等边三角形的面积为1,那么还能用 “皮克公式”来计算格点多边形的面积吗?
1、各组依次展示,表明本小组发现的S与L、M之间的关系。 2、点名回答大家发现的S与L、M之间的关系的共同点。
四、背景介绍
皮克,1859~1943年,奥地利数学家。
1889年发现了S、L、N 三者数量关系
的“皮克公式”,并进行了证明,得到 “皮克定理”。
“皮克定理”被誉为有史以来“最重要100个数学定理” 之一。
二、分类讨论
第二阶段 课内活动
1、当N=0时, ①画边上格点(顶点和边上)总数分别为3,4,5,6,…,的格点多边形
②、列表计算面积填表找规律
N
L
S
03
1 2
04
2 2
0
5
3 2
06
4
2
0
7
5 2
0…
…
S与L之间的关系
S 3-2 2
S 4-2 2
S 5-2 2
S 6-2 2
S 7-2 2
…
讨论结果
当N=0时S与L之间 的关系式为:
S L -2 1 L 1 L 1
22
2
2、当N≠0时,为了找到和前面N=0之间的联系,我们应该控
制L变N(由于个人能力问题分为三、四个大组探讨)
第二阶段 课内活动
①画(边上格点数,内部格点数)分别为(3,1),(3,2),(3,3),
(3,4)…(4,1),(4,2),(4,3),(4,4), … (5,1),(5,2),
数格点算面积
福泉四中:刘胜举
第二阶段 课内活动
一、画一画 1、你能画出内部没有格点的格点多边形吗?
第二阶段 课内活动
2、你能画出内部有格点的格点多边形吗?
结论:格点多边形的内部可以有格点也可以无格点,说明要讨论格 点与面积的关系要分成两类来进行讨论。我们设格点多边形的面积 为S,多边形内部的格点数为N,它的边上的格点数为L。第一类为 内部无格点(N=0),第二类为内部有格点(N≠0)
…… …
…
…
结论
S L2N 2
N L S值 当N等于0 当N等于0 在N=0基础之 现S与N、L 时S与N之 时S值 上增加多少 之间的关系
间关系式
结论
15
5
S L2
3
2
2
2
25
7 S L2
3
2
2
2
35
9 S L2
3
2
2
2
…… …
…
1
S L 2 1 2
2
S L22 2
Hale Waihona Puke S L2N23
S L23 2
