2020年河南中考数学总复习考点精讲第13讲几何图形初步(3分)

合集下载

初中数学专题讲解课件专题十三几何图形的相关证明及计算(构造直角三角形)PPT模板

专题十三几何图形的相关证明及计算
（构造直角三角形）初中数学专题讲解课件
汇报人：XXX
2. 如图，点M是正方形ABCD的边BC上一点，连接AM，点E是线段AM上一点， ∠CDE的平分线交AM延长线于点F. (1)如图①，若点E为线段AM的中点，BM∶CM＝1∶2，BE＝，求AB的长； (2)如图②，若DA＝DE，求证：BF＋DF＝AF.
3. (2019重庆实验外国语学校一模)如图，在菱形ABCD中，∠A＝60°，点E、F分别在边AB、BC上． (1)如图①，若△DEF是等边三角形，且AD＝6，AE＝4，求△BEF的面积； (2)如图②，若△DEF是等腰直角三角形，∠EDF＝90°，且DB⊥EF于点Q，过点D 作DH⊥AB交AB于点H，交EF于点G，求证：AB＝DH＋12CF.
专题十三几何图形的相关证明及计算
（构造直角三角形）初中数学专题讲解课件
汇报人：XXX
ห้องสมุดไป่ตู้ 目录
01 考情聚焦 02 考点突破 03 考向课堂 04 其它补充
01
考情聚焦
1. (2019重庆八中一模)如图，在平行四边形ABCD中，AE⊥BD于点E. (1)如图①，若BC＝BD，tan∠ABE＝3，DE＝16，求平行四边形ABCD的周长； (2)如图②，若∠DBC＝45°，对角线AC、BD交于点O，F为AE上一点，且AF＝2EO ，求证：CF＝ 2CD.

2020中考数学复习专项训练第三章图形认识初步(含答案)

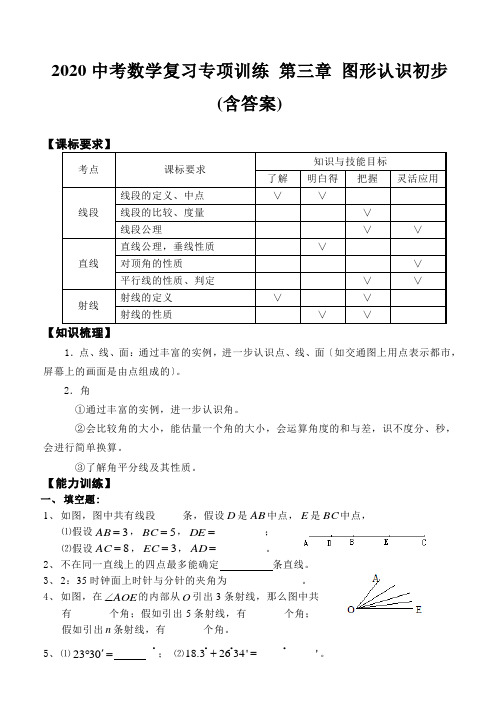
2020中考数学复习专项训练第三章图形认识初步(含答案)考点课标要求知识与技能目标了解明白得把握灵活应用线段线段的定义、中点∨ ∨ 线段的比较、度量 ∨ 线段公理∨ ∨ 直线直线公理，垂线性质∨ 对顶角的性质 ∨ 平行线的性质、判定∨ ∨ 射线射线的定义 ∨ ∨ 射线的性质∨∨【知识梳理】1．点、线、面：通过丰富的实例，进一步认识点、线、面〔如交通图上用点表示都市，屏幕上的画面是由点组成的〕。

2．角①通过丰富的实例，进一步认识角。

②会比较角的大小，能估量一个角的大小，会运算角度的和与差，识不度分、秒，会进行简单换算。

③了解角平分线及其性质。

【能力训练】一、填空题:1、如图，图中共有线段_____条，假设D 是AB 中点，E 是BC 中点，⑴假设3=AB ，5=BC ，=DE _________； ⑵假设8=AC ，3=EC ，=AD _________。

2、不在同一直线上的四点最多能确定条直线。

3、 2：35时钟面上时针与分针的夹角为______________。

4、如图，在AOE ∠的内部从O 引出3条射线，那么图中共有_______个角；假如引出5条射线，有_______个角；假如引出n 条射线，有_______个角。

5、 ⑴='︒0323 ︒； ⑵18.32634'_________'︒︒︒+=。

二、选择题1、关于直线AB ，线段CD ，射线EF ，在以下各图中能相交的是〔〕2、假如1∠与2∠互补，2∠与3∠互余，那么1∠与3∠的关系是〔〕A 、1∠=3∠B 、31801∠-︒=∠C 、3901∠+︒=∠D 、以上都不对 3、如图，P 为直线l 外一点，C B A 、、为l 上三点，且l PB ⊥，那么〔〕A 、PC PB PA 、、三条线段中PB 最短 B 、线段PB 叫做点P 到直线l 的距离C 、线段AB 是点A 到PB 的距离D 、线段AC的长度是点A 到PC 的距离4、如图，115︒∠=,90AOC ︒∠=,点B 、O 、D 在同一直线上，那么2∠的度数为〔〕 A 、75︒ B 、15︒C 、105︒D 、165︒ 5、在海上，灯塔位于一艘船的北偏东40度方向，那么这艘船位于那个灯塔的〔〕A 、南偏西50度方向B 、南偏西40度方向C 、北偏东50度方向D 、北偏东40度方向三、作图并分析1、⑴在图上过A 点画出直线BC 、直线AC 的垂线；⑵在图上过B 点画出直线AC 的垂线，过C 点画出直线AB 的垂线。

2020中考数学专题13—方法技巧之构造与转化

2020中考专题13——方法技巧之构造与转化班级姓名.构造法是一种技巧性很强的解题方法,它能训练思维的创造性和敏捷性.常见的构造形式有:(1)构造方程;(2)构造函数;(3)构造图形.【例题分析】例1例2.如图，已知Rt△ABC中，∠A=90°，AC=3，AB=4，点P为AB边上一动点，连接CP，过点P 作PM⊥CP，交BC于点M，则BM的最大值为____________.例3.如图，在平面直角坐标系xOy中，直线AB经过点A（-4，0）、B（0，4），⊙0的半径为1（O 为坐标原点），点P在直线AB上，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为_________.例4.如图，己知y=12-x2+32x+2与x轴交于A、B两点（点A在点B左侧），与y轴交于C点，现一直线经过B、C两点，点P为BC上方的抛物线上一动点，过点P作PQ⊥BC，求PQ的最大值.【巩固训练】1.设关于x的一元二次方程(x-1)(x-2)=m(m>0)的两根分别为α,β,且α<β,则α,β满足()A.1<α<β<2B.1<α<2<βC.α<1<β<2D.α<1且β>22.关于x的方程a(x+m)2+b=0的解是x1=-2,x2=1(a,m,b均为常数,a≠0),则方程a(x+m+2)2+b=0的解是.3.如图,六边形ABCDEF的六个内角都相等.若AB=1,BC=CD=3,DE=2,则这个六边形的周长等于.第3题图第4题图第5题图4.如图，⊙O的半径为3，点O到直线l的距离为4，点P是直线l上的一个动点，PQ切⊙O于点Q，则PQ的最小值为。

5.如图，△ABC中，∠BAC=60°，∠ABC=45°，AB=D是线段BC上的一个动点，以AD为直径作⊙O分别交AB、AC于E、F两点，连接EF，则线段EF长度的最小值为。

2020-2021中考数学专题分类卷专题十三几何初步、相交线与平行线(真题篇)

一、选择题1．不透明袋子中装有一个几何体模型，两位同学摸该模型并描述它的特征，甲同学：它有4个面是三角形；乙同学：它有8条棱，该模型的形状对应的立体图形可能是( )A．三棱柱B．四棱柱C．三棱锥D．四棱锥2．若一个角为75°，则它的余角的度数为( )A. 285°B. 105°C. 75°D. 15°3．如图，直线a，b被直线c所截，那∠1的同位角是( )A．∠2B．∠3C．∠4D．∠54．如图，田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长要小，能正确解释这一现象的数学知识是( )A．垂线段最短B．经过一点有无数条直线C．经过两点，有且仅有一条直线D．两点之间，线段最短5．如图，直线AD，BE被直线BF和AC所截，则∠1的同位角和∠5的内错角分别是( )A．∠4，∠2B．∠2，∠6C．∠5，∠4D．∠2，∠46．如图，AB⊥AC，AD⊥BC，垂足分别为A，D，则图中能表示点到直线距离的线段共有( )A．2条B．3条C，4条D．5条7．如图，直线a，b被直线c所截，下列条件不能判定直线a与b平行的是( )A．∠1= ∠3B．∠2+∠4=180°C．∠1=∠4D．∠3=∠48．如图，直线若∠1=124°，∠2=88°，则∠3的度数为( )A．26°B．36°C．46°D．56°9．如图，AB∥CD,CE平分∠BCD,∠B=36°，则∠DCE等于( )A.18°B．36°C．45°D．54°10. 如图是一个正方体，则它的表面展开图可以是( )A B C D二、填空题1.一个角的度数为20°，则它的补角的度数为________.2．1.45°=________.3.如图，直线AB∥CD，BC平分∠ABD，若∠1=54°，则∠2=________.4. 将一矩形纸条按如图所示折叠，若∠1=40°，则∠2=________.5．如图，AB∥CD，∠CDE=119°，GF交∠DEB的平分线EF于点F，∠AGF=130°，则∠F=________.6. 如图，AB∥CD，AE交CD于点C，DE⊥AE于点E，若∠A=42°，则∠D=________.7.已知直线a∥b，一块直角三角板如图所示放置，若∠1= 37°，则∠2=________.8. 如图，把一块三角板的60°角的顶点放在直尺的一边上，若∠1= 2∠2，则∠1=________.三、应用题1.如图，直线EF∥GH，点A在EF上，AC交GH于点B，若∠FAC=72°，∠ACD=58°；点D在GH上，求∠BDC的度数．2.如图,AE与CD交于点O，∠A=50°，OC= OE，∠C=25°，求证：AB∥CD.一、1．D2．D3．C解析：由同位角的定义可知，∠1的同位角是∠4，故选C．4．D5．B6．D解析：线段AB是点B到AC的距离，线段CA是点C到AB的距离，线段AD是点A到BC的距离，线段BD是点B到AD的距离，线段CD是点C到AD的距离，故选D．7．D8．B解析：如图，∵直线，∴∠1+∠AOB=180°，而∠1=124°，∴∠AOB=56°，∠3=180°-∠2-∠AOB=180°-88°-56°=36°，故选B.9．A10.B解析：A.含有田字形，不能折成正方体，故A错误；B能折成正方体，故B正确；C凹字形，不能折成正方体，故C错误；D含有田字形，不能折成正方体，故D错误．故选B．二、1. 160°2. 87'3. 72°解析：∵AB∥CD，∠1= 54°，∴∠ABC=21=54°，又∵BC平分∠ABD，∴∠CBD=∠ABC= 54°．∵∠CBD+∠BDC+∠DCB=180°，∠1=∠DCB，∠2=∠BDC，∴∠2=180°-∠1-∠CBD=180°-54°-54°=72°．4. 110° 解析：如图；∵AB ∥CD,∴∠3=∠1=40°,∠2+∠4=180°,∵∠4=∠5，∴∠4=∠5=21×(180°- 40°)=70°, ∴∠2 =110°.5.9.5°解析：∵AB ∥CD,∠CDE=119°,∴∠AED=180°-119°=61°,∠DEB=119°. ∵GF 交∠DEB 的平分线EF 于点F,∴∠DEF=21×119°=59. 5°, ∴∠GEF= ∠AED+∠DEF=61°+59.5°=120. 5°. ∵∠AGF=130°,∴∠F=∠AGF -∠GEF=130°-120. 5°=9.5°．6. 48°解析：∵AB ∥CD,∴∠ECD=∠A=42°,又∵DE ⊥AE,∴在Rt △ECD 中，∠D=90°-∠ECD=90°-42°=48°.7. 53°解析：如图，作直线AB ∥a ，∵a ∥b ∴AB ∥a ∥b,∵AB ∥a,∴∠1=∠3,∵AB ∥b,∴∠2=∠4,∵∠3+∠4=90°,∴∠1+∠2=90°,∵∠1=37°,∴∠2=90°-37°=53°.8. 80°解析:如图;∵AB ∥CD ，∴∠3=∠2，∵∠1= 2∠2．∴∠1= 2∠3，∴3∠3+60°=180°，∴∠3= 40°,∴∠1= 80°.三1．解：∵EF∥GH,∴∠ABD+∠FAC=180°,∴∠ABD=180°-72°=108°,∵∠ABD=∠ACD+∠BDC,∴∠BDC=∠ABD-∠ACD=108°-58°=50°.2.证明：∵OC=OE,∠C= 25°,∴∠E=∠C=25°,∴∠DOE=∠C+∠E=50°,∵∠A=50°，∴∠A=∠DOE,∴AB∥CD.。

2020年中考数学专题分类卷专题十三几何初步、相交线与平行线(模拟篇)(含答案)

拓展训练2020年中考数学专题分类卷专题十三几何初步、相交线与平行线（模拟篇）一、选择题1．如图，小李同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长要小，能正确解释这一现象的数学知识是( )A.垂线段最短B．经过一点有无数条直线C．两点之间线段最短D．经过两点有且仅有一条直线2．已知∠A=30°，则这个角的余角是( )A. 30°B. 60°C. 90°D. 150°3．下列图形中，∠1与∠2互为补角的是( )A B C D4．如图，直线AB，CD相交于点O，EO上CD于点O，∠AOE=36°，则∠BOD= ( )A．36°B．44°C．50°D．54°5．如果∠α与∠β的两边分别平行，∠α比∠β的3倍少36°，则∠α的度数是( ) A．18°B．126°C．18°或126°D．以上都不对6．如图，能判定EC∥AB的条件是( )A．∠B=∠ACEB．∠A=∠ECDC．∠B=∠ACBD．∠A=∠ACE7．如图，已知AB∥CD，BC平分∠ABE，∠C= 33°，则∠BED的度数是( )A.16°B．33°C．49°D．66°8．下列计算正确的是( )9．如图，把矩形ABCD沿EF对折，若∠1=50°，则∠AEF等于( )A.50°B．80°C．65°D．115°10.如图，直线AB∥CD，∠C=44°，∠E为直角，则∠1等于( )A.132°B.134°C.136°D.138°二、填空题1.如图，点C是线段AB上一点，AC<CB，M，N分别是AB和CB的中点，AC=8，NB=5，则线段MN=________.2.如图所示，一艘船从A点出发，沿东北方向航行至B，再从B点出发沿南偏东15°方向航行至C点，则∠ABC等于________度．3.如图，直线AB，CD相交于点O，OM上AB于点O，若∠MOD=43°，则∠COB=________度．4．如图，直线a∥b，∠1=85°，∠2=35°，则∠3为________.5.一个正方形的平面展开图如图所示，将它折成正方体后，“保”字对面的字是________.6.如图，给出了过直线外一点作已知直线的平行线的方法，其依据是________.7.如图，直线AB∥CD，直线EF分别于AB，CD交于点E，F，FP⊥EF于点F，且与∠BEF的平分线交于点P，若∠1=20°，则∠P的度数是________.三、应用题1.如图，已知AB=AC=AD，且∠C=2∠D.求证：AD∥BC.2.如图，已知，Rt△ABC的两个顶点A，B分别在直线平分∠ABC，交AC于点D，∠1= 26°，求∠2的度数．一、1．C2．B3．C4．D解析：∵EO⊥CD，∴∠EOD= 90°，又∵∠AOE+ ∠EOD+ ∠BOD= 180°，∠AOE=36°，∴∠BOD=54°，故选D．5．C解析：∵∠α与∠β的两边分别平行，∴∠α比∠β相等或互补，设∠α=x°，∵∠α比∠β的3倍少36°，∴若∠α与∠β相等，则x=3x- 36，解得：x=18，若∠α与∠β互补，则x=3(180-x)-36，解得：x=126，∴∠α的度数是18°或126°．故选C 6．D7．D解析：∵AB∥CD,∠C=33°,∴∠ABC=∠C=33°,∵BC平分∠ABE，∴∠ABE=2∠ABC=66°,∵AB∥CD，∴∠BED=∠ABE= 66°.故选D．8．C解析：9．D解析：如图；∵把矩形ABCD沿EF对折，∴AD∥BC，∠BFE=∠2，∵∠1=50°，∠1+∠2+∠BFE=180°，∴∠BFE=250180︒-︒=65°， ∵∠AEF+∠BFE=180°，∴∠AEF=115°，故选D ．10.B 解析：如图，过点E 作EF ∥AB ，∵ABHCD,∴AB //CD //EF,∴∠C=∠FEC, ∠BAE=∠FEA,∵∠C=44°,∠AEC 为直角 ,∴∠FEC=44°,∠BAE= ∠AEF=90°-44°=46°,∴∠1=180°-∠BAE=180°-46°=134°．故选B二、1.4解析：∵点C 是线段AB 上一点，AC<CB ，M ，N 分别是AB 和CB 的中点，AC=8，NB=5，∴BC=2NB=10,∴AB=AC+BC=8+10=18．∴BM=9．∴MN=BM -NB=9-5=4．2. 60解析：从图中我们发现向北的两条方向线平行，∠NAB=45°，∠MBC=15°，根据平行线的性质：两直线平行，内错角相等，可得∠ABM= ∠NAB=45°，所以∠ABC=45°+15°=60°．3. 133解析：∵OM⊥AB，∴∠AOM= 90°，∵∠MOD= 43°，∴∠AOD= 90°+43°=133°，∴∠COB=133°，4. 50°解析：在△ABC中，∵∠1= 85°，∠2=35°，∴∠4=85°-35°=50°，∵a∥b，∴∠3=∠4=50°，故答案为：50°．5．碳解析：正方体的表面展开图，相对的面之间一定相隔一个正方形，“低”与“绿”是相对面，“碳”与“保”是相对面，“环”与“色”是相对面．6.同位角相等，两直线平行解析：由图形得，有两个相等的同位角，所以只能依据：同位角相等，两直线平行．7. 55°解析：∵AB∥CD，FP⊥EF于点F，∠1= 20°，∴∠BEF=180°-90°-20°=70°，∵∠BEF的平分线为PE，∴∠2=35°，又∵FP⊥EF，∴Rt△EFP中，∠P=90°-35°=55°．三、1．证明：∵AB=AC=AD，∴∠C=∠ABC，∠D=∠ABD，∵∠C=2∠D，∴∠ABC=2∠ABD,∴∠ABD=∠CBD=∠D，∴AD∥BC. 2．解：∴∠ABC=2∠ABD=52°，∵∠C=90°，∴Rt△ABC中，∠2=90°-∠ABC=38°．。

2020年中考数学二轮专项冲刺复习——几何综合、压轴题(含详细解答)

2020年中考数学二轮专项冲刺复习——几何综合、压轴题1、（2019河南•中考第22题•10分）在△ABC中，CA＝CB，∠ACB＝α．点P是平面内不与点A，C重合的任意一点．连接AP，将线段AP绕点P逆时针旋转α得到线段DP，连接AD，BD，CP．（1）观察猜想如图1，当α＝60°时，的值是1，直线BD与直线CP相交所成的较小角的度数是60°．（2）类比探究如图2，当α＝90°时，请写出的值及直线BD与直线CP相交所成的小角的度数，并就图2的情形说明理由．（3）解决问题当α＝90°时，若点E，F分别是CA，CB的中点，点P在直线EF上，请直接写出点C，P，D在同一直线上时的值．【考点】相似形综合题．【分析】（1）如图1中，延长CP交BD的延长线于E，设AB交EC于点O．证明△CAP≌△BAD（SAS），即可解决问题．（2）如图2中，设BD交AC于点O，BD交PC于点E．证明△DAB∽△P AC，即可解决问题．（3）分两种情形：①如图3﹣1中，当点D在线段PC上时，延长AD交BC的延长线于H．证明AD＝DC即可解决问题．②如图3﹣2中，当点P在线段CD上时，同法可证：DA＝DC解决问题．【解答】解：（1）如图1中，延长CP交BD的延长线于E，设AB交EC于点O．∵∠P AD＝∠CAB＝60°，∴∠CAP＝∠BAD，∵CA＝BA，P A＝DA，∴△CAP≌△BAD（SAS），∴PC＝BD，∠ACP＝∠ABD，∵∠AOC＝∠BOE，∴∠BEO＝∠CAO＝60°，∴＝1，线BD与直线CP相交所成的较小角的度数是60°，故答案为1，60°．（2）如图2中，设BD交AC于点O，BD交PC于点E．∵∠P AD＝∠CAB＝45°，∴∠P AC＝∠DAB，∵＝＝，∴△DAB∽△P AC，∴∠PCA＝∠DBA，＝＝，∵∠EOC＝∠AOB，∴∠CEO＝∠OABB＝45°，∴直线BD与直线CP相交所成的小角的度数为45°．（3）如图3﹣1中，当点D在线段PC上时，延长AD交BC的延长线于H．∵CE＝EA，CF＝FB，∴EF∥AB，∴∠EFC＝∠ABC＝45°，∵∠P AO＝45°，∴∠P AO＝∠OFH，∵∠POA＝∠FOH，∴∠H＝∠APO，∵∠APC＝90°，EA＝EC，∴PE＝EA＝EC，∴∠EP A＝∠EAP＝∠BAH，∴∠H＝∠BAH，∴BH＝BA，∵∠ADP＝∠BDC＝45°，∴∠ADB＝90°，∴BD⊥AH，∴∠DBA＝∠DBC＝22.5°，∵∠ADB＝∠ACB＝90°，∴A，D，C，B四点共圆，∠DAC＝∠DBC＝22.5°，∠DCA＝∠ABD＝22.5°，∴∠DAC＝∠DCA＝22.5°，∴DA＝DC，设AD＝a，则DC＝AD＝a，PD＝a，∴＝＝2﹣．如图3﹣2中，当点P在线段CD上时，同法可证：DA＝DC，设AD＝a，则CD＝AD＝a，PD＝a，∴PC＝a﹣a，∴＝＝2+．2、（2019陕西•中考第22题•9分）在图1，2，3中，已知ABCDY，120ABC∠=︒，点E为线段BC上的动点，连接AE，以AE为边向上作菱形AEFG，且120EAG∠=︒．（1）如图1，当点E与点B重合时，CEF∠=60︒；（2）如图2，连接AF．①填空：FAD∠EAB∠（填“>”，“<“，“=”)；②求证：点F在ABC∠的平分线上；（3）如图3，连接EG，DG，并延长DG交BA的延长线于点H，当四边形AEGH是平行四边形时，求BCAB的值．【考点】相似形综合题【分析】（1）根据菱形的性质计算；（2）①证明60DAB FAE∠=∠=︒，根据角的运算解答；②作FM BC⊥于M，FN BA⊥交BA的延长线于N，证明AFN EFM∆≅∆，根据全等三角形的性质得到FN FM=，根据角平分线的判定定理证明结论；（3）根据直角三角形的性质得到2GH AH=，证明四边形ABEH为菱形，根据菱形的性质计算，得到答案．【解答】解：（1）Q四边形AEFG是菱形，18060AEF EAG∴∠=︒-∠=︒，60CEF AEC AEF∴∠=∠-∠=︒，故答案为：60︒；（2）①Q四边形ABCD是平行四边形，18060DAB ABC ∴∠=︒-∠=︒，Q 四边形AEFG 是菱形，120EAG ∠=︒，60FAE ∴∠=︒，FAD EAB ∴∠=∠，故答案为：=；②作FM BC ⊥于M ，FN BA ⊥交BA 的延长线于N ，则90FNB FMB ∠=∠=︒，60NFM ∴∠=︒，又60AFE ∠=︒，AFN EFM ∴∠=∠，EF EA =Q ，60FAE ∠=︒，AEF ∴∆为等边三角形，FA FE ∴=，在AFN ∆和EFM ∆中，AFN EFM FNA FME FA FE ∠=∠⎧⎪∠=∠⎨⎪=⎩，()AFN EFM AAS ∴∆≅∆，FN FM ∴=，又FM BC ⊥，FN BA ⊥，∴点F 在ABC ∠的平分线上；（3）Q 四边形AEFG 是菱形，120EAG ∠=︒，60AGF ∴∠=︒，30FGE AGE ∴∠=∠=︒，Q 四边形AEGH 为平行四边形，//GE AH ∴，30GAH AGE ∴∠=∠=︒，30H FGE ∠=∠=︒，90GAH ∴∠=︒，又30AGE ∠=︒，2GH AH ∴=，60DAB ∠=︒Q ，30H ∠=︒，30ADH ∴∠=︒，AD AH GE ∴==，Q 四边形ABEH 为平行四边形，BC AD ∴=，BC GE ∴=，Q 四边形ABEH 为平行四边形，30HAE EAB ∠=∠=︒，∴平行四边形ABEH 为菱形，AB AH HE ∴==，3GE AB ∴=， ∴3BC AB=．3、（2019上海•中考第22题•10分）图1是某小型汽车的侧面示意图，其中矩形ABCD 表示该车的后备箱，在打开后备箱的过程中，箱盖ADE 可以绕点A 逆时针方向旋转，当旋转角为60︒时，箱盖ADE 落在AD E ''的位置（如图2所示）．已知90AD =厘米，30DE =厘米，40EC =厘米．（1）求点D '到BC 的距离；（2）求E 、E '两点的距离．【考点】解直角三角形的应用；矩形的性质【分析】（1）过点D '作D H BC '⊥，垂足为点H ，交AD 于点F ，利用旋转的性质可得出90AD AD '==厘米，60DAD ∠'=︒，利用矩形的性质可得出90AFD BHD ∠'=∠'=︒，在Rt △AD F '中，通过解直角三角形可求出D F '的长，结合FH DC DE CE ==+及D H D F FH '='+可求出点D '到BC 的距离；（2）连接AE ，AE '，EE '，利用旋转的性质可得出AE AE '=，60EAE ∠'=︒，进而可得出AEE ∆'是等边三角形，利用等边三角形的性质可得出EE AE '=，在Rt ADE ∆中，利用勾股定理可求出AE 的长度，结合EE AE '=可得出E 、E '两点的距离．【解答】解：（1）过点D '作D H BC '⊥，垂足为点H ，交AD 于点F ，如图3所示．由题意，得：90AD AD '==厘米，60DAD ∠'=︒．Q 四边形ABCD 是矩形，//AD BC ∴，90∴∠'=∠'=︒．AFD BHD在Rt△AD F'中，sin90sin60453g厘米．D F AD DAD'='∠'=⨯︒=又40Q厘米，30DE=厘米，CE=∴==+=厘米，FH DC DE CE70∴'='+=+厘米．D H D F FH(45370)答：点D'到BC的距离为(45370)+厘米．（2）连接AE，AE'，EE'，如图4所示．由题意，得：AE AE'=，60∠'=︒，EAE∴∆'是等边三角形，AEE∴'=．EE AEQ四边形ABCD是矩形，90∴∠=︒．ADE在Rt ADEDE=厘米，AD=厘米，30∆中，90223010∴=+=厘米，AE AD DE∴'=厘米．EE3010答：E、E'两点的距离是3010厘米．4、（2019河南•中考第17题•9分）如图，在△ABC中，BA＝BC，∠ABC＝90°，以AB为直径的半圆O交AC于点D，点E是上不与点B，D重合的任意一点，连接AE交BD于点F，连接BE并延长交AC于点G．（1）求证：△ADF≌△BDG；（2）填空：①若AB＝4，且点E是的中点，则DF的长为4﹣2；②取的中点H，当∠EAB的度数为30°时，四边形OBEH为菱形．【考点】圆的综合题．【分析】（1）利用直径所对的圆周角是直角，可得∠ADB＝∠AEB＝90°，再应用同角的余角相等可得∠DAF＝∠DBG，易得AD＝BD，△ADF≌△BDG得证；（2）作FH⊥AB，应用等弧所对的圆周角相等得∠BAE＝∠DAE，再应用角平分线性质可得结论；由菱形的性质可得BE＝OB，结合三角函数特殊值可得∠EAB＝30°．【解答】解：（1）证明：如图1，∵BA＝BC，∠ABC＝90°，∴∠BAC＝45°∵AB是⊙O的直径，∴∠ADB＝∠AEB＝90°，∴∠DAF+∠BGD＝∠DBG+∠BGD＝90°∴∠DAF＝∠DBG∵∠ABD+∠BAC＝90°∴∠ABD＝∠BAC＝45°∴AD＝BD∴△ADF≌△BDG（ASA）；（2）①如图2，过F作FH⊥AB于H，∵点E是的中点，∴∠BAE＝∠DAE∵FD⊥AD，FH⊥AB∴FH＝FD∵＝sin∠ABD＝sin45°＝，∴，即BF＝FD∵AB＝4，∴BD＝4cos45°＝2，即BF+FD＝2，（+1）FD＝2∴FD＝＝4﹣2故答案为．②连接OE，EH，∵点H是的中点，∴OH⊥AE，∵∠AEB＝90°∴BE⊥AE∴BE∥OH∵四边形OBEH为菱形，∴BE＝OH＝OB＝AB∴sin∠EAB＝＝∴∠EAB＝30°．故答案为：30°5、（2019河北•中考第23题•9分）如图，△ABC和△ADE中，AB＝AD＝6，BC＝DE，∠B＝∠D＝30°，边AD与边BC交于点P（不与点B，C重合），点B，E在AD异侧，I为△APC的内心．（1）求证：∠BAD＝∠CAE；（2）设AP＝x，请用含x的式子表示PD，并求PD的最大值；（3）当AB⊥AC时，∠AIC的取值范围为m°＜∠AIC＜n°，分别直接写出m，n的值．【考点】圆的综合题．【分析】（1）由条件易证△ABC≌△ADE，得∠BAC＝∠DAE，∴∠BAD＝∠CAE．（2）PD＝AD﹣AP＝6﹣x，∵点P在线段BC上且不与B、C重合，∴AP的最小值即AP⊥BC时AP的长度，此时PD可得最大值．（3）I为△APC的内心，即I为△APC角平分线的交点，应用“三角形内角和等于180°“及角平分线定义即可表示出∠AIC，从而得到m，n的值．【解答】解：（1）在△ABC和△ADE中，（如图1）∴△ABC≌△ADE（SAS）∴∠BAC＝∠DAE即∠BAD+∠DAC＝∠DAC+∠CAE∴∠BAD＝∠CAE．（2）∵AD＝6，AP＝x，∴PD＝6﹣x当AD⊥BC时，AP＝AB＝3最小，即PD＝6﹣3＝3为PD的最大值．（3）如图2，设∠BAP＝α，则∠APC＝α+30°，∵AB⊥AC∴∠BAC＝90°，∠PCA＝60°，∠P AC＝90°﹣α，∵I为△APC的内心∴AI、CI分别平分∠P AC，∠PCA，∴∠IAC＝∠P AC，∠ICA＝∠PCA∴∠AIC＝180°﹣（∠IAC+∠ICA）＝180°﹣（∠P AC+∠PCA）＝180°﹣（90°﹣α+60°）＝α+105°∵0＜α＜90°，∴105°＜α+105°＜150°，即105°＜∠AIC＜150°，∴m＝105，n＝150．6、（2019海南•中考第21题•13分）如图，在边长为1的正方形ABCD中，E是边CD的中点，点P是边AD上一点（与点A、D不重合），射线PE与BC的延长线交于点Q．（1）求证：△PDE≌△QCE；（2）过点E作EF∥BC交PB于点F，连结AF，当PB＝PQ时，①求证：四边形AFEP是平行四边形；②请判断四边形AFEP是否为菱形，并说明理由．【考点】四边形综合题．【分析】（1）由四边形ABCD是正方形知∠D＝∠ECQ＝90°，由E是CD的中点知DE＝CE，结合∠DEP＝∠CEQ即可得证；（2）①由PB＝PQ知∠PBQ＝∠Q，结合AD∥BC得∠APB＝∠PBQ＝∠Q＝∠EPD，由△PDE≌△QCE知PE ＝QE，再由EF∥BQ知PF＝BF，根据Rt△P AB中AF＝PF＝BF知∠APF＝∠P AF，从而得∠P AF＝∠EPD，据此即可证得PE∥AF，从而得证；②设AP＝x，则PD＝1﹣x，若四边形AFEP是菱形，则PE＝P A＝x，由PD2+DE2＝PE2得关于x的方程，解之求得x的值，从而得出四边形AFEP为菱形的情况．【解答】解：（1）∵四边形ABCD是正方形，∴∠D＝∠ECQ＝90°，∵E是CD的中点，∴DE＝CE，又∵∠DEP＝∠CEQ，∴△PDE≌△QCE（ASA）；（2）①∵PB＝PQ，∴∠PBQ＝∠Q，∵AD∥BC，∴∠APB＝∠PBQ＝∠Q＝∠EPD，∵△PDE≌△QCE，∴PE＝QE，∵EF∥BQ，∴PF＝BF，∴在Rt△P AB中，AF＝PF＝BF，∴∠APF＝∠P AF，∴∠P AF＝∠EPD，∴PE∥AF，∵EF∥BQ∥AD，∴四边形AFEP是平行四边形；②当AP＝时，四边形AFEP是菱形．设AP＝x，则PD＝1﹣x，若四边形AFEP是菱形，则PE＝P A＝x，∵CD＝1，E是CD中点，∴DE＝，在Rt△PDE中，由PD2+DE2＝PE2得（1﹣x）2+（）2＝x2，解得x＝，即当AP＝时，四边形AFEP是菱形．7、（2019福建•中考第21题•8分）在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，将△ABC绕点A顺时针旋转一定的角度α得到△DEC，点A、B的对应点分别是D、E．（1）当点E恰好在AC上时，如图1，求∠ADE的大小；（2）若α＝60°时，点F是边AC中点，如图2，求证：四边形BEDF是平行四边形．【考点】平行四边形的判定；旋转的性质．【分析】（1）如图1，利用旋转的性质得CA＝CD，∠ECD＝∠BCA＝30°，∠DEC＝∠ABC＝90°，再根据等腰三角形的性质和三角形内角和计算出∠CAD，从而利用互余和计算出∠ADE的度数；（2）如图2，利用直角三角形斜边上的中线性质得到BF＝AC，利用含30度的直角三角形三边的关系得到AB ＝AC，则BF＝AB，再根据旋转的性质得到∠BCE＝∠ACD＝60°，CB＝CE，DE＝AB，从而得到DE＝BF，△ACD和△BCE为等边三角形，接着证明△CFD≌△ABC得到DF＝BC，然后根据平行四边形的判定方法得到结论．【解答】（1）解：如图1，∵△ABC绕点A顺时针旋转α得到△DEC，点E恰好在AC上，∴CA＝CD，∠ECD＝∠BCA＝30°，∠DEC＝∠ABC＝90°，∵CA＝CD，∴∠CAD＝∠CDA＝（180°﹣30°）＝75°，∴∠ADE＝90°﹣75°＝15°；（2）证明：如图2，∵点F是边AC中点，∴BF＝AC，∵∠ACB＝30°，∴AB＝AC，∴BF＝AB，∵△ABC绕点A顺时针旋转60得到△DEC，∴∠BCE＝∠ACD＝60°，CB＝CE，DE＝AB，∴DE＝BF，△ACD和△BCE为等边三角形，∴BE＝CB，∵点F为△ACD的边AC的中点，∴DF⊥AC，易证得△CFD≌△ABC，∴DF＝BC，∴DF＝BE，而BF＝DE，∴四边形BEDF是平行四边形．8、（2019北京•中考第20题•5分）如图，在菱形ABCD中，AC为对角线，点E，F分别在AB，AD上，BE＝DF，连接EF．（1）求证：AC⊥EF；（2）延长EF交CD的延长线于点G，连接BD交AC于点O．若BD＝4，tan G＝，求AO的长．【考点】全等三角形的判定与性质；菱形的性质；解直角三角形．【分析】（1）由菱形的性质得出AB＝AD，AC⊥BD，OB＝OD，得出AB：BE＝AD：DF，证出EF∥BD即可得出结论；（2）由平行线的性质得出∠G＝∠ADO，由三角函数得出tan G＝tan∠ADO＝＝，得出OA＝OD，由BD ＝4，得出OD＝2，得出OA＝1．【解答】（1）证明：连接BD，如图1所示：∵四边形ABCD是菱形，∴AB＝AD，AC⊥BD，OB＝OD，∵BE＝DF，∴AB：BE＝AD：DF，∴EF∥BD，∴AC⊥EF；（2）解：如图2所示：∵由（1）得：EF∥BD，∴∠G＝∠ADO，∴tan G＝tan∠ADO＝＝，∴OA＝OD，∵BD＝4，∴OD＝2，∴OA＝1．10、（2019北京•中考第27题•7分）已知∠AOB＝30°，H为射线OA上一定点，OH＝+1，P为射线OB上一点，M为线段OH上一动点，连接PM，满足∠OMP为钝角，以点P为中心，将线段PM顺时针旋转150°，得到线段PN，连接ON．（1）依题意补全图1；（2）求证：∠OMP＝∠OPN；（3）点M关于点H的对称点为Q，连接QP．写出一个OP的值，使得对于任意的点M总有ON＝QP，并证明．【考点】三角形综合题．【分析】（1）根据题意画出图形．（2）由旋转可得∠MPN＝150°，故∠OPN＝150°﹣∠OPM；由∠AOB＝30°和三角形内角和180°可得∠OMP ＝180°﹣30°﹣∠OPM＝150°﹣∠OPM，得证．（3）根据题意画出图形，以ON＝QP为已知条件反推OP的长度．由（2）的结论∠OMP＝∠OPN联想到其补角相等，又因为旋转有PM＝PN，已具备一边一角相等，过点N作NC⊥OB于点C，过点P作PD⊥OA于点D，即可构造出△PDM≌△NCP，进而得PD＝NC，DM＝CP．此时加上ON＝QP，则易证得△OCN≌△QDP，所以OC＝QD．利用∠AOB＝30°，设PD＝NC＝a，则OP＝2a，OD＝a．再设DM＝CP＝x，所以QD＝OC＝OP+PC ＝2a+x，MQ＝DM+QD＝2a+2x．由于点M、Q关于点H对称，即点H为MQ中点，故MH＝MQ＝a+x，DH ＝MH﹣DM＝a，所以OH＝OD+DH＝a+a＝+1，求得a＝1，故OP＝2．证明过程则把推理过程反过来，以OP＝2为条件，利用构造全等证得ON＝QP．【解答】解：（1）如图1所示为所求．（2）设∠OPM＝α，∵线段PM绕点P顺时针旋转150°得到线段PN∴∠MPN＝150°，PM＝PN∴∠OPN＝∠MPN﹣∠OPM＝150°﹣α∵∠AOB＝30°∴∠OMP＝180°﹣∠AOB﹣∠OPM＝180°﹣30°﹣α＝150°﹣α∴∠OMP＝∠OPN（3）OP＝2时，总有ON＝QP，证明如下：过点N作NC⊥OB于点C，过点P作PD⊥OA于点D，如图2∴∠NCP＝∠PDM＝∠PDQ＝90°∵∠AOB＝30°，OP＝2∴PD＝OP＝1∴OD＝∵OH＝+1∴DH＝OH﹣OD＝1∵∠OMP＝∠OPN∴180°﹣∠OMP＝180°﹣∠OPN即∠PMD＝∠NPC在△PDM与△NCP中∴△PDM≌△NCP（AAS）∴PD＝NC，DM＝CP设DM＝CP＝x，则OC＝OP+PC＝2+x，MH＝MD+DH＝x+1∵点M关于点H的对称点为Q∴HQ＝MH＝x+1∴DQ＝DH+HQ＝1+x+1＝2+x∴OC＝DQ在△OCN与△QDP中∴△OCN≌△QDP（SAS）∴ON＝QP11、（2019北京•中考第28题•7分）在△ABC中，D，E分别是△ABC两边的中点，如果上的所有点都在△ABC的内部或边上，则称为△ABC的中内弧．例如，图1中是△ABC的一条中内弧．（1）如图2，在Rt△ABC中，AB＝AC＝，D，E分别是AB，AC的中点，画出△ABC的最长的中内弧，并直接写出此时的长；（2）在平面直角坐标系中，已知点A（0，2），B（0，0），C（4t，0）（t＞0），在△ABC中，D，E分别是AB，AC的中点．①若t＝，求△ABC的中内弧所在圆的圆心P的纵坐标的取值范围；②若在△ABC中存在一条中内弧，使得所在圆的圆心P在△ABC的内部或边上，直接写出t的取值范围．【考点】圆的综合题．【分析】（1）由三角函数值及等腰直角三角形性质可求得DE＝2，最长中内弧即以DE为直径的半圆，的长即以DE为直径的圆周长的一半；（2）根据三角形中内弧定义可知，圆心一定在DE的中垂线上，①当t＝时，要注意圆心P在DE上方的中垂线上均符合要求，在DE下方时必须AC与半径PE的夹角∠AEP满足90°≤∠AEP＜135°；②根据题意，t的最大值即圆心P在AC上时求得的t值．【解答】解：（1）如图2，以DE为直径的半圆弧，就是△ABC的最长的中内弧，连接DE，∵∠A＝90°，AB＝AC＝，D，E分别是AB，AC的中点，∴BC＝＝＝4，DE＝BC＝×4＝2，∴弧＝×2π＝π；（2）如图3，由垂径定理可知，圆心一定在线段DE的垂直平分线上，连接DE，作DE垂直平分线FP，作EG ⊥AC交FP于G，①当t＝时，C（2，0），∴D（0，1），E（1，1），F（，1），设P（，m）由三角形中内弧定义可知，圆心线段DE上方射线FP上均可，∴m≥1，∵OA＝OC，∠AOC＝90°∴∠ACO＝45°，∵DE∥OC∴∠AED＝∠ACO＝45°作EG⊥AC交直线FP于G，FG＝EF＝根据三角形中内弧的定义可知，圆心在点G的下方（含点G）直线FP上时也符合要求；∴m≤综上所述，m≤或m≥1．②如图4，设圆心P在AC上，∵P在DE中垂线上，∴P为AE中点，作PM⊥OC于M，则PM＝，∴P（t，），∵DE∥BC∴∠ADE＝∠AOB＝90°∴AE＝＝＝，∵PD＝PE，∴∠AED＝∠PDE∵∠AED+∠DAE＝∠PDE+∠ADP＝90°，∴∠DAE＝∠ADP∴AP＝PD＝PE＝AE由三角形中内弧定义知，PD≤PM∴AE≤，AE≤3，即≤3，解得：t≤，∵t＞0∴0＜t≤．12、（2019安徽•中考第20题•10分）如图，点E在ABCDY内部，//AF BE，//DF CE．（1）求证：BCE ADF∆≅∆；（2）设ABCDY的面积为S，四边形AEDF的面积为T，求ST的值．【考点】全等三角形的判定与性质；平行四边形的性质【分析】（1）根据ASA 证明：BCE ADF ∆≅∆；（2）根据点E 在ABCD Y 内部，可知：12BEC AED ABCD S S S ∆∆+=Y ，可得结论．【解答】解：（1）Q 四边形ABCD 是平行四边形，AD BC ∴=，//AD BC ，180ABC BAD ∴∠+∠=︒，//AF BE Q ，180EAB BAF ∴∠+∠=︒，CBE DAF ∴∠=∠，同理得BCE ADF ∠=∠，在BCE ∆和ADF ∆中，Q CBE DAF BC AD BCE ADF ∠=∠⎧⎪=⎨⎪∠=∠⎩，()BCE ADF ASA ∴∆≅∆；（2）Q 点E 在ABCD Y 内部，12BEC AED ABCD S S S ∆∆∴+=Y ，由（1）知：BCE ADF ∆≅∆，BCE ADF S S ∆∆∴=，12ADF AED BEC AED ABCD AEDF S S S S S S ∆∆∆∆∴=+=+=Y 四边形， ABCD QY 的面积为S ，四边形AEDF 的面积为T ， ∴212S S T S ==． 13、如图，矩形ABCD 中，点E 在边CD 上，将BCE ∆沿BE 折叠，点C 落在AD 边上的点F 处，过点F 作//FG CD 交BE 于点G ，连接CG ．（1）求证：四边形CEFG 是菱形；（2）若6AB =，10AD =，求四边形CEFG 的面积．【考点】LA：菱形的判定与性质；PB：翻折变换（折叠问题）；LB：矩形的性质【分析】（1）根据题意和翻着的性质，可以得到BCE BFE∆≅∆，再根据全等三角形的性质和菱形的判定方法即可证明结论成立；（2）根据题意和勾股定理，可以求得AF的长，进而求得EF和DF的值，从而可以得到四边形CEFG的面积．【解答】（1）证明：由题意可得，BCE BFE∆≅∆，BEC BEF∴∠=∠，FE CE=，//FG CEQ，FGE CEB∴∠=∠，FGE FEG∴∠=∠，FG FE∴=，FG EC∴=，∴四边形CEFG是平行四边形，又CE FE=Q，∴四边形CEFG是菱形；（2）Q矩形ABCD中，6AB=，10AD=，BC BF=，90BAF∴∠=︒，10AD BC BF===，8AF∴=，2DF∴=，设EF x=，则CE x=，6DE x=-，90FDE=︒Q，2222(6)x x∴+-=，解得，103x=，103CE∴=，∴四边形CEFG的面积是：1020233 CE DF=⨯=g．14、（2019成都•中考第27题•10分）如图1，在ABC∆中，20AB AC==，3tan4B=，点D为BC边上的动点（点D 不与点B ，C 重合）．以D 为顶点作ADE B ∠=∠，射线DE 交AC 边于点E ，过点A 作AF AD ⊥交射线DE 于点F ，连接CF ．（1）求证：ABD DCE ∆∆∽；（2）当//DE AB 时（如图2)，求AE 的长；（3）点D 在BC 边上运动的过程中，是否存在某个位置，使得DF CF =？若存在，求出此时BD 的长；若不存在，请说明理由．【考点】SO ：相似形综合题【分析】（1）根据两角对应相等的两个三角形相似证明即可．（2）解直角三角形求出BC ，由ABD CBA ∆∆∽，推出AB DB CB AB =，可得222025322AB DB CB ===，由//DE AB ，推出AE BD AC BC=，求出AE 即可．（3）点D 在BC 边上运动的过程中，存在某个位置，使得DF CF =．作FH BC ⊥于H ，AM BC ⊥于M ，AN FH ⊥于N ．则90NHM AMH ANH ∠=∠=∠=︒，由AFN ADM ∆∆∽，可得3tan tan 4AN AF ADF B AM AD ==∠==，推出3312944AN AM ==⨯=，推出1697CH CM MH CM AN =-=-=-=，再利用等腰三角形的性质，求出CD 即可解决问题．【解答】（1）证明：AB AC =Q ，B ACB ∴∠=∠，ADE CDE B BAD ∠+∠=∠+∠Q ，ADE B ∠=∠，BAD CDE ∴∠=∠，BAD DCE ∴∆∆∽．（2）解：如图2中，作AM BC ⊥于M ．在Rt ABM∆中，设4BM k=，则3tan434AM BM B k k ==⨯=g，由勾股定理，得到222AB AM BM=+，22220(3)(4)k k∴=+，4k∴=或4-（舍弃），AB AC=Q，AM BC⊥，22432BC BM k∴===g，//DE ABQ，BAD ADE∴∠=∠，ADE B∠=∠Q，B ACB∠=∠，BAD ACB∴∠=∠，ABD CBA∠=∠Q，ABD CBA∴∆∆∽，∴AB DBCB AB=，222025322ABDBCB∴===，//DE ABQ，∴AE BDAC BC=，252012523216AC BDAEBC⨯∴===g．（3）点D在BC边上运动的过程中，存在某个位置，使得DF CF=．理由：作FH BC⊥于H，AM BC⊥于M，AN FH⊥于N．则90NHM AMH ANH∠=∠=∠=︒，∴四边形AMHN为矩形，90MAN∴∠=︒，MH AN=，AB AC=Q，AM BC⊥，11321622BM CM BC∴===⨯=，在Rt ABM ∆中，由勾股定理，得12AM ==， AN FH ⊥Q ，AM BC ⊥，90ANF AMD ∴∠=︒=∠，90DAF MAN ∠=︒=∠Q ，NAF MAD ∴∠=∠，AFN ADM ∴∆∆∽， ∴3tan tan 4AN AF ADF B AM AD ==∠==， 3312944AN AM ∴==⨯=， 1697CH CM MH CM AN ∴=-=-=-=，当DF CF =时，由点D 不与点C 重合，可知DFC ∆为等腰三角形， FH DC ⊥Q ，214CD CH ∴==，321418BD BC CD ∴=-=-=，∴点D 在BC 边上运动的过程中，存在某个位置，使得DF CF =，此时18BD =．。

2020河南中考数学考点突破(课件+训练)：14几何初步与尺规作图

考点研读
栏目索引
考点六尺规作图 1.尺规作图的要求只用不带刻度的直尺和圆规通过有限次操作,完成画图的一种作图方法.尺规作图不一定要写作图步骤,但必须保留作图痕迹. 2.五种基本尺规作图
作角的平分线
步骤:1.以点O为圆心,任意长为半径画弧,分别交OA,OB于点N,M;2.
分别以点M,N为圆心,大于 1MN的 2
命题探究
栏目索引
探究点一与相交线有关的计算例1 (2018湖南益阳)如图,直线AB,CD相交于点O,EO⊥CD.下列说法错误的是 ( C )
A.∠AOD=∠BOC C.∠AOC=∠AOE
B.∠AOE+∠BOD=90° D.∠AOD+∠BOD=180°
考点研读
栏目索引
考点四平行线(高频考点) 1.平行线的定义: 在同一平面内 ,不相交的两条直线叫做平行线. 2.平行公理:经过直线外一点有且只有一条直线与已知直线平行. 3.平行公理的推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行 .
4.平行线的判定和性质 (1)同位角相等⇔两直线平行 ; (2)内错角相等 ⇔两直线平行; (3)同旁内角互补 ⇔两直线平行.
步骤:1.以点O为圆心,任意长为半径向点O两侧作弧,交直线于A,B两
点;2.分别以点A,B为圆心,大于 1
2
AB的长为半径向直线两侧作弧,交点分别为M,N;3.连接MN,则直线 MN即为所求作的垂线
命题探究
栏目索引
命题探究
探究点一与相交线有关的计算探究点二与平行线有关的计算探究点三尺规作图
栏目索引
第一节几何初步与尺规作图
总纲目录
真题演练考点研读命题探究随堂检测

2020届中考数学复习课件：第15讲几何初步 (共28张PPT)

如图,作DE⊥AB,垂足为E,由AD平分∠BAC,得 DE=DC=4.应填4.
第四章
第15讲几何初步课前小练考情分析
知识梳理
例题精讲
随堂练习
-21-
本题考查了作辅助线的方法以及角平分线性质的应用.广东省近几年没有牵涉到此类问题,备考时请关注.
第四章
第15讲几何初步课前小练考情分析
知识梳理
随堂练习
-25-
8.如图AB∥CD,直线EF交AB于点E,交CD于F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2= 65° .
9.如图,在△ABC中,分别以点A和点B为圆心,大于
1 2
AB的长为半径
画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC
的周长为10,AB=7,则△ABC的周长为 17 .
第四章
第15讲几何初步课前小练考情分析
知识梳理
例题精讲
随堂练习
-26-
10. (2018·益阳)如图,AB∥CD,∠1=∠2.求证:AM∥CN.
证明:∵AB∥CD, ∴∠EAB=∠ECD. ∵∠1=∠2, ∴∠EAM=∠ECN, ∴AM∥CN.
第四章
第15讲几何初步课前小练考情分析
知识梳理
第四章
第15讲几何初步
课前小练考情分析知识梳理例题ห้องสมุดไป่ตู้讲随堂练习
-4-
6.如图是由6个相同的小正方体搭成的一个几何体,则它的俯视图是( A )
第四章
第15讲几何初步
课前小练考情分析知识梳理例题精讲随堂练习
-5-
7.如图,已知∠2=40°,AD⊥AC且∠1=50°,求证:AB∥CD.

河南省淮阳中学七年级数学上册第四单元《几何图形初步》知识点总结(课后培优)

一、选择题1．如图，已知点C 为线段AB 的中点，则①AC ＝BC ；②AC ＝12AB ；③BC ＝12AB ；④AB ＝2AC ；⑤AB ＝2BC ，其中正确的个数是（）A ．2B ．3C ．4D ．52．将一张圆形纸片对折后再对折，得到下图，然后沿着图中的虚线剪开，得到两部分，其中一部分展开的平面图形是（）A ．AB ．BC ．CD ．D 3．下面四个图形中，能判断∠1＞∠2的是（）A ．B ．C ．D ． 4．如图，点C 是线段AB 的中点，点D 是线段CB 上任意一点，则下列表示线段关系的式子不正确的是（）A ．AB=2ACB ．AC+CD+DB=ABC ．CD=AD-12AB D ．AD=12（CD+AB ） 5．已知：如图，C 是线段AB 的中点，D 是线段BC 的中点，AB ＝20 cm ，那么线段AD 等于( )A ．15 cmB ．16 cmC ．10 cmD ．5 cm 6．已知∠α与∠β互补，且∠α＞∠β，则∠β的余角可以表示为（）A ．12α∠B ．12β∠C ．()12αβ∠-∠D ．()1+2αβ∠∠ 7．如图，90AOB ∠=︒，AOC ∠为AOB ∠外的一个锐角，且40AOC ∠=︒，射线OM 平分BOC ∠，ON 平分AOC ∠，则MON ∠的度数为（）．A ．45︒B ．65︒C ．50︒D ．25︒8．“枪挑一条线，棍扫一大片”，从数学的角度解释为（）．A ．点动成线，线动成面B ．线动成面，面动成体C ．点动成线，面动成体D ．点动成面，面动成线9．如图．已知//AB CD ．直线EF 分别交,AB CD 于点,,E F EG 平分BEF ∠．若1 50∠=︒．则2∠的度数为（）A ．50︒B ．65︒C ．60︒D ．70︒ 10．如图，把APB ∠放置在量角器上，P 与量角器的中心重合，读得射线PA 、PB 分别经过刻度117和153，把APB ∠绕点P 逆时针方向旋转到A PB ''∠，下列结论： ①APA BPB ''∠=∠；②若射线PA '经过刻度27，则B PA '∠与A PB '∠互补；③若12APB APA ''∠=∠，则射线PA '经过刻度45．其中正确的是（）A ．①②B ．①③C ．②③D ．①②③11．已知线段AB ＝6cm ，反向延长线段AB 到C ，使BC ＝83AB ，D 是BC 的中点，则线段AD 的长为____cmA ．2B ．3C ．5D ．6 12．一根直木棒长10厘米，棒上有刻度如图，若把它作为尺子，只测量一次，能测量的长度共有（）A．7种B．6种C．5种D．4种13．下图是一个三面带有标记的正方体，它的表面展开图是（）A．B．C．D．14．用一个平面去截正方体，所得截面是三角形，留下较大的几何体一定有（）A．7个面B．15条棱C．7个顶点D．10个顶点15．下列图形中，是圆锥的表面展开图的是（）A．B．C．D．二、填空题16．如图，点C，M，N在线段AB上，且M是AC的中点，CN：NB=1：2，若AC=12，MN=15，则线段AB的长是_______.17．在直线AB上，点A与点B的距离是8cm，点C与点A的距离是2cm，点D是线段AB 的中点，则线段CD的长为________.18．用一个平面分别截棱柱、圆锥，都能截出的一个图形是________.19．如图是一个多面体的表面展开图，则折叠后与棱AB重合的棱是________.20．把棱长为1cm的四个正方体拼接成一个长方体，则在所得长方体中，表面积最大等于________2cm.21．下面的图形是某些几何体的表面展开图，写出这些几何体的名称．22．如图，点C 是线段AB 上一点，点M ，N ，P 分别是线段AC ，BC ，AB 的中点.若3AC =，1CP =，则线段PN 的长为________.23．魏老师去农贸市场买菜时发现，若把10千克的菜放在秤上，则指针盘上的指针转了180︒，第二天魏老师请同学们回答以下两个问题：（1）若把0.5千克的菜放在秤上，则指针转过________度；（2）若指针转了243︒，则这些菜共有________千克.24．把命题“等角的余角相等”改写成“如果……那么……”的形式:__________________________. 是______命题(填“真”或“假”)25．已知线段MN=16cm ，点P 为任意一点，那么线段MP 与NP 和的最小值是_____cm ． 26．一个几何体，从不同方向看到的图形如图所示．拼成这个几何体的小正方体的个数为______．三、解答题27．如图，已知OE 是∠AOB 的平分线，C 是∠AOE 内的一点，若∠BOC ＝2∠AOC ，∠AOB ＝114°，则求∠BOC ，∠EOC 的度数．28．已知：点O 为直线AB 上一点，过点O 作射线OC ，100BOC ∠=︒．（1）如图1，求AOC ∠的度数；（2）如图2，过点O 作射线OD ，使90COD ∠=︒，作AOC ∠的平分线OM ，求MOD ∠的度数；（3）如图3，在（2）的条件下，作射线OP ，若BOP ∠与AOM ∠互余，请画出图形，并求COP ∠的度数．29．已知线段AB ＝10cm ，直线AB 上有一点C ，BC ＝6cm ，M 为线段AB 的中点，N 为线段BC 的中点，求线段MN 的长．30．[阅读理解]射线OC 是AOB ∠内部的一条射线，若1,2COA BOC ∠=∠则我们称射线OC 是射线OA 的伴随线．例如，如图1，60 20AOB AOC COD BOD ∠=∠=∠=∠=，，则12AOC BOC ∠=∠，称射线OC 是射线OA 的伴随线：同时，由于12BOD AOD ∠=∠，称射线OD 是射线OB 的伴随线．[知识运用]（1）如图2，120AOB ∠=，射线OM 是射线OA 的伴随线，则AOM ∠= ，若AOB ∠的度数是α，射线ON 是射线OB 的伴随线，射线OC 是AOB ∠的平分线，则NOC ∠的度数是．（用含α的代数式表示）（2）如图，如180AOB ∠=，射线OC 与射线OA 重合，并绕点O 以每秒3的速度逆时针旋转，射线OD 与射线OB 重合，并绕点O 以每秒5的速度顺时针旋转，当射线OD 与射线OA 重合时，运动停止，现在两射线同时开始旋转．①是否存在某个时刻t （秒），使得COD ∠的度数是20，若存在，求出t 的值，若不存在，请说明理由；②当t 为多少秒时，射线OC OD OA 、、中恰好有一条射线是其余两条射线的伴随线．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

七上第五章 P159—P184
八上第十三章 P54—P58，P92—P99.
上一页返回导航下一页
上一页返回导航下一页
上一页返回导航下一页பைடு நூலகம்
直线、射线、线段 1．有关直线的基本事实：① 两两点点确定一条直线． 2．直线上一点及其一旁的部分叫做射线，这个点叫做射线的② 端端点点；直线上两点及两点间的部分叫做线段，这两个点叫做线段的③ 端端点点． 3．有关线段的基本事实：两点之间④ 线线段段最短，连接两点间的线段的长度叫做两点间的距离． 4．线段的中点：把一条线段分成两条相等的线段的点叫做线段的⑤ 中中点点．
第四章三角形
第13讲几何图形初步(3分)
【版本导航】人教：七上第四章 P125—P141
七下第五章 P1—P27
八上第十二章 P48—P52
八上第十三章 P60—P61；
北师：七上第四章 P105—P121
七下第二章 P38—P54
八上第七章 P162—P177
八下第一章 P22—P32；
华师：七上第四章 P138—P153
1．在同一平面内，○22 不不相相交交的两条直线叫做平行线．
2．平行线的判定
(1)同位角○23 相相等等，两直线平行； (2)内错角○24 相相等等，两直线平行； (3)同旁内角○25 互补，两直线平行．
上一页返回导航下一页
注：判断两直线平行还可考虑以下方法： (1)平行于同一条直线的两直线平行； (2)在同一平面内，垂直于同一条直线的两直线平行．
上一页返回导航下一页
(2)线段的垂直平分线：经过线段的中点，并且⑲ 垂垂直直于于这条线段的直线叫做线段的垂直平分线(又称中垂线)．
①性质：线段垂直平分线上的点到线段两端点的距离⑳ 相等． ②判定：到一条线段两端点距离○21 相相等等的点在线段的垂直平分线上．
上一页返回导航下一页
平行线(10 年 5 考)
上一页返回导航下一页
角及角的平分线(高频考点) 1．角的概念：具有公共端点的两条⑥ 射射线线组成的图形叫做角．这个公共端点称为角的顶点，这两条射线是角的两边．角也可以看成是由一条⑦ 射射线线绕其端点旋转而形成的几何图形． 2．角的度量：角的大小用度(°)、分(′)、秒(″)来度量，它们之间是 60 进制的，即 1°＝60′，1′＝60″，1 周角＝⑧ 22倍倍平角＝⑨ 44倍倍直角＝360°.
上一页返回导航下一页
3．余角、补角及其性质 (1)如果两个角的和等于⑩ 909°0°，就说这两个角互为余角． (2)如果两个角的和等于⑪ 118800°°，就说这两个角互为补角． (3)性质：同角(等角）的余角相等，同角(等角）的补角相等．
上一页返回导航下一页
4．角的平分线 (1)角的平分线：从一个角的顶点出发，把这个角分成相等的两个角的射线，叫做这个角的平分线． (2)角平分线定理及其逆定理定理：角平分线上的点到角两边的距离⑫ 相相等等．逆定理：在一个角的内部，到这个角两边距离⑬ 相相等等的点在这个角的平分线上．
上一页返回导航下一页
3．平行线的性质
(1)两直线平行，同位角○26 相等； (2)两直线平行，内错角○27 相等； (3)两直线平行，同旁内角○28 互互补补；
(4)平行公理：经过直线外一点，有且只有一条直线与已知直线平行．
上一页返回导航下一页
命题、定理、证明
1．判断一件事情的语句，叫做命题．命题有题设和结论两部分．正确的命题叫做○29 真真命命题题，错误的命题叫做○30 假假命命题题．
上一页返回导航下一页
序号 1 2 3
中考年份 2019 年 2018 年
2015 年
命题点利用平行线性质求角度利用相交线性质求角度
同位角相等(3) 对顶角相等/余角和邻补角(12)
内错角相等/同位角相等 /同旁内角互补(4)
上一页返回导航下一页
序号
4 5 6 7
中考年份
2014 年 2013 年 2011 年 2010 年
2．一切公理(即基本事实)和定理都是真命题．除基本事实外，其他真命题的正确性
都是通过推理的方法得到证实的，推理的过程叫做○31 证证明明．经过证明的真命题叫做 ○32 定定理理．
上一页返回导航下一页
3．在两个命题中，如果第一个命题的题设是另一个命题的结论，而第一个命题的结论是另一个命题的题设，那么这两个命题叫做互逆命题．如果把其中一个叫做原命题，
那么另一个命题就是它的○33 逆逆命命题题． 4．如果一个定理的逆命题能被证明是真命题，那么就说它是原定理的○34 逆逆定定
理理，这两个定理叫做○35 互逆定理．
上一页返回导航下一页
5．要证明一个命题是假命题，可以用○36 举举反反例例的方法．
6．反证法：假设在原命题的题设下，结论不成立，然后推理出明显矛盾的结果，从而说明假设不成立，原命题得证.
命题点利用平行线性质求角度利用相交线性质求角度
垂线(3) 内错角相等(10) 同旁内角互补(2) 内错角相等(10)
上一页返回导航下一页
利用平行线性质求角度(10 年 5 考) 例 1 (2019·河南 3 题)如图，AB∥CD，∠B＝75°，∠E＝27°，则∠D 的度数为( B )
A．45°
B．48°
C．50°
D．58°
上一页返回导航下一页
【解析】设 BE 与 CD 的交点为 F，如解图所示．∵AB∥CD，∴∠EFC＝∠B＝ 75°.∴∠D＝∠EFC－∠E＝48°，故选 B．
上一页返回导航下一页
相交线(10 年 2 考) 1．对顶角的性质：对顶角⑭ 相相等等． 2．邻补角：两条直线相交所构成的四个角中，有公共顶点且有一条公共边的两个角互为邻补角．
上一页返回导航下一页
3．垂线及性质 (1)垂线段：两条直线相交所成的四个角中，如果有一个角是⑮ 9900°° ，我们就说这两条直线垂直，其中一条直线叫做另一条直线的垂线，它们的交点叫做⑯ 垂足． ①有关垂线的基本事实：在同一平面内，过一点有且只有一条直线与已知直线垂直． ②垂线的性质：直线外一点与直线上各点的所有连线中，⑰ 垂垂线线段段最短．垂线段的长度叫做点到这条直线的⑱ 距距离离．

2020年河南中考数学总复习考点精讲第13讲 几何图形初步(3分)

初中数学专题讲解课件专题十三几何图形的相关证明及计算(构造直角三角形)PPT模板

2020中考数学复习专项训练 第三章 图形认识初步(含答案)

最新2020中考数学典例精做专题13 抛物线与压轴题(1) (教师版)