2014-2015期末——鼓楼区试卷【录入:刘璐 审核:海燕】
2014-2015学年第一学期期末调研试卷
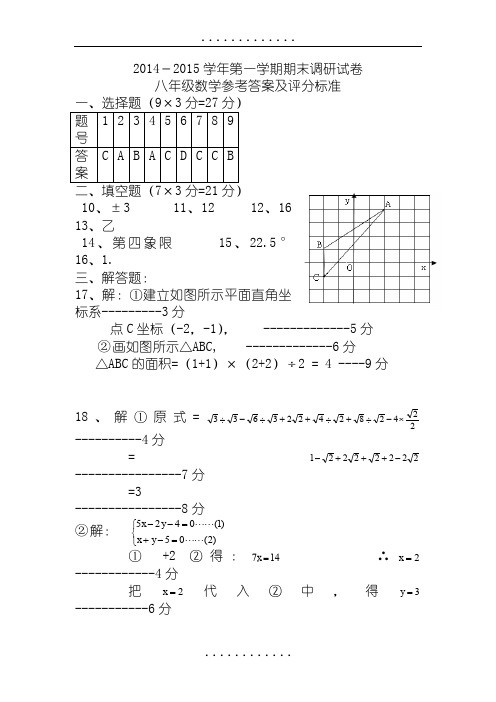
2014-2015学年第一学期期末调研试卷八年级数学参考答案及评分标准一、选择题(9×3分=27分)二、填空题(7×3分=21分) 10、±3 11、12 12、1613、乙14、第四象限 15、22.5°16、1.三、解答题:17、解:①建立如图所示平面直角坐标系---------3分 点C 坐标(-2,-1), -------------5分 ② 画如图所示△ABC, -------------6分△ABC 的面积=(1+1)×(2+2)÷2 = 4 ----9分18、解①原式=2242824223633⨯-÷+÷++÷-÷----------4分=22222221-+++- ----------------7分=3----------------8分② 解: ⎩⎨⎧=-+=--)2(05)1(0425 y x y x① +2 ②得:147=x ∴2=x ------------4分把2=x 代入②中,得3=y-----------6分方程组的解是⎩⎨⎧==32y x----------8分 19、解:连结AC ,∵∠ABC=90°,∴在Rt △ABC 中,AB=1,BC=2,521222=+=AC ∴AC=5 -----------4分∵4222==DC 9322==AD∴222AD DC AC =+ 即∠ACD=90°-------6分四边形面积5152212121+=⨯⨯+⨯⨯=S ---------8分 20、解:①20÷10%=200 所以一共调查200人.---------3分②填对一个得1分--------8分③众数为80人21、解:①设单价5元为x 本,单价8元为y 本。
根据题意得:⎩⎨⎧-+=+=+68133008540y x y x -----------4分解得:⎩⎨⎧==1525y x -----------6分答:单价5元为25本,单价8元为15本② 假如找回68元,设单价5元为x 本。
20142015学年第一学期期末调研考试

2014-2015学年度第一学期期末调研考试七年级数学参考答案注意:本卷三道大题,26小题,总分120。
二、填空题(每小题3分,共18分)17. 140° 18. 11 19. 2 20. 2015元三、解答题(本大题共6个小题,共66分,解答应写出文字说明、证明过程 或演算步骤)21.(满分10分,每小题5分)⑴ 解:原式=-3++5()()………………3分 =2……………………………5分⑵ 解:2632x x -=+……………3分=8x - ……………5分22、(满分10分,每小题5分)(1)解:原式=2252112208a a a a +--+-………3分=2-32213a a +-…………………………5分(2)解:原式=24220x x --……………………………3分 当12x =时,原式=21142202022⨯-⨯-=-()…5分23、(满分10分)解:设粗加工的这种水果的质量是x kg ,则精加工(10000-x )kg …2分由题意得:10000-3200x x =+………………………………………6分解得: 2450x =……………………………………………………9分答:略。
……………………………………………………………………10分24、(满分12分)解:(1)略写:1206060AOD AOC BOD ∠=︒⎧∠=︒⇒⎨∠=︒⎩——————2分30DOM ⇒∠=︒角平分线…………………………4分(2) 60DON ⇒∠=︒直角………………………………6分1206060AOD AON DON ∠=︒⎫⇒∠=︒⎬∠=︒⎭……………………8分 (3)60DON ∠=︒所以,DON ∠的补角是120︒………………………12分25、(本题满分12分)。
(1)-2,10,12x x x ++……………………3分(2)设框内右上角的数为x ,则(-2)(10)(12)192x x x x +++++=……5分解得,43x =………………………………………………7分从而另三个数分别是:41、53和55。
南京市鼓楼区2015-2016学年七年级上期末数学试卷及答案

注意事项:
本试卷共6页.全卷满分100分.考试时间为100分钟.考生答题全部答在答题纸上,答在本试卷上无效.
一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的序号填涂在答题纸相应位置上)
出生年份
2022年年龄(岁)
延迟退休时间(年)
实际退休年Hale Waihona Puke (岁)196755
0.5
55.5
1968
54
1
56
1969
53
1.5
56.5
1970
52
2
57
1971
51
2.5
57.5
1972
50
3
58
……
……
……
……
(1)根据上表,1974年出生的人实际退休年龄将会是▲岁;
(2)若每年延迟退休3个月,则▲年出生的人恰好是65岁退休;
120°、144°、150°、153°、171°的角中,能画出的角有(▲).
A.7个
B.8个
C.9个
D.10个
二、填空题(本题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题纸相应位置上)
7.比较大小:–▲–.
8.多项式ab-2ab2-a的次数为▲.
9.已知5是关于 的方程 的解,则 的值为▲.
②图中线段▲长度表示点A到直线CD的距离.
22. (本题5分)如图,直线AB、CD相交于点O,OE⊥AB,OF⊥CD.
(1)写出图中∠AOF的余角▲;
(2)如果∠EOF=∠AOD,求∠EOF的度数.
2014-2015下学期期末考试高一数学(A卷)试题与答案

答案一、CDABA BACDCDA 13、57-14、3/10 15、017、)4sin(π+x 18、3- 19、解:(1)由条件1OA =,AON θ∠=cos OC θ∴=,sin AC θ= ……2分1sin cos sin 22S θθθ∴== ……4分其中02πθ<< ……6分(2) 02πθ<<,02θπ∴<< ……8分故当22πθ=,即4πθ=时,……10分max 12S =. ……12分20、解:(1) 这二十五个数据的中位数是397.……4分 (2)品种A 亩产量的频率分布表如下:………………………8分(3)品种A 亩产量的频率分布直方图如下:0.0.0.0.0.0.0.0.………12分21、解:(1)由图象知:4()24T πππ=-=,则:22Tπω==,…………2分 由(0)1f =-得:sin 1ϕ=-,即:()2k k z πϕπ=-∈,……………4分∵||ϕπ< ∴ 2πϕ=-。
………………………………6分(2)由(1)知:()sin(2)cos 22f x x x π=-=-,……………………7分∴g()()()1cos )[cos()]12284xx x f x x ππ=--=----2[sin )]12cos 2sin cos 12x x x x x x =+-=+-cos 2sin 2)4x x x π=+=+,………………………10分当[0,]2x π∈时,52[,]444x πππ+∈,则sin(2)[,1]42x π+∈-,∴()g x 的值域为[-。
………………………………………12分22、解:(1)设(14,)P y ,则(14,),(8,3)OP y PB y ==---, ……………1分 由OP PB λ=,得(14,)(8,3)y y λ=---, …………2分 解得7,74y λ=-=-,所以点(14,7)P -。
2014-2015学年七年级期末 数学试卷(人教版)

2014-2015学年七年级期末数学试卷(人教版) 2014.1(试卷共4页,考试时间为90分钟,满分120分)题号一二三总分2122232425262728得分一、选择题(本题共12个小题,每小题3分,共36分.将正确答案的字母填入方框中)题号123456789101112答案1.等于()A.-2 B. C.2 D.2.在墙壁上固定一根横放的木条,则至少需要钉子的枚数是 ( )A.1枚 B.2枚 C.3枚 D.任意枚3.下列方程为一元一次方程的是( )A.y+3= 0 B.x+2y=3 C.x2=2x D.4.下列各组数中,互为相反数的是( )A.与1 B.(-1)2与1 C.与1 D.-12与15.下列各组单项式中,为同类项的是( )A.a与a B.a与2a C.2xy与2x D.-3与a6.如图,数轴A、B上两点分别对应实数a、b,则下列结论正确的是A.a+b>0 B.ab >0 C. D.7.下列各图中,可以是一个正方体的平面展开图的是( )8.把两块三角板按如图所示那样拼在一起,则∠ABC等于( )A.70° B.90° C.105° D.120°9.在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为 ( )A.69° B.111° C.141° D.159°10.一件夹克衫先按成本提高50%标价,再以8折(标价的80%)出售,结果获利28元,若设这件夹克衫的成本是x元,根据题意,可得到的方程是( )A.(1+50%)x×80%=x-28 B.(1+50%)x×80%=x+28C.(1+50%x)×80%=x-28 D.(1+50%x)×80%=x+2811.轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是()A. B. C. D.12.填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值应是()A.110 B.158 C.168 D.178二、填空题(本大题共8个小题;每小题3分,共24分.把答案写在题中横线上)13.-3的倒数是________.14.单项式xy2的系数是_________.15.若x=2是方程8-2x=ax的解,则a=_________.16.计算:15°37′+42°51′=_________.17.青藏高原是世界上海拔最高的高原,它的面积约为2 500 000平方千米.将2 500 000用科学记数法表示应为_________________平方千米.18.已知,a-b=2,那么2a-2b+5=_________.19.已知y1=x+3,y2=2-x,当x=_________时,y1比y2大5.20.根据图中提供的信息,可知一个杯子的价格是________元.三、解答题(本大题共8个小题;共60分)21.(本小题满分6分)计算:(-1)3-×[2-(-3)] .22.(本小题满分6分)一个角的余角比这个角的少30°,请你计算出这个角的大小.23.(本小题满分7分)先化简,再求值:(-4x2+2x-8)-(x-1),其中x=.24.(本小题满分7分)解方程:-=1.25.(本小题满分7分)一点A从数轴上表示+2的点开始移动,第一次先向左移动1个单位,再向右移动2个单位;第二次先向左移动3个单位,再向右移动4个单位;第三次先向左移动5个单位,再向右移动6个单位……(1)写出第一次移动后这个点在数轴上表示的数为;(2)写出第二次移动结果这个点在数轴上表示的数为;(3)写出第五次移动后这个点在数轴上表示的数为;(4)写出第n次移动结果这个点在数轴上表示的数为;(5)如果第m次移动后这个点在数轴上表示的数为56,求m的值.26.(本小题满分8分)如图,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.求:∠COE的度数.27.(本小题满分8分)如图,已知线段AB和CD的公共部分BD=AB=CD,线段AB、CD的中点E、F之间距离是10cm,求AB、CD的长.28.(本小题满分11分)某中学为了表彰在书法比赛中成绩突出的学生,购买了钢笔30支,毛笔45支,共用了1755元,其中每支毛笔比钢笔贵4元.(1)求钢笔和毛笔的单价各为多少元?(2)①学校仍需要购买上面的两种笔共105支(每种笔的单价不变).陈老师做完预算后,向财务处王老师说:“我这次买这两种笔需支领2447元.”王老师算了一下,说:“如果你用这些钱只买这两种笔,那么帐肯定算错了.”请你用学过的方程知识解释王老师为什么说他用这些钱只买这两种笔的帐算错了.②陈老师突然想起,所做的预算中还包括校长让他买的一支签字笔.如果签字笔的单价为小于10元的整数,请通过计算,直接写出签字笔的单价可能为元.2013~2014学年度第一学期七年级期末考试数学试题参考答案及评分说明说明: 1.各校在阅卷过程中,如还有其它正确解法,可参照评分标准按步骤酌情给分.2.坚持每题评阅到底的原则,当学生的解答在某一步出现错误,影响了后继部分时,如果该步以后的解答未改变这一题的内容和难度,可视影响的程度决定后面部分的给分,但不得超过后继部分应给分数的一半;如果这一步后面的解答有较严重的错误,就不给分.一、选择题(每小题3分,共36分)1.C ;2.B ;3.A;4.D;5.B;6. D;7.C;8.D;9.C;10. B;11.A;12.B.二、填空题(每题3分,共24分)13.;14.;15.2;16.58°28′;17.2.5×106;18.9;19.2;20.8.三、解答题(共60分)21.解:原式= -1-×(2-9)………………………………………………………3分=-1+ …………………………………………………………………………5分= ……………………………………………………………………………6分22.解:设这个角的度数为x. ……………………………………………………………1分由题意得:………………………………………………3分解得:x=80 …………………………………………………………………5分答:这个角的度数是80° ……………………………………………………………6分23.解:原式= ………………………………………………3分= ………………………………………………………………4分把x=代入原式:原式==……………………………………………………………5分= ……………………………………………………………………………7分24.解:. ……………………………………………2分. ………………………………………………………4分8x=3. …………………………………………………………6分. …………………………………………………………7分X|k |B| 1 . c|O |m25.解:(1)第一次移动后这个点在数轴上表示的数是3;……………………………1分(2)第二次移动后这个点在数轴上表示的数是4;……………………………2分(3)第五次移动后这个点在数轴上表示的数是7;……………………………3分(4)第n次移动后这个点在数轴上表示的数是n+2;…………………………5分(5)54. ………………………………………………………………………7分26.解:∵∠AOB=90°,OC平分∠AOB∴∠BOC=∠AOB=45°,………………………………………………………2分∵∠BOD=∠COD-∠BOC=90°-45°=45°,………………………………4分∠BOD=3∠DOE∴∠DOE=15,……………………………………………………………………7分∴∠COE=∠COD-∠DOE=90°-15°=75° …………………………………8分27.解:设BD=xcm,则AB=3xcm,CD=4xcm,AC=6xcm.…………………………1分∵点E、点F分别为AB、CD的中点,∴AE=AB=1.5xcm,CF=CD=2xcm.……………………………………………3分∴EF=AC-AE-CF=2.5xcm.………………………………………………………4分∵EF=10cm,∴2.5x=10,解得:x=4.………………………………………………………………6分∴AB=12cm,CD=16cm.……………………………………………………………8分28.解:(1)设钢笔的单价为x元,则毛笔的单价为(x+4)元. ………………………1分由题意得:30x+45(x+4)=1755 ……………………………………………3分解得:x=21则x+4=25. ……………………………………………………………………4分答:钢笔的单价为21元,毛笔的单价为25元. ……………………………………5分(2)设单价为21元的钢笔为y支,所以单价为25元的毛笔则为(105-y)支. …6分根据题意,得21y+25(105-y)=2447.………………………………………………7分解之得:y=44.5 (不符合题意) . ……………………………………………………8分所以王老师肯定搞错了. ……………………………………………………………9分(3)2或6. ………………………………………………………………………11分〖答对1个给1分,答错1个倒扣1分,扣到0分为止〗28.(3)解法提示:设单价为21元的钢笔为z支,签字笔的单价为a元则根据题意,得21z+25(105-z)=2447-a.即:4z=178+a,因为 a、z都是整数,且178+a应被4整除,所以 a为偶数,又因为a为小于10元的整数,所以 a可能为2、4、6、8.当a=2时,4z=180,z=45,符合题意;当a=4时,4z=182,z=45.5,不符合题意;当a=6时,4z=184,z=46,符合题意;当a=8时,4z=186,z=46.5,不符合题意.所以笔记本的单价可能2元或6元.〖本题也可由①问结果,通过讨论钢笔单价得到答案〗。
2015-2016学年江苏省南京市鼓楼区八年级(下)期末数学试卷(解析版)

)
A.不小于 m
3
B.小于 m
3
C.不小于 m
3
D.小于 m
3
6. (2 分)某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如
第 1 页(共 23 页)
图所示的折线图,那么符合这一结果的试验最有可能的是(
)
A.在装有 1 个红球和 2 个白球(除颜色外完全相同)的不透明袋子里随机摸出一个球是 “白球” B.从一副扑克牌中任意抽取一张,这张牌是“红色的” C.掷一枚质地均匀的硬币,落地时结果是“正面朝上” D.只一个质地均匀的正六面体骰子,落地时面朝上的点数是 6 二、填空题:每小题 2 分,共 20 分 7. (2 分)使式子 8. (2 分)计算 ﹣ 有意义的 x 取值范围是 的结果为 . . . .
14. (2 分) 如图, 为了体验四边形的不稳定性, 将四根木条用钉子钉成一个矩形框架 ABCD, B 与 D 两点之间用一根橡皮筋拉直固定,然后向右扭动框架,给出如下的判断: ①四边形 ABCD 为平行四边形;
第 2 页(共 23 页)
②BD 的长度增大; ③四边形 ABCD 的面积不变; ④四边形 ABCD 的周长不变. 其中正确的序号是 .
2015-2016 学年江苏省南京市鼓楼区八年级(下)期末数学试卷
一、选择题:本大题共 6 小题,共 12 分 1. (2 分)计算 A.4 的结果是( B.±4 ) C.2 D.﹣4 )
2. (2 分)下列图形中既是轴对称图形,又是中心对称图形的是(
A.
B.
C. 3. (2 分)如果把分式 A.扩大为原来的 4 倍 C.不变
15. (2 分) 计算 (1﹣ + + )的结果是
2014-2015学年八年级期末试卷
2014-2015学年第一学期期末质量检测八年级历史答题卡(第一面)(开卷考满分:100分考试时间:60分钟)友情提示:请同学们将答案填到答题卡上!答题卡一.选择题(每小题2分,共40分)二、改错题(每小题2分,共10分)21.错误:改正:22.错误:改正:23.错误:改正:24.错误:改正:25.错误:改正:三.辨析题(指出错误给2分,说理正确给3分,共5分)错误:理由:2014-2015学年第一学期期末质量检测八年级历史试卷(开卷考满分:100分考试时间:60分钟)友情提示:请同学们将答案填到答题卡上!一.单项选择题 (请同学们将选择题的正确选项填入对应空格中。
每小题2分,共40分) 1.6月26日是联合国确定的国际禁毒日。
你可知道,历史上一位著名的民族英雄领导人民取得了禁烟斗争的伟大胜利。
这位民族英雄是A.戚继光B.岳飞C.郑成功D.林则徐2.中国近代史开端的标志是A.鸦片战争B.第二次鸦片战争C.中法战争D.甲午中日战争3.第二次鸦片战争前后,俄国共割占了中国东北和西北领土多少平方公里。
A.六十多万B.四十多万C.一百六十多万D.一百五十多万4.在中国人民反抗外国侵略的悲壮历史中,勇击日寇捐躯黄海的民族英雄是:A.林则徐B.邓世昌C.李秀成D.左宗棠5.下列有关《辛丑条约》的内容中哪一项最能说明清政府完全沦为帝国主义统治中国的工具:A.清政府赔偿白银4.5亿两B.清政府保证严禁人民参加反帝活动C.清政府拆毁大沽炮台D.划定北京东交民巷为使馆界,允许各国驻兵保护,不准中国人居住6.某校八年级历史兴趣小组要实地考察辛亥革命爆发的地点,他们应该去:A.北京B.上海C.延安D.武昌7.洋务派开办的第一个军事企业是A.江南制造总局B.福州船政局C.安庆内军械所D.天津机器局8.在下列戊戌变法的内容中,最能体现资产阶级利益的是:A.提倡办实业,奖励兴办工矿企业B.广开言路,裁汰冗官,精简机构C.改革科举制度,开办新式学堂,设立译书局D.训练和装备新式陆、海军9.新文化运动的内容是①提倡民主,反对专制②提倡科学,反对愚昧③提倡新道德,反对旧道德④提倡新文学,反对旧文学A.①②③B.①②③④C.②③④D.①③④10.五四运动所体现的五四精神最突出的是:A.国际主义精神B.科学创新精神C.爱国主义精神D.民主法制精神11.率领第四军独立团屡破强敌的北伐名将是A.贺龙B.周恩来C.叶挺D.刘伯承12.中国共产党打响武装反抗国民党反动统治第一枪的是A.南昌起义B.秋收起义C.广州起义D.武昌起义13.中国共产党提出和平解决西安事变的根本出发点是:A.改善国共两党之间的关系B.粉碎国民党内亲日派的企图C.为全民利益实现共同抗日D.应对蒋介石采取支持的态度14.抗日战争和解放战争时期被誉为革命圣地的是A.延安B.瑞金C.井冈山D.北京15.为争取抗战胜利和实现光明前途准备了条件的会议是A.中共一大B.遵义会议C.中共七大D.十一届三中全会16.右图中毛泽东和蒋介石在重庆的这次合影,曾使无数国人充满希望。
201504鼓楼一模卷(定)
鼓楼区2014-2015学年第二学期期中测试九年级语文试卷2015.4.(分值120分时间120分钟)一、积累与运用。
(26分)1.用诗文原句填空。
(9分)(1)烈士暮年,。
(曹操《龟虽寿》)(2)莫愁前路无知己,。
(高适《别董大》)(3)报君黄金台上意,。
(李贺《雁门太守行》)(4),夜泊秦淮近酒家。
(杜牧《泊秦淮》)(5),西北望,射天狼。
(苏轼《江城子·密州出猎》)(6)马作的卢飞快,。
(辛弃疾《破阵子·为陈同甫赋壮词以寄之》)(7)江山代有才人出,。
(赵翼《论诗》)(8),草色入帘青。
(刘禹锡《陋室铭》)(9)“清明时节雨纷纷,路上行人欲断魂”,这类与传统节日相关的诗句还很多,请再举一例:,。
2.下列加点字读音全部相同....的一项是(2分)()A. 晦.暗欺侮.诲.人不倦B. 伺.候侍.候伺.机而动C. 便笺.缄.默芊.芊细草D. 炽.痛叱.咤敕.勒川3.下列词语书写全部正确....的一项是(2分)()A. 荒谬——杀戳挟持——汗流浃背B. 伧俗——苍海灰尽——死灰复燃C. 攫取——洗濯荣膺——义愤填赝D. 沉湎——腼腆闲暇——闻名遐迩4.书法欣赏。
(4分)(1)“柳体”以瘦劲著称,点画爽利挺秀,骨力矫健,结构严谨。
以下书作中,柳公权的作品是()(2分)[A] [B] [C](2)关于初学者选笔应该用硬毫还是软毫,说法不一。
有同学向他的书法老师询问,下面是老师的回答:打个比方吧:在雕刻艺术上,刀法不高,花纹不明快骏爽,叫太‚肉‛,软毫写出来的笔画是偏‚肉‛的。
除非你喜欢那种没有锋梭芒角,肥软圆熟的书风。
俗语说:‚工欲善其事,必先利其器。
‛庖丁解牛,绝不会去选一把钝刀,用软毫练字,就犹如钝刀子割肉。
如果等刀力练出了再换快刀,那不成了‚工欲善其事,必先钝其器‛嘛!由此看来,这位老师建议选用。
(A.硬毫 B.软毫 C.都可以)(2分)5.阅读下列三则材料,回答问题。
(9分)【材料一】桃之夭夭,灼灼其华。
2014-2015学年第一学期期末调研试卷
WORD 格式-专业学习资料-可编辑学习资料分享2014-2015学年第一学期期末调研试卷九年级数学参考答案及评分标准一、选择题(9×3分=27分) 1.D 2.D 3.C 4.B 5.B 6.A 7.B 8.C 9.A二、填空题(7×3分=21分)10.-49; 11.x=1; 12.20; 13. 答案不唯一,正确即可(∠BAD=∠C 或∠BDA=∠BAC 或BD AB =BA BC ); 14. 75; 15.(-2,1)或(2,-1);16. 8.三、解答题(2)解○1 x 2+x=0 x (x+1)=0………………………7分原方程的解为x 1=0,x 2=-1; ………………………10分其他方程的解法给分类似○1。
(○2的解为x 1=1,x 2=-1;○3的解为x 1=x 2=2;○4的解为x 1,2=251±;○5没有实数根) 18.(本题 10分)该几何体的形状是直四棱柱(答直棱柱,四棱柱,棱柱也给分).………4分由三视图知,棱柱底面菱形的对角线长分别为4cm ,3cm .…………6分∴底面菱形的面积:S 菱=12×4×3=6 ∴V 棱柱= S 菱×高=6×8=48 (cm 3).………10分 19.(本题 10分)(1)P (红球)=23.………4分 (2)解:所有可能出现的结果如图所示:8分共有6种结果,其中两次都摸到红球的有2种,∴P (两次都摸到红球)=2163=.………10分 20. (本题10分)(1)∵A 与C 关于直线MN 对称, ∴AC ⊥MN ∴∠COM=900. ……………… 2分在矩形ABCD 中∠B=900, ∴∠COM=∠B.又∵∠ACB=∠MCO ∴△COM ∽△CBA. ………………6分(2)∵在Rt △CBA 中,AB=6,BC=8, ∴AC=10,∴OC=5. ………………8分又∵△COM ∽△CBA, ∴OC BC = OM AB ∴OM=AB ·OC BC = 154.……………10分 21. (本题11分)解:(1)作AE ⊥y 轴于E ,∵S △AOD =4,OD=2, ∴12OD ·AE=4,∴AE=4,……………2分 ∵AB ⊥OB ,C 为OB 的中点,∴OC=BC ,∠DOC=∠ABC=90°,又∠OCD=∠BCA ,∴Rt △DOC ≌Rt △ABC ∴AB=OD=2 , ∴点A 的坐标为A (4,2),……………4分将A (4,2)代入y 1= k x 中,得k=8,∴反比例函数为y 1= 8x,……………5分 ∴将A (4,2)和D (0,-2)代入y 2=ax+b ,得 解之得:,∴一次函数为y 2=x -2;……………8分(2)在y 轴的右侧,当y 1>y 2时,x 的取值范围是0x 4。
2014-2015学年七年级上册数学期末考试试卷及答案
2013~2014年度第一学期期末考试七年级数学模拟试卷(时间120分钟 满分150分)一、选择题(共10小题,每小题4分,满分40分,在每小题给出的选项中,只有一个符合题意,请将正确的一项代号填入下面括号内)1.我市2013年12月21日至24日每天的最高气温与最低气温如下表:日期 12月21日12月22日12月23日12月24日最高气温 8℃ 7℃ 5℃ 6℃ 最低气温-3℃-5℃-4℃-2℃其中温差最大的一天是………………………………………………………………………………………【 】 A .12月21日 B .12月22日 C .12月23日 D .12月24日 2.如图1所示,A ,B 两点在数轴上,点A 对应的数为2.若线段AB 的长为3,则点B 对应的数为【 】 A .-1B .-2C .-3D .-43.与算式232233++的运算结果相等的是…………………………………………………………………【 】 A .33 B .32 C .53 D .634.化简)3232)21(x --x (+的结果是………………………………………………………………【 】A .317+x -B .315+x -C .6115x -- D .6115+x -5.由四舍五入法得到的近似数3108.8×,下列说法中正确的是………………………………………【 】A .精确到十分位,有2个有效数字B .精确到个位,有2个有效数字C .精确到百位,有2个有效数字D .精确到千位,有4个有效数字6.如下图,下列图形全部属于柱体的是……………………………………………………………………【 】A B C D7.如图2,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=150°,则∠BOC 等于……………【 】 A .30° B .45° C .50° D .60°B 0A 图150c m8.如图3,下列说法中错误..的是……………………………………………………………………………【 】 A .OA 的方向是东北方向 B .OB 的方向是北偏西60° C .OC 的方向是南偏西60° D .OD 的方向是南偏东60°7、我市举行的青年歌手大奖赛今年共有a 人参加,比赛的人数比去年增加 20%还多3人,设去年参赛的人数为x 人,则x 为( ). A 、3120%a ++ B 、(120%)3a ++ C 、 3120%a -+ D 、(120%)3a +- —-—-【 】10. 如图4,宽为50cm 的长方形图案由10个大小相等的小长方形拼成,其中一个小长方形的面积为…【 】A.4000cm 2B 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014-2015学年江苏省南京市鼓楼区九年级(上)期末数学试卷一、选择题(共6小题,每小题2分,满分12分)1.一只不透明的袋子中装有6个黑球3个白球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到白球的概率为()A.B.C.D.2.已知矩形纸片ABCD中,AB=1,如图,剪去正方形ABEF,得到的矩形ECDF与矩形ABCD相似,则AD的长为()A.2 B.C.D.3.已知:⊙O的半径为3cm,圆心O到直线l的距离为1cm,将直线l沿垂直于l的方向平移,使l与⊙O相切,则平移的距离是()A.2cm B.3cm C.4cm D.2cm或4cm4.某商场销售一批衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,商场采取降价措施,假设一定范围内,衬衫单价每降1元,商场平均每天可多售出2件.如果销售这批衬衫每天盈利1250元,设衬衫单价降了x元,根据题意,可列方程()A.(40﹣x)(20+2x)=1250 B.(40﹣2x)(20+x)=1250C.(40+x)(20﹣2x)=1250 D.(40+2x)(20﹣x)=12505.如图,△ABC是⊙O的内接等边三角形,矩形BCDE的边DE与⊙O相切,BE=3,则矩形BCDE的面积是()A.18 B.9 C.18D.96.如图,二次函数y=ax2+bx+c的图象经过点(1,﹣1)和(﹣2,1),下列关于此二次函数的叙述,正确的是()A.当x=0时,y的值小于﹣1 B.当x=﹣3时,y的值大于1C.当x=5时,y的值等于0 D.当x=1时,y的值大于1二、填空题(共10小题,每小题2分,满分20分)7.已知,则=.8.二次函数y=x2+2x﹣5的图象的顶点坐标是.9.已知一元二次方程x2+mx﹣2=0的两个实数根分别为x1,x2,则x1•x2=.10.已知,△ABC的重心G到BC边中点D的距离是2,则BC边上的中线长是.11.将二次函数y=2x2﹣4x+3的图象先向左平移3个单位长度,再向下平移1个单位长度,得到函数的图象的表达式是.12.如图,在▱ABCD中,E是BC边上的一点,且BE:EC=2:1,延长AE交DC延长线于点F,则AB:DF=.13.若二次函数y=ax2+bx+c的x与y的部分对应值如下表:x ﹣7 ﹣6 ﹣5 ﹣4 ﹣3 ﹣2y ﹣27 ﹣13 ﹣3 3 5 3则当x=1时,y的值为.14.关于x的一元二次方程kx2﹣x+1=0有两个不相等的实数根,则k的取值范围是.15.如图,点A、B、C、D在⊙O上,AC、BD交于点E,若CD:AB=1:2,△ABE的周长为8,则△CDE的周长为.16.一张圆心角为45°的扇形纸片按如图方法剪成一个边长为1的正方形,正方形的四个顶点分别在扇形的半径和弧上,那么这个扇形纸片的面积是.三、解答题(共11小题,满分88分)17.(1)解方程(组)①x2+10x+21=0;②(2)利用(1)中解方程(组)使用的方法,可求得方程组的解为.18.(1)根据表1中甲、乙两组数据,完成表2.表1A B C D E F G H甲 5 5 6 6 6 6 7 7乙 3 3 3 6 7 8 8 10表2平均数中位数众数方差甲 6 6 6乙 6 6.5(2)根据表中,回答下列问题:①若项目A~H表示某品牌薯片的8种口味,甲数据表示一天内这8种口味的薯片销售情况,那么作为商家,应该关心表2中的;②若项目A~H表示某公司8位业务员,乙数据表示他们某一个月的销售额,那么作为第9位业务员,想让自己的销售额达到中等以上水平,应该关心表2中的;③若甲、乙表示的两位射击运动爱好者,项目A~H表示8次射击练习中他们命中的环数,那么教练想从中选出一位参加比赛,应选择哪一位?为什么?19.从某班4名团员中随机抽取2名参加学校团员竞赛,这4名团员中有3名男生和1名女生,求抽到两名男生的概率.20.如图是一块矩形铁皮,将四个角各剪去一个边长为2米的正方形后(剩下的部分做成一个)容积为90立方米的无盖长方体箱子,已知长方体箱子底面积的长比宽多4米,求矩形铁皮的面积.21.如图,△ABC中,∠C=90°,∠A=30°,BC=2.(1)用直尺和圆规作△ABC的内切圆⊙O(保留作图痕迹,不写作法);(2)求∠BOC的度数和⊙O的半径.22.如图,夜晚路灯下,小明在点D处测得自己影长DE=4m,在点G处测得自己影长DG=3m,E、D、G、B在同一条直线上,已知小明身高为1.6m,求灯杆AB的高度.23.请用二次函数的知识进行解释,在所有周长相等的矩形中,正方形面积最大.24.如图,AB是⊙O的直径,点C、D在圆上,=,过点C作CE⊥AD延长线于点E.(1)求证:CE是⊙O的切线;(2)若BC=3,AC=4,求CE和AD的长.25.如图是我们熟悉的“勾股树”,图中的三角形都是直角三角形,四边形都是正方形,其中∠ACB=∠A1C1B1=∠A2C2B2=90°,正方形①和②的面积比、正方形③和④的面积比均为1:2.(1)求证:△A1B1C1∽△A2B2C2;(2)若△ABC、△A1B1C1、△A2B2C2的面积分别标记为S、S1、S2,猜想S、S1、S2之间的关系,并说明理由.26.某种药物有三种不同的配方,如图,三条抛物线表示这三种配方在给药量相同的情况下,每毫升血液中的含药量y(微克)随时间x(小时)的变化情况,这种药物每毫升血液中的含药量大于9微克,则会发生中毒,小于5微克,则没有疗效.(1)药厂会旋转该药品的第种配方(填写序号即可),你的理由是.(2)根据图象,求出(1)中选择的配方的有效时间是多长?(3)如果加大给药量,(1)中选择的配方对应的抛物线的形状不变,但位置发生变化,那么该配方的最大有效时间是小时.27.【学习新知】定义:直角三角形的三个顶点分别在矩形的三条边上,并且这个三角形把矩形分割得到若干个三角形,若其中两个三角形均与这个直角三角形相似,我们就把这个直角三角形叫做这个矩形的内接相似直角三角形.【解决问题】矩形ABCD中,AB=4,AD=8,△EFG的三个顶点E、F、G分别在AD、DC、BC上.(1)如图,点E与点A重合,∠EFG=90°.①求证:△EDF∽△FCG;②若△EFG是矩形ABCD的内接相似直角三角形,求DF的长;(2)若△EFG是矩形ABCD的内接相似直角三角形,且它的三个顶点与矩形各顶点都不重合,求DF的长.2014-2015学年江苏省南京市鼓楼区九年级(上)期末数学试卷参考答案与试题解析一、选择题(共6小题,每小题2分,满分12分)1.(2分)(2014秋•南京期末)一只不透明的袋子中装有6个黑球3个白球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到白球的概率为()A.B.C.D.【考点】概率公式.【分析】由一只不透明的袋子中装有6个黑球3个白球,这些球除颜色外都相同,直接利用概率公式求解即可求得答案.【解答】解:∵一只不透明的袋子中装有6个黑球3个白球,这些球除颜色外都相同,∴搅匀后从中任意摸出1个球,摸到白球的概率为:=.故选A.【点评】此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.2.(2分)(2014秋•南京期末)已知矩形纸片ABCD中,AB=1,如图,剪去正方形ABEF,得到的矩形ECDF与矩形ABCD相似,则AD的长为()A.2 B.C.D.【考点】相似多边形的性质.【专题】计算题.【分析】设AD=x,根据正方形的性质得AF=AB=EF=1,则FD=x﹣1,在根据相似多边形的性质得到DF:AB=EF:AD,即(x﹣1):1=1:x,然后解方程即可得到AD的长.【解答】解:设AD=x,∵四边形ABEF为正方形,∴AF=AB=EF=1,∴FD=x﹣1,∵矩形ECDF与矩形ABCD相似,∴DF:AB=EF:AD,即(x﹣1):1=1:x,整理得x2﹣x﹣1=0,解得x1=,x2=(舍去),即AD的长为.故选D.【点评】本题考查了相似多边形的性质:相似多边形对应边的比叫做相似比;对应角相等;对应边的比相等;相似多边形面积的比等于相似比的平方.也考查了等腰直角三角形.3.(2分)(2014秋•南京期末)已知:⊙O的半径为3cm,圆心O到直线l的距离为1cm,将直线l沿垂直于l的方向平移,使l与⊙O相切,则平移的距离是()A.2cm B.3cm C.4cm D.2cm或4cm【考点】直线与圆的位置关系.【分析】根据直线和圆相切的数量关系,可得点O到l的距离为1cm,可向上或向下平移,使l与⊙O相切,即可得出答案.【解答】解:如图,当l与圆第一次相切时,平移的距离为3﹣1=2cm;当l移动到l″时,平移的距离为3﹣1+2=4cm;故选D.【点评】本题考查了直线和圆的位置关系以及平移的性质,是基础知识要熟练掌握.4.(2分)(2014秋•南京期末)某商场销售一批衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,商场采取降价措施,假设一定范围内,衬衫单价每降1元,商场平均每天可多售出2件.如果销售这批衬衫每天盈利1250元,设衬衫单价降了x元,根据题意,可列方程()A.(40﹣x)(20+2x)=1250 B.(40﹣2x)(20+x)=1250C.(40+x)(20﹣2x)=1250 D.(40+2x)(20﹣x)=1250【考点】由实际问题抽象出一元二次方程.【专题】销售问题.【分析】由题意,可设衬衫的单价应下降x元.则每天可售出(20+2x)件,每件盈利(40﹣x)元.再根据相等关系:每天的获利=每天售出的件数×每件的盈利;列方程即可.【解答】解:设每件应降价x元/m3,根据题意,得(40﹣x)(20+2x)=1250.故选A.【点评】考查了一元二次方程的应用,找到题目的相等关系:每天的获利=每天售出的件数×每件的盈利;是解答本题的关键,注意判断所求的解是否符合题意.5.(2分)(2014秋•南京期末)如图,△ABC是⊙O的内接等边三角形,矩形BCDE的边DE与⊙O相切,BE=3,则矩形BCDE的面积是()A.18 B.9 C.18D.9【考点】切线的性质.【分析】连接OB、OC,作OF⊥ED,交BC于G,根据已知求得∠OBC=30°,OG=OB=OF,BG=BC,进而求得OB=6,根据勾股定理求得BG,即可求得BC,最后根据矩形的面积公式即可求得.【解答】解:连接OB、OC,作OF⊥ED,交BC于G,∵△ABC是⊙O的内接等边三角形,∴∠ABC=60°,∠OBC=30°,∵OF⊥ED,∴OF是圆O的半径,OG⊥BC,∴OG=OB=OF,BG=BC,∴GF=OG,∵GF=BE=3,∴OB=OF=6,∴BG==3,∴BC=2BG=6,∴矩形BCDE的面积=3×6=18.故选C.【点评】本题考查了切线的性质,垂径定理,等边三角形的性质和矩形的性质,熟练掌握和运用这些性质是解题的关键.6.(2分)(2014秋•南京期末)如图,二次函数y=ax2+bx+c的图象经过点(1,﹣1)和(﹣2,1),下列关于此二次函数的叙述,正确的是()A.当x=0时,y的值小于﹣1 B.当x=﹣3时,y的值大于1C.当x=5时,y的值等于0 D.当x=1时,y的值大于1【考点】二次函数图象上点的坐标特征.【专题】数形结合.【分析】根据抛物线与y轴的交点位置对A进行判断;根据二次函数的性质,当x=﹣2时,y=1,则x=﹣3时,y>1,于是可对B进行判断;根据图象,当x=5时,不能确定函数值等于0,则可对C进行判断;根据二次函数图象上点的坐标特征对D进行判断.【解答】解:A、抛物线与y轴的交点在x轴下方,且在点(1,﹣1)上方,所以x=0时,﹣1<y<0,所以A选项错误;B、当x=﹣3时,y>1,所以B选项正确;C、当x=5时,不能确定函数值等于0,所以C选项错误;D、当x=1时,y=﹣1,所以D选项错误.故选B.【点评】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.二、填空题(共10小题,每小题2分,满分20分)7.(2分)(2014秋•南京期末)已知,则=.【考点】比例的性质.【分析】根据比例的性质,可用x表示y,根据分式的性质,可得答案.【解答】解:由,得3(3x﹣4y)=2(x﹣2y).化简,得y=x.==,故答案为:.【点评】本题考查了比例的性质,利用了比例的性质,分式的性质.8.(2分)(2014秋•南京期末)二次函数y=x2+2x﹣5的图象的顶点坐标是(﹣1,﹣6).【考点】二次函数的性质.【分析】将函数解析式整理成顶点式形式,然后写出顶点坐标即可.【解答】解:∵y=x2+2x﹣5=(x+1)2﹣6,∴二次函数y=x2+2x﹣5的图象的顶点坐标是(﹣1,﹣6).故答案为:(﹣1,﹣6).【点评】本题考查了二次函数的性质,将函数解析式整理成顶点式形式求解更简便.9.(2分)(2011•来宾)已知一元二次方程x2+mx﹣2=0的两个实数根分别为x1,x2,则x1•x2=﹣2.【考点】根与系数的关系.【专题】计算题;压轴题.【分析】根据一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:设方程的两根分别为x1,x2,则x1+x2=﹣,x1•x2=即可得到答案.【解答】解:∵一元二次方程x2+mx﹣2=0的两个实数根分别为x1,x2,∴x1•x2==﹣2.故答案为﹣2.【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:设方程的两根分别为x1,x2,则x1+x2=﹣,x1•x2=.10.(2分)(2013•长宁区二模)已知,△ABC的重心G到BC边中点D的距离是2,则BC 边上的中线长是6.【考点】三角形的重心.【分析】根据三角形重心的性质:三角形的重心到顶点的距离是它到对边中点的距离的2倍求解即可.【解答】解:∵G是△ABC的重心,∴AG=2GD=4;∴AD=AG+GD=6,即BC边上的中线长是6.故答案为:6.【点评】此题考查了重心的概念和性质:三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍.11.(2分)(2014秋•南京期末)将二次函数y=2x2﹣4x+3的图象先向左平移3个单位长度,再向下平移1个单位长度,得到函数的图象的表达式是y=2(x+2)2或y=2x2+8x+8.【考点】二次函数图象与几何变换.【分析】首先将原式转化为顶点式,进而利用二次函数平移规律进而求出即可.【解答】解:∵y=2x2﹣4x+3=2(x﹣1)2+1,∴抛物线y=2x2﹣4x+3先向左平移3个单位,再向下平移1个单位,平移后的函数关系式是:y=2(x+2)2或y=2x2+8x+8.故答案为:y=2(x+2)2或y=2x2+8x+8.【点评】本题主要考查的是二次函数的图象与几何变换,熟知“上加下减,左加右减”的原则是解答此题的关键.12.(2分)(2014秋•南京期末)如图,在▱ABCD中,E是BC边上的一点,且BE:EC=2:1,延长AE交DC延长线于点F,则AB:DF=2:3.【考点】相似三角形的判定与性质;平行四边形的性质.【分析】根据平行四边形的对边相等,得△ABE∽△FCE,AB=CD,由相似三角形的对应边成比例来求AB:DF的值.【解答】解:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴△ABE∽△FCE,∴AB:FC=BE:EC=2:1,∴AB:DF=AB:(AB+CF)=2:3,故答案是:2:3.【点评】本题考查了相似三角形的判定与性质、平行四边形的性质.三角形相似的判定一直是中考考查的热点之一,在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边,对顶角相等等隐含条件.13.(2分)(2013•如皋市校级模拟)若二次函数y=ax2+bx+c的x与y的部分对应值如下表:x ﹣7 ﹣6 ﹣5 ﹣4 ﹣3 ﹣2y ﹣27 ﹣13 ﹣3 3 5 3则当x=1时,y的值为﹣27.【考点】待定系数法求二次函数解析式.【分析】首先观察表格可得二次函数y=ax2+bx+c过点(﹣4,3)与(﹣2,3),则可求得此抛物线的对称轴,然后有对称性求得答案.【解答】解:∵二次函数y=ax2+bx+c过点(﹣4,3)与(﹣2,3),∴此抛物线的对称轴为:直线x==﹣3,∴横坐标为:x=1的点的对称点的横坐标为:x=﹣7,∴当x=1时,y=﹣27.故答案为:﹣27.【点评】此题考查了二次函数的对称性.此题难度不大,注意抛物线上对称的两点的纵坐标相等.14.(2分)(2012•资阳)关于x的一元二次方程kx2﹣x+1=0有两个不相等的实数根,则k 的取值范围是k<且k≠0.【考点】根的判别式.【专题】方程思想.【分析】根据一元二次方程kx2﹣x+1=0有两个不相等的实数根,知△=b2﹣4ac>0,然后据此列出关于k的方程,解方程即可.【解答】解:∵kx2﹣x+1=0有两个不相等的实数根,∴△=1﹣4k>0,且k≠0,解得,k<且k≠0;故答案是:k<且k≠0.【点评】本题主要考查了一元二次方程的根的判别式.解题时,注意一元二次方程的“二次项系数不为0”这一条件.15.(2分)(2014秋•南京期末)如图,点A、B、C、D在⊙O上,AC、BD交于点E,若CD:AB=1:2,△ABE的周长为8,则△CDE的周长为4.【考点】圆周角定理;相似三角形的判定与性质.【分析】根据圆周角定理得出∠A=∠D,∠B=∠C,根据相似三角形的判定推出△ABE∽△DCE,根据相似三角形的性质得出=,代入求出即可.【解答】解:∵根据圆周角定理得:∠A=∠D,∠B=∠C,∴△ABE∽△DCE,∵CD:AB=1:2,∴==2,∵△ABE的周长为8,∴△CDE的周长为4,故答案为:4.【点评】本题考查了相似三角形的性质和判定,圆周角定理的应用,解此题的关键是根据相似三角形的性质得出==2,难度适中.16.(2分)(2014秋•南京期末)一张圆心角为45°的扇形纸片按如图方法剪成一个边长为1的正方形,正方形的四个顶点分别在扇形的半径和弧上,那么这个扇形纸片的面积是π.【考点】勾股定理;圆的认识.【分析】先求出扇形的半径,再根据面积公式求出面积.【解答】解:如图1,连接OD,∵四边形ABCD是边长为1的正方形,∴∠DCB=∠ABO=90°,AB=BC=CD=1,∵∠AOB=45°,∴OB=AB=1,由勾股定理得:OD==,∴扇形的面积是=π;故答案是:π.【点评】本题考查了正方形性质,勾股定理,扇形的面积公式的应用,解此题的关键是求出扇形的半径,题目比较好,难度适中.三、解答题(共11小题,满分88分)17.(9分)(2014秋•南京期末)(1)解方程(组)①x2+10x+21=0;②(2)利用(1)中解方程(组)使用的方法,可求得方程组的解为,.【考点】解一元二次方程-因式分解法;解二元一次方程组;高次方程.【分析】(1)①分解因式,即可得出两个一元一次方程,求出方程的解即可;②把②代入①得出关于x的方程,求出x的值,代入②求出y即可;(2)把②代入①得出关于x的方程,求出x的值,代入②求出y即可.【解答】解:(1)①x2+10x+21=0,(x+3)(x+7)=0,x+3=0,x+7=0,x1=﹣3,x2=﹣7;②把②代入①得:2x+3(x﹣1)=2,解得:x=1,把x=1代入②得:y=1﹣1=0,所以方程组的解为;(2)把②代入①得:x2+10(x﹣1)+31=0,解得:x1=﹣3,x2=﹣7,代入②得:y1=﹣4,y2=﹣8,所以方程组的解为,,故答案为:,.【点评】本题考查了解一元二次方程和解二元二次方程组的应用,解此题的关键是能把一元二次方程转化成一元一次方程,把二元二次方程组转化成一元二次方程,难度适中.18.(7分)(2014秋•南京期末)(1)根据表1中甲、乙两组数据,完成表2.表1A B C D E F G H甲 5 5 6 6 6 6 7 7乙 3 3 3 6 7 8 8 10表2平均数中位数众数方差甲 6 6 6 0.5乙 6 6.53 6.5(2)根据表中,回答下列问题:①若项目A~H表示某品牌薯片的8种口味,甲数据表示一天内这8种口味的薯片销售情况,那么作为商家,应该关心表2中的众数;②若项目A~H表示某公司8位业务员,乙数据表示他们某一个月的销售额,那么作为第9位业务员,想让自己的销售额达到中等以上水平,应该关心表2中的中位数;③若甲、乙表示的两位射击运动爱好者,项目A~H表示8次射击练习中他们命中的环数,那么教练想从中选出一位参加比赛,应选择哪一位?为什么?【考点】方差;算术平均数;中位数;众数.【分析】(1)按照众数、中位数、方差的求法,可得乙组的中位数是6.5,众数是3,方差为0.5;甲组的方差是0.5;(2)根据统计量的意义,结合数据,逐一选择得出答案即可.【解答】解:(1)表2平均数中位数众数方差甲 6 6 6 0.5乙 6 6.5 3 6.5(2)①若项目A~H表示某品牌薯片的8种口味,甲数据表示一天内这8种口味的薯片销售情况,那么作为商家,应该关心表2中的众数;②若项目A~H表示某公司8位业务员,乙数据表示他们某一个月的销售额,那么作为第9位业务员,想让自己的销售额达到中等以上水平,应该关心表2中的中位数;③若甲、乙表示的两位射击运动爱好者,项目A~H表示8次设计练习中他们命中的环数,那么教练想从中选出一位参加比赛,应当选择甲,因为甲的方差比乙的小,发挥稳定.【点评】此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的计算方法及意义.19.(6分)(2014秋•南京期末)从某班4名团员中随机抽取2名参加学校团员竞赛,这4名团员中有3名男生和1名女生,求抽到两名男生的概率.【考点】列表法与树状图法.【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与抽到两名男生的情况,再利用概率公式即可求得答案.【解答】解:画树状图得:∵共有12种等可能的结果,抽到两名男生的有6种情况,∴抽到两名男生的概率为:=.【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.20.(7分)(2014秋•南京期末)如图是一块矩形铁皮,将四个角各剪去一个边长为2米的正方形后(剩下的部分做成一个)容积为90立方米的无盖长方体箱子,已知长方体箱子底面积的长比宽多4米,求矩形铁皮的面积.【考点】一元二次方程的应用.【专题】几何图形问题.【分析】设矩形铁皮的宽为x米,则长为(x+4)米,无盖长方体箱子的底面长为(x+4﹣4)米,底面宽为(x﹣4)米,根据运输箱的容积为90立方米建立方程求出其解即可.【解答】解:设矩形铁皮的宽为x米,则长为(x+4)米,由题意,得x(x﹣4)×2=90,解得:x1=9,x2=﹣5(舍去),所以矩形铁皮的长为:9+4=13米,矩形铁皮的面积是:13×9=117(平方米).答:矩形铁皮的面积是117平方米.【点评】本题考查了长方体的体积公式的运用,矩形的面积公式的运用,列一元二次方程解实际问题的运用,解答时由无盖长方体箱子的容积为90立方米建立方程是关键.21.(6分)(2014秋•南京期末)如图,△ABC中,∠C=90°,∠A=30°,BC=2.(1)用直尺和圆规作△ABC的内切圆⊙O(保留作图痕迹,不写作法);(2)求∠BOC的度数和⊙O的半径.【考点】作图—复杂作图;三角形的内切圆与内心.【分析】(1)作出△ABC的角平分线的交点就是O,然后作OD⊥BC于点D,以O为圆心,以OD为半径作圆即可;(2)根据内心是角平分线的交点,利用三角形的内角和定理求解.【解答】解:(1)如图所示:⊙O就是所求的圆;(2)∵在直角△ABC中,∠A=30°,∴∠ABC=60°,又∵O是△ABC的内心,∴∠OBC=∠ABC=30°,∠OCB=∠ACB=45°,∴∠BOC=180°﹣30°﹣45°=105°.∵在直角△ABC中,∠A=30°,∴AB=2BC=4,AC===2.∴⊙O的半径是:=﹣1.【点评】本题考查了尺规作图,三角形的内心是三角形的角平分线的交点,到三角形的三边的距离相等.22.(8分)(2014秋•南京期末)如图,夜晚路灯下,小明在点D处测得自己影长DE=4m,在点G处测得自己影长DG=3m,E、D、G、B在同一条直线上,已知小明身高为1.6m,求灯杆AB的高度.【考点】相似三角形的应用.【专题】计算题.【分析】先证明△ECD∽△EAB,利用相似比得到=,即=,再证明△DFG∽△DAB,利用相似比得到=,即=,于是得到=,可解得BG=9,然后利用=求AB的长.【解答】解:∵CD∥AB,∴△ECD∽△EAB,∴=,即=,∵FG∥AB,∴△DFG∽△DAB,∴=,即=,∴=,解得BG=9,∴=,∴AB=6.4(m),即灯杆AB的高度为6.4m.【点评】本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.23.(8分)(2014秋•南京期末)请用二次函数的知识进行解释,在所有周长相等的矩形中,正方形面积最大.【考点】二次函数的应用.【分析】设长方形的周长为l,长为x,则宽为,长方形的面积S=x•=﹣(x﹣)2+,根据二次函数的性质即可得出结论.【解答】解:∵设长方形的周长为l,长为x,则宽为,∴长方形的面积S=x•=﹣(x﹣)2+,∵当x=时,S最大=,此时矩形的宽为,即此时为正方形.【点评】本题考查的是二次函数的应用,熟知二次函数的最值问题是解答此题的关键.24.(9分)(2014秋•南京期末)如图,AB是⊙O的直径,点C、D在圆上,=,过点C作CE⊥AD延长线于点E.(1)求证:CE是⊙O的切线;(2)若BC=3,AC=4,求CE和AD的长.【考点】切线的判定.【分析】(1)连接OC,OA=OC,则∠OCA=∠OAC,再由已知条件,可得∠OCE=90°;(2)由CE是⊙O的切线,得∠DCE=∠CAE=∠CAB,从而求得△CDE∽△ABC,△ACE∽△ABC,根据相似三角形对应边成比例即可求得.【解答】解:(1)连接OC,∵OA=OC,∴∠OCA=∠OAC,∵=∴DC=BC,∴∠BAC=∠CAD,∴∠OCA=∠CAD,∴OC∥AE,∵∠E=90°∴OC⊥CE,∴CE是⊙O的切线;(2)∵CE是⊙O的切线,∴∠DCE=∠CAE=∠CAB,∵AB是⊙O的直径,∴∠ACB=90°,∴∠ACB=∠E,∴△CDE∽△ABC,△ACE∽△ABC,∴==,=∵BC=3,AC=4,∴AB=5,CD=3,∴=,=,=∴CE=,ED=,AE=,∴AD=AE﹣ED=.【点评】考查了切线的判定定理和勾股定理,三角形相似的判定和性质,都是基础知识要熟练掌握.25.(8分)(2014秋•南京期末)如图是我们熟悉的“勾股树”,图中的三角形都是直角三角形,四边形都是正方形,其中∠ACB=∠A1C1B1=∠A2C2B2=90°,正方形①和②的面积比、正方形③和④的面积比均为1:2.(1)求证:△A1B1C1∽△A2B2C2;(2)若△ABC、△A1B1C1、△A2B2C2的面积分别标记为S、S1、S2,猜想S、S1、S2之间的关系,并说明理由.【考点】相似三角形的判定与性质;勾股定理.【分析】(1)根据面积之比可得===,再加上夹角相等可得△A1B1C1∽△A2B2C2;(2)根据面积之比设A1C1=x,C1B1=x,A2C2=y,C2B2=y,然后表示出S、S1、S2,再根据三者的面积可得S1•S2=S2.【解答】(1)证明:∵正方形①和②的面积比、正方形③和④的面积比均为1:2,∴===,∵∠A1C1B1=∠A2C2B2=90°,∴△A1B1C1∽△A2B2C2;(2)解:∵正方形①和②的面积比、正方形③和④的面积比均为1:2,∴设A1C1=x,C1B1=x,A2C2=y,C2B2=y,∴S1=•x x=x2,S2=•y y=y2,A1B1=x,A2B2=y,∴S1•S2=x2y2,S=xy,∴S1•S2=S2.【点评】此题主要考查了相似三角形的判定,以及勾股定理,关键是正确表示出S、S1、S2.26.(10分)(2014秋•南京期末)某种药物有三种不同的配方,如图,三条抛物线表示这三种配方在给药量相同的情况下,每毫升血液中的含药量y(微克)随时间x(小时)的变化情况,这种药物每毫升血液中的含药量大于9微克,则会发生中毒,小于5微克,则没有疗效.(1)药厂会旋转该药品的第②种配方(填写序号即可),你的理由是这种药物每毫升血液中的含药量最高时小于9微克,且在高于5微克时持续一段时间..(2)根据图象,求出(1)中选择的配方的有效时间是多长?(3)如果加大给药量,(1)中选择的配方对应的抛物线的形状不变,但位置发生变化,那么该配方的最大有效时间是6小时.【考点】二次函数的应用.【分析】(1)根据“这种药物每毫升血液中的含药量最高时小于9微克,且在高于5微克时持续一段时间”进行解答;(2)令y=5,解出x,求出x之间的距离即可;(3)当图象最高点上升至9时,配方的有效时间最长.此时令y=5,解出x,求出x之间的距离即可.【解答】解:(1)药厂会旋转该药品的第②种配方(填写序号即可),你的理由是:这种药物每毫升血液中的含药量最高时小于9微克,且在高于5微克时持续一段时间.(2)设②的解析式为y=a(x﹣3)2+7,把(0,3)代入解析式得a(0﹣3)2+7=3,解得a=﹣,函数解析式为y=﹣(x﹣3)2+7,当y=5时,﹣(x﹣3)2+7=5,解得x1=3+,x2=3﹣;可知(1)中选择的配方的有效时间是x1﹣x2=3小时.(3)当图象最高点上升至9时,配方的有效时间最长.则函数解析式化为y=﹣(x﹣3)2+9,当y=5时,﹣(x﹣3)2+9=5,解得x1=6,x2=0②,该配方的最大有效时间为x1﹣x2=6小时.故答案为②;这种药物每毫升血液中的含药量最高时小于9微克,且在高于5微克时持续一段时间;6.【点评】本题考查了二次函数的应用.熟悉二次函数最值得求法,熟悉二次函数的性质,熟悉二次函数的性质是解题的关键.27.(10分)(2014秋•南京期末)【学习新知】。
