有理数的意义
2.2有理数与无理数

课题:2.2有理数与无理数
班级:姓名:
【学习目标】
1.理解有理数的意义和会对有理数进行分类;
2.了解无理数的意义.
【学习重点】
1.有理数的意义和分类;
2.无理数的意义
活动一、有理数的分类
我们学过整数(正整数、负整数、零)和分数(正分数、负分数).实际上,
所有整数都可以写成分母为1的分数的形式.如
5
5=,
1
4
4=,
1
--
0=.
1
我们把能写成分数形式m
n
(m、n是整数,n≠0)的数叫做有理数.
想一想:小学里学过的有限小数和无限循环小数是有理数吗?
归纳:有理数的分类(两种)
活动二、无理数
议一议:是不是所有的数都是有理数呢?
将两个边长为1的小正方形,沿图中红线剪开,重新拼成一个大正方形,它的面积为2.
如果大正方形的边长为a,那么a2=2.a是有理数吗?
归纳:无理数。
有理数的意义-知识讲解

有理数的意义(知识讲解)【课程目标】1.掌握用正负数表示实际问题中具有相反意义的量;2.理解正数、负数、有理数的概念;3. 掌握有理数的分类方法,初步建立分类讨论的思想.【重点梳理】KP1:正数与负数像+3、+1.5、12+、+584等大于0的数,叫做正数; 像-3、-1.5、12-、-584等在正数前面加“-”号的数,叫做负数. 注意:(1)一个数前面的“+”“-”是这个数的性质符号,“+”常省略,但“-”不能省略.(2)用正数和负数表示具有相反意义的量时,哪种为正可任意选择,但习惯把“前进、上升”等规定为正,而把“后退、下降”等规定为负.(3)0既不是正数也不是负数,它是正数和负数的“分水岭”.KP2:有理数的分类(1)按整数、分数的关系分类 (2)按正数、负数与0的关系分类有理数{ 整数{正整数0负整数分数{正分数负分数 有理数{正有理数{正整数负分数0负有理数{负整数负分数 注意:(1)有理数都可以写成分数的形式,整数也可以看作是分母为1的数.(2) 分数与有限小数、无限循环小数可以互化,所以有限小数和无限循环小数可看作分数, 但无限不循环小数不是分数,例如π.(3)正数和零统称为非负数;负数和零统称为非正数;正整数、0、负整数统称整数.【典型例题】类型一、正数与负数例1.若把向北走7km 记为-7km ,则+10km 表示的含义是( ).A .向北走10kmB .向西走10kmC .向东走10kmD .向南走10km【答案】D【解析】正和负相对,-7km 表示向北走7km ,则+10km 表示向南走10km ,所以答案D.【升华】正负数表示具有相反意义的量.如果一个量为正数,则与其相反意义的量就是负数 反之,如果一个量为负数,则与其相反意义的量就是正数,且这两个量的单位相同. 举一反三:【栗子1】一种大米的质量标识为“(50±0.5)千克”,下列各袋大米中质量不合格是( )A .50.0千克B .50.3千克C .49.7千克D .49.1千克【答案】D【解析】“50±0.5千克”表示最多为50.5千克,最少为49.5千克.【栗子2】(1)如果收入300元记作+300元,那么支出500元用表示,0元表示 .(2)若购进50本书,用-50本表示,则盈利30元如何表示?【答案】(1)-500元;既没有收入也没有支出.(2)不是一对具有相反意义的量,不能表示.【栗子3】如果60m表示“向北走60m”,那么“向南走40m”可以表示为().A.-20m B.-40m C.20m D.40m【答案】B例2.体育课上,某学校对九年级男生进行了引体向上测试,以能做7个为标准,超过的次数记为正数,不足的次数记为负数,其中8名男生的成绩如下:2,-1,0,3,-2,-3,1,0(1)这8名男生有百分之几达到标准?(2)他们共做了多少引体向上?【答案】(1)由题意可知:正数或0表示达标,而正数或0的个数共有5个,所以百分率为:5100%62.5% 8⨯=;所以,这8名男生有62.5%达到标准.(2)(7+2)+(7-1)+7+(7+3)+(7-2)+(7-3)+(7+1)+7=56(个)所以,他们共做了引体向上56个.【升华】一定要先弄清题目的“基准”.类型二、有理数的分类例3.下面说法中正确的是().A.非负数一定是正数;B.有最小的正整数,有最小的正有理数;C. −a一定是负数;D.正整数和正分数统称正有理数.【答案】D【解析】A不对,因为非负数还包括0;B最小的正整数为1,但没有最小的正有理数; C不对,当a为负数或0时,则−a为正数或0,而不是负数;D对.举一反三:【栗子1】判断题:(1)0是自然数,也是偶数.()(2)0既可以看作是正数,也可以看成是负数.()(3)整数又叫自然数.()(4)非负数就是正数,非正数就是负数.()【答案】√,⨯,⨯,⨯【栗子2】下列四种说法,正确的是( ).A .所有的正数都是整数B .不是正数的数一定是负数C .正有理数包括整数和分数D .0不是最小的有理数 【答案】D例4.请把下列各数填入它所属于的集合的大括号里.1, 0.0708, -700, -3.88, 0, 3.14159265, −723,0.23. 正整数集合:{ …},负整数集合:{ …},整数集合:{ …},正分数集合:{ …},负分数集合:{ …},分数集合:{ …},非负数集合:{ …},非正数集合:{ …}.【答案】正整数:1;负整数:-700;整数:1,0,-700;正分数:0.0708,3.14159265,0.23;负分数:-3.88,−723;分数:0.0708,3.14159265,0.23,-3.88,−723;非负数:1,0.0708,3.14159265,0,0.23;非正数:-700, -3.88, 0, −723.【升华】填数的方法有两种:一种是逐个考察,一一进行填写;二是逐个填写相关的集合, 从给出的数中找出属于这个集合的数.此外注意几个概念:非负数包括0和正数; 非正数包括0和负数.举一反三:【栗子】在有理数−23、-5、3.14中,属于分数的个数共有 个.【答案】2.类型三、探索规律例5. 某校生物教师李老师在生物实验室做实验时,将水稻种子分组进行发芽试验:第1组取3粒,第2组取5粒,第3组取7粒,第4组取9粒,L .按此规律,那么请你推测第n 组应该有种子是 粒.【答案】12+n【解析】第1组取3粒,第2组取5粒,第3组取7粒,第4组取9粒,L ,由此我们观察到的粒数与组数之间有一定关系:1123+⨯=,1225+⨯=, 1327+⨯=,1429+⨯=,L ,按此规律,第n 组应该有种子数(12+n )粒.【升华】研究一列数的排列规律时,其中的数与符号往往都与序数有关.举一反三:【栗子1】有一组数列:2,-3,2,-3,2,-3,L ,根据这个规律,那么第2010个数是:【答案】-3【栗子2】观察下列有规律的数:,,301,201,121,61,21 根据其规律可知第9个数是: . 【答案】901。
上海市六年级(下)数学同步讲义 第1讲 有理数(解析版)
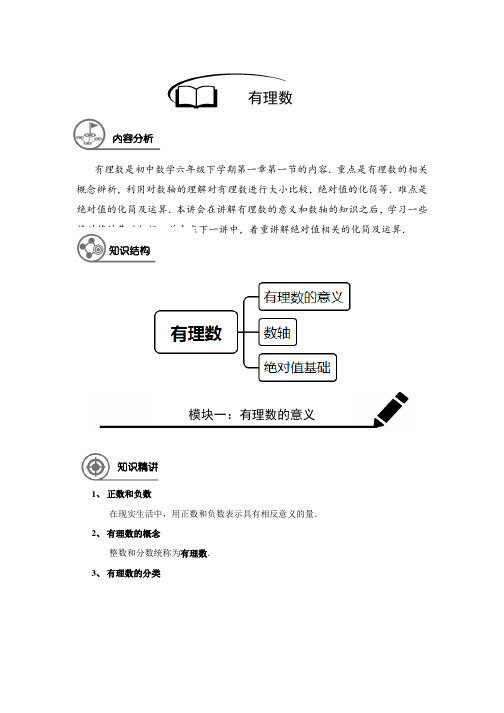
有理数内容分析有理数是初中数学六年级下学期第一章第一节的内容.重点是有理数的相关概念辨析,利用对数轴的理解对有理数进行大小比较,绝对值的化简等.难点是绝对值的化简及运算.本讲会在讲解有理数的意义和数轴的知识之后,学习一些绝对值的基础知识,并会在下一讲中,着重讲解绝对值相关的化简及运算.知识结构模块一:有理数的意义知识精讲1、正数和负数在现实生活中,用正数和负数表示具有相反意义的量.2、有理数的概念整数和分数统称为有理数.3、有理数的分类按意义分:⎧⎧⎪⎪⎨⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩正整数整数零负整数有理数正分数分数负分数;按符号分:⎧⎧⎪⎨⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩正整数正有理数正分数有理数零负整数负有理数负分数.注意:(1)零既不是正数,也不是负数,零是正数和负数的分界;(2)零和正数统称为非负数;零和负数统称为非正数.【例1】下列说法错误的是()A.盈利2000元和亏损100元是相反意义的量B.向西走5千米和向北走5千米是相反意义的量C.增加20人和减少10人是相反意义的量D.支出600元和收入800元是相反意义的量【答案】B【解析】B答案错误,向西走5千米和向东走5千米是相反意义的量.【总结】考察正数、负数表示的意义.【例2】如果5-米表示向南走5米,那么下列各数分别表示什么意义?(1)8+米;(2)3-米;(3)0米;(4)6米.【答案】(1)向北走8米;(2)向南走3米;(3)停留在原地;(4)向北走6米.【解析】向南为负数,则向北为正数.【总结】考察正数、负数表示的意义.【例3】下列说法错误的是()A.正整数、0、负整数统称整数B.0既不是正数,也不是负数例题解析2/ 17C.有理数包括正数和负数D.有理数包括整数和分数【答案】C【解析】C答案错误,有理数包括正数和负数和0.【总结】考察有理数的分类.【例4】判断题:(1)小数都是有理数;()(2)大于负数的数是正数;()(3)有理数中不是正数就是负数.()【答案】(1)×;(2)×;(3)×【解析】(1)小数分为有限小数和无限小数,而无限小数分为无限循环小数和无限不循环小数;其中有限小数和无限循环小数称为有理数,无限不循环小数为无理数;(2)大于负数的数也可以是0;(3)有理数分为正数、负数、0.【总结】考察有理数的分类,注意0既不属于正数也不属于负数.【例5】若人口增加2万人,记作+2万人,那么人口减少1万人,记作______.【答案】-1万人.【解析】增加为+,则减少为-.【总结】考察正负数的意义.-元表示______.【例6】若盈利100元记作+100元,则50【答案】亏损50元【解析】盈利为+,则亏损为-.【总结】考察正负数的意义.【例7】把下列各数填入它所属的圈内:11,18-,5-,215,158-,0.3, 5.67-,π,0,5.5555,20-,0.3,567.【答案】正整数:11,567;负数:18-,5-,158-, 5.67-,20-;正分数:215,0.3,5.5555,0.3;非负数:11,215,0.3,π,0,5.5555,0.3,567;有理数:11,18-,5-,215,158-,0.3, 5.67-,0,5.5555,20-,0.3,567;非负有理数:11,215,0.3,0,5.5555,0.3,567.【解析】有理数分为整数和分数,注意无限不循环小数属于无理数.【总结】考察实数的分类.【例8】六(2)班在一次期中测验中,数学平均分为87分,若把高于平均分的部分记为正数,小智得93分,应记为多少?小方被记为9-分,他实际得分是多少?【答案】+6;78.【解析】小智得93分,记为93-87=6;小方记作-9分,则他实际得分为87-9=78分.【总结】考察正负数的意义及简单运算.【例9】a-表示的数一定是()A.负数B.正数C.正数或负数D.正数或负数或0【答案】D【解析】因为a有可能为正数、负数、0,则a-可能是正数或负数或0.【总结】考察正负数的意义.【例10】按照一定的规律填数:(1)1,2-,4,8-,16,______,______,______;(2)1,2-,3,4,5-,6,7,8-,9,______,______,…,______(第2017个数).4/ 17【答案】(1)-32,64,-128;(2)10,-11,2017.【解析】(1)可找出规律:后面的数字是前面的数字的2倍,第奇数个数字为正数,第偶数个数字为负数.则可得答案.(2)可找出规律:除了1之外,后面的符号规律是一负两正. ()67232016312017=÷=÷- 则第2017个数正数,为2017. 【总结】考察数字找规律.1、 数轴规定了原点、正方向和单位长度的直线叫做数轴. 任何一个有理数都可以用数轴上的一个点表示. 在数轴上表示的数,右边的数总比左边的数大. 2、 相反数只有符号不同的两个数,我们称其中一个数为另一个数的相反数,也称这两个数互为相反数.互为相反数的两个数的和为零. 零的相反数是零.在数轴上,表示互为相反数的两个点位于原点的两侧,并且与原点的距离相等.【例11】 填空:(1)数轴的三要素是______、______、______;(2)在数轴上表示的两个数,______边的数总比______边的数小;例题解析模块二:数轴知识精讲6 / 17A B C DE 012(3)正数都_____0,负数都______0,正数______负数.(填“>”、“ < ”或“=”) 【答案】(1)原点、正方向、单位长度;(2)左,右;(3)>;< ;>. 【解析】考察数轴的基本要素.【例12】 在下图所示的数轴上,写出A 、B 、C 、D 、E 各点分别表示什么数. 【答案】10.50 1.5 1.25A B C D E ==-===-,,,,. 【解析】考察数轴上数字的表示方法.【例13】 下列说法正确的是( )A .任何有理数一定都有相反数,但不一定都有倒数B .任何有理数一定都有倒数,但不一定都有相反数C .任何有理数一定既有相反数,也有倒数D .任何一个正有理数的倒数都比1小 【答案】A【解析】任何有理数一定有相反数,但是除了0之外都有倒数.D 答案错误,如0.5的倒数 为2,比1大.【总结】考察相反数和倒数的意义.【例14】 判断题:(1)数轴上原点及原点右边的点表示的是非负数.( ) (2)一个数的相反数的相反数是它本身.( ) (3)正数和负数互为相反数.( ) 【答案】(1)√;(2)√;(3)×【解析】0和正数统称为非负数;1(正数)和-2(负数)不是互为相反数. 【总结】考察相反数的意义.【例15】 7的相反数是______, 3.2-是______的相反数. 【答案】-7;3.2【解析】正数的相反数是在数字前面加负号,负数的相反数是去掉数字前面的负号. 【总结】考察相反数的表示方法.【例16】 先画出数轴,然后在数轴上画出表示3-、32-、0、2及它们的相反数的点,并将它们从小到大排列起来.【答案】A 、B 、C 、D 、E 、F 、G 所代表的数字分别为3-、32-、0、2、3、32、-2它们从小到大排列为3-<-2<32-<0<32<2<3.【解析】考察数轴上有理数的表示方法.【例17】 数轴上到原点距离为2个单位的点表示的数有______,是______; 数轴上到表示1的点的距离为2个单位的点表示的数为______. 【答案】2个;2和-2;3和-1 【解析】可利用画数轴得到答案.【总结】考察对绝对值几何意义的理解及运用,注意两解的讨论.【例18】 到原点距离不大于1的数有( ) A .2个B .3个C .4个D .无数个【答案】D【解析】数轴上-1到1之间的实数有无数个. 【总结】考察实数比较大小.【例19】 已知数轴上有A 、B 两点,A 、B 之间的距离为1,点A 与原点O 的距离为3,那么所有满足条件的点B 与原点O 的距离之和等于多少?【答案】12.【解析】设A 点表示的有理数为x ,B 点表示的有理数为y .因为A 点与原点O 的距离为3,则3=x ,∴3=x 或-3 又因为A 、B 两点之间的距离为1,则1=-x y ,即1±=-x y ,8 / 17abOA B C D 因为3=x 或-3,所以B 点表示的有理数有四种情况:4-=y 或-2或2或4. 所有满足条件的点B 与原点O 的距离之和为124224=+-++- 【总结】考察数轴上有理数的表示和有理数的加法.【例20】a 、b 在数轴上的位置如图所示,M a b =+,N a b =-+,H a b =-,G a b =--, 求它们的大小关系.(用“>”连接) 【答案】M N H G >>>. 【解析】由数轴可得:0<<a b ,则0>--=b a G ,0<+=b a M ,0<+-=b a N ,0>-=b a H 【总结】考察数轴上有理数的大小比较.【例21】 数轴上表示的数是整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2017厘米的线段AB ,则线段AB 盖住的整点的有多少个? 【答案】2018个或2017个【解析】当A 、B 为整点时,线段AB =2017盖住的整点个数是2018个; 当A 、B 分别不是整点时,线段AB =2017盖住的整点个数是2017个. 【总结】考察数轴上有理数的表示,综合性较强,注意分类讨论.【例22】 如图,数轴上标出若干个点,每相邻两点相距1个单位,点A 、B 、C 、D 对应的数分别是整数a 、b 、c 、d ,且210d a -=,那么数轴的原点应是哪个点?【答案】B【解析】若原点为A ,则07a d ==,,此时72=-a d ,和已知不符,排除; 若原点为B ,则34a d =-=,,此时102=-a d ,和已知相符,正确. 【总结】考察数轴上有理数的表示.模块三:绝对值基础1、 绝对值的概念一个数在数轴上所对应的点与原点的距离,叫做这个数的绝对值.一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;零的绝对值是零. 2、 绝对值的数学表达用符号a 表示数a 的绝对值. ()()()0000a a a a a a >⎧⎪==⎨⎪-<⎩3、 有理数的比较大小正数大于零,零大于负数,正数大于负数; 两个负数,绝对值大的反而小.【例23】 5的绝对值是______,记作_______;3-的绝对值是______,记作______. 【答案】5;5;3;3-.【解析】考察绝对值的求法和记法.【例24】 5.3=______,213=______,0=______, 2.6-=_______. 【答案】5.3;321;0;2.6.【解析】考察绝对值的求法.【例25】 3-的倒数的绝对值是______.知识精讲例题解析10 / 17【答案】31.【解析】-3的倒数是31-,则其绝对值是31.【总结】考察绝对值和倒数的求法.【例26】 判断题:(1)如果一个数的绝对值是它本身,那么这个数是0或1.( ) (2)如果说“一个数的绝对值是负数”,那么这句话是错的.( ) (3)如果一个数的绝对值是它的相反数,那么这个数是负数.( ) 【答案】(1)×;(2)√;(3)×.【解析】(1)如果一个数的绝对值是它本身,那么这个数是0或正数.(3)如果一个数的绝对值是它的相反数,那么这个数是负数或0. 【总结】考察绝对值的求法.【例27】 绝对值等于12的数是______,绝对值小于3的整数是______,绝对值不大于4的非负整数有______个. 【答案】12±;210±±,,;5 【解析】绝对值不大于4的非负整数有0、1、2、3、4,共5个. 【总结】考察绝对值的求法,注意对非负整数的理解.【例28】 当3x =时,7x -一定等于4-吗? 【答案】不一定.【解析】由题意可得:x 为3或-3.当x =3时,47-=-x ;当3-=x 时,107-=-x . 【总结】考察绝对值的求法.【例29】 若0a b +=,则a 与b 的关系是( )A .不相等B .异号C .互为倒数D .0a b ==【答案】D【解析】两个非负数相加等于0,则这两个数都需为0. 【总结】考察绝对值的非负性.【例30】 数a 在数轴上的位置如图所示,试把a ,a 的相反数,a 的倒数和a 的倒数的绝对值用“<”联结起来. 【答案】aa a a 11-<-<<. 【解析】∵01<<-a , ∴10<-<a ,11-<a,11>-a∴aa a a 11-<-<< 【总结】考察实数比较大小.【习题1】 任意写出5个正数与5个负数,分别把它们填入相应的大括号里.正数:{ } 负数:{}【答案】正数:1、3.5、4.2、6、7.8等,负数:5 3.26110.8-----、、、、等. 【解析】考察有理数的分类.【习题2】 关于数字0,下面说法中,错误的是( ) A .是整数,也是有理数 B .既不是正整数,也不是负整数 C .是整数,也是自然数随堂检测0 1a12 / 17D .既不是自然数,也不是有理数 【答案】D【解析】0属于有理数,也属于整数,也属于自然数. 【总结】考察有理数的分类.【习题3】 写出小于5的所有非负整数______________________________; 写出大于162-的所有负数________________________________.【答案】0、1、2、3、4; -6、-5、-4、-3、-2、-1【解析】考察有理数比较大小,注意准确理解题目中的要求.【习题4】 填空:223+=______, 4.3-=______,6--=______. 【答案】322;4.3;-6. 【解析】考察绝对值的求法.【习题5】 如果a 的相反数是最大的负整数,b 是绝对值最小的数,则a b +=______. 【答案】1【解析】由题意可得:1=a ,0=b ,则1=+b a 【总结】考察有理数比较大小.【习题6】 比较大小: (1)37-和25-;(2)311-和0.273-. 【答案】(1)5273-<-;(2)273.0113->-. 【解析】(1)因为5273>,所以5273-<-; (2)因为273.0113<,所以273.0113->-. 【总结】考察有理数比较大小.A BC D 0【习题7】 如图,数轴上A 、B 、C 、D 四个点分别表示数a 、b 、c 、d ,用“<”连接:1a 、1b 、1c 、1d:_____________________. 【答案】ab dc 1111<<<. 【解析】因为b a c d <<<<0, 所以011<<d c ,011>>ba , 所以ab dc 1111<<<. 【总结】考察有理数的比较大小.【习题8】 计算:111111201720162016201520172015-+---. 【答案】0. 【解析】111111201720162016201520172015-+--- 0201712015120161201512017120161201712015120161201512017120161=+--+-=⎪⎭⎫ ⎝⎛---+-=【总结】考察有理数的大小比较及有理数的绝对值的求法.【习题9】 若a 、b 互为相反数,c 、d 互为倒数,m 的绝对值等于2,求a b c d m +++的值. 【答案】3或-1.【解析】由题意可得:0=+b a ,1=cd ,2±=m 所以()13210-=±++=+++或m cd b a14 / 17【总结】考察相反数、倒数、绝对值的定义,注意分类讨论.【习题10】 已知4x =,5y =,且x > y ,则x + y =______. 【答案】-1或-9.【解析】由题意可得:45x y ==-,或45x y =-=-,, 所以91--=+或y x .【总结】考察绝对值的求法和有理数比较大小.【作业1】 关于 2.2-,下面说法正确的是( )A .是负数,不是有理数B .不是分数,是有理数C .是负数,也是分数D .是负数,不是分数【答案】C【解析】有限小数属于分数,也属于有理数 【总结】考察有理数分类.【作业2】 把下列各数分别填到相应的横线上:1-,0.3505-,0,2,56-,33.33%.正数:____________________________; 负数:____________________________; 非负数:____________________________; 非正有理数数:____________________________.课后作业【答案】正数:2,33.33%;负数:1-,0.3505-,56-;非负数:0,2,33.33%;非正有理数数:1-,0.3505-,0,56-.【解析】考察有理数的分类.【作业3】 3π-的倒数是_______,相反数是______,绝对值是______. 【答案】π-31;3-π;3-π. 【解析】考察倒数、相反数、绝对值的求法.【作业4】 若x < 0,则23x x x-=______.【答案】-1.【解析】因为0<x ,所以223313333x x x x x xxxxx-----====-. 【总结】考察绝对值的求法.【作业5】 比较大小,用“<”连接:89-、1112-、1415-.【答案】1411815129-<-<-. 【解析】因为•=8.098,•=691.01211,•=39.01514, 所以1514121198<<, 所以1411815129-<-<-. 【总结】考察负数的比较大小,绝对值大的反而小.16 / 17ABC【作业6】 绝对值大于10且不大于15的负整数的和是_______. 【答案】-65.【解析】绝对值大于10且不大于15的负整数有-11、-12、-13、-14、-15,则其和为-65. 【总结】考察绝对值的运用.【作业7】 填空(填“>”,“<”或“=”):(1)若1a a=-,则a ______0;(2)若0a >,0b >,a b ->-,则a ______b . 【答案】(1)<;(2)<. 【解析】(1)当0<a 时,1-=-=aaa a ; (2)因为ab ->-,所以0a b <<,所以b a <. 【总结】考察有理数比较大小和绝对值运算.【作业8】 如图,数轴上A 、B 、C 四个点分别表示数a 、b 、c , 化简:b a b c a b c -++---. 【答案】b 3-.【解析】由题意可得:0>a ,0<b ,0<c ,0>+b a ,0<-a c ,0>-c b 所以b a b c a b c -++---()()()b a b c a b c =--+---- 3b a b c a b c b =----+-+=-. 【总结】考察绝对值的化简.【作业9】 解方程:931x --=. 【答案】13=x 或5x =.【解析】49=-x ,则49=-x 或4-, 所以13=x 或5x =. 【总结】考察含绝对值的方程的求法,综合性较强,注意分类.【作业10】 比较大小:(提示:分类讨论).(1)a 与a -; (2)a 与1a. 【答案】见解析.【解析】(1)当0=a 时,a a -=; 当0<a 时,a a -<; 当0>a 时,a a ->.(2)令aa 1=,则1±=a , 当1-<a 时,a a 1<; 当1-=a 时,a a 1=; 当01<<-a 时,a a 1>; 当10<<a 时,a a 1<; 当1=a 时,a a 1=; 当1>a 时,aa 1>. 【总结】考察有理数比较大小,综合性较强,注意分类讨论.。
有理数和元理数的定义

有理数和元理数的定义好的,以下是为您生成的关于“有理数和无理数的定义”的文章:---# 【有理数和无理数的定义】## 开场白嘿,朋友!你有没有在数学课上被有理数和无理数搞得晕头转向?其实啊,这俩家伙就在我们的生活中,只是我们可能没有特意去留意。
想象一下,当我们在买东西计算价格,或者测量房间的大小的时候,这些数字背后可都藏着有理数和无理数的身影呢!今天,咱们就一起来揭开它们神秘的面纱。
## 什么是有理数和无理数?简单来说,有理数就是能写成两个整数之比的数,像咱们熟悉的整数、有限小数、无限循环小数都是有理数。
比如说 3 可以写成 3/1,0.25 可以写成 1/4,0.3333... 可以写成 1/3。
无理数呢,则是无限不循环小数,不能写成两个整数之比。
最典型的就是圆周率π,约等于 3.1415926...,还有像根号 2 约等于1.4142135... 这些数。
在生活中,有理数就像我们买东西时找的零钱,清楚明白,有固定的规律。
而无理数呢,就像是一些难以捉摸的神秘现象,没有规律可循。
这里要纠正一个常见的误区,有人可能会觉得无限小数就是无理数,其实不是的,只有无限不循环小数才是无理数,无限循环小数那可是有理数哦!## 关键点解析### 有理数的核心特征或要素1. 整数:像 -2、0、5 这样的整数,是有理数中最直观的一部分。
比如说你有 5 个苹果,这个 5 就是整数形式的有理数。
2. 有限小数:比如 0.5 ,它可以写成 1/2,有明确的结束点。
就像你跑步跑了 0.5 公里,距离是有限且明确的。
3. 无限循环小数:像 0.333... 可以写成 1/3,虽然它的小数位一直延续,但有循环规律。
就像时钟的指针,一直在转,但总是按照一定的规律循环。
### 无理数的核心特征或要素1. 无限性:无理数的小数位是无限延伸的,没有尽头。
比如π,计算起来永远没有结束。
2. 不循环性:没有重复出现的数字序列。
这就好像是随机生成的一串没有规律的数字。
初中数学人教七年级上册第一章有理数有理数 市一等奖PPT

• 最大的自然数.
都是
• 2.自然不数都与是整数的关系:自然数( )整数,但
整数( )自然数单. 位“1” • 3.分数的概念:把( )平均分分成数若干份,
表示这样的一份或几份的数,叫做( ).
一、相反意义的量
在日常生活中我们会遇到这样一些量:
前进100米和后退70米;收入700元和支出600元 ;零上6℃ 和零下6℃ ……
× 7、带有“+”的数是正数,带有“-”的数是负数。( )
我能选
• 1.下面说法中,正确的个数是( B )
• (1)一个有理数,不是整数就是分数;(2)一 个有理数,不是正数就是负数;(3)一个整数, 不是正的就是负的;(4)一个分数不是正的就是 负的.
• A . 1 B. 2
C. 3 D. 4
• 2.下列说法正确的是( C )
将所有学过的数分类,并与同伴交流
整数(integer)
正整数:如 1,2,3,…
零
负整数:如-1,-2,-3,…
分数(fraction)
正分数:如,1 ,5.2,… 2
负分数:如,
1 2
,-3.5,…
整数与分数统称为有理数
按数系扩张的自然顺序
有理数还可以这样分类:
(按认识有理数的先后顺序)
有理数
• A.整数包括正数和负数
• B.有理数包括正有理数和负有理数
• C.负整数是整数也是有理数
• D.有理数就是分数
例 1 下列说法正确的是( ) A.一个有理数不是整数就是分数 B.正整数和负整数统称整数 C.正整数、负整数、正分数、负分数统称有理 数 D.0不是有理数
分析:首先要明确有理数的意义及分类.整数包 括正整数、0、负整数,因此B不对;有理数包括整数 和分数,0是有理数,因此C、D不对.
有理数

-3和-5哪个大?-3和-1.5哪个大?
两个负数,绝对值小的反而大。
例题
比较下列各数的大小
(1)-3与-100
(2) 2 与- 3 35
练习
比较下列各数的大小
21与31 32
0.1与 0.9
与3.14
0.67与 2 3
两个有理数的比较
2.3 2.5
①两个正数: 绝对值大的数大
(4) 3 4,(因为 3 3=21,| 4 | 4 = 20 ,故 21 20 ,即3 4,所以 3 4 .)
57
5 5 35 7 7 35 35 35 5 7
57
说明:两个负数比较,绝对值大的反而小.
3. 在数轴上画出表示下列各数的点,并且把这些数用“<”号连接起来:
1, 3
BC距离: I-1.5-0I=1.5
AD距离: I-3-4I=7
(1)
A
B
C
-6
-5
-4 -3
-2 -1
0
1
D
2
34
5
6
(2)1.5,7
(3) 1, 1 ,0,1 1 ,5 1 2 22
有理数
正有理数
0
正整数 正分数
负有理数
正整数 负整数
例1:下列判断正确的是( )
A,所有的整数都是正数
与表示-4的点距离为5个单位的点所表示的数是
。
2、(1)-5的相反数是
;
(3)
和-3.5互为相反数;
(5)+5.2的绝对值是
;
(7)0.5的绝对值是
;
1. +2和 -2 1和-9 ; 2. 5 -1 3.5 0 5.2 10 0.5 7/3
有理数的定义和性质
有理数的定义和性质在数学中,有理数是指能用两个整数之间的比值来表达的数。
有理数的定义是一个比较基础的概念,但对于理解整个数学体系具有重要意义。
在整数的基础上,有理数的产生体现了人们在实践中对于数学的发展,也是人们在探索具有理性的世界的一项重要成果。
那么究竟什么是有理数呢?一起来深入探讨一下有理数的定义和性质。
有理数的定义有理数是由整数组成的分数,分母不为0。
可以表示为p/q的形式,其中p,q为整数,q≠0,简称有理数。
举个例子:-1,3/5,100/7,1/2等都是有理数。
若有理数q=p/q,其中p与q都为整数,那么它还可以表示为其他形式的分数。
即若q≠±1,那么可以约分至最简分数,使分母q的正负与数本身的符号一致。
例如,3/6和1/2其实是一个数。
有理数的性质1. 唯一分解定理唯一分解定理表明,每个正整数都可以唯一地表示为若干个质数的乘积,而且可以按质数从小到大的顺序来进行表示。
同样的,每个整数也可以写成一些互不相同质数的积,而且这些质数及其指数是唯一的。
唯一分解定理同样适用于所有整系数和有理数,不管这些数正负如何以及它们是不是整数。
2. 加减法性质对于任意的有理数a、b和c,都有:a+b=b+a (加法交换律)a+(b+c)=(a+b)+c (加法结合律)a+0=0+a=a (零元素)a+(-a)=0 (负元素)a-b=a+(-b) (减法变成加法)3. 乘除法性质对于任意的有理数a、b和c,都有:a×b=b×a (乘法交换律)a×(b×c)=(a×b)×c (乘法结合律)a×1=1×a=a (乘法单位元)a×0=0×a=0 (零元素)a×-a=(-a)×a=-(a×a) (负元素)若a≠0,则a/a=1,1/a是a的倒数,即1/a×a=14. 分数的加减乘除法有理数的加减乘除法可以归结为有理数加减乘除分数的运算。
第一讲 有理数的认识
有理数的认识一、相反意义的量:一般情况下,规定收入、增加、上升、零上、高于海平面等为正,另一相反意义的量支出、减少、下降、零下、低于海平面等规定为负,但也可以随意规定,要看实际题目中所给出的标准。
二、正数、负数的概念:大于0的数叫做正数;小于0的数叫做负数。
注意:0既不是正数,也不是负数。
三、有理数的概念:正整数、0、负整数统称为正数;正分数、负分数统称为分数;整数和分数统称为有理数。
⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数正整数整数有理数0⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数正分数正整数正有理数有理数0四、数轴:概念及画法:规定了原点、正方向和单位长度的直线叫做数轴。
数轴的定义包括3层含义:(1)数轴是一条直线,可以向两端无限延伸;(2)数轴有三要素:原点、正方向、单位长度,三者缺一不可;(3)原点位置的选择,单位长度大小的确定都是根据实际而定的,一般取向右的方向为正方向。
数轴的画法则是先画一条水平的直线,再在这条直线上画出数轴的三要素即可。
数轴的性质:1、数轴上表示的两个数,右边的数总比左边的数大。
2、正数都大于零,负数都小于零,正数大于一切负数。
五、相反数的概念:定义:只有符号不同的两个数互为相反数,其中一个数是另一个数的相反数;0的相反数是0.通常情况下,在一个数的前面加上一个负号就得到了这个数的相反数。
即:正数的相反数是负数;负数的相反数是正数,零的相反数是它本身。
几何意义:在数轴上,表示互为相反数的两个点,它们分别位于原点的两侧,而且与原点的距离相等。
六、绝对值:几何意义:在数轴上把表示数a 的点与原点的距离叫做数a 的绝对值。
记作|a|,读作“a 的绝对值”。
代数意义:一个正数的绝对值是它的本身,一个负数的绝对值是它的相反数;0的绝对值是0,它既可以说成“本身”,又可以说成“相反数”。
七、有理数大小的比较:利用绝对值比较两个负数的法则:(1)两个负数,绝对值大的反而小。
有理数的意义、数轴、相反数、绝对值
有理数的意义、数轴、相反数、绝对值三、知识体系一、有理数的概念1.把下列各数分类: 1,53-,8。
2,—7,71,0,—3。
5,1008,-0。
5,-10正数: 负数:整数: 分数: 有理数: 2、(一)、有理数的概念 ★整数和分数统称为有理数。
⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负分数零正整数整数有理数⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 一、知识分类 知识点1.有理数的分类 知识点2.数轴 知识点3. 相反数 知识点4. 绝对值二、重难点1、能分清哪些是有理数,哪些不是有理数,并对有理数再进行细分2、会画数轴,会利用数轴来比较数的大小3、掌握相反数的性质4、理解绝对值的含义,会熟练的去绝对值符号(二)、什么是数轴呢?★数轴三要素:原点,正方向、单位长度 ★任何一个有理数都能够在数轴上表示。
★数轴的数的大小比较方法。
(三)、什么是相反数?★数字相同、符号不同的两个数,我们称其中一个数为另一个数的相反数,也称这两个数互为相反数。
★几何意义: ★零的相反数为零。
★互为相反数的两个数之和为零。
★ a 的相反数是-a ★a 与-a 的大小比较(分类讨论)(四)、什么是绝对值?★一个数在数轴上所对应的点与原点的距离,叫做这个数的绝对值。
用符号“”表示,例如:33=,5252=-,00=。
★运算方法:★⎪⎩⎪⎨⎧==)<()>0(-)000(a a a a a a ★两个负数,绝对值大的那个数反而小。
★任何数的绝对值都是非负数。
一个正数的绝对值就是它本身;一个负数的绝对值就是它的相反数; 零的绝对值就是零。
( 五 )非负数、非正数的认识与性质 ★非正数:负数与零。
★常见的非负数:平方数、绝对值。
(a+b )2★非负数:正数与零。
★非负数的性质:几个非负数的和等于零,则它们都是零。
★★12, —3, —31, +0。
01, +56, 0, +52, 正数: 负数:整数: 分数: 有理数:3、最小的正整数是_________,最大的负整数是________.4、零不是( )A. 正数 B. 整数 C 。
有理数的定义及相关概念
拓展题
0是整数吗?自然数一定是整数吗?0一定是正整数 吗?整数一定是自然数吗?
2、下列说法正确的是( ) A.正整数和正分数统称为正有理数。 B.正整数和负分数统称为整数。 C.正整数、负整数、正分数、负分数统称为有理数。 D.0不是有理数。
3、既不是正数又不是整数的有理数是( )
A.0和正分数
B.只有负分数
C.负整数和负分数
D.正整数和正分数
4、下列不是有理数的有( )
1、数集可以用大括号表示,也可以用圆圈表示。
2、一个数集内的数有无限多个时,我们不能全部写 出,要用“…”,如非负整数集{0,1,2,3,4…}。
3、一个数集内不能有两个一样的数。 4、所有的有理数组成的数集叫做有理数集;
那么,什么叫做整数集,正数集, 自然数集,非负 整数集?
知 1、把下列各数填入相应的集合
A.3.1415926 B.0
C.0.666……
D.π
5、下列说法错误的是( A.自然数一定是有理数 C.自然数一定是非负数
) B.自然数一定是整数 D.整数一定是自然数
6.说出下列生活情景中用到的数所属的集合. ⑴摩托车的里程表上读出的数;
⑵中央电视台播放的天气预报中,播报各地的 气温所用到的数; ⑶老师批改试卷时用到的数; ⑷烤鸭店的柜台上的电子秤上读出的数; ⑸表示某关概念 整数和分数统称为有理数。
正整数、零和负整数统称为整数,正分数和 负分数统称为分数。
非负数:大于等于0的数叫非负数即a≥0 非正数:小于等于0的数叫非正数即a≤0
非正整数: 小于等于0的整数; 非负整数: 大于等于0的整数
2:数的分类
按定义来分
正整数
整数零
…0.…67
