五年高考真题分类汇编(指数对数)

合集下载

专题5—指数函数、对数函数-近8年高考真题分类汇编—2022届高三数学一轮复习

专题5—指数函数、对数函数考试说明：1、了解指数函数模型的实际背景；2、理解指数函数的概念，理解指数函数的单调性，掌握指数函数的图像通过特殊点；3、理解对数函数的概念及其运算性质，知道用换底公式能将一般对数转化成自然对数或常用对数；了解对数在简化运算中的作用；4、理解对数函数的概念，理解对数函数的单调性，掌握对数函数图像通过的特殊点。

5、知道指数函数、对数函数是一类重要的函数模型。

高频考点：1、指数幂、对数式的化简与求值；2、指数函数、对数函数的图像与性质的应用；3、指数函数、对数函数的综合应用问题。

指数函数、对数函数是非常重要的基本函数，是高考中的高频考点，在选择题、填空题中考查其基本性质，在大题中，与导数结合的解答题年年必考。

一、典例分析1．（2019•新课标Ⅰ）已知2log 0.2a =，0.22b =，0.30.2c =，则( ) A ．a b c <，0.300.21<<，从而得出a ，b ，c 的大小关系．解答：解：22log 0.2log 10a =<=， 0.20221b =>=，0.3000.20.21<<=，0.30.2(0,1)c ∴=∈，a cb ∴<<，故选：B ．点评：本题考查了指数函数和对数函数的单调性，增函数和减函数的定义，属基础题． 2．（2013•重庆）函数的定义域为( ) A ． B ．C ．(2，3)(3⋃，)+∞D ．(2，4)(4⋃，)+∞分析：根据“让解析式有意义”的原则，对数的真数大于0，分母不等于0，建立不等式，解之即可．解答：解：要使原函数有意义，则，解得：23x <<，或3x >所以原函数的定义域为(2，3)(3⋃，)+∞．故选：C ．点评：本题主要考查了函数的定义域及其求法，求定义域常用的方法就是根据“让解析式有意义”的原则，属于基础题．3．（2019•北京）在天文学中，天体的明暗程度可以用星等或亮度来描述．两颗星的星等与亮度满足121252Em m lg E -=，其中星等为k m 的星的亮度为．已知太阳的星等是26.7-，天狼星的星等是 1.45-，则太阳与天狼星的亮度的比值为( ) A ．10.110B ．10.1C ．10.1lgD ．10.110-分析：把已知熟记代入121252Em m lg E -=，化简后利用对数的运算性质求解．解答：解：设太阳的星等是126.7m =-，天狼星的星等是2 1.45m =-，由题意可得：1251.45(26.7)2Elg E ---=，1250.510.15E lgE ==，则10.11210E E =．故选：A ．点评：本题考查对数的运算性质，是基础的计算题．4．（2020•新课标Ⅲ）已知5458<，45138<．设5log 3a =，8log 5b =，13log 8c =，则( )A ．a b c <，得到c b >，即可确定a ，b ，c 的大小关系．解答：解：由58335844log log =，345553log log >，而348885log log < 58log 3log 5∴<，即a b <；5458<，554log 8∴<，5log 8 1.25∴>，8log 50.8b ∴=<； 45138<，1345log 8∴<，13log 80.8c ∴=>，c b ∴>，综上，c b a >>．故选：A ．点评：本题考查了三个数大小的判断，指数对的运算和基本不等式的应用，考查了转化思想，是基础题．5．（2016•新课标Ⅰ）若0a b >>，01c <<，则( ) A ．log log a b c c 分析：根据指数函数，对数函数，幂函数的单调性结合换底公式，逐一分析四个结论的真假，可得答案．解答：解：0a b >>，01c <<， log log c c a b ∴<，故B 正确；当1a b >>时，，故A 错误； c c a b >，故C 错误； a b c c <，故D 错误；故选：B ．点评：本题考查的知识点是指数函数，对数函数，幂函数的单调性，难度中档．6．（2016•新课标Ⅱ）下列函数中，其定义域和值域分别与函数10lgx y =的定义域和值域相同的是( ) A ．y x =B ．y lgx =C ．2x y =D ．y=分析：分别求出各个函数的定义域和值域，比较后可得答案．解答：解：函数10lgx y =的定义域和值域均为(0,)+∞，函数y x =的定义域和值域均为R ，不满足要求；函数y lgx =的定义域为(0,)+∞，值域为R ，不满足要求；函数2x y =的定义域为R ，值域为(0,)+∞，不满足要求；函数y=(0,)+∞，满足要求；故选：D ．点评：本题考查的知识点是函数的定义域和值域，熟练掌握各种基本初等函数的定义域和值域，是解答的关键．7．（2014•山东）已知函数log ()(a y x c a =+，c 为常数，其中0a >，1)a ≠的图象如图所示，则下列结论成立的是( )A ．1a >，1c >B ．1a >，01c <<C ．01a <<，1c >D ．01a <<，01c <<分析：根据对数函数的图象和性质即可得到结论．解答：解：函数单调递减，01a ∴<<，当1x =时log ()log (1)0a a x c c +=+<，即11c +>，即0c >，当0x =时log ()log 0a a x c c +=>，即1c <，即01c <<，故选：D ．点评：本题主要考查对数函数的图象和性质，利用对数函数的单调性是解决本题的关键，比较基础．8．（2012•新课标）已知函数1()(1)f x ln x x=+-，则的图象大致为( )A ．B ．C ．D ．分析：考虑函数()f x 的分母的函数值恒小于零，即可排除A ，C ，由()f x 的定义域能排除D ，这一性质可利用导数加以证明解答：解：设()(1)g x ln x x =+- 则()1x g x x'=-+ 在上为增函数，在(0,)+∞上为减函数 ()(0)0g x g ∴<= 1()0()f xg x ∴=< 得：0x >或10x -<<均有()0f x <排除A ，C ，又1()(1)f x ln x x=+-中，，能排除D ．故选：B ．点评：本题主要考查了函数解析式与函数图象间的关系，利用导数研究函数性质的应用，排除法解图象选择题，属基础题 9．（2020•新课标Ⅰ）若，则( ) A ．2a b >B ．2a b <C ．2a b >D ．2a b <分析：先根据指数函数以及等式的性质得到；再借助于函数的单调性即可求解结论．解答：解：因为；因为即；令2()2log x f x x =+，由指对数函数的单调性可得()f x 在(0,)+∞内单调递增；且f （a ）(2)2f b a b <⇒<；故选：B ．点评：本题主要考查指数函数和对数函数的应用，属于基础题．10．（2014•山东）已知实数x ，y 满足(01)x y a a a <<<，则下列关系式恒成立的是( ) A ．33x y >B ．sin sin x y >C ．22(1)(1)ln x ln y +>+D ．分析：本题主要考查不等式的大小比较，利用函数的单调性的性质是解决本题的关键．解答：解：实数x ，y 满足(01)x y a a a <<<，x y ∴>，A ．当x y >时，33x y >，恒成立，B ．当x π=，2y π=时，满足x y >，但sin sin x y >不成立．C ．若22(1)(1)ln x ln y +>+，则等价为22x y >成立，当1x =，1y =-时，满足x y >，但22x y >不成立．D ．若，则等价为2211x y +<+，即22x y <，当1x =，1y =-时，满足x y >，但22x y <不成立．故选：A ．点评：本题主要考查函数值的大小比较，利用不等式的性质以及函数的单调性是解决本题的关键．二、真题集训1．（2020•新课标Ⅲ）设3log 2a =，5log 3b =，23c =，则( ) A ．a c b <且1)a ≠的最大值与最小值之和为3，则22(a a -+= )A ．9B ．7C ．6D ．54．（2017•全国）设01a <<，则( )A ．2log a >B ．aC ．2log a <D ．log <5．（2019•浙江）在同一直角坐标系中，函数1x y a =，1log ()(02a y x a =+>且1)a ≠的图象可能是( ) A ．B ．C ．D ．6．（2019•新课标Ⅲ）函数在，6]的图象大致为( ) A ． B ．C ．D ．7．（2015•四川）某食品保鲜时间y （单位：小时）与储藏温度x （单位：C)︒满足函数关系( 2.718kx b y e e +==⋯为自然对数的底数，k ，b 为常数）．若该食品在0C ︒的保鲜时间是192小时，在22C ︒的保鲜时间是48小时，则该食品在33C ︒的保鲜时间是( ) A ．16小时B ．20小时C ．24小时D ．28小时8．（2014•山东）已知实数x ，y 满足(01)x y a a a <<<，则下列关系式恒成立的是( ) A ．B ．22(1)(1)ln x ln y +>+C ．sin sin x y >D ．33x y >9．（2018•新课标Ⅰ）已知函数22()log ()f x x a =+，若f （3），则a = ． 10．（2013•北京）函数12,1()2,1x log x x f x x ⎧⎪=⎨⎪<⎩的值域为．11．（2015•福建）若函数且1)a ≠的值域是[4，)+∞，则实数a 的取值范围是． 12．（2014•重庆）函数22()log log (2)f x x x =的最小值为．13．（2012•上海）已知函数||()(x a f x e a -=为常数）．若()f x 在区间[1，)+∞上是增函数，则a 的取值范围是．14．（2011•上海）已知函数，其中常数a ，b 满足0a b ⋅≠ （1）若0a b ⋅>，判断函数()f x 的单调性；（2）若0a b ⋅<，求时的x的取值范围．真题集训答案1．解：32log 23alog log ===， 52log 33b log log ===，23c =， a c b ∴<<．故选：A ．2．解：0.20.3log 0.35lg a lg ==-，20.3log 0.32lg b lg ==， 50.30.30.30.3(52)2252525lg lglg lg lg lg lg a b lg lg lg lg lg lg -+=-==， 100.30.30.332525lg lg lg lg ab lg lg lg lg ⋅=-⋅=，，，0ab a b ∴<+<．故选：B ．3．解：函数且1)a ≠在[1-，1]上单调，当1x =-时，1y a -=；当1x =时，y a =．则13a a -+=，两边同时平方得：2229a a -++=，227a a -∴+=．故选：B ．4．解：01a <<，201a a ∴<<<，在A中，2log a =A 错误；在B中，，故B 正确；在C中，2log a >，故C 错误；在D中，log ，故D 错误．故选：B ． 5．解：由函数1x y a =，1log ()2a y x =+，当1a >时，可得1xy a =是递减函数，图象恒过(0,1)点，函数1log ()2a y x =+，是递增函数，图象恒过1(2，0)；当10a >>时，可得1xy a =是递增函数，图象恒过(0,1)点，函数1log ()2a y x =+，是递减函数，图象恒过1(2，0)；满足要求的图象为：D 故选：D ．6．解：由32()22x xx y f x -==+在，6]，知，()f x ∴是，6]上的奇函数，因此排除C又f （4）1182721=>+，因此排除A ，D ．故选：B ．7．解：( 2.718kx b y e e +==⋯为自然对数的底数，k ，b 为常数）．当0x =时，192b e =，当22x =时2248k b e +=， 224811924k e ∴== 1112k e =192b e =当33x =时，3311331()()()192242k b k b e e e +==⨯=故选：C ．8．解：实数x ，y 满足(01)x y a a a <<<，x y ∴>，A ．取2x =，1y =-，不成立；B ．取0x =，1y =-，不成立C ．取x π=，y π=-，不成立；D ．由于3y x =在R 上单调递增，因此正确故选：D ．9．解：函数22()log ()f x x a =+，若f （3），可得：，可得7a =-．故答案为：7-．10．解：当1x 时，；当1x <时，10()222x f x <=<=．所以函数12,1()2,1x log x x f x x ⎧⎪=⎨⎪<⎩的值域为．故答案为．11．解：由于函数且1)a ≠的值域是[4，)+∞，故当2x 时，满足()64f x x =-．①若1a >，()3log a f x x =+在它的定义域上单调递增，当2x >时，由()3log 4a f x x =+，log 1a x ∴，log 21a ∴，12a ∴<． ②若01a <<，()3log a f x x =+在它的定义域上单调递减， ()3log 3log 23a a f x x =+<+<，不满足()f x 的值域是[4，)+∞．综上可得，12a <，故答案为：(1，2]． 12．解：22()log log (2)fx x x=21()log(2)2f x x ∴=21log (2)4x x=14x x =+12)4x x =+211(1)44=+-，当10x +=即x =时，函数()f x 的最小值是14-．故答案为：14-13．解：因为函数||()(x a f x e a -=为常数）．若()f x 在区间[1，)+∞上是增函数由复合函数的单调性知，必有在区间[1，)+∞上是增函数又在区间[a ，)+∞上是增函数所以[1，)[a +∞⊆，)+∞，故有1a 故答案为(-∞，1]14．（解：（1）①若0a >，0b >，则2x y a =⋅与3x y b =⋅均为增函数，所以在R 上为增函数； ②若0a <，0b <，则2x y a =⋅与3x y b =⋅均为减函数，所以在R 上为减函数．（2）①若0a >，0b <，由得112323x x x x a b a b ++⋅+⋅>⋅+⋅，化简得223x x a b ⋅>-⋅，即22()3x b a->，解得232log b x a -<； ②若0a <，0b >，由可得22()3x b a-<，解得232log b x a ->．。

历年高考真题分类汇编---指数、对数、幂函数.doc

考点7 指数函数、对数函数、幂函数一、选择题1. （2013·大纲版全国卷高考文科·Ｔ6）与（2013·大纲版全国卷高考理科·Ｔ5）相同函数)0)(11(log )(2>+=x xx f 的反函数()1=f x -（）A.()1021x x >- B.()1021xx ≠- C.()21x x R -∈ D.()210xx -> 【解题指南】首先令)11(log 2xy +=求出x ，然后将y x ,互换，利用反函数的定义域为原函数的值域求解.【解析】选A.由)11(log 2xy +=，0>x ，得函数的值域为0>y ，又x y 112+=，解得121-=y x ，所以()1=f x -121-x )0(>x 2.(2013·北京高考理科·T5)函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=e x 关于y 轴对称,则f(x)= ( )A.e x+1B.e x-1C.e -x+1D.e -x-1 【解题指南】把上述变换过程逆过来,求出y=e x 关于y 轴对称的函数,再向左平移1个单位长度得到f(x).【解析】选D.与y=e x 关于y 轴对称的函数应该是y=e -x ,于是f(x)可由y=e -x 向左平移1个单位长度得到,所以f(x)=e -(x+1)=e -x-1. 3.（2013·广东高考文科·Ｔ2）函数lg(1)()1x f x x +=-的定义域是（）A ．(1,)-+∞B ．[1,)-+∞C ．(1,1)(1,)-+∞D ．[1,1)(1,)-+∞ 【解题指南】函数的定义域有两方面的要求：分母不为零，真数大于零，据此列不等式即可获解.【解析】选C. 解不等式10,10x x +>-≠可得1,1x x >-≠是定义域满足的条件.4.（2013·山东高考文科·Ｔ5）函数()f x =（）A.(-3，0]B.(-3，1]C.(,3)(3,0]-∞--D.(,3)(3,1]-∞--【解题指南】定义域的求法:偶次根式为非负数，分母不为0.【解析】选A. ⎩⎨⎧>+≥-03021x x ，解得03≤<-x .5.（2013·陕西高考文科·Ｔ3）设a, b, c 均为不等于1的正实数, 则下列等式中恒成立的是 ( ) A ．·log log log a c c b a b =B. b a b c c a log log log =⋅C. c b bc a a a log log )(log ⋅=D.()log g og o l l a a a b b c c +=+【解题指南】a, b,c ≠1，掌握对数两个公式:abb y x xyc c a a a a log log log ,log log log =+= 并灵活转换即可得解.【解析】选B.对选项A: bab a b bc c a c c a log log log log log log =⇒=⋅,显然与第二个公式不符，所以为假。

2020-2022全国高考真题数学汇编：指数函数与对数函数

2020-2022全国高考真题数学汇编指数函数与对数函数一、单选题1．（2022·天津·高考真题）化简()()48392log 3log 3log 2log 2++的值为（） A ．1B ．2C ．4D ．62．（2022·浙江·高考真题）已知825,log 3a b ==，则34a b −=（）A ．25B ．5C ．259 D ．533．（2022·全国·高考真题（文））已知910,1011,89m m m a b ==−=−，则（） A ．0a b >>B ．0a b >>C ．0b a >>D ．0b a >>4．（2022·北京·高考真题）已知函数1()12xf x =+，则对任意实数x ，有（） A ．()()0f x f x B ．()()0f x f x −−= C ．()()1f x f x −+=D ．1()()3f x f x −−=5．（2021·天津·高考真题）若2510a b ==，则11a b+=（）A ．1−B ．lg 7C ．1D ．7log 106．（2021·天津·高考真题）函数2ln ||2x y x =+的图像大致为（） A ． B ．C ．D ．7．（2021·全国·高考真题（文））下列函数中是增函数的为（）A ．()f x x =−B ．()23xf x ⎛⎫= ⎪⎝⎭C ．()2f x x = D ．()f x8．（2021·全国·高考真题（文））青少年视力是社会普遍关注的问题，视力情况可借助视力表测量．通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L 和小数记录表的数据V 的满足5lg L V =+．已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据为（ 1.259≈） A ．1.5B ．1.2C ．0.8D ．0.69．（2020·山东·高考真题）已知函数()y f x =是偶函数，当(0,)x ∈+∞时，()01x y a a =<<，则该函数在(,0)−∞上的图像大致是（）A ．B ．C ．D ．10．（2020·山东·高考真题）函数()1lg f x x=的定义域是（） A ．()0,∞+B ．()()0,11,+∞ C ．[)()0,11,+∞D ．()1,+∞11．（2020·海南·高考真题）已知函数2()lg(45)f x x x =−−在(,)a +∞上单调递增，则a 的取值范围是（） A ．(2,)+∞B ．[2,)+∞C ．(5,)+∞D ．[5,)+∞12．（2020·天津·高考真题）设0.80.70.713,,log 0.83a b c −⎛⎫=== ⎪⎝⎭，则,,a b c 的大小关系为（）A ．a b c <<B ．b a c <<C ．b c a <<D ．c a b <<13．（2020·天津·高考真题）已知函数3,0,(),0.x x f x x x ⎧=⎨−<⎩若函数2()()2()g x f x kx xk =−−∈R 恰有4个零点，则k的取值范围是（）A ．1,(22,)2⎛⎫−∞−+∞ ⎪⎝⎭B ．1,(0,22)2⎛⎫−∞− ⎪⎝⎭C ．(,0)(0,22)−∞D ．(,0)(22,)−∞+∞14．（2020·北京·高考真题）已知函数()21x f x x =−−，则不等式()0f x >的解集是（）． A ．(1,1)− B ．(,1)(1,)−∞−+∞ C ．(0,1)D ．(,0)(1,)−∞⋃+∞15．（2020·海南·高考真题）基本再生数R 0与世代间隔T 是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数，世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段，可以用指数模型：(e )rt I t =描述累计感染病例数I (t )随时间t (单位:天)的变化规律，指数增长率r 与R 0，T 近似满足R 0 =1+rT .有学者基于已有数据估计出R 0=3.28，T =6.据此，在新冠肺炎疫情初始阶段，累计感染病例数增加1倍需要的时间约为(ln2≈0.69) （） A ．1.2天 B ．1.8天 C ．2.5天D ．3.5天16．（2020·全国·高考真题（理））在新冠肺炎疫情防控期间，某超市开通网上销售业务，每天能完成1200份订单的配货，由于订单量大幅增加，导致订单积压.为解决困难，许多志愿者踊跃报名参加配货工作.已知该超市某日积压500份订单未配货，预计第二天的新订单超过1600份的概率为0.05，志愿者每人每天能完成50份订单的配货，为使第二天完成积压订单及当日订单的配货的概率不小于0.95，则至少需要志愿者（） A ．10名B ．18名C ．24名D ．32名17．（2020·全国·高考真题（理））若2233x y x y −−−<−，则（） A ．ln(1)0y x −+>B ．ln(1)0y x −+<C ．ln ||0x y −>D ．ln ||0x y −<18．（2020·全国·高考真题（理））已知55<84，134<85．设a =log 53，b =log 85，c =log 138，则（） A ．a <b <cB ．b <a <cC ．b <c <aD ．c <a <b19．（2020·全国·高考真题（文））Logistic 模型是常用数学模型之一，可应用于流行病学领域．有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I (t )(t 的单位：天)的Logistic 模型：0.23(53)()=1et I K t −−+，其中K 为最大确诊病例数．当I (*t )=0.95K 时，标志着已初步遏制疫情，则*t 约为（）（ln19≈3） A ．60B ．63C ．66D ．6920．（2020·全国·高考真题（文））设3log 2a =，5log 3b =，23c =，则（） A ．a c b <B ．2a b <C ．2a b >D ．2a b <23．（2020·全国·高考真题（理））设函数()ln |21|ln |21|f x x x =+−−，则f (x )（）A ．是偶函数，且在1(,)2+∞单调递增B ．是奇函数，且在11(,)22−单调递减C ．是偶函数，且在1(,)2−∞−单调递增 D ．是奇函数，且在1(,)2−∞−单调递减二、双空题24．（2022·全国·高考真题（文））若()1ln 1f x a b x++−=是奇函数，则=a _____，b =______．三、填空题25．（2022·天津·高考真题）设a ∈R ，对任意实数x ，记(){}2min 2,35f x x x ax a =−−+−．若()f x 至少有3个零点，则实数a 的取值范围为______.26．（2020·山东·高考真题）若212log log 40x −=，则实数x 的值是______.27．（2020·北京·高考真题）函数1()ln 1f x x x =++的定义域是____________．参考答案1．B 【解析】根据对数的性质可求代数式的值. 【详解】原式2233111(2log 3log 3)(log 2log 2)232=⨯++2343log 3log 2232=⨯=，故选：B 2．C 【解析】根据指数式与对数式的互化，幂的运算性质以及对数的运算性质即可解出．【详解】因为25a=，821log 3log 33b ==，即323b =，所以()()22323232452544392a aa b b b −====．故选：C. 3．A 【解析】根据指对互化以及对数函数的单调性即可知9log 101m =>，再利用基本不等式，换底公式可得lg11m >，8log 9m >，然后由指数函数的单调性即可解出．【详解】由910m=可得9lg10log 101lg9m ==>，而()222lg9lg11lg99lg9lg111lg1022+⎛⎫⎛⎫<=<= ⎪ ⎪⎝⎭⎝⎭，所以lg10lg11lg9lg10>，即lg11m >，所以lg11101110110m a =−>−=．又()222lg8lg10lg80lg8lg10lg922+⎛⎫⎛⎫<=< ⎪ ⎪⎝⎭⎝⎭，所以lg9lg10lg8lg9>，即8log 9m >，所以8log 989890m b =−<−=．综上，0a b >>．故选：A. 4．C 【解析】直接代入计算，注意通分不要计算错误．【详解】()()1121112121212x x x x xf x f x −−+=+=+=++++，故A 错误，C 正确； ()()11212121121212122121x x x x x xx xf x f x −−−−=−=−==−++++++，不是常数，故BD 错误；故选：C．5．C【解析】由已知表示出,a b，再由换底公式可求. 【详解】2510a b==，25log10,log10a b∴==，251111lg2lg5lg101log10log10a b∴+=+=+==.故选：C.6．B【解析】由函数为偶函数可排除AC，再由当()0,1∈x时，()0f x<，排除D，即可得解. 【详解】设()2ln||2xy f xx==+，则函数()f x的定义域为{}0x x≠，关于原点对称，又()()()2ln||2xf x f xx−−==−+，所以函数()f x为偶函数，排除AC；当()0,1∈x时，2ln0,20x x+，所以()0f x<，排除D.故选：B.7．D【解析】根据基本初等函数的性质逐项判断后可得正确的选项.【详解】对于A，()f x x=−为R上的减函数，不合题意，舍.对于B，()23xf x⎛⎫= ⎪⎝⎭为R上的减函数，不合题意，舍.对于C，()2f x x=在(),0−∞为减函数，不合题意，舍.对于D，()f x=R上的增函数，符合题意，故选：D.8．C【解析】根据,L V关系，当 4.9L=时，求出lg V，再用指数表示V，即可求解.【详解】由5lgL V=+，当 4.9L=时，lg0.1V=−，则10.110110100.81.259V−−===≈≈.故选：C.9．B 【解析】根据偶函数，指数函数的知识确定正确选项. 【详解】当(0,)x ∈+∞时，()01xy a a =<<，所以()f x 在()0,∞+上递减，()f x 是偶函数，所以()f x 在(),0−∞上递增.注意到01a =，所以B 选项符合. 故选：B 10．B 【解析】根据题意得到0lg 0x x >⎧⎨≠⎩，再解不等式组即可.【详解】由题知：0lg 0x x >⎧⎨≠⎩，解得0x >且1x ≠.所以函数定义域为()()0,11,+∞.故选：B 11．D 【解析】首先求出()f x 的定义域，然后求出2()lg(45)f x x x =−−的单调递增区间即可. 【详解】由2450x x −−>得5x >或1x <− 所以()f x 的定义域为(),1(5,)−∞−⋃+∞ 因为245y x x =−−在(5,)+∞上单调递增所以2()lg(45)f x x x =−−在(5,)+∞上单调递增所以5a ≥ 故选：D 【点睛】在求函数的单调区间时一定要先求函数的定义域. 12．D 【解析】利用指数函数与对数函数的性质，即可得出,,a b c 的大小关系. 【详解】因为0.731a =>，0.80.80.71333b a −⎛⎫==>= ⎪⎝⎭，0.70.7log 0.8log 0.71c =<=，所以1c a b <<<. 故选：D. 【点睛】本题考查的是有关指数幂和对数值的比较大小问题，在解题的过程中，注意应用指数函数和对数函数的单调性，确定其对应值的范围.比较指对幂形式的数的大小关系，常用方法：（1）利用指数函数的单调性：x y a =，当1a >时，函数递增；当01a <<时，函数递减；（2）利用对数函数的单调性：log a y x =，当1a >时，函数递增；当01a <<时，函数递减；（3）借助于中间值，例如：0或1等. 13．D 【解析】由(0)0g =，结合已知，将问题转化为|2|y kx =−与()()||f x h x x =有3个不同交点，分0,0,0k k k =<>三种情况，数形结合讨论即可得到答案. 【详解】注意到(0)0g =，所以要使()g x 恰有4个零点，只需方程()|2|||f x kx x −=恰有3个实根即可，令()h x =()||f x x ，即|2|y kx =−与()()||f x h x x =的图象有3个不同交点. 因为2,0()()1,0x x f x h x x x ⎧>==⎨<⎩，当0k =时，此时2y =，如图1，2y =与()()||f x h x x =有1个不同交点，不满足题意；当0k <时，如图2，此时|2|y kx =−与()()||f x h x x =恒有3个不同交点，满足题意；当0k >时，如图3，当2y kx =−与2yx 相切时，联立方程得220x kx −+=，令0∆=得280k −=，解得k =k >综上，k 的取值范围为(,0)(22,)−∞+∞. 故选：D.【点晴】本题主要考查函数与方程的应用，考查数形结合思想，转化与化归思想，是一道中档题. 14．D 【解析】作出函数2x y =和1y x =+的图象，观察图象可得结果. 【详解】因为()21xf x x =−−，所以()0f x >等价于21x x >+，在同一直角坐标系中作出2x y =和1y x =+的图象如图：两函数图象的交点坐标为(0,1),(1,2)，不等式21x x >+的解为0x <或1x >.所以不等式()0f x >的解集为：()(),01,−∞⋃+∞. 故选：D.【点睛】本题考查了图象法解不等式，属于基础题. 15．B 【解析】根据题意可得()0.38rt tI t e e ==，设在新冠肺炎疫情初始阶段，累计感染病例数增加1倍需要的时间为1t 天，根据10.38()0.382t t t e e +=，解得1t 即可得结果.【详解】因为0 3.28R =，6T =，01R rT =+，所以 3.2810.386r −==，所以()0.38rt tI t e e ==，设在新冠肺炎疫情初始阶段，累计感染病例数增加1倍需要的时间为1t 天，则10.38()0.382t t t e e +=，所以10.382t e =，所以10.38ln 2t =，所以1ln 20.691.80.380.38t =≈≈天. 故选：B. 【点睛】本题考查了指数型函数模型的应用，考查了指数式化对数式，属于基础题. 16．B 【解析】算出第二天订单数，除以志愿者每天能完成的订单配货数即可. 【详解】由题意，第二天新增订单数为50016001200900+−=， 9001850=，故至少需要志愿者18名. 故选：B 【点晴】本题主要考查函数模型的简单应用，属于基础题. 17．A 【解析】将不等式变为2323x x y y −−−<−，根据()23t tf t −=−的单调性知x y <，以此去判断各个选项中真数与1的大小关系，进而得到结果. 【详解】由2233x y x y −−−<−得：2323x x y y −−−<−，令()23t tf t −=−，2x y =为R 上的增函数，3x y −=为R 上的减函数，()f t ∴为R 上的增函数， x y ∴<，0y x −>，11y x ∴−+>，()ln 10y x ∴−+>，则A 正确，B 错误；x y −与1的大小不确定，故CD 无法确定.故选：A.【点睛】本题考查对数式的大小的判断问题，解题关键是能够通过构造函数的方式，利用函数的单调性得到,x y 的大小关系，考查了转化与化归的数学思想.18．A【解析】由题意可得a 、b 、()0,1c ∈，利用作商法以及基本不等式可得出a 、b 的大小关系，由8log 5b =，得85b =，结合5458<可得出45b <，由13log 8c =，得138c =，结合45138<，可得出45c >，综合可得出a 、b 、c 的大小关系. 【详解】由题意可知a 、b 、()0,1c ∈，()222528log 3lg 3lg81lg 3lg8lg 3lg8lg 241log 5lg 5lg 522lg 5lg 25lg 5a b ⎛⎫⎛⎫++⎛⎫==⋅<⋅==< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，a b ∴<；由8log 5b =，得85b =，由5458<，得5488b <，54b ∴<，可得45b <；由13log 8c =，得138c =，由45138<，得451313c <，54c ∴>，可得45c >. 综上所述，a b c <<.故选：A.【点睛】本题考查对数式的大小比较，涉及基本不等式、对数式与指数式的互化以及指数函数单调性的应用，考查推理能力，属于中等题.19．C【解析】将t t *=代入函数()()0.23531t K I t e −−=+结合()0.95I t K *=求得t *即可得解.【详解】 ()()0.23531t KI t e −−=+，所以()()0.23530.951t KI t K e **−−==+，则()0.235319t e *−=，所以，()0.2353ln193t *−=≈，解得353660.23t *≈+≈. 故选：C.【点睛】本题考查对数的运算，考查指数与对数的互化，考查计算能力，属于中等题. 20．A【解析】分别将a ,b 改写为331log 23a =，351log 33b =，再利用单调性比较即可.因为333112log 2log 9333a c =<==，355112log 3log 25333b c =>==，所以a c b <<.故选：A.【点晴】本题考查对数式大小的比较，考查学生转化与化归的思想，是一道中档题.21．B【解析】根据已知等式，利用指数对数运算性质即可得解【详解】由3log 42a =可得3log 42a =，所以49a =，所以有149a −=，故选：B.【点睛】本题考查的是有关指对式的运算的问题，涉及到的知识点有对数的运算法则，指数的运算法则，属于基础题目. 22．B【解析】设2()2log x f x x =+，利用作差法结合()f x 的单调性即可得到答案.【详解】设2()2log x f x x =+，则()f x 为增函数，因为22422log 42log 2log a b b a b b +=+=+所以()(2)f a f b −=2222log (2log 2)a b a b +−+=22222log (2log 2)b b b b +−+21log 102==−<，所以()(2)f a f b <，所以2a b <.2()()f a f b −=22222log (2log )a b a b +−+=222222log (2log )b b b b +−+=22222log b b b −−，当1b =时，2()()20f a f b −=>，此时2()()f a f b >，有2a b >当2b =时，2()()10f a f b −=−<，此时2()()f a f b <，有2a b <，所以C 、D 错误.故选：B.【点晴】本题主要考查函数与方程的综合应用，涉及到构造函数，利用函数的单调性比较大小，是一道中档题. 23．D【解析】根据奇偶性的定义可判断出()f x 为奇函数，排除AC ；当11,22x ⎛⎫∈− ⎪⎝⎭时，利用函数单调性的性质可判断出()f x 单调递增，排除B ；当1,2x ⎛⎫∈−∞− ⎪⎝⎭时，利用复合函数单调性可判断出()f x 单调递减，从而得到结果.由()ln 21ln 21f x x x =+−−得()f x 定义域为12x x ⎧⎫≠±⎨⎬⎩⎭，关于坐标原点对称，又()()ln 12ln 21ln 21ln 21f x x x x x f x −=−−−−=−−+=−，()f x ∴为定义域上的奇函数，可排除AC ；当11,22x ⎛⎫∈− ⎪⎝⎭时，()()()ln 21ln 12f x x x =+−−， ()ln 21y x =+在11,22⎛⎫− ⎪⎝⎭上单调递增，()ln 12y x =−在11,22⎛⎫− ⎪⎝⎭上单调递减， ()f x ∴在11,22⎛⎫− ⎪⎝⎭上单调递增，排除B ；当1,2x ⎛⎫∈−∞− ⎪⎝⎭时，()()()212ln 21ln 12ln ln 12121x f x x x x x +⎛⎫=−−−−==+ ⎪−−⎝⎭， 2121x μ=+−在1,2⎛⎫−∞− ⎪⎝⎭上单调递减，()ln f μμ=在定义域内单调递增，根据复合函数单调性可知：()f x 在1,2⎛⎫−∞− ⎪⎝⎭上单调递减，D 正确. 故选：D.【点睛】本题考查函数奇偶性和单调性的判断；判断奇偶性的方法是在定义域关于原点对称的前提下，根据()f x −与()f x 的关系得到结论；判断单调性的关键是能够根据自变量的范围化简函数，根据单调性的性质和复合函数“同增异减”性得到结论.24． 12−； ln 2．【解析】根据奇函数的定义即可求出．【详解】因为函数()1ln 1f x a b x ++−=为奇函数，所以其定义域关于原点对称．由101a x +≠−可得，()()110x a ax −+−≠，所以11a x a+==−，解得：12a =−，即函数的定义域为()()(),11,11,−∞−⋃−⋃+∞，再由()00f =可得，ln 2b =．即()111ln ln 2ln 211x f x x x +=−++=−−，在定义域内满足()()f x f x −=−，符合题意．故答案为：12−；ln 2． 25．10a ≥【解析】设()235g x x ax a =−+−，()2h x x =−，分析可知函数()g x 至少有一个零点，可得出0∆≥，求出a 的取值范围，然后对实数a 的取值范围进行分类讨论，根据题意可得出关于实数a 的不等式，综合可求得实数a 的取值范围.【详解】设()235g x x ax a =−+−，()2h x x =−，由20x −=可得2x =±.要使得函数()f x 至少有3个零点，则函数()g x 至少有一个零点，则212200a a ∆=−+≥，解得2a ≤或10a ≥.①当2a =时，()221g x x x =−+，作出函数()g x 、()h x 的图象如下图所示：此时函数()f x 只有两个零点，不合乎题意；②当2a <时，设函数()g x 的两个零点分别为1x 、()212x x x <，要使得函数()f x 至少有3个零点，则22x ≤−，所以，()2224550a g a ⎧<−⎪⎨⎪−=+−≥⎩，解得a ∈∅；③当10a =时，()21025g x x x =−+，作出函数()g x 、()h x 的图象如下图所示：由图可知，函数()f x 的零点个数为3，合乎题意；④当10a >时，设函数()g x 的两个零点分别为3x 、()434x x x <，要使得函数()f x 至少有3个零点，则32x ≥，可得()222450a g a ⎧>⎪⎨⎪=+−≥⎩，解得4a >，此时10a >.综上所述，实数a 的取值范围是[)10,+∞.故答案为：[)10,+∞.【点睛】方法点睛：已知函数有零点（方程有根）求参数值（取值范围）常用的方法：（1）直接法：直接求解方程得到方程的根，再通过解不等式确定参数范围；（2）分离参数法：先将参数分离，转化成求函数的值域问题加以解决；（3）数形结合法：先对解析式变形，进而构造两个函数，然后在同一平面直角坐标系中画出函数的图象，利用数形结合的方法求解.26．14【解析】根据对数运算化简为2log 2x =−，求解x 的值.【详解】21222log log 40log log 40x x −=⇔+=，即2log 2x =−，解得：14x =. 故答案为：1427．(0,)+∞【解析】根据分母不为零、真数大于零列不等式组，解得结果.【详解】由题意得010x x >⎧⎨+≠⎩，0x ∴> 故答案为：(0,)+∞【点睛】本题考查函数定义域，考查基本分析求解能力，属基础题.。

高考数学历年(2018-2022)真题按知识点分类(指数函数、对数函数、幂函数)练习

高考数学历年（2018-2022）真题按知识点分类（指数函数、对数函数、幂函数）练习一、单选题1．（2022ꞏ天津ꞏ统考高考真题）化简()()48392log 3log 3log 2log 2++的值为（） A ．1B ．2C ．4D ．62．（2022ꞏ天津ꞏ统考高考真题）已知0.72a =，0.713b ⎛⎫= ⎪⎝⎭，21log 3c =，则（）A ．a c b >>B ．b c a >>C ．a b c >>D ．c a b >>3．（2022ꞏ浙江ꞏ统考高考真题）已知825,log 3ab ==，则34a b -=（）A ．25B ．5C ．259 D ．534．（2022ꞏ全国ꞏ统考高考真题）已知910,1011,89m m m a b ==-=-，则（） A ．0a b >>B ．0a b >>C ．0b a >>D ．0b a >>5．（2022ꞏ北京ꞏ统考高考真题）已知函数1()12xf x =+，则对任意实数x ，有（） A ．()()0f x f x -+= B ．()()0f x f x --= C ．()()1f x f x -+=D ．1()()3f x f x --=6．（2022ꞏ北京ꞏ统考高考真题）在北京冬奥会上，国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术，为实现绿色冬奥作出了贡献．如图描述了一定条件下二氧化碳所处的状态与T 和lg P 的关系，其中T 表示温度，单位是K ；P 表示压强，单位是bar ．下列结论中正确的是（）A ．当220T =，1026P =时，二氧化碳处于液态B ．当270T =，128P =时，二氧化碳处于气态C ．当300T =，9987P =时，二氧化碳处于超临界状态D ．当360T =，729P =时，二氧化碳处于超临界状态7．（2022ꞏ全国ꞏ统考高考真题）设0.110.1e ,ln 0.99a b c ===-，，则（）A ．a b c <<B ．c b a <<C ．c<a<bD ．a c b << 8．（2021ꞏ天津ꞏ统考高考真题）设0.3212log 0.3,log 0.4,0.4a b c ===，则a ，b ，c 的大小关系为（） A ．a b c <<B ．c<a<bC ．b<c<aD ．a c b <<9．（2021ꞏ天津ꞏ统考高考真题）若2510a b ==，则11a b+=（） A ．1- B ．lg 7 C ．1D ．7log 1010．（2021ꞏ天津ꞏ统考高考真题）函数2ln ||2x y x =+的图像大致为（） A ． B ．C ．D ．11．（2021ꞏ全国ꞏ统考高考真题）已知5log 2a =，8log 3b =，12c =，则下列判断正确的是（）A ．c b a <<B ．b a c <<C ．a c b <<D ．a b c <<12．（2021ꞏ全国ꞏ统考高考真题）设2ln1.01a =，ln1.02b =，1c =-．则（） A ．a b c <<B ．b<c<aC ．b a c <<D ．c<a<b13．（2021ꞏ全国ꞏ高考真题）青少年视力是社会普遍关注的问题，视力情况可借助视力表测量．通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L 和小数记录表的数据V 的满足5lg L V =+．已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据为（）（ 1.259≈） A ．1.5 B ．1.2 C ．0.8 D ．0.614．（2021ꞏ全国ꞏ统考高考真题）下列函数中最小值为4的是（） A ．224y x x =++ B ．4sin sin y x x=+ C ．2y 22x x -=+D ．4ln ln y x x=+15．（2020ꞏ山东ꞏ统考高考真题）函数()1lg f x x=的定义域是（） A ．()0,∞+ B ．()()0,11,+∞C ．[)()0,11,+∞UD ．()1,+∞16．（2020ꞏ山东ꞏ统考高考真题）已知函数()y f x =是偶函数，当(0,)x ∈+∞时，()01x y a a =<<，则该函数在(,0)-∞上的图像大致是（）A ．B ．C ．D ．17．（2020ꞏ海南ꞏ高考真题）已知函数2()lg(45)f x x x =--在(,)a +∞上单调递增，则a 的取值范围是（）A ．(2,)+∞B ．[2,)+∞C ．(5,)+∞D ．[5,)+∞18．（2020ꞏ天津ꞏ统考高考真题）设0.80.70.713,,log 0.83a b c -⎛⎫=== ⎪⎝⎭，则,,a b c 的大小关系为（）A ．a b c <B ．ln(1)0y x -+<C ．ln ||0x y ->D ．ln ||0x y -<20．（2020ꞏ全国ꞏ统考高考真题）已知55<84，134<85．设a =log 53，b =log 85，c =log 138，则（）A ．a <b <cB ．b <a <cC ．b <c <aD ．c <a <b21．（2020ꞏ全国ꞏ统考高考真题）Logistic 模型是常用数学模型之一，可应用于流行病学领域．有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I (t )(t 的单位：天)的Logistic 模型：0.23(53)()=1e t I K t --+，其中K 为最大确诊病例数．当I (*t )=0.95K 时，标志着已初步遏制疫情，则*t 约为（）（ln19≈3）A ．60B ．63C ．66D ．6922．（2020ꞏ全国ꞏ统考高考真题）设3log 2a =，5log 3b =，23c =，则（） A ．a c b <<B ．a b c <<C ．b<c<aD ．c<a<b23．（2020ꞏ全国ꞏ统考高考真题）设3log 42a =，则4a -=（） A ．116B ．19C ．18D ．1624．（2020ꞏ全国ꞏ统考高考真题）设函数()ln |21|ln |21|f x x x =+--，则f (x )（）A ．是偶函数，且在1(,)2+∞单调递增B ．是奇函数，且在11(,)22-单调递减C ．是偶函数，且在1(,2-∞-单调递增D ．是奇函数，且在1(,)2-∞-单调递减25．（2019ꞏ全国ꞏ高考真题）已知0.20.32log 0.2,2,0.2a b c ===，则A ．a b c <b ，则 A ．ln(a −b )>0 B ．3a <3b C ．a 3−b 3>0D ．│a │>│b │27．（2019ꞏ北京ꞏ高考真题）在天文学中，天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足212152–lg E m m E =，其中星等为mk 的星的亮度为Ek （k =1,2）.已知太阳的星等是–26.7，天狼星的星等是–1.45，则太阳与天狼星的亮度的比值为A ．1010.1B ．10.1C ．lg10.1D ．10.110-28．（2019ꞏ天津ꞏ高考真题）已知2log 7a =，3log 8b =，0.20.3c =，则,,a b c 的大小关系为A ．c b a <<B ．a b c <<C ．b<c<aD ．c<a<b29．（2019ꞏ天津ꞏ高考真题）已知5log 2a =，0.5log 0.2b =，0.20.5c =，则,,a b c 的大小关系为A ．a c b <>B ．b a c >>C ．c b a >>D ．c a b >>31．（2018ꞏ全国ꞏ高考真题）设0.2log 0.3a =，2log 0.3b =，则 A ．0a b ab +<< B ．0ab a b <+< C ．0a b ab +<<D ．0ab a b <<+32．（2018ꞏ全国ꞏ高考真题）下列函数中，其图像与函数ln y x =的图像关于直线1x =对称的是A ．ln(1)y x =-B ．ln(2)y x =-C ．ln(1)y x =+D ．ln(2)y x =+33．（2018ꞏ天津ꞏ高考真题）已知13313711log ,(),log 245a b c ===，则,,a b c 的大小关系为A ．a b c >>B ．b a c >>C ．c b a >>D ．c a b >>二、多选题34．（2020ꞏ海南ꞏ统考高考真题）信息熵是信息论中的一个重要概念.设随机变量X 所有可能的取值为1,2,,n ，且1()0(1,2,,),1ni i i P X i p i n p ===>==∑ ，定义X 的信息熵21()log ni i i H X p p ==-∑.（）A ．若n =1，则H (X )=0B ．若n =2，则H (X )随着1p 的增大而增大C ．若1(1,2,,)i p i n n== ，则H (X )随着n 的增大而增大D ．若n =2m ，随机变量Y 所有可能的取值为1,2,,m ，且21()(1,2,,)j m j P Y j p p j m +-==+= ，则H (X )≤H (Y )三、填空题35．（2020ꞏ山东ꞏ统考高考真题）若212log log 40x -=，则实数x 的值是______.36．（2020ꞏ北京ꞏ统考高考真题）函数1()ln 1f x x x =++的定义域是____________． 37．（2020ꞏ江苏ꞏ统考高考真题）已知y =f (x )是奇函数，当x ≥0时，()23 f x x = ，则f (-8)的值是____.38．（2018ꞏ全国ꞏ高考真题）已知函数()()22log f x x a =+，若()31f =，则=a ________．四、双空题39．（2022ꞏ全国ꞏ统考高考真题）若()1ln 1f x a b x++-=是奇函数，则=a _____，b =______．参考答案1．B【要点分析】根据对数的性质可求代数式的值.【答案详解】原式2233111(2log 3log 3)(log 2log 2)232=⨯++2343log 3log 2232=⨯=，故选：B2．C【要点分析】利用幂函数、对数函数的单调性结合中间值法可得出a 、b 、c 的大小关系. 【答案详解】因为0.70.7221120log 1log 33⎛⎫>>=> ⎪⎝⎭，故a b c >>.故答案为：C.3．C【要点分析】根据指数式与对数式的互化，幂的运算性质以及对数的运算性质即可解出．【答案详解】因为25a=，821log 3log 33b ==，即323b =，所以()()22323232452544392a aa bb b -====．故选：C.4．A【要点分析】法一：根据指对互化以及对数函数的单调性即可知9log 101m =>，再利用基本不等式，换底公式可得lg11m >，8log 9m >，然后由指数函数的单调性即可解出．【答案详解】［方法一］：（指对数函数性质）由910m=可得9lg10log 101lg 9m ==>，而()222lg 9lg11lg 99lg 9lg111lg1022+⎛⎫⎛⎫<=<= ⎪ ⎪⎝⎭⎝⎭，所以lg10lg11lg 9lg10>，即lg11m >，所以lg11101110110m a =->-=. 又()222lg8lg10lg80lg8lg10lg 922+⎛⎫⎛⎫<=< ⎪ ⎪⎝⎭⎝⎭，所以lg 9lg10lg8lg 9>，即8log 9m >，所以8log 989890m b =-<-=.综上，0a b >>. ［方法二］：【最优解】（构造函数）由910m =，可得9log 10(1,1.5)m =∈．根据,a b 的形式构造函数()1(1)m f x x x x =--> ，则1()1m f x mx -'=-，令()0f x '=，解得110m x m -= ，由9log 10(1,1.5)m =∈ 知0(0,1)x ∈ .()f x 在 (1,)+∞ 上单调递增，所以(10)(8)f f > ，即 a b > ，又因为9log 10(9)9100f =-= ，所以0a b >> .故选：A.【整体点评】法一：通过基本不等式和换底公式以及对数函数的单调性比较，方法直接常用，属于通性通法；法二：利用,a b 的形式构造函数()1(1)m f x x x x =-->，根据函数的单调性得出大小关系，简单明了，是该题的最优解．5．C【要点分析】直接代入计算，注意通分不要计算错误．【答案详解】()()1121112121212x xx x x f x f x --+=+=+=++++，故A 错误，C 正确； ()()11212121121212122121x x x x x x x x f x f x ----=-=-==-++++++，不是常数，故BD 错误；故选：C ．6．D【要点分析】根据T 与lg P 的关系图可得正确的选项.【答案详解】当220T =，1026P =时，lg 3P >，此时二氧化碳处于固态，故A 错误. 当270T =，128P =时，2lg 3P <<，此时二氧化碳处于液态，故B 错误.当300T =，9987P =时，lg P 与4非常接近，故此时二氧化碳处于固态，对应的是非超临界状态，故C 错误.当360T =，729P =时，因2lg 3P <<, 故此时二氧化碳处于超临界状态，故D 正确. 故选：D7．C【要点分析】构造函数()ln(1)f x x x =+-，导数判断其单调性，由此确定,,a b c 的大小.【答案详解】方法一：构造法设()ln(1)(1)f x x x x =+->-，因为1()111x f x x x'=-=-++，当(1,0)x ∈-时，()0f x '>，当,()0x ∈+∞时()0f x '<，所以函数()ln(1)f x x x =+-在(0,)+∞单调递减，在(1,0)-上单调递增，所以1((0)09f f <=，所以101ln 099-<，故110ln ln 0.999>=-，即b c >，所以1()(0)010f f -<=，所以91ln +01010<，故1109e 10-<，所以11011e 109<，故a b <，设()e ln(1)(01)xg x x x x =+-<<，则()()21e 11()+1e 11xx x g x x x x -+'=+=--, 令2()e (1)+1x h x x =-，2()e (21)x h x x x '=+-，当01x <<时，()0h x '<，函数2()e (1)+1x h x x =-单调递减，11x <<时，()0h x '>，函数2()e (1)+1x h x x =-单调递增，又(0)0h =，所以当01x <<时，()0h x <，所以当01x <<时，()0g x '>，函数()e ln(1)x g x x x =+-单调递增，所以(0.1)(0)0g g >=，即0.10.1e ln 0.9>-，所以a c > 故选：C. 方法二：比较法解： 0.10.1a e = ， 0.110.1b =- ， ln(10.1)c =-- ， ①ln ln 0.1ln(10.1)a b -=+- ，令 ()ln(1),(0,0.1],f x x x x =+-∈ 则 1()1011x f x x x-'=-=<-- ，故 ()f x 在 (0,0.1] 上单调递减，可得 (0.1)(0)0f f <= ，即 ln ln 0a b -< ，所以 a b < ；②0.10.1ln(10.1)a c e -=+- ，令 ()ln(1),(0,0.1],x g x xe x x =+-∈则 ()()()1111'11x xxx x e g x xe e x x+--=+-=-- ，令 ()(1)(1)1x k x x x e =+-- ，所以 2()(12)0x k x x x e '=--> ，所以 ()k x 在 (0,0.1] 上单调递增，可得 ()(0)0k x k >> ，即 ()0g x '> ，所以 ()g x 在 (0,0.1] 上单调递增，可得 (0.1)(0)0g g >= ，即 0a c -> ，所以 .a c > 故 .c a b <<8．D【要点分析】根据指数函数和对数函数的性质求出,,a b c 的范围即可求解. 【答案详解】22log 0.3log 10<= ，<0a ∴，122225log 0.4log 0.4log log 212=-=>= ，1b ∴>， 0.3000.40.41<<= ，01c ∴<<， a c b ∴<<. 故选：D.9．C【要点分析】由已知表示出,a b ，再由换底公式可求. 【答案详解】 2510a b ==，25log 10,log 10a b ∴==， 251111lg 2lg 5lg101log 10log 10a b ∴+=+=+==. 故选：C.10．B【要点分析】由函数为偶函数可排除AC ，再由当()0,1∈x 时，()0f x <，排除D ，即可得解.【答案详解】设()2ln ||2x y f x x ==+，则函数()f x 的定义域为{}0x x ≠，关于原点对称，又()()()2ln ||2x f x f x x --==-+，所以函数()f x 为偶函数，排除AC ；当()0,1∈x 时，2ln 0,20x x + ，所以()0f x <，排除D.故选：B.11．C【要点分析】对数函数的单调性可比较a 、b 与c 的大小关系，由此可得出结论.【答案详解】5881log 2log log log 32a b =<==<=，即a c b <<. 故选：C.12．B【要点分析】利用对数的运算和对数函数的单调性不难对a ,b 的大小作出判定，对于a 与c ，b 与c 的大小关系，将0.01换成x ,分别构造函数()()2ln 11f x x =+,()()ln 121g x x =++，利用导数要点分析其在0的右侧包括0.01的较小范围内的单调性，结合f (0)=0,g (0)=0即可得出a 与c ，b 与c 的大小关系. 【答案详解】[方法一]：2ln1.01a =2ln1.01=()2ln 10.01=+()2ln 120.010.01=+⨯+ln1.02b >=，所以b a <；下面比较c 与,a b 的大小关系.记()()2ln 11f x x =+，则()00f =，()2121x f x x -='=+，由于()()2214122x x x x x x +-+=-=-所以当0<x <2时，()21410x x +-+>()1x >+，()0f x ¢>，所以()f x 在[]0,2上单调递增，所以()()0.0100f f >=，即2ln1.011>，即a c >；令()()ln 121g x x =++，则()00g =，()212212x g x x --==+' 由于()2214124x x x +-+=-，在x >0时，()214120x x +-+<，所以()0g x '<，即函数()g x 在[0，+∞)上单调递减，所以()()0.0100g g <=，即ln1.021<，即b <c ；综上，b<c<a ，故选：B. [方法二]：令()21ln 1(1)2x f x x x ⎛⎫+=--> ⎪⎝⎭()()221-01x f x x =+'-<，即函数()f x 在（1，+∞)上单调递减()10,ff b c <=∴<令()232ln 1(13)4x g x x x ⎛⎫+=-+<< ⎪⎝⎭()()()21303x x g x x --+'=>，即函数()g x 在（1，3)上单调递增()10,gg a c =∴综上，b<c<a ，故选：B.【名师点睛】本题考查比较大小问题，难度较大，关键难点是将各个值中的共同的量用变量替换，构造函数，利用导数研究相应函数的单调性，进而比较大小，这样的问题，凭借近似估计计算往往是无法解决的.13．C【要点分析】根据,L V 关系，当 4.9L =时，求出lg V ，再用指数表示V ，即可求解. 【答案详解】由5lg L V =+，当 4.9L =时，lg 0.1V =-，则10.110110100.81.259V --===≈≈. 故选：C.14．C【要点分析】根据二次函数的性质可判断A 选项不符合题意，再根据基本不等式“一正二定三相等”，即可得出,B D 不符合题意，C 符合题意．【答案详解】对于A ，()2224133y x x x =++=++≥，当且仅当=1x -时取等号，所以其最小值为3，A 不符合题意；对于B ，因为0sin 1x <≤，4sin 4sin y x x=+≥=，当且仅当sin 2x =时取等号，等号取不到，所以其最小值不为4，B 不符合题意；对于C ，因为函数定义域为R ，而20x >，2422242x x xx y -=+=+≥=，当且仅当22x =，即1x =时取等号，所以其最小值为4，C 符合题意；对于D ，4ln ln y x x=+，函数定义域为()()0,11,+∞ ，而ln x R ∈且ln 0x ≠，如当ln 1x =-，5y =-，D 不符合题意．故选：C ．【名师点睛】本题解题关键是理解基本不等式的使用条件，明确“一正二定三相等”的意义，再结合有关函数的性质即可解出．15．B【要点分析】根据题意得到0lg 0x x >⎧⎨≠⎩，再解不等式组即可.【答案详解】由题知：0lg 0x x >⎧⎨≠⎩，解得0x >且1x ≠.所以函数定义域为()()0,11,+∞ . 故选：B16．B【要点分析】根据偶函数，指数函数的知识确定正确选项.【答案详解】当(0,)x ∈+∞时，()01xy a a =<<，所以()f x 在()0,∞+上递减，()f x 是偶函数，所以()f x 在(),0∞-上递增. 注意到01a =，所以B 选项符合. 故选：B17．D【要点分析】首先求出()f x 的定义域，然后求出2()lg(45)f x x x =--的单调递增区间即可. 【答案详解】由2450x x -->得5x >或1x <- 所以()f x 的定义域为(),1(5,)-∞-⋃+∞因为245y x x =--在(5,)+∞上单调递增所以2()lg(45)f x x x =--在(5,)+∞上单调递增所以5a ≥ 故选：D【名师点睛】在求函数的单调区间时一定要先求函数的定义域.18．D【要点分析】利用指数函数与对数函数的性质，即可得出,,a b c 的大小关系. 【答案详解】因为0.731a =>，0.80.80.71333b a -⎛⎫==>= ⎪⎝⎭，0.70.7log 0.8log 0.71c =<=，所以1c a b <<<. 故选：D.【名师点睛】本题考查的是有关指数幂和对数值的比较大小问题，在解题的过程中，注意应用指数函数和对数函数的单调性，确定其对应值的范围. 比较指对幂形式的数的大小关系，常用方法：（1）利用指数函数的单调性：x y a =，当1a >时，函数递增；当01a <<时，函数递减；（2）利用对数函数的单调性：log a y x =，当1a >时，函数递增；当01a <<时，函数递减；（3）借助于中间值，例如：0或1等.19．A【要点分析】将不等式变为2323x x y y ---<-，根据()23t tf t -=-的单调性知x y <，以此去判断各个选项中真数与1的大小关系，进而得到结果. 【答案详解】由2233x y x y ---<-得：2323x x y y ---<-，令()23t tf t -=-，2x y = 为R 上的增函数，3x y -=为R 上的减函数，()f t ∴为R 上的增函数， x y ∴<，0y x ->Q ，11y x ∴-+>，()ln 10y x ∴-+>，则A 正确，B 错误；x y -Q 与1的大小不确定，故CD 无法确定.故选：A.【名师点睛】本题考查对数式的大小的判断问题，解题关键是能够通过构造函数的方式，利用函数的单调性得到,x y 的大小关系，考查了转化与化归的数学思想.20．A【要点分析】由题意可得a 、b 、()0,1c ∈，利用作商法以及基本不等式可得出a 、b 的大小关系，由8log 5b =，得85b =，结合5458<可得出45b <，由13log 8c =，得138c =，结合45138<，可得出45c >，综合可得出a 、b 、c 的大小关系. 【答案详解】由题意可知a 、b 、()0,1c ∈，()222528log 3lg 3lg81lg 3lg8lg 3lg8lg 241log 5lg 5lg 522lg 5lg 25lg 5a b ⎛⎫⎛⎫++⎛⎫==⋅<⋅==<⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，a b ∴<；由8log 5b =，得85b =，由5458<，得5488b <，54b ∴<，可得45b <；由13log 8c =，得138c =，由45138<，得451313c <，54c ∴>，可得45c >.综上所述，a b c <<. 故选：A.【名师点睛】本题考查对数式的大小比较，涉及基本不等式、对数式与指数式的互化以及指数函数单调性的应用，考查推理能力，属于中等题.21．C【要点分析】将t t *=代入函数()()0.23531t K I t e--=+结合()0.95I tK *=求得t*即可得解.【答案详解】()()0.23531t K I t e--=+ ，所以()()0.23530.951t K I t K e**--==+，则()0.235319t e*-=，所以，()0.2353ln193t *-=≈，解得353660.23t *≈+≈. 故选：C.【名师点睛】本题考查对数的运算，考查指数与对数的互化，考查计算能力，属于中等题.22．A【要点分析】分别将a ,b 改写为331log 23a =，351log 33b =，再利用单调性比较即可.【答案详解】因为333112log 2log 9333a c =<==，355112log 3log 25333b c =>==，所以a c b <<. 故选：A.【点晴】本题考查对数式大小的比较，考查学生转化与化归的思想，是一道中档题.23．B【要点分析】根据已知等式，利用指数对数运算性质即可得解【答案详解】由3log 42a =可得3log 42a=，所以49a =，所以有149a-=，故选：B.【名师点睛】本题考查的是有关指对式的运算的问题，涉及到的知识点有对数的运算法则，指数的运算法则，属于基础题目.24．D【要点分析】根据奇偶性的定义可判断出()f x 为奇函数，排除AC ；当11,22x ⎛⎫∈- ⎪⎝⎭时，利用函数单调性的性质可判断出()f x 单调递增，排除B ；当1,2x ⎛⎫∈-∞- ⎪⎝⎭时，利用复合函数单调性可判断出()f x 单调递减，从而得到结果.【答案详解】由()ln 21ln 21f x x x =+--得()f x 定义域为12x x ⎧⎫≠±⎨⎬⎩⎭，关于坐标原点对称，又()()ln 12ln 21ln 21ln 21f x x x x x f x -=----=--+=-， ()f x \为定义域上的奇函数，可排除AC ；当11,22x ⎛⎫∈- ⎪⎝⎭时，()()()ln 21ln 12f x x x =+--，()ln 21y x =+Q 在11,22⎛⎫- ⎪⎝⎭上单调递增，()ln 12y x =-在11,22⎛⎫- ⎪⎝⎭上单调递减，()f x \在11,22⎛⎫- ⎪⎝⎭上单调递增，排除B ；当1,2x ⎛⎫∈-∞- ⎪⎝⎭时，()()()212ln 21ln 12ln ln 12121x f x x x x x +⎛⎫=----==+ ⎪--⎝⎭，2121x μ=+- 在1,2⎛⎫-∞- ⎪⎝⎭上单调递减，()ln f μμ=在定义域内单调递增，根据复合函数单调性可知：()f x 在1,2⎛⎫-∞- ⎪⎝⎭上单调递减，D 正确.故选：D.【名师点睛】本题考查函数奇偶性和单调性的判断；判断奇偶性的方法是在定义域关于原点对称的前提下，根据()f x -与()f x 的关系得到结论；判断单调性的关键是能够根据自变量的范围化简函数，根据单调性的性质和复合函数“同增异减”性得到结论.25．B【要点分析】运用中间量0比较,a c ，运用中间量1比较,b c【答案详解】22log 0.2log 10,a =<=0.20221,b =>=0.3000.20.21,<<=则01,c a c b <<<<．故选B ．【名师点睛】本题考查指数和对数大小的比较，渗透了直观想象和数学运算素养．采取中间变量法，利用转化与化归思想解题．26．C【要点分析】本题也可用直接法，因为a b >，所以0a b ->，当1a b -=时，ln()0a b -=，知A 错，因为3x y =是增函数，所以33a b >，故B 错；因为幂函数3y x =是增函数，a b >，所以33a b >，知C 正确；取1,2a b ==-，满足a b >，12a b =<=，知D 错．【答案详解】取2,1a b ==，满足a b >，ln()0a b -=，知A 错，排除A ；因为9333a b =>=，知B 错，排除B ；取1,2a b ==-，满足a b >，12a b =<=，知D 错，排除D ，因为幂函数3y x =是增函数，a b >，所以33a b >，故选C ．【名师点睛】本题主要考查对数函数性质、指数函数性质、幂函数性质及绝对值意义，渗透了逻辑推理和运算能力素养，利用特殊值排除即可判断．27．A【解析】由题意得到关于12,E E 的等式，结合对数的运算法则可得亮度的比值. 【答案详解】两颗星的星等与亮度满足12125lg 2E m m E -=,令211.45,26.7m m =-=-, ()10.111212222lg( 1.4526.7)10.1,1055E E m m E E =⋅-=-+==. 故选A.【名师点睛】本题以天文学问题为背景,考查考生的数学应用意识､信息处理能力､阅读理解能力以及指数对数运算.28．A【要点分析】利用利用0,1,2等中间值区分各个数值的大小．【答案详解】0.200.30.31c =<=；22log 7log 42>=；331log 8log 92<<=．故c b a <<．故选A ．【名师点睛】利用指数函数、对数函数的单调性时要根据底数与1的大小区别对待．29．A【解析】利用10,,12等中间值区分各个数值的大小．【答案详解】551log 2log 2a =<<， 0.50.5log 0.2log 0.252b =>=， 10.200.50.50.5<<，故112c <<，所以a c b <<．故选A ．【名师点睛】本题考查大小比较问题，关键选择中间量和函数的单调性进行比较．30．D【答案详解】要点分析：由题意结合对数函数的性质整理计算即可求得最终结果. 答案详解：由题意结合对数函数的性质可知： 2log e >1a =，()21ln 20,1log ==∈b e ，12221log log 3log 3c e ==>，据此可得：c a b >>. 本题选择D 选项.名师点睛：对于指数幂的大小的比较，我们通常都是运用指数函数的单调性，但很多时候，因幂的底数或指数不相同，不能直接利用函数的单调性进行比较．这就必须掌握一些特殊方法．在进行指数幂的大小比较时，若底数不同，则首先考虑将其转化成同底数，然后再根据指数函数的单调性进行判断．对于不同底而同指数的指数幂的大小的比较，利用图象法求解，既快捷，又准确．31．B【答案详解】要点分析：求出0.2211log0.3,0.3log a b ==，得到11a b+的范围，进而可得结果．答案详解：.0.30.3log0.2,2a b log == 0.2211log0.3,0.3log a b∴== 0.3110.4log a b∴+= 1101a b∴<+<,即01a bab +<< 又a 0,b 0><ab 0∴<即ab a b 0<+<故选B.名师点睛：本题主要考查对数的运算和不等式，属于中档题．32．B【答案详解】要点分析：确定函数y lnx =过定点（1，0）关于x=1对称点，代入选项验证即可．答案详解：函数y lnx =过定点（1，0），（1，0）关于x=1对称的点还是（1，0），只有()y ln 2x =-过此点．故选项B 正确名师点睛：本题主要考查函数的对称性和函数的图像，属于中档题．33．D【答案详解】要点分析：由题意结合对数的性质，对数函数的单调性和指数的性质整理计算即可确定a ,b ,c 的大小关系.答案详解：由题意可知：3337392log log log <<，即12a <<，13111044⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭=，即01b <<， 133317552log log log =>，即c a >，综上可得：c a b >>.本题选择D 选项. 名师点睛：对于指数幂的大小的比较，我们通常都是运用指数函数的单调性，但很多时候，因幂的底数或指数不相同，不能直接利用函数的单调性进行比较．这就必须掌握一些特殊方法．在进行指数幂的大小比较时，若底数不同，则首先考虑将其转化成同底数，然后再根据指数函数的单调性进行判断．对于不同底而同指数的指数幂的大小的比较，利用图象法求解，既快捷，又准确．34．AC【要点分析】对于A 选项，求得()H X ，由此判断出A 选项；对于B 选项，利用特殊值法进行排除；对于C 选项，计算出()H X ，利用对数函数的性质可判断出C 选项；对于D 选项，计算出 ()(),H X H Y ，利用基本不等式和对数函数的性质判断出D 选项.【答案详解】对于A 选项，若1n =，则11,1i p ==，所以()()21log 10H X =-⨯=，所以A 选项正确.对于B 选项，若2n =，则1,2i =，211p p =-，所以()()()121121X log 1log 1H p p p p =-⋅+-⋅-⎡⎤⎣⎦，当114p =时，()221133log log 4444H X ⎛⎫=-⋅+⋅ ⎪⎝⎭，当13p 4=时，()223311log log 4444H X ⎛⎫=-⋅+⋅ ⎪⎝⎭，两者相等，所以B 选项错误. 对于C 选项，若()11,2,,i p i n n== ，则 ()222111log log log H X n n n n n ⎛⎫=-⋅⨯=-= ⎪⎝⎭，则()H X 随着n 的增大而增大，所以C 选项正确.对于D 选项，若2n m =，随机变量Y 的所有可能的取值为1,2,,m ，且 ()21j m j P Y j p p +-==+（ 1,2,,j m = ）.()2222111log log m mi i i i i iH X p p p p ===-⋅=⋅∑∑ 122221222122121111log log log log m m m mp p p p p p p p --=⋅+⋅++⋅+⋅ . ()H Y =()()()122221212122211111log log log m m m m m m m m p p p p p p p p p p p p -+-++⋅++⋅+++⋅+++ 12222122212221221121111log log log log m m m m m mp p p p p p p p p p p p ---=⋅+⋅++⋅+⋅++++ 由于()01,2,,2i p i m >= ，所以 2111i i m i p p p +->+，所以 222111log log i i m ip p p +->+，所以222111log log i i i i m ip p p p p +-⋅>⋅+，所以()()H X H Y >，所以D 选项错误. 故选：AC【名师点睛】本小题主要考查对新定义“信息熵”的理解和运用，考查要点分析、思考和解决问题的能力，涉及对数运算和对数函数及不等式的基本性质的运用，属于难题.35．14【要点分析】根据对数运算化简为2log 2x =-，求解x 的值. 【答案详解】21222log log 40log log 40x x -=⇔+=，即2log 2x =-，解得：14x =. 故答案为：1436．(0,)+∞【要点分析】根据分母不为零、真数大于零列不等式组，解得结果.【答案详解】由题意得010x x >⎧⎨+≠⎩，0x ∴> 故答案为：(0,)+∞【名师点睛】本题考查函数定义域，考查基本要点分析求解能力，属基础题.37．4-【要点分析】先求(8)f ，再根据奇函数求(8)f - 【答案详解】23(8)84f ==，因为()f x 为奇函数，所以(8)(8)4f f -=-=-故答案为：4-【名师点睛】本题考查根据奇函数性质求函数值，考查基本要点分析求解能力，属基础题. 38．-7【答案详解】要点分析：首先利用题的条件()31f =，将其代入解析式，得到()()2391f log a =+=，从而得到92a +=，从而求得7a =-，得到答案.答案详解：根据题意有()()2391f log a =+=，可得92a +=，所以7a =-，故答案是7-. 名师点睛：该题考查的是有关已知某个自变量对应函数值的大小，来确定有关参数值的问题，在求解的过程中，需要将自变量代入函数解析式，求解即可得结果，属于基础题目.39． 12-； ln 2．【要点分析】根据奇函数的定义即可求出．【答案详解】[方法一]：奇函数定义域的对称性若0a =，则()f x 的定义域为{|1}x x ≠，不关于原点对称 0a ∴≠ 若奇函数的1()||1f x ln a b x =++-有意义，则1x ≠且101a x +≠- 1x ∴≠且11x a ≠+，函数()f x 为奇函数，定义域关于原点对称， 111a ∴+=-，解得12a =-，由(0)0f =得，102ln b +=，2b ln ∴=，故答案为：12-；2ln ． [方法二]：函数的奇偶性求参111()111a ax ax a f x ln a b ln b ln b x x x -+--=++=+=+--- 1()1ax a f x ln b x++-=++ 函数()f x 为奇函数11()()2011ax a ax a f x f x ln ln b x x--++∴+-=++=-+ 2222(1)201a x a lnb x -+∴+=- 22(1)1210112a a a a +∴=⇒+=⇒=- 1222241,22b ln b ln a b ln ln-==-⇒=∴=-= [方法三]：因为函数()1ln 1f x a b x ++-=为奇函数，所以其定义域关于原点对称．由101a x+≠-可得，()()110x a ax -+-≠，所以11a x a +==-，解得：12a =-，即函数的定义域为()()(),11,11,-∞-⋃-⋃+∞，再由()00f =可得，ln 2b =．即()111ln ln 2ln 211x f x x x+=-++=--，在定义域内满足()()f x f x -=-，符合题意．故答案为：12-；ln 2．。

考点04 指数、对数、幂函数-2019年江苏高考数学五年真题与三年模拟试题考点分类解读(解析版)

1、了解幂函数的概念，掌握常见的幂函数的图像；2、理解指数函数的概念，以及指数函数的图像与性质。

会用指数函数模型解决简单的实际问题；3、理解对数函数的概念及其性质，了解对数函数的换底公式，理解对数函数的性质，会画对数函数的图像；指数函数、对数函数作为一类特殊的函数，在江苏高考中往往作为一种载体与其他函数结合考查，重点考查与指数、对数函数有关的综合函数的单调性、奇偶性以及与不等式等知识点的综合，难度往往较大。

幂函数在江苏高考中的要求较低，近几年江苏高考中还没有涉及，在平时的复习中可以适当的关注。

在高考复习中要注意以下几点：①要善于用指数函数的图像和性质，研究指数函数的单调性，对于这类问题考查的热点是对含参的讨论。

在有关根式的变形或者求值的过程中，要善于用转化的思想和方程观点处理问题；②研究对数问题尽量华为同底，另外对数问题中要注意定义域的限制，充分对对数函数的概念、图像、性质讨论一些与之有关的复合函数的限制；③对于与指数函数、对数函数有关的综合体现要善于运用数形结合的思想以及等价转化的思想，注意与其他知识点的结合。

学科@网1、(14年江苏)已知函数f (x )＝e x ＋e －x ，其中e 是自然对数的底数．(1) 证明：f (x )是R 上的偶函数；(2) 若关于x 的不等式mf (x )≤e －x ＋m －1在(0，＋∞)上恒成立，求实数m 的取值范围；(3) 已知正数a 满足：存在x 0∈[1，＋∞)，使得f (x 0)<a (－x 30＋3x 0)成立．试比较ea－1与a e－1的大小，并证明你的结论．【解析】： (1) 因为对任意x ∈R ，都有f (－x )＝e －x ＋e－(－x )＝e －x ＋e x ＝f (x )，所以f (x )是R 上的偶函数．(3) 令函数g (x )＝e x ＋1e x －a (－x 3＋3x )，则g ′(x )＝e x －1e x ＋3a (x 2－1)．当x ≥1时，e x －1ex >0，x 2－1≥0.又a >0，故g ′(x )>0，所以g (x )是[1，＋∞)上的单调增函数，因此g (x )在[1，＋∞)上的最小值是g (1)＝e ＋e －1－2a .由于存在x 0∈[1，＋∞)，使e x 0＋e －x 0－a (－x 30＋3x 0)<0成立，当且仅当最小值g (1)<0. 故e ＋e －1－2a <0，即a >e ＋e －12.解法2 由于e a－1与a e－1均为正数，同取自然底数的对数，即比较(a －1)lne 与(e －1)ln a 的大小，即比较lne e －1与ln aa －1的大小. 构造函数h (x )＝ln xx －1，则h ′(x )＝1－1x －ln x(x －1)2.设m (x )＝1－1x －ln x ，则m ′(x )＝1－x x2.令m ′(x )＝0，得x ＝1.当x >1时，m ′(x )<0；当0<x <1时，m ′(x )>0.所以m (x )在(1，＋∞)上单调递减，此时m (x )<m (1)＝0，所以h ′(x )<0在(1，＋∞)上恒成立，所以h (x )＝ln xx －1在(1，＋∞)上单调递减．所以当e ＋e －12<a <e 时，a e －1>e a －1；当a ＝e 时，e a －1＝a e －1；当a >e 时，a e －1<e a －1.解法3 因为ae －1＝e(e －1)ln a，所以a e －1ea －1＝e (e －1)ln a －(a －1)，故只要比较a －1与(e －1)ln a 的大小.令h (x )＝(e －1)ln x －(x －1)，那么h ′(x )＝e －1x －1.令h ′(x )＝0，得x ＝e －1.当x >e －1时，h ′(x )<0；当0<x <e －1时，h ′(x )>0.所以h (x )在(0，e －1)上是增函数；在(e －1，＋∞)上是减函数．又h (e)＝0，h (1)＝0，则h (e －1)>0，h ⎝⎛⎭⎫e ＋e －12>0.那么当e ＋e －12<a <e 时，h (a )>0，所以e h (a )>1，所以a e－1>e a －1；当a ＝e 时，h (a )＝0，所以e a －1＝a e －1；当a >e 时，h (a )<0，所以0<e h (a )<1，所以a e －1<e a －1.综上所述，当e ＋e －12<a <e 时，a e －1>e a －1；当a ＝e 时，e a －1＝a e －1；当a >e 时，a e －1<e a －1.2、（15年江苏）.不等式224x x-<的解集为________.3、(16年江苏)已知函数f (x )＝a x ＋b x(a >0，b >0，a ≠1，b ≠1)．(1) 设a ＝2，b ＝12.①求方程f (x )＝2的根；②若对于任意x ∈R ，不等式f (2x )≥mf (x )－6恒成立，求实数m 的最大值； (2) 若0<a <1，b >1，函数g (x )＝f (x )－2有且只有1个零点，求ab 的值．思路分析第1问的第2小题，通过将变量m 分离出来，将问题转化为求分离出的函数的最小值则可．第2问，注意到g (0)＝0，从而得0是函数g (x )的一个零点，为此，只需说明函数g (0)为函数g (x )的最大值或者最小值，进而说明它的某个极值点与0相等，由此来求出ab 的值．(2) 解法1 因为函数g (x )＝f (x )－2只有1个零点，而g (0)＝f (0)－2＝a 0＋b 0－2＝0，所以0是函数g (x )的唯一零点．因为g ′(x )＝a x ln a ＋b x ln b ，又由0<a <1，b >1知ln a <0，ln b >0，所以g ′(x )＝0有唯一解x 0＝log b a ⎝⎛⎭⎫－ln a ln b . 令h (x )＝g ′(x )，则h ′(x )＝(a x ln a ＋b x ln b )′＝a x (ln a )2＋b x (ln b )2，从而对任意x ∈R ，h ′(x )>0，所以g ′(x )＝h (x )是(－∞，＋∞)上的单调增函数．于是当x ∈(－∞，x 0)时，g ′(x )<g ′(x 0)＝0；当x ∈(x 0，＋∞)时，g ′(x )>g ′(x 0)＝0.因而函数g (x )在(－∞，x 0)上是单调减函数，在(x 0，＋∞)上是单调增函数．下证x 0＝0.若x 0<0，则x 0<x 02<0，于是g ⎝⎛⎭⎫x 02<g (0)＝0.又g (log a 2)＝a log a 2＋b log a 2－2>a log a 2－2＝0，且函数g (x )在以x 02和log a 2为端点的闭区间上的图像不间断，所以在x 02和log a 2之间存在g (x )的零点，记为x 1.因为0<a <1，所以log a 2<0.又x 02<0，所以x 1<0，与“0是函数g (x )的唯一零点”矛盾．若x 0>0，同理可得，在x 02和log b 2之间存在g (x )的非0的零点，矛盾．因此，x 0＝0.于是－ln aln b＝1，故ln a ＋ln b ＝0，所以ab ＝1.解后反思本题考查了指数方程的求解，以及换元思想在解题中的应用，利用导数研究函数的性质．对于本题的第2问，我们也可以从函数图像的交点的角度来加以思考，从而通过分析函数的图像来帮助我们得到问题的【答案】．由g (x )＝0得a x －2＝－b x ，即F (x )＝a x －2与G (x )＝－b x 有且只有一个交点，通过图像观察得，此交点即为(0，－1)，为此只需两个函数在x ＝0处有相同的切线，即a 0ln a ＝－b 0ln b ，所以有ab ＝1，通过这一图形的关系，我们可以得到问题的【答案】，从而通过理论来加以说明，这说明了“形”在代数论证中的价值．题型一：指数、对数函数的简单运用1、(2018南京、盐城、连云港二模）函数f(x)＝lg (2－x)的定义域为________．【答案】： (－∞，2)【解析】：由题意得2－x>0，即x<2，所以函数f(x)＝lg (2－x)的定义域为(－∞，2)．2、(2018盐城三模）函数()ln(1f x =的定义域为．【答案】：(2,3]【解析】：由题意，10->，1<，即031x ≤-<，解得23x <≤.3、(2017南京、盐城二模）函数f (x )＝ln 11－x的定义域为________．【答案】： (－∞，1) 由11－x＞0，得1－x ＞0，即x ＜1. 易错警示定义域应该写成集合(或区间)形式，区间是某些集合的缩写． 4、(2017苏锡常镇调研（一））函数f (x )＝1ln (4x －3)的定义域为________．5、(2018苏州期末）已知4a ＝2，log a x ＝2a ，则正实数x 的值为________．【答案】：. 12【解析】：由4a＝2，得22a＝21，所以2a ＝1，即a ＝12.由log 12x ＝1，得x ＝⎝⎛⎭⎫121＝12.6、(2015苏州期末）已知函数f (x )＝lg ⎝⎛⎭⎫1－a 2x 的定义域是⎝⎛⎭⎫12，＋∞，则实数a 的值为________．【答案】2解法1 由1－a 2x >0，得2x >a .显然a >0，所以x >log 2a .由题意，得log 2a ＝12，即a ＝ 2.解法2 (秒杀解法)当x ＝12时，必有1－a2x ＝0，解得a ＝ 2.学科@网7、(2017徐州、连云港、宿迁三检）如图，已知正方形ABCD 的边长为2，BC 平行于x 轴，顶点A ，B 和C 分别在函数13log a y x =，22log a y x =和3log a y x =(1a >)的图象上，则实数a 的值为．【答案】：．2设)log 3,(t t A a （0>t ），因为正方形ABCD 的边长为2，所以)log 2,(t t B a ，)log 2,(2t t C a ，则⎩⎨⎧=-=-2log 2log 322t t t t a a ，即⎩⎨⎧==--2log 022t t t a ，解之得⎩⎨⎧==22a t ，即所求的实数a 的值为2． 8、(2016镇江期末）已知函数f (x )是定义在R 上的奇函数，当x >0时，f (x )＝1－log 2x ，则不等式f (x )<0的解集是________．【答案】： (－2,0)∪(2，＋∞)9、(2016常州期末）. 函数f (x )＝log 2(－x 2＋22)的值域为________．【答案】：. ⎝⎛⎦⎤－∞，32 【解析】：由题意可得－x 2＋22>0，即－x 2＋22∈(0,22]，故所求函数的值域为⎝⎛⎦⎤－∞，32.10、(2017南京学情调研）已知f (x )，g (x )分别是定义在R 上的奇函数和偶函数，且f (x )＋g (x )＝⎝⎛⎭⎫12x.若存在x 0∈⎣⎡⎦⎤12，1，使得等式af (x 0)＋g (2x 0)＝0成立，则实数a 的取值范围是________．【答案】： ⎣⎡⎦⎤22，522思路分析由于所给出的是一个函数方程，因此，根据函数的奇偶性，可以得到另外一个函数方程，从而可求出f (x )，g (x )的【解析】式，通过将等式af (x 0)＋g (2x 0)＝0中的a 分离出来，转化为求分离之后的函数的值域问题．解后反思已知方程有解求参数取值范围常用的方法和思路：(1)直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数的范围；(2)分离参数法：先将参数分离，转化成求函数的值域问题加以解决；(3)数形结合法：先对【解析】式进行变形，在同一平面直角坐标系中，画出函数的图像，然后利用数形结合法进行求解．本题所采用的是分离参数法．11、(2016镇江期末）已知函数f (x )＝4x －2x ，实数s ，t 满足f (s )＋f (t )＝0，设a ＝2s ＋2t ，b ＝2s ＋t .(1) 当函数f (x )的定义域为[－1,1]时，求f (x )的值域； (2) 求函数关系式b ＝g (a )，并求函数g (a )的定义域； (3) 求8s ＋8t 的取值范围．【解析】： (1) 若x ∈[－1,1]，令m ＝2x ∈⎣⎡⎦⎤12，2，(1分) f (x )＝l (m )＝m 2－m ＝⎝⎛⎭⎫m －122－14在⎣⎡⎦⎤12，2上为增函数，(2分) f (x )min ＝l (m )min ＝l ⎝⎛⎭⎫12＝－14，f (x )max ＝l (m )max ＝l (2)＝2，(3分) 所以f (x )的值域为⎣⎡⎦⎤－14，2.(4分) (2) 实数s ，t 满足f (s )＋f (t )＝0，则4s －2s ＋4t －2t ＝0，则(2s ＋2t )2－2×2s ＋t －(2s ＋2t )＝0，(6分)而a ＝2s ＋2t ，b ＝2s ＋t ，所以a 2－2b －a ＝0，b ＝g (a )＝12(a 2－a )．(7分)由题意，b >0，a >0，则12(a 2－a )>0，所以a >1.(8分)又2s＋2t＝4s＋4t≥2×⎝⎛⎭⎫2s＋2t22，即a ≥a 22，所以a ≤2，当且仅当s ＝t 时取得等号．(9分)综上所述，g (a )的定义域为(1,2]．(10分)题型二：指数、对数函数的综合运用1、(2018苏锡常镇调研（一））已知函数f(x)＝⎩⎪⎨⎪⎧a －e x ，x<1，x ＋4x ，x ≥1(e 是自然对数的底)．若函数y ＝f(x)的最小值是4，则实数a 的取值范围为________．【答案】：. [e ＋4，＋∞)解法1 在x ≥1时，f(x)min ＝f(2)＝4.所以当x<1时，a －e x ≥4恒成立．转化为a ≥e x ＋4对x<1恒成立．因为e x ＋4在(－∞，1)上的值域为(4，e ＋4)，所以a ≥e ＋4.解法2 当x<1时，f(x)＝a －e x >a －e ，当x ≥1时，f(x)＝x ＋4x ≥4，当且仅当x ＝4x ，即x ＝2时，取“＝”，故函数f(x)的值域是[e ＋4，＋∞) .解后反思解法1中，因为e x ＋4在x<1上没有最大值，所以要特别注意边界值e ＋4能否取到． 2、(2017镇江期末）已知函数y ＝2x ＋12x ＋1与函数y ＝x ＋1x 的图像共有k (k ∈N *)个公共点：A 1(x 1，y 1)，A 2(x 2，y 2)，…，A k (x k ，y k )，则∑(x i ＋y i )＝________.【答案】： 2思路分析函数y ＝2x ＋12x ＋1可变形为y ＝2－22x ＋1，则函数y ＝2x ＋12x ＋1在R 上单调递增，也可变形为y ＝2x －12x＋1＋1，则函数y ＝2x ＋12x ＋1图像关于点(0,1)对称；函数y ＝x ＋1x 图像也关于点(0,1)对称，在(－∞，0)和(0，＋∞)上都是减函数．如图，函数y ＝2x ＋12x ＋1与函数y ＝x ＋1x 的图像都关于点(0,1)成中心对称，所以它们的交点也关于点(0,1)成中心对称，且只有两个交点，所以∑i ＝0，∑i ＝2，则∑(x i ＋y i )＝2.3、(2017镇江期末）不等式log a x －ln 2x ＜4(a ＞0且a ≠1)对任意x ∈(1,100)恒成立，则实数a 的取值范围为________．【答案】： (0,1)∪(e 14，＋∞)【解析】：思路分析不等式恒成立问题常用方法是参变量分离，为了实现参变量分离，本题需要把log a x 化成ln x ln a.不等式log a x －ln 2x ＜4可化为ln x ln a －ln 2x ＜4，即1ln a ＜4ln x＋ln x 对任意x ∈(1,100)恒成立．因为x ∈(1,100)，所以ln x ∈(0,2ln10)，4ln x ＋ln x ≥4，故1ln a ＜4，解得ln a ＜0或ln a ＞14，即0＜a ＜1或a ＞e 14. 4、(2016南京、盐城、连云港、徐州二模）（C13,14. 若存在两个正实数x ，y ，使得等式x ＋a (y －2e x )(ln y －ln x )＝0成立，其中e 为自然对数的底数，则实数a 的取值范围为________．【答案】： (－∞，0)∪（1e，＋∞）解题反思本题的解题思路清晰：二元化一元→分离参数→导数研究函数的性质→数形结合→问题得解．可以看出，考生在复习备考过程中能掌握扎实的数学基本知识和数学基本思想方法至关重要．5、(2017南通、扬州、淮安、宿迁、泰州、徐州六市二调）已知函数f (x )＝1e x ，g (x )＝ln x ，其中e 为自然对数的底数．(1) 求函数y ＝f (x )g (x )在x ＝1处的切线方程；(2) 若存在x 1，x 2(x 1≠x 2)，使得g (x 1)－g (x 2)＝λ[f (x 2)－f (x 1)]成立，其中λ为常数，求证：λ＞e ； (3) 若对任意的x ∈(0,1]，不等式f (x )g (x )≤a (x －1)恒成立，求实数a 的取值范围．思路分析 (1) 记φ(x )＝ln xex ，所求的切线方程为y －φ(1)＝φ′(1)(x －1)．(2) 记p (x )＝λf (x )＋g (x )，则存在x 1，x 2(x 1≠x 2)，使p (x 1)＝p (x 2)，即函数p (x )在定义域(0，＋∞)上不是单调函数．可先考虑其对立情况：函数p (x )在定义域(0，＋∞)上是单调函数，求得λ≤e.(3) 由第(1)题，画出曲线y ＝ln x e x (x ∈(0,1])及切线y ＝1e (x －1)，可猜想，a ≤1e. 考虑到当x ＝1时，ln xe x 与x －1均等于零，所以用分离参数的方法不太合适．因为f (x )g (x )－a (x －1)＝ln x e x －a (x －1)＝1e x [ln x －a (x －1)e x ]．可设F (x )＝ln x －a (x －1)e x ，注意到F (1)＝0.再证，当a ≤1e 时，F (x )≤F (1)对x ∈(0,1]恒成立；当a ＞1e 时，存在x 0∈(0,1)，使得F (x 0)＞F (1)．规范解答 (1) 函数y ＝ln x e x ，y ′＝⎝⎛⎭⎫1x －ln x 1e x ，当x ＝1时，y ＝0，y ′＝1e . 所求的切线方程为y ＝1e(x －1)，即x －e y －1＝0.(2分)(3) 因为f (x )g (x )－a (x －1)＝ln x e x －a (x －1)＝1ex [ln x －a (x －1)e x ]．设F (x )＝ln x －a (x －1)e x，则F (x )≤0对x ∈(0,1]恒成立．考虑F ′(x )＝1x－ax e x ＝x e x ⎝⎛⎭⎫1x 2e x －a . 当x ∈(0,1]时，1x 2ex 单调递减，取值范围为⎣⎡⎭⎫1e ，＋∞. ①当a ≤1e 时，F ′(x )≥0对x ∈(0,1]恒成立，所以F (x )在(0,1]上单调递增，F (x )max ＝F (1)＝0，满足题意；(12分)②当a ＞1e时，F ′(x )在(0,1]上有唯一零点x 0∈(0,1)．易得F (x )在(0，x 0]上单调递增，在[x 0,1]上单调递减，所以F (x 0)＞F (1)＝0，不合题意．综上所述，实数a 的取值范围是⎝⎛⎦⎤－∞，1e .(16分) 学科@网解后反思第(2)题也可考虑用反证法：假设λ≤e ，则可证p ′(x )≥0恒成立，即p (x )在(0，＋∞)上单调递增，得出矛盾．第(3)题中，对某些函数(或式子)作变形处理，可减少一些运算量．6、已知函数f (x )＝axe x 在x ＝0处的切线方程为y ＝x .(1) 求实数a 的值；(2) 若对任意的x ∈(0,2)，都有f (x )<1k ＋2x －x 2成立，求实数k 的取值范围；(3) 若函数g (x )＝ln f (x )－b 有两个零点为x 1，x 2，试判断g ′⎝⎛⎭⎫x 1＋x 22的正负，并说明理由．思路分析第(2)问，求参数k 的取值范围，常用的方法是将参数进行分离，然后将问题转化为求相应的函数的最值．分析2：注意到g ′(x)＝1－x x (x>0)，从而得到g ′(x 1＋x 22)＝2x 1＋x 2－1 (*)，再注意到x 1，x 2是函数g(x)＝ln x －x －b 的两个零点，从而有ln x 1－x 1－b ＝0，ln x 2－x 2－b ＝0，消去参数b 得ln x 2x 1＝x 2－x 1，即lnx 2x 1x 2－x 1＝1，将此式代入(*)式，从而g ′(x 1＋x 22)＝2x 1＋x 2－lnx 2x 1x 2－x 1＝1x 2－x 1·(2x 2－2x 1x 1＋x 2)－ln x 2x 1＝1x 2－x 1(2t －2t ＋1－ln t)，至此来构建以t ＝x 2x 1为元的函数加以解决．规范解答 (1) 由题意得f ′(x)＝a (1－x )e x，因为函数在x ＝0处的切线方程为y ＝x ，所以f ′(0)＝a1＝1，得a ＝1.(4分)(2) 由(1)知f(x)＝x e x <1k ＋2x －x 2对任意x ∈(0,2)都成立，所以k ＋2x －x 2>0，即k>x 2－2x 对任意x ∈(0,2)都成立，从而k ≥0.(6分)又不等式整理可得k<e x x ＋x 2－2x ，令h(x)＝e x x ＋x 2－2x ，所以h ′(x)＝e x (x －1)x 2＋2(x －1)＝(x －1)(e x x 2＋2)＝0，得x ＝1，(8分)当x ∈(1,2)时，h ′(x)>0，函数h(x)在(1,2)上单调递增，同理，函数h(x)在(0,1)上单调递减，所以k<h(x)min ＝h(1)＝e －1. 综上所述，实数k 的取值范围是[0，e －1)．(10分)解法2 可知函数g(x)＝ln x －x －b ，所以g ′(x)＝1x －1＝1－x x，因为x 1，x 2是函数g(x)的两个零点，所以⎩⎨⎧x 1＋b ＝ln x 1，x 2＋b ＝ln x 2，相减得ln x 2－ln x 1＝x 2－x 1.由定义域知x 1>0，x 2>0，不妨令x 2x 1＝t>1，则g ′(x 1＋x 22)＝2x 1＋x 2－1＝2x 1＋x 2－ln x 2－ln x 1x 2－x 1＝1x 2－x 12x 2－2x 1x 1＋x 2－(ln x 2－ln x 1)＝1x 2－x 12t －2t ＋1－ln t.(14分)令φ(t)＝2×t －1t ＋1－ln t ，因为φ′(t)＝4(t ＋1)2－1t ＝－(t －1)2t (t ＋1)2<0，所以φ(t)在(1，＋∞)上单调递减，所以φ(t)<φ(1)＝0，又因为x 2－x 1>0，所以g ′(x 1＋x 22)<0.(16分)解后反思由恒成立问题来求参数的取值范围，一般有两种思维方式：一是将参数分离出来后，转化为求一个已知函数在某个范围内的最值问题；二是将问题看作以范围已知的量为元的函数，通过分类讨论来求函数的最值来解决问题．在应用这两种思维方式时，要根据不同的问题，进行合理地选择． 7、已知函数f (x )＝g (x )·h (x )，其中函数g (x )＝e x ，h (x )＝x 2＋ax ＋a .(1) 求函数g (x )在(1，g (1))处的切线方程；(2) 当0＜a ＜2时，求函数f (x )在x ∈[－2a ，a ]上的最大值；(3) 当a ＝0时，对于给定的正整数k ，问函数F (x )＝e·f (x )－2k (ln x ＋1)是否有零点？请说明理由．(参考数据e ≈2.718，e ≈1.649，e e ≈4.482，ln2≈0.693)规范解答 (1) g ′(x )＝e x ，故g ′(1)＝e ，所以切线方程为y －e ＝e(x －1)，即y ＝e x .(3分)(2) f (x )＝e x ·(x 2＋ax ＋a ), 故f ′(x )＝(x ＋2)(x ＋a )e x ，令f ′(x )＝0，得x ＝－a 或x ＝－2. ①当－2a ≥－2，即0＜a ≤1时，f (x )在[－2a ，－a ]上单调递减，在[－a ，a ]上单调递增，所以f (x )max ＝max{f (－2a )，f (a )}．由于f (－2a )＝(2a 2＋a )e－2a，f (a )＝(2a 2＋a )e a ，故f (a )＞f (－2a )，所以f (x )max ＝f (a )．(5分)(3) 结论：当k ＝1时，函数F (x )无零点；当k ≥2时，函数F (x )有零点．(9分) 理由如下：①当k ＝1时，实际上可以证明：e x ＋1x 2－2ln x －2＞0.证法1 直接证明F (x )＝e x ＋1x 2－2ln x －2的最小值大于0，可以借助虚零点处理．F ′(x )＝(x 2＋2x )e x ＋1－2x ，显然可证F ′(x )＝(x 2＋2x )e x ＋1－2x在(0，＋∞)上单调递增．因为F ′⎝⎛⎭⎫1e ＝e 1e ＋1⎝⎛⎭⎫1e 2＋2e －2e ＝ee 1e 1e 2＋2e －2＜e ⎣⎡⎦⎤e 12⎝⎛⎭⎫1e 2＋2e －2＝e ⎝ ⎛⎭⎪⎫1＋2e e e －2＜0，F ′⎝⎛⎭⎫12＝54e e －4＞0，所以存在x 0∈⎝⎛⎭⎫1e ，12，使得F ′(x 0)＝(x 20＋2x 0)e x 0＋1－2x 0＝0，即x 20e x 0＋1＝2x 0＋2，所以当x ∈(0，x 0)时，F (x )单调递减；当x ∈(x 0，＋∞)时，F (x )单调递增，所以 F (x )min ＝F (x 0)＝x 20e x 0＋1－2ln x 0－2＝2⎝⎛⎭⎫1x 0＋2－ln x 0－1，其中x 0∈⎝⎛⎭⎫1e ，12，而φ(x )＝2⎝⎛⎭⎫1x ＋2－ln x －1单调递减，所以φ(x )＞φ⎝⎛⎭⎫12＝2⎝⎛⎭⎫ln2－35＞0，所以F (x )min ＞0，所以命题得证．(14分)证法2 转化为证明e x ＋1x ＞2(ln x ＋1)x 3，下面分别研究左右两个函数．令p (x )＝e x ＋1x，则可求得p (x )min ＝p (1)＝e 2.令q (x )＝2(ln x ＋1)x 3，则可求得q (x )max ＝q (e －23)＝23e 2，即p (x )min ＞g (x )max ，所以命题得证．(14分) 证法3 先放缩，再证明．可先证明不等式e x ≥e x (参考第1小题，过程略)，然后就有e x ＋1x 2≥e 2x 3成立，所以只要证e 2x 3＞2ln x ＋2.令h (x )＝e 2x 3－2ln x －2，则可求得h (x )min ＝h ⎝⎛⎭⎫⎝⎛⎭⎫23e 213＝23ln 32＞0，所以命题得证．(14分)解后反思 (1) 已知切点求切线，这是送分题．(2) 求函数在闭区间上的最大值，这也是常规题，只是需对极值点是否在给定的闭区间内，展开讨论．分类讨论思想几乎是每份试卷中函数大题都要涉猎的．(3) 对于问题(3)尤其值得反思：①常见的不等关系如：e x ≥e x ，e x ＞x 2(x ≥2)，虽然不能直接引用，但为证题指明了方向；②虚零点处理方法；③当k ≥2时，函数F (x )有零点，这里的12，e k 通常称为支撑点，它是如何寻找的．问题(3)虽然难，但这几点在今后的解题中值得借鉴和尝试．。

(完整版)指数函数与对数函数高考题及答案

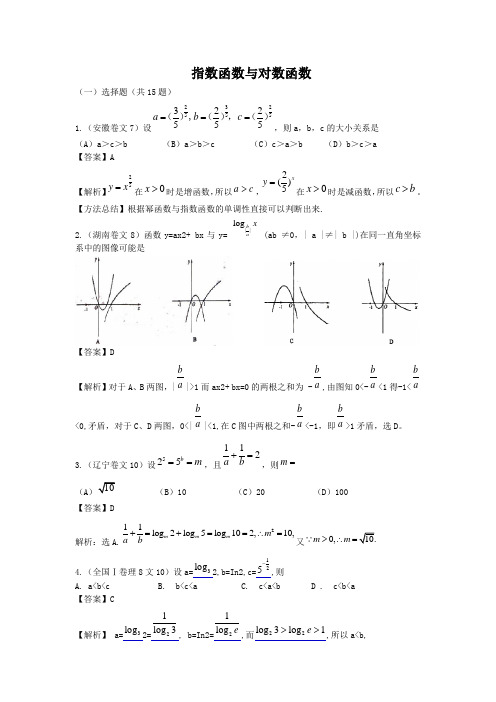
指数函数与对数函数（一）选择题（共15题）1.（安徽卷文7）设232555322555a b c ===（）,（），（），则a ，b ，c 的大小关系是（A ）a ＞c ＞b （B ）a ＞b ＞c （C ）c ＞a ＞b （D ）b ＞c ＞a【答案】A【解析】25y x =在0x >时是增函数，所以a c >，2()5xy =在0x >时是减函数，所以c b >。

【方法总结】根据幂函数与指数函数的单调性直接可以判断出来.2.（湖南卷文8）函数y=ax2+ bx 与y= ||log b ax(ab ≠0，| a |≠| b |)在同一直角坐标系中的图像可能是【答案】D【解析】对于A 、B 两图，|b a |>1而ax2+ bx=0的两根之和为 -b a ,由图知0<-b a <1得-1<ba <0,矛盾，对于C 、D 两图，0<|b a |<1,在C 图中两根之和-b a <-1，即ba >1矛盾，选D 。

3.（辽宁卷文10）设525bm ==，且112a b +=，则m =（A（B ）10 （C ）20 （D ）100 【答案】D解析：选A.211log 2log 5log 102,10,m m m m a b +=+==∴=又0,m m >∴=4.（全国Ⅰ卷理8文10）设a=3log 2,b=In2,c=125-,则A. a<b<cB. b<c<aC. c<a>,所以a<b,c=125-=,而222log 4log 3>=>,所以c<a,综上c<a<b.【命题意图】本小题以指数、对数为载体，主要考查指数函数与对数函数的性质、实数大小的比较、换底公式、不等式中的倒数法则的应用.5.（全国Ⅰ卷理10）已知函数F(x)=|lgx|,若0<a<b,且f(a)=f(b),则a+2b 的取值范围是(A))+∞(B))+∞ (C)(3,)+∞ (D)[3,)+∞【答案】A【命题意图】本小题主要考查对数函数的性质、函数的单调性、函数的值域，考生在做本小题时极易忽视a 的取值范围，而利用均值不等式求得a+2b 2a a =+>,从而错选A,这也是命题者的用苦良心之处.【解析】因为 f(a)=f(b),所以|lga|=|lgb|,所以a=b(舍去)，或1b a =，所以a+2b=2a a +又0<a<b,所以0<a<1f(1)=1+21=3,即a+2b 的取值范围是(3,+∞).6.（全国Ⅰ卷文7）已知函数()|lg |f x x =.若a b ≠且，()()f a f b =，则a b +的取值范围是(A)(1,)+∞ (B)[1,)+∞ (C) (2,)+∞ (D) [2,)+∞【答案】C【命题意图】本小题主要考查对数函数的性质、函数的单调性、函数的值域，考生在做本小题时极易忽视a 的取值范围，而利用均值不等式求得a+b=12a a +≥,从而错选D,这也是命题者的用苦良心之处. 7.（山东卷文3）函数()()2log 31x f x =+的值域为A.()0,+∞ B. )0,+∞⎡⎣ C. ()1,+∞ D. )1,+∞⎡⎣ 【答案】A【解析】因为311x+>，所以()()22log 31log 10x f x =+>=，故选A 。

专题02 指数运算与对数运算(解析版)-高考数学计算题型精练(新高考通用版)

指数与对数运算1．求值：(1))20.51π316-⎛⎫+- ⎪⎝⎭；(2)2ln 31274e log 9log 8lg 4lg 25-⋅++．【答案】(1)0(2)12【详解】（1）原式123493711041644⎛⎫=+-=+-= ⎪⎝⎭（2）原式ln923e log 3log 2lg10091212=+⋅+=++=．2．计算(1)1223182π4-⎛⎫-+ ⎪⎝⎭(2)2log 321log lg 2lg 528--+【答案】(1)5(2)1-【详解】（1）()1122222333132282π214154233--⎡⎤⎛⎫⎛⎫-++++-++=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦（2）()2log 321log lg 2lg 523lg 2lg 5318--+=--++=-3．求值：(1)(213103531732248---⎛⎫⎛⎫++-⨯ ⎪ ⎪⎝⎭⎝⎭；(2)2ln3427elog 9log 8lg4lg25-⋅++．【答案】(1)3(2)10【详解】（1）(213103531732248---⎛⎫⎛⎫++-⨯ ⎪⎪⎝⎭⎝⎭()()1132533353122224--=+-⨯+⨯123233122222=+-⨯+⨯12331882+=+-+12=+3=；（2）原式ln 923elog 3log 2lg10091210=-⋅+=-+=；综上，（1）原式=3；（2）原式=10.4．计算:(1)341lg2lg 3lg5log 2log 94-+-⨯；(2)21log 3231lglog 3log log 52100+-⨯++.【答案】(1)2(2)4【详解】（1）341lg2lg 3lg5log 2log 94-+-⨯2232log 9lg2lg23lg5log 2log 4-=-+-⨯32lg22lg23lg5log 2log 3=++-⨯3(lg2lg5)1=+-3lg101=-31=-2=.（2）21log 3231lglog 3log log 52100+-⨯+2log 322222log log 512log 322log 5log 32=--⨯++⨯112622=--++4=.5．求下列各式的值：(1)()10.52332770.02721259-⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭＋－；(2)55557log 352log log 7log 1.83-+-.【答案】(1)9100(2)2【详解】（1）原式210.5332333351053-⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫=+-⎢⎥⎢⎥⎢⎥ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦95510033=+-9100=（2）原式5555499log 35log log 7log 95=-+-5499log 35795⎛⎫=÷⨯÷ ⎪⎝⎭5log 252==6．计算：(2)()()2266661log 2log 33log 2log log 23⎛⎫++⨯ ⎪⎝⎭【答案】(1)4-(2)1【详解】（11128125lg 25lg10lg10-⨯⨯=⨯()2lg10112=⨯-4=-；（2）()()2266661log 2log 33log 2log log 23⎛⎫++⨯ ⎪⎝⎭()()226666log 2log 33log 2log =++⨯()()22666log 2log 33log 2log =++⨯()()226666log 2log 32log 2log 3=++⨯()266log 2log 3=+1=．7．计算或化简下列各式：(1)()1223164⎛⎫-+ ⎪⎝⎭(2)228393(log 3log 9)(log 4log 8log 2)(lg 2)lg 20lg5+++++⨯【答案】(1)3(2)172【详解】（1）原式221111111113332362362222255122ln e 333233422++⎛⎫⎛⎫⎛⎫=⨯-++⨯⨯=-++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭（2）原式=()22233322log 3log 32log 2log 2log 2lg 2lg 20lg 533⎛⎫⎛⎫+++++⨯ ⎪⎪⎝⎭⎝⎭()()()22235915log 3log 2lg 2lg 20lg5lg 2lg 21lg5322=⨯++⨯=+++⨯()()()215151517lg 2lg 2lg5lg5lg 2lg 2lg5lg5lg 2lg52222=+++=+++=++=8．计算下列各式的值：(1)2237828-⎛⎫--+⎪⎝⎭；(2)2log 331log 27lg2100++．【答案】(1)1π4+(2)92【详解】（1）02237828-⎛⎫--+⎪⎝⎭()23321213π2=-+-+141π34=-+-+1π4=+；（2）21log 33223311l 2og 27lg 2log 3lg10ln e 332310092-++=+++=-=++．9．计算下列各式的值：(1)213112726-⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭；(2)3332log 2log 32log 8-+.【答案】(1)5.5(2)0【详解】（1）原式230.52120.54 5.5=-+-=-+=；（2）原式3333348log 4log 32log 8log log 1032⨯=-+===.10．计算下列两个小题：(1)ln 31e2lg15lg 3++；(2)0.25608π+．【答案】(1)4(2)75【详解】（1）ln 3111e2lg15lg 3lg 2lg15lg 3lg 2154333⎛⎫++=+++=+⨯⨯= ⎪⎝⎭.（2）660.750.2650.25085221289π17=⨯+⨯+=+⨯=++.11．求下列式子的值：(1)()()12623129.684-⎛⎫+--- ⎪⎝⎭.(2)ln334lg252lg2log 16log 3e +-⋅+.【答案】(1)0(2)3【详解】（1）()()()()126203122332129.68931912412 1.05444--⎛⎫+--- ⎪⎝⎭⎛⎫⎡⎤+--- ⎪⎣⎦⎝⎭==+--=（2）ln33434lg252lg2log 16log 3e lg25lg42log log 33lg1002324233+-⋅++-⋅+=-+=-+==12．计算与化简：(1)453log 27log 8log 25⨯⨯(2)12271112333662228a a b a b ---⎛⎫⎛⎫⎛⎫⋅-÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.(3)10220.51392(0.01)54-⎛⎫⎛⎫+⨯- ⎪ ⎪⎝⎭⎝⎭(4)222lg5lg8lg5lg20(lg2)3++⋅+.【答案】(1)9(2)b -(3)5140(4)3【详解】（1）原式3lg 33lg 22lg 592lg 2lg 5lg 3=⨯⨯=；（2）原式12711122363262328a b b-+--⎛⎫⎛⎫⎛⎫- ⎪==- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭（3）原式131511421040=+⨯-=（4）原式()()22lg 52lg 2lg 5lg 52lg 2lg 2=++++()()22lg 5lg 2lg 2lg 5=+++2213=+=13．（1）21023213(2)(9.6)(3)(1.5)48---+；（2）log 535﹣2log 573+log 57﹣log 595.【答案】（1）12；（2）2【详解】解：（1）21023213(2)(9.6)(3)(1.5)48---+1﹣2327()8+2.25＝32﹣1﹣2333(2⎡⎤⎢⎥⎣⎦+2.25＝32﹣1﹣94+94＝12；（2）log 535﹣2log 573+log 57﹣log 595＝log 5[35÷（499）×7÷95]＝log 5（35×949×7×59）＝log 525＝2．14．化简求值：(1)2133325-⎛⎫+ ⎪⎝⎭；(2)7log 2log lg 25lg 47++.【答案】(1)12-(2)112【详解】（1）原式1213331182212122-=-⨯+=-+=-.（2）原式331311log 3lg100222222=++=++=.15．化简或求值：(1)0.5207120.1π93-⎛⎫+-+⎪⎝⎭；(2)7lg142lg lg 7lg183-+-；【答案】(1)101；(2)0；(3)1.【详解】（1）0.5207120.1π93-⎛⎫+-+ ⎪⎝⎭1225151100110011019333⎛⎫=+-+=+-+= ⎪⎝⎭；（2）7lg142lg lg 7lg183-+-27lg14lg lg 7lg183⎛⎫=-+- ⎪⎝⎭9lg 1471849⎛⎫=⨯⨯÷ ⎪⎝⎭lg1=0=；（3211-=.16．计算：(1))()1211610.259-⎛⎫-- ⎪⎝⎭(2)25lg 42lg 5log 5log 8lg10++⨯+．【答案】(1)23-(2)6【详解】（1）原式4214333=--+=-（2）原式2lg 5lg8lg 4lg 51lg 2lg 5=++⨯+3222log 813log 26=++=+=17．计算下列各式的值：(1)()6221103321642e 453π-⎛⎫⎛⎫+--+⨯ ⎪ ⎪⎝⎭⎝⎭；(2)ln 2352log 27lg2lg5log 16log e ---⋅．【答案】(1)2023(2)2【详解】（1）()6221103321642e π453-⎛⎫⎛⎫+--+⨯ ⎪⎪⎝⎭⎝⎭611223243245⎛⎫=+-+⨯ ⎪⎝⎭232345=+⨯2023=．（2）()ln 235log 27lg2lg5log 16log e-+-⋅ln25=31log 16log e --⋅()ln 2521=24log 2log 5e =2222-⋅+-+=2．18．计算下列各题：(1)()20.5312816410.751627---⎛⎫⎛⎫+-÷+ ⎪ ⎪⎝⎭⎝⎭；(2)()70log 23log lg 25lg 479.8+++-.【答案】(1)94(2)132【详解】（1）原式20.523814279999116364416164⎛⎫⎛⎫⎛⎫=-÷+=-+= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭.（2）原式323100313log 3lg lg 4212lg 4lg 43422=++++=+-++=.19．化简求值(1)1131227(0.002)2)8--⎛⎫+- ⎪⎝⎭；(2)()266661log 3log 2log 18log 4⎡⎤-+⨯÷⎣⎦．【答案】(1)372-(2)1【详解】（1）原式)113131232271350010285002-⨯⎛⎫⎛⎫⎛⎫=+=+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭3372022=+-=-.（2）原式()()266666612log 3log 3log log 63log 43⎡⎤=-++⋅⨯÷⎢⎥⎣⎦()()()26666612log 3log 31log 31log 3log 4⎡⎤=-++-+÷⎣⎦()()22666612log 3log 31log 3log 4⎡⎤=-++-÷⎣⎦()666666621log 3log 6log 3log 212log 2log 2log 2--====.20．（1）计算：1222301322(2.5)3483-⎛⎫⎛⎫⎛⎫---+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭；（2）已知7log 23log 27lg252lg27x a =++-，求33x xx xa a a a--++的值．【答案】（1）12；（2）739．【详解】（1）原式123232223333391991122222444212⎛⎫⎛⎫⎛⎫⎛⎫+=--+=-+=⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎡⎤⎡⎤=--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎭⎦⎝⎭．（2）()33log 32lg52lg2232lg5lg223223x a =++-=++-=+-=，所以()()()()3322331xx xx x xx xx x x xx xa a aa a a a a a a a a a a -------++⋅-++==+++()()()22222222117311131.39xxxxxx aaaa aa --⎛⎫⎛⎫=+-=+-=+-=+-= ⎪ ⎪⎝⎭⎝⎭21．求值：(1))1213250.02719-⎛⎫+-⎪⎝⎭；(2)2350.2log 27log 82log 10log 4⨯--．【答案】(1)4(2)7【详解】（1）)()12131121233255351020.02710.31149310333---⎡⎤⎛⎫⎛⎫⎛⎫⎡⎤+-=+-=+-=+=⎢⎥ ⎪ ⎪ ⎪⎣⎦⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦.（2）()13322350.25555ln 3ln 23ln 33ln 2log 27log 82log 10log 42log 25log 22log 212log 292ln 2ln 3ln 2ln 3-⨯--=⨯-⨯-=⨯-++=-=.22．求值：()1220348π49-⎛⎫+-+ ⎪⎝⎭;(2)3323log 54log 2log 3log 4-+⋅.【答案】(1)172；(2)5.【详解】（11215321022532233317(2)(2)1[(]22122248(π4)()9-=++++-+=++=+.（2）322332332322log 454log 54log 2log 3log 4log log 3log 3log 23252log 3-+⋅=+⋅=+=+=.23．计算下列式子(1)()7l 0o 2g lg25+lg4l 79og .8+++-2334lo g log ⨯【答案】(1)132(2)8-【详解】（1）()7l 0o 2g lg25+lg4l 79og .8+++-3233133lg1002122122log =+++=+++=.（22334lo g log ⨯()222log lo 4lg100036281312g log =-⨯=--=-⨯-.24．计算：()031438162-⎛⎫---+ ⎪ ⎪⎝⎭；(2)223lg 2lg 5log log 64++-．【答案】(1)118(2)-2【详解】（1）原式()13314334311111122124488⨯⎛⎫⨯- ⎪⨯⎝⎭⎛⎫=---+=-++= ⎪⎝⎭（2）原式()22lg 25log 32log 312=⨯+---=-25．计算：223327-⋅+；(2)()()()221004lg 2log 2lg 5lg 23++-．【答案】(1)27-(2)1【详解】（1）依题意，223327⋅+()22233433=--⋅+(2224332=--⋅+(224272=--+231227=-+=-（2）()()()221004lg 2log 2lg 5lg 23++-()()4lg 2lg 2lg 5lg 2lg 5lg 23lg100⎛⎫=+++- ⎪⎝⎭4lg 2lg 2lg 5lg 232⎛⎫=++- ⎪⎝⎭43lg 25lg 322=⋅+52lg 2lg2=+25lg 2lg 2=+5lg 412⎛⎫=⋅= ⎪⎝⎭26．求值：(1)01310.0277-⎛⎫+- ⎪⎝⎭；(2)ln 21lg20lg4lg e 5-++.【答案】(1)73；(2)2.【详解】（1）()()111341334170.0270.3120.31273---⎛⎫+-+-=+-=⎪⎝⎭；（2）ln 21201lg20lg4lg e lg 2lg122545⎛⎫-++=⨯+=+= ⎪⎝⎭.27．求值：(1)))2202220223272264-⎛⎫-+-+ ⎪⎝⎭；(2)()9log 1620427log 9log 643lg 2lg 5lg 12022lg 5⨯++⨯+++．【答案】(1)3(2)7【详解】（1）原式()20222162113999++-=++=.（2）原式()3log 4223log 3log 43lg 2lg 5lg 2lg 524lg 2lg 5lg 2lg 5=⨯++⨯++=++++6lg 2lg5617=++=+=.28．计算(1))2log 3lg12lg1001-+-(2))0.523124-⎛⎫+⎪⎝⎭【答案】(1)2；(2)1π3-.【详解】（1）)2log 3lg12lg1001-+-)32lg101=-+-321=-+2=；（2）)0.523124-⎛⎫+ ⎪⎝⎭20.5233233π22-⎡⎤⎛⎫⎛⎫=+-+⎢⎥ ⎪⎪⎝⎭⎢⎥⎝⎭⎣⎦13π322-⎛⎫=+-+ ⎪⎝⎭1π3=-.29．计算下列各式的值：(1)11421481⎛⎫+ ⎪⎝⎭；(2)33252log 2log 12l 8og 5log -+⨯.【答案】(1)143(2)2【详解】（1）114211423314813⎛⎫ ⎪⎝⎭=+-=．（2）33252log 2log 12l 8og 5log -+⨯321log log 32381==-+=+．30．求下列各式的值：(1)134440.06425--⎛⎫---⋅⎪⎝⎭(2)2log 3232lg25lg8log 27log 223+-⨯+．【答案】(1)1516(2)2【详解】（1）原式1159151910.41621616=--⨯=--=．（2）原式()232lg52lg23log 3log 232lg5lg2332=+-⨯+=+-+=．31．求解下列问题：(1)2433641)27--⎛⎫++ ⎪⎝⎭；(2)2log 3491lg2log 27log 8100--⋅．【答案】(1)2916(2)74-【详解】（1）2433641)27--⎛⎫++ ⎪⎝⎭24333324123--⎡⎤⎛⎫⎛⎫=++⎢⎥ ⎪ ⎪⎝⎭⎢⎥⎝⎭⎣⎦224123--⎛⎫=++ ⎪⎝⎭9129116416=++=.（2）2log 3491lg2log 27log 8100--⋅221233223lg10ln e 3log 3log 2-=-+-⋅2313323log 3log 2222=--+-⋅192324=--+-74=-.32．计算下列各式的值：(1)2log 23log lg 5lg 22++．(2)cos 20sin 50cos50cos70︒︒-︒︒．【答案】(1)72(2)12【详解】（1）2log 2317log lg 5lg 22lg10222++=++=；（2）cos 20sin 50cos50cos70cos 20sin 50cos50sin 20︒︒-︒︒=︒︒-︒︒()1sin 50202=︒-︒=.33．计算下列各式，写出演算过程(1)1222318324272-⎛⎫⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭；(2)5525lg 42lg 52log 10log 20log 5log 8++---⋅.【答案】(1)72(2)12-【详解】（1）解：原式23324344722392992⎡⎤⎛⎫=-+=+-+=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦.（2）解：原式()225101ln 53ln 211lg 45log 213202ln 2ln 522=⨯+--⋅=+--=-.34．化简求值：(1)213240330.250.53π)0.0648---⎛⎫⨯--+ ⎪⎝⎭(2)2log 314319lg 25lg 2log 9log 822-++-⨯++．【答案】(1)7318；(2)4.【详解】（1）213240330.250.53π)0.0648---⎛⎫⨯---++ ⎪⎝⎭212433331132124225---⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=⨯--++⎢⎥⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦45731129218=--++=；（2）2log 314319lg 25lg 2log 9log 822-++-⨯++2221221log 322233312log 3lg 5lg 2log 3log 2ln e 22=++-⨯++323314log 3lg 5lg 2log 33log 222=++-⨯++()32314lg 52log 33log 222=+⨯-⨯++41324=+-+=.35．求值：(1)()11202929.3log 443-⎛⎫⎛⎫---+ ⎪ ⎪⎝⎭⎝⎭(2)5log 2lg2lg5lg15+++【答案】(1)1(2)3【详解】（1）()111222029233339.3log 412121432222-⎡⎤⎛⎫⎛⎫⎛⎫---+=--+=--+=⎢⎥ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦.（2）5log 2lg 2lg 5lg15lg1002123+++=++=+=.36．化简求值：1020.5+(2)0.21log 53212lg5log 25lg 4-⎛⎫-++ ⎪⎝⎭.【答案】(1)3(2)2【详解】（1）原式3322=++=（2）原式155log 522lg5log 22lg 25=-++()15log 52112lg 5lg 2log 255-⎛⎫=+-+ ⎪⎝⎭151log 511552⎛⎫-+ ⎪⎝⎭=11255=-+2=37．计算下列各式的值：(1)1013352943-⎛⎫⎛⎫⨯-+ ⎪ ⎪⎝⎭⎝⎭(2)1433log lg 253log 3lg 43+-+【答案】(1)3(2)1【详解】（1）解：113352943-⎛⎫⎛⎫⨯-+ ⎪ ⎪⎝⎭⎝⎭112133334413355⎛⎫⎛⎫=⨯+⨯- ⎪ ⎪⎝⎭⎝⎭11213333443355+⎛⎫⎛⎫=-+= ⎪ ⎪⎝⎭⎝⎭；（2）1433log lg 253log 3lg 4+-+343331log 3log 32lg53log 32lg 24=-+-⨯+3312(lg5lg 2)44=-++-12lg101=-+=.38．化简求值：(1)312log 14lg 2lg529-⎛⎫++- ⎪⎝⎭；(2)71113sin cos tan 634πππ++.【答案】(1)32(2)1【详解】（1）原式()1220233lg 25211322-⎡⎤⎛⎫=+⨯-=+-=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦（2）原式πππsin πcos 4πtan2ππ634⎛⎫⎛⎫⎛⎫=++-+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭πππsincos tan π634⎛⎫=-+++ ⎪⎝⎭11πtan 1224=-++=39．化简或求值(1)11034781(0.064)()()|0.1|816---++-(2)7lg142lg lg 7lg183-+-【答案】(1)3110(2)0(3)5π-【详解】（1）11034781(0.064)()()|0.1|816---++-1310.10.42=-++53112210=-++1310=+31.10=（2）27lg142lg lg 7lg1837lg14lg lg 7lg1839lg 1471849lg10.-+-⎛⎫=-+- ⎪⎝⎭⎛⎫=⨯⨯÷ ⎪⎝⎭==（3）325.πππ+=-+-=--=-40．计算求值(1)2ln 38916log 27log 6log 6e ⨯÷+；(2)419log 8log 34--【答案】(1)11(2)2-【详解】（1）2ln 38916log 27log 6log 6e⨯÷+ln92361log 3log 64log 2e 2=⨯⨯+62236log 22log 392log 3log 2911log 3=⨯+=⨯+=；（2）419log 8log 34--2331log 2log 322=---314222=+-=-.41．计算：(1)()110520.01321π---+；(2)3log 22log 8lg 2lg53++-．【答案】(1)5(2)2【详解】（1）()110520.01321102125π---+=---=；（2）()3log 22log 8lg 2lg 53lg 25223=+++-⨯-=．42．计算：(1)1123182427-⎛⎫-+ ⎛⎫ ⎪⎝⎪⎭⎝⎭(2)2lg 2lg 2lg5(lg5)+⋅+.【答案】(1)94(2)1【详解】（1）解：1123182427-⎛⎫-+ ⎛⎫ ⎪⎝⎪⎭⎝⎭1132233223-⎡⎤⎛⎫-⎢⎥ =⎪⎝⎭⎢⎥⎡⎤⎛⎫⎢⎥ ⎪⎝⎭⎢⎥⎣⎦⎣⎦1123223323232⎛⎫⨯⨯- ⎪⎝⎭⎛⎫⎛⎫-+ ⎪ ⎪⎛⎫= ⎪⎝⎝⎭⎭⎝⎭33992244-+==.（2）解：2lg 2lg 2lg5(lg5)+⋅+()lg 2lg5lg 2lg5=++()lg 2lg 5lg 25=+⋅⨯()lg 2lg 5lg 251=+=⨯=.43．化简求值：)2138227--⎛⎫++⎪⎝⎭；(2)3log 211lg 9lg 240292361lg 27lg 35+-+-+.【答案】π(2)3【详解】（1）原式2335259π32π3π4344⎛⎫⨯- ⎪⎝⎭⎛⎫=-+-=-+++-= ⎪⎝⎭．（2）原式32log 21lglg10lg 3lg 24083414336lg8lg10lg 9lg 5+-=+=+=-+=-+.44．求值：(1)230323(8)π)-+-；(2)()22824log 27(lg 5)(lg 2)lg 5lg log 16log 9+-+⨯．【答案】(1)2(2)0【详解】（1）2331032223(π)3313212-=-+⨯=-+=（2）()22824log 27(lg 5)(lg 2)lg 5lg log 16log 9+-+⨯32322222log 3(lg 5)(lg 2)2lg 5lg 2log 3=+-+⨯2(lg 5lg 2)1110=+-=-=45．计算：(1)ln 2lg252lg2e ++(2)()20.5133890.1252749--⎛⎫⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭【答案】(1)4(2)19【详解】（1）原式lg25lg42lg1002224=++=+=+=.（2）原式2132(0.5)3()332313724712939⨯⨯-⨯-⎛⎫⎛⎫⎛⎫=-+=-+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.46．（1）求值：3204161)++；（2）求值：5log 2lg25lg45log +++．【答案】（1）12；（2）112．【详解】（1）原式()343432132112=++=++=（2）原式()323lg 2542log 3=⨯++3lg10022=++112=47．求值：(1)()1430513π38-⎛⎫-- ⎪⎝⎭；(2)()2273log 8log 7log log 81+⨯．【答案】(1)4(2)5【详解】（1）()143015545143π32312381-+⎛⎫-- =+=⎝+⎭-⎪-=；（2）()2273274log 8log 7log log 813log 7log +⨯=+⨯273log 72l 5og 22==++=⨯.48．（1）)1334ln 22811e 162022⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭（2）()314163log 4log 2log log 3⎛⎫+ ⎪⎝⎭【答案】（1）5；（2）12．【详解】（1）原式31442433333214152222⨯⎛⎫⎛⎫=++-=++-= ⎪ ⎪⎝⎭⎝⎭．（2）原式()(3344341log 4log 2log log log 2log 32=-=⨯=．49．计算：(1)212232327(1)(()[(3)]28--+⋅+-；(2)232lg5lg 4log 3log 4log +-⋅+【答案】(1)5(2)32【详解】（1）22122233323272349(1)()()[(3)]1()[()]3135283294--+⋅+-=+⋅+=+⨯+=（2）232lg5lg 4log 3log 4log +-⋅+lg 32lg 23332lg 52lg 22(lg 5lg 2)2lg 2lg 3222=+-⨯+=+-+=50．计算下列各式的值：(1)2ln 21elglg 202--；(2)232lg 25lg8log 27log 23+-⨯.【答案】(1)3.(2)1-.【详解】（1）22ln 2ln 2111e lg lg 20e (lg lg 20)4lg(20)4lg10413222--=-+=-⨯=-=-=.（2）2232323232lg 25lg8log 27log 2lg(258)log 27log 2lg103log 3log 22313+-⨯=⨯-⨯=-⨯=-=-.51．化简下列各式：(1)75sincos cos(5)tan 224ππππ++-+；(2)24log 32log 0.252lg 42lg 5⋅++++⋅【答案】(1)-1(2)1592【详解】（1）原式3sincos cos 11011122πππ=+++=-+-+=-.（2）原式421log 322242221log ln e 2lg 4lg55123)log (lg 24lg 4-=++++=++++1159281lg100222=-+++-=.52．计算下列各式的值：(1)()2223327389.682--⎛⎫⎛⎫---+ ⎪ ⎪⎝⎭⎝⎭；(2)07log 2(9.8)log lg25lg47+-++.【答案】(1)3；(2)132【详解】（1）原式2323334122⎛⎫⨯-- ⎪⎝⎭⎛⎫⎛⎫=--+ ⎪ ⎪⎝⎭⎝⎭3=（2）原式()323log 3lg 25421=+⨯++3232=++132=53．计算求值：(1))()140231101108200-⎛⎫-++- ⎪⎝⎭；(2)(42log 923lg 2lg 250082log 9log 4⨯+⨯++⋅．【答案】(1)36(2)9【详解】（1）原式()()43431010220236⎡⎤=++-=+-=⎣⎦；（2）原式()2log 3212lg 32lg 2lg 22lg 528lg 524lg 2lg 3⎛⎫=++⨯++⋅ ⎪⎝⎭()22lg 2lg 52lg 22lg 5342lg 5lg 2lg 52lg 27=++++=+++()2lg 5lg 27279=++=+=.54．计算下列各式的值：(1)(332212234-⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭(2)5log 3333322log 4log log 2527-++【答案】(1)1(2)6【详解】（1）(33332221392213424-⎛⎫⎛⎫⎛⎫⎛⎫+-=+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭33233233331112222⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+-=+-=⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦（2）5log 3333322log 4log log 2527-++23332log 423log 27333627⎛⎫=÷⨯+=+=+= ⎪⎝⎭55．求下列各式的值：(1)1220.2531222854--⎛⎫⎛⎫+⨯ ⎪ ⎪⎝⎭⎝⎭；(2)158311lglog 9log 125log 10032+--.【答案】(1)56-(2)163-【详解】（1）()112112220.25344311315222812212544266---⎡⎤⎛⎫⎛⎫⎛⎫+⨯-=+⨯-⨯=+-=-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦.（2）3235158352311516lglog 9log 125log lg10log 9log 5log 22231003233--+--=---=---+=-.56．化简求值：())13320,0a b a b ->>；(2)7log 52225lg5lg 2lg 2lg5log 5log 47+++⨯+.【答案】(1)1(2)7【详解】（1）因为0,0a b >>()31332221b a ab --⎡⎤==⎢⎥⎣⎦，()31333222a a b b --=，所以原式332233221a b a b--==；（2）7log 52225lg5lg 2lg 2lg5log 5log 47+++⨯+()25lg 5lg 2lg 2lg 5log 5log 25=+++⨯+()25lg 5lg 2lg 2lg 5log 5log 25=+++⨯+lg 5lg 2157=+++=.57．计算：(1)21304816π27-⎛⎫-+ ⎪⎝⎭；(2)3ln 22552lg 4lg log 5log 4e 8++⋅+.【答案】(1)154-(2)11【详解】（1）解：原式()231344291521524344-⎡⎤⎛⎫=-+-=--=-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦.（2）解：原式()32ln 25ln 52ln 2lg 4e 128118ln 2ln 5⎛⎫=⨯+⋅+=++= ⎪⎝⎭.58．计算：(1)5log 3311845log 11log 27log 2log 8-⋅++；(2)若33m m --=99m m -+的值.【答案】(1)116(2)9914m m -+=.【详解】（1）原式31122133log 113log 3log 2log 232=-⨯++131133326=-++=.（2）将等式33m m --=99212m m -+-=，则9914m m -+=.。

五年(2016-2020年)高考数学(理)真题知识分布与解析：对数与对数函数(原卷版+解析版)

第二章函数概念与基本初等函数对数与对数函数考点1 对数函数的图象与性质1. 【2020年高考全国Ⅲ卷理数12】已知544558,138<<．设5813log 3,log 5,log 8a b c ===，则（）A ．a b c <<B ．b a c <<C ．b c a <<D ．c a b << 2. 【2020年高考北京卷11】函数1()=ln 1f x x x ++的定义域是__________．考点2 与对数函数相关的综合问题1. 【2020年高考全国Ⅲ卷文理数4】Logistic 模型是常用数学模型之一，可应用于流行病学领域．有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数()I t （t 的单位：天）的Logisic 模型：()()0.23531et K I t --=+，其中K 为最大确诊病例数．当()0.95I tK *=时，标志着已初步遏制疫情，则t*约为（ln193≈）（）A ．60B ．63C ．66D ．69 2. 【2019年高考天津理数】已知5log 2a =，0.5og 2.l 0b =，0.20.5c =，则,,a b c 的大小关系为 A ．a c b <> B ．b a c >> C ．c b a >>D ．c a b >>4. 【2018年高考全国Ⅲ卷理数】设0.2log 0.3a =，2log 0.3b =，则 A ．0a b ab +<< B ．0ab a b <+< C ．0a b ab +<<D ．0ab a b <<+5. 【2017年高考北京理数】根据有关资料，围棋状态空间复杂度的上限M 约为3361，而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与M N最接近的是（参考数据：lg3≈0.48）A ．1033B ．1053C ．1073D ．10936. 【2017年高考全国Ⅰ卷理数】设x 、y 、z 为正数，且235x y z ==，则 A ．2x <3y <5z B ．5z <2x <3y C ．3y <5z <2x D ．3y <2x <5z。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

五年高考真题分类汇编
指数对数
1.（19全国1文、理）已知0.2
0.3
2
log 0.220.2a b c ===，，，则（）
A ．a b c <<
B ．a c b <<
C ．c a b <<
D ．b c a <<
2.（19全国2理）已知()f x 是奇函数，且当0x <时，
()e ax f x =-.若(ln 2)8f =，
则a =___–3____.
3.（19全国2文）设f (x )为奇函数，且当x ≥0时，f(x)=e 1x -，则当x<0时，f(x)=（）
A ．e 1x --
B ．e 1x -+
C ．e 1x ---
D ．e 1x --+
4.（19全国3文理）设()f x 是定义域为R 的偶函数，且在()0,∞单调递减，则（）
A ．f （log 314
）＞f （
3
2
2
-
）＞f （
23
2-
）
B ．f （log 314
）＞f （232-）＞f （322-） C ．f （322-）＞f （232-）＞f （log 314）
D ．f （232-）＞f （322-）＞f （log 314
） 5.（18全国1文）设函数()20
1 0x x f x x -⎧=⎨>⎩
，≤，，则满足()()12f x f x +<的x 的取值范围是（）
A ．(]1-∞-，
B ．()0+∞，
C ．()10-，
D ．()0-∞，
6.（18全国1理）已知函数．若g （x ）存在2个零点，则a 的取值范围是（）
A ．[–1，0）
B ．[0，+∞）
C ．[–1，+∞）
D ．[1，+∞）
7.（18全国3文）下列函数中，其图像与函数的图像关于直线对称的是（） A ． B ． C ．
D ．
e 0()ln 0x x
f x x x ⎧≤=⎨
>⎩，，
，，
()()g x f x x a =++ln y x =1x =ln(1)y x =-ln(2)y x =-ln(1)y x =+ln(2)y x =+
8.（18全国2文理）函数的图像大致为（ B ）
9.（18全国3理）设，，则（）
A ．
B ．
C ．
D ．
10.（18全国1文）已知函数()()
2
2log f x x a =+，若()31f =，则a =_____．
11.（18全国3文）已知函数，，则___2-_____．
12.（17全国1文）已知函数()ln ln(2)f x x x =+-，则（）
A ．()f x 在（0，2）单调递增
B ．()f x 在（0，2）单调递减
C ．y=()f x 的图像关于直线x=1对称
D ．y=()f x 的图像关于点（1，0）对称
13.（17全国1理）函数()f x 在(,)-∞+∞单调递减，且为奇函数．若(11)f =-，则满足
21()1x f --≤≤的x 的取值范围是（）
A ．[2,2]-
B ．[1,1]-
C ．[0,4]
D ．[1,3] 14.（17全国1理）设x 、y 、z 为正数，且235x y z ==，则（）
A ．2x<3y<5z
B ．5z<2x<3y
C ．3y<5z<2x
D ．3y<2x<5z
15.（17全国2文）函数2
()ln(28)f x x x =--的单调递增区间是( ) A ．(,2)-∞- B ． (,1)-∞ C ． (1,)+∞ D ． (4,)+∞ 16.（16全国1文）若0a b >>,01c <<,则（） A. log a c<log b c B. l og c a<log c b C. a c
c b
17.（16全国1理）若101a b c >><<，,则 ( )
A. c c a b <
B. c c ab ba <
C. log log b a a c b c <
D. log log a b c c < 18.（16全国2文）下列函数中，其定义域和值域分别与函数y=10lgx
的定义域和值域相同的是（）
A. y=x
B. y=lgx
C. y=2
x
D. y =
19.（16全国3文理）已知421
3
3
3
2,3,25a b c ===，则（） A. b a c << B. a b c <<
C. b c a <<
D. c a b <<
20.(15全国1文)已知函数，且，则（）
A.
B. C. D. ()2
e e x x
f x x --=0.2lo
g 0.3a =2log 0.3b =0a b ab +<<0ab a b <+<0a b ab +<<0ab a b <<+7-())1f x x =+()4f a =()f a -=1222,1
()log (1),1
x x f x x x -⎧-≤=⎨-+>⎩()3f a =-(6)f a -=
74-
54-34-14
-
21.(15全国1文)设函数的图像与的图像关于直线对称，且
，则( )
A. B. C. D.
22.(15全国2理)设函数211log (2),1,
()2,1,
x x x f x x -+-<⎧=⎨≥⎩,2(2)(log 12)f f -+=( )
A ．3
B ．6
C ．9
D ．12
()y f x =2x a
y +=y x =-(2)(4)1f f -+-=a =1-124。