组合变形与强度理论
工程力学弯扭组合
Fy
Fz
A 1 B 100 300
Fy F'y
d
C
F'y Fz
1
D 300 2
2 F'z
F'z
D1 D2
上海应用技术学院
Fy Fz
A 1 B 100 300
Fy F'y
d
C
F'y
Fz
1 2
11
2 F'z
300
D
F'z
Fy M1 Fz
A
y M2
B
F'y
C
D1 D2
D
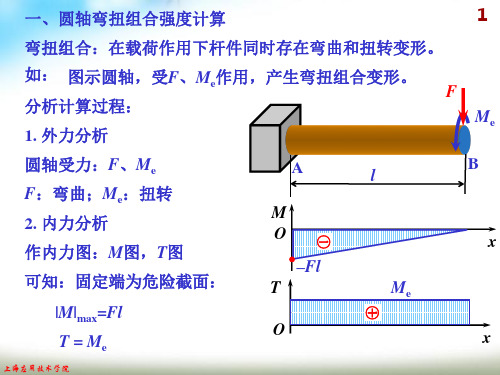
z 解:1. 外力分析
x
32 M 0.75 T 2 πd 3
2
O
x
32 1.0642 106 0.75 1 106 99.4MPa [σ ] 3 π 0.052
∴ 轴满足强度要求。
上海应用技术学院
例4 已知一单级直齿圆柱齿轮减速器输出轴,齿轮轮齿受力:14 Ft= 4053 N,Fr=1475.2 N,输出转矩T= 664669 N· mm,支 承间跨距 l=180mm,齿轮对称布置,轴的材料为 45钢,许 用应力[s ]=100 MPa。 试按第三强度理论确定该轴危险截面处的直径 d。
上海应用技术学院
㊀
x Me
–Fl
O
x
3. 应力分析 由危险截面上的s、t 分布可知: a、b点为危险点: 取单元体: a b A M O T
㊉
F
2 MesMa来自lBsM
M σM W T T sM τT Wp 2W
tT tT
b
工程力学第十一章 组合变形

土建工程中的混凝土或砖、石偏心受压柱,往往不 允许横截面上出现拉应力。这就是要求偏心压力只能作 用在横截面形心附近的截面核心内。
要使偏心压力作用下杆件横截面上不出现拉应力, 那么中性轴就不能与横截面相交,一般情况下充其量只能 与横截面的周边相切,而在截面的凹入部分则是与周边外 接。截面核心的边界正是利用中性轴与周边相切和外接时 偏心压力作用点的位置来确定的。
解:拉扭组合:
7kNm T
50kN FN
安全
例11-8 直径为d的实心圆轴,
·B
P 若m=Pd,指出危险点的位置, 并写出相当应力 。
x
m
解:偏拉与扭转组合
z
C P P 例11-9 图示折角CAB,ABC段直径
d=60mm,L=90mm,P=6kN,[σ]=
BA
60MPa,试用第三强度理论校核轴 x AB的强度。
例11-6 图示圆轴.已知,F=8kN,Me=3kNm,[σ]=100MPa, 试用第三强度理论求轴的最小直径.
解:(1) 内力分析
4kNm M
3kNm T
(2)应力分析
例11-7 直径为d=0.1m的圆杆受力如图,T=7kNm,P=50kN, []=100MPa,试按第三强度理论校核此杆的强度。
至于发生弯曲与压缩组合变形的杆件,轴向压力 引起的附加弯矩与横向力产生的弯矩为同向,故只有 杆的弯曲刚度相当大(大刚度杆)且在线弹性范围内 工作时才可应用叠加原理。
A M
F FN
+ ql2/8
+
B
+
=
C 10kN
A 1.6m
1.6m
10kN
1.2m
例11-3 两根无缝钢管焊接 而成的折杆。钢管外径 D=140mm,壁厚t=10mm。求 危险截面上的最大拉应力和 B 最大压应力。
压缩与弯曲的组合变形

FN Pe l A WZ
代入已知数据得
150102 600104 35 2 3 πd 4 πd 32
第11章 组合变形
解上式即可求得立柱的直径d。因为这是一个三次方程,
求解较繁。因为一般在偏心距较大的情况下,偏心拉伸(或 压缩)杆件的弯曲正应力是主要的,所以可先按弯曲强度条 件求出立柱的一个近似直径,然后将此直径的数值稍稍增大, 再代入偏心拉伸的强度条件中进行校核,如数值相差较大,
第11章 组合变形
第11章 组合变形
11.1 概述 11.2 拉伸(压缩)与弯曲的组合变形 11.3 应力状态 11.4 强度理论
11.5 弯曲与扭转的组合变形
思考题 习 题
第11章 组合变形
11.1 概 述
在实际工程中,杆件在受力后,往往同时产生两种或两种以 上基本变形的组合,这种杆件的变形称为组合变形。例如,
再作适当变更,以试凑的方法进行设计计算,最后即可求得
满足此方程的直径。
第11章 组合变形 先考虑弯曲强度条件 10 35 3 d 32
4
得直径,将其稍稍加大,现取,心拉伸的强度条件进行校核,得
150102 600104 l max 32.4MPa 35MPa 2 3 3.14125 4 3.14125 32
l max
FN M max l A WZ
FN M max y max y A WZ
第11章 组合变形
例11-1
如图11-5(a)所示钻床受压力P=15kN作用,已知偏
心距 e=0.4m ,铸铁立柱的许用拉应力[ σl ] =35MPa ,许用压 应力[σy]=120 MPa。试求铸铁立柱所需的直径。 解(1) 分析立柱变形。 将P力平移到立柱轴线上,同时附加一个力偶Mf=Pe。在P 和Mf的共同作用下, 立柱发生弯曲和拉伸的组合变形。
工程力学之组 合 变 形

工程力学第10章组合变形学习目标(1)了解组合变形的概念及其强度问题的分析方法;(2)掌握斜弯曲、拉伸(压缩)与弯曲和偏心压缩的应力及强度计算。
10.1 组合变形的概念例如,烟囱的变形,除自重W引起的轴向压缩外,还有水平风力引起的弯曲变形,同时产生两种基本变形,如图10-1(a)所示。
又如图10-1(b)所示,设有吊车的厂房柱子,作用在柱子牛腿上的荷载F,它们合力的作用线偏离柱子轴线,平移到轴线后同时附加力偶。
此时,柱子既产生压缩变形又产生弯曲变形。
再如图10-1(c)所示的曲拐轴,在力F作用下,AB 段同时产生弯曲变形和扭转变形。
10.1 组合变形的概念图10-110.1 组合变形的概念上述这些构件的变形,都是两种或两种以上的基本变形的组合,称为组合变形。
研究组合变形问题依据的是叠加原理,进行强度计算的步骤如下:(1)将所作用的荷载分解或简化为几个只引起一种基本变形的荷载分量。
(2)分别计算各个荷载分量所引起的应力。
(3)根据叠加原理,将所求得的应力相应叠加,即得到原来荷载共同作用下构件所产生的应力。
(4)判断危险点的位置,建立强度条件。
10.2例如图10-2(a)所示的横截面为矩形的悬臂梁,外力F作用在梁的对称平面内,此类弯曲称为平面弯曲。
斜弯曲与平面弯曲不同,如图10-2(b)所示同样的矩形截面梁,外力F的作用线通过横截面的形心而不与截面的对称轴重合,此梁弯曲后的挠曲线不再位于梁的纵向对称面内,这类弯曲称为斜弯曲。
斜弯曲是两个平面弯曲的组合,本节将讨论斜弯曲时的正应力及其强度计算。
10.2图10-210.210.2.1 正应力计算斜弯曲时,梁的横截面上同时存在正应力和切应力,但因切应力值很小,一般不予考虑。
下面结合图10-3(a)所示的矩形截面梁说明斜弯曲时正应力的计算方法。
图10-310.2.1 正应力计算10.2.1.1 外力的分解由图10-3(a)可知:10.2.1.2 内力的计算如图10-3(b)所示,距右端为a 的横截面上由F y 、F z 引起的弯曲矩分别是:10.2 10.2.1 正应力计算10.2.1.3 应力的计算由M z 和M y (即F y 和F z )在该截面引起K 点的正应力分别为:F y 和F z 共同作用下K 点的正应力为:10.210-110.210.2.1 正应力计算10.2.1.3 应力的计算通过以上分析过程,我们可以将组合变形问题计算的思路归纳为“先分后合”,具体如下:10.210.2.2 正应力强度条件同平面弯曲一样,斜弯曲梁的正应力强度条件仍为:10-2即危险截面上危险点的最大正应力不能超过材料的许用应力[σ]。
材料力学第9章 强度理论
由于物体在外力作用下所发生的弹性变形既包括 物体的体积改变,也包括物体的形状改变,所以可推 断,弹性体内所积蓄的变形比能也应该分成两部分: 一部分是形状改变比能(畸变能) ,一部分是体积改 变比能 。 在复杂应力状态下,物体形状的改变及所积蓄的 形状改变比能是和三个主应力的差值有关;而物体体 积的改变及所积蓄的体积改变比能是和三个主应力的 代数和有关。
注意:图示应力状态实际上为弯扭组合加载对 应的应力状态,其相当应力如下:
r 3 2 4 2 [ ] 2 2 [ ] r 4 3
可记住,便于组合变形的强度校核。
例1 对于图示各单元体,试分别按第三强度理论及第四强度理论 求相当应力。
120 MPa 140 MPa
r4
1 2 2 2 [(0 120) ( 120 120) ( 120 0) ] 120MPa 2
140 MPa
(2)单元体(b)
σ1 140MPa
σ 2 110MPa
σ3 0
110 MPa
σr 3 σ1 σ 3 140MPa 1 2 2 2 σr 4 [30 110 ( 140) ] 128MPa 2
1u
1u
E
b
E
1 1 1 2 3 E
1u
1u
E
b
E
1 2 3 b
强度条件为: 1 2 3
b
n
[ ]
实验验证: a) 可解释大理石单压时的纵向裂缝; b) 脆性材料在双向拉伸-压缩应力状态下,且压应 力值超过拉应力值时,该理论与实验结果相符合。
σ1 94 .72MPa σ 3 5 .28MPa
9.组合变形

2 y
2 z
设挠度 的方向与Y轴间的夹角 ,则:
z Iz tg tg y Iy
讨论:由上式可看出:要使得 必须:I z I y 即,只 有在 I z I y 的条件下,才是平面弯曲, 否则是斜弯 曲。
思考题
正方形,圆形,当外力作用线通过截面形心时,为平面弯曲还 是斜弯曲?
总目录
本章要点
(1)斜弯曲 (2)偏心压缩 (3)弯扭组合变形
重要概念
组合变形、斜弯曲、偏心压缩、弯扭组合
§9-1 概述
*工程中几种常见的组合变形:
斜弯曲 —————斜屋架上的檩条 拉弯组合 ————冻结管 偏心压缩 ————设有吊车的厂房柱子 弯扭组合变形——机床中靠齿轮传递的轴
由于组合变形是几种基本变形相互组合的结果, 因此,在进行组合变形下的强度和刚度计算时,只 需分别计算形成这种组合变形的几种基本变形下的 应力和变形,然后进行叠加即可得到组合变形下的 应力和变形。 计算组合变形强度问题的步骤如下:
可得中性轴的方程式为:
yP y z P z 1 2 2 0 iz iy
根据该方程式可知中性轴是不过形心的直线。
现令:应力零线N-N,它在y、z轴上的截距分别为 a y a z 分别将 a y ,0 0, az 代入 k 表达式得:
iZ 2 ay yP
aZ
2 1 2 2 1 2 2 3 3 1 2
将C式代入上式,简化整理后可得:
W 3
2
2 n
代入<a><b>式即可得:
1 W
M W 0.75Tn2
材料力学知识点总结

材料力学知识点总结材料力学是研究材料在各种外力作用下产生的应变、应力、强度、刚度和稳定性的学科。
它是工程力学的一个重要分支,对于机械、土木、航空航天等工程领域的设计和分析具有重要意义。
以下是对材料力学主要知识点的总结。
一、基本概念1、外力与内力外力是指物体受到的来自外部的作用力,包括集中力、分布力等。
内力则是物体内部各部分之间的相互作用力,当物体受到外力作用时,内力会随之产生以抵抗外力。
2、应力与应变应力是单位面积上的内力,它反映了材料内部受力的强弱程度。
应变是物体在受力作用下形状和尺寸的相对变化,分为线应变和切应变。
3、杆件的基本变形杆件在受力作用下主要有四种基本变形形式:拉伸(压缩)、剪切、扭转和弯曲。
二、拉伸与压缩1、轴力与轴力图轴力是指杆件沿轴线方向的内力。
通过绘制轴力图,可以直观地表示出轴力沿杆件轴线的变化情况。
2、横截面上的应力在拉伸(压缩)情况下,横截面上的应力均匀分布,其大小等于轴力除以横截面面积。
3、材料在拉伸与压缩时的力学性能通过拉伸试验,可以得到材料的强度指标(屈服强度、抗拉强度)和塑性指标(伸长率、断面收缩率)。
不同材料具有不同的力学性能,如低碳钢的屈服和强化阶段,铸铁的脆性等。
4、胡克定律在弹性范围内,应力与应变成正比,即σ =Eε ,其中 E 为弹性模量。
5、拉伸(压缩)时的变形计算根据胡克定律,可以计算杆件在拉伸(压缩)时的变形量。
三、剪切1、剪切内力与剪切应力剪切内力通常用剪力表示,剪切应力则是单位面积上的剪力。
2、剪切实用计算在工程中,通常采用实用计算方法来确定剪切面上的平均应力。
四、扭转1、扭矩与扭矩图扭矩是指杆件在扭转时横截面上的内力偶矩。
扭矩图用于表示扭矩沿杆件轴线的变化。
2、圆轴扭转时的应力与变形圆轴扭转时,横截面上的应力分布呈线性规律,其最大应力发生在圆周处。
扭转角的计算与材料的剪切模量、扭矩和轴的长度等因素有关。
五、弯曲1、剪力与弯矩弯曲内力包括剪力和弯矩,它们的计算和绘制剪力图、弯矩图是弯曲分析的重要内容。
弯曲与扭转组合变形的强度计算_工程力学_[共6页]
![弯曲与扭转组合变形的强度计算_工程力学_[共6页]](https://img.taocdn.com/s3/m/6ab7e43c6294dd88d1d26b3e.png)
σ1
σ+ 2
σ 2
2
+τ
2
,,
σ2
=
0
σ3
=
σ 2
−
σ 2
2
+τ2
对于塑性材料,通常选第三或第四强度理论,强度条件分别为
σ r3 = σ 2 + 4τ 2 ≤≤[σ≤] , σ r4 σ 2 + 3τ 2 [σ ]
(10.6)
将式(a)代入式(10.6)并注意到 Wp=2Wz,得到圆杆弯扭组合变形以内力表示的强度条件
= σ eq3
M 2 + = MT2 Wz
7.62 + 62 × 106 =
50.5 MPa <= [σ ]
80 MPa
π × 1253
32
计算结果表明轴 OA 的强度是足够的。
162
− 1125 × 103 1003 / 6
=6.99 MPa < [σ ]
故梁是安全的。
10.2 弯曲与扭转组合变形的强度计算
弯曲与扭转组合变形在机械工程中是很常见的,例如皮带轮传动轴、齿轮轴、曲柄轴等轴
类构件,在传递扭矩的同时往往还发生弯曲变形。
如图 10-5(a)所示水平直角曲拐,AB 段为圆杆,受集中力 F 作用。将 F 向 AB 杆的 B 端
σr3
= 1 M 2 + M Wz
2 n
≤≤[σ
]
,
σr4
= 1 M 2 + 0.75 Wz
M
2 n
[σ ]
(10.7)
工程中除了弯扭组合的杆件外,还有拉(压)与扭转的组合,或者拉压、弯曲与扭转的组 合变形,运用相同的分析方法,仍可用式(10.6)进行强度计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
组合变形和强度理论习题及解答 题1.图示,水平放置圆截面直角钢杆(2ABCp?),直径100dmm=,2lm=,1qkNm=,MPa160,试校核该杆的强度。
AB
Cl
lq
q
解: 1)各力向根部简化,根截面A为危险面
扭矩:212nAMql=,弯矩 232zAMql=+,剪力2AQql=
2) 2348ZAMqlWdsp==, 3132Wdp=,3116pWdp=, 扭转剪应力:23810.18nPMqlMPaWdtp===,
3) []22364.42znrMMMPaWss+==<, ∴梁安全 题2、 平面曲杆在C端受到铅重力P作用。材料的[]=160MPa。若P=5KN,l=1m,a=0.6m。试根据第四强度理论设计轴AB的直径d. 解:属于弯扭组合变形 危险面A处的内力为:
53zMkNmTkNm=?
A
B
C
l
Pad42263
50.7535.63325.631071160rMkNmdmmp=+? 创==´
题3、平面曲拐在C端受到铅垂力P作用,材料的[]=160MPa,E=2.1105MPa,。 杆的直径d=80mm,l=1.4m,a=0.6m,l1=1.0m。若P=5KN (1) 试用第三强度理论校核曲拐的强度。 (2) 求1-1截面顶端处沿45方向的正应变。
解: (1)危险A上的内力为:51.47zMkNm=? 50.63TkNm=?
[]333
2234464
737.62805.0310327.62101511605.0310rzrrzMkNmWmmMMPaMPaWpss=+=?? ´===<=´
曲拐安全 (2)1-1截面内力:5,3zMkNmTkNm=? 顶点的应力状态
450 64510
99.45.0310MPas´==´
64310
29.825.0310MPat´==
创
ABCP
l1
450
a
I79.52219.882MPaMPaabsstsst=+==-= 45579.5219.880.283.52102.1102.110ae-=-=
创
题4. 图示一悬臂滑车架,杆AB为18 号工字钢,其长度为2.6lm=。试求当荷载F=25kN作用在AB的中点D处时,杆内的最大正应力。设工字钢的自重可略去不计。
AC
BD
ll/2
F
ADB
Fl/2
FAx
FAy
解:18号工字钢43421851030610.,.WmAm--=? AB杆系弯庄组合变形。
()0
0033
44300302521263025162522232510162510287837079491851030610maxmaxcos,sin.,.sin........中中压BCABCBCBCMFWAlMFlFFkNlMFkNmMPass-
=+==?=?创=创´
=+=+=创
å
题5. 砖砌烟囱高30hm=,底截面mm-的外径13dm=,内径22dm=,自重2000PkN=,受1/qkNm=的风力作用。试求:
(1)烟囱底截面上的最大正应力; (2)若烟囱的基础埋深04hm=,基础及填土自重按21000PkN=计算,土壤的许用应力[]0.3MPas=圆形基础的直径D应为多大?
注:计算风力时,可略去烟囱直径的变化,把它看作是等截面的。
hq
h0
mm
P1
D 解:烟囱底截面上的最大正应力: 2323
12244
11103020001022323214643205080212max()()/..()压qhP
WA
MPaMPaspp创 ´=+=+--´=+
[]012
22
33
6
22
666
3243230110304200010001020310432382105811003103825810417maxmaxmax()()().......2
3
土壤中的最大正应力即 D即 0.3D解得:hqhhPPDDDDDDDmsssppspp++=+
创?+
=+4
创+4
--==
题6. 受拉构件形伏如图,已知截面尺寸为405mmmm´,承受轴向拉力12FkN=。现拉杆开有切口,如不计应力集中影响,当材料的[]100MPas=时,
试确定切口的最大许可深度,并绘出切口截面的应力变化图。 FFAAx5
A-AA-A放大
h
bxx/2
h/2(h-x)/2
解: []33362912101012102100105401061286400525max().-62即 (40-x)510整理得 x解得:FMAWxxxxmmss--
=+ 创 ´
+4? 创
-+==
题7. 试确定图示各截面的截面核心边界。
zABC
D123
4
y800
8005
40
o
oy 解:① 截面几何 2222612444412242228005401044411101264180054010126429961000729().()..yzyyzAbdmbIIdmIiimApppp--
--
=-=-创= ==-
=?创= ===
② 截面核心 2131400007290182400100,..设中性轴为边,yzzyABammaiymaz-
== =-=-=-´
=
相应荷载作用点为点1;利用对称性,同样可得荷载作用点2 , 3 , 4 。因此截面核心为点1 , 2 , 3 . 4 组成的正方形,该正方形的对角线长度:
13018220364364..lmm=?=
题8. 试确定图示各截面的截面核心边界。 z
R=200
123
4
zyy0
DAo
B
d
解:① 截面几何 2262232044124420042244442222400106283102482240010849103400106283102642646283106283108491017541062831010010628310..........zyyzzdAmdzmdImIIAzmIimAppppp--
--
--
------
-
==创= ´
创===
==创= 创
=-
=?创 = ´=== ´
4232217541027910628310...yyIimA--
-
´=== ´
② 截面核心 设中性轴为AB边,2y8.4910, zama-=-? ,则相应的荷载作用点1的坐标为: 231212791000329849100...yzizmay-
-´
=-=-=+-
=
分别设中性轴与点AB、 和C相切,则其截跟以及相应的荷载作用点2 , 3 和4 的坐标分别为:中性轴截距:200115,;,zyzyaammamma=??= 相应点坐标:
2323440502430,,,;.,.zymmzmmy==?-=
中性轴由点A的切线绕角点A转至AB边和由AB边绕角B转至点B的切线,相应的荷载作用点的轨迹为直线,故分别以直线连接点1 、2 和点1 、3 。中性轴从点A的切线沿半圆孤ACB过渡到B 点的切线(始终与圆周相切),则相应的荷载作用点的轨迹必为一曲线,于是以适应的曲线连接点2 、4 、3 即得该截面的截面核心,如图中阴影区域所示,为一扇形面积。
题9. 曲拐受力如图示,其圆杆部分的直径50dmm=。试画出表示A点处应力状态的单元体,求其主应力及最大切应力。
