第八章组合变形构建的强度习题答案.
《材料力学》第八章课后习题参考答案
解题方法与技巧归纳
受力分析
在解题前首先要对物体进行受力分析， 明确各力的大小和方向，以便后续进 行应力和应变的计算。
图形结合
对于一些复杂的力学问题，可以画出 相应的示意图或变形图，帮助理解和 分析问题。
公式应用
熟练掌握材料力学的相关公式，能够 准确应用公式进行计算和分析。
检查结果
在解题完成后，要对结果进行检查和 验证，确保答案的正确性和合理性。
压杆稳定
探讨细长压杆在压缩载荷作用下的稳定性问题。
解题方法与技巧
准确理解题意
仔细审题，明确题目要求和考查的知识点。
选择合适的公式
根据题目类型和所给条件，选用相应的公式 进行计算。
注意单位换算
在计算过程中，要注意各物理量的单位换算， 确保计算结果的准确性。
检查答案合理性
得出答案后，要检查其是否符合实际情况和 物理规律，避免出现错误。
相关题型拓展与延伸
组合变形问题
超静定问题
涉及多种基本变形的组合，如弯曲与扭转 的组合、拉伸与压缩的组合等，需要综合 运用所学知识进行分析和计算。
超静定结构是指未知力数目多于静力平衡 方程数目的结构，需要通过变形协调条件 或力法、位移法等方法进行求解。
稳定性问题
疲劳强度问题
研究细长压杆在压力作用下的稳定性问题 ，需要考虑压杆的临界力和失稳形式等因 素。
研究材料在交变应力作用下的疲劳破坏行为 ，需要了解疲劳极限、疲劳寿命等概念和计 算方法。
THANKS FOR WATCHING
感谢您的观看
重点知识点回顾
材料的力学性质
包括弹性、塑性、强度、硬度等基本概念和 性质。
杆件的拉伸与压缩
涉及杆件在拉伸和压缩状态下的应力、应变及 变形分析。
第八章 组合变形 构件的强度计算1
P
D1
=159.4MPa<[ ]
图示矩形截面梁，截面宽度b＝90mm，高度h＝180mm。 梁在两个互相垂直的平面内分别受有水平力F1和铅垂 力F2 。若已知F1＝800N， F2＝1650N， L ＝1m，试 求梁内的最大弯曲正应力并指出其作用点的位置。 M y = F1 L F2 M z = F2 L
或单向压缩)，故：
FN M z ,max s max = + A Wz
强度条件
max≤ [ ]
例1
• 最大吊重P=8kN的起重机， AB杆的工字钢，材料为A3 钢，[]=100MPa，选择工 字钢型号。
“M”
“N”
Mmax=12kN· m
N=40kN
先按弯曲正应力选择工字钢型号； 再按组合变形的最大正应力校核强度，必要 时选择大一号或大二号的工字钢； 若剪力较大时，还需校核剪切强度。
-3
2
求内力(作用于截面形心) 取研究对象如图
N=P kN, -2 My =42.5´ 10 P kNm
危险截面 各截面相同 应力分布
危险截面 各截面相同 应力分布
N引起的应力
My引起的应力
N P = MPa σ¢ = A 15
σⅱ t max =
M y zo Iy M y z1 Iy
z
x
F1
L L
σ max =
My Wy
+
Mz Wz
材料力学习题册参考答案
材料力学习题册参考答案材料力学习题册参考答案（无计算题）第1章：轴向拉伸与压缩一：1（ABE ）2（ABD ）3（DE ）4（AEB ）5（C ）6（ＣＥ）７（ABD ）8（C ）9（BD ）10（ADE ）11（ACE ）12（D ）13（CE ）14（D ）15（ＡＢ）１６（BE ）17（D ）二：1对2错3错4错5对6对7错8错9错10错11错12错13对14错15错三：1：钢铸铁 2：比例极限p σ 弹性极限e σ 屈服极限s σ 强度极限b σ3.横截面 45度斜截面4. εσE =， EAFl l =5.强度，刚度，稳定性；6.轴向拉伸（或压缩）；7. llb b ?μ?=8. 1MPa=106 N/m 2 =1012 N/mm 2 9. 抵抗伸缩弹性变形，加载方式 10. 正正、剪 11.极限应力 12. >5% <5% 13. 破坏s σ b σ 14.强度校核截面设计荷载设计15. 线弹性变形弹性变形 16.拉应力 45度 17.无明显屈服阶段的塑性材料力学性能参考答案：1. A 2. C 3. C 4. C 5. C 6. 5d ; 10d 7. 弹塑8. s2s 9. 0.1 10. 压缩11. b 0.4σ 12. <；< 剪切挤压答案：一：1.（C ），2.（B ），3.（A ），二：1. 2bh db 2. b(d+a) bc 3. 4a δ a 2 4. F第2章：扭转一：1.（B ） 2.（C D ） 3.（C D ） 4. （C ） 5. （A E ） 6. （A ）7. （D ）8. （B D ） 9.（C ） 10. （B ） 11.（D ） 12.（C ）13.（B ）14.（A ） 15.（A E ）二：1错 2对 3对 4错 5错 6 对三：1. 垂直 2. 扭矩剪应力 3.最外缘为零4. p ττ< 抗扭刚度材料抵抗扭转变形的能力5. 不变不变增大一倍6. 1.5879τ7.实心空心圆8. 3241)(α- 9. m ax m in αττ= 10. 长边的中点中心角点 11.形成回路（剪力流）第3章：平面图形的几何性质一：1.（C ），2.（A ），3.（C ），4.（C ），5.（A ），6.（C ），7.（C ），8.（A ），9.（D ）二：1）. 1；无穷多；2）4)4/5(a ； 3），84p R I π=p 4z y I 16R I I ===π4）12/312bh I I z z ==；5）)/(/H 6bh 6BH W 32z -= 6）12/)(2211h b bh I I I I z y z y +=+=+；7）各分部图形对同一轴静矩8）两轴交点的极惯性矩；9）距形心最近的；10）惯性主轴；11）图形对其惯性积为零三：1：64/πd 114； 2.（0 , 14.09cm ）(a 22，a 62)3： 4447.9cm 4， 4：0.00686d 4 ，5: 77500 mm 4 ;6: 64640039.110 23.410C C C C y y z z I I mm I I mm ==?==?第4章：弯曲内力一：1.（A B ）2.（D ）3.（B ）4.（A B E ）5.（A B D ）6.（ACE ） 7.（ABDE ） 8.（ABE ）9. （D ） 10. （D ） 11.（ACBE ） 12.（D ） 13.（ABCDE ）二：1错 2错 3错 4对 5错 6对 7对三：1. 以弯曲变形 2.集中力 3. KNm 2512M .max =4. m KN 2q = 向下 KN 9P = 向上5.中性轴6.荷载支撑力7. 小8. 悬臂简支外伸9. 零第5章：弯曲应力一：1（ＡＢＤ）２．（C ）3.（BE ）4.（A ）5.（C ）6.（C ）7.（B ）8.（C ）9.（BC ）二：1对 2错 3错 4 对 5 错 6错 7 对三：1.满足强度要求更经济、更省料2. 变成曲面，既不伸长也不缩短3.中性轴4.形心主轴5.最大正应力6.剪力方向7.相等8.平面弯曲发生在最大弯矩处9.平面弯曲第6章：弯曲变形一：1（B ），2（B ），3（A ），4（D ），5（C ），6（A ），7（C ），8（B ），9（A ）10（B ），11（A ）二：1对2错3错4错5错6对7错8错9错10对11错12对三：1.（转角小量:θθtan ≈）（未考虑高阶小量对曲率的影响）2. 挠曲线采用近似微分方程导致的。
(材料力学课件)第8章组合变形作业
F
4
d2
4
80103 222 106
F
组
52.61MPa[ ]130MPa
bF 1
合 变
(2) 挤压强度计算
形 作 业
bsF Abbss4F d 4282011003106
题 90.91MPa[bs]
Fs
Fs
Fs
3F/4
Fs
F
1F
(3) 板拉伸强度计算
上板轴力图
F/4
（+）
2 孔 F 面 A N 4 ( b 3 F 2 d d ) 4 ( 8 1 0 3 2 8 0 2 1 0 3 1 2 ) 0 1 0 6 0 1.7 6 M 6 [P ] a
故接头符合强度条件
8-27 解: (1) 由剪切强度条件
b
F
F
F A ss b F l 255 01 10 30 0 3l[]1160
a
l
l
第 得: l0.2m (2) 由挤压强度条件
8 章 组
b s F A b bs s a F ba 5 2 0 1 5 1 30 0 3 0[b]s 1 0 160
作
业 题
1 O 1 A C 1 A O C 2.7 1 1 (22 .4 3 ) 8 3.4 3 M 5 Pa
2 0
3 O 3 O A C C 3 A 1.7 1 4 2.7 1 1 9 .9M 7 Pa
8-20 解: (1) 剪切强度计算
Fs FAs
轴 卡环
380
30 40
第 A F s 3 18 4 4 0 5 1 0 3 0 1 00 63.3 0M 7 Pa
8 章
故卡环符合剪切强度条件
第八章-组合变形及连接部分的计算-习题选解.docx
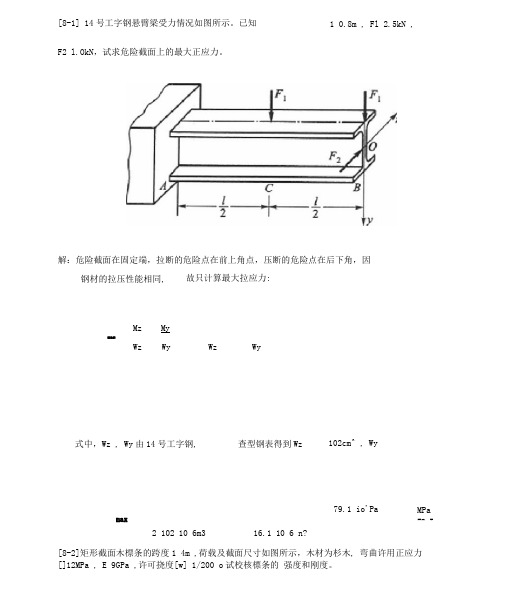
[8-1] 14号工字钢悬臂梁受力情况如图所示。
已知F2 l.OkN，试求危险截面上的最大正应力。
解：危险截面在固定端，拉断的危险点在前上角点，压断的危险点在后下角，因[8-2]矩形截面木標条的跨度1 4m ,荷载及截面尺寸如图所示，木材为杉木, 弯曲许用正应力[]12MPa , E 9GPa ,许可挠度[w] 1/200 o试校核標条的强度和刚度。
1 0.8m , Fl 2.5kN ,钢材的拉压性能相同, 故只计算最大拉应力:maxMz MyWz Wy Wz Wy式中，Wz , Wy由14号工字钢, 查型钢表得到Wz 102cm^ , Wymax79.1 io'Pa MPa79 J2 102 10 6m3 16.1 10 6 n?■ . , ■ l ・6kN/m ________A 戈HHluq习题8解：（1）受力分析COS1.6 cos26° 34 1.431(/ kN mq z q sin 1.6 sin26°340.716( kN/m)(2)内力分析My .max4qz 1 81 2-q yl 2 8(3)应力分析Mz.max-4 0.716 8-1 1.432 84 2 1.432(kN m) 4? 2.864(kN m) 最大的拉应力出现在跨中截面的右上角点， 最大压应力出现在左下角点。
M y ・ maxz.maxmax式中,160 11026322667 mm?maxWz110 16O 26469333mm^1.432 1()6 N mm2.86425 心隔（4）强度分析 因为max（5）变形分析322667 mm?469333mm310.54MPa , [ ] 12MPa ,即max［所以杉木的强度足够。
最大挠度出现在跨中，查表得:■1-60-1-1^ 17746667 (mn?)12（6）刚度分析 12屮一37546667 mm^12Wcy5qyl4 5 1.431N/mm 4000^ mm^ 384EIz 384 9 1()3 N/mn? 37546667mm^14.12mmwcz5qzl^ 5 0.716N/mm 400()4 mn? 384EIy384 9103 N/mm217746667mm° 14.94.mm (Wc/ \i4.12 214.94220,56(mm)式中，ly12因为WmaxWc 20・56(mm) , [ w]400020(mm),即 Wmax [w],200 200 所以，从理论上讲，变形过大，不符合刚度要求。
第八章组合变形时的强度计算
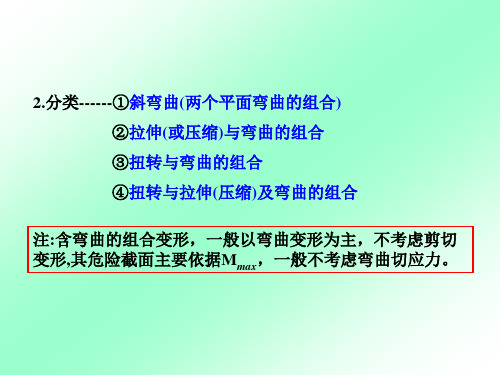
Iy
IY
由 mz 产生的正应力
s"' MZ .y Fyp y
IZ
IZ
假设C 点在第一象限内,根据杆件的变形可知, s ',s '',s ''' 均为拉应
力，由叠加原理，即得 C点处的正应力为：
σ σ' σ'' σ'''
任意横截面 n-n上的 C点的正应力为
c
σ F F zP z F yP y
与y轴的夹角θ为：
tgθ z0 Mz Iy Iy tgφ y0 My Iz Iz
公式中角度 是横截面上合成弯矩 M 的矢量与 y 轴的夹角 . 横截面上合成弯矩 M 为：
M
M
2 y
M
2 z
tgθ Iy tgφ Iz
讨论：
（1） 一般情况下，截面的 IzIy ,故中性轴与合成弯矩 M 所在平面不垂直，此为斜弯曲的受力特征。导致挠曲线与外 力（合成弯矩）所在面不共面,此为斜弯曲的变பைடு நூலகம்特征。
s s ' s '' My z - Mz y
Iy
Iz
式中，Iy和Iz分别为横截面对于两对称轴y和z的惯性矩； M y和Mz分别是截面上位于水平和铅垂对称平面内的弯矩，且 其力矩矢量分别与y轴和z轴的正向相一致。在具体计算中，
也可以先不考虑弯矩M y、Mz和坐标y、z的正负号，以它们的 绝对值代入，然后根据梁在P1和P2分别作用下的变形情况， 来判断上式右边两项的正负号。
FN A
Mz Wz
158 MPa
s
所以强度是安全
【例8-4】矩形截面柱如图所示。P1的作用线与杆轴线重合， P2作用在 y 轴上。已知， P1= P2=80kN，b=24cm , h=30cm。 如要使柱的m—m截面只出现压应力，求P2的偏心距e。
结构设计原理 第八章 变形 习题及答案
第八章钢筋混凝土构件裂缝及变形的验算一、填空题1.混凝土构件裂缝开展宽度及变形验算属于极限状态的设计要求，验算时材料强度采用。
2. 是提高钢筋混凝土受弯构件刚度的最有效措施。
3. 裂缝宽度计算公式中的，σsk是指，其值是按荷载效应的组合计算的。
4.钢筋混凝土构件的平均裂缝间距随混凝土保护层厚度的增大而。
用带肋变形钢筋时的平均裂缝间距比用光面钢筋时的平均裂缝间距_______（大、小）些。
5.钢筋混凝土受弯构件挠度计算中采用的最小刚度原则是指在弯矩范围内，假定其刚度为常数，并按截面处的刚度进行计算。
6.结构构件正常使用极限状态的要求主要是指在各种作用下和不超过规定的限值。
7.裂缝间纵向受拉钢筋应变的不均匀系数Ψ是指之比，反映了裂缝间参与工作的程度。
8.平均裂缝宽度是指位置处构件的裂缝宽度。
二、选择题1. 计算钢筋混凝土梁的挠度时，荷载采用（）A、平均值；B、标准值；C、设计值。
2. 当验算受弯构件挠度时，出现f>[f]时，采取（）措施最有效。
A、加大截面的宽度；B、提高混凝土强度等级；C、加大截面的高度；D、提高钢筋的强度等级。
3. 验算受弯构件裂缝宽度和挠度的目的是（）。
A、使构件能够带裂缝工作；B、使构件满足正常使用极限状态的要求；C、使构件满足承载能力极限状态的要求；D、使构件能在弹性阶段工作。
4. 钢筋混凝土轴心受拉构件的平均裂缝间距与纵向钢筋直径及配筋率的关系是（）。
A、直径越大，平均裂缝间距越小；B、配筋率越大，平均裂缝间距越大；C、直径越小，平均裂缝间距越小；5. 钢筋混凝土梁截面抗弯刚度随荷载的增加及持续时间增加而（）。
A、逐渐减小；B、逐渐增加；C、保持不变；D、先增加后减小。
6. 裂缝间钢筋应变的不均匀系数Ψ的数值越大，说明（）。
A、裂缝之间混凝土的应力越大；B、裂缝之间钢筋应力越小；C、裂缝之间混凝土的应力越小；D、裂缝之间钢筋应力为零。
7. 当其他条件完全相同，根据钢筋面积选择钢筋直径和根数时，对裂缝有利的选择是（）。
第八章 组合变形的强度计算
FAx A FAy FN
l/2
F2
C
B F1
b
cmax
σcmax
l/2
FB F1
h
z
y
＋
z
=
z
M
M max F2 l 4
tmax
Mmax max Wz
σtmax
5.强度计算 （脆性材料）
F M max 1 max t t max A Wz F M c max max 1 max c A Wz
y My M y max Wy
z
My
讨论：无棱角的截面如何确定危险点
b
h
z
y
z
z
Mz
My
y
z
F
y
F
y
t max
Mz M y Wz Wy
Mz M y c max Wz Wy
此时，应先找出组合变形的 中性轴，距中性轴最远的点有最 大的正应力。
F
l
Mz Fy x Fx cos
M y Fz x Fx sin
3.应力计算 (计算A(y，z)点的正应力)
Mz A Mz y Iz
A A A
Mz y M y z A Iz Iy
M y A
M yz Iy
§8-3
概述 两相互垂直平面内的弯曲
拉伸（压缩）与弯曲
§8-4
扭转与弯曲
§8-1 概述
组合变形：由两种或两种以上基本变形组合形成的变形。 工程实例：
组合变形及强度理论
组合变形和强度理论习题及解答题1．图示，水平放置圆截面直角钢杆（2ABCp ?），直径100d mm =，2l m =，1q k N m =，[]MPa 160=σ，试校核该杆的强度。
解：1）各力向根部简化，根截面A 为危险面 扭矩：212nA Mql =，弯矩 232zA M ql =+，剪力2A Q ql = 2) 2348ZA M ql W d s p ==， 3132W d p =，3116p W d p =， 扭转剪应力：23810.18n P M ql MPa W dt p ===，3) []364.42r MPa s s ==<，∴梁安全题2、 平面曲杆在C 端受到铅重力P 作用。
材料的[σ]=160MPa 。
若P=5KN ，l =1m ，a=0.6m 。
试根据第四强度理论设计轴AB 的直径d. 解：属于弯扭组合变形危险面A 处的内力为：题3、平面曲拐在C 端受到铅垂力P 作用，材料的[σ]=160MPa ，E=2.1⨯105MPa ，。
杆的直径d=80mm ，l =1.4m ，a=0.6m ，l 1=1.0m 。
若P=5KN (1) 试用第三强度理论校核曲拐的强度。
(2) 求1-1截面顶端处沿45︒方向的正应变。
解：（1）危险A 上的内力为：5 1.47z M kN m =??B曲拐安全 （2）1-1截面内力：5,3z M kN mT kN m =?? 顶点的应力状态题4. 图示一悬臂滑车架，杆AB 为18 号工字钢，其长度为 2.6l m =。
试求当荷载F =25kN 作用在AB 的中点D 处时，杆内的最大正应力。
设工字钢的自重可略去不计。
B解：18号工字钢43421851030610.,.W m A m --=??AB 杆系弯庄组合变形。
题5. 砖砌烟囱高30h m =，底截面m m -的外径13d m =，内径22d m =，自重2000P kN =，受1/q kN m =的风力作用。
第8章组合变形及连接部分的计算（答案）
第8章组合变形及连接部分的计算（答案）8.1梁的截⾯为2100100mm ?的正⽅形，若kN P30=。
试作轴⼒解：求得约束反⼒24Ax F KN =,9Ay F KN =，9B F KN =为压弯组合变形，弯矩图、轴⼒图如右图所⽰可知危险截⾯为C 截⾯最⼤拉应⼒maxmax 67.5ZM MPa W σ== 最⼤压应⼒max max69.9N Z M FMPa W Aσ=+=8.2若轴向受压正⽅形截⾯短柱的中间开⼀切槽，其⾯积为原来⾯积的⼀半，问最⼤压应⼒增⼤⼏倍？解：如图，挖槽后为压弯组合变形挖槽前最⼤压应⼒挖槽后最⼤压应⼒22222286/)2/(4/2/a P a a Pa a P W M A N c =+=+=σ8//82212==a P a P c c σσ211a P A N c ==σ8.3外悬式起重机，由矩形梁AB （2=bh尺⼨。
解：吊车位于梁中部的时候最危险，受⼒如图解得BC F P =,2Ax F P =，2Ay P F =梁为压弯组合变形，危险截⾯为梁中N F =压)，4PL M =(上压下拉)[]max4NZ F PL W A σσ=+≤,代⼊()226Z b b W =，A bh =，由2h b = 解得125b mm =， 250h mm =8.4图⽰为⼀⽪带轮轴（1T 、2T 与3T 相互垂直）。
已知1T 和2T 均为kN 5.1，1、2轮的直径均为mm 300，3轮的直径为mm 450，轴的直径为mm 60。
若M P a 80][=σ，试按第三强度理论校核该轴。
解：由已知条件解得32T KN = 内⼒图如右：最⼤弯矩所在截⾯可能为：1C M KN m ==?1.2D M KN m =?故危险截⾯为D 截⾯32T KN =由第三强度理论[]360r MPa σσ==故安全38.5铁道路标圆信号板装在外径mm D 60=的空⼼圆柱上，若信号板上所受的最⼤风载2/2m kN p =，MPa 60][=σ，试按第三强度理论选择空⼼柱的厚度。
第八章组合变形习题集
8-2 人字架及承受的荷载如图所示。
试求m-m 截面上的最大正应力和A 点的正应力。
m解：（1）外力分析，判变形。
由对称性可知，A 、C 两处的约束反力为P/2 ，主动力、约束反力均在在纵向对称面内，简支折将发生压弯组合变形。
引起弯曲的分力沿y 轴，中性轴z 过形心与对称轴y 轴垂直。
截面关于y 轴对称，形心及惯性矩1122123122328444A A 20010050200100(100100)125A +A 200100+200100200100200100(12550)12100200100200(300125100)123.0810 3.0810C z zzy y y I I I -+⨯⨯+⨯⨯+===⨯⨯⨯=+=+⨯⨯-⨯++⨯⨯--=⨯=⨯mmmm m(2)内力分析，判危险面：沿距B 端300毫米的m-m 横截面将人字架切开，取由左边部分为研究对象，受力如图所示。
梁上各横截面上轴力为常数：,m-m 250(1.80.3sin )(1.80.3202.5(k 22250cos =100(k )22y N P M P F ϕϕ=⨯-=⨯-=⋅=⨯=N m)N(3)应力分析，判危险点，如右所示图①m-m 截面上边缘既有比下边缘较大的弯曲压应力，还有轴力应力的压应力，故该面上边缘是出现最大压应力。
m mmax33410010202.510(0.30.125)(Pa) 2.5115.06MPa 117.56MPa 2(0.20.1) 3.0810N zF M y A I σ---=+⋅-⨯⨯=-⨯-=--=-⨯⨯⨯上② A 点是压缩区的点，故m m33410010202.510(0.30.1250.1)(Pa) 2.549.31MPa 51.83MPa 2(0.20.1) 3.0810N a a zF M y A I σ--=+⋅-⨯⨯=-⨯--=--=-⨯⨯⨯注意：最大拉应力出现在下边缘m mmax33410010202.5100.125(Pa) 2.582.18MPa 79.68MPa2(0.20.1) 3.0810N zF M y A I σ---=+⋅-⨯⨯=+⨯=-+=⨯⨯⨯下8-3 图示起重机的最大起吊重量为W=35kN ，横梁AC 由两根NO.18槽钢组成。
组合变形习题讲解[1]
![组合变形习题讲解[1]](https://img.taocdn.com/s3/m/db62dabd1a37f111f1855b16.png)
第八章 组合变形习题讲解【习题5-29】解：矩形截面木榫头在力F 作用下可能发生挤压、剪切、横截面强度破坏，因此应分别满足这三方面的强度条件。
（1）挤压强度校核挤压面：BC 面，挤压面积：0.25b s A a=；挤压力：50b sF F k N==于是有，35010[]0.25b s b sb s b sF A a σσ⨯==≤⨯ 则20a m m≥（2）剪切强度校核剪切面：BE 和CD 面，剪切面积：0.25sA l=；剪切力：50sF F k N==于是有，35010[]0.25s ssF A l στ⨯==≤⨯则 200l m m ≥ （3）横截面强度校核1-1截面（如图（a ）所示）：由于只有轴力150N k N=，所以按照轴向拉压强度条件进行强度校核。
即：31115010[](2)0.25t N A a c σσ⨯==≤+⨯则 233.3a c m m+≥。
2-2截面：截面上存在轴力250N k N=，弯矩0.5()M F a c =+，所以应按照组合变形（偏心拉伸）来考虑。
根据2-2截面上的内力分量可知：危险点位于该截面的下边缘，应力为：题 5-29 图（a ）题 5-29 图（b ）233222250100.55010()[]10.250.256t N M a c A Wccσσ⨯⨯⨯⨯+=+=+≤⨯⨯⨯则146.9c m m≥【习题5-32】解：（1）外力分析以ABC 横梁为研究对象，受力图如图所示（a ）。
列静力平衡方程()00.1120A B D x B D y M F F F F =⨯+⨯-⨯=∑其中，B D xB D yF F =。
则27.272B D xB D y F F k N==绘制ABC 横梁的受力简图如图（b ）所示。
其中0.1 2.7272B D x M F k N m=⨯=⋅（2）内力分析根据横梁上作用的载荷可知，AE 段发生弯曲与拉伸的组合变形，EC 段发生平面弯曲变形。
第八章组合变形构件的强度-
Fx F cos; Fy F sin 2.内力分析
FN Fx F cos FS Fy F sin M z Fy (l x) 上侧受拉
F sin(l x)
m
xm l
z
Fx
x
Fy
F
y
z
FS
FN x
y Mz
§8-2 弯曲与拉伸(或压缩)得组合
一、拉(压)与弯曲组合变形
第八章组合变形构件的强度
第八章 组合变形构件得强度
轴向拉(压)
F
内
FN
力
FN F
扭转
m
x
T
T m
F
应
T
力
FN (x)
A
max
(ρ) T ρ Ip
对称弯曲
FS
M
σ
τ FS
M
My
;
FS
S
z
Iz
bI z
§8-1 概述 一、组合变形
F2
F1
Me
F1 — 轴向拉伸 F2 — 弯曲变形 Me — 扭转变形
F2
2
F1
1
z
FN F1
A bh
x 3
My Wy
F1 b h b2
2 6
3F1 bh
4
l
l
y
Mz Wz
F1 h b h2
2 6
3F1 bh
1
F1 bh
3F1 bh
3F1 bh
F1 bh
3
2
F1 bh
3F1 bh
3F1 bh
7 F1 bh
4
F1 bh
3F1 bh
3F1 bh
第八章组合变形构件的强度
偏心距e。
P
εa
P
e e h
【解】1）将P向轴线平移。
M e Pe
P
2）由虎克定律得：
Me
z
εb
b
εa
P
εb
Me
a b
a
E
b
E
1 E
1 E
P A
P A
Me Wz
Me Wz
1 E
1 E
P bh P bh
12Pe b h3
12Pe b h3
P
Ebh( a
2
e
h(
a
b)
6( a b)
A
F
+
σ'
2)当梁上只有P作用时，其弯
P ab
矩图和应力图为：
A
B
C
σ''
正应力：σ M (x) y
Iz
3)F、P同时作用时正应力：
Pab/(a+b)
+
AC
B
σmin σ σmax
F M (x) y
A
Iz
4)整个梁正应力在C截面上 下边缘取得极值：
Hale Waihona Puke 5)梁处于单向应力状 态，强度条件为：
σ
态，处于二向应力状态。
τ
5)强度计算：
eq3 2 4 2
2 m
ax
4
2max
M ma Wz
x
2
4
Tm W
ax t
2
M max Wz
2
4
T max 2W z
2
1 W
z
M
2 m
ax
T
结构力学 第八章
根据工字形截面的特点,可知,截面的最大弯曲正应力为
σ max
8-2、受集度为 q 的均布荷载作用的矩形截面简支梁，其荷载作用面与梁的纵向对称面间的夹角为α=30o， 如图所示。己知该梁材料的弹性模量 E=10GPa；梁的尺寸为 l=4m，h=160mm；b=120mm；许用应力 [σ]=l20MPa;许可挠度[w]=l/1150。试校核梁的强度和刚度。
max My = F2 l = 1.0 × 0.8 = 0.8 ( kN .m )
14 号工字钢的抗弯截面模量分别为
Wz = 102cm3 ;
Wy = 16.1cm3
max 3 × 103 0.8 ×103 M zmax M y = + = + = 79.1× 106 ( Pa ) −6 −6 102 × 10 16.1×10 Wz Wy
8-10、受拉构件形状如图，己知截面尺寸为 40mm×5mm，承受轴向拉力 F=l2kN。现拉杆开有切口，如不 计应力集中影响，当材料的[σ]=100MPa 时，试确定切口的最大许可深度，并绘出切口截面的应力变 化图。
38MPa
100 MPa A-A 截面应力分布图
解、由于切口的存在，在切口截面载荷为偏心力，切口截面上的轴力和弯矩分别为
3 3 2⎤ ⎡1 ⎤ ⎡1 I zC = ⎢ ( 4a )( 2a ) + ( 4a )( 2a ) a 2 ⎥ + ⎢ a ( 4a ) + ( 4a )( a )( 2a ) ⎥ = 32a 4 ⎣12 ⎦ ⎣12 ⎦ 1 1 3 I yC = ( 2a )( 4a ) + ( 4a ) a 3 = 11a 4 12 12
2
, FN = qx x = qx sin α
材料力学习题册答案-第8章 组合变形
第 八 章 组 合 变 形一、选择题1、偏心拉伸（压缩）实质上是（B ）的组合变形。
A ．两个平面弯曲B ．轴向拉伸（压缩）与平面弯曲C ．轴向拉伸（压缩）与剪切D ．平面弯曲与扭转 2、图示平面曲杆，其中AB ⊥BC 。
则AB 部分的 变形为( B )。
A ． 拉压扭转组合B ．弯曲扭转组合C ．拉压弯曲组合D ．只有弯曲二、计算题1、如图所示的悬臂梁，在全梁纵向对称平面内承受均布荷载 q=5kN/m ，在自由端的水平对称平面内受集中力P=2kN 的作用。
已知截面为25a 工字钢，材料的弹性模量E=2×105MPa ，求： （1）梁的最大拉、压应力（2）若[σ]=160MPa ，校核梁的强度是否安全。
解：（1）固定端截面为危险截面。
22max 115210kN m 22z M ql ==⨯⨯=⋅max 224kN m y M Pl ==⨯=⋅查表得：3348.283cm ,401.883cm y z W W ==由于截面对称，最大拉、压应力相等。
33max max max max661010410()Pa 108MPa 401.8831048.28310y z t c z y M M W W σσ--⨯⨯==+=+=⨯⨯（2）校核梁的强度[]max 108MPa 160MPaσσ=<=可见，梁的强度是足够的。
2、矩形截面木檩条，尺寸及受载情况如图所示。
已知q=2.1kN/m,木材许用拉应力[σt ]=11MPa ，许用挠度[w]= l ／200，弹性模量E=10GPa 。
校核其强度和刚度。
ABCq解：（1）受力分析，计算内力。
根据梁的受力特点可知梁将产生斜弯曲。
因此，将载荷q 沿两对称轴分解为cos y q q ϕ= , sin z q q ϕ=在q 作用下，梁跨中截面的弯矩最大，为危险截面。
由q z 、q y 引起的最大弯矩M ymax 、M zmax 为202max 202max112.1sin 2634'4 1.88kN m 88112.1cos 2634'43.76kN m 88y z z y M q l M q l ==⨯⨯⨯=⋅==⨯⨯⨯=⋅（2）确定危险点位置，计算危险点应力。
(材料力学课件)第8章组合变形作业
组
③
②
合 (2) 中性轴的截距（m） ay 0.4,az 0
800
变
形 作 业
y
iy2 ay
0.18,3z
0
确定点1
同理求出点2,3,4
题
当中性轴绕棱角点旋转时，外力作用点移动轨迹为直线。
故点1和2间亦为直线。
第
8 章 组 合 变 形 作 业 题
第
8 章 组 合 变 形 作 业 题
8-20 解: (1) 剪切强度计算
Fs
Fs
Fs
3F/4
Fs
F
1F
(3) 板拉伸强度计算
上板轴力图
F/4
（+）
2 孔 F 面 A N 4 ( b 3 F 2 d d ) 4 ( 8 1 0 3 2 8 0 2 1 0 3 1 2 ) 0 1 0 6 0 1.7 6 M 6 [P ] a
故接头符合强度条件
8-27 解: (1) 由剪切强度条件
b
F
F
F A ss b F l 255 01 10 30 0 3l[]1160
a
l
l
第 得: l0.2m (2) 由挤压强度条件
8 章 组
b s F A b bs s a F ba 5 2 0 1 5 1 30 0 3 0[b]s 1 0 160
合
变
得: a0.02m
形
作
业 故取
ቤተ መጻሕፍቲ ባይዱ
[l]0.2m ,[a]0.0m 2
w m a[x w ] 1% 0 0 2 .0 6 2 1% 0 0 3 % 故强度和刚度均满足要求
[w ]
2
8-5 解: (1) m-m截面上内力
《材料力学》第8章 组合变形及连接部分的计算 习题解
第八章 组合变形及连接部分的计算 习题解[习题8-1] 14号工字钢悬臂梁受力情况如图所示。
已知m l 8.0=，kN F 5.21=，kN F 0.12=，试求危险截面上的最大正应力。
解：危险截面在固定端，拉断的危险点在前上角点，压断的危险点在后下角，因钢材的拉压性能相同，故只计算最大拉应力：式中，z W ，y W 由14号工字钢，查型钢表得到3102cm W z =，31.16cm W y =。
故MPa Pa mm N m m N 1.79101.79101.168.0100.11010228.0105.236363363max=⨯=⨯⨯⨯+⨯⨯⨯⨯⨯=--σ [习题8-2] 受集度为 q 的均布荷载作用的矩形截面简支梁，其荷载作用面与梁的纵向对称面间的夹角为 030=α，如图所示。
已知该梁材料的弹性模量 GPa E 10=；梁的尺寸为m l 4=，mm h 160=，mm b 120=；许用应力MPa 12][=σ；许用挠度150/][l w =。
试校核梁的强度和刚度。
解：（1）强度校核)/(732.1866.0230cos 0m kN q q y =⨯== （正y 方向↓）)/(15.0230sin 0m kN q q z =⨯== （负z 方向←）)(464.34732.1818122m kN l q M y zmaz ⋅=⨯⨯== 出现在跨中截面)(241818122m kN l q M z ymaz ⋅=⨯⨯== 出现在跨中截面)(5120001601206161322mm bh W z =⨯⨯==)(3840001201606161322mm hb W y =⨯⨯==最大拉应力出现在左下角点上：yy z z W M W M maxmax max +=σ MPa mmmm N mm mm N 974.1138400010251200010464.33636max=⋅⨯+⋅⨯=σ因为 MPa 974.11max =σ，MPa 12][=σ，即：][max σσ<所以 满足正应力强度条件，即不会拉断或压断，亦即强度上是安全的。
组合变形构件的强度
组合变形构件的强度一、单项选择题：1．在偏心拉伸（压缩）情况下，受力杆件中各点的应力状态为（ ）。
A ．单向应力状态； Ｂ．二向应力状态；Ｃ．单向或二向应力状态； Ｄ．单向应力状态或零应力状态。
2．圆截面折杆ABCDEF 在端部受一对集中力P 作用，力P 与Z 轴平行，如图所示。
该折杆处于弯扭组合变形状态的部分是（ ）。
A ．杆BC 和杆DE ； Ｂ．杆CD ；Ｃ．杆BC 、杆CD 和杆DE ； Ｄ．无。
3．圆截面悬臂梁受载如图，固定端横截面上的最大拉、压应力为（ ）。
A ．)(z y yW Mz W M +±； Ｂ． )32(322d M M z y π+±； Ｃ．)16(322d M M z y π+±； Ｄ． )(1z y zM M W +±。
4．图（1）杆件承受轴向拉力F ，若在杆上分别开一侧、两侧切口如图（2）、图（3）所示。
令杆（1）、（2）、（3）中的最大拉应力分别为、max 1σ、max 2σ和max 3σ，则下列结论中（ ）是错误的。
A. max 1σ一定小于max 2σB. max 1σ一定小于max 3σC. max 3σ一定大于max 2σD. max 3σ可能小于max 2σ5．某构件横截面上危险点处的应力：弯曲正应力z W M =σ，扭转切应力t W T=τ。
按第三强度理论的强度条件为（ ）。
题2图题3图题4图A ．t W T M 22+=σ≤[σ]； Ｂ．2)(42)(tW T z W M +=σ≤[σ]； Ｃ．2)(32)(tW T z W M +=σ≤[σ]； Ｄ．t W T z W M +=σ≤[σ]。
6．图示刚架BACD ，处于弯扭组合变形的是（ ）段。
A ．AB ,CD 段； Ｂ．AC ,CD 段； Ｃ．AB,AC 段； Ｄ．CD 段。
7．图示结构中AB 杆将发生（ ）。
A ．弯曲变形； Ｂ．拉伸变形； Ｃ．弯曲和拉伸的组合变形； Ｄ．弯曲和压缩的组合变形。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第八章 组合变形构件的强度习题答案
一、填空题
1、组合
二、计算题
1、解：31
7888010157.610(N mm)4M =⨯⨯⨯=⨯⋅
336
78810141.8410(N mm)2T =⨯⨯=⨯⋅
33
800.1r d
σ=
=≤ 解得
d ≥30mm
2
、解：(1) 轴的计算简图
画出铰车梁的内力图：
险截面在梁中间截面左侧,P T P M 18.02.0max ==
(2) 强度计算
第三强度理论:()
()[]σπσ≤+=+=
2
2
322318.02.032
P P d
W T M Z r
[]()()()()
mm
m d 5.320325.010118.01012.010
8032
10118.01012.032
3
2
32
36
32
32
3==⨯⨯+⨯⨯⨯⨯=⨯⨯+⨯⨯≥πσπ
所以绞车的轴的最小直径为32.5mm 。
3、解：
m kN 8.1⋅
m kN 2.4⋅
（1）外力分析，将作用在胶带轮上的胶带拉力F 1、F 2向轴线简化，结果如图b ． 传动轴受竖向主动力：
kN 1436521=++=++=F F G F ， 此力使轴在竖向平面内弯曲。
附加力偶为：
()()m kN 8.16.03621⋅=⨯-=-=R F F M e ， 此外力偶使轴发生变形。
故此轴属于弯扭组合变形。
（2）内力分析
分别画出轴的扭矩图和弯矩图如图（c ）、（d ） 危险截面上的弯矩m kN 2.4⋅=M ，扭矩m kN 8.1⋅=T （3）强度校核
()()
[]σπσ≤=⨯⨯+⨯=
+=
MPa W T
M Z
r 6.4632
1.0108.110
2.43
2
32
32
23
故此轴满足强度要求。
4、解：1）外力分析
kN F Q Q F 625
.01==∴⨯=⨯Θ
2）内力分析，做内力图
2222
22
37.65.3.7.653600.1d
0.1d 111eq z M kN m T kN m M
T M T W d mm σ==+++=
=
=
≤>L L
3）求直径 []MPa
801.010375.0)1065.7(1.075.075.03
2
62
63
2
2
z
2
2
4r =≤⨯⨯⨯+⨯=⨯+=+=
σσd d T M W T M ）（mm 101≥d
5、
F
m B
mm N F ⋅140
mm N F ⋅150
解：
mm
N F T mm
N F M ⋅=⋅=140150()()
22
22
4150140[]160r z
F F M T Mpa W σσ++=
=
≤=
2353N 2.4kN F ≤≈ 故此结构的许可载荷F 为2.4kN 。
6、解 简化力系
()
()()
[]
200mm
d 32
109.11025.1W T M m 25KN .12
1
5.22D F -2F M 9.5KN
522.52F F F F 3
2
62
6Z
2
Max
2Max r3P ≈≤⨯+⨯=
+=⋅=⨯===++=++=解出总σπσd。