福田+小数+工程
2023-2024深圳福田区六年级(上)期中数学试卷答案

2023-2024深圳福田区六年级(上)期中数学试卷参考答案一、认真观察,细心计算。
1.【分析】根据分数、百分数加减乘除法的计算方法以及四则混合运算的顺序,直接进行口算即可。
【解答】解:2+12%=2.1210÷10%=100====2.【分析】(1)根据乘法分配律计算简便;(2)根据乘法分配律计算简便;(3)先算小括号里面的减法算式和加法算式,最后算括号外面的除法算式。
【解答】解:(1)=18×=6﹣4+15=2+15=17(2)=(45%+0.55)×==(3)==3.【分析】(1)先化简,然后根据等式的性质方程两边同时除以4.8;(2)根据等式的性质,方程两边同时减,然后方程两边同时乘2;(3)先化简,然后根据等式的性质方程两边同时乘4。
【解答】解:(1)5x﹣20%x=19.24.8x=19.24.8x÷4.8=19.2÷4.8x=4(2)x=(3)x﹣75%x=40.25x=40.25x×4=4×4x=16二、填空。
4.【分析】依据分数与比、除法的关系,利用分数的基本性质,结合题中小数0.6分别去计算即可。
【解答】解:0.6===12÷200.6=60%=六折故答案为:20;60;六。
5.【分析】1小时是60分,要求1小时的是多少分,用60乘求解;把要求的数看作单位“1”,它的1+对应的具体的数量是8吨,用8除以对应分率,即得单位“1”的量。
【解答】解:1小时是60分60×=15(分)8÷(1+)=8÷=6(吨)答:1小时的是15分,8吨比6吨多。
故答案为:15;6。
6.【分析】将若干个小正方体,摆成一个大正方体,那么这个正方体的每个棱长上至少有2个小正方体,由此即可计算得出小正方体的总个数。
【解答】解:根据小正方体拼组大正方体的特点可知:将若干个小正方形,摆成一个大正方体,那么这个正方体的每个棱长上至少有2个小正方体,所以组成的这个大正方体中,小正方体的个数至少有2×2×2=8(个)。
深圳市福田区三好学生事迹简介

深圳市福田区三好学生事迹简介——第四届“福田好少年”事迹福田区外国语学校香蜜校区罗羽菲:热爱祖国,善于创作,撰写创作的《歌唱祖国》、《我是一只快乐的幸福鸟》获得童话节创作优秀奖。
她兴趣广泛,全面发展,获得书法、美术、大提琴等多项等级证书,创作画作《夏夜石榴》荣获全国青少年美术创作大赛水彩三等奖。
她勇敢勤奋,积极参加义工活动,既延续了深圳这座城市的精神血脉,又学到了很多有用的实践知识,在奉献他人的过程中更加珍惜眼前生活,玫瑰余香更加坚定了个人价值。
她遵纪正心,坦率正直,积极进取,曾连续三年荣获“深圳市优秀少先队员”称号、第二届“最美南粤少年”深圳提名奖、第四届最美南粤少年“福田区最美少年”称号、“福田区优秀少先队员”称号,多次荣获校“三好学生”“优秀学生干部”“鸣天骄子学习之星”等荣誉。
梅林中学赖静茹:乐于助人,参加校学生会纪检工作。
在学校活动期间参加义工工作。
她担任班级里的生物课代表,尽己所能为同学们答疑解惑,帮助同学。
她才艺出众,曾在第十二届香港国际青年艺术节中获得银奖,曾获得意大利瓦雷泽国际青少年大赛三等奖。
在2015年未来之星全国特长生文化艺术广东赛区获得了A组优秀奖,以及2014年获得了青苗杯少儿才艺大赛A组舞蹈生特等奖。
2017年申请国家实用新型专利证书,2018年通过专利。
2014年获得深圳市青少年科技体育活动建筑模型类一等奖,2016年获得深圳市航空航天模型优胜奖,深圳市车辆模型三等奖,深圳市航空航天模型三等奖,宝安区车辆模型教育竞赛第一名,宝安区中小学航空航天模型教育竞赛优胜奖。
景田小学曾泓萱:才艺出众,是景田小学小有名气的主持人。
她已取得播音主持10级证书并连续两届在“深圳市少儿语言大赛”中获得儿童组的铜奖和银奖。
她曾在“谁是故事大王·第二季”深圳晋级赛中,因扮演的花木兰形象深入人心,得到“小小花木兰”的美誉。
她才思敏捷,兴趣广泛,作为景田小学国际象棋校队的女棋手,她在各项国际象棋等级比赛中斩获女子组的冠军和亚军。
深圳市建筑工程消耗量定额

总说明一、《深圳市建筑工程消耗量定额》下简称"本定额是指在正常施工条件下完毕规定计量单位的合格建筑工程所需的人工费、材料及施工机械台班消耗量的基准。
二、本定额与《深圳市建设工程计价规程》、《深圳市建设工程计价费率标准》配合使用,合用于深圳市辖区范围内新建、扩建、改建的工业与民用建筑工程。
三、本定额是合理拟定和有效控制工程造价的基础,可作为编制国有投资工程估算、设计概算、施工图预算、招标控制价的依据,也可作为编制投标报价的参考。
四、本定额的编制依据为:1.《建设工程工程量淸单计价规范》》(GB 50500—2023);2.《房屋建筑与装饰工程工程量计算规范》(GB 50854—2023);3.《房屋建筑与装饰工程消耗量定额》(TY 01—31—2023);4.《全国统一建设劳动定额(建筑工程)》(LD/T 72.1~11—2023);5.《深圳市建筑工程消耗量标准》(2023);6.《深圳市建设工程施工机械台班定额》(2023);7.《混凝土结构工程施工质量验收规范》(GB50204——2023);8.其他有关现行产品标准、设计规范、施工及验收规范、技术操作规程、质量评估标准和安全操作规程;9.深圳市近年来具有代表性的建筑工程设计文献、施工组织文献、工程计价文献及其他资料;10.编制期建筑市场价格行情调研资料。
五、本定额内容组成1.本定额由总说明、工程畳计算规则总则、土壤及岩石分类表、建筑物超髙增长费说明、分部分项工程部分、措施项目部分以及附录等七部分组成。
2.本定额中分部分项工程部分、措施项目部分按章、节、项目、子目顺序排列,各章均涉及说明、工程量计算规则、定额子目构成表三部分。
定额子目构成表由工作内容、计量单位、消耗量表格及必要的附注组成。
3.分部分项工程部分涉及:第一章土(石)方工程,第二章地基解决与边坡支护工程,第三章桩基础工程,第四章砌筑工程,第五章混凝土及钢筋混凝土工程,第六章厂库房大门、特种门及木结构工程,第七章屋面及防水工程,第八章防腐、保溫与隔热工程。
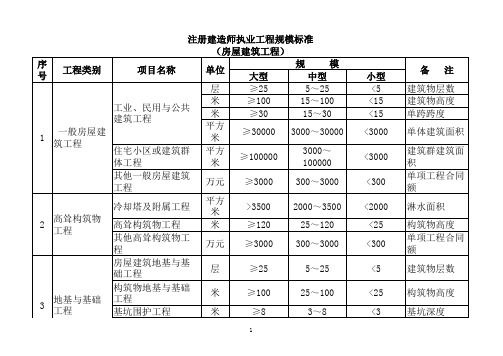
大,中,小型工程规模划分标准
万元 ≥200
50~200
米
≥80
层
≥25
米
≥80
15~80
5~25 15~80
3
小型 <10 <100 <3000 <10 <50 <200
<300
<50
<50
<15
<5 <15
备注
钢结构跨度 总重量
单体建筑面积
网架工程边长 总重量
单体建筑面积
单项工程合同 额 单项工程合同 额 单项工程合同 额
高度
1000~8000
万元 ≥500
100~500
米
≥30
10~30
万元 ≥800
100~800
级
≥C
D~C
级
≥B
D~B
万元 ≥500
200~500
小型 <1000
<100 <10 <100 <D
备注
单体建筑面积
单项工程合同 额 跨度 单项工程合同 额 爆破等级
<D
爆破等级
<200
单项工程合同 额
4
序 号
工程类别
项目名称
高尔夫球场、室内 外迷你高尔夫球场 和练习场工程
13
体育场地设 施工程
14
特种专业工 程
体育场田径场地设 施工程
体育馆(包括游泳 馆、冬季项目馆) 设施工程
合成面层网球、篮 球、排球场地设施 工程 其他体育场地设施 工程 建筑物纠偏和平移 等工程
(房屋筑工程)
单位
大型
规模 中型
公顷 ≥55
项目名称
福田区厨房工程招标文件

一、招标公告1. 项目名称:福田区厨房工程2. 招标单位:福田区某机关单位3. 项目地点:福田区某机关单位内部食堂4. 招标范围:包括但不限于厨房设备采购、安装、调试及售后服务等。
5. 招标方式:公开招标6. 招标时间:自本公告发布之日起至2023年X月X日止。
7. 投标截止时间:2023年X月X日17:00时。
8. 开标时间:2023年X月X日9:00时。
9. 开标地点:福田区某机关单位会议室。
二、项目概况1. 项目规模:本工程主要建设内容包括厨房设备采购、安装、调试及售后服务等。
2. 工程预算:项目预算总额为人民币XXX万元。
3. 工程工期:合同签订后,在30个工作日内完成设备安装调试并交付使用。
三、投标人资格要求1. 投标人须具备独立法人资格,注册资金不少于人民币XXX万元;2. 投标人须具备有效的营业执照、税务登记证、组织机构代码证;3. 投标人须具备有效的安全生产许可证;4. 投标人须具备厨房工程相关的专业资质证书;5. 投标人须有良好的商业信誉和健全的财务会计制度;6. 投标人须有类似项目业绩,并在近三年内无不良记录;7. 本项目不接受联合体投标;8. 本项目不接受代理商投标。
四、投标文件要求1. 投标文件应包含以下内容:(1)投标函;(2)法定代表人身份证明或授权委托书;(3)企业法人营业执照副本、税务登记证、组织机构代码证复印件;(4)安全生产许可证复印件;(5)相关资质证书复印件;(6)类似项目业绩证明材料;(7)投标报价文件;(8)售后服务承诺书;(9)其他相关证明材料。
2. 投标文件应密封完好,并在封口处加盖公章;3. 投标文件份数:正本1份,副本1份;4. 投标文件装订要求:采用线装或胶装,封面注明项目名称、招标单位名称、投标单位名称、日期等;5. 投标文件提交地点:福田区某机关单位招标办公室;6. 投标文件提交时间:自本公告发布之日起至2023年X月X日17:00时止;7. 逾期提交的投标文件,招标人不予受理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工程问题(1个课时) 工程问题在近年来的小升初考试中单独考的比较多,题型多以解答题的形式出现,所占分值4--10分不等,这跟所给题目的难易程度相关,纵观历年考题,工程问题考的大类主要有“求合作”和“求独干”两类。在做这类题时要时刻把握住工作总量,工作时间,工作效率三者之间关系。
完成一项工程,甲队单独做40天完成,乙队单独做要30天完成。甲队先干了这项工程的后,乙队又加入施工,两队合作了多少天完成这项工程? 考点:简单工程合作问题
解析:把整个工程总量看作单位“1”,由题意可知,甲队干了这项工程的81后,还剩87的工作量,剩下的工作
量由甲、乙合作完成,甲的工作效率是401,乙的工作效率是301,两队的工作效率之和是(401+301),那么剩下的工作量两队合作需要的天数是87÷(401+301)=15(天) 解答:(1-81)÷(401+301)=15(天) 答:两队合作了15天完成了这项工作。 点评:先求出甲乙要合干的工作总量,再把握住工作总量,工作时间,工作效率三者之间关系。
拓展一 完成一项工程,甲队单独做15天完成,乙队单独做要20天完成。甲队先干了这项工程的51后,乙队又加入施工,两队合作了多少天完成这项工程?
拓展二 完成一批零件,甲单独做12个小时完成,乙单独做要15个小时完成,丙单独做需要9小时,甲先完成了这批
零件的152后,乙、丙又加入其中,三人合作了多长时间完成这批零件?
(2012·小升初·解答题19)(4分)完成一项工程,甲队单独做20天完成,乙队单独做要30天完成。甲队先干了这项工程的41后,乙队又加入施工,两队合作了多少天完成这项工程?(9天)
(2011·外国语中学(东区)·小升初32).6分)单独完成一项工程,甲队要24天,乙队要30天.现在甲、乙两队合作4天后,丙队参加进来又经过7天完成全工程.如果一开始三队就一起工作,多少天可以完成全工程?10(天) (桐柏路一中· 解答题·2)(7分) 有一个水箱上装有两个进水管,单开1号水管15分钟可以把空水箱注满水,单开2号水管10分钟可以把空水箱注满水.如果要求不超过8分钟把空水箱注满水,那么两个水管至少应同时打开多长时间?
一项工作,第一天甲、乙两人合做4小时,完成全部工作的21 ;第二天乙又独做了5小时,还剩全部工作的
51没完成.这件工作由甲一人独做完成需要多少小时?
解析:把整个工程总量看作单位“1”,由题意可知,第一天,甲、乙两队4小时干了这项工程的21后,还剩2
1
的工作量,第二天,乙5小时干了(21-51)=103的工作量,那么,乙的工作效率是103÷5=503,由于两队的工作效率之和是21÷4=81,那么剩甲的工作效率就是81-503=20013,家独自一人需1÷20013=13515(小时) 解答:(1-21-51)÷5=503
21÷4 -503=20013
1÷20013=13515(小时) 答:两队合作了13515小时完成了这项工作。 点评:本题主要考查学生依据工作总量,工作时间以及工作效率之间等量关系解决问题的能力,解答本题的关键是求出甲的工作效率. 拓展一
一项工程,第一次甲、乙两对合做4天,完成全部工作的157 ;第二次乙队独做了5天,还剩全部工程的132没完成.这项工程由甲队独做需多少天完成? 拓展二
要生产一批零件,甲、乙两个车间生产了10天,完成了这批零件的52 ;因加车间设备出现问题,乙车间单独生产
了15天,还剩全部零件的81没生产完.如果这批零件由甲车间单独生产,需多少天?
拓展三 一个水池,有甲、乙、丙三个水龙头注水,同时打开甲、乙两个水龙头4小时可以把水池注满,同时打开乙、丙两个水龙头5小时可以把水池注满,现在先打开甲、丙两个水龙头2小时,余下的由乙水龙头用6小时注满,那么甲水龙头单独注水需要几小时注满? (2011·12“大山杯”数学邀请赛·初赛·解答题14)(8分)一个水池,甲乙两管同时打开,5小时能灌满;乙丙两管同时打开,4小时能灌满;如果乙管打开6小时,还需要甲丙两管同时开2小时才能灌满,那么单开乙管多少小时可以灌满?
(2012·市七十三中·4月份·小升初·应用题14)(10分)一件工作,有甲、乙合作5小时可以完成,乙、丙合作6小时可以完成,现在由甲、丙合作2小时,余下的乙又用8小时做完,那么甲单独完成这件工作需要几小时?
(2012·枫杨外国语·应用题·3)(8分)一项工作,甲、乙两人合作8天完成,乙、丙两人合作9天完成。丙、甲两人合作18天完成,那么丙一个人来做,完成这项工作需要多少天?
(枫杨·2012·应用题·13) 一项工程,甲先单独做2天,然后与乙合作7天,这样才完成全工程的一半。已知甲、乙工作效率的比为3:2,如果这件工作由乙单独做,需要多少天才能完成?
(2013·7月7日·枫杨·填空)10、一件工作,甲的工作效率是乙丙工作效率之和,乙的工作效率是甲丙之和的15。如果三人合作1天就可以完成,那么乙单独完成需要 天。
练习题 2.一项工作,甲、乙两人合作6天完成,乙、丙两人合作10天完成。现在由甲、乙、丙合作3天后,余下的乙再做6天可以完成,乙独坐需要几天可以完成? 完成一项工程,甲队单独做15天完成,乙队单独做要20天完成。甲队先干了这项工程的51后,乙队又加入施工,两队合作了多少天完成这项工程? 1÷15=151 1÷20=201 1-51=54 54÷(151+201)=7
66(天) 完成一批零件,甲单独做12个小时完成,乙单独做要15个小时完成,丙单独做需要9小时,甲先完成了这批
零件的152后,乙、丙又加入其中,三人合作了多长时间完成这批零件? 1÷12=121 1÷15=151 1÷9=91 1-152=1513 1513÷(121+151+91)=47153(小时) 1÷25=251 1÷15=151 1÷20=201 1—253—(152+101)=150127 150127÷(251+151+201)=47195(天) (2012·小升初·解答题19)(4分)完成一项工程,甲队单独做20天完成,乙队单独做要30天完成。甲队
先干了这项工程的41后,乙队又加入施工,两队合作了多少天完成这项工程? (9天) (2011·外国语中学(东区)·小升初32).6分)单独完成一项工程,甲队要24天,乙队要30天.现在甲、乙两队
合作4天后,丙队参加进来又经过7天完成全工程.如果一开始三队就一起工作,多少天可以完成全工程? 10(天)
(桐柏路一中·解答题·2)(7分) 有一个水箱上装有两个进水管,单开1号水管15分钟可以把空水箱注满水,单开2号水管10分钟可以把空水箱注满水.如果要求不超过8分钟把空水箱注满水,那么两个水管至少应同时打开多长时间?
(1-101×8)÷151=3(分钟) 一项工程,第一次甲、乙两对合做4天,完成全部工作的157 ;第二次乙队独做了5天,还剩全部工程的132没完成.这项工程由甲队独做需多少天完成? 1—157—132=19574 19574÷5=97574 157÷4=607 1÷(607—975
74)=532824(天)
要生产一批零件,甲、乙两个车间生产了10天,完成了这批零件的52 ;因加车间设备出现问题,乙车间单独
生产了15天,还剩全部零件的81没生产完.如果这批零件由甲车间单独生产,需多少天?
52÷10=251 1—52—81=4019 4019÷15=60019 251—60019=1201 1÷1201=120(天)
一个水池,有甲、乙、丙三个水龙头注水,同时打开甲、乙两个水龙头4小时可以把水池注满,同时打开乙、
丙两个水龙头5小时可以把水池注满,现在先打开甲、丙两个水龙头2小时,余下的由乙水龙头用6小时注满,那么甲水龙头单独注水需要几小时注满?
甲效+乙效=41 乙效+丙效=51 2甲效+2丙效+6乙效=1 甲效+丙效+2乙效=209
2甲效+2丙效+4乙效=2018 2乙效=101 乙效=201 甲效=51 1÷51=5(小时) (2011·12“大山杯”数学邀请赛·初赛·解答题14)(8分)一个水池,甲乙两管同时打开,5小时能灌满;乙丙两管同时打开,4小时能灌满;如果乙管打开6小时,还需要甲丙两管同时开2小时才能灌满,那么单开乙管多少小时可以灌满?
(20个小时) (2012·市七十三中·4月份·小升初·应用题14)(10分)一件工作,有甲、乙合作5小时可以完成,乙、丙合作6小时可以完成,现在由甲、丙合作2小时,余下的乙又用8小时做完,那么甲单独完成这件工作需要几小时?
(217小时) (2012·枫杨外国语·应用题·3)(8分)一项工作,甲、乙两人合作8天完成,乙、丙两人合作9天完成。丙、甲两人合作18天完成,那么丙一个人来做,完成这项工作需要多少天? (24天)
(枫杨·2012·应用题·13) 一项工程,甲先单独做2天,然后与乙合作7天,这样才完成全工程的一半。已知甲、乙工作效率的比为3:2,如果这件工作由乙单独做,需要多少天才能完成?
(3113天)
(2013·7月7日·枫杨·填空)10、一件工作,甲的工作效率是乙丙工作效率之和,乙的工作效率是甲丙之和的15。如果三人合作1天就可以完成,那么乙单独完成需要_6_天
练习题 2.(7天) 2.一项工作,甲、乙两人合作6天完成,乙、丙两人合作10天完成。现在由甲、乙、丙合作3天后,余下的乙再做6天可以完成,乙独坐需要几天可以完成? (15天)
