高一数学暑假学习材料09
最新人教版高一数学知识点总结暑假作业必备优秀名师资料

人教版高一数学知识点总结暑假作业必备高中数学必修1知识点第一章集合与函数概念【1.1.1】集合的含义与表示(1)集合的概念集合中的元素具有确定性、互异性和无序性.(2)常用数集及其记法NN表示自然数集,或表示正整数集,表示整数集,表示有理数集,表示实数集. ,NQZR,(3)集合与元素间的关系aM,aM,对象与集合的关系是,或者,两者必居其一. aM(4)集合的表示法?自然语言法:用文字叙述的形式来描述集合.?列举法:把集合中的元素一一列举出来,写在大括号内表示集合.?描述法:{|具有的性质},其中为集合的代表元素. xxx?图示法:用数轴或韦恩图来表示集合.(5)集合的分类?含有有限个元素的集合叫做有限集.?含有无限个元素的集合叫做无限集.?不含有任何元素的集合,叫做空集().1.1.2】集合间的基本关系【(6)子集、真子集、集合相等名称记号意义性质示意图(1)A,A A,B(或,,AA中的任一元素都属(2) A(B)子集 BAA,BBC,AC,(3)若且,则于B B,A)或 A,BBA,AB,(4)若且,则AB (1)(A为非空子集) ,,,A,,A,B,且B中至真子集 BA少有一元素不属于A (或BA) (2)若且,则 ,AB,BC,AC,,,,,A中的任一元素都属,集合 B (1)AA(B)于B,B中的任一元素AB, ,相等 (2)BA 都属于Annn221,21,(7)已知集合有个元素,则它有个子集,它有个真子集,它有个非空子集,nn(1),An22,它有非空真子集.【1.1.3】集合的基本运算(8)交集、并集、补集名称记号意义性质示意图AAA:, (1)且{|,xxA,AB:A:,,,(2) 交集 ABABA:, (3) xB,}ABB:,AAA:, (1)或{|,xxA,AB:AA:,,(2) 并集 BAABA:, (3) xB,}ABB:,2 1AAU:()ð,AA:()ð,,UU{|,}xxUxA,,且痧()()()ABAB::, UUU补集ðAU痧ABAB::, ()()() UUU【补充知识】含绝对值的不等式与一元二次不等式的解法(1)含绝对值的不等式的解法不等式解集||(0)xaa,,{|}xaxa,,,或 ||(0)xaa,,xxa|,,xa,}axb,看成一个整体,化成,把||xa,||,||(0)axbcaxbcc,,,,,型不等式来求解 ||(0)xaa,,(2)一元二次不等式的解法判别式,,0,,0,,0 2,,,bac4二次函数2yaxbxca,,,,(0)O的图象2一元二次方程,,,bbac4x,1,2b22axx,,, 无实根 axbxca,,,,0(0)122axx,)的根 (其中 122baxbxca,,,,0(0)或 x,,}{|xxx,xx,}{|x R122a的解集2axbxca,,,,0(0) {|}xxxx,,,, 12的解集〖1.2〗函数及其表示【1.2.1】函数的概念(1)函数的概念?设、是两个非空的数集,如果按照某种对应法则,对于集合中任何一个数,在集合xfABAB中都有唯一确定的数和它对应,那么这样的对应(包括集合,以及到的对应法则)fx()fABAB叫做集合到的一个函数,记作( fAB:,AB?函数的三要素:定义域、值域和对应法则(?只有定义域相同,且对应法则也相同的两个函数才是同一函数()区间的概念及表示法 (2ab,axb,,?设是两个实数,且,满足的实数的集合叫做闭区间,记做;满足xab,[,]abaxb,,axb,,axb,,的实数的集合叫做开区间,记做;满足,或的实数的xx(,)ab集合叫做半开半闭区间,分别记做,;满足的实数的集x[,)ab(,]abxaxaxbxb,,,,,,,合分别记做( [,),(,),(,],(,)aabb,,,,,,,, b注意:对于集合与区间,前者可以大于或等于,而后者必须 a(,)ab{|}xaxb,, ab,((3)求函数的定义域时,一般遵循以下原则:?fx()是整式时,定义域是全体实数(?fx()是分式函数时,定义域是使分母不为零的一切实数(fx()?是偶次根式时,定义域是使被开方式为非负值时的实数的集合( ?对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1(,xkkZ,,,()yx,tan?,中,( 2?零(负)指数幂的底数不能为零(fx()?若是由有限个基本初等函数的四则运算而合成的函数时,则其定义域一般是各基本初等函数的定义域的交集(一般步骤是:若已知?对于求复合函数定义域问题,的定义域为,其复合函数fx()[,]abfgx[()]的定义域应由不等式解出( agxb,,()?对于含字母参数的函数,求其定义域,根据问题具体情况需对字母参数进行分类讨论( ?由实际问题确定的函数,其定义域除使函数有意义外,还要符合问题的实际意义((4)求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的(事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值(因此求函数的最值与值域,其实质是相同的,只是提问的角度不同(求函数值域与最值的常用方法:?观察法:对于比较简单的函数,我们可以通过观察直接得到值域或最值( ?配方法:将函数解析式化成含有自变量的平方式与常数的和,然后根据变量的取值范围确定函数的值域或最值(?判别式法:若函数可以化成一个系数含有的关于的二次方程xyfx,()y2,则在时,由于为实数,故必须有xy,ay()0,ayxbyxcy()()()0,,,2,从而确定函数的值域或最值( ,,,,,byaycy()4()()0?不等式法:利用基本不等式确定函数的值域或最值(?换元法:通过变量代换达到化繁为简、化难为易的目的,三角代换可将代数函数的最值问题转化为三角函数的最值问题(?反函数法:利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值( ?数形结合法:利用函数图象或几何方法确定函数的值域或最值( ?函数的单调性法(【1.2.2】函数的表示法(5)函数的表示方法表示函数的方法,常用的有解析法、列表法、图象法三种(解析法:就是用数学表达式表示两个变量之间的对应关系(列表法:就是列出表格来表示两个变量之间的对应关系(图象法:就是用图象表示两个变量之间的对应关系((6)映射的概念?设、是两个集合,如果按照某种对应法则f,对于集合中任何一个元素,在集合中都ABAB有唯一的元素和它对应,那么这样的对应(包括集合,以及到的对应法则f)叫做集合ABABA到的映射,记作fAB:,( Bba?给定一个集合到集合的映射,且aAbB,,,(如果元素和元素对应,那么我们把元素ABbbaa叫做元素的象,元素叫做元素的原象(〖1.3〗函数的基本性质【1.3.1】单调性与最大(小)值(1)函数的单调性?定义及判定方法函数的定义图象判定方法性质如果对于属于定义域I内某(1)利用定义个区间上的任意两个自变量(2)利用已知函数的yy=f(X)的值x、x,当x< x时,都1212f(x )((单调性 2(((有f(x)<f(x),那么就说12(((3)利用函数图象(在(((((((((f(x )1f(x)在这个区间上是增函数( 某个区间图 (((o 象上升为增) xxx12 函数的 (4)利用复合函数单调性 (1)利用定义如果对于属于定义域I内某(2)利用已知函数的yy=f(X)个区间上的任意两个自变量单调性 f(x )1的值x、x,当x< x时,都1212(((3)利用函数图象(在(((f(x )2有f(x)>f(x),那么就说12((某个区间图(((((((((f(x)在这个区间上是减函数( ox象下降为减) (((xx12(4)利用复合函数 ?在公共定义域内,两个增函数的和是增函数,两个减函数的和是减函数,增函数减去一个减函数为增函数,减函数减去一个增函数为减函数(?对于复合函数,令,若为增,为增,则yfu,()yfgx,[()]ugx,()ugx,()为增;若为减,为减,则为增;若为yfu,()yfu,()yfgx,[()]ugx,()yfgx,[()]增,为减,则为减;若为减,为增,则yfu,()ugx,()yfgx,[()]ugx,()y为减( yfgx,[()]afxxa()(0),,,(2)打“?”函数的图象与性质 xfx()分别在、上为增函数,分别在(,],,,a[,)a,,o x、上为减函数( [,0),a(0,]a(3)最大(小)值定义yfx,() ?一般地,设函数的定义域为,如果存在实数满足:(1)IMxI,对于任意的fxM(),,都有;xI,fxM(),fx() (2)存在,使得(那么,我们称是函数的最大值,记作M00 ( fxM(),maxxI,?一般地,设函数的定义域为,如果存在实数满足:(1)对于任意的,都有myfx,()I;(2)存在,使得(那么,我们称是函数的最小值,记作xI,fxm(),mfxm(),fx()00( fxm(),max【1.3.2】奇偶性(4)函数的奇偶性?定义及判定方法函数的定义图象判定方法性质如果对于函数f(x)定义域内(1)利用定义(要先任意一个x,都有f(,x)=,判断定义域是否关于(((((((f(x),那么函数f(x)叫做奇函原点对称) ((((((数( (2)利用图象(图象(关于原点对称)函数的奇偶性如果对于函数f(x)定义域内(1)利用定义(要先任意一个x,都有f(,x)=f(x),判断定义域是否关于(((((((((( 那么函数f(x)叫做偶函数( 原点对称) ((((2)利用图象(图象关于y轴对称)x,0?若函数为奇函数,且在处有定义,则( fx()f(0)0,?奇函数在轴两侧相对称的区间增减性相同,偶函数在轴两侧相对称的区间增减性相反( yy?在公共定义域内,两个偶函数(或奇函数)的和(或差)仍是偶函数(或奇函数),两个偶函数(或奇函数)的积(或商)是偶函数,一个偶函数与一个奇函数的积(或商)是奇函数(〖补充知识〗函数的图象(1)作图利用描点法作图:?确定函数的定义域; ?化解函数解析式;?讨论函数的性质(奇偶性、单调性); ?画出函数的图象(利用基本函数图象的变换作图:要准确记忆一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等各种基本初等函数的图象(?平移变换hh,0,左移个单位yfxyfxh,,,,,,,,,,,()()hh,0,|右移|个单位kk,上移个单位0,yfxyfxk,,,,,,,,,,,()() kk,下移|个单位0,|?伸缩变换01,,,,伸 yfxyfx,,,,,,,()(),,1,缩,01,,,A缩 yfxyAfx,,,,,,,()()A,1,伸?对称变换y轴x轴 yfxyfx,,,,,,,()()yfxyfx,,,,,,,()()直线yx,原点,1 yfxyfx,,,,,,,,()()yfxyfx,,,,,,,()()去掉轴左边图象yyfxyfx,,,,,,,,,,,,,,,,,,()(||) 保留轴右边图象,并作其关于轴对称图象yy保留轴上方图象x yfxyfx,,,,,,,,,,,,()|()|将轴下方图象翻折上去x(2)识图对于给定函数的图象,要能从图象的左右、上下分别范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性,注意图象与函数解析式中参数的关系((3)用图函数图象形象地显示了函数的性质,为研究数量关系问题提供了“形”的直观性,它是探求解题途径,获得问题结果的重要工具(要重视数形结合解题的思想方法(第二章基本初等函数(?)〖2.1〗指数函数【2.1.1】指数与指数幂的运算 (1)根式的概念n?如果,且,那么叫做的次方根(当是奇数时,nN,xannxaaRxRn,,,,,,,1,nnaa的次方根用符号表示;当是偶数时,正数的正的次方根用符号表示,负的次方annannn,a根用符号表示;0的次方根是0;负数没有次方根( nanna?式子叫做根式,这里叫做根指数,叫做被开方数(当为奇数时,为任意实数;当nanaa,0n为偶数时,(nnnnaa,?根式的性质:;当n为奇数时,;当n为偶数时, ()aa,aa (0),,nn( aa,,||,,,aa (0) ,(2)分数指数幂的概念mnmnaaamnN,,,(0,,,?正数的正分数指数幂的意义是:且n,1)(0的正分数指数,幂等于0(mm, 11mnnnaamnN,,,,()()(0,,,?正数的负分数指数幂的意义是:n,1)且(0,aa 的负分数指数幂没有意义( 注意口诀:底数取倒数,指数取相反数( (3)分数指数幂的运算性质rsrs,rsrs? ? aaaarsR,,,,(0,,)()(0,,)aaarsR,,,rrr? ()(0,0,)abababrR,,,,【2.1.2】指数函数及其性质 (4)指数函数函数名称指数函数x定义函数且叫做指数函数 a,1)yaa,,(0a,101,,axxy yy,ay,a图象 (0,1)y,1y,1 (0,1)1 1 OOxx0 0定义域 R值域 (0,),,过定点 x,0图象过定点,即当时,( (0,1)y,1奇偶性非奇非偶单调性在上是增函数在上是减函数 RRxxax,,1(0)ax,,1(0)函数值的 xx ax,,1(0)ax,,1(0)变化情况 xxax,,1(0)ax,,1(0)aaa变化对图象的影响在第一象限内,越大图象越高;在第二象限内,越大图象越低( 〖2.2〗对数函数【2.2.1】对数与对数运算(1)对数的定义xNxN,logxaa ?若,则叫做以为底的对数,记作,其中叫做底数,aNaa,,,(0,1)且aN叫做真数(?负数和零没有对数(xxNaNaaN,,,,,,log(0,1,0)?对数式与指数式的互化:( a(2)几个重要的对数恒等式b,,( log10,log1a,logab,aaa(3)常用对数与自然对数lnNe,2.71828常用对数:,即;自然对数:,即(其中…)( logNlogNlgN10e(4)对数的运算性质如果,那么 aaMN,,,,0,1,0,0M?加法: ?减法:logloglog MN,,logloglog()MNMN,,aaaaaaNlogNna?数乘: ? aN,nMMnRloglog(),,aanlogNnb?loglog(0,) ?换底公式: MMbnR,,,log(0,1)Nbb,,,且baaablogab【2.2.2】对数函数及其性质 (5)对数函数函数对数函数名称定义函数且叫做对数函数 yxa,,log(0a,1)aa,101,,ax,1x,1yyyx,log yx,logaa图象 (1,0)1 1OO(1,0)xx 0 0定义域 (0,),,值域 R过定点 x,1图象过定点,即当时,y,0( (1,0)奇偶性非奇非偶(0,),,(0,),,在上是增函数在上是减函数单调性log0(1)xx,,log0(1)xx,,aa函数值的 log0(1)xx,,log0(1)xx,,aa变化情况log0(01)xx,,,log0(01)xx,,,aa变化对图象的影响在第一象限内,越大图象越靠低;在第四象限内,越大图象越靠高( aaa(6)反函数的概念C设函数的定义域为,值域为,从式子中解出,得式子(如xyfx,()yfx,()xy,,()AC果对于在中的任何一个值,通过式子,在中都有唯一确定的值和它对应,那么式xxy,,()yA,1子表示是的函数,函数叫做函数的反函数,记作,xxy,,()xy,,()yfx,()xfy,()y,1习惯上改写成( yfx,()(7)反函数的求法,1?确定反函数的定义域,即原函数的值域;?从原函数式中反解出;yfx,()xfy,(),1,1?将改写成,并注明反函数的定义域( xfy,()yfx,()(8)反函数的性质,1 ?原函数与反函数的图象关于直线对称( yx,yfx,()yfx,(),1?函数的定义域、值域分别是其反函数的值域、定义域( yfx,()yfx,()',1?若在原函数的图象上,则在反函数的图象上( Pab(,)yfx,()Pba(,)yfx,() ?一般地,函数要有反函数则它必须为单调函数( yfx,()〖2.3〗幂函数(1)幂函数的定义, 一般地,函数叫做幂函数,其中x为自变量,,是常数( yx,(2)幂函数的图象(3)幂函数的性质?图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象(幂函数是偶函数时,图象分布在第一、二象限(图象关于轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶y函数时,图象只分布在第一象限(?过定点:所有的幂函数在都有定义,并且图象都通过点( (0,),,(1,1),,0,,0?单调性:如果,则幂函数的图象过原点,并且在上为增函数(如果,则幂函数[0,),,的图象在上为减函数,在第一象限内,图象无限接近轴与轴( x(0,),,y q?奇偶性:当为奇数时,幂函数为奇函数,当为偶数时,幂函数为偶函数(当(其中互pq,,,,,pqqpp质,和),若为奇数为奇数时,则是奇函数,若为奇数为偶数时,则qZ,yx,yx,ppqpqqp是偶函数,若为偶数为奇数时,则是非奇非偶函数( yx,pq,,,101,,x?图象特征:幂函数,当时,若,其图象在直线yx,下方,若yxx,,,,,(0,)x,1,,101,,xx,1yx,yx,,其图象在直线上方,当时,若,其图象在直线上方,若,yx,其图象在直线下方(〖补充知识〗二次函数(1)二次函数解析式的三种形式22?一般式:?顶点式:?两根式:fxaxbxca()(0),,,,fxaxhka()()(0),,,, fxaxxxxa()()()(0),,,,(2)求二次函数解析式的方法 12?已知三个点坐标时,宜用一般式(?已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式(xfx()?若已知抛物线与轴有两个交点,且横线坐标已知时,选用两根式求更方便( (3)二次函数图象的性质b2x,,,?二次函数的图象是一条抛物线,对称轴方程为顶点坐标是fxaxbxca()(0),,,,2a2bacb4,( (,),24aabbba,0?当时,抛物线开口向上,函数在上递减,在上递增,当时,(,],,,[,),,,x,,2a2a2a24acb,bba,0;当时,抛物线开口向下,函数在上递增,在上(,],,,[,),,,fx(),min2a2a4a24acb,b递减,当时,( x,,fx(),max2a4a22?二次函数当时,图象与轴有两个交点,,,,bac40xfxaxbxca()(0),,,, ,( MxMxMMxx(,0),(,0),||||,,,11221212||a2(4)一元二次方程根的分布 axbxca,,,,0(0)一元二次方程根的分布是二次函数中的重要内容,这部分知识在初中代数中虽有所涉及,但尚不够系统和完整,且解决的方法偏重于二次方程根的判别式和根与系数关系定理(韦达定理)的运用,下面结合二次函数图象的性质,系统地来分析一元二次方程实根的分布(2 设一元二次方程的两实根为,且(令xx,xx,axbxca,,,,0(0)1212b2x,,,从以下四个方面来分析此类问题:?开口方向: ?对称轴位置: afxaxbxc(),,,2a?判别式: ?端点函数值符号( ,?k,x?x ,12yybx,,a,0f(k),02a,OOkkxxxx2112xx,bf(k),0x,,a,02a ?x?x,k ,12yybf(k),0x,,a,02a,OOkx2kxxx211xx,ba,0f(k),0x,,2a?x,k,x af(k),0 ,12yya,0f(k),0,OkOxxxxk2112xx,f(k),0a,0?k,x?x,k ,1122ya,0byx,,2a,fk,()01()0fk,2,kxk1x221OOxx2kk1xx12,,()0fk,1bf(k),02x,,a,02a?有且仅有一个根x(或x)满足k,x(或x),k f(k)f(k)0,并同时考虑f(k)=0,,121122121或f(k)=0这两种情况是否也符合 2yya,0,fk,fk,()0()011,kxk212xOOxx12kk2xx11,,()0fk,2a,0()0fk,2?k,x,k?p,x,p ,112122此结论可直接由?推出(2(5)二次函数在闭区间[,]pq上的最值 fxaxbxca()(0),,,,1xpq,,()mfx()[,]pq 设在区间上的最大值为,最小值为,令( M02a,0(?)当时(开口向上)bbbbpq,,,mf,,(),,p,,q?若,则mfp,() ?若,则 ?若,则2a2a2a2amfq,() y b , a 0 , , x y y , b , b a 0 a 0 2 a , , , , x x 2 a 2 a ffff (q) (p) (p) p (q) q q O x p q p O O x x f bbbff(),f(),(p) f(),bb2a2a2a?若,,x,则 ?,,x,则 Mfq,()Mfp,()(q) 002a2ay , b a 0 b , , y x , a 0 , , x 2 a 2 a fa,0(?)当时(开口向下) f(p) q xbbbb0(q) xp pq,,,?若Mf,,(),则 ?若,则 ?若,则,,p,,qMfp,()0 p O x2a2a2a2aq O x b Mfq,()fff(),2ab(p) (q) f(), 2ay , ba 0 y y , , bbf(),a 0 a 0 ff(),f(), 2a2a2a(q) ffp (p) (p) q q q O x p p O O x x fffb , , b b x , , , , x x (p) (q)(q) 2 a 2 a 2 a bb,,x,,x?若,则 ?,则( mfq,()mfp,()002a2ay y b, a 0 , ba 0 f(),f(),f2a2a f(q) (p) xq p 0x0 p O x q O x ffbb , , x , , (q)x 2 a (p) 2 a 第三章函数的应用一、方程的根与函数的零点x1、函数零点的概念:对于函数,把使成立的实数叫做函数y,f(x)(x,D)f(x),0 的零点。
高一数学必修一(暑期自学材料,非常详细)

高一数学必修一(暑期自学材料,非常详细)第一章集合§1.1 集合与集合的表示方法1.1.1 集合的概念1.元素与集合的概念(1)集合:一般地,把一些能够____________对象看成一个整体,就说这个整体是由这些对象的______构成的集合(或集).通常用英语大写字母表示.(2)元素:构成集合的________叫做这个集合的元素(或成员),通常用英语小写字母表示. 2.集合中元素的特性:________、________. 3.元素与集合的关系(1)如果a是集合A的元素,就说________,记作_____________________________. (2)如果a不是集合A的元素,就说__________,记作______.4.实数集、有理数集、整数集、非负整数集、正整数集分别用字母____、____、____、____、____或____来表示.5.集合的分类?集合??非空集合:空集:不含任何元素,记作 .按含有元素?? :含有有限个元素?的个数分为?? :含有无限个元素一、选择题1.下列语句能确定是一个集合的是( )A.著名的科学家 B.留长发的女生 C.2021年广州亚运会比赛项目 D.视力差的男生 2.集合A只含有元素a,则下列各式正确的是( ) A.0∈A ;B.a?A ;C.a∈A ;D.a=A3.已知M中有三个元素可以作为某一个三角形的边长,则此三角形一定不是( ) A.直角三角形; B.锐角三角形;C.钝角三角形; D.等腰三角形4.由a2,2-a,4组成一个集合A,A中含有3个元素,则实数a的取值可以是( ) A.1 ; B.-2;C.6 ; D.25.已知集合A是由0,m,m2-3m+2三个元素组成的集合,且2∈A,则实数m为( ) A.2 ;B.3;C.0或3 ;D.0,2,3均可36.由实数x、-x、|x|、x2及-x3所组成的集合,最多含有( ) A.2个元素;B.3个元素;C.4个元素;D.5个元素二、填空题7.由下列对象组成的集体属于集合的是________.(填序号) ①不超过π的正整数;②本班中成绩好的同学;③高一数学课本中所有的简单题;④平方后等于自身的数.8.集合A中含有三个元素0,1,x,且x2∈A,则实数x的值为________. 9.用符号“∈”或“?”填空-2_______R,-3______Q,-1______N,π________Z. 三、解答题10.判断下列说法是否正确?并说明理由.(1)参加2021年广州亚运会的所有国家构成一个集合; (2)未来世界的高科技产品构成一个集合;31(3)1,0.5,,组成的集合含有四个元素; (4)高一(三)班个子高的同学构成一个集合.22- 1 -11.已知集合A是由a-2,2a+5a,12三个元素组成的,且-3∈A,求a.能力提升12.设P、Q为两个非空实数集合,P中含有0,2,5三个元素,Q中含有1,2,6三个元素,定义集合P+Q中的元素是a+b,其中a∈P,b∈Q,则P+Q中元素的个数是多少?113.设A为实数集,且满足条件:若a∈A,则∈A (a≠1).1-a求证:(1)若2∈A,则A中必还有另外两个元素; (2)集合A不可能是单元素集.1.考查对象能否构成一个集合,就是要看是否有一个确定的特征(或标准),能确定一个个体是否属于这个总体,如果有,能构成集合,如果没有,就不能构成集合. 2.集合中元素的三个性质(1)确定性:指的是作为一个集合中的元素,必须是确定的,即一个集合一旦确定,某一个元素属于不属于这个集合是确定的.要么是该集合中的元素要么不是,二者必居其一,这个特性通常被用来判断涉及的总体是否构成集合.(2)互异性:集合中的元素必须是互异的,就是说,对于一个给定的集合,它的任何两个元素都是不同的.2- 2 -第一章集合§1.1 集合与集合的表示方法1.1.1 集合的概念知识梳理1.(1)确定的不同的全体 (2)每个对象 2.确定性互异性3.(1)a属于A a∈A (2)a不属于集合A a?A 4.R Q Z N N* N+ 5.? 有限集无限集作业设计1.C [选项A、B、D都因无法确定其构成集合的标准而不能构成集合.]2.C [由题意知A中只有一个元素a,∴0?A,a∈A,元素a与集合A的关系不应用“=”,故选C.] 3.D [集合M的三个元素是互不相同的,所以作为某一个三角形的边长,三边是互不相等的,故选D.] 4.C [因A中含有3个元素,即a2,2-a,4互不相等,将选项中的数值代入验证知答案选C.] 5.B [由2∈A可知:若m=2,则m2-3m+2=0,这与m2-3m+2≠0相矛盾;若m2-3m+2=2,则m=0或m=3,当m=0时,与m≠0相矛盾,当m=3时,此时集合A={0,3,2},符合题意.]36.A [因为|x|=±x,x2=|x|,-x3=-x,所以不论x取何值,最多只能写成两种形式:x、-x,故集合中最多含有2个元素.] 7.①④解析①④中的标准明确,②③中的标准不明确.故答案为①④. 8.-1解析当x=0,1,-1时,都有x2∈A,但考虑到集合元素的互异性,x≠0,x≠1,故答案为-1. 9.∈ ∈ ? ?10.解 (1)正确.因为参加2021年广州亚运会的国家是确定的,明确的. (2)不正确.因为高科技产品的标准不确定.1(3)不正确.对一个集合,它的元素必须是互异的,由于0.5=,在这个集合中只能作为一元素,故这个集合含2有三个元素.(4)不正确,因为个子高没有明确的标准.311.解由-3∈A,可得-3=a-2或-3=2a2+5a,∴a=-1或a=-.22则当a=-1时,a-2=-3,2a+5a=-3,不符合集合中元素的互异性,故a=-1应舍去.373当a=-时,a-2=-,2a2+5a=-3,符合题意.∴a=-.22212.解∵当a=0时,b依次取1,2,6,得a+b的值分别为1,2,6;当a=2时,b依次取1,2,6,得a+b的值分别为3,4,8;当a=5时,b依次取1,2,6,得a+b的值分别为6,7,11. 由集合元素的互异性知P+Q中元素为1,2,3,4,6,7,8,11共8个.1113.证明 (1)若a∈A,则∈A. 又∵2∈A,∴=-1∈A.1-a1-211111∵-1∈A,∴=∈A. ∵∈A,∴=2∈A. ∴A中另外两个元素为-1,.2121-?-1?21-211(2)若A为单元素集,则a=,即a2-a+1=0,方程无解.∴a≠,∴A不可能为单元素集.1-a1-a- 3 -1.1.2 集合间的基本关系和基本运算一、基础过关1.下列集合中,结果是空集的是A.{x∈R|x2-1=0} C.{(x,y)|x2+y2=0}( )B.{x|x>6或x<1} D.{x|x>6且x<1}( )2.集合P={x|y=x+1},集合Q={y|y=x-1},则P与Q的关系是 A.P=Q C.P��Q 3.下列命题:B.P��Q D.P∩Q=?①空集没有子集;②任何集合至少有两个子集;③空集是任何集合的真子集;④若?��A,则A≠?. 其中正确的个数是 A.0( )B.1 C.2 D.3( )4.下列正确表示集合M={-1,0,1}和N={x|x2+x=0}关系的Venn图是5.已知M={x|x≥22,x∈R},给定下列关系:①π∈M;②{π}��M;③π��M;④{π}∈M.其中正确的有________.(填序号)6.已知集合A={x|1<x<2},B={x|x<a},若A��B,则实数a的取值范围是________. 7.已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B?A,求实数m的取值范围. 8.若集合A={x|x2+x-6=0},B={x|x2+x+a=0},且B?A,求实数a的取值范围.二、能力提升9.适合条件{1}?A��{1,2,3,4,5}的集合A的个数是A.15个B.16个( )C.31个 D.32个10.集合M={x|x=3k-2,k∈Z},P={y|y=3n+1,n∈Z},S={z|z=6m+1,m∈Z}之间的关系是( )A.S��P��M C.S��P=MB.S=P��MD.P=M��S11.已知集合A��{2,3,7},且A中至多有1个奇数,则这样的集合共有________个. 12.已知集合A={x|1<ax<2},B={x|-1<x<1},求满足A?B的实数a的取值范围.- 4 -三、探究与拓展13.已知集合A={x||x-a|=4},B={1,2,b}.问是否存在实数a,使得对于任意实数b(b≠1,b≠2)都有A?B.若存在,求出对应的a值;若不存在,说明理由.- 5 -感谢您的阅读,祝您生活愉快。
初高中教材衔接第二讲 因式分解2009 2010年江苏靖江市新高一生初高中数学衔接内容暑期作业

第二讲因式分解因式分解是代数式的一种重要的恒等变形,它与整式乘法是相反方向的变形.在分式运算、解方程及各种恒等变形中起着重要的作用.是一种重要的基本技能.平方差公式和完全平方(因式分解的方法较多,除了初中课本涉及到的提取公因式法和公式法、十字相乘法和分组分解法等等.)外,还有公式法(立方和、立方差公式)公式)立方和、立方差公式一、公式法(在第一讲里,我们已经学习了乘法公式中的立方和、立方差公式:3322b?)b)(a??ab?ba(a?) 立方和公式(3322b?)(a??ab?ba)(a?b)立方差公式( 由于因式分解与整式乘法正好是互为逆变形,所以把整式乘法公式反过来写,就得到:2233)?ab??(a?b)(aa?bb2323)b?abb?(a?)(aa?b?这就是说,两个数的立方和(差),等于这两个数的和(差)乘以它们的平方和与它们积的差(和).运用这两个公式,可以把形式是立方和或立方差的多项式进行因式分解.【例1】用立方和或立方差公式分解下列各多项式:33b270.125?8?x(1) (2)33330.125?0.5,27b?(3b)28?.,(1)中,(2)中分析:3332)2xx?2?x?(2?x)(4?8?x? (1) 解:22333](3b)?b?(3)?(0.5?3b)[0.50.5?3b??0.125?27b0.5(2)2)b?9b)(0.25?1.5b3?(0.5?3338ab?(2ab),(1) 说明:在运用立方和(差)公式分解因式时,经常要逆用幂的运算法则,如nnn b?a(ab)一定要看准因式中各项的公式分解因式时,(2) 这里逆用了法则;在运用立方和(差) 符.【例2】分解因式:4367b?81b3aaba? (2) (1)66b?a,可看中提取公因式后,括内出现分析:(1) 中应先提取公因式再进一步分解;(2) 32223323)(ba)?b(a)?()(.着是或233234)?9bb)(a?3ab(b3a?81b?3b(a?27b)?3ba?3 (1) .解:33376663)a?ab?a(a?b)?a(ab)(a??b(2)2222)a?b)(ab?ab?a(a?b)(a?ab?b?)(2222)?ab?bab?a(a?b)(a?b)(a??b)(a二、分组分解法从前面可以看出,能够直接运用公式法分解的多项式,主要是二项式和三项式.而对于四项nb?ma?mb?na既没有公式可用,也没有公因式可以提取.因此,可以先以上的多项式,如将多项式分组处理.这种利用分组来因式分解的方法叫做分组分解法.分组分解法的关键在于如何分组.1.分组后能提取公因式bxby?2ax?10ay?5把分解因式.【例3】x 的降幂排列,然后从把多项式的四项按前两项与后两项分成两组,并使两组的项按分析:y5x?b?2a两组分别提出公因式,这时另一个因式正好都是,这样可以继续提取公因式.与)y)(2a?b5(x?y)?(x?55?2ax?10ay?5bybx?2a(x?y)?b解:用分组分解法,一定要想想分组后能否继续完成因式分解,由此合理选择分组的方说明:法.本题也可以将一、四项为一组,二、三项为一组,同学不妨一试.2222cd))c?d?(a?bab(分解因式.4 【例】把按照原先分组方式,无公因式可提,需要把括打开后重新分组,然后再分解因式.分析:22222222cdcd?ba)cd?abc?abd?b?cab(?d)(a?解:2222)bcd?(abc?aabdcd)?(?)?bd?(bcad)(ac)(adac?(bc?)?bdbc?ad?可以看出,分组时运用了加法结合律,而为了合理分组,先运用了加法4说明:由例3、例交换律,分组后,为了提公因式,又运用了分配律.由此可以看出运算律在因式分解中所起的作用.2.分组后能直接运用公式22ay?axyx??】5【例把分解因式.把第一、二项为一组,这两项虽然没有公因式,但可以运用平方差公式分解因式,其分析:a yxx?y?.后,另一个因式也是;把第三、四项作为另一组,在提出公因式中一个因式是22)?a)(x?y)?a(x?y)?(x?y?x?y?ax?ay?(x?y)(xy解:222z?82x?4xy?2y 6】把分解因式.【例222z4?y?2x?xy,其中前三项作为一组,它是一个完全2提出后,得到分析:先将系数平方式,再和第四项形成平方差形式,可继续分解因式.222222)?2(zy?4x?2xy?2x?4xy?2y?8z解:22)zy?22(?x?y?2z)(?2[(x?y)x?(2z)?]可以看出:如果一个多项式的项分组后,各组都能直接运用公式或提取说明:从例5、例6公因式进行分解,并且各组在分解后,它们之间又能运用公式或有公因式,那么这个多项式就可以分组分解法来分解因式.三、十字相乘法2pqq)x?x?(p? 1 .型的因式分解这类式子在许多问题中经常出现,其特点是:(2) 常数项是两个数之积;(3) 一次项系数是常数项的两个因数之和.(1) 二次项系数是1;22)q)(x???p)?(xp?qx?xpq?(x?p)?q(xxq?(p?)x?pq?x?px2)x?q?(x?p)(xx?(p?q)?pq因此,运用这个公式,可以把某些二次项系数为1的二次三项式分解因式.把下列各式因式分解:【例7】2236x?x?13x?7x?6 (2) (1)7???(?6)? 6?(?1)?(?6),(1) (1) 解:2)?)(6?]x(?x1][6?x?(?1)x[??(6)xx??7?.13?9? 36?4?9,4 (2)2(?4x)(?x13x?36?9)? x?说明:此例可以看出,常数项为正数时,应分解为两个同因数,它们的符与一次项系数的符相同.【例8】把下列各式因式分解:2215?224x?xxx?5?(1) (2)?24?(?3)?8,(?3)?8?5解:(1)2)?8)x(?x3)(2?4?x[?(?3)x](?8? x??5x2??5)?3,(?5)?3( ?15??(2)2)3(?x5)(??x[?(5)x](?3?)x? x?2x?15?此例可以看出,常数项为负数时,应分解为两个异的因数,其中绝对值较大的因数与说明:一次项系数的符相同.9】把下列各式因式分解:【例22222128(x?x?xy?6y)?(x?x)?x(2) (1) 222y?6x?xyy?6x y,看成,一次项系数是的二次三项式,这时常数项是分析:(1) 把2y?6y)??(?2y?2y3yy3的积,而把分解成,正好是一次项系数.与2x?xa,可不必写出,只当作分解二次三由换元思想,只要把整体看作一个字母(2)212?a?8a.项式2222)2y?(x?3y)(x??x?xy?6yx?yx?6解:(1)222222)x?x?)x?x)?8(x?x?12?(x?x?6)(((2)1)?2)(x?(x?3)(x?2)(x?2c?ax?bx 2.一般二次三项式型的因式分解2cx?c?(acac)xax?c)(a?c)?aax?(.大家知道,?cc,,a,acaacca11,这分解2111222212112)cx?x?c)(ac?a)x?cc?(a(aax?ac反过来,就得到:221121222111ca成写成分解成,把,常数项我们发现,二次项系数21212211ca222caac?c?ax?bx b,,如果它正好等于的一次项系数里按斜线交叉相乘,再相加,就得到11222)c)(ax?c(ax?ca,c,ac??bxax位于上一行,,其中就可以分解成那么位于下一行.22112211这种借助画十字交叉线分解系数,从而将二次三项式分解因式的方法,叫做十字相乘法.必须注意,分解因数及十字相乘都有多种可能情况,所以往往要经过多次尝试,才能确定一个二次三项式能否用十字相乘法分解.】把下列各式因式分解:10 【例222yxy?5x6?82125?xx? (2) (1)2?3?21)???5x?2?(3x2)(4x12x解:(1) 14y 21?22)x?2yy?4)(5x5x?6xy?8y?( (2) y45?时较困难,具体分解时,1说明:用十字相乘法分解二次三项式很重要.当二次项系数不是,看是否符合一”为提高速度,可先对有关常数分解,交叉相乘后,若原常数为负数,用减法”凑”凑”绝对值,然后调整,添加正、负.,先次项系数,否则用加法”凑”四、其它因式分解的方法.配方法1216?6x?x分解因式11【例】2222225?3)?(?2?x?3?3?3?16?x16x?6x??x解:2)8)(x??5)?(x?(?x?3?5)(x?3配方后将二次三项式化为两个平方式,说明:这种设法配成有完全平方式的方法叫做配方法,然后用平方差公式分解.当然,本题还有其它方法,请大家试验..拆、添项法2234?x?3x】【例12分解因式细查式中无一次项,分组也不易进行.分析:此多项式显然不能直接提取公因式或运用公式,了,可考虑通0如果它能分解成几个因式的积,那么进行乘法运算时,必是把一次项系数合并为过添项或拆项解决.22333)x???4?(x1)?(3?x3x解:221)]??3(xx?x?1)1)1)??3(x?1)(x??(x?1)[(x?(?1)(x?x222)?x(?1)(x?1)(x?4x?4)?x?(的和,将多项式分成两组,满足系数对应成比例,造成与34拆成1说明:本解法把原常数222y?4xx3?,将多项式分成两组拆成可以用公式法及提取公因式的条件.本题还可以将223)(x?x4??4x和.一般地,把一个多项式因式分解,可以按照下列步骤进行:(1) 如果多项式各项有公因式,那么先提取公因式;(2) 如果各项没有公因式,那么可以尝试运用公式来分解;(3) 如果用上述方法不能分解,那么可以尝试用分组或其它方法(如十字相乘法)来分解;(4) 分解因式,必须进行到每一个多项式因式都不能再分解为止.练习A 组1.把下列各式分解因式:3338?27x8?m?27a? (3) (2) (1)111113333333x?yp?q?c?xy8(6)(5) (4) 216271258642.把下列各式分解因式:n?3n343yx?xx?xy(1) (2)22333222y)??2x)?aby(xa(m?n (4) (3)3.把下列各式分解因式:22226??11x?37x?36x?3x?2xx(2) (1) (3)222228b)?b)?11(a?(a?mx?6x?27?4mn?5n (4) (6) (5)4.把下列各式分解因式:2221n?3n2n?54?9x(x)?2bax?10ax?16ax6ab?a?a (1) (3) (2)22242y?15x?26xy83?6x?7x?x?7x18(6) (4) (5)2227(a?b)?5(a?b)?2(6x?7x)?25(8) (7)5.把下列各式分解因式:2223y6??2xy5x?15xy3ax?3ay??yx1?8x?4x2x? (2) (3) (1)2242222243yx?44xy?1?abb??a36b?aab?4a20ab?25b?(5) (4) (6)6632)?x?y1(xyx(x?1)?x?y2x?(7) (8)组B1.把下列各式分解因式:222222)bacd(?(abc?d)?n4?8mn?x?4mx (2) (1)3223234y8x2y?4x?xy?x?11x?31x?2164?x (4) (3) (5)22222ab?2ab?ab2aab,?b??的值..已知2,求代数式3.53n?4n?5nn 3.证明:当2为大于的整数时,120整除.能被32230?b?a?ac?bc?abc0a?b?c?.已知,求证:.4第二讲因式分解答案A组222),x6x?9m?m),(2?3x)(4??(a?3)(a?3a?9),(2m)(4?2 1.112112222222)4c?22xy?c)(xpq?qxyc),(2xy?)(4xyy???xy?),(2p?q)(4p(?2 64552521622n22x(x?y)(y?xy?x),x(x?y)(x?xy?y),2.22222432?2xx??4x)?b1)],y?(x?1)3(an(m?n?b)[(m?)x?b(m?n(x?2)(x?1),(x?36)(x?1),(x?13)(x?2),(x?9)(x?3) 3.(x?9)(x?3),(m?5n)(m?n),(a?b?4)(a?b?7)3n22?2)3)(xx?3)(x?3)(x?1)(xx?2?3),((x?2)(x?8),a)((a?3ba?2b),(x?ax.42(2x?3)(x3?1)x(?3?(x 1),(x?2x?5)(675a?))1x,(?2yx?(4y15a),(b7?7?2b?).52(2x?1),(x?3)(5x?2y),(2a?),(2x?1)5b?6)( 2a?5b?6)a(x?y)(3?y23333),x(x?y)(xy?)(xy?1?y?a?2x?y)(12x?y),ab(?b)b(a?),(x1)?1?(1?.B组228),??4x8)(),(x?4x?x24adbc?)(ac?bd),(x?m?2n)(x?n(.12y2x)?(y2),)?x((x?1x7)x?(3(?).28 2.353n?5n?4n?(n?2)(n?1)n(n?1)(n?2) 3.223223)baba???bc?aa?cabcb(??)(b?a?c.4.。
人教版高中数学-高一数学导学案09 正切函数的图像与性质
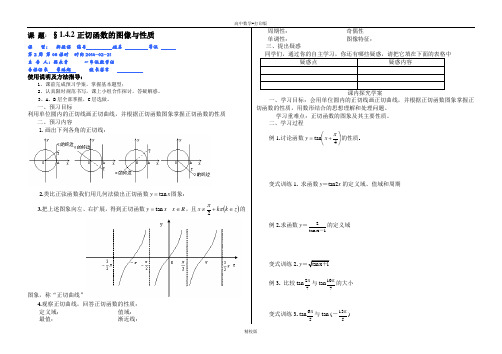
课 题:§1.4.2正切函数的图像与性质课 型: 新授课 编号 姓名 等级 第2周 第08课时 时间2014-02-21 主 备 人:张永章 一年级数学组备课组长 李鸿超 段长签字使用说明及方法指导:1、课前完成预习学案,掌握基本题型;2、认真限时规范书写,课上小组合作探讨,答疑解惑。
3、A 、B 层全部掌握,C 层选做。
一、预习目标利用单位圆内的正切线画正切曲线,并根据正切函数图象掌握正切函数的性质二、预习内容1.画出下列各角的正切线:2.类比正弦函数我们用几何法做出正切函数x y tan =图象:3.把上述图象向左、右扩展,得到正切函数R x x y ∈=tan ,且()z k k x ∈+≠ππ2的图象,称“正切曲线”4.观察正切曲线,回答正切函数的性质: 定义域: 值域: 最值: 渐近线:周期性: 奇偶性 单调性: 图像特征: 三、提出疑惑同学们,通过你的自主学习,你还有哪些疑惑,请把它填在下面的表格中疑惑点 疑惑内容课内探究学案一、学习目标:会用单位圆内的正切线画正切曲线,并根据正切函数图象掌握正切函数的性质,用数形结合的思想理解和处理问题。
学习重难点:正切函数的图象及其主要性质。
二、学习过程例1.讨论函数⎪⎭⎫ ⎝⎛+=4tan πx y 的性质变式训练1. 求函数y =tan2x 的定义域、值域和周期例2.求函数y =2tan x 1-的定义域变式训练2. y =tan x 1+例3. 比较tan 27π与tan 107π的大小变式训练3. tan 65π与tan (-135π)。
高一数学-09暑假18

高一数学暑假班测试卷班级姓名 得分 一、填空:本大题共18小题;每小题4分,共计72分. 1.若1a b -+与24a b ++是互为相反数,则()2008a b += 2.计算:11111335572121n n +++++++-++的结果为 。
3.已知集合{}1,3A =,集合{}30B x mx =-=,且,B A B A φ≠=,则m 的值是 .4.已知全集{}3U x x =≥-,集合{}1A x x =>,则A 的补集U C A = .5.已知集合{}{}22,21,1,1,3,1M x x x N x x =---=+-+,且{}0,3M N =-,则x 的值为 .6.不等式31>x 的解集是 . 7.不等式()()110x x +->的解是 .8.已知关于x 不等式20x ax b --<的解为23x <<,则不等式210bx ax -->的解为 .9.若,αβ是关于x 的二次方程()222350x k x k k --+++=(k 为实数)的两实根,则22αβ+的最大值等于 .10.设关于x 的方程()2290x a x a +++=,有两个不等的实数根12,x x ,且121x x <<,那么a 的取值范围是 .11.若0b a -<<,且函数()f x 定义域是[],a b ,则函数()()()F x f x f x =+-的定义域是 . 12.函数2231218423y x x x x =-+--的值域是 . 13.函数223y x x =--的递增区间是_______________________14.已知函数242y x ax =-+在4x ≥上,y 随x 的增加而增加,则实数a 的取值范围是 .15.已知集合{}{}22,,2,P y y x x R Q y y x x R ==-+∈==-+∈,那么P Q = .16.若函数()()221,2f x x g x x =+=+满足()()()()f g x g f x =,则x = .17.已知函数()21xf x x =+,求()f f x ⎡⎤⎣⎦= .18.已知是()f x 定义在R 上的偶函数,且当0x <时,()23f x x =-,则当0x >时,函数的解析式()f x =____________.二.解答题:本大题共4小题;前两小题每小题10分,共计 38分1.已知全集U ={小于10的自然数},其子集为,A B 满足{}1,9U U C A C B =,{}2A B =,{}4,6,8U C A B =,分别求集合,A B2设{}(){}22240,2110A x x x B x x a x a =+==+++-=,若B B A = ,求实数a 的取值范围.3.奇函数()x f 在定义域()1,1-内是单调递增的函数,且()()0112<-+-a f a f ,求a 的取值范围.4.讨论函数()()201ax f x a x =≠-,在()1,1x ∈-上的增减情况,并加以证明。
高一数学暑假学习材料

暑期专题辅导材料五(旧课)5一、教学进度:1.4 含绝对值的不等式解法 1.5 一元二次不等式解法 教学内容1.c b ax <+和c b ax >+ 型的不等式2.一元二次不等式02<++c bx ax 和02>++c bx ax (0≠a )的解法 二、重点难点剖析1.实数的大小比较a-b >0⇔a >b ,a-b=0⇔a=b a-b <0⇔a <b. 2.不等式的基本性质a >b ⇒a+c >b+c a >b ,c >0⇒ac >bc ,a >b ,c <0⇒ac <bc. 3.绝对值的意义a (a >0)a 0(a=0)-a(a <0=4.最简绝对值的解法|x|>a(a >0)⇔x >a 或x <-a , |x|<a(a >0)⇔-a <x <a.5.|ax+b|>c (c >0),|ax+b |<c (c >0)型6.|ax+b |<c 或|ax+b |<c (c >0)这两种类型的不等式的解题方法是利用了最简绝对值不等式的思想,把绝对值不等式化为代数不等式来解决。
7.在具体变形时要注意同解变形;(1)|ax+b |<c (c >0)⇔ax+b >c 或ax+b <-c ; (2)|ax+b |<c (c >0)⇔-c <ax+b <c.然后再根据a 的正、负解出相应绝对值的解。
8.解含绝对值不等式的基本思想:含绝对值不等式 不含绝对值符号不等式9.脱去绝对符号的方法有:(1)化归法,化为|x|<a 或|x|>a (a >0)型。
(2)零点分段法,找绝对值为零的点,分段讨论。
(3)数形结合。
(4)平方法,化为一元二次不等式(后面将会学到)。
10.c b ax <+和c b ax >+型的不等式(1)解含绝对值的不等式的基本方法体现了“化归”的数学思想,即将含绝对值的不等式化归为不含绝对值的“普通不等式”,在化归时要注意绝对值的含意. (2)对含绝对值的不等式,一般地有如不结论:①当0>c ,c b ax <+;c b ax c <+<- c b ax >+c b ax >+ 或.c b ax -<+②当0=c ,c b ax <+的解集为Φ;b ax >+c b ax ≠+. ③当0<a ,c b ax <+的解集为Φ;c b ax >+的解集为R .化归 脱去绝对值符号【例1】 求满足4213-=+x x 的x 值.解:由绝对值的定义得,4213-=+x x ,或13+x ∴5-=x ,或53=x . 【例2】 求不等式1≤2x-1≤5112<-x . ②由①,2x-1≥1 或 2x-1≤≤0.由②,-5<2x-1<5, ∴ ∴原不等式的解集为 评析 由绝对值的意义,|21-x |221的点的坐标是0和1,该距离等于25的点的坐标是-2和3,由数轴可见,原不等式的解是{x|-2<x ≤0,或1≤x<3}.【例3】 求下列不等式的解集:(1)|4x-3|≤x+1; (2)|3x+5|>2x-1. 解 (1) ∵|4x-3|≤x+1,∴-(x+1) ≤4x-3≤x+1, 即 –x-1≤4x-3, ① 4x-3≤x+1. ②由①得 52≥x , 由②得 34≤x .∴原不等式的解集为 {x|3452≤≤x }. (2) ∵|3x+5|>2x-1,∴3x+5>2x-1, ① 或 3x+5<-(2x-1) ② 由①得 x>-6, 由②得 x<54-. ∴原不等式的解集为{x|x ∈R}.【例4】 求关于x 的不等式|2x+1|≤t+1 (t ∈R)的解集. 解 当t+1<0,即t<-1时,不等式的解集为φ.当t+1=0,即t=-1时,2x+1=0,x=21-,不等式的解集为{21-}. 当t+1>0,即t>-1时,-(t+1) ≤2x+1≤t+1,-t-2≤2x ≤t,t x t 21121≤≤--,不等-2-10123x式的解集为{x|t x t 21121≤≤--}. 评析 所谓“关于x 的不等式”是指除x 以外的其他字母均表示常数.由于t+1的符号不确定,因此这里需对t 的不同情况分别求解.(3)对于含有几个绝对值的方程或不等式,可以用零点分段的方法除去绝对值符号: 【例5】(1)解方程:|x-3|+|x+2|=6; (2)解不等式:|x-1|+|x+2|<5. 解(1)零点为3,-2,分三段讨论. 25-; 当x>3,方程为x-3+x+2=6,x=2. ∴ 方程的解集为{25-,27}. (2)零点为1,-2,分三段讨论.当x<-2,不等式为(1-x)-(x+2)<5,x>-3, ∴-3<x<-2; 当-2≤x ≤1,不等式为(1-x)+(x+2)<5,3<5, ∴-2≤x ≤1; 当x>1,不等式为(x-1)+(x+2)<5,x<2, ∴1<x<2. ∴不等式的解集为{x|-3<x<2}.评析 ①所谓“零点”,即使绝对值为零的x 的值.若有n 个零点,则分n+1个情况讨论.由于每种情况都可以去掉绝对值符号,就把含有绝对值的方程或不等式转化为普通的方程或不等式去解.②在每一种情况求方程或不等式的解时,所求得的解必须满足相应的条件.③上面的方法是解含有绝对值的问题的基本方法。
高一数学暑假预习必备高一数学第一学期授课讲义共11份人教课标版3教案
讲义九:函数的基天性质单调性和最值 ()(一)、基本看法及知识系统:教课要求:更进一步理解函数单调性的看法及证明方法、鉴识方法,理解函数的最大(小) 值及其几何意义 .教课要点:娴熟求函数的最大(小)值。
教课难点:理解函数的最大(小)值,能利用单调性求函数的最大(小)值。
教课过程:一、复习准备:.指出函数 () = 2 ++ (>) 的单调区间及单调性,并进行证明。
. () = 2 ++的最小值的状况是如何的? .知识回顾:增函数、减函数的定义。
二、解说新课:.教课函数最大(小)值的看法:①指出以下函数图象的最高点或最低点,→能表现函数值有什么特色?f ( x)2x 3 , f ( x)2 x3 x[ 1,2] ; f ( x) x 2 2 x 1 , f ( x) x 22x 1 x [ 2,2]②定义最大值:设函数 ()的定义域为,假如存在实数满足:对于任意的∈,都有()≤;存在∈,使得 () . 那么,称 是函数 ()的最大值() ③商讨:模拟最大值定义,给出最小值()的定义.→一些什么方法可以求最大(小)值?(配方法、图象法、单调法)→试举例说明方法 ..教课例题: ①出示★例题:一枚炮弹发射,炮弹距地面高度(米)与时间(秒)的变化规律是 h 130t 5t 2 ,那么什么时辰距离达到最高?射高是多少?(学生谈论方法→师生共练:配方、分析结果→研究:经过多少秒落地?) ②练习:一段篱笆笆长20 米,围成一面靠墙的矩形菜地,如何设计使菜地面积最大?(指引:审题→设变量→建立函数模型→研究函数最大值;→小结:数学建模)③出示★例:求函数 y3 在区间 [,]上的最大值和最小值 .x 2分析:函数 y3 , x [3,6] 的图象→方法:单调性求最大值和最小值. x 2→板演→小结步骤:先按定义证明单调性,再应用单调性获得最大(小)值 .→变式练习: y3x,x [3,6]x 233④研究: y的图象与 y 的关系?x 2x⑤练习: 求函数 y2xx 1 的最小值 .(解法一:单调法;解法二:换元法). 看书 例题→口答练习→小结:最大(小)值定义;三种求法.三、牢固练习:. 求以下函数的最大值和最小值:() y 3 2 x x 2 , x [5 , 3 ] ;() y | x 1| | x 2 |2 2 房价(元)住宅率().一个星 级酒店有个标准房,经过一段时间的经营,经理获得一些定价和住宅率的数据如右:欲使每日的的营业额最高,应如何定价?(分析变化规律→建立函数模型→求解最大值) . 课堂作业:书组题;组、题.四、备采纳思虑题:【题】、二次函数 () (为常数且≠ )满足 () ()且方程 ()有等根;①求()的分析式;②能否存在实数、( <) 使 ()定义域为 [ , ],值域为 [ , ] ,若存在,求出、之值,若不存在,说明原由解、① ()②因为 ()的值域是 ()≤,则≤,即≤,所以有 () 3m 且 ()∴存在实数使 ()定义域为 [, ] ,值域为 [ , ]★例:某产品单价是元,可销售万件。
高一数学必修一(暑期自学材料,非常详细)
高一数学必修一(暑期自学材料,非常详细)第一章集合§1.1集合与集合的表示方法1.1.1集合的概念1.元素与集合的概念(1)集合:一般来说,把一些______________________________(2)元素:构成集合的________叫做这个集合的元素(或成员),通常用英语小写字母表示.2.集合中元素的特性:________、________.3.元素与集合的关系(1)如果a是集合a的一个元素,比如说,记为,如果a不是集合a的一个元素,比如,记为__4.实数集、有理数集、整数集、非负整数集、正整数集分别用字母____、____、____、____、____或____来表示.5.集合的分类集合?非空集:空集:不含任何元素,记作.按元素?:包含有限个元素的个数分为??:含有无限个元素一、多项选择题1.下列语句能确定是一个集合的是()著名的科学家B.长头发的女孩C 2022广州亚运会的事件D视力低下的男孩2。
集合a 只包含元素a,那么下面的正确表达式是()a.0∈ A.b、 a?a、中情局∈a、 d.a=a3.已知m中有三个元素可以作为某一个三角形的边长,则此三角形一定不是()a.直角三角形;b.锐角三角形;c.钝角三角形;d.等腰三角形4.集合A由a2、2-A和4组成。
如果a包含三个元素,实数a的值可以是()a.1;b、-2;c.6;d.25.已知集合a是由0,m,m2-3m+2三个元素组成的集合,且2∈a,则实数m为()a.2;b.3;c.0或3;d.0,2,3均可三6.由实数x、-x、|x|、x2及-x3所组成的集合,最多含有()a.2个元素;b.3个元素;c.4个元素;d.5个元素二、填空题以下第7组(填写序列号)① 不超过π的正整数;② 这个班成绩好的学生;③高一数学课本中所有的简单题;④平方后等于自身的数.8.集合a包含三个元素0、1、x和X2∈ a、那么实数x的值是__9。
高一数学暑假讲义
目录第1讲集合的含义及其表示 (1)第2讲集合的子集与补集 (6)第3讲解不等式 (11)第4讲交集与并集(一) (16)第5讲交集与并集(二) (21)第6讲函数的概念及定义域 (26)第7讲函数的解析式 (31)第8讲函数的值域(一) (36)第9讲函数的值域(二) (41)第10讲函数的单调性 (46)第11讲函数的奇偶性 (51)第12讲函数习题课 (56)第13讲分数指数幂 (61)第14讲指数函数 (66)第15讲对数(一) (71)第16讲对数(二) (76)第17讲对数函数 (81)第一讲 集合的含义及其表示【知识要点】1.集合的定义2.集合元素的特征: ①确定性;②互异性;③无序性3.集合的表示方法: ①列举法;②描述法;③文氏图法;④特殊集合4.元素与集合的关系:①属于关系,用“∈”表示;②不属于关系,用“∉”表示【典型例题】例1.判断下列各组对象能否构成集合.(1)不小于2008且不大于2012的所有正整数;(2)比较矮的人(3)身高超过170cm 的人(4)方程2102x x -+=的实根;例2.元素互异性的检验问题(1)设{}24,3,A a a =-,且A ∈9,求实数a 的值.(2)已知2是集合{}21,,x x x -中的元素,试求出x 的值.例3.集合的表示方法(1)用列举法表示集合{}234A x x x =+=. (2)用列举法表示集合{}24,,B y y x x y N ==-∈. (3)用列举法表示集合(){}2,4,,C x y y x x y N ==-∈. (4)用列举法表示集合6,3D x Z x N x ⎧⎫=∈∈⎨⎬-⎩⎭. (5)用描述法表示100内被3整除余2的正整数所组成的集合P(6)平面直角坐标系内在x 轴上方的点组成的集合例4. 已知集合{}R x R a x ax x A ∈∈=++=,,0122.(1)若A 是空集,求a 的取值范围.(2)若A 是单元素集,求a 的值.(3)若A 中至多只有一个元素,求a 的取值范围.例5.设集合{},,P x y x y xy =-+,{}2222,,0Q x y x y =+-,若P Q =,求,x y 的值及集合P 、Q .例6.(1)已知集合{}2,,0,,,1b b a Q b b a P +=⎭⎬⎫⎩⎨⎧=且Q P =.求20072007b a +的值.(2)已知{}{}2,,1,21,1,1r r B d d A =++=,其中1,0≠≠r d ,当r d ,满足什么条件时, B A =?并求出这种情形下的集合A1.下列各组对象不能形成集合的是( )A .高一全体女生B .高三(1)班家长全体C .高中所有课程D .高一(1)班中个子较高的学生2.下列表述中正确的是( )A.{}0=∅B.{}{}1,33,1=C.{}∅=∅D.0N ∉3.定义集合运算:A ⊙B={}B y A x y x xy Z Z ∈∈+=,);(,其中{}{}3,2,1,0==B A ,则集合A ⊙B 的所有元素之和为( )A .0B .6C .12D .18 4.,a b 均为非零实数,且a b y a b=+,则y 可能取值的集合为 5.已知集合{}33,)1(,222++++=a a a a A ,若1A ∈,求a 的值.6.设P 、Q 为两个非空数集,定义集合{|,}P Q a b a P b Q +=+∈∈,若{0,2,5},P = }6,2,1{=Q ,则P Q +中元素的个数是1.下列给出的对象中,能表示集合的是( )A.一切很大的数B.无限接近零的数C.聪明的人D.方程22-=x 的实数根2.集合{5|<∈+x N x }的另一种表示法是( )A.{0,1,2,3,4}B.{1,2,3,4}C.{0,1,2,3,4,5}D.{1,2,3,4,5}3.由大于-3且小于11的偶数所组成的集合是( )A.{x|-3<x<11,Q x ∈}B.{x|-3<x<11}C.{x|-3<x<11,x=2k,N k ∈}D.{x|-3<x<11,x=2k,Z k ∈}4.方程的解集为{}22320x x x --=,用列举法表示为_______ ____5.在平面直角坐标系内第二象限的点组成的集合为______ _____ ___6.设集合A={(x,y)|x+y=6,,x N y N **∈∈} ,用列举法表示集合A=7.已知集合A=126x N N x ⎧⎫∈∈⎨⎬-⎩⎭,用列举法表示集合A= 8.已知A={28160x kx x -+=}中只有一个元素,则实数k 的取值范围为≠⊂第二讲 集合的子集与补集【知识要点】1.集合间的关系:①包含用“⊆”表示;②真包含用“ ”表示;③相等;④不相等2.子集与真子集3.全集与补集的定义【典型例题】例1.集合{,,,}a b c d 的子集有多少个?非空真子集有多少个?例2.已知{}{},,,,,a b A a b c d e ⊆⊆,求满足条件的A .例3.非空数集{}1,2,3,4,5A ⊆,满足若A a ∈,则A a ∈-6的非空集合A 有多少个?写出这些集合例4.判断如下A 与B 之间有怎样的包含或相等关系:(1)A ={x |x =2k -1,k ∈Z },B ={x |x =2m +1,m ∈Z }(2)A ={x |x =2m ,m ∈Z },B ={x |x =4n ,n ∈Z }例5.子集综合题(1)已知集合{}}01|{,06|2=+==-+=ax x S x x x P 若P S ⊆,求实数a 的值 (2)已知集合{}{}312,35A x a x a B x x =-<<+=≤≤,若B A ⊆,求a 的范围(3)若集合{}2|10,A x x ax x R =++=∈,集合{}1,2B =,且A B ⊆,求实数a 的取值范围.例6.集合A ={x |-2≤x ≤5},B ={x |m +1≤x ≤2m -1},(1)若B ⊆A ,求实数m 的取值范围.(2)当x ∈Z 时,求A 的非空真子集个数.(3)当x ∈R 时,没有元素x 使x ∈A 与x ∈B 同时成立,求实数m 的取值范围.例7.已知全集{}{}{}22,3,23,1,2,3U U a a A a C A a =+-=+=+,求a 的值.【课堂练习】1.下列命题正确的是( )A.无限集的真子集是有限集B.任何一个集合必定有两个子集C.自然数集是整数集的真子集D.{1}是质数集的真子集2.以下五个式子中,错误的个数为( )①{1}∈{0,1,2} ②{1,-3}={-3,1} ③{0,1,2}⊆{1,0,2} ④∅∈{0,1,2} ⑤∅∈{0}A.5B.2C.3D.43.已知集合{}{}12,,A x x B x x a A B =<<=<⊆若,则实数a 的取值范围是( )A. 2a ≤B. 2a <C. 2a >D. 2a ≥4.满足{}{}1,21,2,3,4,5X ⊆⊆的集合X 的个数是( )A .8B .7C .6D .45.设{}{}0,1,2,B A x x B ==⊆,是A 与B 的关系是( )A.A B ⊆B.B A ⊆C.A B ∈D.B A ∈6.(1)设全集{}{}22,3,1,3,2U a a A =--=,若{}1U C A =,则实数a 的值为_______ (2)集合A ={-1,3,2m -1},集合B ={3,2m }.若B ⊆A ,则实数m =(3)已知{1,3,}A m =-,集合{3,4}B =,若B A ⊆,则实数m =(4)已知2{|2530}M x x x =--=,{|1}N x mx ==,若N M ⊆,则适合条件的实数m 的集合P 为 ;P 的子集有 个;P 的非空真子集有 个.7.判断正误(1)空集没有子集 ( )(2)空集是任何一个集合的真子集 ( )(3)任一集合必有两个或两个以上子集 ( )(4)若B ⊆A ,那么凡不属于集合A 的元素,则必不属于B ( )【课后作业】1.下列八个关系式①{0}=φ ②φ=0 ③φ⊆{φ} ④φ∈{φ} ⑤{0}⊇φ ⑥0∉φ ⑦φ≠{0} ⑧φ≠{φ}其中正确的个数( ) A.4 B.5 C.6 D.72.集合{1,2,3}的真子集共有( )A.5个B.6个C.7个D.8个 3.满足条件{1,2,3}⊂≠M ⊂≠{1,2,3,4,5,6}的集合M 的个数是( )A.5个B.6个C.7个D.8个4.集合A={x |x =3k -2,k ∈Z},B={y |y=3n +1,n ∈Z},S={y |y =6m +1,m ∈Z}之间的关系是( ) A.SBA B.S=BA C.SB=A D.SB=A5.已知A ={x |x <3},B ={x |x <a } (1)若B ⊆A ,则a 的取值范围是______ (2)若A B ,则a 的取值范围是______6.设A ={x |x 2-8x +15=0},B ={x |a x -1=0},若B ⊆A ,则实数a 组成的集合为7.设集合A={23≤≤-x x },B={x 1212+≤≤-k x k },且A ⊇B ,则实数k 的取值范围为第三讲 解不等式【知识要点】1.你会解一元二次不等式及分式不等式吗?2.你知道一元二次不等式,一元二次函数,一元二次方程之间的关系吗? 3.你会解绝对值不等式吗?如a x ≥及a x ≤的解集, 不等式c b ax >+或)0(><+c c b ax 的解集【典型例题】例1.解关于x 的不等式:(1)2210x x -+≥ (2)0322>-+x x例2.解关于x 的不等式:(1)0713224<--x x (2)032>-+x x (3)83402≤++≤x x例3.解关于x 的不等式:(1)2102x x ->- (2)222102x x ->+ (3)2112x x ->- (4) 2112x x +≥+例4.解关于x 的不等式:(1)37x +≤ (2)17x -≥ (3)2323x ≤-≤(4)1x x -≤ (5)123x x ->- (6)|21||2|4x x ++->例5.二次函数的恒成立问题(1)若不等式22(2)40x a x +-+>对一切x R ∈成立,求a 的取值范围(2)对于任意实数x ,不等式240mx mx ++>恒成立,求m 的取值范围.例6.绝对值不等式的恒成立问题(1)对任意实数x ,|1||2|x x a ++->恒成立,则a 的取值范围是 ;(2)对任意实数x ,|1||3|x x a --+<恒成立,则a 的取值范围是 .1.与不等式202xx-<+有相同解集的是( ) A .22x -<< B .22x x ><-或 C .2x > D .2x < 2.集合{}25A x x =+≥,则A =( )A .RB .{}73x x x ≤-≥或 C .{}71x x x ≤->或 D .{}35x x ≤< 3.集合{}2650B x x x =--->,则B =( )A .RB .{}5x x >- C .{}15x x x >-<-或 D .{}51x x -<<- 4.不等式722xx -≥+的解集为 5.不等式25x +<的解集为 6.解下列不等式:(1)22470x x -+< (2)3222xx -≥+1.解不等式(1)24120x x --≥ (2)2650x x --≥(3)2045x x ≤+≤ (4)424120x x --≥2.解不等式 (1)203x x -≥+ (2)213xx -≥+3.解不等式(1)235x +≥ (2)1235x ≤+≤第四讲 交集与并集(一)【知识要点】1.理解交集、并集的概念2.AB A A B =⇔⊆,A B A A B =⇔⊇;3.能利用数轴或文氏图进行集合的运算4.()()()U U U C A C B C A B =, ()()()U U U C A C B C AB =【典型例题】例1.基本训练(1)已知全集{}{}{}5,4,1,5,3,0,5,4,3,2,1,0===N M ,求)(N C M . (2)设{}{}Q x x x B N k k x x A ∈≤=∈+==,6,,15,求B A . (3)集合{}{}2,,3,A x x K K N B x x K K N ++==∈==∈,求A B .例2.交并集的运算(1)已知集合{}{}1 5,36A x x x B x x =≤-≥=-<<或求,AB A B(2)已知集合{}{}2|3760,|114,A x x x B x x =--≤=<+≤求,AB A B例3.已知数集{}{}}3{,1,12,3,3,1,22-=⋂+--=-+=B A a a a B a a A ,求A B .例4.已知全集U R =,{}{}2241,,23,A y y x x x R B y y x x x R ==++∈==-++∈,求B A 与()U C B A例5.数集和点集的理解(1)已知集合{}2|2,p y y x x R ==-+∈,{}|2,Q y y x x R ==-+∈,求pQ(2)已知集合{}{}1),(,2),(2+==++==x y y x B mx x y y x A ,若φ≠B A ,求m 的取值范围.例6.已知集合{}{}a x x B x x A >=≤≤-=,42. (1)若φ≠B A ,求a 的范围. (2)若A B A ≠ ,求a 的范围.(3)若φ≠B A 且A B A ≠ ,求a 的范围.例7.(1)已知集合{}|1A x x a =-≤,{}2540B x x x =-+≥.若AB =∅,则实数a 的取值范围为 (2)设集合3(,)12y M x y x ⎧-⎫==⎨⎬-⎩⎭,(){},5N x y y kx ==+,若M N φ=,则k =【课堂练习】1.设集合{}{}{}4,3,2,3,2,1,2,1===C B A ,则C B A )(=( ) A.{1,2,3}B.{1,2,4}C .{2,3,4} D.{1,2,3,4}2.若集合{}{}03,22=-=≤=x x x N x x M ,则N M =( ) A.{3}B.{0}C .{0,2} D.{0,3}3.设集合{}{}{}3,,1,2,2,1,2U x x x Z A B =<∈==--,则()U A C B =( )A.{1}B.{1,2}C .{2} D.{0,1,2}4.设集合{}2,1=A ,则满足{}3,2,1=B A 的集合B 的个数是( ) A.1B.3 C .4D.85.若A 、B 、C 为三个集合,A B B C =,则一定有( )A.C A ⊆B.A C ⊆C.C A ≠D.φ=A 6.设集合{}{}12,M x x N x x a =-≤<=≤.若M N ≠∅,则a 的取值范围是( )A.](,2-∞ B.()1,-+∞ C.)1,-+∞⎡⎣ D.[]1,1- 7.设全集{}{}{}17,25,36U x x A x x B x x =<<=≤≤=≤≤,则()C A B =____ _ 8.全集U R =,集合{}{}|02,|13,A x x x B x x =<>=-<<或()U C AB 则=9.集合{}{}24,21,,5,1,9A a a B a a =--=--,又已知{}9AB =,求a 的值.【课后作业】1.已知集合{}}8,7,3{},9,6,3,1{,5,4,3,2,1,0===C B A ,则C B A )(等于( ) A.{0,1,2,6} B.{3,7,8,} C.{1,3,7,8} D.{1,3,6,7,8}2.设集合{}x A ,4,1=,{}2,1x B =,且{}x B A ,4,1=⋃,则满足条件的实数x 的个数是( )A.1个B.2个C.3个D.4个3.集合A 含有10个元素,集合B 含有8个元素,集合A∩B 含有3个元素,则集合A ∪B 的元素个数为( )A.10个B.8个C.18个D.15个4.设A={x 0152=+-∈px x Z },B={x 052=+-∈q x x Z },若A ⋃B={2,3,5},A 、B 分别为( )A.{3,5}、{2,3}B.{2,3}、{3,5}C.{2,5}、{3,5}D.{3,5}、{2,5}5.若{}23100A x x x =+-<, {}33B x x =-<<,全集U=R ,则()U A C B ⋃=6.集合M={y ∣y= x 2 +1,x ∈ R },N={t ∣t=5- x 2,x ∈ R },则M ∪N=7.已知集合A ={-1,1},B ={x |mx =1},且A ∪B =A ,则m 的值为8.已知集合}33|{≤≤-=x x U ,}11|{<<-=x x M ,}20|{<<=x x N C U 那么集合=N ,=⋂)(N C M U ,=⋃N M .第五讲 交集与并集(二)【知识要点】1.重要的等价关系:B A B B A A B A ⊆⇔=⋃⇔=⋂2.利用文氏图进行集合的运算3.容斥原理:card(A ∪B)= card(A)+card(B)- card(A ∩B).4.区间的概念【典型例题】例 1.{}{}22|20,|6(2)50A x x px q B x x p x q =-+==++++=,1AB=2⎧⎫⎨⎬⎩⎭若求A B例2.A ={x |a ≤x ≤a +3},B ={x |x <-1或x >5} ①若A ∩B =∅,求a 的取值范围. ②若A ∩B =A , 求a 的取值范围.例3.已知{}250,U x x x N =<∈,(){}1,6U C M N ⋂=,(){}2,3U M C N ⋂=(){}0,4U C M N ⋃=,求M 和N例4.某班级共有48人,其中爱好体育的25名,爱好文艺的24名,体育和文艺都爱好的9名,试求体育和文艺都不爱好的有几名?例5.已知集合{}{}k x k x B x x A 21,52<<+=≤≤-=.若A B A = ,求k 的取值范围.例6. {}{}{}2222190560,280A x x ax a B x x x C x x x =-+-==-+==+-=, 且A B ≠∅,A C =∅,求实数a 的值.例7.已知集合{}{}22320,B 20A x x x x x mx =-+==-+=,且B B A=.求实数m 的取值范围.例8.U R =,{}2120,A x x px X N +=++=∈, {}250,B x x x q X N +=-+=∈且(){}2U C A B =.(){}4U A C B =.求p q +的值.1.已知集合U ={1,2,3,4,5,6,7}, A ={2,4,5,7},B ={3,4,5},则(u A )∪(u B )=( ) A .{1,6} B .{4,5} C .{1,2,3,4,5,7} D .{1,2,3,6,7}2.已知,M ={3,a },N ={x |x 2-3x <0,x ∈Z},M ∩N ={1},P =M ∪N ,则集合P 的子集的个数为( ) A .3B .7C .8D .163.已知集合M 、N 满足,card M =6,card N =13,若card (M ∩N )=6,则card (M ∪N )=_____ _ ;若M ∩N =∅,则card(M ∪N )=_______.4.已知全集U={- 4,-3,-2,-1,0},集合M={- 2,-1,0},N={-4,-3,0},则()U C M N ⋂=5.已知集合{}2,A x x x x R ==∈,则满足条件AB A =的所有集合B 的个数为______6.已知U={},8,7,6,5,4,3,2,1(){},8,1=⋂B C A U (){},6,2=⋂B A C U()(){},7,4=⋂B C A C U U 则集合A=7.设U 是一个全集,A 、B 为U 的两个子集,试用阴影线在图甲和图乙中分别标出下列集合.①C U (A ∪B )∪(A ∩B ) ②(C U A )∩B8.已知全集U ={x |x 2-3x +2≥0},A ={x |x <1或x >3},B ={x |x ≤1或x >2},求C U B ,A ∪B ,(C U A )∩(C U B ),C U (A ∪B ).1.已知集合P M ,满足M P M = ,则一定有( )A.P M =B.P M ⊇C.M P M =D.P M ⊆2.设U={1,2,3,4,5},A ,B 为U 的子集,若A ⋂B={2},(C U A )⋂B={4},(C U A )⋂(C U B )={1,5},则下列结论正确的是( )A.3B A ∉∉3,B.3B A ∈∉3,C.3B A ∉∈3,D.3B A ∈∈3, 3.全集},|),{(R y x y x U ∈=,}123|),{(=--=x y y x M ,}1|),{(+≠=x y y x N ,那么)(M C U ∩)(N C U = ( )A.φB.{(2,3)}C.(2,3)D.}1|),{(+≠x y y x4.已知集合A 中有10个元素,B 中有6个元素,全集U 有18个元素,≠⋂B A φ。
人教版高一学生初高中数学衔接教材暑假补课资料
二、根式
式子 叫做二次根式,其性质如下:
(1) (2)
(3) (4)
【例6】化简下列各式:
(1) (2)
解:(1) 原式=
(2) 原式=
说明:请注意性质 的使用:当化去绝对值符号但字母的范围未知时,要对字母的取值分类讨论.
【例7】计算(没有特殊说明,本节中出现的字母均为正数):
说明:从例5、例6可以看出:如果一个多项式的项分组后,各组都能直接运用公式或提取公因式进行分解,并且各组在分解后,它们之间又能运用公式或有公因式,那么这个多项式就可以分组分解法来分解因式.
三、十字相乘法
1. 型的因式分解
这类式子在许多问题中经常出现,其特点是:
(1) 二次项系数是1;(2) 常数项是两个数之积;(3) 一次项系数是常数项的两个因数之和.
因此,
运用这个公式,可以把某些二次项系数为1的二次三项式分解因式.
【例7】把下列各式因式分解:
(1) (2)
解:(1)
.
(2)
说明:此例可以看出,常数项为正数时,应分解为两个同号因数,它们的符号与一次项系数的符号相同.
【例8】把下列各式因式分解:
(1) (2)
解:(1)
(2)
说明:此例可以看出,常数项为负数时,应分解为两个异号的因数,其中绝对值较大的因数与一次项系数的符号相同.
三、分式
当分式 的分子、分母中至少有一个是分式时, 就叫做繁分式,繁分式的化简常用以下两种方法:(1) 利用除法法则;(2) 利用分式的基本性质.
【例10】化简
解法一:原式=
解法一:原式=
说明:解法一的运算方法是从最内部的分式入手,采取通分的方式逐步脱掉繁分式,解法二则是利用分式的基本性质 进行化简.一般根据题目特点综合使用两种方法.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
暑期专题辅导材料九(旧课) 复习与测试(第一章 集合与简易逻辑) 本章的重点是: (1)有关集合的基本概念、术语和符号; (2) x<a与x>a(a>0)型的不等式的解法,一元二次不等式的解法; (3)逻辑联结词“或”、“且”、“非”与充分条件和必要条件.
本章的难点是: (1)有关集合的各个概念的涵义、它们之间的区别与联系; (2)对绝对值意义的理解; (3)弄清一元二次函数、一元二次方程、一元二次不等式的关系; (4)对一些数学命题真假的判断、关于充要条件的判断和反证法的运用.
本章内容是高中数学的基础知识,其中集合论是由18世纪德国数学家康托尔创始的,是近、现代数学的一个重要基础;逻辑是研究思想形式及其规律的一门基础学科,它们今后学习的内容有着密切联系,学好本章内容必将为进一步学习其它知识奠定坚实的基础.
【基本概念】 1.集合:一般地,某些指定的对象集在一起就成为一个集合,也简称集.表示集合的方法有列举法、描述法和图示法,集合可分为有限集和无限集. 2.空集:一般地,我们把不含任何元素的集合叫做空集,记作. 3.子集:一般地,对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,我们就说集合A包含于集合B,或集合B包含集合A,记作 AB(或BA). 这时我们也说集合A是集合B的子集. 当集合A不包含于集合B,或集合B不包含集合A时,则记作 BA(或AB)
我们规定:空集是任何集合的子集.也就是说,对任何一个集合A,有
A
4.等集:一般地,对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,同时集合B的任何一个元素都是集合A的元素,我们就说集合A等于集合B,记作 A=B 5.全集:如果集合S含有我们所要研究的各个集合的全部元素,这个集合就可以看作一个全集,全集通常用U表示. 6.补集:一般地,设S是一个集合,A是S的一个子集(即AS),由S中所有不属于A的元素组成的集合,叫做S中子集A的补集(或余集),记作CSA,即 CSA={x|x∈S,且xA}. 7.交集,并集:一般地,由所有属于集合A且属于集合B的元素所组成的集合,叫做A与B的交集,记作A∩B(读作“A交B”),即 A∩B={x|x∈A,且x∈B}. 而由所有属于集合A或属于集合B的元素所组成的集合,叫做A与B的并集,记作A∪B(读作“A并B”),即 A∪B={x|x∈A,或x∈B}. 对于交集“A∩B={x|x∈A,且x∈B}”,不能简单地认为A∩B中的任一元素都是A与B的公共元素,或者简单认为A与B的公共元素都属于A∩B,这是因为并非任何两个集合总有公共元素.当集合A与B没有公共元素时,不能说A与B没有交集,而是A∩B=. 对于并集“A∪B={x|x∈A,或x∈B}”,不能简单地理解为A∪B是由A的所有元素与B的所有元素组成的集合,这是因为A与B可能有公共元素,故上述理解与集合的互异性不符. 8.逻辑联结词:“或”、“且”、“非”这些词叫做逻辑联结词.不含逻辑联结词,是简单命题;由简单命题与逻辑联结词构成,是复合命题. 9.四种命题:在两个命题中,如果第一个命题的条件(或题设)是第二个命题的结论,且第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题;如果把其中一个命题叫做原命题,那么另一个叫做原命题的逆命题. 一个命题的条件和结论分别是另一个命题的条件的否定和结论的否定,这样的两个命题叫做互否命题.把其中一个命题叫做原命题,另一个就叫做原命题的否命题. 一个命题的条件和结论分别是另一个命题的结论的否定和条件的否定,这样的两个命题叫做互为逆否命题.把其中一个命题叫做原命题,另一个就叫做原命题的逆否命题. 10.充要条件:一般地,如果已知 pq, 那么我们说,p是q的充分条件,q是p的必要条件. 一般地,如果既有pq,又有qp,就记作 pq. 这时,p既是q的充分条件,又是q的必要条件,我们就说p是q的充分必要条件,简称充要条件.
【基本性质】 1.基本符号 ∈ x∈A x属于A;x是集合A的一个元素 yA y不属于A;y不是集合A的一个元素 {,...,} {a,b,c,...n} 诸元素a,b,c,...n构成的集合 {|} {x|p(x),x∈A} 使命题p(x)为真的A中诸元素之集合 空集 N 非负整数集;自然数集 N*或N+ 正整数集 Z 整数集 Q 有理数集 R 实数集 C 复数集 BA B包含于A;B是A的子集 BA B真包含于A;B是A的真子集 BA B不包含于A;B不是A的子集 ∩ A∩B A与B的交集 ∪ A∪B A与B的并集 C CAB A中子集B的补集或余集 2.集合部分: A;A(A非空);AA;(CUA)∩A=;(CUA)∪A=U;CU(CUA)=A;
ABCAC;ABCAC;A∩BA;BA∪B;CU=U;CUU=;ABA∩B=A;ABA∪B=B;CU(A∩B)=(CUA)∪(CUB);CU(A∪B)=(CUA)∩(CUB) 3. |ax+b|≤c(c>0) -c≤ax+b≤c |ax+b|≥c(c>0) ax+b≥c或ax+b≤-c
【基本规律】 1.复合命题真假判断表 非p形式复合命题的真假可以用下表表示. p 非p 真 假 假 真
p且q形式复合命题的真假可以用下表表示. p q P且q 真 真 真 真 假 假 假 真 假 假 假 假 p或q形式复合命题的真假可以用下表表示. p q p或q 真 真 真 真 假 真 假 真 真 假 假 假 2.四种命题之间的相互关系 四种命题之间的相互关系,如图所示.
我们已经知道,原命题为真,它的逆命题不一定为真.一般地一个命题的真假与其他三个命题的真假有如下三条关系. (1)原命题为真,它的逆命题不一定为真. (2)原命题为真,它的否命题不一定为真. (3)原命题为真,它的逆否命题一定为真.
【基本方法与思想】 1.绝对值不等式的解法:|x|<a(a>0)的解集是 {x|-a<x<a}; |x|>a(a>0)的解集是 {x|x<-a,或x>a}. 注:对于|ax+b|>c(或<c,其中c>0)的解法可用换元法解. 2.一元二次不等式的解法: 一元二次不等式ax2+bx+c>0(a>0)的解集如下表. 判别式△=b2-4ac △>0 △=0 △<0
二次函数y=ax2+bx+c(a>0)的图像 y=ax2+bx+c y=ax2+bx+c y=ax2+bx+c
一元二次方程ax2+bx+c=0(a>0)的根 有两相异实根x1,x2(x1<x2) 有两相等实根x1=x2=-ab2 没有实根 ax2+bx+c>0(a>0)的解集 {x|x<x1或x>x2} {x|x≠-ab2} R ax2+bx+c<0(a>0)的解集 {x|x1<x<x2}
对于绝对值不等式|ax+b|>c(或<c,其中c>0)可采用平方去绝对值法,即化为(ax+b)2>c2(或<c2) 3.充要条件的判定方法:若pq但qp,则p只是q的充分不必要条件; 若pq,但qp,则p只是q的必要不充分条件; 若pq,且qp,则p只是q的充要条件; 注:必须看两个方向,即pq,qp结果如何?才能下结论. 4.反证法:反证法是“原命题与其逆否命题同真同假”这一理论的具体体现,用反证法证明命题的一般步骤如下: (1)假设命题的结论不成立,即假设结论的反面成立; (2)从这个假设出发,经过推理论证,得出矛盾; (3)由矛盾判定假设不正确,从而肯定命题的结论正确.
学习要求和需要注意的问题: 1.学习要求 (1)集合 ①理解集合、子集、交集、并集、补集的概念 ②了解空集和全集的意义 ③了解属于、包含、相等关系的意义 ④会用集合的有关术语和符号表示一些简单的集合. ⑤掌握简单的绝对值不等式与一元二次不等式的解法. (2)简易逻辑 ①了解命题的概念和命题的构成. ②理解逻辑联结词“或”、“且”、“非”的含义. ③掌握四种命题及其相互关系. ④初步掌握充要条件. 2.需要注意的问题 (1)集合与集合的元素是两个不定义的概念,教科书中是通过描述给出的,这与平面几何中的点与直线的概念类似,但是,应该清楚集合中的元素具有确定性,互异性.确定性是指给定一个集合,一个对象属于不属于这个集合就是明确的,象很大的数,不能组成一个集合.互异性是指在一个集合中,任何两个元素是不同的对象,相同的对象只能算作这个集合的一个元素.此外,集合中的元素还具有无序性,例如, {1,2,4}={4,2,1}. (2)容易混淆的符号 ①∈与的区别:∈符号是表示元素与集合之间关系的,例如,有1∈N,-1N等;符号是表示集合与集合之间关系的,例如,有NR,R等.
②a与{a}的区别:一般地,a表示一个元素,而{a}表示只有一个元素的集合,例如,有1∈{1,3,4},0∈{0},{1}{1,3,4}等,不能写成0={0},{1}∈{1,3,4},1{1,3,4}.
