有限元作业—三梁平面框架结构的有限元分析
有限元受力分析--结构梁-力-计算

有限元受力分析–结构梁-力-计算1. 前言受力分析是工程设计中至关重要的一环,能够帮助工程师完善设计并避免安全事故的发生。
在此,我们将介绍有限元受力分析在结构梁设计中的应用。
本文将重点讲解有限元受力分析的相关理论和计算方法。
2. 有限元受力分析有限元分析是数值计算的一种方法,可用于解决工程中的受力分析问题。
它把结构离散为有限个单元,然后对每个单元进行分析。
有限元分析可分为线性有限元分析和非线性有限元分析两种类型。
本文我们只讨论线性有限元分析。
在有限元分析中,结构被分解为离散的单元,每个单元都是基于解析解的一部分。
有限元的形状、尺寸和材料属性可以通过计算机程序进行定义。
使用数学模型和有限元方法,可以计算单元的应力、变形和应变,从而进行结构的受力分析。
3. 结构梁结构梁相信大家应该都知道,它是工程中最为常用的结构之一。
它具有一定的强度和刚度,可以支撑和传递载荷。
一般来说,结构梁通常由简单的杆件单元组成。
在进行结构梁受力分析时,我们需要考虑弯曲、剪切和挤压等不同形式的载荷,以及结构在工作条件下的应变和应力分布情况。
有限元受力分析对于这些问题的研究提供了很好的解决方案。
4.力的分析在受力分析中,载荷是非常关键的参数。
载荷可以是点载荷、均布载荷、集中荷载等。
在本文中,我们将分别介绍这些载荷类型的有限元分析方法。
4.1 点载荷分析点载荷通常是一个单点受到的载荷。
对于点载荷的有限元分析,我们可以通过构建一个网格模型,然后将点载荷作用在网格的节点上。
此外,还需要设定材料的弹性模量和截面的截面面积,以计算结构的应力和变形。
需要注意的是,点载荷分析过程中的网格划分应当尽量精细,以达到更为优秀的数值精度。
4.2 均布载荷分析均布载荷是沿着梁的长度方向均匀分布的载荷,例如一根梁的自重、荷载等。
在进行均布载荷的有限元分析时,我们可以在网格的中央位置放置均布载荷,然后将梁的边缘节点设置为固定的约束条件。
同样,需要设定材料的弹性模量和截面的截面面积以计算结构的应力和变形。
ANSYS案例—— 例ANSYS 实例
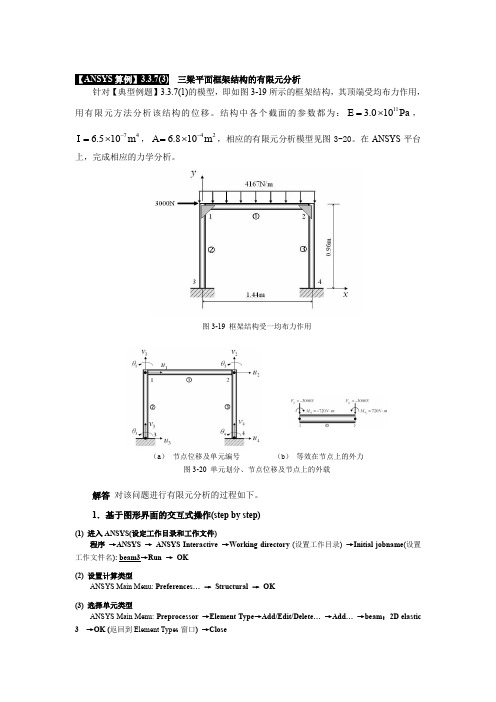
【ANSYS 算例】3.3.7(3) 三梁平面框架结构的有限元分析针对【典型例题】3.3.7(1)的模型,即如图3-19所示的框架结构,其顶端受均布力作用,用有限元方法分析该结构的位移。
结构中各个截面的参数都为:113.010Pa E =⨯,746.510m I -=⨯,426.810m A -=⨯,相应的有限元分析模型见图3-20。
在ANSYS 平台上,完成相应的力学分析。
图3-19 框架结构受一均布力作用(a ) 节点位移及单元编号 (b ) 等效在节点上的外力图3-20 单元划分、节点位移及节点上的外载解答 对该问题进行有限元分析的过程如下。
1.基于图形界面的交互式操作(step by step)(1) 进入ANSYS(设定工作目录和工作文件)程序 →ANSYS → ANSYS Interactive →Working directory (设置工作目录) →Initial jobname (设置工作文件名): beam3→Run → OK(2) 设置计算类型ANSYS Main Menu: Preferences… → Structural → OK(3) 选择单元类型ANSYS Main Menu: Preprocessor →Element Type →Add/Edit/Delete… →Add… →beam :2D elastic 3 →OK (返回到Element Types 窗口) →Close(4) 定义材料参数ANSYS Main Menu:Preprocessor →Material Props →Material Models→Structural →Linear →Elastic→Isotropic: EX:3e11 (弹性模量) →OK →鼠标点击该窗口右上角的“ ”来关闭该窗口(5) 定义实常数以确定平面问题的厚度ANSYS Main Menu: Preprocessor →Real Constant s… →Add/Edit/Delete →Add →Type 1 Beam3→OK→Real Constant Set No: 1 (第1号实常数), Cross-sectional area:6.8e-4 (梁的横截面积) →OK →Close(6) 生成几何模型生成节点ANSYS Main Menu: Preprocessor →Modeling →Creat→Nodes→In Active CS→Node number 1 →X:0,Y:0.96,Z:0 →Apply→Node number 2 →X:1.44,Y:0.96,Z:0 →Apply→Node number 3 →X:0,Y:0,Z:0→Apply→Node number 4 →X:1.44,Y:0,Z:0→OK生成单元ANSYS Main Menu: Preprocessor →Modeling →Create →Element →Auto Numbered →Thru Nodes →选择节点1,2(生成单元1)→apply →选择节点1,3(生成单元2)→apply →选择节点2,4(生成单元3)→OK(7)模型施加约束和外载左边加X方向的受力ANSYS Main Menu:Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择节点1→apply →Direction of force: FX →V ALUE:3000 →OK→上方施加Y方向的均布载荷ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Pressure →On Beams →选取单元1(节点1和节点2之间)→apply →V ALI:4167→V ALJ:4167→OK左、右下角节点加约束ANSYS Main Menu:Solution →Define Loads →Apply →Structural →Displacement →On Nodes →选取节点3和节点4 →Apply →Lab:ALL DOF →OK(8) 分析计算ANSYS Main Menu:Solution →Solve →Current LS →OK →Should the Solve Command be Executed? Y→Close (Solution is done! ) →关闭文字窗口(9) 结果显示ANSYS Main Menu: General Postproc →Plot Results →Deformed Shape … →Def + Undeformed →OK (返回到Plot Results)(10) 退出系统ANSYS Utility Menu: File→Exit …→Save Everything→OK(11) 计算结果的验证与MA TLAB支反力计算结果一致。
平面框架结构的有限元分析

三梁平面框架结构的有限元分析一、问题说明如图1所示的框架结构,其顶端受均布载荷作用,用有限元方法分析该结构的位移。
结构中各个部分的参数为:弹性模量E=300GPa,截面惯性矩I=6.5×105mm4,横截面积A=680mm2。
相应的有限元分析模型见图2,利用梁板壳分析程序完成该模型的力学分析。
图1框架结构图2有限元分析模型二.Fortran程序的输入数据(1)Facile.11 4 3 6 0 12 42 1 11 1 11 3 51 2 2 3 3 40 0 0 0 1000 01000 1000 0 1000 0 0(2)Facile.2111 211 1111 0 0 0 1 03E5 1.6E5680 6.5E5 6.5E5 6.5E50 0(3)Facile.312 41 02 03 04 05 06 0 19 0 20 0 21 0 22 023 0 24 08 -1200 12 -200000 14 -1200 18 200000输出的数据文件为:Facile7和Facile8,其中各节点位移结果在文件Facile8中。
三.计算结果各节点的位移计算结果见表1。
四.Ansys分析结果Ansys计算结果如下图所示,图3为节点x方向的位移云图,图4为节点y 方向的位移云图,图5为节点转角云图。
图3 节点x方向的位移图4 节点y方向的位移图5 节点转角各节点的位移值见表2。
五.结果对比通过对比表1和表2中的数据可以发现,Fortran程序与Ansys分析的结果十分接近。
实例3 平面框架结构的有限元分析

三梁平面框架结构的有限元分析如图框架结构,顶端受均布力作用,各个截面的参数都为:E =3.0 ×1011 Pa ,I =6.5 ×10−7 m 4 ,A =6.8 ×10−4 m 21 基于图形界面(GUI)的交互式操作(1) 进入A NSYS(设定工作目录和工作文件)程序→ANSYS →ANSYS Interactive →Working directory (设置工作目录) →Initial jobname(设置工作文件名): beam3→Run →OK(2) 设置计算类型ANSYS Main Menu: Preferences… →Structural →OK(3) 选择单元类型ANSYS Main Menu: Preprocessor →Element Type→Add/Edit/Delet e… →Add… →beam:2D elastic 3OK (返回到E lement Types 窗口) →Close(4) 定义材料参数ANSYS Main Menu: Preprocessor →Material Props →Material Models→Structural →Linear →Elastic→Isotropic: EX:3e11 (弹性模量) →OK →鼠标点击该窗口右上角的“U”来关闭该窗口(5) 定义实常数以确定平面问题的厚度ANSYS Main Menu: Preprocessor →Real Constants… →Add/Edit/Delete →Add →Type 1 Beam3→OK→Real Constant Set No: 1 (第1号实常数), Cross-sectional area:6.8e-4 (梁的横截面积) →OK →Close(6) 生成几何模型生成节点ANSYS Main Menu: Preprocessor →Modeling →Creat→Nodes→In Active CS→Nodenumber 1 →X:0,Y:0.96,Z:0 →Apply→Node number 2 →X:1.44,Y:0.96,Z:0 →Apply→Node number 3 →X:0,Y:0,Z:0→Apply→Node number 4 →X:1.44,Y:0,Z:0→OK生成单元ANSYS Main Menu: Preprocessor →Modeling →Create →Element →Auto Numbered →Thru Nodes →选择节点1、2(生成单元1)→apply →选择节点1、3(生成单元2)→apply →选择节点2、4(生成单元3)→OK(7) 模型施加约束和外载左边加X方向的受力ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes→选择节点1→apply →Direction of force: FX →V ALUE:3000 →OK→上方施加Y方向的均布载荷ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Pressure →On Beams →选取单元1(节点1和节点2之间)→apply →V ALI:4167→V ALJ:4167→OK左、右下角节点加约束ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Displacement →On Nodes →选取节点3和节点4→Apply →Lab:ALL DOF →OK(8) 分析计算ANSYS Main Menu: Solution →Solve →Current LS →OK →Should The Solve Command beExecuted? Y→Close (Solution is done! ) →关闭文字窗口(9) 结果显示ANSYS Main Menu: General Postproc →Plot Results →Deformed Shape … →Def + Undeformed →OK (返回到P lot Results)(10) 退出系统ANSYS Utility Menu: File→Exit …→Save Everything→OK(11) 计算结果的验证与M A TLAB 支反力计算结果一致。
有限元(梁系)

u
(e)
(e )
i
vi i u j v j j
xi
( e )T
单元结点力列向量: F
F
Fyi M i Fxj Fyj M j
( e )T
单元的自由度:单元的自由度为单元全部结点自由度之和 每结点自由度:3个
2.单元的位移函数(displacement function) 单元位移函数:用来描述单元内位移分布规律的函数 (插值函数)(interpolating function)
(3-1a),(3-1b)或(3-2a),(3-2b)称为二维梁单元的位移函数
二、结点位移(杆端位移)与杆端力的关系 1、 对于轴力有:
E
Fx A
EA 所以: x EA F ui u j l
du 1 1 因为: ui u j dx l l
y
y
Fyi Fxi sin Fyi cos M i M i
Fxj Fxj cos Fyj sin Fyj Fxj sin Fyj cos M j M j
vj
vi
i i
vj
uj uj
结构刚度矩阵(Structure Stiffness Matrix)
用力的平衡关系建立结构的刚度方程。 先把单元局部坐标系下的各物理量变换到统一的坐标系 下——结构坐标系下。
一、结构坐标系
我们把任意的一个单元取出来,放在结构坐标系下,考 察一下该单元在两种坐标系下的物理量。 首先定义一下结构坐标系x-y与局部坐标系 x y 的夹角符 号: x-y坐标系沿逆时针转动到与 x y 坐标系重合,则x-y坐 标系转过的角度 为正。
有限元作业—三梁平面框架结构的有限元分析

三梁平面框架结构的有限元分析针对如图1所示的框架结构,其顶端受均布力作用,用有限元方法分析该结构的位移。
结构中各个截面的参数都为:E=3.0 10 Pa,I =6.5 10〃m,2A =6.8 10 m,生成相应的有限元分析模型。
在ANSY平台上,完成相应的力学分析。
416~N nt3000N② ③144mI ------------------------------------------------------------------------------------------ |图1框架结构受一均布力作用ANSYS军答:对该问题进行有限元分析的过程如下。
(1)进入ANSYS设定工作目录和工作文件)程序—An sys —ANSYS In teractive —Worki ng directory (设置工作目录)—Initial jobname(设置工作文件名):beam3 —Run —OK(2)设置计算类型ANSYS Main Menu: Preferences , —Structural —OK(3)选择单元类型ANSYS Main Me nu: Preprocessor —Eleme nt Type —Add/Edit/Delete , —Add, —beam 2node188 —OK (返回到Element Types 窗口)—CloseCross-sectional area:6.8e-4 (梁的横截面积)—OK —Close八 Library of Element Types Library of Element TypesElement type referenc ■亡 number(4)定义材料参数ANSYS Mai n Me nu: Preprocessor — Material Props — Material Models —Structural — Lin ear — Elastic — Isotropic: EX:3e11 ( 弹性模量)—OKANSYS Main Menu: Preprocessor — Real Constants , — Add/Edit/Delete —Add — Type 1 Beam3 — OK — Real Constant Set No: 1 ( 第 1 号实常数),Ry finite 戟『気2 node 1882 node 188Canttl—鼠标点击该窗口右上角的“ ”来关闭该窗口。
梁的有限元分析原理

梁的有限元分析原理梁的有限元分析原理是一种工程结构分析方法,广泛应用于建筑、桥梁、航空航天、汽车等领域。
它通过将连续的结构离散化为有限数量的小单元,通过数学模型进行计算,得出结构的力学性能和响应情况。
梁的有限元分析原理是有限元分析的基础,下面将对其进行详细介绍。
首先,梁的有限元分析原理基于梁理论,即在横向较小、纵向较长的情况下,结构可以近似为一维梁。
梁的有限元分析原理通过将梁划分为多个单元,每个单元内部可以看作两个节点之间的一段杆件,通过建立节点之间的力学关系方程,得到整个结构的力学性能。
其次,梁的有限元分析原理利用了变分原理,即将结构的势能取极小值,建立了结构的力学方程。
通过对于梁的弯曲、剪切和轴向力等方面的力学模型进行合理的假设与简化,可以得到结构的位移与力的关系,从而解决结构的力学问题。
在梁的有限元分析中,需要进行以下几个步骤:1.几何离散化:将梁结构划分为多个单元,每个单元具有相同的形状与尺寸,通常为矩形或三角形。
2.模型建立:根据梁理论以及力学方程的简化假设,建立节点的力学关系方程,包括位移、应力、应变等参数。
3.材料性能定义:确定梁材料的力学性能参数,如弹性模量、截面惯性矩等。
这些参数对梁结构的力学性能具有重要影响。
4.边界条件施加:根据实际问题设定边界条件,包括固定支座、约束条件等。
这些条件对于解决梁结构的位移、应力等问题至关重要。
5.方程求解:通过数学方法求解得到节点之间的力学关系方程,利用数值计算技术进行迭代求解,得到梁结构的位移、应力等参数。
6.结果分析:根据求解得到的结果,进行力学性能分析,如最大应力、挠度、模态分析等。
根据分析结果评估结构的强度与稳定性。
总结起来,梁的有限元分析原理是一种基于梁理论的工程结构分析方法,通过将结构离散化为多个小单元,利用力学关系方程和数值计算技术求解得到结构的力学性能。
通过梁的有限元分析原理,工程师可以更加准确地评估结构的强度与稳定性,对结构进行优化设计。
钢筋混凝土框架结构的有限元分析

钢筋混凝土框架结构的有限元分析[摘要]利用ANSYS软件建立一榀三层框架模型,对该结构模型进行非线性有限元分析,得出框架结构在一定荷载作用下的破坏特征。
【关键词】ANSYS;框架;非线性1、框架尺寸和材料参数框架模型为单跨三层结构,跨度和层高尺寸见图1,结构选用混凝土等级为C30,梁柱截面尺寸及配筋情况见图2。
钢筋及砼强度设计值通过查阅《混凝土结构设计规范》取得。
2、分离式建模采用link8,Solid65单元分别模拟钢筋和混凝土,保护层厚度取2cm。
ANSYS 中对模型的网格划分方法有映射网格划分和自由网格划分两种。
自由网格划分对于单元形状没有限制,并且没有特定的准则,映射网格划分对单元形状有限制。
且须满足特定规则,映射面网格只包含四边形和三角形单元,映射体网格只包含六面体单元,映射网格具有规则的形状,明显成排的单元,如果要用这种网格类型,须将模型划分成相当规则的体和面,但映射网格有利于结点数据的储存,使得计算速度快耗时少。
由于框架几何形状比较规则,采用映射划分网格,单元均采用六面体划分网格,单元最小尺寸为2cm(见图3)。
为避免加载点砼出现局部破坏而影响计算结果,在加载点设置垫块并将集中荷载等效为垫块区域均布荷载。
3、有限元计算与结果分析一次性施加竖向荷载,在左侧柱顶分步逐级施加水平右向荷载(加载图参见图1),图4、图5分别为开裂裂缝图和破坏裂缝图,结构开始出现裂缝时的荷载为6KN,钢筋屈服荷载为36KN,结构破坏荷载58KN。
当荷载加至6KN时,梁端最先出现裂缝,然后裂缝向梁中间延伸,随着梁端裂缝的增长增多,柱子底部出现水平裂缝和拉裂裂缝,裂缝不断增多并向上延伸,当荷载加至36KN时,梁端钢筋开始屈服,标志着结构从弹性阶段开始过度到弹塑性阶段,由于顶梁比第一、二层梁截面尺寸和配筋小,顶梁裂缝最多破坏最严重,当荷载加至58KN时,梁端纵筋和柱底纵筋达到极限强度,梁柱节点区域出现许多裂缝,以致整个结构彻底破坏而计算停止。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三梁平面框架结构的有限元分析
针对如图1所示的框架结构,其顶端受均布力作用,用有限元方法分析该结
构的位移。
结构中各个截面的参数都为:113.010Pa E =⨯,746.510m I -=⨯,
426.810m A -=⨯,生成相应的有限元分析模型。
在ANSYS 平台上,完成相应的力学分析。
图1 框架结构受一均布力作用
ANSYS 解答 :对该问题进行有限元分析的过程如下。
(1) 进入ANSYS(设定工作目录和工作文件)
程序 →Ansys → ANSYS Interactive →Working directory (设置工作目录) →Initial jobname(设置工作文件名): beam3→Run → OK
(2) 设置计算类型
ANSYS Main Menu: Preferences … → Structural → OK
(3) 选择单元类型
ANSYS Main Menu: Preprocessor →Element Type →Add/Edit/Delete … →Add … →beam :2node188 →OK (返回到Element Types 窗口) →Close
(4) 定义材料参数
ANSYS Main Menu: Preprocessor →Material Props →Material Models →Structural →Linear →Elastic→ Isotropic: EX:3e11 (弹性模量) → OK →鼠标点击该窗口右上角的“ ”来关闭该窗口。
(5)定义实常数以确定平面问题的厚度
ANSYS Main Menu: Preprocessor →Real Constants…→Add/Edit/Delete →Add →Type 1 Beam3→ OK→Real Constant Set No: 1 (第1号实常数), Cross-sectional area:6.8e-4 (梁的横截面积) →OK →Close
(6) 生成几何模型
生成节点
ANSYS Main Menu: Preprocessor →Modeling →Creat→Nodes→ In Active CS→Node number 1 →X:0,Y:0.96,Z:0 →Apply→Node number 2 →X:1.44,Y:0.96,Z:0 →Apply→Node number 3 → X:0,Y:0,Z:0→Apply→Node number 4 → X:1.44,Y:0,Z:0→OK
生成单元
ANSYS Main Menu: Preprocessor → Modeling → Create →Element →Auto Numbered → Thru Nodes →选择节点 1,2(生成单元1)→ apply →选择节点 1, 3(生成单元2)→ apply →选择节点 2, 4(生成单元3)→OK
(7) 模型施加约束和外载
左边加X方向的受力
ANSYS Main Menu:Solution → Define Loads → Apply →Structural →Force/Moment → On Nodes →选择节点1→ apply →Direction of force: FX
→VALUE:3000 → OK
上方施加Y方向的均布载荷
ANSYS Main Menu: Solution→ Define Loads → Apply →Structural →Pressure →On Beams →选取单元1(节点1和节点2之间)→ apply →VALI:4167→VALJ:4167→OK
左、右下角节点加约束
ANSYS Main Menu: Solution → Define Loads → Apply →Structural →Displacement → On Nodes →选取节点3和节点4 → Apply → Lab:ALL DOF → OK
(8) 分析计算
ANSYS Main Menu: Solution → Solve → Current LS →OK → Should the Solve Command be Executed? Y→ Close (Solution is done! ) →关闭文字窗口
(9) 结果显示
ANSYS Main Menu: General Postproc →Plot Results →Deformed Shape …→ Def + Undeformed → OK (返回到Plot Results)
各节点位移计算结果
NODE UX UY ROTZ
1 0.41034E-05 -0.14768E-01 -0.62904E-05
2 0.23191E-06 -0.14773E-01 -0.48275E-06
3 0.0000 0.0000 0.0000
4 0.0000 0.0000 0.0000
节点最大位移计算结果
MAXIMUM ABSOLUTE VALUES
NODE 1 2 1
VALUE 0.41034E-05 -0.14773E-01 -0.62904E-05
所有单元内力计算结果
单元编号轴力轴向应力轴向应变
ELEM MFORX SAXL EPELAXL
1 -0.52427 -0.80657E+06 -0.26886E-05
2 -2999.7 -0.46150E+10 -0.15383E-01
3 -3000.7 -0.46165E+10 -0.15388E-01
轴力、向应力和轴向应变的最小值所在单元
ELEM 3 3 3
VALUE -3000.7 -0.46165E+10 -0.15388E-01
轴力、向应力和轴向应变的最大值及所在单元
ELEM 1 1 1
VALUE -0.52427 -0.80657E+06-0.26886E-05
(10) 退出系统
ANSYS Utility Menu:File→ Exit …→ Save Everything→OK
完全的命令流
/ PREP7 !进入前处理
ET,1,beam3 !选择单元类型
R,1,6.5e-7,6.8e-4 !给出实常数(横截面积、惯性矩)
MP,EX,1,3e11 !给出材料的弹性模量
N,1,0,0.96,0 !生成4个节点,坐标(0,0.96,0),以下类似
N,2,1.44,0.96,0
N,3,0,0,0
N,4,1.44,0,0
E,1,2 !生成单元(连接1号节点和2号节点) ,以下类似E,1,3
E,2,4
D,3,ALL !将3号节点的位移全部固定
D,4,ALL !将4号节点的位移全部固定
F,1,FX,3000 !在1号节点处施加X方向的力(3000) SFBEAM,1,1,PRESS,4167 !施加均布压力
FINISH !结束前处理状态
/SOLU !进入求解模块
SOLVE !求解
FINISH !结束求解状态
/POST1 !进入后处理
PLDISP,1 !显示变形状况
FINISH !结束后处理。
