高观点下的中学数学作业四(陕师大)
“高观点”下的中学数学的实践与认识

“高观点”下的中学数学的实践与认识一、本文概述《“高观点”下的中学数学的实践与认识》是一篇旨在探讨如何在中学数学教育中融入高观点教学理念的文章。
文章首先介绍了“高观点”教学理念的定义和内涵,指出这种教学理念对于提升学生数学素养、培养学生的创新能力和解决问题的能力具有重要意义。
接着,文章分析了当前中学数学教育面临的挑战,如教学内容单教学方法陈旧、学生缺乏实践机会等问题,并提出了在“高观点”下解决这些问题的策略和方法。
文章强调,中学数学教育的目标不仅仅是传授知识,更重要的是培养学生的数学思维和解决问题的能力。
因此,文章提倡将高观点教学理念引入到中学数学教学中,通过引导学生从更高的层次和更广阔的视角去理解和应用数学知识,提升学生的数学素养和创新能力。
文章还指出,实现这一目标需要教师不断更新教育观念,改进教学方法,为学生提供更多的实践机会和探究空间。
在文章的结构上,本文先对“高观点”教学理念进行阐述,然后分析当前中学数学教育的问题和挑战,接着提出在“高观点”下解决这些问题的策略和方法,最后对实施这些策略和方法可能遇到的困难和挑战进行讨论和展望。
通过这篇文章,我们希望能够引起广大中学数学教师和教育管理者的关注,共同推动中学数学教育的发展和进步。
二、“高观点”下的中学数学教学实践“高观点”下的中学数学教学,不仅要求教师对数学知识有深入的理解和掌握,还需要他们具备从更高层次、更宽广的视角去看待和教授数学知识的能力。
这种教学方法的实践,能够帮助学生更好地理解和掌握数学知识,提高他们的数学素养和解决问题的能力。
将高等数学的知识和思维方法引入中学数学教学。
高等数学的知识和思维方法往往具有更高的抽象性和普适性,能够帮助学生更好地理解和掌握中学数学知识。
例如,在中学数学中引入微积分、线性代数等高等数学的知识,可以帮助学生更好地理解函数的性质、变量的变化等概念。
注重数学知识的应用和问题解决。
数学是一门应用广泛的学科,将数学知识应用到实际问题中,能够帮助学生更好地理解数学的应用价值,提高他们的数学素养和解决问题的能力。
高观点下的中学数学作业四(陕师大)
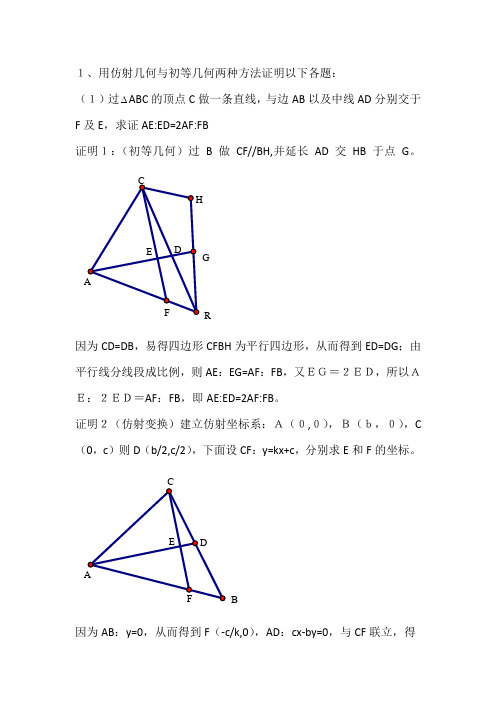
1、用仿射几何与初等几何两种方法证明以下各题:(1)过 ABC 的顶点C 做一条直线,与边AB 以及中线AD 分别交于F 及E ,求证AE:ED=2AF:FB证明1:(初等几何)过B 做CF//BH,并延长AD 交HB 于点G 。
因为CD=DB ,易得四边形CFBH 为平行四边形,从而得到ED=DG ;由平行线分线段成比例,则AE :EG=AF :FB ,又EG=2ED,所以AE:2ED=AF :FB ,即AE:ED=2AF:FB 。
证明2(仿射变换)建立仿射坐标系:A(0,0),B(b,0),C (0,c )则D (b/2,c/2),下面设CF :y=kx+c ,分别求E 和F 的坐标。
因为AB :y=0,从而得到F (-c/k,0),AD :cx-by=0,与CF 联立,得R GBE (bc/(c-kb),c^2/(c-kb))AF :FB=-c/k ((b+c/k )=-c/(kb+c),AE:ED=bc/(c-kb):[b/2-bc(c-kb)]=-2c/(kb+c))所以,AE:ED=2AF:FB(2)(梅耐劳斯定理)设L ,N ,M 分别在∆ABC 的边AB,AC,BC(或延长线)上,求证:L ,N ,M 三点共线的充要条件是1AL BM CM LB MC MA⋅⋅= 证明:如图,建立仿射坐标系:以BC 为x 轴,以BA 为y 轴,B (0,0),C (a ,0),A (0,b ),00(,0),(0,)M x N y ,则直线AC 的方程为:1x y a b+=, 0000000000000000000000000000000000ML 1()()(,)()(),,()()()1()x y N x y ax b y by b y bx ay bx ay ax b y a b y x bx ay y x a AL BM CN ax b y LB y MC x a NA x b y bx ay b y x y x a AL BM CN LB MC NA y x a x b y +=---------====------⋅⋅=⋅⋅=--直线的方程为:,联立上述方程,可求得点坐标为所以,故本题结论得证(3)已知∆ABC 中,D是BC 边上的中点,G 是AD 上的任一点,连MCB接BG 并延长交AC 于E ,连接并延长交DG,AB于F,求证FE//BC证明:如图,延长AD至K使得DG=DK,由于BD=DC,所以四边形BKCG为平行四边形,所以进一步得到FG//BK,KC//GE,在∆ABK和∆AKC中,根据平行线分线段成比例知:,,//AF AG AE AG AF AE FE BC FB GK EC GK FB EC==,从而所以2、利用“圆的仿射变换像是椭圆”这一结论,试将与圆有关的一些结论移植到椭圆上去,并给出证明K CB,,22222222,222,,,2,21(0)1(0),OAB O A a O A a 12OAB OA B x y a b ab a bx y a b a bx x x y a y ya S S a ππ∆∆+=>>+=>>⎧=+=∆⎨=⎩===椭圆的面积是证明:设椭圆方程:,则其经过仿射变换,对应图形为圆椭圆内的各定点的坐标为(0,0),(,0),B(0,b),圆中对应的三角形顶点坐标为(0,0),(,0),B(0,a)椭圆的面积圆的面积所以,即椭圆的ab π面积为。
高观点下的的中学数学

高观点下的中学数学高观点下的的初等数学,这一重要思想发端于19世纪末,20世纪初的一场教育教学改革运动—克莱因·贝利运动.其中菲利克斯·克莱因不仅是一位伟大的数学家,也是现代国际数学教育的奠基人.他主张在现代数学观点指导下研究“高数”与“中数”之间的联系,高等数学中有许多方法,可以和中学数学相通,有些也可以迁移到中学数学中,高等数学的方法不仅可以使我们居高临下地观察初等数学问题,帮助我们确定解题思路,有时还能帮助我们发现某些初等问题的实质,寻求更一般、更简捷的解决问题的方法.(一)高观点下研究中学数学的必要性新一轮课程改革无论是从形式上还是从内容上,都对中学数学提出了许多新的课题,从内容上高等数学内容不断地下放到中学,从形式上,更强调教学活动的设计、开放性的教学和研究性的学习,更关注培养学生解决问题、分析问题的能力,以及所教知识的来龙去脉,这就使得高观点下研究中学数学,不仅是教学改革的迫切任务,也是新课改形势下中学数学教学改革的一个主流方向.具体表现为(1) 教学过程中,创设问题情境的需要. ◆例1:等差数列求和10012310010150S =++++=⨯L(1)(1)2123112(1)22n n n n n n S n n n n n ⎧+⎪+⎪=++++==⎨-+⎪++⎪⎩L 为奇数为奇数2(1)n S n n =+从高斯求和开始,再到一般等差数列的求和,从问题所呈现形式出发,引导学生积极思考倒写相加法是如何想到的,还原问题发生发展的过程。
把知识变得有血有肉,从而激发学生积极探索的兴趣. 例2 数列的递推公式 ◆河内塔问题相传在越南的某寺庙中有一个用n 个带孔的大小不等的圆盘磊成的塔,僧侣们每天挪动一次圆盘,一次只能挪动一个,任何时候大盘不得在小盘之上,将全部n个圆盘从A处挪到C处,最少需要多少天?(可放回B处)AB C1231,3,7,.a a a ===L 121,21n n n n a a a +=+=-教师要有渊博的数学知识,这样才能让你的课堂变得更加充实.本例想说明两点,一是已知递推公式,可以求出数列的任何一项,二是在有些计数问题中,我们也可利用数列的递推公式求解,这实际上也是递推公式的应用,通过这样的教学手段,将是课本知识变得更加丰富,更有活力. ◆例 平面上n条两两相交且无三条共点的直线可把平面分成几部分?11(1)2,1,12n n n n n a a a n a ++==++=+◆例 (F数列)有一儿童要上n阶楼梯,他一步可上一阶也可上两阶,问有多少不同上法?12(3)n n n a a a n --=+≥( 2 ) 高考题和竞赛题经常会有高等数学的背景 ◆例1 用四种不同颜色给图中区域染色,要求相邻区域不同色,,有多少不同染色方法? 这是著名的四色问题解法Ⅰ加法原理和乘法原理4312124321214321111120⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯=分1、4同色与1、4不同色(2、4同色与2、4不同色)解法Ⅱ 本例也可以利用递推方法, 当4n ≥时,113432,4n n n a a a --+=⨯⨯=!教师站的越高,才能更容易指导学生掌握知识,抓住问题的实质,学生才能用更少的时间掌握通性同法.( 3 ) 学生的求知欲对教师提出了更高的要求 当今学生接受知识的渠道越来越多,知识面越来越广,老师必须有一桶水,才能教给学生一碗水. ◆例 四人各写一张明信片,然后交换,每人都收到不是自己写的明信片,有多少种不同方法?(高考题)分析:这是组合数学中错排问题,因为数比较小,可简单的分类,利用两个原理来解决,但若学生提出100人的错排,应如何解决呢?一般地,1,2,3,…,n的全排列,其中i(1≤i≤n)不在第i位,这样的错排共有多少个?解 1 (容斥原理) 用i A 表示i 在第i 位的全排列(n i ,,2,1Λ=),则nn A A A D I ΛI I 21==∑∑∑-+++-n n j i i A A A A A A S I ΛI I ΛI 21)1(=!0)1()!2()!1(!21nn n n nC n C n C n -++-+--Λ=)!1)1(!31!2111(!n n n -++-+-Λ解2 (递推公式)设n a a a Λ,,21为n Λ,2,1的一个错排,显然i a a i≠≠,11,分两类(1) 第1a 位是1,共2-n D 种方法;(2)第1a 位不是1,有1-n D 种方法.又1a 有(1-n )种取法,故))(1(21--+-=n n nD D n D 其中1,021==D D)!2(1)!1(1!21-+--=--n D n n D n n n D n n n 令!n D E nn=,则2111--+-=n n nE nE n n E !1)1()(1211n E E n E E n n n n n -==--=----Λ,又01=E!1)1(!31!21n E n n -++-=Λ,因此)!1)1(!31!21!111(!n n D n n -++-+-=Λ.◆例 2 过:,0:22221111=++=++c y b x a l c y b x a l 交点),(00y x P 的直线系0)()(22221111=+++++c y b x a c y b x a λλ),(),,(222111b a n b a n ==,1n 与2n 线性无关,可作为二维空间的一组基底,由平面向量基本定理可知该直线包含过),(00y x P 的任何直线.而0)()(222111=+++++c y b x a c y b x a λ表示的直线系不含2l ,原因是21n n λ+与2n 不共线. (二)排列组合的有关问题(1)多重复的排列和组合◆例1,一排七盏路灯,关掉其中互不相邻的三盏,且不关两端的路灯,有多少种方法?分析:4个a ,3个b 的全排列,要求b 互不相邻且不在两端的方法有34C◆例2:100=++z y x 的正整数解的个数?方法Ⅰ:98+97+…+1=299C方法Ⅱ:对应于97///=++z y x 非负整数解个数,又可转化为97个球与两个竖线的全排列方法数299C(也可理解为{a,b,c}的一个97可重组合,97个相同的球放入三个不同的盒子中的方法数).古典组合数学的主要原理有: ①两个基本原理 ②容斥原理③一一对应,和中学要求一致.(2)分配问题(k n ≥)◆例:4人分配到3个工厂,每个工厂至少1人的方法数为 3324A C .一般地,n 个人分配到k 个工厂,(n ≥k ),每个工厂至少1人的方法数?解:用i A 表示第i 个工厂空的方法数,(i =1,2…k )kk n A A A S k ⋅⋅⋅=⋅I I 21!=n k k k n k n k n k k C k C k C k )()1()2()1(21--+⋅⋅⋅--+--现代组合数学工具还有母函数和Fevver 图,在数学竞赛中经常看到,例如解决整数的分拆. (三)有关根据递推公式,求通项公式 (1))(1n f a a n n =-+型与)(1n f a a n n •=+型.利用累加法与累乘法. (2)q pa a n n +=+1型.◆例:,1,1211=+=+a a a n n 求?=na解:)1(211+=++n n a a ,令}{,1n n n b a b +=是等比数列,n n b 2= 12-=n n a(3))(1n f pa a n n +=+◆例:,1,3211=+=+a a a n n n 求n a解:)3(2311n n n n a a -=-++ 令}{,3n n n n b a b -=是等比数列,n n b 2-= 所以n n n a 23-=.也可化为(1)型(2)型 ◆例: ,1,211=+=+a n a a n n 求n a 解: ),1(21)1(1++=++++n a n a n n 1231--⨯=-n a n n(4) 11-++=n n n qa pa a 型解:特征方程:02=--q px x ,若有两个不相等实根βα,,则n n n a βλαλ21+=, 若有两个相等实根βα=,则n n n a αλλ)(21+=,若无实根,周期数列. ◆例: F 数列,)3(,1,12121≥+===--n a a a a a n n n ,求 n a解:特征方程: 251,012±==--x x x , nn n a )251()251(21-++=λλ 21,λλ 由21,a a 确定. (注:也可以化为一阶递推公式,再求通项公式) (5)分数型递推公式)(,)(1n n a f a dcx bax x f =++=+构造数列}{n a 当x x f =)(有两个不等实根βα,时,(即)(x f 有两个不动点),则k a a k a a n n n n (11βαβα--⋅=--++为常数). 当x x f =)(有两个相等实根0x 时,(即)(x f 有唯一不动点),则存在常数k 使得k x a x a n n +-=-+00111.当x x f =)(无不动点时,往往是周期数列. 此种形式的数列,有时也可采用倒数法或三角换元. ◆例: 2,1111=-+=+a a a a nnn 求 n a解: x xx f -+=11)(, 方程x xx =-+11无实根,则数列{n a }是一周期数列,(周期是4).+===θθtan(,tan 221a a л/4)…,)1(tan[-+=n a n θ л/4](6)生成函数,例F 函数由递推公式求通项公式,往往是通过构造新数列,把递推公式变形成等差或等比数列,通过求新数列通项公式,再求原数列通项,差分方程中有太多这样的例子.以上只是我对这两部分的一些简单认识,其余章节也有一些类似的问题.。
高等数学观点下的中学数学

高等数学观点下的中学数学高等数学观点下的中学数学,这个话题听上去有点儿高大上,对吧?说白了,就是把那些看似复杂的数学概念,搬到我们熟悉的中学数学里,没错,咱们都曾在课堂上认真听讲的那些内容。
说到高等数学,大家脑海里肯定浮现出那一堆看起来像外星文的公式和符号,让人头大。
但是,如果你稍微把视角拉回一点,看看中学数学,哎,真的有惊喜。
先说说代数。
大家应该都经历过那个让人捧心口的“解方程”的过程,哎,心里想着:“这玩意儿到底有什么用?”当我们用高等数学的眼光去看待代数,哇,发现它其实是解谜的游戏。
就像找寻宝藏一样,把未知数藏在方程里,咱们用各种方法挖掘出来,真是过瘾!你看,代数的公式就像是魔法,运用得当,什么都能解决。
想想看,生活中那些看似复杂的问题,其实归根结底也是在“解方程”嘛。
无论是购物算折扣,还是计划行程,都可以用代数的方式来思考。
再聊聊几何。
几何就像是在画画,线条、角度、面积……都是画布上的元素。
高等数学里的几何则把这些元素放大,变成一幅幅美丽的画卷。
想象一下,平面图形转化成立体,真是像魔法一样!中学的时候,咱们常常用直尺和圆规,画出各种图形,嘿,实际上,高等数学告诉我们,这些图形背后还有深刻的逻辑和美感。
比如,圆的性质让人感叹,什么直径、弦、切线,简直像是在解读宇宙的奥秘!我们用几何学来理解世界,理解那些隐藏在平凡背后的不平凡。
再看看函数,啊,函数可谓是数学中的明星。
中学的时候,我们学习的那些图像,像是抛物线、正弦波,简直就是数学的舞蹈。
高等数学则把这些舞蹈推向了更高的境界。
想象一下,把函数的变化当作生活中的各种情绪波动,是不是更贴近我们自己的经历?生活不就是一场函数的图像吗?高兴时,上升,低落时,下降。
用函数来解释生活的起伏,听起来是不是特别有意思?当你能用函数去描绘自己的生活状态,那种感觉就像是找到了人生的说明书。
还有微积分,哎呀,这个东西初听起来就让人觉得复杂,它就像是观察时间的流逝和变化。
最新陕西省师大附中高三数学四模考试试题 理(含解析)(含答案解析)

陕西师大附中高考数学四模试卷(理科) 一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出地四个选项中,只有一项是符合题目要求地.1.(5分)已知全集U={﹣1,1,2,3,4},集合A={1,2,3},B={2,4},则(∁U A )∪B 为( ) A . {1,2,4} B .{2,3,4} C .{﹣1,2,4} D . {﹣1,2,3,4}考点:交、并、补集地混合运算. 专计算题.题:分析: 利用补集运算求出∁U A ,然后直接利用交集运算求解.解答: 解:因为集合A={1,2,3},U={﹣1,1,2,3,4}, 所以∁U A={﹣1,4},所以(∁U A )∪B={﹣1,4}∪{2,4}={﹣1,2,4}. 故选C .点评: 本题考查了交、并、补集地混合运算,是基础地概念题.2.(5分)如果复数z=,则( )A .|z|=2 B .z 地实部为1 C . z 地虚部为﹣1 D .z 地共轭复数为1+i考点:复数代数形式地乘除运算;复数地基本概念. 专题:计算题. 分析: 直接利用复数地除法运算化简,求出复数地模,然后逐一核对选项即可得到答案. 解解:由z=,答: 所以,z 地实部为﹣1,z 地虚部为﹣1,z 地共轭复数为﹣1+i , 故选C .点评: 本题考查了复数代数形式地乘除运算,考查了复数地基本概念,是基础题.3.(5分)(2012•安徽模拟)已知双曲线地一个焦点与抛物线y 2=4x 地焦点重合,且双曲线地离心率等于,则该双曲线地方程为( ) A .B .C .D .考点: 双曲线地标准方程;抛物线地简单性质;双曲线地简单性质. 专题:计算题;压轴题. 分析: 先根据抛物线方程求得焦点坐标,进而确定双曲线地焦点,求得双曲线中地c ,根据离心率进而求得长半轴,最后根据b 2=c 2﹣a 2求得b ,则双曲线地方程可得.解答:解:抛物线y 2=4x 地焦点F (1,0), 双曲线地方程为故选D点评: 本题主要考查了双曲线地标准方程.考查了对圆锥曲线基础知识地综合运用.4.(5分)已知地二项展开式地各项系数和为32,则二项展开式中x 4地系数为( ) A . 5 B .10 C .20 D .40考点:二项式系数地性质. 专题:计算题.分析: 先对二项式中地x 赋值1求出展开式地系数和,列出方程求出n 地值,代入二项式;再利用二项展开式地通项公式求出展开式地通项,令通项中地x 地指数为4,求出r ,将r 地值代入通项求出二项展开式中x 4地系数. 解答: 解:在中,令x=1得到二项展开式地各项系数和为2n∴2n=32 ∴n=5 ∴其展开式地通项为T r+1=C 5r x 10﹣3r令10﹣3r=4得r=2∴二项展开式中x 4地系数为C 52=10 故选B .点评: 求二项展开式地系数和常用地方法是给二项式中地x 赋值;解决二项展开式地特定项问题常用地方法是利用二项展开式地通项公式.5.(5分)(2013•汕头一模)采用系统抽样方法从960人中抽取32人做问卷调查为此将他们随机编号为1,2…960,分组后在第一组采用简单随机抽样地方法抽到地号码为9,抽到地32人中,编号落入区间[1,450]地人做问卷A ,编号落人区间[451,750]地人做问卷B ,其余地人做问卷C .则抽到地人中,做问卷C 地人数为( )A . 15B .10 C .9 D .7考点:系统抽样方法. 专题:概率与统计. 分析: 根据系统抽样地方法和步骤,我们可将960人分为32组,每组30个人,则由此可计算出做问卷AB 地组数和做问卷C 地组数,即相应地人数. 解答: 解:用系统抽样方法从960人中抽取32人 可将960人分为32组,每组30个人由于分组后在第一组采用简单随机抽样地方法抽到地号码为9,故编号为[1,750]中共有750÷30=25组 即做问卷C 地有32﹣25=7组 故做问卷C 地人数为7人 故选D点评: 本题考查地知识点是系统抽样方法,熟练掌握系统抽样地方法和步骤是解答地关键.6.(5分)(2012•浙江)把函数y=cos2x+1地图象上所有点地横坐标伸长到原来地2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到地图象是( )A .B .C .D .考点:函数y=Asin (ωx+φ)地图象变换. 专题:证明题;综合题. 分析: 首先根据函数图象变换地公式,可得最终得到地图象对应地解析式为:y=cos (x+1),然后将曲线y=cos (x+1)地图象和余弦曲线y=cosx 进行对照,可得正确答案.解解:将函数y=cos2x+1地图象上所有点地横坐标答:伸长到原来地2倍(纵坐标不变),得到地图象对应地解析式为:y=cosx+1,再将y=cosx+1图象向左平移1个单位长度,再向下平移 1个单位长度,得到地图象对应地解析式为:y=cos(x+1),∵曲线y=cos(x+1)由余弦曲线y=cosx左移一个单位而得,∴曲线y=cos(x+1)经过点(,0)和(,0),且在区间(,)上函数值小于0由此可得,A选项符合题意.故选A点本题给出一个函数图象地变换,要我们找出符合地评:选项,着重考查了函数图象变换规律和函数y=Asin(ωx+φ)地图象变换公式等知识点,属于基础题.7.(5分)(2010•青岛模拟)在区间[﹣π,π]内随机取两个数分别记为a,b,则使得函数f(x)=x2+2ax ﹣b2+π有零点地概率为()A .B.C.D.考点:等可能事件地概率.专题:压轴题. 分析: 先判断概率地类型,由题意知本题是一个几何概型,由a ,b 使得函数f (x )=x 2+2ax ﹣b 2+π有零点,得到关于a 、b 地关系式,写出试验发生时包含地所有事件和满足条件地事件,做出对应地面积,求比值得到结果.解答: 解:由题意知本题是一个几何概型,∵a ,b 使得函数f (x )=x 2+2ax ﹣b 2+π有零点, ∴△≥0 ∴a 2+b 2≥π试验发生时包含地所有事件是Ω={(a ,b )|﹣π≤a ≤π,﹣π≤b ≤π} ∴S=(2π)2=4π2,而满足条件地事件是{(a ,b )|a 2+b 2≥π}, ∴s=4π2﹣π2=3π2, 由几何概型公式得到P=, 故选B .点评: 高中必修中学习了几何概型和古典概型两种概率问题,先要判断该概率模型是不是古典概型,再要找出随机事件A 包含地基本事件地个数和试验中基本事件地总数.再看是不是几何概型,它地结果要通过长度、面积或体积之比来得到.8.(5分)如果执行如图地程序框图,那么输出地值是( )A . 0B .C .D .﹣1考点:循环结构. 专题:图表型.分析: 题目给出了当型循环结构框图,首先引入累加变量s和循环变量n ,由判断框得知,算法执行地是求cos 值地和,n 从1取到2013. 解答: 解:第一次循环:,满足条件n <2013,n=n+1=2;第二次循环:,满足条件n <2013,n=n+1=3; 第三次循环:,满足条件n <2013,n=n+1=4; 第四次循环:,满足条件n <2013,n=n+1=5; 第五次循环:,满足条件n <2013,n=n+1=6; 第六次循环:,满足条件n <2013,n=n+1=7; 第七次循环:,满足条件n <2013,n=n+1=8; …易知:S 地值以6为周期进行循环,所以最后输出地S 地值为﹣1. 故选D .点评: 本题考查了程序框图中地当型循环结构,当型循环结构是先判断再执行,若满足条件进入循环,否则结束循环,循环结构主要用在一些规律地重复计算,如累加、累积等,在循环结构中框图中,特别要注意条件应用,如计数变量和累加变量等.9.(5分)已知实数a ,b ,c ,d 成等比数列,且对函数y=ln (x+2)﹣x ,当x=b 时取到极大值c ,则ad 等于( ) A . ﹣1 B .0 C .1 D .2考点:数列与函数地综合. 专计算题.题:分析: 首先根据题意求出函数地导数为f ′(x )=,再结合当x=b 时函数取到极大值c ,进而求出b 与c 地数值,再利用等比数列地性质得到答案. 解答: 解:由题意可得:函数y=ln (x+2)﹣x , 所以f ′(x )=.因为当x=b 时函数取到极大值c , 所以有且ln (b+2)﹣b=c ,解得:b=﹣1,c=1.即bc=﹣1. 因为实数a ,b ,c ,d 成等比数列, 所以ad=bc=﹣1. 故选A .点评: 解决此类问题地关键是熟练掌握导数地作用,即求单调区间,求切线方程,以及求函数地极值与最值等.10.(5分)(2011•双流县三模)定义在R 上地函数y=f (x )是减函数,且函数y=f (x ﹣1)地图象关于(1,0)成中心对称,若s ,t 满足不等式f (s 2﹣2s )≤﹣f (2t ﹣t 2).则当1≤s ≤4时,地取值范围是( )A .B .C .D .考点: 奇偶性与单调性地综合;函数解析式地求解及常用方法.专题:计算题;综合题;压轴题.分析: 首先由由f (x ﹣1)地图象关于(1,0)中心对称知f (x )地图象关于(0,0)中心对称,根据奇函数定义与减函数性质得出s 与t 地关系式,然后利用不等式地基本性质即可求得结果.解答: 解析:由f (x ﹣1)地图象关于(1,0)中心对称知f (x )地图象关于(0,0)中心对称, 故f (x )为奇函数得f (s 2﹣2s )≤f (t 2﹣2t ), 从而t 2﹣2t ≤s 2﹣2s ,化简得(t ﹣s )(t+s ﹣2)≤0,又1≤s ≤4,故2﹣s ≤t ≤s ,从而,而, 故. 故选C .点评: 题综合考查函数地奇偶性、单调性知识;同时考查由最大值、最小值求取值范围地策略,以及运算能力,属中档题.二、填空题:本大题共7小题,每小题5分,共25分.将答案填写在题中地横线上.11.(5分)已知等差数列{a n }地前n 项和为S n ,a 5=5,S 5=15,则数列地前100项和为 .考点:数列地求和.专题:计算题;等差数列与等比数列.分析: 等差数列{a n }中,由a 5=5,S 5=15,解得a 1=1,d=1,故==,由此利用裂项求和法能够求了数列地前100项和.解答: 解:等差数列{a n }中,∵a 5=5,S 5=15, ∴,解得a 1=1,d=1,∴a n =1+(n ﹣1)=n , ∴==,∴数列地前100项和S 100=(1﹣)+()+()+…+()=1﹣=. 故答案为:.点评: 本题考查数列地前100项和地求法,解题时要认真审题,仔细解答,注意等差数列地通项公式和前n项和公式地求法,注意裂项求和法地合理运用.12.(5分)已知函数f (x )满足:x ≥4,则f (x )=;当x <4时f (x )=f (x+1),则f (2+log 23)═ .考点:分段函数地应用.专题:计算题.分析:判断地范围代入相应地解析式求值即可 解答: 解:∵2+log 23<4,∴f (2+log 23)=f (3+log 23)=f (log 224)== 故应填点评: 本题考查分段函数求值及指数对数去处性质,对答题者对基本运算规则掌握地熟练程度要求较高13.(5分)一个几何体地三视图如图π×12×1=π所示,则该几何体地体积为.考点:由三视图求面积、体积.专题:计算题.分析: 由三视图知:原几何体是一个圆柱和三棱锥地组合体,且圆柱地底面半径为1,高为1,三棱锥地底面是等腰直角三角形,两直角边为,高为,分别求出棱柱与圆柱地体积,进而可求该几何体地体积.解答: 解:由三视图知:原几何体是一个圆柱和三棱锥地组合体,其中圆柱地底面半径为1,高为1,所以圆柱地体积为π×12×1=π; 三棱锥地底面是等腰直角三角形,两直角边为,高为, 所以三棱柱地体积为, 所以该几何体地体积为. 故答案为. 点本题考查由几何体地三视图求原几何体地体积问评:题,属于基础题.14.(5分)已知,,如果与地夹角为锐角,则λ地取值范围是.考点:数量积表示两个向量地夹角.专题:计算题.分析: 根据题意,若与地夹角为锐角,则有•>0且与不平行,由•>0可得3λ2+4λ>0,由若与不平行,可得≠且2λ×3λ≠2λ,解可得λ地范围,综合可得答案.解答: 解:根据题意,若与地夹角为锐角,则有•>0且与不平行, 由•>0,可得3λ2+4λ>0,解可得λ<﹣或λ>0, 若与不平行,则有≠且2λ×3λ≠2λ,即λ≠0且λ≠,综合可得,λ<﹣或λ>0且λ≠,即λ地取值范围是(﹣∞,﹣)∪(0,)∪(,+∞); 故答案为(﹣∞,﹣)∪(0,)∪(,+∞). 点本题考查数量积地运用,注意向量夹角为锐角地充评:要条件,其次要排除向量平行地情况.15.(5分)(不等式选做题)若不存在实数x 使|x ﹣3|+|x ﹣1|≤a 成立,则实数a 地取值集合是 {a|a <2} .考点:绝对值不等式.专题:计算题;函数地性质及应用;不等式地解法及应用. 分析: 根据绝对值地几何意义得y=|x ﹣3|+|x ﹣1|地几何意义是数轴上点x 到点3和1地距离和,由此可得|x ﹣3|+|x ﹣1|地最小值为2.再由题意不存在实数x 使|x ﹣3|+|x ﹣1|≤a 成立,可知|x ﹣3|+|x ﹣1|地最小值大于a ,由此即可得到实数a 地取值集合.解答: 解:∵设y=|x ﹣3|+|x ﹣1|,此函数地几何意义是数轴上地点x 到点3和1地距离之和,∴当1≤x ≤3时,y=|x ﹣3|+|x ﹣1|达到最小值,最小值为2.∵不存在实数x 使|x ﹣3|+|x ﹣1|≤a 成立,∴y=|x ﹣3|+|x ﹣1|地最小值要大于a ,故2>a , 得实数a 地取值集合是{a|a <2}.故答案为:{a|a <2}点评: 本题给出含有绝对值地不等式,在不等式解集为空集地情况下求参数a 地取值集合.着重考查了绝对值地几何意义、不等式地性质和函数最值地求法等知识,属于中档题.16.(2012•天津)如图,已知AB 和AC 是圆地两条弦,过点B 作圆地切线与AC 地延长线相交于点D ,过点C 作BD 地平行线与圆相交于点E ,与AB 相交于点F ,AF=3,FB=1,EF=,则线段CD 地长为.考点:与圆有关地比例线段.专题:计算题;压轴题.分析: 由相交弦定理求出FC ,由相似比求出BD ,设DC=x ,则AD=4x ,再由切割线定理,BD 2=CD •AD 求解. 解答: 解:由相交弦定理得到AF •FB=EF •FC ,即3×1=×FC ,FC=2,在△ABD 中AF :AB=FC :BD ,即3:4=2:BD ,BD=,设DC=x ,则AD=4x ,再由切割线定理,BD 2=CD •AD ,即x •4x=()2,x= 故答案为:点评: 本题主要考查了平面几何中直线与圆地位置关系,相交弦定理,切割线定理,相似三角形地概念、判定与性质.17.(坐标系与参数方程选做题) 已知直线l 1:(t 为参数)与圆C 2:(θ为参数)地位置关系不可能是 相离 .考点:圆地参数方程;直线地参数方程.专题:压轴题;直线与圆.分析: 先把直线l 1与圆C 2地参数方程化为普通方程,再利用点到直线地公式求出圆心到直线地距离,再与半径1比较即可.解答: 解:把直线l 1地方程:(t 为参数)化为直角坐标方程为xtan α﹣y ﹣tan α=0,把圆C 2地方程:(θ为参数)化为直角坐标方程为x 2+y 2=1,圆心(0,0),半径r=1.圆心到直线地距离为:.点评: 熟练掌握参数方程化为普通方程地方法、点到直线地公式、直线与圆地位置关系地判定方法是解题地关键.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.18.(12分)已知△ABC地三个内角A、B、C地对边分别为a、b、c,且b2+c2=a2+bc,求:(1) 2sinBcosC ﹣sin(B﹣C)地值;(2)若a=2,求△ABC周长地最大值.解三角形;三角函数地恒等变换及化简求值.考点:专计算题.题:分(1)根据余弦定理表示出cosA,把已知得等式变析:形后代入即可求出cosA 地值,由A 地范围,利用特殊角地三角函数值即可求出A 地度数,然后把所求地式子利用两角和与差地正弦函数公式及诱导公式化简,将sinA 地值代入即可求出值;(2)由a=2和sinA 地值,根据正弦定理表示出b 和c ,代入三角形地周长a+b+c 中,利用两角和与差地正弦函数公式及特殊角地三角函数值化为一个角地正弦函数,根据正弦函数地值域即可得到周长地最大值.解答: 解:(1)∵b 2+c 2=a 2+bc ,∴a 2=b 2+c 2﹣bc , 结合余弦定理知cosA===, 又A ∈(0,π),∴A=,∴2sinBcosC ﹣sin (B ﹣C )=sinBcosC+cosBsinC =sin (B+C )=sin[π﹣A]=sinA=;(2)由a=2,结合正弦定理得: ====, ∴b=sinB ,c=sinC ,则a+b+c=2+sinB+sinC =2+sinB+sin (﹣B ) =2+2sinB+2cosB=2+4sin (B+),可知周长地最大值为6.点评: 此题考查学生灵活运用正弦、余弦定理化简求值,灵活运用两角和与差地正弦函数公式化简求值,掌握正弦函数地值域,是一道中档题.19.(12分)已知函数f(x)=x2﹣2(n+1)x+n2+5n ﹣7.(Ⅰ)设函数y=f(x)地图象地顶点地纵坐标构成数列{an },求证:{an}为等差数列;(Ⅱ)设函数y=f(x)地图象地顶点到x轴地距离构成数列{bn },求{bn}地前n项和Sn.考点:数列与函数地综合;等差关系地确定;数列地求和.专题:综合题.分析: (Ⅰ)配方,确定函数y=f (x )地图象地顶点地纵坐标,从而可求数列{a n }地通项,再证明为等差数列;(Ⅱ)确定数列{b n }地通项,进而可分段求出{b n }地前n 项和S n .解答: (Ⅰ)证明:∵f (x )=x 2﹣2(n+1)x+n 2+5n ﹣7=[x ﹣(n+1)]2+3n ﹣8,∴a n =3n ﹣8,﹣﹣﹣﹣﹣﹣﹣﹣﹣(2分) ∴a n+1﹣a n =3(n+1)﹣8﹣(3n ﹣8)=3,∴数列{a n }为等差数列.﹣﹣﹣﹣﹣﹣﹣﹣﹣(4分)(Ⅱ)解:由题意知,b n =|a n |=|3n ﹣8|,﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)∴当1≤n ≤2时,b n =8﹣3n ,;﹣﹣﹣﹣(8分)当n ≥3时,b n =3n ﹣8,S n =b 1+b 2+b 3+…+b n =5+2+1+…+(3n ﹣8)=.﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分) ∴.﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分) 点评: 本题考查数列与函数地关系,考查等差数列地证明,考查数列地求和,考查分类讨论地数学思想,正确求数列地通项是关键.20.(12分)如图,四棱锥P ﹣ABCD 地底边ABCD 为直角梯形,其中BA ⊥AD ,CD ⊥AD ,CD=AD=2AB ,PA ⊥底面ABCD ,E 是PC 地中点.(Ⅰ)求证:BE ∥平面PAD ;(Ⅱ)若BE ⊥平面PCD ,求平面EBD 与平面CBD 夹角地余弦值.考点: 用空间向量求平面间地夹角;直线与平面平行地判定;向量语言表述线面地垂直、平行关系. 专计算题;证明题.题:分析: (I )以A 为坐标原点,AB 为x 轴,AD 为y 轴,AP为z 轴,建立空间直角坐标系,写出要用地点地坐标,根据向量地共线关系得到线与线之间地平行关系,得到线与面平行地结论.(II )根据面面垂直得到线线垂直,得到两个向量地数量积等于0,求出两个字母之间地关系,设出平面地法向量,根据数量积等于0,做出法向量,进而求出面面角.解答: 解:设AB=a ,PA=b ,以A 为坐标原点,AB 为x 轴,AD为y 轴,AP 为z 轴,建立空间直角坐标系,则A (0,0,0),B (a ,0,0),P (0,0,b ),C (2a ,2a,0),D(0,2a,0),E(a,a,).(Ⅰ)证明:,∴.又∵BE⊄平面PAD∴BE∥平面PAD.(Ⅱ)∵BE⊥平面PCD,∴BE⊥PC,即.又∵,∴.即b=2a在平面BDE和平面BDC中,,∴平面BDE地一个法向量为,平面BDC地一个法向量为,∴.∴平面EBD 与平面CBD 夹角地余弦值为.点评: 本题第一小题考查空间中直线与平面地位置关系地证明,主要应用线面平行判断定理,本题获得定理成立地条件方法是向量法,第二小题考查用空间向量求二面角,本题解题地关键是建立坐标系,把难度比较大地二面角地求法,转化成了数字地运算.21.(12分)(2012•芜湖二模)某品牌地汽车4S店,对最近100位采用分期付款地购车者进行统计,统计结果如右表所示:已知分3期付款地频率为0.2,4S店经销一辆该品牌地汽车,顾客分1期付款,其利润为1万元;分2期或3期付款其利润为1.5万元;分4期或5期付款,其利润为2万元.用η表示经销一辆汽车地利润.(1)求上表中地a,b值;(2)若以频率作为概率,求事件A:“购买该品牌汽车地3位顾客中,至多有1位采用3期付款”地概率P(A);(3)求η地分布列及数学期望Eη.考点:离散型随机变量地期望与方差.专题:计算题;应用题;综合题.分析: (1)根据分3期付款地频率为0.2,得到a 除以100值为0.2,求出a 地值,根据总体数是100,求出b 地值.(2)记分期付款地期数为ξ,则ξ地可能取值是1,2,3,4,5,结合变量对应地事件写出变量地概率,根据独立重复试验地概率公式得到购买该品牌汽车地3位顾客中至多有1位采用3期付款地概率.(3)η表示经销一辆汽车地利润,η地可能取值为:1,1.5,2,结合变量对应地事件,根据η和ξ之间地关系,写出变量地概率,得到分布列. 解答: 解:(1)由得a=20∵40+20+a+10+b=100∴b=10(2)记分期付款地期数为ξ,则ξ地可能取值是1,2,3,4,5, 依题意得:,,P (ξ=3)=0.2,,则“购买该品牌汽车地3位顾客中至多有1位采用3期付款”地概率10.2×(1﹣0.2)2=0.896P(A)=0.83+C3(3)∵η地可能取值为:1,1.5,2(单位万元)P(η=1)=P(ξ=1)=0.4P(η=1.5)=P(ξ=2)+P(ξ=3)=0.4P(η=2)=P(ξ=4)+P(ξ=5)=0.1+0.1=0.2∴η地分布列为:∴η地数学期望Eη=1×0.4+1.5×0.4+2×0.2=1.4(万元)点本题考查离散型随机变量地分布列和期望,考查独。
陕西省西安中学2022届高三下学期四模文科数学试题(含答案解析)

陕西省西安中学2022届高三下学期四模文科数学试题学校:___________姓名:___________班级:___________考号:___________ 一、单选题 1.“0a b >>”是“1ab>”的( ) A .充要条件 B .充分不必要条件 C .必要不充分条件D .既不充分也不必要条件2.函数 f (x )=lnx+2x-6的零点x 0所在区间是( ) A .()0,1B .()1,2C .()2,3D .()3,43.某旅游者爬山的高度h (单位:m)是时间t (单位:h)的函数,关系式是h =-100t 2+800t ,则他在2 h 这一时刻的高度变化的速度是( ) A .500 m/h B .1 000 m/h C .400 m/hD .1 200 m/h4.已知流程图如右图所示,该程序运行后,为使输出的b 值为16, 则循环体的判断框内①处应填A .2B .3C .4D .55.某几何体的三视图如图所示,主视图和左视图是高为个半径为2和4的同心圆,则该几何体侧面展开成的扇环所对的圆心角为( )A .πB .34π C .23π D .2π 6.已知关于x 的方程(x 2+mx )+2x i =-2-2i (m ①R )有实数根n ,且z =m +n i ,则复数z 等于( ) A .3+i B .3-i C .-3-i D .-3+i7.已知322παπ<<( ) A .1sin α-B .1sin αC .2sin α-D .2sin α8.第24届冬季奥林匹克运动会,将于2022年2月4日~2月20日在北京和张家口联合举行.为了更好地安排志愿者工作,现需要了解每个志愿者掌握的外语情况,已知志愿者小明只会德、法、日、英四门外语中的一门.甲说,小明不会法语,也不会日语:乙说,小明会英语或法语;丙说,小明会德语.已知三人中只有一人说对了,由此可推断小明掌握的外语是( ) A .德语B .法语C .日语D .英语9.已知半径为2的圆经过点(5,12),则其圆心到原点的距离的最小值为( ) A .10B .11C .12D .1310.已知球O 表面上的四点A ,B ,C ,P 满足AC BC ==2AB =,若四面体PABC 体积的最大值为23,则球O 的表面积为( )A .254π B .259π C .2516π D .8π11.某人准备到某接种点接种新冠疫苗加强针,该接种点在前一天已用完全部疫苗,新的疫苗将于当天上午8:00~11:00之间随机送达,若他在9:00~12:00之间随机到达该接种点,则他到达时疫苗已送达的概率是( ) A .29B .59C .23D .7912.已知梯形ABCD 中,AD BC ∥,π3B ∠=,2AB =,4BC =,1AD =,点P ,Q 在线段BC 上移动,且1PQ =,则DP DQ ⋅的最小值为( )A .1B .112C .132D .114二、填空题13.直线20x my +-=和直线(21)0mx m y --=垂直,则实数m =__________.14.在等差数列{}n a 中,72615,18a a a =+=,若数列{}(1)nn a -的前n 项之和为n S ,则100S =__________.15.已知F 是双曲线221412x y -=的左焦点,()1,4A ,P 是双曲线右支上的动点,则PF PA +的最小值为________.16.若过定点(1,e)P 恰好可作曲线e (0)x y a a =>的两条切线,则实数a 的取值范围是__________. 三、解答题17.函数π()sin()(0,0,||)2f x A x A ωϕωϕ=+>><的部分图象如图所示:(1)求函数()f x 的解析式与单调递减区间;(2)求函数()f x 在[0,]2π上的值域.18.某地医疗机构承担了该地的新冠疫苗接种任务,现统计了前5天每天(用1,2,3,4,5t =表示)前来接种的人数y 的相关数据,如下表所示:(1)根据表格,请利用线性回归模型拟合y 与t 的关系,求出y 关于t 的回归方程,并求出第6天前来接种人数的预报值;(2)若用分层抽样的方法从第2天和第4天前来接种的人群中随机抽取6人作样本分析,并打算对样本6人中的两人随机进行电话回访,则被回访的两人接种日期不同的回归直线ˆˆˆybx a =+的斜率和截距的最小二乘估计分别为:1221ˆˆˆni ii nii x y nxyb ay bx xnx==-==--∑∑, 19.如图,在ABC 中,AB ①B C ,AB =3,BC =4,D ,E 分别为BC ,AC 的中点.将CDE △沿DE 折起到PDE △的位置,连接P A ,PB ,得到四棱锥P -ABDE .(1)证明:平面P AB ①平面PBD ;(2)若PD ①BD ,F 为PB 的一个靠近点B 的三等分点,求三棱锥P -AEF 的体积. 20.动圆P 与直线1x =-相切,点(1,0)F 在动圆上. (1)求圆心P 的轨迹Q 的方程;(2)过点F 作曲线O 的两条互相垂直的弦AB ,CD ,设AB ,CD 的中点分别为M ,N ,求证:直线MN 必过定点. 21.已知函数()1x f x e x =--. (1)求函数()f x 的单调区间和极值; (2)当0x ≥时,求证:21()1cos 2f x x x x ++≥+. 22.在直角坐标系xOy 中,曲线E 的参数方程为2223141t x tt y t ⎧-=⎪⎪+⎨⎪=⎪+⎩(t 为参数),以O 为极点,x 轴非负半轴为极轴建立极坐标系,直线l 的极坐标方程为()6R πθρ=∈,l 交曲线E 于点A ,B .(1)求曲线E 的极坐标方程; (2)求||AB .23.若关于x 的不等式||x m n +的解集为[6,2]-. (1)求实数m ,n 的值;(2)若实数y ,z 满足1||3my z +<,1||3y nz -<,求证:1||9z <.参考答案:1.B 【解析】 【分析】根据充分条件、必要条件的定义判断即可; 【详解】解:由0a b >>,得1a b >,反之不成立,如2a =-,1b =-,满足1ab>,但是不满足0a b >>,故“0a b >>”是“1ab>”的充分不必要条件. 故选:B 2.C 【解析】 【分析】判断函数是连续增函数,利用函数的领导品牌定理,从而得到函数f (x )=lnx+2x-6的零点所在的区间. 【详解】①连续函数f (x )=lnx+2x-6是增函数,①f (2)=ln2+4-6=ln2-2<0,f (3)=ln3>0, ①f (2)•f (3)<0,故函数f (x )=lnx+2x-6的零点所在的区间为(2,3), 故选C . 【点睛】本题主要考查函数的零点的判定定理的应用,属于基础题. 3.C 【解析】 【分析】求函数导数,再取x=2时的导数值即可得解. 【详解】解析:h ′(t )=-200t +800,①h ′(2)=-200×2+800=400(m/h). 答案:C 【点睛】本题考查了导数的物理意义瞬时速度,属于基础题. 4.B 【解析】 【详解】试题分析:1,1a b ==;2,2b a ==;4,3b a ==;16,4b a ==;输出16b =,所以框内填3a ≤.考点:程序框图. 5.A 【解析】 【分析】由给定的三视图可得一圆台,再利用圆台侧面展开图计算作答. 【详解】还原三视图,得如图所示的几何体,它是上底面圆半径12r =,下底面圆半径24r =,高为则有此圆台的母线长4l ==,作出圆台的侧面展开图为如图所示的扇环,设扇环所对的圆心角为θ,于是得扇环小圆半径12r OB πθ=,大圆半径22r OA πθ=,由OA OB l -=, 即844ππθθ-=,解得:θπ=,所以该几何体侧面展开成的扇环所对的圆心角为π. 故选:A6.B 【解析】 【分析】根据复数相等得出,m n 的值,进而得出复数z . 【详解】由题意知(n 2+mn )+2n i =-2-2i ,即220220n mn n ⎧++=⎨+=⎩,解得3,1m n =⎧⎨=-⎩,3i z ∴=-故选:B 7.C 【解析】 【分析】利用平方关系,根号下分子分母同乘分子,将被开方数化为完全平方,然后可得. 【详解】 因为322παπ<<,所以sin 0α<,0cos 1α<<,=1cos 1cos 2sin sin sin ααααα+-=+=---另解:因为342παπ<<,所以sin 02α>,cos 02α<,所以=cos sin22sin cos22αααα⎛⎫⎪==-+ ⎪ ⎪⎝⎭= 22sin 2sincos22ααα=-=-.故选:C8.B【解析】【分析】根据题意,分“甲说对,乙、丙说错”、“乙说对,甲、丙说错”、“丙说对,甲、乙说错”三种情况进行分析,即可得到结果.【详解】若甲说对,乙、丙说错:甲说对,小明不会法语也不会日语;乙说错,则小明不会英语也不会法语;丙说错,则小明不会德语,由此可知,小明四门外语都不会,不符合题意;若乙说对,甲、丙说错:乙说对,则小明会英活或法语;甲说错,则小明会法语或日语;丙说错,小明不会德语;则小明会法语;若丙说对,甲、乙说错:丙说对,则小明会德语;甲说错,到小明会法语或日语;乙说错,则小明不会英语也不会法语;则小明会德语或日语,不符合题意;综上,小明会法语.故选:B.9.B【解析】【分析】由条件可得圆心的轨迹是以点()5,12为圆心,半径为2的圆,然后可得答案.【详解】因为半径为2的圆经过点(5,12),所以圆心的轨迹是以点()5,12为圆心,半径为2的圆,211=,故选:B10.A【解析】由已知条件和平面几何知识得出关于外接球的半径的方程,由球的表面积公式可得出选项.【详解】设ABC的外接圆心为1O,由2AB BC AC===和四面体PABC体积的最大值为2 3得,12PO =,设球的半径为r,则有2r =,解得54r =,则该球的表面积为225254444r πππ⎛⎫=⨯=⎪⎝⎭. 故选:A. 【点睛】本题考查四面体的外接球的表面积,关键在于确定外接球的球心和半径,属于中档题. 11.D 【解析】 【分析】根据题意作出试验的全部结果所构成的区域及所求事件构成的区域,再利用几何概型概率公式即求. 【详解】设8:00为初始时刻0,则9:00,10:00,11:00,12:00分别为时刻1,2,3,4,设新的疫苗送达的时刻为 x ,某人到接种点的时刻为 y ,记他到达时疫苗已送达为事件A ,则试验的全部结果所构成的区域为(){}Ω,03,14x y x y =≤≤≤≤,事件A 所构成的区域为{}(,),03,14A x y y x x y =≥≤≤≤≤,如图阴影区域,则()1332272339A S P A S Ω⨯-⨯⨯===⨯.故选:D. 12.D 【解析】 【分析】如图以B 为坐标原点,BC 所在的直线为x 轴建立平面直角坐标系,设(),0P x ,则()()1,003Q x x +≤≤,然后表示出DP DQ ⋅,求其最小值即可,【详解】如图,以B 为坐标原点,BC 所在的直线为x 轴建立平面直角坐标系, 因为AD BC ∥,π3B ∠=,2AB =,1AD =,所以(D ,不妨设(),0P x ,()()1,003Q x x +≤≤,则((()()223112,1,2133524DP DQ x x x x x x x ⎛⎫⋅=-⋅-=--+=-+=-+ ⎪⎝⎭,所以当32x =时,DP DQ ⋅取得最小值114, 故选:D13.0或1##1或0 【解析】 【分析】根据给定条件,利用两直线垂直关系直接列式计算作答. 【详解】因直线20x my +-=和直线(21)0mx m y --=垂直,则有1[(21)]0m m m ⋅+--=,即2220m m -=,解得0m =或1m =, 所以0m =或1m =. 故答案为:0或114.100 【解析】 【分析】根据给定条件,利用等差数列性质计算首项、公差,再借助并项求和法求解作答. 【详解】设等差数列{}n a 公差为d ,由426218a a a =+=得:49a =,则741592743a a d --===-, ()4421n a a n d n =+-=+,当n 为偶数时,()()111112n nn n n n a a a a d ----+-=-==,所以100214310099()()()502100a a a a a a S =-+-++-=⨯=.故答案为:100 15.9 【解析】作出图形,设双曲线的右焦点为M ,根据双曲线的定义可得4PF PM =+,可得出4PF PA PM PA +=++,利用A 、P 、M 三点共线时PF PA +取得最小值即可得解. 【详解】对于双曲线221412x y -=,则2a =,b =4c =,如下图所示:设双曲线的右焦点为M ,则()4,0M ,由双曲线的定义可得4PF PM -=,则4PF PM =+,所以,4449PF PA PM PA AM +=++≥+==,当且仅当A 、P 、M 三点共线时,等号成立. 因此,PF PA +的最小值为9. 故答案为:9. 【点睛】关键点点睛:利用双曲线的定义求解线段和的最小值,有如下方法:(1)求解椭圆、双曲线有关的线段长度和、差的最值,都可以通过相应的圆锥曲线的定义分析问题;(2)圆外一点到圆上的点的距离的最值,可通过连接圆外的点与圆心来分析求解. 16.(1,)+∞ 【解析】 【分析】求出函数的导数,设切点为(,)m n ,由导数的几何意义和两点的斜率公式可得e(2)e m m a-=-,设()(2)e x f x x =-,利用导数求出其单调区间和极值,再画出函数的图象,结合图象可得a 的取值范围 【详解】由e (0)x y a a =>,得e x y a '=,切点为(,)m n ,则切线的斜率为e m a , 所以切线方程为e ()m y n a x m -=-, 因为e m n a =,所以e e ()m m y a a x m -=-, 因为点(1,e)P 在切线上, 所以e e e (1)m m a a m -=-,得e(2)e m m a-=-, 令()(2)e x f x x =-,则()(1)e x f x x '=-, 当1x >时,()0f x '>,当1x <时,()0f x '<, 所以()f x 在(1,)+∞上递增,在(,1)-∞上递减, 所以()f x 在1x =处取得极小值e -,当x →-∞时,()0f x →,当x →+∞时,()f x →+∞, 由题意可得直线ey a=-与函数()f x 的图象有两个交点,所以ee 0a-<-<,解得1a >,所以实数a 的取值范围为(1,)+∞,故答案为:(1,)+∞17.(1)()2sin(2)4f x x π=+,单调递减区间5,(Z)88k k k ππππ⎡⎤++∈⎢⎥⎣⎦(2)[2] 【解析】 【分析】(1)根据图像即可写出2A =,再由图像过30088ππ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,、,即可求出其周期,则可求出2ω=,在将点08π⎛⎫- ⎪⎝⎭,带入()f x ,则可求出4πϕ=.由sin y x =在区间32,2,Z 22k k k ππππ⎡⎤++∈⎢⎥⎣⎦上单调递减,则可求出()f x 的单调递减区间.(2)由52,sin 2()[[0,]2]24444x x f x x πππππ⎡⎤⎡⎤⎛⎫+∈⇒+∈⇒∈⎢⎥ ⎪⎢⎥⎣⎦⎝⎭⎣⎦∈⇒. (1)观察图象得:2A =,令函数()f x 的周期为T ,则322,288T T ππππω⎛⎫=⨯+=== ⎪⎝⎭, 由08f π⎛⎫-= ⎪⎝⎭得:22,Z 8k k πϕπ⎛⎫⨯-+=∈ ⎪⎝⎭,而||2ϕπ<,于是得0,4πϕ==k ,所以函数()f x 的解析式是()2sin(2)4f x x π=+.由3222,Z 242k x k k πππππ+≤+≤+∈解得:5,Z 88k x k k ππππ+≤≤+∈, 所以()f x 的单调递减区间是5,(Z)88k k k ππππ⎡⎤++∈⎢⎥⎣⎦.(2)由(1)知,当0,2x π⎡⎤∈⎢⎥⎣⎦时,52444x πππ≤+≤,则当242x ππ+=,即8x π=时max ()2f x =,当5244x ππ+=,即2x π=时,min ()f x =所以函数()f x 在0,2π⎡⎤⎢⎥⎣⎦上的值域是[2].18.(1)113y t =-,63 (2)815【解析】 【分析】(1)根据已知数据和公式直接求解即可,(2)先根据题意求出第二天抽取2人,第4天抽取4人,然后利用列举法求解即可 (1) 123458202940533,3055t y ++++++++====2221555560590ˆˆ11,30113355535i ii iii x y xyba y bx xx =-=--⨯∴====-=-⨯=--⨯-∑∑ y ∴关于t 的线性回归方程为113y t =-当6t =时,66363,y =-=∴第6天前来接种人数的预报值为63 (2)由题意可得第二天抽取2人,第4天抽取4人,记第二天的2人为12,A A ,第4天的4人为1234,,,B B B B ,所有基本事件为 121112131421222324121314232434,,,,,,,,,,,,,,A A A B A B A B A B A B A B A B A B B B B B B B B B B B B B ,共十五种,两人来自不同日期的事件有8种, 815m P n ∴==. 19.(1)证明见解析;(2)43. 【解析】 【分析】(1)根据给定条件证明AB ①平面PBD ,再利用面面垂直的判定推理作答.(2)求出三棱锥P -ABE 的体积,再借助等体积法及同高的两个三棱锥体积关系计算作答. (1)在ABC 中,D ,E 分别为BC ,AC 的中点,有//DE AB ,又AB BC ⊥,则DE BC ⊥, 在四棱锥P -ABDE 中,DE PD ⊥,于是得PD AB ⊥,而AB BD ⊥,PD BD D ⋂=,,PD BD ⊂平面PBD ,因此,AB ①平面PBD ,又AB 平面P AB ,所以面P AB ①平面PBD . (2)连接BE ,如图,因PD BD ⊥,PD AB ⊥,,AB BD ⊂平面ABDE ,AB BD B =,则有PD ①平面ABDE ,即P 到平面ABDE 的距离2PD =, 显然1132322ABESAB BD =⋅=⨯⨯=,则1132233P ABE ABEV SPD -=⋅=⨯⨯=, 依题意,23PF PB =,则23APFAPBS S =,于是得22242=3333P AEF E APF E APB P ABE V V V V ----====⨯所以,三棱锥P -AEF 的体积为43.20.(1)24y x = (2)证明见解析 【解析】 【分析】(1)设(,)P x y ,然后根据题意列方程化简可得圆心P 的轨迹Q 的方程, (2)由题意,知直线AB 的斜率存在且不为0所以设直线()():(1),,,,AB A A B B l y k x A x y B x y =-,然后将直线方程代入抛物线方程中消去y 后,利用根据与系数的关系结合中点坐标公式表示出点M 的坐标,同理表示出点N 的坐标,从而可表示出直线MN 的方程,进而可证得结论 (1)设(,)P x y1x =+,化简,得24y x =, 即圆心P 的轨迹Q 的方程为24y x =. (2)由题意,知直线AB 的斜率存在且不为0. 设直线()():(1),,,,AB A A B B l y k x A x y B x y =-,代入24y x =,得()2222220k x k x k -++=,所以()2222A B k x x k ++=.因为M 是线段AB 的中点,所以2222,k M kk ⎛⎫+ ⎪⎝⎭.因为AB CD ⊥,所以将点M 坐标中的k 换成1k-,即得()221,2N k k +-.当222221k k k+=+,即1k =±时,直线3MN l x ⋅=;当1k ≠±时.直线()222222:221221MNk k l y k x k k k k--+=--++-. 整理,得()21(3)k y k x -=-,所以直线MN 过定点(30),. 综上所述,不论k 为何值,直线MN 必过定点(30),. 21.(1)单调递增区间为(0,)+∞,单调递减区间为(,0)-∞,极小值为(0)0f =,没有极大值 (2)证明见解析 【解析】 【分析】(1)求f (x )的导数,利用导数即可求f (x )单调区间,根据单调性即可求其极值; (2)化简要证明的不等式,构造新函数,利用sinx≥-1放缩,转化为已知函数求解. (1)易知函数()f x 定义域为R ,①()1x f x e x =--,①()1xf x e '=-,令()10xf e x ='->,解得0x >,()f x 在(0,)+∞上单调递增,()10x f e x ='-<,解得0x <,()f x 在(,0)-∞上单调递减, 即()f x 的单调递增区间为(0,)+∞,单调递减区间为(,0)-∞, ①函数()f x 的极小值为(0)0f =,没有极大值; (2)解法一:要证21()1cos 2f x x x x ++≥+, 即证21cos 02xe x x --≥,设21()cos 2xg x e x x =--,要证原不等式成立即证()0g x ≥成立,①()sin x g x e x x '=-+①sin 1x ≥-,①()sin 1x x g x e x x e x '=-+≥--(当且仅当22x k π=-+π,k Z ∈时等号成立),由(1)知10x e x --≥(0x =等号成立),①()0g x '>,①()g x 在(0,)+∞单调递增,①()(0)0g x g ≥= ①当0x ≥时,21()1cos 2f x x x x ++≥+得证. 解法二:要证21()1cos 2f x x x x ++≥+, 即证21cos 02xe x x --≥设21()cos 2xg x e x x =--,要证原不等式成立即证()0g x ≥成立,①()sin x g x e x x '=-+, 设()()sin x h x g x e x x '==-+,则()1cos x h x e x '=-+,令m (x )=()h x ', 则()sin x m x e x '=-①0x ≥,1x e ∴≥,又|sin |1x ≤,①()sin 0x m x e x '=->, 即()1cos x h x e x '=-+在[0,)+∞单调递增, ①()(0)10h x h ''≥=>,即()h x 在[0,)+∞单调递增, ①()(0)10h x h ≥=>,①()0g x '>,即()g x 在[0,)+∞单调递增,①()(0)0g x g ≥= ①当0x ≥时,21()1cos 2f x x x x ++≥+得证. 【点睛】本题关键在于利用sin x ≥-1对函数进行放缩,将构造的新函数转化为已知的函数求解,(2)问的解法二关键在于利用多次求导判断函数的单调性求函数的最值. 22.(1)22cos 30()ρρθθπ--=≠【解析】 【分析】(1)消参即可得到曲线E 的普通方程,利用222cos ,sin ,x y x y ρθρθρ==+=即可化为极坐标方程. (2)将()6R πθρ=∈带入曲线E 的极坐标方程.利用韦达定理即可求出答案.(1)2223141t x t t y t ⎧-=⎪⎪+⎨⎪=⎪+⎩①②,[1]+÷①②得:111x y t y t x +=⇒=+, 代入(2)中,得:22(1)4x y -+=, 由于22234111t t t-=-+++,且223131t t --<≤+, 所以22(1)4(1)x y x -+=≠-;由2222(1)4230x y x y x -+=⇒+--=, 极坐标方程为22cos 30()ρρθθπ--=≠. (2)将直线l 的极坐标方程为6πθ=,代入22cos 30ρρθ--=,得230ρ-=设点A 、B 对应的极径为12,ρρ,则12123ρρρρ+=- 故12||AB ρρ=-==23.(1)24m n =⎧⎨=⎩;(2)见解析【解析】 【分析】(1)由题得n m x n m ---,解方程组62n m n m --=-⎧⎨-=⎩,,即得m,n 的值;(2)()()9224224z y z y z y z y z =+--++-,再结合已知证明.【详解】(1)由x m n +,得n x m n -+,即n m x n m ---,则62n m n m --=-⎧⎨-=⎩,,解得24m n =⎧⎨=⎩,. (2)由(1)可知123y z +<,143y z -<,又因为()()1192242242133z y z y z y z y z =+--++-<+⨯=,所以19z <. 【点睛】本题主要考查绝对值不等式的解法和绝对值不等式的证明,意在考查学生对这些知识的理解掌握水平和分析推理能力.。
陕西师大附中高级第四次模拟考试数学试题文理.4
陕西师大附中高级第四次模拟考试数学试题一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,有且只有一项是正确的.请把答案填在答题卷上)1.(理)设a 是实数,且211ai i+++是实数,则a =( )A .1- B .12 C .1 D .32(文)已知全集{0,1,2,3,4,5,6,7,8,9}U =,集合2{|980}M x Z x x =∈-+<,则U M =( )A .{0,9}B .{0,1,8,9}C .{2,3,4,5,6,7}D .{1,2,3,4,5,6,7,8}2.(理)设集合{|3,(,0)}tP m R m t =∈=∈-∞,13{|log ,(0,1)}Q m R m t t =∈=∈,则( )A .P Q ⊆B .Q P ⊆C .P Q =D .P Q =∅(文)已知α是第三象限角,并且4sin 5α=-,则tan α等于( ) A .34B .43C .34-D .43-3.设n S 是等差数列{}n a 的前n 项和,5283()S a a =+,则53a a 的值为( )A .16 B .13 C .35 D .564.已知条件p :3k =,条件q :直线2y kx =+与圆221x y +=相切,则p 是q 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件5.某中学开学后从高一年级的学生中随机抽取90名学生进行家庭情况调查,经过一段时间后再次从这个年级随机抽取100名学生进行学情调查,发现有20名同学上次被抽到过,估计这个学校高一年级的学生人数为( )A .180B .400C .450D .20006.若()f x 在0x =处连续,且0x ≠时,311()11x f x x +-=--,则(0)f =( )A .1B .23-C .0D .32-(文)设函数2)(+=ax x f ,且)(1x fy -=的图象过点)1,2(-,则=-)(1a f( )A .23B .34C .43 D .32 7.已知函数2()2||f x x x =-,方程|()|f x a =有6个不同的实根,则实数a 的取值范围是( )A .1a <-B .10a -<<C .01a <<D .1a >8.双曲线12222=-b y a x 与椭圆22221(0,0)x y a m b m b+=>>>的离心率之积大于1,则以,,a b m 为边长的三角形一定是( )A .等腰三角形B .锐角三角形C .直角三角形D .钝角三角形9.若向量(,),(,)a m n b p q ==,且5,3m n p q +=+=,则||a b +的最小值为( )A .4B .42C .62D .810.在正三棱锥S ABC -中,E 为SA 的中点,F 为ABC ∆的中心,2SA BC ==,则直线EF 与平面SAB 所成角的正弦值为( )A .364 B .63C .63D .26911.来自中国、英国、瑞典的乒乓球裁判各两名,执行北京奥运会的一号、二号和三号场地的乒乓球裁判工作,每个场地由两名来自不同国家的裁判组成,则不同的安排方案总数有( )A .12种B .48种C .90种D .96种12.(理)给定*(1)log (2)()n n a n n N +=+∈,定义使乘积12k a a a ⋅⋅⋅为整数的()k k N *∈叫做理想数,则区间[1,2009]内的所有理想数的和为 ( )A .2026B .2016C .2009D . 2008(文)设函数()||f x x x bx c =++,给出下列四个命题:①当0c =时,()y f x =是奇函数;②当0,0b c =>时,方程()0f x =只有一个实根;③函数()y f x =的图象关于点(0,)c 对称;④方程()0f x =至多有两个实根.其中正确命题的个数为( )A .1个B .2个C .3个D .4个二、填空题(本大题共4小题,每小题4分,满分16分.请把答案填在答题卷上) 13.函数2()12cos 2f x x =-的最小正周期为 .14.已知满足条件25020x y y a x x ⎧-+≥⎪≥⎨⎪-≤⎩的平面区域的面积是5,则实数a = .15.设n a 为1*(1)()n x n N ++∈的展开式中2x 项的系数,则数列{}n a 的前12项和为 .16.P 为棱长为1的正方体1111ABCD A B C D -表面上的动点,且2AP =,则动点P 的轨迹的长度为________________.三、解答题(本大题共6小题,满分74分.解答应写出文字说明、证明过程和演算步骤) 17.(本小题满分12分)已知(2,0),(0,2),(cos ,sin A B C θθ),O 为坐标原点.(Ⅰ)13AC BC •=-,求sin 2θ的值; (Ⅱ)若||7,OA OC +=且(,0)θπ∈-,求OB OC 与的夹角.18. ( 本小题满分12分)某地机动车驾照考试规定:每位考试者在一年内最多有3次参加考试的机会,一旦某次考试通过,便可领取驾照,不再参加以后的考试,否则就一直考到第三次为止,如果小王决定参加驾照考试,设他一年中三次参加考试通过的概率依次为0.6,0.7,0.8. (理)(Ⅰ)求小王在一年内领到驾照的概率;(Ⅱ)求在一年内小王参加驾照考试次数ξ的分布列和ξ的数学期望. (文)(Ⅰ)求小王在第三次考试中通过而领到驾照的概率; (Ⅱ)求小王在一年内领到驾照的概率. 19.(本小题满分12分)如图,等腰梯形12ABPP 中,21AB P P ,12BC PP ⊥于C ,12AD PP ⊥于D ,2AB BC ==,26AP 2P AD ∆和1P BC ∆分别沿着AD 和BC 折起,使21,P P 重合于一点P ,AC 与BD 交于M 点,折起之后:(Ⅰ)求证:平面PBC ⊥平面PAD ; (Ⅱ)求异面直线PD 和AC 所成的角; (Ⅲ)(理)求二面角A PM B --的大小.20. (本小题12分)(理)已知函数tx e x f x-+=)1ln()(. (Ⅰ)求)(x f 的单调区间;(Ⅱ)当01t <<时,记min ()f x =)(t ϕ,求()t ϕ的最大值. (文)已知函数32()4()f x x ax a R =-+-∈.(Ⅰ)若函数)(x f y =的图象在点(1,(1))P f 处的切线的倾斜角为4π,求a 的值; (Ⅱ)设()f x 的导函数是()f x ',在(Ⅰ)的条件下,若[],1,1m n ∈-,求()()f m f n '+的最小AABP 1 P 2 CDBCDPM值.21. (本小题12分)已知数列{n a }的前n 项的和为n S ,对一切正整数n 都有22n n S n a =+.(Ⅰ)求数列{n a }的通项公式;(Ⅱ)(理)当n N *∈,证明:111172122212n n n aa a ++++≥++. (文)若*21()3nn a n b n N -=∈,证明:1213n b b b +++≥.22.(本小题满分14分)过双曲线1:22=-y x C 的右焦点2F 的直线与右支交于,A B 两点,且线段22,AF BF 的长度分别为,,m n m n ≥.(Ⅰ)求证:1mn ≥;(Ⅱ)当直线AB 的斜率5,3]k ∈时,求nm的取值范围.陕西师大附中高级第四次模拟考试数学答题纸一、选择题(每小题5分,共60分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案二、填空题(每小题4分,共16分)13. ; 14. ;15. ; 16. .三、解答题(本大题共6小题,满分74分.解答应写出文字说明、证明过程和演算步骤)17.解:18. 解:19.解:AA B P1P2 CDB CDPM20. 解21.22.陕西师大附中高级第四次模拟考试数学参考答案及评分标准一、选择题(每小题5分,共60分)题号12345 6 7 8 9 10 11 12答案 ()C B ()A B D A C ()D A C D B D B ()A C 二、填空题(每小题4分,共16分)13.2π 14.72 15.364 16.34π三、解答题17.(本小题满分12分)解:(Ⅰ)∵(cos 2,sin )AC θθ=-,(cos ,sin 2)BC θθ=-由13AC BC •=-,得2cos sin 3θθ+=两边平方:1sin 2θ+=49,∴sin 2θ=59- ………………6分 (Ⅱ)∵(cos 2,sin )OA OC θθ+=+,||7,OA OC +=∴22(cos 2)sin 7θθ++=,解得1cos 2θ=,又∵(,0)θπ∈-, ∴3sin 2θ=-,∴13(,)22OC =-,3OB OC •=-,设OB OC 与的夹角为α,则cos α=32=-,∴56πα=即OB OC 与的夹角为56π. …………… 12分18. (本小题满分12分)解:(理)(Ⅰ)小王在一年内领到驾照的概率为:1(10.6)(10.7)(10.8)0.976P =----=………………………( 4分)(Ⅱ)ξ的取值分别为1,2,3.(1)0.6P ξ==,(2)(10.6)0.70.28P ξ==-⨯=(3)(10.6)(10.7)0.12P ξ==-⨯-=………………………( 8分)所以小王参加考试次数ξ的分布列为:ξ 1 2 3 P0.60.280.12所以ξ的数学期望为 1.52E ξ= ……………………12分(文)(Ⅰ)小王在第三次考试中通过而领到驾照的概率为:(10.6)(10.7)0.80.096P =-⨯-⨯=………………………6分 (Ⅱ)小王在一年内领到驾照的概率为:1(10.6)(10.7)(10.8)0.976P =----=………………12分19.(本小题满分12分)(Ⅰ)证明:由已知得2,2PC PD CD ===,所以090CPD ∠=,即PC PD ⊥,又PD AD ⊥,||AD BC ,∴PD BC ⊥, PD ⊥平面PBC∴平面PBC ⊥平面PAD .……………………………4分(文6分)(Ⅱ)解:设PB 的中点为N ,连接MN ,则PD ∥NM ,∴CMN ∠是异面直线PD 和AC 所成的角或其补角 由(Ⅰ)知MN CN ⊥,在Rt CMN ∆中,2CM =22MN =, ∴60OCMN ∠=.所以异面直线PD 和AC 所成的角为060.…………………8分(文12分)(Ⅲ)(解法一)由已知得四边形ABCD 是正方形,∴,CM DM =又PC PD =,∴PMC PMD ∆≅∆, 过点C 做CE PM ⊥于E ,连接DE ,则DE PM ⊥, 则CED ∠即二面角A PM B --的平面角, 在PMC ∆中,2PM PC CM ===,所以62CE DE ==, 又2CD =,由余弦定理得1cos 3CED ∠=-, 所以二面角A PM B --的大小为1arccos 3π-.……………12分 (解法二)向量法设O 为CD 的中点,则PO CD PO OM ⊥⊥,,以O 为坐标原点,OM OC OP 、、所在直线分别为x y z 、、轴建立空间直角坐标系,则(001)(010)P C ,,,,,,(100)(210)(210)M B A -,,,,,,,,, (110)(101)MB MP ==-,,,,,,设平面PMB 的法向量1(1,,),n y z =由10,n MB ⋅=得1,y =-由10,n MP ⋅=得1,z =所以1(1,1,1),n =- 同理得平面PMA 的法向量2(1,1,1),n =1212121cos ,3||||n n n n n n ⋅<>==-,所以所求二面角的大小为1-arccos3π.………………12分 20.(本小题满分12分)解:(理)(Ⅰ)(1)()11x x x xe t e tf x t e e--'=-=++ 当0t ≤时,()0f x '>,∴()f x R 的递增区间为.当),1(ln ,1ln0)(10+∞-∴->>'<<t tt t x x f ,t 递增区间为得令时 )1ln ,(1ln 0)(tt,t t x x f --∞∴-<<'递减区间为得令R x f x f ,t 的递减区间为时当)(,0)(1∴<'≥……………6分(Ⅱ)当(0,1)t ∈时,由(Ⅰ)的讨论可知()(ln )ln(1)ln()111t t tt f t t t tϕ==+---- 即1()ln[ln ln(1)]ln (1)ln(1)1t t t t t t t t tϕ=---=-+--- ∴()(1)ln(1)ln (01)t t t t t t ϕ=---<<11()ln(1)(1)ln 1ln1tt t t t t tϕ--'=-+---=-得 1()02t t ϕ'==令得 110()0,()(0,)22t t t ϕϕ'<<>∴当时,在上递增111()0,()(,1)22t t t ϕϕ'<<<∴当时,在上递减 ∴max 11111()()ln ln ln 222222t ϕϕ==--=………………12分(文)(Ⅰ)∵2()32f x x ax '=-+据题意,(1)tan 14f π'==,∴321,2a a -+==即 ………………………4分(Ⅱ)由(Ⅰ)知32()24f x x x =-+-,∴32()24f m m m =-+-则2()34f m m m '=-+ m 1- (1,0)- 0(0,1) 1 ()f m ' 7- - 0+ 1()f m 1- 4- 3-∴对于[]1,1m ∈-,()f m 最小值为(0)4f =- ………………… 8分∵2()34f n n n '=-+的对称轴为23x =,且抛物线开口向下, ∴[]1,1n ∈-时,)(x f '最小值为(1)f '-与(1)f '中较小的,∵(1)1,(1)7f f ''=-=-,∴当[]1,1n ∈-时,()f n '的最小值是-7.∴()()f m f n '+的最小值为-11. ………………………12分21.(本小题满分12分)解:(Ⅰ)∵221112222n n n n a a n n S S +++=+=+(),, ∴11112121222n n n n n n n a a n a S S a a n +++++=-=+-+=+,即 ∴11n n a n a n +-+=--()()令n n b a n =-,则1n n b b +=-,∴11(1)n n b b -=-11111122a a S a ==+=又得,∴1110b a =-= ∴0n n b a n ==,即.……………6分(Ⅱ)(理)证明:111()(*)122f k k N k k k=+++∈++构造 111111(1)()()()2322122f k f k k k k k k k +-=+++-++++++++ 1102122k k =->++ ∴()f k k 关于是递增的,又∵22(*)n n N ≥∈,∴(2)(2)n f f ≥ ∴1111117(2)(2)212223412n n n n f f +=+++=+=++的最小值为 ∴111121222n n n ++++≥++712.………………12分 (文)证明:由(Ⅰ)知:*21()3n n n b n N -=∈ 记1223135213333n n n n S b b b -=+++=++++ 用错位相减法求和得:113n n n S +=- 令13n n n c +=, ∵1112210333n n n n n n n n c c +++++-=-=> ∴数列{}n c 是递减数列,∴123n c c ≤=, ∴12111333n n n S +=-≥-=. 即1213n b b b +++≥.………………………12分 (由111133n n n S +=->>证明也给满分) 22.(本小题满分14分)解:(Ⅰ)①当直线AB x ⊥轴时,则2,1),2,1)A B -,此时1m n ==,∴1mn =.(不讨论扣1分)②当直线AB 不垂直于x 轴时,m n >,设双曲线的右准线为l , 作1AA l ⊥于1A ,作1BB l ⊥于1B ,作1BK AA ⊥于K 且交x 轴于M根据双曲线第二定义有:1122||,||22AA m BB n ==, 而2F 到准线l 的距离为22. 由22||||||||BF MF BA KA =,得:22222222n m n m n =+-, ∴22mn m n mn =+≥,∴1mn ≥,∵此时m n ≠,∴1mn > 综上可知1mn ≥.………………………………………7分(Ⅱ)设AB :2x ty =+22(1)2210t y ty -++= ∴11,122221221-=-=+t y y t t y y 令λ=nm ,则1>λ,且12y y λ=-代入上面两式得: 2222(1)1t y t λ-=-- ① 22211y t λ-=- ② 由①②消去2y 得22218)1(tt -=-λλ 即2221862181t t t -+-=+-=+λλ ③ 由5,3]k ∈有:22111[,]95t k =∈,综合③式得134λλ≤+≤ 由1λ>得⎪⎩⎪⎨⎧≤+-≥+-01401322λλλλ,解得35[,23]2λ+∈+ ∴m n 的取值范围为35[23]+…………………………14分。
《高观点下中学数学——分析学》练习题答案
《高观点下中学数学——分析学》练习题一参考答案一、填空题1.⊂,2.}},{},{},{}{,{b a b a a ,∅,3. 满射,4.代数数,5.)1ln()(x x f +=,6.下凸7.传递的;8.双射;9.)()(lim a f x f ax =→;10.1))()(),(),,0(,y x y x y x ϕϕϕ+=+∞∈∀;11.1))()()()()(τττs t s c t c t c +=-, 12. xFy 。
13.⊂;14、{,{∅甲},{乙},{甲,乙}};15、单射;16、未知函数;17、1)2(=πf ;18、上凸; 19.传递性; 20.0x <-εβ;21.可导; 22. )()()(y f x f y x f =+;23. )()(2)()(τττc t c t c t c =-++;24.b ax +(其中b a ,为常数).25.C A -; 26.⊂; 27.,E x ∈∀有β≤x ; 28.收敛的子列}{k n x ; 29.)()(y L x L -;30.1-.二、单项选择题1.B ;2.A ;3.C ;4.D ;5.D ;6.C ;7.C ;8.C ;9.D ;10.B ;11. D ;12. A13.D; 14.B; 15.C; 16.C; 17.D; 18. A; 19.C; 20.B; 21.A; 22.B; 23.D ;24.A; 25D ; 27B ; 27. A ;28.C ; 29.D ;30.A三、计算题 1解 iyx iy x z +-=, 2分22y x iy x +=-,22y x iy x +=+ 7分故1=z 8分2设xt 2=,则t x 2log =, 3分 代入得t t t f 222log sin )(log )(+=x x x f 222log sin )(log )(+= 8分3.解]cos )sin 1(cos )sin 2[()sin 2(1)(2x x x x x x f ++--=' 3分令0)(='x f ,得0cos =x ,22ππ±=k x易验证22ππ+=k x 是极大值点,22ππ-=k x 是极小值点, 6分极大值21211)22(=-+=+ππk f ,极小值0)22(=-ππk f 8分 4.解 显然1+<n n a a ,且40<<n a ,即数列}{n a ,单调增加且有上界,故n n a ∞→lim 存在, 设a a n n =∞→lim ,由18-+=n n a a 可得a a +=8, 5分即082=--a a , 解得)331(212)3211(+=++=a5.解 首先计算过点M 的切线的斜率16822=='===x x x y k 4分 所求的切线方程为 )2(1619-=-x y即 1316-=x y 8分 6.解 已知x xf x f 3)1()(2=+ (1)将x1代替x ,得 xx f x f 3)()1(2=+ (2) 4分)2(2)1(-⨯得x x x f x f x f x f 36)()1(2)1(2)(4-=--+xx x f 12)(-= 8分7.解 已知在),0(π内,x sin 是上凸函数,由上凸函数的定义有224sin 2sin )sin (sin 21==+≥+πy x y x 5分 即 2sin sin ≥+y x而且当4π==y x 时,24sin4sin=+ππ,故2是y x sin sin +的最小值。
陕西师范大学附中中考四模--数学(解析版)
陕西师范大学附中中考数学四模试卷一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)1.在|﹣2|,20,2﹣1,这四个数中,最大的数是()A.|﹣2|B.20C.2﹣1D.2.如图是一个螺母的示意图,它的俯视图是()A.B.C.D.3.如图,在菱形ABCD中,AB=5,∠BCD=120°,则对角线AC等于()A.20 B.15 C.10 D.54.若正比例函数的图象经过点(﹣1,2),则这个图象必经过点()A.(1,2)B.(﹣1,﹣2)C.(2,﹣1)D.(1,﹣2)5.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为()A.1 B.2 C.3 D.46.在同一直角坐标系下,直线y=x+1与双曲线的交点的个数为()A.0个B.1个C.2个D.不能确定7.为了美化城市,经统一规划,将一正方形草坪的南北方向增加3m,东西方向缩短3m,则改造后的长方形草坪面积与原来正方形草坪面积相比()A.增加6m2 B.增加9m2C.减少9m2D.保持不变8.如图,⊙O的半径为2,弦AB=,点C在弦AB上,AC=AB,则OC的长为()A.B.C.D.9.如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则的值为()A.B.C.D.10.已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a >2;④4a﹣2b+c>0.其中正确结论的个数是()A.1 B.2 C.3 D.4二、填空题(共4小题,每小题3分,计12分)11.请给出一元二次方程x2﹣8x+ =0的一个常数项,使这个方程有两个不相等的实数根.12.如图,小丽荡秋千,秋千链子的长OA为2.5米,秋千向两边摆动的角度相同,摆动的水平距离AB为3米,则秋千摆至最高位置时与最低价位置时的高度之差(即CD)为米.13.如图,点A在双曲线y=(x>0)上,点B在双曲线y=(x>0)上(点B在点A的右侧),且AB∥x轴.若四边形OABC是菱形,且∠AOC=60°,则k=.14.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是.三、解答题(共11小题,计78分)第17题图aAB15.计算:()﹣2﹣(π﹣)0+|﹣2|+4sin60°.16.先化简,再求值:÷(1+),其中x=﹣1.17.如图,已知线段a.只用直尺(没有刻度的尺)和圆规,求作一个直角三角形ABC,以AB和BC分别为两条直角边,使AB=a,BC=a(要求保留作图痕迹,不必写出作法)18.为了推动课堂教学改革,打造“贵生课堂”,我县某中学对该校八年级部分学生就一学期以来“分组合作学习”方式的支持程度进行调查,统计情况如图,请根据图中提供的信息,回答下列问题:(1)本次调查的八年级部分学生共有名;请补全条形统计图;(2)若该校八年级学生共有540人,请你估计该校八年级有多少名学生支持“分组合作学习”方式(含“非常喜欢”和“喜欢”两种情况的学生)?19.在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P,(1)求证:△ABF≌△ACE;(2)求证:PB=PC.20.我国南水北调中线工程的起点是丹江水库,按照工程计划,需对原水库大坝进行混凝土加高,使坝高由原来的162米增加到176.6米,以抬高蓄水位.如图是某一段坝体加高工程的截面示意图,其中原坝体的高为BE,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡坡底端水平方向增加的宽度AC(结果精确到0.1米.参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50,).21.附中现要从甲、乙两位男生和丙、丁两位女生中,选派两位同学分别作为①号选手和②号选手代表学校参加全市汉字听写大赛.(1)请用树形图或列表法列举出各种可能选派的结果;(2)求恰好选派一男一女两位同学参赛的概率.22.某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:①金卡售价600元/张,每次凭卡不再收费.②银卡售价150元/张,每次凭卡另收10元.暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;(3)请根据函数图象,直接写出选择哪种消费方式更合算.23.如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE 的延长线交切线DB于点F,AF交⊙O于点H,连接BH.(1)求证:AC=CD;(2)若OB=2,求BH的长.24.如图,抛物线y=﹣x2+2x+3与x轴交与A,B两点(点A在点B的左侧),与y轴交于点C.点D和点C关于抛物线的对称轴对称,直线AD与y轴相交于点E.(1)求直线AD的解析式;(2)如图1,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH的周长的最大值;(3)点M是抛物线的顶点,点P是y轴上一点,点Q是坐标平面内一点,以A,M,P,Q为顶点的四边形是AM为边的矩形,若点T和点Q关于AM所在直线对称,求点T的坐标.25.已知四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.(1)如图1,P为AB边上的一点,以PD、PC为边作▱PCQD,请问对角线PQ,DC的长能否相等,为什么?(2)如图2,若P为AB边上一点,以PD,PC为边作▱PCQD,请问对角线PQ的长是否存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.(3)若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE、PC为边作▱PCQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.(4)如图3,若P为DC边上任意一点,延长PA到E,使AE=nPA(n为常数),以PE、PB为边作▱PBQE,请探究对角线PQ的长是否也存在最小值?如果存在,直接写出最小值,如果不存在,请说明理由.2016年陕西师范大学附中中考数学四模试卷参考答案与试题解析一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)1.在|﹣2|,20,2﹣1,这四个数中,最大的数是()A.|﹣2|B.20C.2﹣1D.【考点】实数大小比较;零指数幂;负整数指数幂.【分析】正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,首先求出|﹣2|,20,2﹣1的值是多少,然后根据实数比较大小的方法判断即可.【解答】解:|﹣2|=2,20=1,2﹣1=0.5,∵,∴,∴在|﹣2|,20,2﹣1,这四个数中,最大的数是|﹣2|.故选:A.2.如图是一个螺母的示意图,它的俯视图是()A.B.C.D.【考点】简单组合体的三视图.【分析】根据从上面看得到的图形是俯视图,可得答案.【解答】解:从上面看外面是一个正六边形,里面是一个没有圆心的圆,故选:B.3.如图,在菱形ABCD中,AB=5,∠BCD=120°,则对角线AC等于()A.20 B.15 C.10 D.5【考点】菱形的性质;等边三角形的判定与性质.【分析】根据菱形的性质及已知可得△ABC为等边三角形,从而得到AC=AB.【解答】解:∵AB=BC,∠B+∠BCD=180°,∠BCD=120°∴∠B=60°∴△ABC为等边三角形∴AC=AB=5故选D.4.若正比例函数的图象经过点(﹣1,2),则这个图象必经过点()A.(1,2)B.(﹣1,﹣2)C.(2,﹣1)D.(1,﹣2)【考点】待定系数法求正比例函数解析式.【分析】求出函数解析式,然后根据正比例函数的定义用代入法计算.【解答】解:设正比例函数的解析式为y=kx(k≠0),因为正比例函数y=kx的图象经过点(﹣1,2),所以2=﹣k,解得:k=﹣2,所以y=﹣2x,把这四个选项中的点的坐标分别代入y=﹣2x中,等号成立的点就在正比例函数y=﹣2x的图象上,所以这个图象必经过点(1,﹣2).故选D.5.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为()A.1 B.2 C.3 D.4【考点】平行线分线段成比例.【分析】根据平行线分线段成比例可得,代入计算即可解答.【解答】解:∵DE∥BC,∴,即,解得:EC=2,故选:B.6.在同一直角坐标系下,直线y=x+1与双曲线的交点的个数为()A.0个B.1个C.2个D.不能确定【考点】反比例函数与一次函数的交点问题.【分析】根据一次函数与反比例函数图象的性质作答.【解答】解:y=x+1的图象过一、二、三象限;函数的中,k>0时,过一、三象限.故有两个交点.故选:C.7.为了美化城市,经统一规划,将一正方形草坪的南北方向增加3m,东西方向缩短3m,则改造后的长方形草坪面积与原来正方形草坪面积相比()A.增加6m2 B.增加9m2C.减少9m2D.保持不变【考点】平方差公式.【分析】根据正方形和长方形的面积公式求出原来正方形草坪面积和改造后的长方形草坪面积,比较即得结论.【解答】解:设正方形草坪的原边长为a,则面积=a2;将一正方形草坪的南北方向增加3m,东西方向缩短3m后,边长为a+3,a﹣3,面积为a2﹣9.故减少9m2.故选C.8.如图,⊙O的半径为2,弦AB=,点C在弦AB上,AC=AB,则OC的长为()A.B.C.D.【考点】垂径定理;勾股定理.【分析】首先过点O作OD⊥AB于点D,由垂径定理,即可求得AD,BD的长,然后由勾股定理,可求得OD 的长,然后在Rt△OCD中,利用勾股定理即可求得OC的长.【解答】解:过点O作OD⊥AB于点D,∵弦AB=2,∴AD=BD=AB=,AC=AB=,∴CD=AD﹣AC=,∵⊙O的半径为2,即OB=2,∴在Rt△OBD中,OD==1,在Rt△OCD中,OC==.故选D.9.如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则的值为()A.B.C.D.【考点】旋转的性质;含30度角的直角三角形;等腰直角三角形.【分析】根据旋转得出∠NCE=75°,求出∠NCO,设OC=a,则CN=2a,根据△CMN也是等腰直角三角形设CM=MN=x,由勾股定理得出x2+x2=(2a)2,求出x=a,得出CD=a,代入求出即可.【解答】解:∵将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,∴∠ECN=75°,∵∠ECD=45°,∴∠NCO=180°﹣75°﹣45°=60°,∵AO⊥OB,∴∠AOB=90°,∴∠ONC=30°,设OC=a,则CN=2a,∵等腰直角三角形DCE旋转到△CMN,∴△CMN也是等腰直角三角形,设CM=MN=x,则由勾股定理得:x2+x2=(2a)2,x=a,即CD=CM=a,∴==,故选C.10.已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a >2;④4a﹣2b+c>0.其中正确结论的个数是()A.1 B.2 C.3 D.4【考点】二次函数图象与系数的关系.【分析】①首先根据抛物线开口向上,可得a>0;然后根据对称轴在y轴左边,可得b>0;最后根据抛物线与y轴的交点在x轴的上方,可得c>0,据此判断出abc>0即可.②根据二次函数y=ax2+bx+c+2的图象与x轴只有一个交点,可得△=0,即b2﹣4a(c+2)=0,b2﹣4ac=8a>0,据此解答即可.③首先根据对称轴x=﹣=﹣1,可得b=2a,然后根据b2﹣4ac=8a,确定出a的取值范围即可.④根据对称轴是x=﹣1,而且x=0时,y>2,可得x=﹣2时,y>2,据此判断即可.【解答】解:∵抛物线开口向上,∴a>0,∵对称轴在y轴左边,∴b>0,∵抛物线与y轴的交点在x轴的上方,∴c+2>2,∴c>0,∴abc>0,∴结论①不正确;∵二次函数y=ax2+bx+c+2的图象与x轴只有一个交点,∴△=0,即b2﹣4a(c+2)=0,∴b2﹣4ac=8a>0,∴结论②不正确;∵对称轴x=﹣=﹣1,∴b=2a,∵b2﹣4ac=8a,∴4a2﹣4ac=8a,∴a=c+2,∵c>0,∴a>2,∴结论③正确;∵对称轴是x=﹣1,而且x=0时,y>2,∴x=﹣2时,y>2,∴4a﹣2b+c+2>2,∴4a﹣2b+c>0.∴结论④正确.综上,可得正确结论的个数是2个:③④.故选:B.二、填空题(共4小题,每小题3分,计12分)11.请给出一元二次方程x2﹣8x+ 12(答案不唯一)=0的一个常数项,使这个方程有两个不相等的实数根.【考点】根的判别式.【分析】方程有两个不相等的实数根,则△>0,建立关于c的不等式,求出c的取值范围.【解答】解:由题意知,△=64﹣4c>0,∴c<16,即当c取小于16时就能满足题意.比如c=12满足方程有两个不相等的实数根.12.如图,小丽荡秋千,秋千链子的长OA为2.5米,秋千向两边摆动的角度相同,摆动的水平距离AB为3米,则秋千摆至最高位置时与最低价位置时的高度之差(即CD)为0.5米.【考点】垂径定理的应用;勾股定理.【分析】由题意知,秋千摆至最低点时,点C为弧AB的中点,由垂径定理知AB⊥OC,AD=BD=AB=1.5米.再根据勾股定理求得OD即可.【解答】解:∵点C为弧AB的中点,O为圆心由垂径定理知:AB⊥OC,AD=BD=AB=1.5米,在Rt△OAD中,根据勾股定理,OD==2(米),∴CD=OC﹣OD=2.5﹣2=0.5(米);故答案为0.5.13.如图,点A在双曲线y=(x>0)上,点B在双曲线y=(x>0)上(点B在点A的右侧),且AB∥x轴.若四边形OABC是菱形,且∠AOC=60°,则k=.【考点】菱形的性质;反比例函数图象上点的坐标特征.【分析】首先根据点A在双曲线y=(x>0)上,设A点坐标为(a,),再利用含30°直角三角形的性质算出OA=2a,再利用菱形的性质进而得到B点坐标,即可求出k的值.【解答】解:因为点A在双曲线y=(x>0)上,设A点坐标为(a,),因为四边形OABC是菱形,且∠AOC=60°,所以OA=2a,可得B点坐标为(3a,),可得:k=,故答案为:14.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是.【考点】正方形的性质;直角三角形斜边上的中线;勾股定理.【分析】根据正方形的性质求出AB=BC=1,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,求出AM=4,FM=2,∠AMF=90°,根据正方形性质求出∠ACF=90°,根据直角三角形斜边上的中线性质求出CH=AF,根据勾股定理求出AF即可.【解答】解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,∴AB=BC=1,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,则AM=BC+CE=1+3=4,FM=EF﹣AB=3﹣1=2,∠AMF=90°,∵四边形ABCD和四边形GCEF是正方形,∴∠ACD=∠GCF=45°,∴∠ACF=90°,∵H为AF的中点,∴CH=AF,在Rt△AMF中,由勾股定理得:AF===2,∴CH=,故答案为:.三、解答题(共11小题,计78分)第17题图aAB15.计算:()﹣2﹣(π﹣)0+|﹣2|+4sin60°.【考点】实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.【分析】原式第一项利用负整数指数幂法则计算,第二项利用零指数幂法则计算,第三项利用绝对值的代数意义化简,最后一项利用特殊角的三角函数值计算即可得到结果.【解答】解:原式=4﹣1+2﹣+4×=5+.16.先化简,再求值:÷(1+),其中x=﹣1.【考点】分式的化简求值.【分析】分式的化简,要熟悉混合运算的顺序,分子、分母能因式分解的先因式分解;除法要统一为乘法运算,注意化简后,将,代入化简后的式子求出即可.【解答】解:=÷(+)=÷=×=,把,代入原式====.17.如图,已知线段a.只用直尺(没有刻度的尺)和圆规,求作一个直角三角形ABC,以AB和BC分别为两条直角边,使AB=a,BC=a(要求保留作图痕迹,不必写出作法)【考点】作图—复杂作图.【分析】先画线段AB=a,再作AB的垂直平分线得到其中点D,接着过B点作l⊥AB,然后再l上截取BC=BD,则△ABC满足条件.【解答】解:如图,△ABC为所作.18.为了推动课堂教学改革,打造“贵生课堂”,我县某中学对该校八年级部分学生就一学期以来“分组合作学习”方式的支持程度进行调查,统计情况如图,请根据图中提供的信息,回答下列问题:(1)本次调查的八年级部分学生共有54名;请补全条形统计图;(2)若该校八年级学生共有540人,请你估计该校八年级有多少名学生支持“分组合作学习”方式(含“非常喜欢”和“喜欢”两种情况的学生)?【考点】条形统计图;用样本估计总体;扇形统计图.【分析】(1)根据喜欢的人数是18人,根据对应的圆心角即可求得所占的比例,利用18除以所占的比例即可求得总人数,进而求得非常喜欢的人数,从而补全条形统计图;(2)利用总人数540乘以对应的比例即可求解.【解答】解:(1)本次调查的八年级部分学生共有18÷=54(人),“非常喜欢”的人数为:54﹣18﹣6=30(人),补全条形统计图如图:(2)×540=480(人),答:估计该校八年级有480名学生支持“分组合作学习”方式.故答案为:(1)54.19.在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P,(1)求证:△ABF≌△ACE;(2)求证:PB=PC.【考点】全等三角形的判定与性质;等腰三角形的性质.【分析】(1)根据AE=AF,AB=AC,∠A=∠A即可证明三角形全等;(2)根据(1)结论可证∠ABF=∠ACE,即可证明∠PBF=∠PCE,即可解题.【解答】证明:(1)在△ABF和△ACE中,,∴△ABF≌△ACE(SAS);(2)∵AB=AC,∴∠ABC=∠ACB,∵△ABF≌△ACE,∴∠ABF=∠ACE,∴∠PBF=∠PCE,∴BP=CP.20.我国南水北调中线工程的起点是丹江水库,按照工程计划,需对原水库大坝进行混凝土加高,使坝高由原来的162米增加到176.6米,以抬高蓄水位.如图是某一段坝体加高工程的截面示意图,其中原坝体的高为BE,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡坡底端水平方向增加的宽度AC(结果精确到0.1米.参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50,).【考点】解直角三角形的应用-坡度坡角问题.【分析】在Rt△BAE中,根据BE=162米,∠BAE=68°,解直角三角形求出AE的长度,然后在Rt△DCE中解直角三角形求出CE的长度,然后根据AC=CE﹣AE求出AC的长度即可.【解答】解:在Rt△BAE中,∵BE=162米,∠BAE=68°,∴AE===64.8(米),在Rt△DCE中,∵DE=176.6米,∠DCE=60°,∴CE===≈102.1(米),则AC=CE﹣AE=102.1﹣64.8=37.3(米).答:工程完工后背水坡坡底端水平方向增加的宽度AC约为37.3米.21.附中现要从甲、乙两位男生和丙、丁两位女生中,选派两位同学分别作为①号选手和②号选手代表学校参加全市汉字听写大赛.(1)请用树形图或列表法列举出各种可能选派的结果;(2)求恰好选派一男一女两位同学参赛的概率.【考点】列表法与树状图法.【分析】(1)利用列表法展示所有有12种等可能的选派方案;(2)找出恰有一男一女参赛的结果数,然后根据概率公式求解.【解答】解:(1)列表如下:甲乙丙丁甲乙甲丙甲丁甲乙乙甲乙丙乙丁丙丙甲丙乙丙丁丁丁甲丁乙丁丙共有12种等可能的选派方案;(2)恰有一男一女参赛共有8种可能,所以P(一男一女)==.22.某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:①金卡售价600元/张,每次凭卡不再收费.②银卡售价150元/张,每次凭卡另收10元.暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;(3)请根据函数图象,直接写出选择哪种消费方式更合算.【考点】一次函数的应用.【分析】(1)根据银卡售价150元/张,每次凭卡另收10元,以及旅游馆普通票价20元/张,设游泳x次时,分别得出所需总费用为y元与x的关系式即可;(2)利用函数交点坐标求法分别得出即可;(3)利用(2)的点的坐标以及结合得出函数图象得出答案.【解答】解:(1)由题意可得:银卡消费:y=10x+150,普通消费:y=20x;(2)由题意可得:当10x+150=20x,解得:x=15,则y=300,故B(15,300),当y=10x+150,x=0时,y=150,故A(0,150),当y=10x+150=600,解得:x=45,则y=600,故C(45,600);(3)如图所示:由A,B,C的坐标可得:当0<x<15时,普通消费更划算;当x=15时,银卡、普通票的总费用相同,均比金卡合算;当15<x<45时,银卡消费更划算;当x=45时,金卡、银卡的总费用相同,均比普通票合算;当x>45时,金卡消费更划算.23.如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE 的延长线交切线DB于点F,AF交⊙O于点H,连接BH.(1)求证:AC=CD;(2)若OB=2,求BH的长.【考点】切线的性质.【分析】(1)连接OC,只要证明OC∥BD即可.(2)在Rt△ABF中,根据BH=计算即可.【解答】证明(1)连接OC.∵C是中点,AB是○O的直径∴OC⊥AB,∵BD是○O切线,∴BD⊥AB.∴OC∥BD.∵AO=BO,∴AC=CD(2)∵E是OB中点,∴OE=BE在△COE与△FBE中,∠CEO=∠FEBOE=BE∠COE=∠FBE△COE≌△FBE(ASA)∴BF=CO∵OB=2,∴BF=2∴AF===2,∵AB是直径∴BH⊥AF∴AB•BF=AF•BH∴BH===.24.如图,抛物线y=﹣x2+2x+3与x轴交与A,B两点(点A在点B的左侧),与y轴交于点C.点D和点C关于抛物线的对称轴对称,直线AD与y轴相交于点E.(1)求直线AD的解析式;(2)如图1,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH的周长的最大值;(3)点M是抛物线的顶点,点P是y轴上一点,点Q是坐标平面内一点,以A,M,P,Q为顶点的四边形是AM为边的矩形,若点T和点Q关于AM所在直线对称,求点T的坐标.【考点】二次函数综合题.【分析】(1)求出A、D两点坐标,利用待定系数法即可解决问题.(2)首先证明△FHG是等腰直角三角形,构建二次函数利用函数性质解决问题即可.(3)分两种情形①如图2中,若AP为对角线,利用相似三角形性质求出点T坐标.②如图3中,若AQ为对角线,利用相似三角形性质即可解决问题.【解答】解:(1)∵抛物线y=﹣x2+2x+3与x轴交与A,B两点(点A在点B的左侧),与y轴交于点C,∴点A坐标(﹣1,0),点B坐标(3,0),点C坐标(0,3),∵抛物线对称轴x=1,D、C关于对称轴对称,∴点D坐标(2,3),设直线AD为y=kx+b.则解得;∴直线AD解析式为:y=x+1.(2)如图1中,∵OA=OE=1,∴∠EAO=45°,∵FH∥AB,∴∠FHA=∠EAO=45°,∵FG⊥AH,∴△FGH是等腰直角三角形,设点F坐标(m,﹣m2+2m+3),∴点H坐标(﹣m2+2m+2,﹣m2+2m+3),∴FH=﹣m2+m+2,∴△FGH的周长=(﹣m2+m+2)+2×(﹣m2+m+2)=﹣(1+)(m﹣)2+∴△FGH的周长最大值为.(3)①如图2中,若AP为对角线作PS⊥对称轴于于S,对称轴与x轴的交点为R,∵∠PMS+∠MPS=90°,∠PMS+∠AMR=90°,∴∠MPS=∠AMR,∵∠PSM=∠MRA,∴△PMS∽△MAR可得=,∴=,∴SM=,∴点P坐标(0,)由点的平移可知Q(﹣2,)故Q点关于直线AM的对称点T为(0,﹣).②如图3中,若AQ为对角线,作AR∥y轴,MR∥x轴,AS∥y轴,PS∥AB,同理可证△ARM∽△PSA,∴=,∴AS=∴点P坐标(0,﹣),由点的平移可知Q(2,),故Q点关于直线AM的对称点T为(0,).25.已知四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.(1)如图1,P为AB边上的一点,以PD、PC为边作▱PCQD,请问对角线PQ,DC的长能否相等,为什么?(2)如图2,若P为AB边上一点,以PD,PC为边作▱PCQD,请问对角线PQ的长是否存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.(3)若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE、PC为边作▱PCQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.(4)如图3,若P为DC边上任意一点,延长PA到E,使AE=nPA(n为常数),以PE、PB为边作▱PBQE,请探究对角线PQ的长是否也存在最小值?如果存在,直接写出最小值,如果不存在,请说明理由.【考点】相似形综合题.【分析】(1)由四边形PCQD是平行四边形,若对角线PQ、DC相等,则四边形PCQD是矩形,得出∠DPC=90°,由勾股定理得出DC=2,设PB=x,则AP=2﹣x,在Rt△DPC中,由勾股定理得出方程,方程无解,得出对角线PQ与DC不可能相等.(2)过点Q作QH⊥BC,交BC的延长线于H,由AAS证明△ADP≌△HCQ,得出AD=HC求出BH=4,当PQ ⊥AB时,PQ的长最小,即为4.(3)设PQ与DC相交于点G,由平行线得出=,得出G是DC上一定点,作QH⊥BC,交BC的延长线于H,证明Rt△ADP∽Rt△HCQ,得出=,求出CH=2得出BH=BG+CH=5,当PQ⊥AB时,PQ 的长最小,即为5.(4)设PQ与AB相交于点G,由平行线得出=,作QH∥PD,交CB的延长线于H,过点C作CK ⊥CD,交QH的延长线于K,证明△ADP∽△BHQ,得出=,求出BH=n+1,得出CH=BH+BC=n+4,过点D作DM⊥BC于M,则四边形ABND是矩形,得出BM=AD=1,DM=AB=2,证出∠KCH=45°,由三角函数得出CK=CH•cos45°=(n+4),即可得出结果.【解答】解:(1)对角线PQ与DC不可能相等,理由如下:∵四边形PCQD是平行四边形,若对角线PQ、DC相等,则四边形PCQD是矩形,∴∠DPC=90°,∵AD=1,AB=2,BC=3,∴DC=2,设PB=x,则AP=2﹣x,在Rt△DPC中,PD2+PC2=DC2,即x2+32+(2﹣x)2+12=(2)2,整理得:x2﹣2x+3=0,∵△=(﹣2)2﹣4×1×3=﹣8<0,∴方程无解,∴对角线PQ与DC不可能相等.(2)存在,理由如下:如图2,在平行四边形PCQD中,设对角线PQ与DC相交于点G,则G是DC的中点,过点Q作QH⊥BC,交BC的延长线于H,∵AD∥BC,AB⊥BC,∴AD⊥AB,∠ADC=∠DCH,即∠ADP+∠PDG=∠DCQ+∠QCH,∵PD∥CQ,∴∠PDC=∠DCQ,∴∠ADP=∠QCH,在△ADP和△HCQ中,,∴△ADP≌△HCQ(AAS),∴AD=HC,∵AD=1,BC=3,∴BH=4,∴当PQ⊥AB时,PQ的长最小,即为4.(3)存在,理由如下:如图3,设PQ与DC相交于点G,∵PE∥CQ,PD=DE,∴=,∴G是DC上一定点,作QH⊥BC,交BC的延长线于H,同(2)得:∠ADP=∠QCH,∴Rt△ADP∽Rt△HCQ,∴=,∴CH=2,∴BH=BG+CH=3+2=5,∴当PQ⊥AB时,PQ的长最小,即为5.(4)存在,理由如下:如图4,设PQ与AB相交于点G,∵PE∥BQ,AE=nPA,∴=,作QH∥PD,交CB的延长线于H,过点C作CK⊥CD,交QH的延长线于K,∵AD∥BC,AB⊥BC,∴∠ADP=∠QHC,∠DAP+∠PAG=∠QBH+∠QBG=90°,∠PAG=∠QBG,∴∠QBH=∠PAD,∴△ADP∽△BHQ,∴=,∵AD=1,∴BH=n+1,∴CH=BH+BC=3+n+1=n+4,过点D作DM⊥BC于M,则四边形ABND是矩形,∴BM=AD=1,DM=AB=2∴CM=BC﹣BM=3﹣1=2=DM,∴∠DCM=45°,∴∠KCH=45°,∴CK=CH•cos45°=(n+4),∴当PQ⊥CD时,PQ的长最小,最小值为(n+4).。
高观点下中学数学-代数学练习题
《高观点下中学数学—代数学》练习题一一、填空1、由A →B 的单映射σ的定义为()。
2、由A →B 的满映射σ的定义为()。
3、自然数a 与b 相乘的定义中两个条件为()。
4、环的理想定义为( )。
5、剩余类环12Z 中可逆元素为( )。
6、π为有理数域上的( )。
A 、代数元 B 、超越元7、y=lg x 则( )A 、y 是上凸函数B 、y 是下凸函数8、++21x x ……+n x =m 的非负整数解的个数为( )。
9、下面不等式A 、212121)(21Sinx Sinx x x Sin +≥+ B 、212121)(21Sinx Sinx x x Sin +≤+ 正确的是( )。
10、n 个数码的扰乱排列总数为( )。
11、在二阶方阵环(实数域上)中找出两个零因子( )。
12、素元素的定义为( )。
13、不可约元素的定义为( )。
14、rn C 1-+11--r n C =( )。
15、在剩余类环8Z 中不可逆的元素为( )。
16、若|A|=m ,|B|=n ,则A →B 的所有不同映射的个数为 A 、n m B 、m n C 、n ×m 17、皮阿罗公理中的归纳公式为( )。
18、由A →B 的单映射的定义为( )。
19、自然数a 与b 加法的定义中两个条件为( )。
20、若f(x) =kx 为上凸函数则( )。
A 、k>1 B 、0<k<1 C 、k<021、自然数的加法的定义中两个条件为( )。
22、自然数a>b 的定义为( )。
23、在整数集合中求两个数的最大公因数( )。
A 、是代数运算B 、不是代数运算24、若集合|A|=n ,则集合A →A 的映射共有( )种。
25、素元素的定义为( )。
二.计算题1.若a>b>c>0,且a+b+c=1,求(1)、2abc 的极大值。
(2)a ×b ×c=1, 求2a+b+4c 的极小值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、用仿射几何与初等几何两种方法证明以下各题:
(1)过 ABC 的顶点C 做一条直线,与边AB 以及中线AD 分别交于F 及E ,求证AE:ED=2AF:FB
证明1:(初等几何)过B 做CF//BH,并延长AD 交HB 于点G 。
因为CD=DB ,易得四边形CFBH 为平行四边形,从而得到ED=DG ;由平行线分线段成比例,则AE :EG=AF :FB ,又EG=2ED,所以AE:2ED=AF :FB ,即AE:ED=2AF:FB 。
证明2(仿射变换)建立仿射坐标系:A(0,0),B(b,0),C (0,c )则D (b/2,c/2),下面设CF :y=kx+c ,分别求E 和F 的坐标。
因为AB :y=0,从而得到F (-c/k,0),AD :cx-by=0,与CF 联立,得
R G
B
E (bc/(c-kb),c^2/(c-kb))
AF :FB=-c/k ((b+c/k )=-c/(kb+c),AE:ED
=bc/(c-kb):[b/2-bc(c-kb)]=-2c/(kb+c))
所以,AE:ED=2AF:FB
(2)(梅耐劳斯定理)设L ,N ,M 分别在∆ABC 的边AB,AC,BC(或延长线)上,求证:L ,N ,M 三点共线的充要条件是1AL BM CM LB MC MA
⋅⋅= 证明:如图,建立仿射坐标系:以BC 为x 轴,以BA 为y 轴,B (0,0),
C (a ,0),A (0,b ),
00(,0),(0,)M x N y ,则直线AC 的方程为:1x y a b
+=, 00
00000000
00000000
0000000000000000ML 1()()(,)()
(),,()()
()1()
x y N x y ax b y by b y bx ay bx ay ax b y a b y x bx ay y x a AL BM CN ax b y LB y MC x a NA x b y bx ay b y x y x a AL BM CN LB MC NA y x a x b y +=---------====------⋅⋅=⋅⋅=--直线的方程为:,联立上述方程,可求得点坐标为所以,故本题结论得证
(3)已知∆ABC 中,D是BC 边上的中点,G 是AD 上的任一点,连M
C
B
接BG 并延长交AC 于E ,连接并延长交DG,AB于F,求证FE//BC
证明:如图,延长AD至K使得DG=DK,
由于BD=DC,所以四边形BKCG为平行四边形,所以进一步得到FG//BK,KC//GE,在∆ABK和∆AKC中,根据平行线分线段成比例知:
,,//AF AG AE AG AF AE FE BC FB GK EC GK FB EC
==,从而所以
2、利用“圆的仿射变换像是椭圆”这一结论,试将与圆有关的一些结论移植到椭圆上去,并给出证明
K C
B
,,22
2222
22,
222,,,2
,21(0)1(0),OAB O A a O A a 12OAB OA B x y a b ab a b
x y a b a b
x x x y a y y
a S S a ππ∆∆+=>>+=>>⎧=+=∆⎨=⎩===椭圆的面积是证明:设椭圆方程:,则其经过仿射变换,对应图形为圆椭圆内的各定点的坐标为(0,0),(,0),B(0,b),圆中对应的三角形顶点
坐标为(0,0),(,0),B(0,a)
椭圆的面积圆的面积所以,即椭圆的ab π面积为。
