常州市教育局直属义务教育学校轮岗交流教师基数统计表
2024-2025学年江苏省常州市实验中学、二十四中学等学校八年级(上)期中数学试卷(含答案)

2024-2025学年常州市实验中学、二十四中学等学校八年级(上)期中数学试卷一、选择题:本题共8小题,每小题3分,共24分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.下面四幅作品分别代表二十四节气中的“立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是( )A. B. C. D.2.下列各组数据为勾股数的是( )A. 1,2,3B. 1, 3,2C. 9,40,41D. 14,15,133.下列说法错误的是( )A. ±3是9的平方根B. 16的平方根为±4C. 25的平方根为±5D. 负数没有平方根4.如图,AC 和BD 相交于O 点,若OA =OD ,不能证明▵AOB≅▵DOC 的是( )A. AB =DCB. OB =OCC. ∠A =∠DD. ∠B =∠C5.如图,在△ABC 中,PM 、QN 分别是线段AB 、AC 的垂直平分线,若∠BAC =110°,则∠PAQ 的度数是( )A. 40°B. 50°C. 60°D. 70°6.如图,在ΔABC 中,已知CD 是AB 边上的高线,BE 平分∠ABC ,交CD 于点E ,BC =5,DE =2,则ΔBCE的面积等于( )A. 5B. 6C. 8D. 107.如图,▵ABD和▵BCD都是边长为2的等边三角形,点E,F分别在边AB,AD上,将▵AEF沿直线EF折叠,点A恰好落在边BC的中点G处,则AF的长度是( )A. 1B. 74C. 32D. 538.如图,点A是射线OM上一个定点,点B是射线ON上的一个动点,OM⊥ON,以线段OB为边在ON右侧作等边三角形,以线段AB为边在AB上方作等边三角形,连接CD,随点B的移动,下列说法中正确的是( )①▵BOA≌▵BDC;②∠ODC=150∘;③直线CD与射线OM所夹的锐角的度数不变;④随点B的移动,线段CD的值逐渐增大.A. ①②B. ①②③C. ①②④D. ①②③④二、填空题:本题共10小题,每小题3分,共30分。
常教人200752号

常教人〔2007〕52号关于公布沈亚东等673人具备中学高级教师资格的通知各辖市(区)教育局(教育文体局、社会事业局)、局属各单位及有关学校:接常州市人事局常人职〔2007〕76号文件,沈亚东等673人经常州市中学教师高级专业技术资格评审委员会评审,已具备中学高级教师资格(名单附后),现将名单公布。
上述人员的高级专业技术资格从2007年8月3日起算。
二〇〇七年十一月十五日主题词:教师职称通知常州市教育局办公室2007年11月19日印发附名单:中学高级教师(共673人):江苏省常州高级中学沈亚东、任小庆、管凌云、胡静常州西藏民族中学崔夕凤常州外国语学校赵敏芝、李雪彬、倪爱平、蒋晓峰吕秋溪常州市正衡中学尹雪霞、杜娟花常州市同济中学张克荣常州市田家炳实验中学姜亚东、汪明、许波勤、周存军戴慧、郑惠娟、陈晓鹏常州市市北实验初级中学李梅先、侯亚芳、薛惠娟常州市实验小学周旸、曲晓红、陆春燕、冯茹霞丁国芳、杨静娟、周红、潘勤华郝慧、陈慧华常州市实验初级中学王德文、沈帆、丁燕、谢敏常州市清潭中学陈冬娣、冯秋萍、陈九梅、王翔江芳、郑建琴、张锡琴、丁文黎王蕾、窦有志常州市聋哑学校徐鸿冰、杨颜华常州市丽华中学钱红武、于德娜、徐秋月、秦香娟常州市蓝天实验学校许晓曙、许中兴常州市兰陵中学储红仙、陈祥凤、徐建远、程文彬常州市局前街小学丁轶敏、李娜、邓方红、马蕙吕战亚、曹之杰常州市教育信息中心李冬梅常州市花园中学刘慧娟、王兴华、蔡留娣、张霞王秀芬、周炜常州市红溪实验幼儿园徐璋莉常州市电化教育馆华泽峰常州市第一中学梁修安、程代军、赵志清、何华周瑞平常州市第五中学曹莉婷、丁庆云、顾美华、汪洋史晓瑾、俞丽芬、肖志民、季宁常州市第三中学李文伟常州市第三职业高级中学刘彩凤、杭国金、朱勤、李新常州市第二中学徐蕾、梅润清、陆萍、蒋峰艳张华、李琴、许冰常州市第二实验小学朱丽萍、高鸣鸿、赵菊玉、马美南张林、蒋旭英、梁小红常州市第二十四中学赵军、戴黎军、谢鹏、赵敏慧常州市翠竹中学朱学勤常州市朝阳中学王梅、朱福、李高峰常州市北郊中学杭佳楣、徐晶磊、邓兆华、王小琴刘莹、金伟清、邰玉韦、吴晓波常州市北环中学蒋丽华、蔡忠军、丁志芬、宋宝珊陈广余、李承送、高志平、张海涛常州旅游学校丁皓、王劲、仇献忠、杜月红沈凤君常州刘国钧高等职业技术学校毛平、姜丹、朱静波、傅旭红黄小璜、沈凤琴、张小谋、孙琳张伟峰、刘琦华常州市戚墅堰先行小学钱卫文常州市戚墅堰实验中学孙瑾常州市潞城中学章建国常州市青龙中学尹亚萍、田先明常州市青龙中心小学徐卫琦常州市浦前中心小学张惠芬常州市解放路小学缪亚芬、潘晨阳、吴明珠常州市雕庄中学彭皓常州市第八中学李久和常州市翠竹新村小学张岭、尹静、周志萍常州市博爱小学巫惠群、韦晶、莫东英常州市北郊小学陆梅芳常州市北环路小学朱丽芬、任洁、张静虹江苏省武进职业高级中学谢莉琴、王险峰、何伟明、符爱萍江苏省武进西林职业高级中学施银燕、徐敏莉、秦建宇、吴文杰宣丽琴、李巧娣、钱华、姚强周月蓉江苏省武进高级中学周彩珠、陆静芬、蒋惠良、贺建刚王芳、杨丽芳、陈书俊江苏省前黄高级中学郝干伟、陈中奇、张雷、顾文明马莉莉、朱劭晨、顾亚玉、唐文洁管黎平、杨鸿斌、吴忠波江苏省奔牛高级中学戴亚军、李平、陈伟常州市武进区邹区中心小学周丽媛、朱小砂常州市武进区政平小学吴静波常州市武进区郑陆中心小学邱金兰、周刚常州市武进区郑陆幼儿园夏历芳常州市武进区郑陆初级中学刘玉峰、唐勇常州市武进区寨桥初级中学魏丽芬、蒋晓鞠、邵震宇常州市武进区运村初级中学顾益平常州市武进区育才职业中学王维群、陆文君、李珊珊常州市武进区遥观中心小学戈彩萍、戚伯萍、周桂芳、宣桃芬常州市武进区遥观初级中学钱英姿、梅建芳常州市武进区淹城初级中学陈英常州市武进区雪堰中心小学李向红常州市武进区雪堰初级中学王小玉常州市武进区星辰实验学校曹叶娟、梁万兵、刘玉兰、花丽娟常州市武进区星辰实验学校汤荣斌、毛秋娟、戴金龙常州市武进区夏溪中心小学王玉华常州市武进区泰村实验学校王霞常州市武进区三河口中学沈智瑜、汤亚芳、张丽群、殳妤岚常州市武进区三河口小学杨剑英、王丽芳常州市武进区前黄实验学校徐文娟、杨志明常州市武进区前黄初级中学朱红惠常州市武进区潘家中心小学杨丽娟、蒋丽、张良、周黎洪常州市武进区潘家初级中学盖秋芳、吴梅育常州市武进区牛塘初级中学高爱武、沈兰芳常州市武进区南宅初级中学承志渊、王志琴、承博渊、杨乐民陈宏常州市武进区南夏墅中心小学周小芬、马祥美常州市武进区鸣凰中学杨维明、张菊、杨玲瑾、吴建新薛文彬、王成常州市武进区鸣凰中心小学陈建伟常州市武进区马杭中心小学蒋素芬、王红梅、周小萍、杨筱艳常州市武进区马杭初级中学壮旭东、姚静霞常州市武进区洛阳中学李成荣、许虹、杨小波、刘海燕常州市武进区洛阳中心小学邓瑞芳常州市武进区卢家巷实验学校邓耀琴、卢波常州市武进区礼嘉中学吴业庭、刘春根常州市武进区礼嘉中心小学邵小芳常州市武进区礼河实验学校吴留珍、潘红梅常州市武进区九里初级中学李明正、夏忠新常州市武进区焦溪初级中学徐建华、顾新华、李燕云、吴红亚周惠华常州市武进区剑湖初级中学祁玉琴、吴彩虹常州市武进区嘉泽初级中学周建琴、商战军常州市武进区机关幼儿园刘尧常州市武进区湟里中心小学刘伟莉常州市武进区湟里高级中学钱文良常州市武进区湟里初级中学薛国春、金文华、储正伟常州市武进区湖塘中心幼儿园裴文娟常州市武进区湖塘实验初级中学巢浩云、杨娴、秦燕、梅建芬常州市武进区湖塘桥中心小学孟亦萍、马伟国、龚小鹰、张亚锋钱国芬、宋志英、唐英、周美娟庄惠芬常州市武进区湖塘桥实验小学蒋惠琴、黄炎常州市武进区湖塘桥初级中学周红梅、周建中、管菊芳、郭曙叶蓉晖、林卫青、刘静亚、李建伟戴国伟、刘玉敏、朱小红、宋玉珍裴阿良、周玉芬常州市武进区厚余初级中学邢亚春常州市武进区横山桥中学周玉建、王延峰、赵洁、陆建洪常州市武进区横山桥中心小学周月萍常州市武进区横林中学王哲、查君蕾常州市武进区横林中心小学单芙玉、徐敏怡常州市武进区横林实验小学邵莉萍、易敏常州市武进区芙蓉初级中学张国民、莫建军常州市武进区东青实验学校张丽玉、姚军华常州市武进区东安初级中学陈玉梅、戴国兴、路正兴、张卫明常州市武进区戴溪初级中学陆立新常州市武进区崔桥小学孙明丽、徐国荣常州市武进区崔桥初级中学丁雪珍常州市武进区成章小学朱爱芳、徐文娟、朱国洪常州市武进区成章初级中学薛炜、王甦、韩文娟常州市武进区成人教育培训中心蒋杏芬、张晓燕、钱瑾红常州市武进区漕桥中心小学金云霞、胥志东常州市武进区漕桥初级中学陈景宏、王建英常州市武进区卜弋中心小学江晓燕常州市武进区卜弋初级中学蒋息芳、姜华琴、陈丽萍、何群张宁芳常州市武进区奔牛实验幼儿园巢燕常州市武进区奔牛实验小学范丽萍常州市武进区奔牛初级中学巢丽娟、周峻、叶冬梅、史振宇张志坚常州市武进区坂上幼儿园潘丽洁常州市新桥中学秦菊珍常州市新北区薛家中学徐春凤、贾峻峰常州市新北区新桥中心小学张红梅、韩燕清常州市新北区孝都中学商彩芳、仇亚芳常州市新北区孝都小学周琴秀常州市新北区小河中心小学李忠顺、周立萍常州市新北区西夏墅中心小学殷玉明常州市新北区魏村中学陈昌荣常州市新北区圩塘中学包秀芳常州市新北区泰山小学宣静娴常州市新北区实验中学杨萍、刘仁兴、钱文娟、张爱红常州市新北区三井中心幼儿园茅春雷常州市新北区浦河中学刘建云、巢军英常州市新北区孟河中学汤建芬、孔颖悟常州市新北区孟河中心幼儿园马群敏常州市新北区孟河中心小学王彩群常州市新北区吕墅中学张泰南常州市新北区吕墅幼儿园陈玉华常州市新北区龙虎塘中学蒋瑞琴、柴娟芳、盛文芳常州市新北区龙虎塘中心幼儿园姚建琴常州市新北区百丈中学谈小东常州市小河中学董红方、储岩、周华伟、巢萍仙马文艳常州市西夏墅中学符婉婷、陶志强、钱曙明、金红霞黄秋霞常州市安家中学沈亚黎、王书本常州国际学校汪晓军、孙亚敏常州市永红中心小学刘丽霞常州市西新桥二小徐志彤常州市西林实验学校殷文华、王建瑛、赵建国、齐燕岳贤常州市谭市小学王辉常州市清潭实验小学胡丹凤常州市觅渡桥小学姜晖、洪敏亚常州市怀德苑小学叶斌常州市北港中学张卫国殷雪梅小学周卫星金坛市朱林中学韩菊芳金坛市朱林中心小学丁网青金坛市指前中学焦建忠金坛市职业教育中心李雪琴、窦粉林、霍洪舜、朱夕青贺罗保金坛市直溪中心小学田粉兰金坛市直溪高级中学张建华、黄国强金坛市尧塘中心小学张仁荣、程建华金坛市洮西中学赵金赛金坛市涑渎中学王宛庆金坛市少体校朱生群金坛市金沙高级中学印小英、张清早、史建明、杜永红孔祥贞金坛市金城镇中心小学蒋守成金坛市教育局教研室王志忠金坛市建昌中心小学张立俊金坛市华罗庚实验学校贺勤芳、何瑛、袁雷群、张五芳彭燕梅、郭晓晴、王息英、顾雪松唐辉、于秀成、姜菊蓉、龚爱武贺莉、赵煜、王华金坛市华城实验小学李新梅、黄波、张勇卫金坛市后阳中心小学包建平金坛市河头中学蒋荣春、王松林金坛市河头中心小学虞国俊、徐锁平金坛市河滨小学倪网苟、吴春梅、张吉娣、杨月凤周夕中、陈杏芳、朱小芳金坛市第一中学冯菊英、陈金平、汤红卫、徐青娥曹建国、洪秀华、于文忠金坛市第五中学盛春梅、徐蓉芬、王建良、汤炳述金坛市第四中学高雪梅、葛水英、阚和明、蔡爱芳王旭霞、杨玉梅、管松金坛市第三中学吴双美、刘俊、张锁庆、黄小卫张仁俊、汤婷婷、郑忠美、杨建国王建军、宫爱梅、李慧珍、彭留英金坛市第二中学冯菊芳、王秀珍、袁平、王玉芳王霞、李朵朵、陈坚梅、顾红军金坛市城西中心小学吴惠娟金坛市朝阳小学秦晓云、田洪军、施月琴金坛市常胜小学祝文祥、尹文琴、杨蓉凤、周俊华金坛市白塔中学耿玉华金坛实验幼儿园蔡伟、袁英江苏省华罗庚中学李贵莲、蒋润强溧阳市竹箦中学陈德华、黄永才、陆新华、张久耕蒋春玲、刘昌友溧阳市竹箦中心小学孙正香溧阳市周城中学彭达、朱正兴溧阳市永和小学张世生溧阳市燕山中学宋国庆、吴小兵、项菊萍、王田方陈金晶、卢云娟、芮曙、周文娟李幸福、李坚兰、刘小妹、黄科伟郭珺溧阳市新昌中学潘利平、周洪炳溧阳市新昌中心小学周田贇溧阳市文化小学王梅兰、沈乐涯、杨一波、许红萍高金花、苏瑜、蓝秀一、狄国琴溧阳市天目湖实验学校汪国初、司志君溧阳市汤桥初级中学邢国平溧阳市实验幼儿园金玉琴溧阳市实验小学杨云亮、童春芳、马瑛琴、陶春萍孙玉梅、陈翠萍、史红、陈蓉杨志斌、王云南、方莉华溧阳市实验初级中学张跃生、沈琴、彭娟、赵建华溧阳市社渚中心小学吴汉平、费成义溧阳市社渚初级中学虞永水、潘耕幸、虞爱云溧阳市少体校吕志祥溧阳市上兴中学蒋敏溧阳市上沛中学冯贵伢、蒋筱芸溧阳市上黄中学杨双庚溧阳市上黄中心小学黄丽君、蒋法平溧阳市清安小学王小卫溧阳市前马初级中学谢海春溧阳市南门街小学王欣瑾、方建华溧阳市南渡中心小学李莉溧阳市南渡高级中学杭红娟、朱阿龙、黄可平、李松法黄晓勤、薛锡良溧阳市南渡初级中学陈建新溧阳市溧城中心小学潘婕溧阳市溧城镇平陵小学马坤明溧阳市昆仑小学王红兵、邵菊华、湛伟俊、蒋梅蓉史燕君溧阳市后六初级中学薛盘才、梁惠珍溧阳市河口小学沈国清溧阳市河口初级中学毛平荣溧阳市光华高级中学周文俊、史永红溧阳市光华初级中学曹新溧阳市古渎初级中学徐红香溧阳市第五中学潘惠英、陈双庆溧阳市第四中学谢茂芳溧阳市第三中学陈晟、金尚平、周文跃、蒋学平吴小平、张晓飞溧阳市第三职业高级中学王远捷溧阳市第六中学孙菊岚溧阳市第二中学濮云娣、周美俊、李敏、马秀华溧阳市戴埠中心小学朱春梅溧阳市戴埠初级中学许庚保溧阳市埭头中学史小康、葛燕芳、马伟清溧阳市城南小学庄亚云、贺志荣、郜立青溧阳市别桥中学吕尚志溧阳第二职业高级中学王志伟、张志明江苏省溧阳中学罗志强、许六三、尤丽群罗宏伟、陈俊林、彭卫清江苏省溧阳职业教育中心史春华、严爱琴、史惠芬。
2011常州非义务教育绩效工资管理办法

2011常州非义务教育绩效工资管理办法附件:常州市教育局直属非义务教育事业单位及人员绩效考核指导意见依据市人力资源和社会保障局、市财政局《关于印发〈常州市其他事业单位绩效工资实施办法〉的通知》(常人社发〔2011〕218号)、《关于贯彻我市公共卫生与基层医疗卫生和其他事业单位绩效工资实施办法中若干问题的处理意见》(常人社发〔2011〕219号)文件精神,为推进局属非义务教育事业单位顺利实施绩效工资,特制订本指导意见。
一、指导思想以党中央、国务院关于事业单位实施绩效工资三步走的决策为指导,以市人社局、财政局关于其他事业单位实施绩效工资的文件为依据,着力构建符合学校发展规律和教师职业特点的导向明确、标准科学、体系完善的学校及教师绩效考核评价制度,调动教师教书育人的积极性、主动性和创造性,促进学校办学水平的全面提高,推动常州教育事业高位均衡可持续发展。
二、基本原则(一)分类考核原则。
非义务教育学校及校外教育机构的绩效考核依据各自特点分别实施。
工作人员的绩效考核按照专业技术、管理、工勤岗位及等级分类实施。
(二)激励导向原则。
建立健全科学有效的激励约束机制,将绩效考核结果作为财政拨款、机构主要负责人和工作人员收入待遇的主要依据。
(三)客观公正原则。
注重考核过程的透明度和绩效考核结果的信度与效度,确保公开、公平、公正。
(四)公益性原则。
突出非义务教育学校和校外教育机构的公益性质,坚持绩效考核与社会效益、岗位职责、工作业绩和实际贡献相挂钩。
(五)可操作原则。
绩效考核工作要因地制宜,考核指标与方法应科学合理,力求客观、适宜、有效、可行。
三、考核范围按国家规定执行事业单位岗位绩效工资制度的局属非义务教育学校、非校事业单位及其在编在岗的人员。
四、考核内容(一)学校绩效主要考核学校规模、发展规划与组织实施、课程建设与教学改革、学校文化建设、师资队伍建设、学生发展、德育工作、校企合作与社会服务等方面的实绩。
1.发展规划。
小学教师交流轮岗方案通用版

小学教师交流轮岗方案通用版(实用版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的实用范文,如学习资料、英语资料、学生作文、教学资源、求职资料、创业资料、工作范文、条据文书、合同协议、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this shop provides various types of practical sample essays, such as learning materials, English materials, student essays, teaching resources, job search materials, entrepreneurial materials, work examples, documents, contracts, agreements, other essays, etc. Please pay attention to the different formats and writing methods of the model essay!小学教师交流轮岗方案通用版小学教师交流轮岗方案通用版(7篇)在交流轮岗中应该优先保障教师发展,对交流轮岗教师在考核晋升中优先考虑、在津贴待遇中优先保障、在成长需求中优先满足,充分调动教师交流积极性,解决教师‘后顾之忧’。
江苏省常州市教育会业水平监测2024-2025学年九年级数学第一学期开学联考模拟试题【含答案】

江苏省常州市教育会业水平监测2024-2025学年九年级数学第一学期开学联考模拟试题题号一二三四五总分得分A 卷(100分)一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、(4分)一个多边形为八边形,则它的内角和与外角和的总度数为()A .1080°B .1260°C .1440°D .540°2、(4分)五箱梨的质量(单位:千克)分别为:18,20,21,18,19,则这五箱梨质量的中位数和众数分是()A .20和18B .20和19C .18和18D .19和183、(4分)甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数都为8.8环,方差分别为20.63S =甲,20.51S =乙,2S 丙=0.48,2S 丁=0.45,则四人中成绩最稳定的是()A .甲B .乙C .丙D .丁4、(4分)正方形具有而菱形不一定具有的性质是()A .四边相等B .对角线相等C .对角线互相垂直D .对角线互相平分5、(4分)如图,矩形ABCD 中,AB=8,BC=4,P ,Q 分别是直线AB ,AD 上的两个动点,点E 在边CD 上,2DE =,将DEQ ∆沿EQ 翻折得到FEQ ∆,连接PF ,PC ,则PF PC +的最小值为()A .2-B .8C .10D .26、(4分)有下列说法:①平行四边形既是中心对称图形,又是轴对称图形;②正方形有四条对称轴;③平行四边形相邻两个内角的和等于180︒;④菱形的面积计算公式,除了“=菱形S 底×高”之外,还有“=菱形S 两对角线之积”;⑤矩形和菱形均是特殊的平行四边形,因此具有平行四边形的所有性质.其中正确的结论的个数有()A .1B .2C .3D .47、(4分)已知a <b ,下列不等关系式中正确的是()A .a+3>b+3B .3a >3b C .﹣a <﹣b D .﹣2a >﹣2b 8、(4分)下列图案既是轴对称图形,又是中心对称图形的是()A .4个B .3个C .2个D .1个二、填空题(本大题共5个小题,每小题4分,共20分)9、(4分)已知一次函数y=mx+n(m≠0,m,n 为常数),x 与y 的对应值如下表:x ﹣2﹣10123y ﹣101234那么,不等式mx+n<0的解集是_____.10、(4分)如图,直线243y x =+与x 轴、y 轴分别交于点A 和点B ,点C ,D 分别为线段AB ,OB 的中点,点P 为OA 上一动点,PC PD +值最小时,点P 的坐标为______.11、(4分)如果向量AD BC =,那么四边形ABCD 的形状可以是_______________(写出一种情况即可)12、(4分)如图△ABC 中,∠BAC=90°,将△ABC 绕点A 按顺时针方向旋转一定角度得到△ADE,点B 的对应点D 恰好落在BC 边上,若,∠B=60∘,则CD 的长为____13、(4分)在“童心向党,阳光下成长”的合唱比赛中,30个参赛队的成绩被分为5组,第1~4组的频数分别为2,10,7,8,则第5组的频率为________.三、解答题(本大题共5个小题,共48分)14、(12分)暑假期间,两名教师计划带领若干名学生去旅游,他们联系了报价均为每人500元的两家旅行社.经协商,甲旅行社的优惠条件是:两名教师全额收费,学生都按七折收费;乙旅行社的优惠条件是:教师、学生都按八折收费.请你帮他们选择一下,选哪家旅行社比较合算.15、(8分)如图,在平行四边形ABCD 中,点E 是对角线AC 上一点,连接BE 并延长至F ,使EF =BE .求证:DF ∥AC .16、(8分)我市遗爱湖公园内有一块四边形空地,如图所示,景区管理人员想在这块空地上铺满观赏草坪,需要测量其面积.经技术人员测量,,米,米,米,米.(1)请你帮助管理人员计算出这个四边形对角线的长度;(2)请用你学过的知识帮助管理员计算出这块空地的面积.17、(10分)某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:甲1061068乙79789经过计算,甲进球的平均数为8,方差为3.2.(1)求乙进球的平均数和方差;(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?18、(10分)在研究反比例函数y =﹣1x 的图象时,我们发现有如下性质:(1)y =﹣1x 的图象是中心对称图形,对称中心是原点.(2)y =﹣1x 的图象是轴对称图形,对称轴是直线y =x ,y =﹣x .(3)在x <0与x >0两个范围内,y 随x 增大而增大;类似地,我们研究形如:y =﹣12x -+3的函数:(1)函数y =﹣12x -+3图象是由反比例函数y =﹣1x 图象向____平移______个单位,再向_______平移______个单位得到的.(2)y =﹣12x -+3的图象是中心对称图形,对称中心是______.(3)该函数图象是轴对称图形吗?如果是,请求出它的对称轴,如果不是,请说明理由.(4)对于函数y =3224x x ---,x 在哪些范围内,y 随x 的增大而增大?B 卷(50分)一、填空题(本大题共5个小题,每小题4分,共20分)19、(4分)=__.20、(4分)函数2(1)1y x =-+向右平移1个单位的解析式为__________.21、(4分)若关于x 的方程21122x mx x +-=++有增根,则m 的值为________.22、(4分)如图,一次函数y=-2x+2的图象与轴、轴分别交于点、,以线段为直角边在第一象限内作等腰直角三角形ABC ,且,则点C 坐标为_____.23、(4分)若不等式组+0122x a x x ≥⎧⎨->-⎩有且仅有3个整数解,则a 的取值范围是___________.二、解答题(本大题共3个小题,共30分)24、(8分)某学校为改善办学条件,计划采购A 、B 两种型号的空调,已知采购3台A 型空调和2台B 型空调,需费用39000元;4台A 型空调比5台B 型空调的费用多6000元.(1)求A 型空调和B 型空调每台各需多少元;(2)若学校计划采购A 、B 两种型号空调共30台,且A 型空调的台数不少于B 型空调的一半,两种型号空调的采购总费用不超过217000元,该校共有哪几种采购方案?(3)在(2)的条件下,采用哪一种采购方案可使总费用最低,最低费用是多少元?25、(10分)计算:(1;(2)+26、(12分)哈市某专卖店销售某品牌服装,设服装进价为80元,当每件服装售价为240元时,月销售为200件,该专卖店为提高经营利润,准备采取降价的方式进行促销,经市场调查发现:当每件价格每下降10元时,月销售量就会增加20件,设每件服装售价为x(元),该专卖店的月利润为y(元).(1)求出y 与x 的函数关系式(不要求写出x 的取值范围);(2)该专卖店要获得最大月利润,售价应定为每件多少元?最大利润是多少?参考答案与详细解析一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、C 【解析】直接利用多边形的内角和与外角和定义分析得出答案.【详解】八边形的内角和为:(8﹣2)×180°=1080°,八边形的外角和为:360°,故八边形的内角和与外角和的总度数为:1440°.故选C .本题考查了多边形的内角和与外角和,正确把握相关定义是解题的关键.2、D 【解析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.【详解】解:从小到大排列此数据为:1、1、19、20、21,数据1出现了三次最多,所以1为众数;19处在第3位是中位数.∴本题这组数据的中位数是19,众数是1.故选:D .本题属于基础题,考查了确定一组数据的中位数和众数的能力.要明确定义,一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项,注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.3、D【解析】根据方差的意义进行判断.【详解】解:∵2S 丁<2S 丙<2S 乙<2S 甲∴四人中成绩最稳定的是丁.故选:D .本题考查了方差:方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.4、B 【解析】观察四个选项,分别涉及了四条边和对角线,我们应对照正方形和菱形边及对角线的性质,找出不同即可.【详解】正方形和菱形的四条边均相等,每条对角线均平分一组对角,正方形两条对角线相等且互相垂直平分,菱形对角线互相垂直且平分,但不相等.故选B.本题考查了正方形和菱形性质的知识,解决本题的关键是熟练掌握正方形和菱形的性质.5、B 【解析】作点C 关于AB 的对称点H ,连接PH ,EH ,由已知求出CE =6,CH =8,由勾股定理得出EH ,由SAS 证得△PBC ≌△PBH ,得出CP =PH ,PF +PC =PF +PH ,当E 、F 、P 、H 四点共线时,PF +PH 值最小,即可得出结果.【详解】解:作点C 关于AB 的对称点H ,连接PH ,EH ,如图所示:∵矩形ABCD 中,AB =8,BC =4,DE =2,∴CE =CD−DE =AB−DE =6,CH =2BC =8,∴EH ==10,在△PBC 和△PBH 中,90BC BH PBC PBH PB PB ⎧⎪∠∠︒⎨⎪⎩====,∴△PBC ≌△PBH (SAS ),∴CP =PH ,∴PF +PC =PF +PH ,∵EF =DE =2是定值,∴当E 、F 、P 、H 四点共线时,PF +PH 值最小,最小值=10−2=8,∴PF +PD 的最小值为8,故选:B .本题考查翻折变换、矩形的性质、全等三角形的判定与性质、勾股定理等知识,解题的关键是学会利用轴对称,根据两点之间线段最短解决最短问题.6、C 【解析】根据特殊平行四边形的性质即可判断.【详解】①平行四边形既是中心对称图形,不是轴对称图形,故错误;②正方形有四条对称轴,正确;③平行四边形相邻两个内角的和等于180︒,正确;④菱形的面积计算公式,除了“=菱形S 底×高”之外,还有“=菱形S 12两对角线之积”,故错误;⑤矩形和菱形均是特殊的平行四边形,因此具有平行四边形的所有性质,正确.故②③⑤正确,选C 此题主要考查特殊平行四边形的性质,解题的关键是熟知特殊平行四边形的特点与性质.7、D【解析】根据不等式的性质逐一判断即可.【详解】A :不等式两边都加3,不等号的方向不变,原变形错误,故此选项不符合题意;B :不等式两边都乘以3,不等号的方向不变,原变形错误,故此选项不符合题意;C :不等式两边都乘﹣1,不等号的方向改变,原变形错误,故此选项不符合题意;D 不等式两边都除以﹣2,不等号的方向改变,原变形正确,故此选项符合题意;故选:D .本题主要考查了不等式的性质,熟记不等式在两边都乘除负数时,不等式符号需要改变方向是解题关键.8、B 【解析】轴对称图形的定义:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形;中心对称图形的定义:一个图形绕一点旋转180°后能够与原图形完全重合即是中心对称图形.【详解】解:选项B 只是轴对称图形,其它三个均既是轴对称图形,又是中心对称图形,故选B .本题考查轴对称图形与中心对称图形的定义,本题属于基础应用题,只需学生熟练掌握轴对称图形与中心对称图形的定义,即可完成.二、填空题(本大题共5个小题,每小题4分,共20分)9、x<﹣1【解析】由表格得到函数的增减性后,再得出0y =时,对应的x 的值即可.【详解】当1x =-时,0y =,根据表可以知道函数值y 随x 的增大而增大,故不等式0mx n +<的解集是1x <-.故答案为:1x <-.此题考查了一次函数与一元一次不等式,认真体会一次函数与一元一次方程及一元一次不等式之间联系.理解一次函数的增减性是解决本题的关键.10、(-32,0)【解析】根据一次函数解析式求出点A 、B 的坐标,再由中点坐标公式求出点C 、D 的坐标,根据对称的性质找出点D′的坐标,结合点C 、D′的坐标求出直线CD′的解析式,令y=0即可求出x 的值,从而得出点P 的坐标.【详解】作点D 关于x 轴的对称点D′,连接CD′交x 轴于点P ,此时PC+PD 值最小,如图所示.令y=23x+4中x=0,则y=4,∴点B 的坐标为(0,4);令y=23x+4中y=0,则23x+4=0,解得:x=-6,∴点A 的坐标为(-6,0).∵点C 、D 分别为线段AB 、OB 的中点,∴点C (-3,1),点D (0,1).∵点D′和点D 关于x 轴对称,∴点D′的坐标为(0,-1).设直线CD′的解析式为y=kx+b ,∵直线CD′过点C (-3,1),D′(0,-1),∴有232k b b -+-⎧⎨⎩==,解得:423k b --⎧⎪⎨⎪⎩==,∴直线CD′的解析式为y=-43x-1.令y=-43x-1中y=0,则0=-43x-1,解得:x=-32,∴点P 的坐标为(-32,0).故答案为:(-32,0).本题考查了待定系数法求函数解析式、一次函数图象上点的坐标特征以及轴对称中最短路径问题,解题的关键是找出点P 的位置.11、平行四边形【解析】根据相等向量的定义和四边形的性质解答.【详解】如图:∵AD uuu v =BC ,∴AD ∥BC ,且AD=BC ,∴四边形ABCD 的形状可以是平行四边形.故答案为:平行四边形.此题考查了平面向量,掌握平行四边形的判定定理(有一组对边平行且相等的四边形是平行四边形)是解题的关键.12、4【解析】先在直角三角形ABC 中,求出AB ,BC ,然后判断出BD=AB=4,简单计算即可【详解】在Rt △ABC 中∠B=60°,∴AB=4,BC=8,由旋转得,AD=AB ,∵∠B=60°,∴BD=AB=4,∴CD=BC−BD=8−4=4故答案为:4此题考查含30度角的直角三角形,旋转的性质,解题关键在于求出AB ,BC 13、0.1.【解析】直接利用频数÷总数=频率,进而得出答案.【详解】解:∵30个参赛队的成绩被分为5组,第1~4组的频数分别为2,10,7,8,∴第5组的频率为:(30-2-10-7-8))÷30=0.1.故答案为:0.1.本题考查频数与频率,正确掌握频率求法是解题关键.三、解答题(本大题共5个小题,共48分)14、①当两名家长带领的学生少于4人时,应该选择乙旅行社;②当两名家长带领的学生为4人时,选择甲、乙两家旅行社都一样;③当两名家长带领的学生多于4人时,应该选择甲旅行社.【解析】(1)根据甲旅行社的收费=两名家长的全额费用+学生的七折费用,可得到y 1与x 的函数关系式;再根据乙旅行社的收费=两名家长的八折费用+学生的八折费用,可得到y 2与x 的函数关系式;(2)首先分三种情况讨论:①y 1>y 2,②y 1=y 2,③y 1<y 2,针对每一种情况,分别求出对应的x 的取值范围,然后比较哪种情况下选谁更合适,即可判断选择哪家旅行社.解答:【详解】解:设x 名学生,则在甲旅行社花费:y 1=2500500x 0.7350x 1000⨯+⨯=+,在乙旅行社的花费:y 2=()x 25000.8400x 800+⨯⨯=+,当在乙旅行社的花费少时:y 1>y 2350x 1000400x 800+>+,解得x 4<;在两家花费相同时:y 1=y 2350x 1000400x 1800+=+,解得x 4=;当在甲旅行社的花费少时:y 1<y 2350x 1000400x 800+<+,解得x 4>.综上,可得①当两名家长带领的学生少于4人时,应该选择乙旅行社;②当两名家长带领的学生为4人时,选择甲、乙两家旅行社都一样;③当两名家长带领的学生多于4人时,应该选择甲旅行社.本题考查了一次函数的应用:根据题意列出一次函数关系式y=kx+b(k≠0),然后比较函数值的大小得到对应的x 的取值范围,从而确定省钱的方案.15、见解析;【解析】连接BD 交AC 于点O ,根据平行四边形的性质证明即可.【详解】连接BD 交AC 于点O .∵四边形ABCD 是平行四边形,∴BO =OD ,而BE =EF ,∴OE ∥DF ,即AC ∥EF .本题考查了平行四边形的性质,关键是根据平行四边形的性质和三角形中位线定理解答.16、(1)25米;(2)234米2【解析】(1)连接,利用勾股定理求出AC 即可;(2)利用勾股定理的逆定理证明∠ADC =90°,计算两个直角三角形面积即可解决问题【详解】(1)连接.在中,由勾股定理得:(米).(2)在中,∵,∴.∴(米2).本题考查勾股定理及其逆定理的应用,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.17、(1)乙平均数为8,方差为0.8;(2)乙.【解析】(1)根据平均数、方差的计算公式计算即可;(2)根据平均数相同时,方差越大,波动越大,成绩越不稳定;方差越小,波动越小,成绩越稳定进行解答.【详解】(1)乙进球的平均数为:(7+9+7+8+9)÷5=8,乙进球的方差为:15[(7﹣8)2+(9﹣8)2+(7﹣8)2+(8﹣8)2+(9﹣8)2]=0.8;(2)∵二人的平均数相同,而S 甲2=3.2,S 乙2=0.8,∴S 甲2>S 乙2,∴乙的波动较小,成绩更稳定,∴应选乙去参加定点投篮比赛.本题考查了方差的定义:一般地设n 个数据,x 1,x 2,…x n 的平均数为x ,则方差S 21n =[x 1x -)2+(x 2x -)2+…+(x n x -)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.也考查了平均数.18、(1)右,2,上,1;(2)(2,1);(1)是轴对称图形,对称轴是:y =x+1和y =﹣x+2;(4)x<2或x>2.【解析】(1)根据图象平移的法则即可解答;(2)根据平移的方法,函数y=﹣1x的中心原点平移后的点就是对称中心;(1)图象平移后与原来的直线y=x和y=-x平行,并且经过对称中心,利用待定系数法即可求解;(4)把已知的函数y=3224xx---变形成的形式43x-22--,类比反比例函数性质即可解答.【详解】解:(1)函数y=﹣12x-+1图象是由反比例函数y=﹣1x图象向右平移2个单位,再向上平移1个单位得到的.故答案为:右2上1.(2)y=﹣12x-+1的图象是中心对称图形,对称中心是(2,1).故答案为:(2,1).(1)该函数图象是轴对称图形.∵y=﹣1x的图象是轴对称图形,对称轴是直线y=x,y=﹣x.设y=﹣12x-+1对称轴是y=x+b,把(2,1)代入得:1=2+b,∴b=1,∴对称轴是y=x+1;设y=﹣12x-+1对称轴是y=﹣x+c,把(2,1)代入得:1=﹣2+c,∴c=2.∴对称轴是y=﹣x+2.故答案为:y=x+1和y=﹣x+2.(4)对于函数y=3224xx---,变形得:y=3224xx---=3(2)82(2)xx---=43x-22--,则其对称中心是(2,32-).则当x<2或x>2时y随x的增大而增大.故答案为:x <2或x >2本题考查了反比例函数的图象与性质,以及待定系数法求函数的解析式,正确理解图象平移的方法是关键.一、填空题(本大题共5个小题,每小题4分,共20分)【解析】分析:先将二次根式化为最简,然后合并同类二次根式即可.详解:原式点睛:本题考查了二次根式的加减运算,解答本题得关键是掌握二次根式的化简及同类二次根式的合并.20、22()1y x =-+或245y x x =-+【解析】根据“左加右减,上加下减”的规律即可求得.【详解】解:∵抛物线()211y x =-+向右平移1个单位∴抛物线解析式为()221y x =-+或245y x x =-+.本题考查的是二次函数,熟练掌握二次函数的平移是解题的关键.21、3-;【解析】先将m 视为常数求解分式方程,得出方程关于m 的解,再根据方程有增根判断m 的值.【详解】21122x mx x +-=++去分母得:2x+1-x-2=m解得:x=m+1∵分式方程有增根∴m+1=-2解得:m=-1故答案为;-1.本题考查解分式方程增根的情况,注意当方程中有字母时,我们通常是将字母先视为常数进行计算,后续再讨论字母的情况.22、(3,1);【解析】先求出点A ,B 的坐标,再判断出△ABO ≌△CAD ,即可求出AD=2,CD=1,即可得出结论;【详解】如图,过点C 作CD ⊥x 轴于D ,令x=0,得y=2,令y=0,得x=1,∴A(1,0),B(0,2),∴OA=1,OB=2,∵△ABC 是等腰直角三角形,∴AB=AC,∠BAC=90°,∴∠BAO+∠CAD=90°,∵∠ACD+∠CAD=90°,∴∠BAO=∠ACD ,∵∠BOA=∠ADC=90°,∴△ABO ≌△CAD ,∴AD=BO=2,CD=AO=1,∴C(3,1);此题考查一次函数综合,解题关键在于作辅助线23、1≤a <2【解析】此题需要首先解不等式,根据解的情况确定a 的取值范围.特别是要注意不等号中等号的取舍.【详解】解:解不等式x+a≥0得:x≥-a ,解不等式1-1x >x-1得:x <1,∵此不等式组有2个整数解,∴这2个整数解为-1,-1,0,∴a 的取值范围是-2<a≤-1.故答案为:1≤a <2.此题考查一元一次不等式组的解法.解题关键在于要注意分析不等式组的解集的确定.二、解答题(本大题共3个小题,共30分)24、(1)A 型空调和B 型空调每台各需9000元、6000元;(2)共有三种采购方案,方案一:采购A 型空调10台,B 型空调20台,方案二:采购A 型空调11台,B 型空调19台,案三:采购A 型空调12台,B 型空调18台;(3)采购A 型空调10台,B 型空调20台可使总费用最低,最低费用是210000元.【解析】分析:(1)根据题意可以列出相应的方程组,从而可以解答本题;(2)根据题意可以列出相应的不等式组,从而可以求得有几种采购方案;(3)根据题意和(2)中的结果,可以解答本题.详解:(1)设A 型空调和B 型空调每台各需x 元、y 元,3239000456000x y x y +⎧⎨-⎩==,解得,90006000x y ⎧⎨⎩==,答:A 型空调和B 型空调每台各需9000元、6000元;(2)设购买A 型空调a 台,则购买B 型空调(30-a )台,()()13029000600030217000a a a a ⎧≥-⎪⎨⎪+-≤⎩,解得,10≤a≤1213,∴a=10、11、12,共有三种采购方案,方案一:采购A 型空调10台,B 型空调20台,方案二:采购A 型空调11台,B 型空调19台,方案三:采购A 型空调12台,B 型空调18台;(3)设总费用为w 元,w=9000a+6000(30-a )=3000a+180000,∴当a=10时,w取得最小值,此时w=210000,即采购A 型空调10台,B 型空调20台可使总费用最低,最低费用是210000元.点睛:本题考查一次函数的应用、一元一次不等式组的应用、二元一次方程组的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用函数和不等式的思想解答.25、()()125【解析】(1)先化简二次根式,再加减;(2)根据平方差公式进行计算.【详解】==;(2)(22835+=-=-=考核知识点:二次根式的运算.掌握运算法则是关键.26、(1)y=−2x 2+840x−54400;(2)售价应定为每件210元,最大利润是33800元.【解析】(1)由题意得到每件服装的利润为x−80元,则可得月销售量为200+2402010x-⨯,再根据月利润等于总销量乘以每件服装的利润即可得到;(2)由(1)得到y=−2x 2+840x−54400经过变形得到y=−2(x−210)2+33800,即可得到答案.【详解】解:(1)每件服装的利润为x−80元,月销售量为200+2402010x-⨯,所以月利润:y=(x-80)⋅(200+2402010x-⨯)=(x−80)(680−2x)=−2x2+840x−54400,所以函数关系式为y=−2x2+840x−54400;(2)y=−2x2+840x−54400=−2(x−210)2+33800所以,当x=210时,y最大=33800.即售价应定为每件210元,最大利润是33800元.答:售价应定为每件210元,最大利润是33800元.本题考查一元二次函数的实际应用,解题的关键是读懂题意,得到等式关系.。
(完整版)教师家访记录表表格
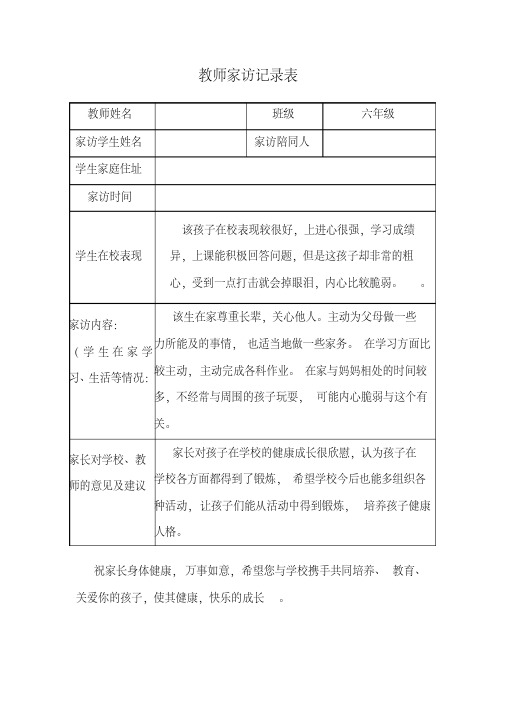
教师姓名班级六年级家访学生姓名家访陪同人学生家庭住址家访时间学生在校表现该孩子在校表现较很好,上进心很强,学习成绩异,上课能积极回答问题,但是这孩子却非常的粗心,受到一点打击就会掉眼泪,内心比较脆弱。
家访内容:(学生在家学习、生活等情况:该生在家尊重长辈,关心他人。
主动为父母做一些力所能及的事情,也适当地做一些家务。
在学习方面比较主动,主动完成各科作业。
在家与妈妈相处的时间较多,不经常与周围的孩子玩耍,可能内心脆弱与这个有关。
家长对学校、教师的意见及建议家长对孩子在学校的健康成长很欣慰,认为孩子在学校各方面都得到了锻炼,希望学校今后也能多组织各种活动,让孩子们能从活动中得到锻炼,培养孩子健康人格。
祝家长身体健康,万事如意,希望您与学校携手共同培养、教育、关爱你的孩子,使其健康,快乐的成长。
教师姓名班级家访学生姓名家访陪同人学生家庭住址家访时间学生在校表现该孩子在校是个有礼貌的孩子,但脾气较暴躁,虽然脑袋灵活,但学习习惯不是很好,比较拖拉。
家访内容:(学生在家学习、生活等情况:)孩子的父母很负责,对孩子的学习抓的很紧,但孩子在生活上不太善于收拾,学习时也总是注意力分散,思想不容易集中,完成作业自觉性不够,需要家长守着。
家长对学校、教师的意见及建议家长希望老师多给孩子鼓励,作业时多盯紧她,家长也会积极配合老师帮助孩子改正缺点,养成良好的学习习惯。
祝家长身体健康,万事如意,希望您与学校携手共同培养、教育、关爱你的孩子,使其健康,快乐的成长。
教师姓名班级家访学生姓名家访陪同人学生家庭住址家访时间学生在校表现该生在校行为规范,能与同学和睦相处,自觉遵守学校及班级规章制度,不足的是该生在课堂上的注意力不够集中,所完成的各科作业字迹较为潦草。
家访内容:(学生在家学习、生活等情况:)该生父母生意较忙,没有时间顾及到孩子的学习,只是把孩子的学习都归咎为老师。
在学习上也显得不够主动,比较好玩,没有进取心。
家长对学校、教师的意见及建议希望在校期间,老师能够更加严格的监督、管理,改掉拖拉的毛病,养成良好的学习习惯,提高学习质量。
轮岗交流方案
轮岗交流方案轮岗交流方案1为了促进基础教育的改革和发展,建立符合我校特点的教师管理制度,促进教育公平和均衡发展,不断提升办学水平和效益,努力办好让人民满意的教育。
经研究,决定建立本校教师轮岗支教交流实施方案。
一、指导思想以“三个代表”重要思想和科学发展观为指导,认真贯彻落实赵化学区教育工作督导组和xx镇政府关于均衡发展教育的精神,以关注每一个学生健康成长为宗旨,以全面推进素质教育、全面提高教育质量为根本任务,立足本校实际,建立和完善教师轮岗支教交流制度,积极推动我校教师轮岗交流工作。
二、基本原则按照“以人为本、统筹兼顾、增强活力、和谐稳定”的工作要求,本着“资源共享、协调发展”的原则,做到三个结合,即:建立教师轮岗交流机制与建立健全科学合理的教师职务晋级和奖惩机制相结合;建立教师轮岗交流机制与弘扬艰苦奋斗、爱岗敬业的师德教育相结合;建立教师轮岗交流机制与确保教育系统安定稳定、推动教育事业持续健康发展相结合。
三、基本情况本校下辖青山、杨寺村小。
青山村小现有五个教学班,学生110余人,教师6名。
杨寺村小现有四个教学班,学生90多人,代课教师4名。
三、实施办法(一)轮岗对象1、凡我校完小的在编在岗专任教师,均为轮岗对象。
2、当村小一旦出现差缺教师时,在完小教师中按照下列次序确定交流对象:(1)教师自愿申报到村小任教。
由本人提出申请,学校根据学科结构等情况确定是否安排轮岗支教。
(2)在近一学年期末统考中,所任教学科平均分与学区平均分差距最大者【教多班科的取平均,再乘以系数(1-0.1x),x为教师任教的统考班科数】,按照轮岗支教人数,按平均分差距从大到小依次确定。
(3)若统考成绩名次相同,则年龄较小者为轮岗支教交流对象。
3、符合下列条件者,不作为轮岗交流的'对象:(1)男教师年龄58周岁以上,女教师53周岁以上的专任教师(时间截至到当年8月31日为准)。
(2)校委会成员。
(3)孕妇、身体残疾或长期病假的教师(以县级以上医院出具的诊断证明为准)。
2025年常州市教育系统“优才计划”公开招聘教师报名表
2025年常州市教育系统“优才计划”公开招聘教师报名表
2-1.有效期内的身份证正面
2-2.有效期内的身份证反面
3.就业推荐表
4.最高学历的毕业证书/教育部学历认证证明
5.学位证书
6.最高学历的学籍在线验证报告或学历证书电子注册备案表
(中国高等教育学生信息网下载)
7.养老保险缴纳证明(时间为毕业后至报名时)
和本人实际报名前的离职证明
8.教师资格证书照片
(报考初中、高中、中等职业学校公共课的人员上传)
9-1.奖学金证书(证明)-1
9-2.奖学金证书(证明)-2
10-1.“三好学生”、“优秀学生”、“优秀毕业生”证书-1
10-2.“三好学生”、“优秀学生”、“优秀毕业生”证书-2
11. 师范生基本功大赛(技能竞赛)证书
12.英语专业八级证书照片
13.其他材料。
某教育局教育工作督导评估与考核细则
附:
常州市2021年辖市区教育局教育工作督导评估与考核细那么
常州市2021年辖市区教育局教育工作督导评估与考核细那么
常州市2021年辖市区教育局教育工作督导评估与考核细那么
常州市2021年辖市区教育局教育工作督导评估与考核细那么
常州市2021年辖市区教育局教育工作督导评估与考核细那么
常州市2021年辖市区教育局教育工作督导评估与考核细那么
常州市2021年辖市区教育局教育工作督导评估与考核细那么
常州市2021年辖市区教育局教育工作督导评估与考核细那么
常州市2021年辖市区教育局教育工作督导评估与考核细那么
警示指标
凡发生以下情况的,每条扣20分。
1.发生越级到省、国家上访事件,产生恶劣碍事的。
2.发生重大学生损害事故的〔一次事故造成1人死亡或2人重伤〕。
3.发生校园内侵害师生人身平安的刑事案件的。
4.发生重大传染病疫情或食物中毒等突发性公共卫生事件的。
5.教师违反“八要十不〞师德自律,造成恶劣碍事的。
6.因违规收费向省、部举报并查实,造成重大、恶劣碍事的。
7.未创立成标准收费示范市〔区〕或已创立成但又被摘牌的。
8.公务员和校级领导因违纪违法受司法查处或D政纪处理的。
9.因行政执法过错受到责任追究的。
小学轮岗交流教师实施方案(合集7篇)
小学轮岗交流教师实施方案(合集7篇)小学轮岗交流教师实施方案(合集7篇)小学轮岗交流教师实施方案1为进一步增强教师队伍建设,规范教师交流管理,科学配置教师资源,推进全县教育优质平衡发展,依据《__县人民政府关于全面深化新时代教师队伍建设改革的实施观点》(太政(2023)67号)《__县人民政府关于推动县域内义务教育学校校长教师交流轮岗的实施观点》(x政秘(2023)129号)文件精神,特制定本方案。
一、交流原则(一)编制掌握原则。
教师交流应在编制限额内进行。
超编学校不得交流进教师,学科教师多余的学校不得交流进同学科教师超编学校教师应向空编学校流淌。
(二)推进平衡原则。
平衡在理配置教师资源,优化教师队伍的学科构造、年龄构造、职称构当前隐藏内容免费查看造和性别构造等,缩小城乡差距、校际差距,推进学校优质平衡发展。
(三)统筹聘用原则。
职称岗位由流入学校统筹聘用,凡申请交流的教师,由乡镇学校交流到城区学校,中心学校或城区学校之间教师交流,在职称岗位聘用时,流入学校依据职称岗位余缺情况,统筹聘用,有岗可按现聘岗位聘用,无岗降岗聘用。
(四)以人为本原则。
关怀爱怀一线教师,优先解决优秀教师夫妻两地分居、照顾家庭困难等情形。
(五)公平公开公正原则。
交流步骤公开,交流结果公示。
规范操作,严格纪律,增强监督。
具备下列行为的不予交流:1.近三年来有擅自离岗现象的;2.正在接受有关部门调查处理或受到纪律处分未废除处分的;3.近三年年度考察、师德师风考察有不达标的;4.在教师交流过程中弄虚作假、供应虚假证明的;5.违反法律、法规、规章制度等相关规定及其他不宜交流情形。
二、交流管理(一)乡镇到城区学校交流1.城区学校范围本方案所指城区学校包括县直城区学校(含三中东校区)、北城中心学校、南城中心学校、新城中心学校和局直属学校(下同)。
2.交流计划今年拟交流进城教师40人。
3.申请交流教师必需具备以下条件:(1)具备与申请交流的学段、学科相适应的学历、教师资格;(2)在我县乡镇学校工作6年以上,且在现任教乡镇中心学校持续工作3年以上;(3)近3年来年度考察均在“达标”等次以上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-9-
附件1
常州市教育局直属义务教育学校轮岗交流教师基数统计表
专任教师(不含骨干) 单位 高级职称 人数
北郊初中 田初中 勤业中学 朝阳中学 同济中学 实验初中 二十四中 市北初中 清潭中学 花园中学 丽华中学 兰陵中学 北环中学 翠竹中学 民族中学 合计 14 6 14 8 6 15 24 8 19 11 10 5 10 13 3 166
2 0 0 4 9 4 2 2 3 2 1 2 4 0 38 0 0 0 0 0 3 0 0 1 0 0 0 0 0 4 3 8 2 9 18 16 7 13 15 7 3 12 8 2 132 0 1 0 1 3 2 1 2 2 1 0 2 1 0 17 10 2 1 3 2 1
最终 需流 动数
0 0 1 0 1 0 0 0 2 2 1 0 0 0 0 7
中级职称 人 数
21 8 12 8 7 7 18 11 21 23 9 12 8 14 4 183
本 硕 科 士
14 6 14 8 6 15 24 8 18 10 10 5 10 13 3 164 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 2
专 科
0 0 0 0 0 0 1 2 1 1 0 0 0 1 0 6
教 坛 新 秀
2 0 6 1 2 5 2 2 5 6 3 0 3 3 1 41
教 学 能 手
4 1 2 1 3 4 7 3 6 5 2 2 7 1 干 15% 动、支 带头 小计 教 需交 教、系 人 师 流数 统内调 动人数 3 0 9 1 1
本 科
20 7 12 8 7 7 17 8 19 19 9 12 8 12 4 169
硕 士
1 1 0 0 0 0 0 1 1 3 0 0 0 1 0 8
按 集团流动 最终 15% 、支教、 小计 需流 需交 系统内调 人 专 本 动数 流数 动人数 数 科 科 初级职称
8 0 7 1 2 4 4 3 12 5 2 1 2 3 0 54 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 8 0 7 1 2 4 4 3 11 5 2 1 2 3 0 53 43 14 33 17 15 26 46 22 52 39 21 18 20 30 7 403 6 2 5 3 2 4 7 3 8 6 3 3 3 5 1 61 31 1 3 5 1 4 7 1 2 1 6 0 2 3 2 2 0 0 2 8 5 3 2 0 0 1 30
