初二数学动点问题练习

合集下载

(完整)初二数学动点问题归类复习(含例题、练习及答案)(2)

初二数学动点问题归类复习（含例题、练习及答案）所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想：分类思想数形结合思想转化思想本文将初一至二学习过的有关知识，结合动点问题进行归类复习，希望对同学们能有所帮助。

一、等腰三角形类：因动点产生的等腰三角形问题例1：（2013年上海市虹口区中考模拟第25题）如图1，在Rt△ABC中，∠A＝90°，AB＝6，AC ＝8，点D为边BC的中点，DE⊥BC交边AC于点E，点P为射线AB上的一动点，点Q为边AC 上的一动点，且∠PDQ＝90°．（1）求ED、EC的长；（2）若BP＝2，求CQ的长；（3）记线段PQ与线段DE的交点为F，若△PDF为等腰三角形，求BP的长．图1 备用图思路点拨1．第（2）题BP＝2分两种情况．2．解第（2）题时，画准确的示意图有利于理解题意，观察线段之间的和差关系．3．第（3）题探求等腰三角形PDF时，根据相似三角形的传递性，转化为探求等腰三角形CDQ．解答：（1）在Rt△ABC中，AB＝6，AC＝8，所以BC＝10．在Rt△CDE中，CD＝5，所以315tan544ED CD C=⋅∠=⨯=，254EC=．（2）如图2，过点D作DM⊥AB，DN⊥AC，垂足分别为M、N，那么DM、DN是△ABC的两条中位线，DM＝4，DN＝3．由∠PDQ＝90°，∠MDN＝90°，可得∠PDM＝∠QDN．因此△PDM∽△QDN．所以43PM DMQN DN==．所以34QN PM=，43PM QN=．图2 图3 图4 ①如图3，当BP＝2，P在BM上时，PM＝1．此时3344QN PM==．所以319444CQ CN QN=+=+=．②如图4，当BP＝2，P在MB的延长线上时，PM＝5．此时31544QN PM ==．所以1531444CQ CN QN =+=+=．（3）如图5，如图2，在Rt △PDQ 中，3tan 4QD DN QPD PD DM ∠===．在Rt △ABC 中，3tan 4BA C CA ∠==．所以∠QPD ＝∠C ．由∠PDQ ＝90°，∠CDE ＝90°，可得∠PDF ＝∠CDQ ．因此△PDF ∽△CDQ ．当△PDF 是等腰三角形时，△CDQ 也是等腰三角形．①如图5，当CQ ＝CD ＝5时，QN ＝CQ －CN ＝5－4＝1（如图3所示）．此时4433PM QN ==．所以45333BP BM PM =-=-=． ②如图6，当QC ＝QD 时，由cos CHC CQ =，可得5425258CQ =÷=．所以QN ＝CN －CQ ＝257488-=（如图2所示）．此时4736PM QN ==．所以725366BP BM PM =+=+=． ③不存在DP ＝DF 的情况．这是因为∠DFP ≥∠DQP ＞∠DPQ （如图5，图6所示）．图5 图6考点伸展：如图6，当△CDQ 是等腰三角形时，根据等角的余角相等，可以得到△BDP 也是等腰三角形，PB ＝PD ．在△BDP 中可以直接求解256BP =．二、直角三角形：因动点产生的直角三角形问题例2：（2008年河南省中考第23题）如图1，直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ，点A 的坐标是（-2，0）．（1）试说明△ABC 是等腰三角形；（2）动点M 从A 出发沿x 轴向点B 运动，同时动点N 从点B 出发沿线段BC 向点C 运动，运动的速度均为每秒1个单位长度．当其中一个动点到达终点时，他们都停止运动．设M 运动t 秒时，△MON 的面积为S ． ① 求S 与t 的函数关系式；② 设点M 在线段OB 上运动时，是否存在S ＝4的情形？若存在，求出对应的t 值；若不存在请说明理由；③在运动过程中，当△MON 为直角三角形时，求t 的值．图1思路点拨：1．第（1）题说明△ABC 是等腰三角形，暗示了两个动点M 、N 同时出发，同时到达终点． 2．不论M 在AO 上还是在OB 上，用含有t 的式子表示OM 边上的高都是相同的，用含有t 的式子表示OM 要分类讨论．3．将S ＝4代入对应的函数解析式，解关于t 的方程．4．分类讨论△MON 为直角三角形，不存在∠ONM ＝90°的可能．解答：（1）直线434+-=x y 与x 轴的交点为B （3，0）、与y 轴的交点C （0，4）． Rt △BOC 中，OB ＝3，OC ＝4，所以BC ＝5．点A 的坐标是（-2，0），所以BA ＝5．因此BC ＝BA ，所以△ABC 是等腰三角形．（2）①如图2，图3，过点N 作NH ⊥AB ，垂足为H ．在Rt △BNH 中，BN ＝t ，4sin 5B =，所以45NH t =．如图2，当M 在AO 上时，OM ＝2－t ，此时211424(2)22555S OM NH t t t t =⋅⋅=-⨯=-+．定义域为0＜t ≤2．如图3，当M 在OB 上时，OM ＝t －2，此时211424(2)22555S OM NH t t t t =⋅⋅=-⨯=-．定义域为2＜t ≤5．图2 图3②把S ＝4代入22455S t t =-，得224455t t -=．解得1211t =，2211t =．因此，当点M 在线段OB 上运动时，存在S ＝4的情形，此时211t = ③如图4，当∠OMN ＝90°时，在Rt △BNM 中，BN ＝t ，BM 5t =-，3cos 5B =，所以535tt-=．解得258t=．如图5，当∠OMN＝90°时，N与C重合，5t=．不存在∠ONM＝90°的可能．所以，当258t=或者5t=时，△MON为直角三角形．图4 图5考点伸展：在本题情景下，如果△MON的边与AC平行，求t的值．如图6，当ON//AC时，t＝3；如图7，当MN//AC时，t＝2.5．图6 图7三、平行四边形问题：因动点产生的平行四边形问题例3：（2010年山西省中考第26题）在直角梯形OABC中，CB//OA，∠COA＝90°，CB＝3，OA＝6，BA＝35．分别以OA、OC边所在直线为x轴、y轴建立如图1所示的平面直角坐标系．（1）求点B的坐标；（2）已知D、E分别为线段OC、OB上的点，OD＝5，OE＝2EB，直线DE交x轴于点F．求直线DE的解析式；（3）点M是（2）中直线DE上的一个动点，在x轴上方的平面内是否存在另一点N，使以O、D、M、N为顶点的四边形是菱形？若存在，请求出点N的坐标；若不存在，请说明理由．图1 图2思路点拨：1．第（1）题和第（2）题蕴含了OB与DF垂直的结论，为第（3）题讨论菱形提供了计算基础．2．讨论菱形要进行两次（两级）分类，先按照DO为边和对角线分类，再进行二级分类，DO与DM、DO与DN为邻边．解答：(1)如图2，作BH⊥x轴，垂足为H，那么四边形BCOH为矩形，OH＝CB＝3．在Rt△ABH中，AH＝3，BA＝35，所以BH＝6．因此点B的坐标为(3,6)．(2) 因为OE＝2EB，所以223E Bx x==，243E By y==，E(2,4)．设直线DE的解析式为y＝kx＋b，代入D(0,5)，E(2,4)，得5,2 4.bk b=⎧⎨+=⎩解得12k=-，5b=．所以直线DE的解析式为152y x=-+．(3) 由152y x=-+，知直线DE与x轴交于点F(10,0)，OF＝10，DF＝55．①如图3，当DO为菱形的对角线时，MN与DO互相垂直平分，点M是DF的中点．此时点M的坐标为(5,52)，点N的坐标为(－5,52)．②如图4，当DO、DN为菱形的邻边时，点N与点O关于点E对称，此时点N的坐标为(4,8)．③如图5，当DO、DM为菱形的邻边时，NO＝5，延长MN交x轴于P．由△NPO∽△DOF，得NP PO NODO OF DF==，即51055NP PO==．解得5NP=，25PO=．此时点N的坐标为(25,5)-．图3 图4考点伸展如果第（3）题没有限定点N在x轴上方的平面内，那么菱形还有如图6的情形．图5 图6四、相似三角形：因动点产生的相似三角形问题例4：（2013年苏州中考28题）如图，点O为矩形ABCD的对称中心，AB=10cm，BC=12cm，点E、F、G分别从A、B、C三点同时出发，沿矩形的边按逆时针方向匀速运动，点E的运动速度为1cm/s，点F的运动速度为3cm/s，点G的运动速度为1.5cm/s，当点F到达点C（即点F与点C重合）时，三个点随之停止运动．在运动过程中，△EBF关于直线EF的对称图形是△EB′F．设点E、F、G运动的时间为t（单位：s）．（1）当t=s时，四边形EBFB′为正方形；（2）若以点E、B、F为顶点的三角形与以点F，C，G为顶点的三角形相似，求t的值；（3）是否存在实数t，使得点B′与点O重合？若存在，求出t的值；若不存在，请说明理由．思路点拨：（1）利用正方形的性质，得到BE=BF，列一元一次方程求解即可；（2）△EBF与△FCG 相似，分两种情况，需要分类讨论，逐一分析计算；（3）本问为存在型问题．假设存在，则可以分别求出在不同条件下的t值，它们互相矛盾，所以不存在．解答：（1）若四边形EBFB′为正方形，则BE=BF，即：10﹣t=3t，解得t=2.5；（2）分两种情况，讨论如下：①若△EBF∽△FCG，则有，即，解得：t=2.8；②若△EBF∽△GCF，则有，即，解得：t=﹣14﹣2（不合题意，舍去）或t=﹣14+2．∴当t=2.8s或t=（﹣14+2）s时，以点E、B、F为顶点的三角形与以点F，C，G为顶点的三角形相似．（3）假设存在实数t，使得点B′与点O重合．如图，过点O作OM⊥BC于点M，则在Rt△OFM中，OF=BF=3t，FM=BC﹣BF=6﹣3t，OM=5，由勾股定理得：OM2+FM2=OF2，即：52+（6﹣3t）2=（3t）2解得：t=；过点O作ON⊥AB于点N，则在Rt△OEN中，OE=BE=10﹣t，EN=BE﹣BN=10﹣t﹣5=5﹣t，ON=6，由勾股定理得：ON 2+EN 2=OE 2，即：62+（5﹣t ）2=（10﹣t ）2解得：t =3.9．∵≠3.9，∴不存在实数t ，使得点B ′与点O 重合．考点伸展：本题为运动型综合题，考查了矩形性质、轴对称、相似三角形的判定性质、勾股定理、解方程等知识点．题目并不复杂，但需要仔细分析题意，认真作答．第（2）问中，需要分类讨论，避免漏解；第（3）问是存在型问题，可以先假设存在，然后通过推导出互相矛盾的结论，从而判定不存在．拓展练习：1、如图1，梯形ABCD 中，AD ∥ BC ，∠B=90°，AB=14cm,AD=18cm,BC=21cm,点P 从A 开始沿AD 边以1cm/秒的速度移动，点Q 从C 开始沿CB 向点B 以2 cm/秒的速度移动，如果P ，Q 分别从A ，C 同时出发，设移动时间为t 秒。

初二数学动点问题练习(含答案) 2 修改版

动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想：分类思想数形结合思想转化思想1、如图1，梯形ABCD中，AD∥BC，∠B=90°，AB=14cm,AD=18cm,BC=21cm,点P从A开始沿AD 边以1cm/秒的速度移动，点Q从C开始沿CB向点B以2 cm/秒的速度移动，如果P，Q分别从A，C 同时出发，设移动时间为t秒。

当t= 时，四边形是平行四边形；6当t= 时，四边形是等腰梯形. 82、如图2，正方形ABCD的边长为4，点M在边DC上，且DM=1，N为对角线AC上任意一点，则DN+MN的最小值为 53、如图，在Rt ABC △中，9060ACB B ∠=∠=°，°，2BC =．点O 是AC 的中点，过点O 的直线l 从与AC 重合的位置开始，绕点O 作逆时针旋转，交AB 边于点D ．过点C 作CE AB ∥交直线l 于点E ，设直线l 的旋转角为α．（1）①当α= 度时，四边形EDBC 是等腰梯形，此时AD 的长为；②当α= 度时，四边形EDBC 是直角梯形，此时AD 的长为；（2）当90α=°时，判断四边形EDBC 是否为菱形，并说明理由．解：（1）①30，1；②60，1.5；（2）当∠α=900时，四边形EDBC 是菱形.∵∠α=∠ACB=900，∴BC //ED . ∵CE //AB , ∴四边形EDBC 是平行四边形在Rt △ABC 中，∠ACB =900，∠B =600,BC =2, ∴∠A =300.∴AB =4,AC 3∴AO =12AC3 .在Rt △AOD 中，∠A =300，∴AD =2.∴BD =2. ∴BD =BC . 又∵四边形EDBC 是平行四边形，∴四边形EDBC 是菱形O E CDA α lOCA （备用图）4、在△ABC 中，∠ACB=90°，AC=BC ，直线MN 经过点C ，且AD ⊥MN 于D ，BE ⊥MN 于E.(1)当直线MN 绕点C 旋转到图1的位置时，求证：①△ADC ≌△CEB ；②DE=AD ＋BE ； (2)当直线MN 绕点C 旋转到图2的位置时，求证：DE=AD-BE ；(3)当直线MN 绕点C 旋转到图3的位置时，试问DE 、AD 、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明. 解：（1）① ∵∠ACD=∠ACB=90° ∴∠CAD+∠ACD=90° ∴∠BCE+∠ACD=90° ∴∠CAD=∠BCE ∵AC=BC ∴△ADC ≌△CEB② ∵△ADC ≌△CEB ∴CE=AD ，CD=BE ∴DE=CE+CD=AD+BE (2) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE 又∵AC=BC ∴△ACD ≌△CBE ∴CE=AD ，CD=BE ∴DE=CE-CD=AD-BE(3) 当MN 旋转到图3的位置时，DE=BE-AD(或AD=BE-DE ，BE=AD+DE 等) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE ，又∵AC=BC ， ∴△ACD ≌△CBE ， ∴AD=CE ，CD=BE ， ∴DE=CD-CE=BE-AD.C B AE D 图1 N M A B C D E M N 图2A CB E D N M 图35、数学课上，张老师出示了问题：如图1，四边形ABCD 是正方形，点E 是边BC 的中点．90AEF ∠=，且EF 交正方形外角DCG ∠的平行线CF 于点F ，求证：AE =EF ．经过思考，小明展示了一种正确的解题思路：取AB 的中点M ，连接ME ，则AM =EC ，易证AME ECF △≌△，所以AE EF =．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其它条件不变，那么结论“AE =EF ”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；（2）小华提出：如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE =EF ”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．解：（1）正确．证明：在AB 上取一点M ，使AM EC =，连接ME ． BM BE ∴=．45BME ∴∠=°，135AME ∴∠=°． CF 是外角平分线，45DCF ∴∠=°，135ECF ∴∠=°． AME ECF ∴∠=∠． 90AEB BAE ∠+∠=°，90AEB CEF ∠+∠=°， ∴BAE CEF ∠=∠． AME BCF ∴△≌△（ASA ）． AE EF ∴=．（2）正确．证明：在BA 的延长线上取一点N ．使AN CE =，连接NE ．BN BE ∴=． 45N PCE ∴∠=∠=°．四边形ABCD 是正方形， AD BE ∴∥． DAE BEA ∴∠=∠． NAE CEF ∴∠=∠．ANE ECF ∴△≌△（ASA ）．AE EF ∴=．A D F CGE B 图1 AD FGE B 图3A DF CG EB 图2AD F C GE B M A DF CG E B N6、如图, 射线MB上,MB=9,A是射线MB外一点,AB=5且A到射线MB的距离为3,动点P从M沿射线MB方向以1个单位/秒的速度移动，设P的运动时间为t.求（1）△PAB为等腰三角形的t值；（2）△PAB为直角三角形的t值；（3）若AB=5且∠ABM=45 °，其他条件不变，直接写出△PAB为直角三角形的t值7、如图，已知ABC △中，10AB AC ==厘米，8BC =厘米，点D 为AB 的中点．(1）如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动 ①若点Q 的运动速度与点P 的运动速度相等，经过1秒后，BPD △与CQP △是否全等，请说明理由；②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使BPD △与CQP △全等？（2）若点Q 以②中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿ABC △三边运动，求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇？解：（1）①∵1t =秒， ∴313BP CQ ==⨯=厘米， ∵10AB =厘米，点D 为AB 的中点， ∴5BD =厘米．又∵8PC BC BP BC =-=，厘米， ∴835PC =-=厘米， ∴PC BD =．又∵AB AC =， ∴B C ∠=∠， ∴BPD CQP △≌△． ②∵P Qv v ≠， ∴BP CQ ≠，又∵BPD CQP △≌△，B C ∠=∠，则45BP PC CQ BD ====，，∴点P ，点Q 运动的时间433BP t ==秒， ∴515443Q CQv t ===厘米/秒。

初二数学-八年级数学动点问题专项训练

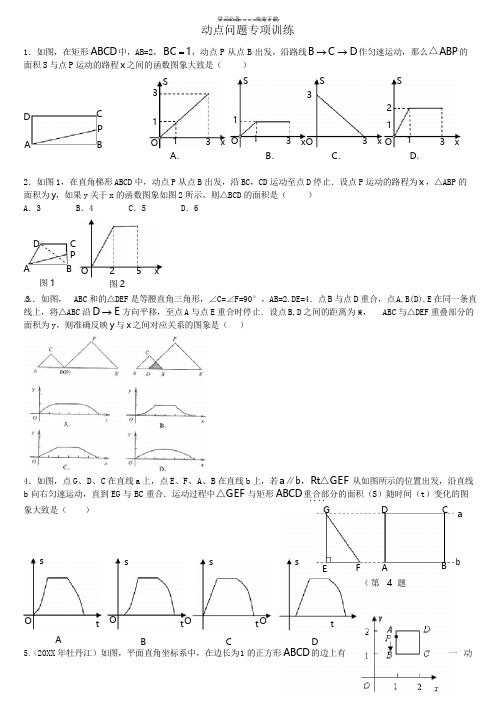
b 向右匀速运动，直到 EG 与 BC 重合．运动过程中 △GEF 与矩形 ABCD 重合部分的面积（S ）随时间（t ）变化的图动点问题专项训练1．如图，在矩形 ABCD 中，AB=2， BC = 1 ，动点 P 从点 B 出发，沿路线 B → C → D 作匀速运动，那么 △ A BP 的面积 S 与点 P 运动的路程 x 之间的函数图象大致是（）SSS S33DAC P B1O 113 x O 13 xO213 x O 13 xA ．B ．C ．D ．2．如图 1，在直角梯形 ABCD 中，动点 P 从点 B 出发，沿 BC ，CD 运动至点 D 停止．设点 P 运动的路程为 x ，△ABP 的面积为 y ，如果 y 关于 x 的函数图象如图 2 所示，则△BCD 的面积是（） A ．3 B ．4 C ．5 D ．6DC PAB O 25 x图 1图 2△3．如图， ABC 和的△DEF 是等腰直角三角形，∠C=∠F=90°，AB=2.DE=4．点 B 与点 D 重合，点 A,B(D),E 在同一条直线上，将△ABC 沿 D → E 方向平移，至点 A 与点 E 重合时停止．设点 B,D 之间的距离为 △x ， ABC 与△DEF 重叠部分的面积为 y ，则准确反映 y 与 x 之间对应关系的图象是（）4．如图，点 G 、D 、C 在直线 a 上，点 E 、F 、A 、B 在直线 b 上，若 a ∥b ，Rt △GEF 从如图所示的位置出发，沿直线．．．．象大致是（）G DC as s s sEFAB b（第 4 题Ot O t O t O tA B C D5．（20XX 年牡丹江）如图，平面直角坐标系中，在边长为 1 的正方形 ABCD 的边上有一动s stOt .（第 6 题图）.O C 8。

点 P 沿 A → B → C → D → A 运动一周，则 P 的纵坐标 y 与点 P 走过的路程 s 之间的函数关系用图象表示大致是（）yy2 2 11 y2 1 y2 1O 1 2 3 4sO 1 2 3 4s O 1 2 3 4 s O 1 2 3 4sABC D6．如图 1，在矩形 ABCD 中，动点 P 从点 B 出发，沿 BC 、CD 、DA 运动至点 A 停止，设点 P 运动的路程为 x ，△ABP 的面积为 y ，如果 y 关于 x 的函数图象如图 2 所示，则矩形 ABCD 的面积是( )A ．10 8．16 C. 20 D ．367．如图，三个大小相同的正方形拼成六边形 ABCDEF ，一动点 P 从点 A 出发沿着 A → B → C → D → E 方向匀速运动，最后到达点 E .运动过程中 ∆PEF 的面积（ s ）随时间（t ）变化的图象大致是（）s sPA · B.C DO8．如图．，点 A 、B 、C 、D 为圆 O 的四等分点，动点 P 从圆心 O 出发，沿 O-C-D-O 的路线作匀速运动.设运动时间为 t 秒,∠APB 的度数为 y 度，则下列图象中表示 y 与 t 之间函数关系最恰当的是9． 13．一张正方形的纸片，剪去两个一样的小矩形得到一个“E ”图案，如图4 所示，设小矩形的长和宽分别为x 、y ，剪去部分的面积为 20，若 2≤x ≤10，则 y 与 x 的函数图象是:10．如图，AB 是半圆 O 的直径，点 P 从点 O 出发，沿 O A - AB - BO 的路径运动一周．设OP 为 s ，运动时间为t ，则QC ，即 6﹣x = （6+x ），解得 x =2。

八年级数学动点问题习题整理归纳

1如图：已知正方形ABCD的边长为8，M在DC上，且DM=2，N是AC上的一动点，求DN+MN的最小值。

2如图，在四边形ABCD中，AD∥BC,且AD>BC，BC=6cm，P、Q分别从A,C同时出发，P以1cm/s的速度由A向D运动，Q以2cm/s的速度由C向B运动，几秒后四边形ABQP是平行四边形？设t秒后，四边形APQB为平行四边形（1分）则AP=t，QC=2t，BQ=6-2t （4分）因为AD//BC所以AP//BQ根据一组对边平行且相等的四边形是平行四边形知：AP=BQ即可（8分）即：t= 6-2t所以t=2（10分）当t=2时，AP=BQ=2<BC<AD ,符合综上，2秒后四边形ABQP是平行四边形3如图，梯形ABCD中AD//BC，∠B=90 °AB=14cm，AD=15cm,BC=21cm，点M从A点开始，沿AD边向D运动，速度为1cm/s，点N从点C开始沿CB边向点B运动，速度为2cm/s，设四边形MNCD的面积为S。

（1）写出面积S与时间t之间的函数关系式。

（2）t为何值时，四边形MNCD是平行四边形？（3）t为何值时，四边形MNCD是等腰梯形？【解析】（1）根据题意得：AM=tcm，CN=2tcm，则MD=AD-AM=15-t（cm），∴S=（MD+CN）•AD=×（15-t+2t）×14=7t+105（cm2）；∴面积S与时间t之间的函数关系式为：S=7t+105；（2）∵点M的速度为1cm/s，点N的速度为2cm/s，∴MD=AD-AM=15-t，CN=2t，四边形MNCD是平行四边形时，MD=CN，∴15-t=2t，解得t=5；∴当t=5时，四边形MNCD是平行四边形；（3）如图，过点D作DE⊥BC于E，∵AD∥BC，∠B=90°，∴四边形ABED是矩形，∴BE=AD=15cm，∴CE=BC-BE=21-15=6cm，四边形MNCD是等腰梯形时，CN=2CE+MD，∴2t=2×6+15-t，解得t=9．∴当t=9时，四边形MNCD是等腰梯形．4如图，在直角梯形ABCD中，∠ABC=90°，DC//AB，BC=3，DC=4，AD=5.动点P从B点出发，由B→C→D→A沿边运动，则△ABP的最大面积为（）A.10B.12C.14D.16如图，在Rt△ABC 中，∠C=90 °，AC=4cm，BC=6cm，动点P从点C沿CA以1cm/s的速度向A运动，同时动点Q从点C沿CB，以2cm/s的速度向点B运动，其中一个动点到达终点时，另一个动点也停止运动。

初二动点问题(含答案)

动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想：分类思想数形结合思想转化思想1、如图1，梯形ABCD 中，AD ∥ BC ，∠B=90°，AB=14cm,AD=18cm,BC=21cm,点P 从A 开始沿AD 边以1cm/秒的速度移动，点Q 从C 开始沿CB 向点B 以2 cm/秒的速度移动，如果P ，Q 分别从A ，C 同时出发，设移动时间为t 秒。

当t= 时，四边形是平行四边形；6 当t= 时，四边形是等腰梯形. 82、如图2，正方形ABCD 的边长为4，点M 在边DC 上，且DM=1，N 为对角线AC 上任意一点，则DN+MN 的最小值为 53、如图，在Rt ABC △中，9060ACB B ∠=∠=°，°，2BC =．点O 是AC 的中点，过点O 的直线l 从与AC 重合的位置开始，绕点O 作逆时针旋转，交AB 边于点D ．过点C 作CE AB ∥交直线l 于点E ，设直线l 的旋转角为α．（1）①当α= 度时，四边形EDBC 是等腰梯形，此时AD 的长为；②当α= 度时，四边形EDBC 是直角梯形，此时AD 的长为；（2）当90α=°时，判断四边形EDBC 是否为菱形，并说明理由．解：（1）①30，1；②60，1.5；（2）当∠α=900时，四边形EDBC 是菱形.∵∠α=∠ACB=900，∴BC //ED . ∵CE //AB , ∴四边形EDBC 是平行四边形在Rt △ABC 中，∠ACB =900，∠B =600,BC =2, ∴∠A =300.∴AB =4,AC =23. ∴AO =12AC=3 .在Rt △AOD 中，∠A =300，∴AD =2.∴BD =2. ∴BD =BC . 又∵四边形EDBC 是平行四边形，∴四边形EDBC 是菱形4、在△ABC 中，∠ACB=90°，AC=BC ，直线MN 经过点C ，且AD ⊥MN 于D ，BE ⊥MN 于E.O E CDA α lOCA （备用图） CB AE D 图1 N M A B C D EM N 图2A CB E D N M 图3(1)当直线MN 绕点C 旋转到图1的位置时，求证：①△ADC ≌△CEB ；②DE=AD ＋BE ； (2)当直线MN 绕点C 旋转到图2的位置时，求证：DE=AD-BE ；(3)当直线MN 绕点C 旋转到图3的位置时，试问DE 、AD 、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明. 解：（1）① ∵∠ACD=∠ACB=90° ∴∠CAD+∠ACD=90° ∴∠BCE+∠ACD=90° ∴∠CAD=∠BCE ∵AC=BC ∴△ADC ≌△CEB② ∵△ADC ≌△CEB ∴CE=AD ，CD=BE ∴DE=CE+CD=AD+BE (2) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE 又∵AC=BC ∴△ACD ≌△CBE ∴CE=AD ，CD=BE ∴DE=CE-CD=AD-BE(3) 当MN 旋转到图3的位置时，DE=BE-AD(或AD=BE-DE ，BE=AD+DE 等) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE ，又∵AC=BC ， ∴△ACD ≌△CBE ， ∴AD=CE ，CD=BE ， ∴DE=CD-CE=BE-AD.5、数学课上，张老师出示了问题：如图1，四边形ABCD 是正方形，点E 是边BC 的中点．90AEF ∠=，且EF 交正方形外角DCG ∠的平行线CF 于点F ，求证：AE =EF ．经过思考，小明展示了一种正确的解题思路：取AB 的中点M ，连接ME ，则AM =EC ，易证AME ECF △≌△，所以AE EF =．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其它条件不变，那么结论“AE =EF ”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；（2）小华提出：如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE =EF ”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．解：（1）正确．证明：在AB 上取一点M ，使AM EC =，连接ME ． BM BE ∴=．45BME ∴∠=°，135AME ∴∠=°． CF 是外角平分线，45DCF ∴∠=°，135ECF ∴∠=°． AME ECF ∴∠=∠． 90AEB BAE ∠+∠=°，90AEB CEF ∠+∠=°， ∴BAE CEF ∠=∠． AME BCF ∴△≌△（ASA ）． AE EF ∴=．（2）正确．证明：在BA 的延长线上取一点N ．使AN CE =，连接NE ．BN BE ∴=． 45N PCE ∴∠=∠=°．四边形ABCD 是正方形， AD BE ∴∥． DAE BEA ∴∠=∠． NAE CEF ∴∠=∠．ANE ECF ∴△≌△（ASA ）． AE EF ∴=．6、如图, 射线MB 上,MB=9,A 是射线MB 外一点,AB=5且A 到射线MB 的距离为3,动点P 从M 沿射线MB 方向以1个单位/秒的速度移动，设P 的运动时间为t. 求（1）△ PAB 为等腰三角形的t 值；（2）△ PAB 为直角三角形的t 值；（3）若AB=5且∠ABM=45 °，其他条件不变，直接写出△ PAB 为直角三角形的t 值AD FC G E B 图1 AD FG B 图3A D FC GE B 图2A D F C GB M A D FC G E B N7、在等腰梯形ABCD中,AD‖BC,E为AB的中点,过点E作EF‖BC交CD于点F.AB=4,BC=6, ∠B=60°。

初二数学动点问题练习

动点问题练习题1、已知：等边三角形ABC的边长为4厘米，长为1厘米的线段MN 在ABC △的边AB 上沿AB 方向以1厘米/秒的速度向B 点运动（运动开始时，点M 与点A 重合，点N 到达点B 时运动终止），过点M N 、分别作AB 边的垂线，与ABC △的其它边交于P Q 、两点，线段MN 运动的时间为t 秒．1、线段MN 在运动的过程中，t 为何值时，四边形MNQP 恰为矩形？并求出该矩形的面积；（2）线段MN 在运动的过程中，四边形MNQP 的面积为S ，运动的时间为t ．求四边形MNQP 的面积S 随运动时间t 变化的函数关系式，并写出自变量t 的取值范围．2、如图，在梯形ABCD 中，35AD BC AD DC ==∥，，动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 点出发沿线段CD 以每秒1个单位长度的速度向终点D （1）求BC 的长．（2）当MN AB ∥时，求t 的值．（3）试探究：t 为何值时，MNC △3、如图，在平面直角坐标系中，四边形OABC (6，0)，点B 的坐标为(4，3)，点C 在y A 点；动点N 在AB 上运动，从A 点出发到B 1个单位长度，当其中一个点到达终点时，t (秒)． (1)求线段AB 的长；当t 为何值时，MN ∥OC ？ (2)设△CMN 的面积为S ，求S 与t 并指出自变量t 的取值范围；S 是否有最小值？若有最小值，最小值是多少？ (3)连接AC ，那么是否存在这样的t ，使MN 与AC 若存在，求出这时的t 值；若不存在，请说明理由．2、如图，在Rt △ABC 中，∠C ＝90°，AC ＝12，BC ＝16C 以每秒3个单位长的速度运动，动点Q 从点C 出发沿CB 边向点B 以每秒4个单位长的速度运动．P ，Q 分别从点A ，C 同时出发，当其中一点到达端点时，另一点也随之停止运动．在运动过程中，△PCQ 关于直线PQ 对称的图形是△PDQ ．设运动时间为t （秒）．（1）设四边形PCQD 的面积为y ，求y 与t 的函数关系式；（2）t 为何值时，四边形PQBA 是梯形？（3）是否存在时刻t ，使得PD ∥AB ？若存在，求出t 的值；若不存在，请说明理由；（4）通过观察、画图或折纸等方法，猜想是否存在时刻t ，使得PD ⊥AB ？若存在，请估计t 的值在括号中的哪个时间段内（0≤t ≤1；1＜t ≤2；2＜t ≤3；3＜t ≤4）；若不存在，请简要说明理由．3、（山东济宁）如图，A 、B 分别为x 轴和y 轴正半轴上的点。

初二动点问题(含答案)

初二动点问题(含答案)动态问题所谓动点型问题是指题设图形中存在一个或多个动点，它们在线段、射线或弧线上运动的一类开放性题目。

解决这类问题的关键是从动中求静，灵活运用有关数学知识解决问题。

关键：从动中求静。

数学思想：分类思想、数形结合思想、转化思想。

类型：1.利用图形想到三角形全等、相似及三角函数。

2.分析题目，了解有几个动点，动点的路程、速度（动点怎么动）。

3.结合图形和题目，得出已知或能间接求出的数据。

4.分情况讨论，把每种可能情况列出来，不要漏。

5.动点一般在中考都是压轴题，步骤不重要，重要的是思路。

6.动点类题目一般都有好几问，前一问大都是后一问的提示，就像几何探究类题一样。

如果后面的题难了，可以反过去看看前面问题的结论。

例题：1.如图1，梯形ABCD中，AD∥BC，∠B=90°，AB=14cm，AD=18cm，BC=21cm，点P从A开始沿AD边以1cm/秒的速度移动，点Q从C开始沿CB向点B以2cm/秒的速度移动。

如果P、Q分别从A、C同时出发，设移动时间为t秒。

当t=时，四边形是平行四边形。

当t=时，四边形是等腰梯形。

2.如图2，正方形ABCD的边长为4，点M在边DC上，且DM=1，N为对角线AC上任意一点，则DN+MN的最小值为1，B=60°，BC=2.点O是AC的中点，过点O的直线为l。

3.如图，在直角三角形ABC中，∠ACB=90°。

从与AC重合的位置开始，绕点O作逆时针旋转，交AB边于点D。

过点C作CE∥AB交直线l于点E，设直线l的旋转角为α。

1）当α=度时，四边形EDBC是等腰梯形，此时AD的长为；②当α=度时，四边形EDBC是直角梯形，此时AD的长为；2）当α=90°时，判断四边形EDBC是否为菱形，并说明理由。

删除问题明显的第四个例题。

对于其他例题，可以稍作改写，使其更加清晰易懂。

25、在正方形ABCD中，点E是边BC的中点，且∠AEF 为直角，EF交正方形外角∠DCG的平行线CF于点F。

初二数学期末复习《一次函数的应用—动点问题》(附练习及答案)

课题一次函数的应用——动点问题教学目标1．学会结合几何图形的性质，在平面直角坐标系中列函数关系式。

2．通过对几何图形的探究活动和对例题的分析，感悟探究动点问题列函数关系式的方法，提高解决问题的能力。

重点、难点理解在平面直角坐标系中，动点问题列函数关系式的方法。

小结：1用函数知识求解动点问题，需要将问题给合几何图形的性质,建立函数模型求解，解要符合题意，要注意数与形结合。

2.以一次函数为背景的问题，要充分运用方程、转化、函数以及数形结合等思想来研究解决，注意自变量的取值范围例题1：如图，直线1l 的解析表达式为33y x =-+，且1l 与x 轴交于点D ，直线2l 经过点A B ，，直线1l ，2l 交于点C ．（1）求点D 的坐标；（2）求直线2l 的解析表达式；（3）求ADC △的面积；（4）在直线2l 上存在异于点C 的另一点P ，使得ADP △与ADC △的面积相等，请直接．．写出点P 的坐标．例题2：如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P 、Q 移动的时间为t 秒．(1) 求直线AB 的解析式；(2) 当t 为何值时，△APQ 的面积为524个平方单位？当堂巩固：如图，直线6y kx =+与x 轴、y 轴分别交于点E 、F ，点E 的坐标为（-8，0），点A 的坐标为（-6，0）。

（1）求k 的值；（2）若点P （x ，y ）是第二象限内的直线上的一个动点，在点P 的运动过程中，试写出△OPA 的面积S 与x 的函数关系式，并写出自变量x 的取值范围；（3）探究：当点P 运动到什么位置时，△OPA 的面积为278，并说明理由。

课后检测： 1、如果一次函数y=-x+1的图象与x 轴、y 轴分别交于点A 点、B 点，点M 在x 轴上，并且使以点A 、B 、M 为顶点的三角形是等腰三角形，那么这样的点M 有（）。

初二数学动点问题练习题

初二数学动点问题练习题 1. 题目描述：一辆汽车匀速行驶，从A地到B地全程100公里，行驶时间为2小时。假设汽车在行驶过程中遇到了一个马路上的动点C，请回答以下问题。

1) 动点C与A地的距离为30公里，汽车在经过C点前后所需的时间各为多少？

2) 假设动点C与B地的距离为40公里，汽车将在何时与动点C相遇？

2. 解题过程：根据题目给出的信息，我们来逐步解决上述两个问题。 1) 动点C与A地的距离为30公里，汽车在经过C点前后所需的时间各为多少？

首先，我们可以先求出汽车的行驶速度。由于汽车匀速行驶，我们可以用速度等于位移除以时间的公式来计算速度。假设汽车的速度为v，则v=100公里/2小时，即v=50公里/小时。

现在，我们已经知道了汽车的速度，我们可以通过距离等于速度乘以时间的公式来求解汽车在经过C点之前和之后所需的时间。

设汽车在经过C点之前所需的时间为t1小时，则距离C点的路程为：30公里 = 50公里/小时 × t1小时解方程可得：t1 = 30/50 = 0.6小时同理，设汽车在经过C点之后所需的时间为t2小时，则距离B点的路程为：70公里 = 50公里/小时 × t2小时

解方程可得：t2 = 70/50 = 1.4小时因此，汽车在经过C点前后所需的时间分别为0.6小时和1.4小时。 2) 假设动点C与B地的距离为40公里，汽车将在何时与动点C相遇？

设汽车和动点C相遇时的时间为t小时，则汽车在行驶过程中分别与A点和C点所需的时间分别为2 - t小时和t小时。

根据题目给出的信息，我们可以得到以下两个方程：距离C点的路程：30公里 = 50公里/小时 × (2 - t)小时距离B点的路程：40公里 = 50公里/小时 × t小时解方程组可得：t = 40 / (50/小时 + 50/小时) = 40 / (100/小时) = 0.4小时

因此，汽车将在0.4小时后与动点C相遇。 3. 总结：通过解题过程，我们得到了以下结论： 1) 汽车在经过C点前需0.6小时，经过C点后需1.4小时。 2) 汽车将在0.4小时后与动点C相遇。以上是初二数学动点问题练习题的解答过程。通过这道题目的解答，我们可以更好地理解动点问题的求解方法，提高我们的数学解题能力。希望这篇文章对你的学习有所帮助。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

初二数学动点问题练习 TTA standardization office【TTA 5AB- TTAK 08- TTA 2C】 O M A N B C

（2）线段MN在运动的过程中，四边形MNQP的面积为S，运动的时间为t．求四边形MNQP的面积S随运动时间t变化的函数关系式，并写出自变量t的取值范围． 2、如图，在梯形ABCD中，354245ADBCADDCABB∥，，，，∠．动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动；动点N同时从C

点出发沿线段CD以每秒1个单位长度的速度向终点D运动．设运动的时间为t秒．（1）求BC的长．（2）当MNAB∥时，求t的值．（3）试探究：t为何值时，MNC△为等腰三角形． 3、如图，在平面直角坐标系中，四边形OABC是梯形，OA∥BC，点A的坐标为(6，0)，点B的坐标为(4，3)，点C在y轴的正半轴上．动点M在OA上运动，从O点出发到A点；动点N在AB上运动，从A点出发到B点．两个动点同时出发，速度都是每秒1个单位长度，当其中一个点到达终点时，另一个点也随即停止，设两个点的运动时间为t(秒)． (1)求线段AB的长；当t为何值时，MN∥OC

C P Q

B A M N

A D

C B M

N (2)设△CMN的面积为S，求S与t之间的函数解析式，并指出自变量t的取值范围；S是否有最小值？

若有是多少？ (3)连接AC，那么是否存在这样的t，使MN与AC互相垂直？若存在，求出这时的t值；若不存在，请说明理由． 2、如图，在Rt△ABC中，∠C＝90°，AC＝12，BC＝16，动点P从点A出发沿AC边向点C以每秒3个单位长的速度运动，动点Q从点C出发沿CB边向点B以每秒4个单位长的速度运动．P，Q分别从点A，C同时出发，当其中一点到达端点时，另一点也随之停止运动．在运动过程中，△PCQ关于直线PQ对称的图形是△PDQ．设运动时间为t（秒）．（1）设四边形PCQD的面积为y，求y与t的函数关系式；（2）t为何值时，四边形PQBA是梯形

（3）是否存在时刻t，使得PD∥AB若存在，求出t的值；若不存在，请说明理由；（4）通过观察、画图或折纸等方法，猜想是否存在时刻t，使得PD⊥AB若存在，请估计t的值在括号中的哪个时间段内（0≤t≤1；1＜t≤2；2＜t≤3；3＜t≤4）；若不存在，请简要说明理由． 3、（山东济宁）如图，A、B分别为x轴和y轴正半轴上的点。OA、OB的长分别是方程x2－14x＋48＝0的两根

A P

C Q B

D (OA＞OB)，直线BC平分∠ABO交x轴于C点，P为BC上一动点，P点以每秒1个单位的速度从B点开始沿BC方向移动。 (1)设△APB和△OPB的面积分别为S1、S2，求S1∶S2

的值； (2)求直线BC的解析式； (3)设PA－PO＝m，P点的移动时间为t。 ①当0＜t≤54时，试求出m的取值范围； ②当t＞54时，你认为m的取值范围如何(只要求写出结论)

4、在ABC中，,4,5,DBCCD3cm,CRtACcmBCcm点在上，且以＝现有两个动点P、Q分别从点A和点B同时出发，其中点P以1cm/s的速度，沿AC向终点C移动；点Q以s的速度沿BC向终点C移动。过点P作PE∥BC交AD于点E，连结EQ。设动点运动时间为x秒。（1）用含x的代数式表示AE、DE的长度；（2）当点Q在BD（不包括点B、D）上移动时，设EDQ的面积为2()ycm，求y与

月份x的函数关系式，并写出自变量x的取值范围；（3）当x为何值时，EDQ为直角三角形。 5、在直角梯形ABCD中，90C，高6CDcm（如图1）。动点,PQ同时从点

B出发，点P沿,,BAADDC运动到点C停止，点Q沿BC运动到点C停止，两点运动时的速度都是1/cms。而当点P到达点A时，点Q正好到达点C。设,PQ同时从点B出发，经过的时间为ts时，BPQ的面积为2ycm（如图2）。分别以,ty为横、纵坐

标建立直角坐标系，已知点P在AD边上从A到D运动时，y与t的函数图象是图3中的线段MN。（1）分别求出梯形中,BAAD的长度；（2）写出图3中,MN两点的坐标；

O A B C P x

y （3）分别写出点P在BA边上和DC边上运动时，y与t的函数关系式（注明自变量的取值范围），并在图3中补全整个运动中y关于t的函数关系的大致图象。

6如图1，在平面直角坐标系中，已知点(043)A，，点B在x正半轴上，且30ABO∠．动点P在线段AB上从点A向点B以每秒3个单位的速度运动，设运动时间为t秒．在x轴上取两点MN，作等边PMN△．（1）求直线AB的解析式；（2）求等边PMN△的边长（用t的代数式表示），并求出当等边PMN△的顶点M运动到与原点O重合时t的值；（3）如果取OB的中点D，以OD为边在RtAOB△内部作如图2所示的矩形ODCE，点C在线段AB上．设等边PMN△和矩形ODCE重叠部分的面积为S，请求出当02t≤≤秒时S与t的函数关系式，并求出S的最大值．

7、两块完全相同的直角三角板ABC和DEF如图1所示放置，点C、F重合，且BC、DF在一条直线上，其中AC=DF=4，BC=EF=3．固定Rt△ABC不动，让Rt△DEF沿CB向左平移，直到点F和点B重合为止．设FC=x，两个三角形重叠阴影部分的面积为y．（1）如图2，求当x=21时，y的值是多少？

（2）如图3，当点E移动到AB上时，求x、y的值；（3）求y与x之间的函数关系式；

CBAD

（图1） CBADPQ（图2）

yt30

（图3）

（图（图 8、如图1所示，一张三角形纸片ABC，∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成11ACD和22BCD两个三角形（如图2所示）.将纸片11ACD沿直线2DB（AB）方向平移（点12,,,ADDB始终在同一直线上），当点1D于点B重合

时，停止平移.在平移过程中，11CD与2BC交于点E,1AC与222CDBC、分别交于点

F、P. （1）当11ACD平移到如图3所示的位置时，猜想图中的1DE与2DF的数量关系，并

证明你的猜想；（2）设平移距离21DD为x，11ACD与22BCD重叠部分面积为y，请写出y与x的函

数关系式，以及自变量的取值范围；（3）对于（2）中的结论是否存在这样的x的值；使得重叠部分的面积等于原ABC

面积的14若不存在，请说明理由.

9. 梯形ABCD中，AD∥BC，∠B=90°，AD=24cm，AB=8cm，BC=26cm，动点P从点A开始，沿AD边，以1厘米/秒的速度向点D运动；动点Q从点C开始，沿CB边，以3厘米/秒的速度向B点运动。已知P、Q两点分别从A、C同时出发，，当其中一点到达端点时，另一点也随之停止运动。假设运动时间为t秒，问：（1）t为何值时，四边形PQCD是平行四边形？

（2）在某个时刻，四边形PQCD可能是菱形吗为什么（3）t为何值时，四边形PQCD是直角梯形？（4）t为何值时，四边形PQCD是等腰梯形

CBDA图1

PEF

AD1BC1D2

图3 C2D2C1BD1A图2

ABCDP

Q A F D P E B Q C

FDBC

D'A A

M O F N E

B C D

10. 如右图，在矩形ABCD中，AB=20cm，BC=4cm，点 P从A开始沿折线A—B—C—D以4cm/s的速度运动，点Q从C 开始沿CD边1cm/s的速度移动，如果点P、Q分别从A、C同时出发，当其中一点到达点D时，另一点也随之停止运动，设运动时间为t(s)，t为何值时，四边形APQD也为矩形？ 11. 如图，在等腰梯形ABCD中，AB∥DC，cmBCAD5,AB=12 cm,CD=6cm , 点P

从A开始沿AB边向B以每秒3cm的速度移动，点Q从C开始沿CD边向D以每秒1cm的速度移动，如果点P、Q分别从A、C同时出发，当其中一点到达终点时运动停止。设运动时间为t秒。

（1）求证：当t=23时，四边形APQD是平行四边形；（2）PQ是否可能平分对角线BD若能，求出当t为何值时PQ平分BD；若不能，请说明理由；（3）若△DPQ是以PQ为腰的等腰三角形，求t的值。 12. 如图所示，△ABC中，点O是AC边上的一个动点，过O作直线MNBCABCAEOFOB如图，矩形ABCD中，AB=8,BC=4,

将矩形沿AC折叠，点D落在点D’处，求重叠部分⊿AFC的面积.

14. 如图所示，有四个动点P、Q、E、F分别从正方形

ABCD的四个顶点出发，沿着AB、BC、CD、DA以同样的速度向B、C、D、A各点移动。（1）试判断四边形PQEF是正方形并证明。（2）PE是否总过某一定点，并说明理由。（3）四边形PQEF的顶点位于何处时，其面积最小，最大各是多少

A B C D Q P

初二数学动点问题练习

(完整)初二数学动点问题归类复习(含例题、练习及答案)(2)

初二数学动点问题练习(含答案) 2 修改版

初二数学-八年级数学动点问题专项训练

八年级数学动点问题习题整理归纳

最新初二数学八年级数学动点问题专项训练

初二动点问题(含答案)

初二数学动点问题练习

初二动点问题(含答案)

初二数学期末复习《一次函数的应用—动点问题》(附练习及答案)

初二数学动点问题练习题