四边简支矩形板计算
矩形板 计算书LB
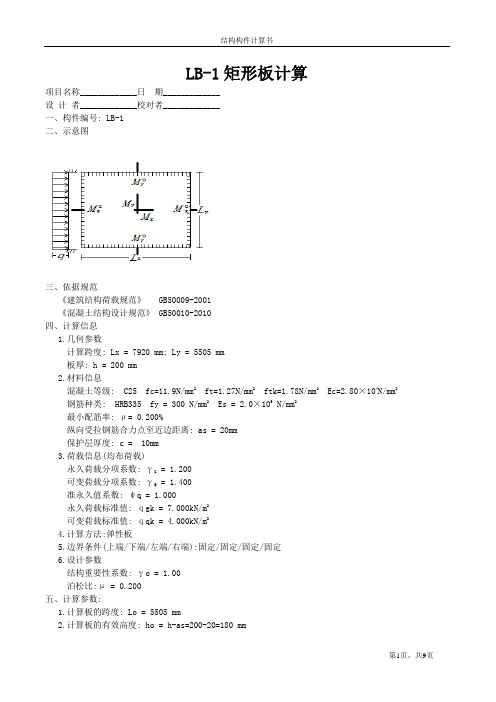
LB-1矩形板计算项目名称_____________日期_____________设计者_____________校对者_____________一、构件编号: LB-1二、示意图三、依据规范《建筑结构荷载规范》 GB50009-2001《混凝土结构设计规范》 GB50010-2010四、计算信息1.几何参数计算跨度: Lx = 7920 mm; Ly = 5505 mm板厚: h = 200 mm2.材料信息混凝土等级: C25 fc=11.9N/mm2 ft=1.27N/mm2 ftk=1.78N/mm2Ec=2.80×104N/mm2钢筋种类: HRB335 fy = 300 N/mm2Es = 2.0×105 N/mm2最小配筋率: ρ= 0.200%纵向受拉钢筋合力点至近边距离: as = 20mm保护层厚度: c = 10mm3.荷载信息(均布荷载)永久荷载分项系数: γG = 1.200可变荷载分项系数: γQ = 1.400准永久值系数: ψq = 1.000永久荷载标准值: qgk = 7.000kN/m2可变荷载标准值: qqk = 4.000kN/m24.计算方法:弹性板5.边界条件(上端/下端/左端/右端):固定/固定/固定/固定6.设计参数结构重要性系数: γo = 1.00泊松比:μ = 0.200五、计算参数:1.计算板的跨度: Lo = 5505 mm2.计算板的有效高度: ho = h-as=200-20=180 mm六、配筋计算(lx/ly=7920/5505=1.439<2.000 所以按双向板计算):1.X向底板钢筋1) 确定X向板底弯矩Mx = 表中系数(γG*qgk+γQ*qqk)*Lo2= (0.0111+0.0323*0.200)*(1.200*7.000+1.400*4.000)*5.5052 = 7.463 kN*m2) 确定计算系数αs = γo*Mx/(α1*fc*b*ho*ho)= 1.00*7.463×106/(1.00*11.9*1000*180*180)= 0.0193) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.019) = 0.0204) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*11.9*1000*180*0.020/300= 140mm25) 验算最小配筋率ρ = As/(b*h) = 140/(1000*200) = 0.070%ρ<ρmin = 0.200% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.200%*1000*200 = 400 mm2采取方案 8@125, 实配面积402 mm22.Y向底板钢筋1) 确定Y向板底弯矩My = 表中系数(γG*qgk+γQ*qqk)*Lo2= (0.0323+0.0111*0.200)*(1.200*7.000+1.400*4.000)*5.5052 = 14.663 kN*m2) 确定计算系数αs = γo*My/(α1*fc*b*ho*ho)= 1.00*14.663×106/(1.00*11.9*1000*180*180)= 0.0383) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.038) = 0.0394) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*11.9*1000*180*0.039/300= 277mm25) 验算最小配筋率ρ = As/(b*h) = 277/(1000*200) = 0.138%ρ<ρmin = 0.200% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.200%*1000*200 = 400 mm2采取方案 8@125, 实配面积402 mm23.X向支座左边钢筋1) 确定左边支座弯矩M o x = 表中系数(γG*qgk+γQ*qqk)*Lo2= 0.0569*(1.200*7.000+1.400*4.000)*5.5052= 24.149 kN*m2) 确定计算系数αs = γo*M o x/(α1*fc*b*ho*ho)= 1.00*24.149×106/(1.00*11.9*1000*180*180)= 0.0633) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.063) = 0.0654) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*11.9*1000*180*0.065/300 = 462mm25) 验算最小配筋率ρ = As/(b*h) = 462/(1000*200) = 0.231%ρ≥ρmin = 0.200% 满足最小配筋要求采取方案 10@160, 实配面积490 mm24.X向支座右边钢筋1) 确定右边支座弯矩M o x = 表中系数(γG*qgk+γQ*qqk)*Lo2= 0.0569*(1.200*7.000+1.400*4.000)*5.5052= 24.149 kN*m2) 确定计算系数αs = γo*M o x/(α1*fc*b*ho*ho)= 1.00*24.149×106/(1.00*11.9*1000*180*180)= 0.0633) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.063) = 0.0654) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*11.9*1000*180*0.065/300 = 462mm25) 验算最小配筋率ρ = As/(b*h) = 462/(1000*200) = 0.231%ρ≥ρmin = 0.200% 满足最小配筋要求采取方案 10@160, 实配面积490 mm25.Y向上边支座钢筋1) 确定上边支座弯矩M o y = 表中系数(γG*qgk+γQ*qqk)*Lo2= 0.0738*(1.200*7.000+1.400*4.000)*5.5052= 31.313 kN*m2) 确定计算系数αs = γo*M o y/(α1*fc*b*ho*ho)= 1.00*31.313×106/(1.00*11.9*1000*180*180)= 0.0813) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.081) = 0.0854) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*11.9*1000*180*0.085/300= 606mm25) 验算最小配筋率ρ = As/(b*h) = 606/(1000*200) = 0.303%ρ≥ρmin = 0.200% 满足最小配筋要求采取方案 10@125, 实配面积628 mm26.Y向下边支座钢筋1) 确定下边支座弯矩M o y = 表中系数(γG*qgk+γQ*qqk)*Lo2= 0.0738*(1.200*7.000+1.400*4.000)*5.5052= 31.313 kN*m2) 确定计算系数αs = γo*M o y/(α1*fc*b*ho*ho)= 1.00*31.313×106/(1.00*11.9*1000*180*180)= 0.0813) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.081) = 0.0854) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*11.9*1000*180*0.085/300= 606mm25) 验算最小配筋率ρ = As/(b*h) = 606/(1000*200) = 0.303%ρ≥ρmin = 0.200% 满足最小配筋要求采取方案 10@125, 实配面积628 mm2七、跨中挠度计算:Mk -------- 按荷载效应的标准组合计算的弯矩值Mq -------- 按荷载效应的准永久组合计算的弯矩值1.计算荷载效应Mk = Mgk + Mqk= (0.0323+0.0111*0.200)*(7.000+4.000)*5.5052 = 11.521 kN*mMq = Mgk+ψq*Mqk= (0.0323+0.0111*0.200)*(7.000+1.0*4.000)*5.5052 = 11.521 kN*m 2.计算受弯构件的短期刚度 Bs1) 计算按荷载荷载效应的两种组合作用下,构件纵向受拉钢筋应力σsk = Mk/(0.87*ho*As) 混规(7.1.4-3)= 11.521×106/(0.87*180*402) = 183.010 N/mmσsq = Mq/(0.87*ho*As) 混规(7.1.4-3)= 11.521×106/(0.87*180*402) = 183.010 N/mm2) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积: Ate = 0.5*b*h = 0.5*1000*200= 100000mm2ρte = As/Ate 混规(7.1.2-4)= 402/100000 = 0.402%3) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψk = 1.1-0.65*ftk/(ρte*σsk) 混规(7.1.2-2)= 1.1-0.65*1.78/(0.402%*183.010) = -0.473因为ψ不能小于最小值0.2,所以取ψk = 0.2ψq = 1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)= 1.1-0.65*1.78/(0.402%*183.010) = -0.473因为ψ不能小于最小值0.2,所以取ψq = 0.24) 计算钢筋弹性模量与混凝土模量的比值αEαE = Es/Ec = 2.0×105/2.80×104 = 7.1435) 计算受压翼缘面积与腹板有效面积的比值γf矩形截面,γf=06) 计算纵向受拉钢筋配筋率ρρ = As/(b*ho)= 402/(1000*180) = 0.223%7) 计算受弯构件的短期刚度 BsBsk = Es*As*ho2/[1.15ψk+0.2+6*αE*ρ/(1+ 3.5γf')](混规(7.2.3-1)) = 2.0×105*402*1802/[1.15*-0.473+0.2+6*7.143*0.223%/(1+3.5*0.0)]= 4.955×103 kN*m2Bsq = Es*As*ho2/[1.15ψq+0.2+6*αE*ρ/(1+ 3.5γf')](混规(7.2.3-1)) = 2.0×105*402*1802/[1.15*-0.473+0.2+6*7.143*0.223%/(1+3.5*0.0)]= 4.955×103 kN*m23.计算受弯构件的长期刚度B1) 确定考虑荷载长期效应组合对挠度影响增大影响系数θ当ρ'=0时,θ=2.0 混规(7.2.5)2) 计算受弯构件的长期刚度 BBk = Mk/(Mq*(θ-1)+Mk)*Bs (混规(7.2.2-1))= 11.521/(11.521*(2.0-1)+11.521)*4.955×103= 2.478×103 kN*m2Bq = Bsq/θ (混规(7.2.2-2))= 4.955×103/2.0= 2.478×103 kN*m2B = min(Bk,Bq)= min(2477.543,2477.543)= 2477.5434.计算受弯构件挠度f max = f*(q gk+Ψq*q qk)*Lo4/B= 0.00212*(7.000+1.0*4.000)*5.5054/2.478×103= 8.656mm5.验算挠度挠度限值fo=Lo/200=5505/200=27.525mmfmax=8.656mm≤fo=27.525mm,满足规范要求!八、裂缝宽度验算:1.跨中X方向裂缝1) 计算荷载效应Mx = 表中系数(qgk+ψqqk)*Lo2= (0.0111+0.0323*0.200)*(7.000+1.00*4.000)*5.5052= 5.864 kN*m2) 光面钢筋,所以取值v i=0.73) 因为C < 20,所以取C = 204) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=5.864×106/(0.87*180*402)=93.144N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*200=100000 mm2ρte=As/Ate 混规(7.1.2-4)=402/100000 = 0.0040因为ρte=0.0040 < 0.01,所以让ρte=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*1.780/(0.0100*93.144)=-0.142因为ψ=-0.142 < 0.2,所以让ψ=0.27) 计算单位面积钢筋根数nn=1000/dist = 1000/125=88) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=8*8*8/(8*0.7*8)=119) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.200*93.144/2.0×105*(1.9*20+0.08*11/0.0100)=0.0229mm ≤ 0.30, 满足规范要求2.跨中Y方向裂缝1) 计算荷载效应My = 表中系数(qgk+ψqqk)*Lo2= (0.0323+0.0111*0.200)*(7.000+1.00*4.000)*5.5052= 11.521 kN*m2) 光面钢筋,所以取值v i=0.73) 因为C < 20,所以取C = 204) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=11.521×106/(0.87*180*402)=183.010N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*200=100000 mm2ρte=As/Ate 混规(7.1.2-4)=402/100000 = 0.0040因为ρte=0.0040 < 0.01,所以让ρte=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*1.780/(0.0100*183.010)=0.4687) 计算单位面积钢筋根数nn=1000/dist = 1000/125=88) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=8*8*8/(8*0.7*8)=119) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.468*183.010/2.0×105*(1.9*20+0.08*11/0.0100)=0.1053mm ≤ 0.30, 满足规范要求3.支座上方向裂缝1) 计算荷载效应M o y = 表中系数((qgk+ψqqk)*Lo2)= 0.0738*(7.000+1.00*4.000)*5.5052= 24.603 kN*m2) 光面钢筋,所以取值v i=0.73) 因为C < 20,所以取C = 204) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=24.603×106/(0.87*180*628)=250.175N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*200=100000 mm2ρte=As/Ate 混规(7.1.2-4)=628/100000 = 0.0063因为ρte=0.0063 < 0.01,所以让ρte=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*1.780/(0.0100*250.175)=0.6387) 计算单位面积钢筋根数nn=1000/dist = 1000/125=88) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=8*10*10/(8*0.7*10)=149) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.638*250.175/2.0×105*(1.9*20+0.08*14/0.0100)=0.2307mm ≤ 0.30, 满足规范要求4.支座下方向裂缝1) 计算荷载效应M o y = 表中系数(qgk+ψqqk)*Lo2= 0.0738*(7.000+1.00*4.000)*5.5052= 24.603 kN*m2) 光面钢筋,所以取值v i=0.73) 因为C < 20,所以取C = 204) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=24.603×106/(0.87*180*628)=250.175N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*200=100000 mm2ρte=As/Ate 混规(7.1.2-4)=628/100000 = 0.0063因为ρte=0.0063 < 0.01,所以让ρte=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*1.780/(0.0100*250.175)=0.6387) 计算单位面积钢筋根数nn=1000/dist = 1000/125=88) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=8*10*10/(8*0.7*10)=149) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.638*250.175/2.0×105*(1.9*20+0.08*14/0.0100)=0.2307mm ≤ 0.30, 满足规范要求5.支座左方向裂缝1) 计算荷载效应M o x = 表中系数(qgk+ψqqk)*Lo2= 0.0569*(7.000+1.00*4.000)*5.5052= 18.974 kN*m2) 光面钢筋,所以取值v i=0.73) 因为C < 20,所以取C = 204) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=18.974×106/(0.87*180*490)=247.276N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*200=100000 mm2ρte=As/Ate 混规(7.1.2-4)=490/100000 = 0.0049因为ρte=0.0049 < 0.01,所以让ρte=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*1.780/(0.0100*247.276)=0.6327) 计算单位面积钢筋根数nn=1000/dist = 1000/160=68) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=6*10*10/(6*0.7*10)=149) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.632*247.276/2.0×105*(1.9*20+0.08*14/0.0100)=0.2261mm ≤ 0.30, 满足规范要求6.支座右方向裂缝1) 计算荷载效应M o x = 表中系数(qgk+ψqqk)*Lo2= 0.0569*(7.000+1.00*4.000)*5.5052= 18.974 kN*m2) 光面钢筋,所以取值v i=0.73) 因为C < 20,所以取C = 204) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=18.974×106/(0.87*180*490)=247.276N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*200=100000 mm2ρte=As/Ate 混规(7.1.2-4)=490/100000 = 0.0049因为ρte=0.0049 < 0.01,所以让ρte=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*1.780/(0.0100*247.276)=0.6327) 计算单位面积钢筋根数nn=1000/dist = 1000/160=68) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=6*10*10/(6*0.7*10)=149) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.632*247.276/2.0×105*(1.9*20+0.08*14/0.0100)=0.2261mm ≤ 0.30, 满足规范要求。
四边简支矩形板稳定问题的精确解

四边简支矩形板稳定问题的精确解四边简支矩形板稳定问题的精确解
“四边简支矩形板稳定性问题”一直是国内外结构工程界的一个热门话题,关
于此问题,很多学者提出了自己的解决方案,但仍未能得出一个明确的精确答案。
因此,四边简支矩形板稳定性问题的精确解非常重要。
首先,要求四边简支矩形板稳定,就需要确定力学模型及其对应的支座位置。
通过有限个节点以及一定的刚度,用支撑力法(support force method)分析问题,可以得到节点的位移。
根据这个位移的大小,以及构成支座的刚度系数,可以得到支座的弹力系数和承载力,最后可以得知四边简支矩形板的稳定性情况。
另外,要求四边简支矩形板稳定,必须建立计算机编程模型,通过C语言或者Fortran等编程语言来实现计算,这样可以更精确地求得四边简支矩形板的稳定性解,使得在设计结构时,能够更好地优化支座的位置,从而使板的稳定性更为明确。
因此,我们可以得出结论,采用正确的力学模型及其对应的支座位置,并建
立计算机编程模型,就可以正确精确地求得四边简支矩形板的稳定性解,从而使得结构物的稳定性更为可靠。
abaqus四边简支板的边界条件

abaqus四边简支板的边界条件全文共四篇示例,供读者参考第一篇示例:在ABAQUS中,四边简支板是一个常见的结构,通常用于测试和学习有限元分析的基本原理。
在进行有限元分析时,正确的设置边界条件至关重要,因为它们直接影响到结果的准确性和可靠性。
下面我们来讨论一下关于ABAQUS四边简支板的边界条件设置。
四边简支板是一种简单的结构,由一个矩形板和四个简支支撑组成。
在有限元分析中,我们需要对这个结构进行几何建模,材料属性定义以及加载和边界条件的设置。
在这里,我们主要关注边界条件的设置。
我们需要定义四边简支板的几何尺寸和材料属性。
在ABAQUS中,我们可以通过几何建模模块来绘制板的几何形状,并通过材料属性来定义板的材料性质,比如弹性模量、泊松比、密度等等。
接下来,我们需要设置四边简支板的边界条件。
在这个问题中,四边简支板的四个边分别是简支边界,所以我们需要将这四个边定义为简支条件。
简支条件意味着这四个边不能有任何位移或旋转,而约束了结构的自由度。
在ABAQUS中,我们可以通过施加位移边界条件或定义边界条件来实现这一设置。
在完成边界条件的设置后,我们还需要定义加载条件。
对于简支板的加载条件,通常可以施加均布载荷、集中载荷或者边界支撑反力等。
通过在适当位置施加加载,我们可以模拟不同的工程情况和应力状态。
我们需要选择适当的求解器和求解算法,运行模拟并分析结果。
通过正确设置边界条件,我们可以得到精确的应力、应变和位移结果,从而评估结构的性能和稳定性,为工程设计提供重要参考。
ABAQUS四边简支板的边界条件设置是有限元分析中的关键步骤,直接影响到结果的准确性和可靠性。
通过正确设置简支条件,加载条件和求解算法,我们可以得到准确的模拟结果,帮助工程师更好地理解和优化结构设计。
希望以上内容能对您有所帮助,谢谢阅读!第二篇示例:Abaqus是一种用于进行有限元分析的强大软件工具,它可以用来研究各种结构的性能和行为。
在实际工程中,我们经常会遇到四边简支板的问题,这种结构在工程设计中应用广泛。
单块矩形板计算典型例题
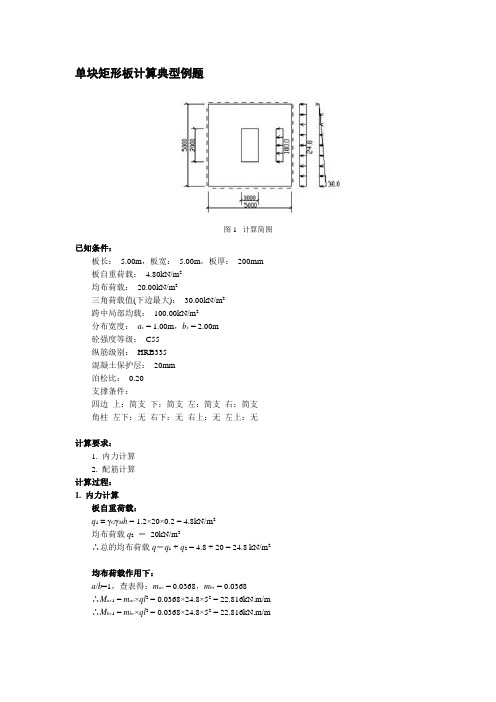
单块矩形板计算典型例题图1 计算简图已知条件:板长: 5.00m,板宽: 5.00m,板厚:200mm板自重荷载: 4.80kN/m2均布荷载:20.00kN/m2三角荷载值(下边最大):30.00kN/m2跨中局部均载:100.00kN/m2分布宽度:a x = 1.00m,b y = 2.00m砼强度等级:C55纵筋级别:HRB335混凝土保护层:20mm泊松比:0.20支撑条件:四边上:简支下:简支左:简支右:简支角柱左下:无右下:无右上:无左上:无计算要求:1. 内力计算2. 配筋计算计算过程:1. 内力计算板自重荷载:q1= γGγM h = 1.2×20×0.2 = 4.8kN/m2均布荷载q2=20kN/m2∴总的均布荷载q=q1 + q2 = 4.8 + 20 = 24.8 kN/m2均布荷载作用下:a/b=1,查表得:m ac = 0.0368,m bc = 0.0368∴M ac1 = m ac×ql2 = 0.0368×24.8×52 = 22.816kN.m/m ∴M bc1 = m bc×ql2 = 0.0368×24.8×52 = 22.816kN.m/m三角形荷载作用下:a/b=1,查表得:m amax = 0.0184,m bmax = 0.0216∴M ac2 = m amax×ql2 = 0.0184×30×52 = 13.8kN.m/m∴M bc2 = m bmax×ql2 = 0.0216×30×52 = 16.2kN.m/m跨中局部均载作用下:a x / a = 1 / 5 = 0.2,b y / b = 2 / 5 = 0.4,b / a = 1查表得:m ac = 0.143,m bc = 0.117∴M ac3 = m ac×qa x b y = 0.143×100×1×2 = 28.6kN.m/m∴M bc3 = m bc×qa x b y = 0.117×100×1×2 = 23.4kN.m/m根据叠加原理,得M ac=M ac1+M ac2+M ac3 = 22.816+13.8+28.6 = 65.216kN.m/mM bc=M bc1+M bc2+M bc3 = 22.816+16.2+23.4 = 62.416kN.m/m∵泊松比=0.2≠0,且板边无自由边,∴必须对跨中弯矩进行调整。
简述用机动法计算钢筋混凝土四边固定矩形双向板极限荷载的要点及步骤

简述用机动法计算钢筋混凝土四边固定矩形双向板极限荷载的要点及步骤钢筋混凝土四边固定矩形双向板是建筑结构中常见的构件之一。
在设计中,计算其极限荷载是非常重要的一步。
本文将简述用机动法计算钢筋混凝土四边固定矩形双向板极限荷载的要点及步骤,希望能对您有所帮助。
1. 前置知识在进行计算之前,需要掌握以下基本知识:1)重力荷载的计算方法,包括自重和活载。
2)双向板的构造形式和受力特点。
3)混凝土和钢筋的弹性模量、黏度、极限应力等材料力学参数。
4)机动法的基本理论和计算步骤。
2. 计算步骤通过以上的前置知识,我们可以开始进行机动法计算钢筋混凝土四边固定矩形双向板极限荷载。
其计算步骤如下:1)确定荷载组合,一般采用组合状况Ⅰ(DL+LL)。
2)确定板的受力状态,即确定板的边界条件,一般分为四边固定和四边自由两种情况。
本文中采用四边固定的情况。
3)确定板的受力方式,即确定板的初始应力分布。
本文中采用等应力分布的方式。
4)进行非线性分析,即通过机动法进行分析计算。
5)反复迭代,直至收敛为止。
以下,我们将具体解释这些步骤。
3. 确定荷载组合荷载组合是指在不同工况下受力的组合方式,对于双向板来说,一般采用组合状况Ⅰ(DL+LL)。
其中DL指自重荷载,LL指活载荷载。
在确定荷载组合之后,我们需要对板进行分析计算。
4. 确定板的受力状态在双向板的受力状态中,根据板的支承和边界条件的不同,受力状态也会有所不同。
一般来说,边界条件分为四边固定和四边自由两种情况。
本文中采用四边固定的情况,即在四个边界都受到约束的情况下进行计算。
5. 确定板的受力方式在四边固定的双向板中,其受力方式有多种。
一般来说,初始应力分布采用等应力分布的方式,即在板的中心部位应力值最大,在板的边缘部位则比较小。
这种应力分布方式可以保证板的整体稳定性。
6. 进行非线性分析进行非线性分析的过程中,我们需要采用机动法进行分析。
机动法是求解结构变形、内力和反力的有效方法。
第二章 薄板振动分析

§2-1 薄板的自由振动
等厚度各向同性薄板的非齐次运动方程为
4w
m D
2w t 2
px, y,t
D
(1)
其中 m 为板的单位面积上的质量。p 为动载荷。
首先考虑齐次运动方程,即自由振动问题
4w m 2w 0 D t 2
(2)
令 w = T(t)W(x,y), 代入齐次方程,两边同除TW, 得
wt
ab 00
mx ny
0 sin a sin b
w sin mx st t0a来自dxdy cosmnt
in
ny
b
dxdy
sinmnt
s
in
mx
asinny
b
讨论 运用分离变量法解偏微分方程,必然导致固有值问题:
•分离变量法要求分离变量后每个函数有非零解,因此要求固有 值存在;
•方程和定解条件要求固有函数具有正交性和完备性; •非齐次初值条件或自由项(受迫振动时)或方程的解等,应能 用固有函数展开成平均收敛的级数。
2
2
dW dr
d2W dr 2
dr
对于夹支圆形薄板,可简化为
(7)
UW
Dr
d2W dr 2
2
1 r
dW dr
2
dr
(8)
设薄板振形泛函为
4W 2 m W 0
D
U
W
2
1 2
m
W
2dxdy
(9)
其中W为可能的振形函数。可以证明由泛函的驻值条件可以 导出方程(4)。
为了求固有频率或固有函数的近似解,设
32D
3a2
2m
矩形容器设计计算

1、类型说明:加固圈数量nE型(垂直横向联合加固型)矩形容器E型矩形容器为四边简支,有顶边和垂直、横向加固件,设计压力为常压,仅承受液体静压的矩形容器。
本计算对壁板,顶板(可选)和底板作强度、刚度分析,对加固件作刚度分析。
604.964188cm49.45256545cm448.17cm4结论:不合格合格111.212693mm结论:选用合格8、顶板强度计算(如不作顶板设计,此可忽略)查图8-15得α=0.048234 1.6885607mm δ=δt+C1+C2= 2.1885607mm 顶板的名义厚度δtn取为:6mm当无拉杆时选用当有拉杆时选用拉杆材质是否是普通碳钢:(碳钢填1,其他填0)当无拉杆时,Hc=H,Lc=L,顶边加固件所需的惯性矩I cT 为:当有拉杆时,Hc=H,Lc=Lp,顶边加固件所需的惯性矩I cT 为:拉杆的最小直径d min 为:顶板承受自重所需的计算厚度δt:选用的顶边加固件惯性矩为:9、顶板刚度校核(如不作顶板设计,此可忽略)查图8-15得β=0.044374顶板有效厚度δte: 5.5mm2.2671066mm23.75结论:选用合格6472.8493mm3= 6.472849cm3顶板加强筋选用:20.47cm3结论:11、底板设计底板计算厚度δb:6.1020518mm δ= 6.6020518mm8mm610.04515mm 结论:合格2)、在平基础上全平面支撑的底板最终取底板厚度:8mm最终取底板名义厚度为型钢的最大跨距Lb,max为:当底板整个表面被支撑时,底板最小厚度常用4mm~6mm,(或与壁板等厚),并考虑腐蚀裕度。
T,W 顶板加强筋截面系数:L100X100X8合格顶板最大挠度f T,max :顶板的许用挠度[f]:。
矩形板计算

LB20矩形板计算项目名称_____________日期_____________设计者_____________校对者_____________一、构件编号: LB20二、示意图三、依据规范《建筑结构荷载规范》 GB50009-2001《混凝土结构设计规范》 GB50010-2010四、计算信息1.几何参数计算跨度: Lx = 4500 mm; Ly = 4550 mm板厚: h = 120 mm2.材料信息混凝土等级: C30 fc=14.3N/mm2 ft=1.43N/mm2 ftk=2.01N/mm2 Ec=3.00×104N/mm2钢筋种类: HRB335 fy = 300 N/mm2Es = 2.0×105 N/mm2最小配筋率: ρ= 0.214%纵向受拉钢筋合力点至近边距离: as = 20mm保护层厚度: c = 10mm3.荷载信息(均布荷载)= 1.200永久荷载分项系数: γG= 1.400可变荷载分项系数: γQ准永久值系数: ψq = 0.500永久荷载标准值: qgk = 5.000kN/m2可变荷载标准值: qqk = 2.000kN/m24.计算方法:弹性板5.边界条件(上端/下端/左端/右端):固定/简支/固定/固定6.设计参数结构重要性系数: γo = 1.00泊松比:μ = 0.200五、计算参数:1.计算板的跨度: Lo = 4500 mm2.计算板的有效高度: ho = h-as=120-20=100 mm六、荷载组合可变荷载控制组合:q = γG*qgk+γQ*qqk= 1.200*5.000+1.400*2.000= 8.800 KN/m2永久荷载控制组合:q = γG*qgk+γQ*qqk= 1.35*qgk+0.7*γQ*qqk= 1.35*5.000+0.7*1.400*2.000= 8.710 KN/m2取较大值荷载控制组合为:q = 8.800 KN/m2七、配筋计算(lx/ly=4500/4550=0.989<2.000 所以按双向板计算):1.X向底板钢筋1) 确定X向板底弯矩Mx = 表中系数q*Lo2= (0.0236+0.0178*0.200)*8.800*4.52= 4.834 kN*m2) 确定计算系数αs = γo*M/(α1*fc*b*ho*ho)= 1.00*4.834×106/(1.00*14.3*1000*100*100)= 0.0343) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.034) = 0.0344) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*100*0.034/300 = 164mm25) 验算最小配筋率ρ = As/(b*h) = 164/(1000*120) = 0.137%ρ<ρmin = 0.214% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.214%*1000*120 = 257 mm2用户选择了底板放大系数,系数值为:1.00所以最后面积As = 257*1.00 = 257 mm2采取方案 12@200, 实配面积565 mm22.Y向底板钢筋1) 确定Y向板底弯矩My = 表中系数q*Lo2= (0.0178+0.0236*0.200)*8.800*4.52= 4.016 kN*m2) 确定计算系数αs = γo*M/(α1*fc*b*ho*ho)= 1.00*4.016×106/(1.00*14.3*1000*100*100)= 0.0283) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.028) = 0.0284) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*100*0.028/300 = 136mm25) 验算最小配筋率ρ = As/(b*h) = 136/(1000*120) = 0.113%ρ<ρmin = 0.214% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.214%*1000*120 = 257 mm2用户选择了底板放大系数,系数值为:1.00所以最后面积As = 257*1.00 = 257 mm2采取方案 12@200, 实配面积565 mm23.X向支座左边钢筋1) 确定左边支座弯矩M o x = 表中系数q*Lo2= 0.0607*8.800*4.52= 10.813 kN*m2) 确定计算系数αs = γo*M/(α1*fc*b*ho*ho)= 1.00*10.813×106/(1.00*14.3*1000*100*100)= 0.0763) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.076) = 0.0794) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*100*0.079/300 = 375mm25) 验算最小配筋率ρ = As/(b*h) = 375/(1000*120) = 0.313%ρ≥ρmin = 0.214% 满足最小配筋要求用户选择了支座放大系数,系数值为:1.00所以最后面积As = 375*1.00 = 375 mm2采取方案 12@200, 实配面积565 mm24.X向支座右边钢筋1) 确定右边支座弯矩M o x = 表中系数q*Lo2= 0.0607*8.800*4.52= 10.813 kN*m2) 确定计算系数αs = γo*M/(α1*fc*b*ho*ho)= 1.00*10.813×106/(1.00*14.3*1000*100*100)= 0.0763) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.076) = 0.0794) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*100*0.079/300= 375mm25) 验算最小配筋率ρ = As/(b*h) = 375/(1000*120) = 0.313%ρ≥ρmin = 0.214% 满足最小配筋要求用户选择了支座放大系数,系数值为:1.00所以最后面积As = 375*1.00 = 375 mm2采取方案 12@200, 实配面积565 mm25.Y向上边支座钢筋1) 确定上边支座弯矩M o y = 表中系数q*Lo2= 0.0552*8.800*4.52= 9.832 kN*m2) 确定计算系数αs = γo*M/(α1*fc*b*ho*ho)= 1.00*9.832×106/(1.00*14.3*1000*100*100)= 0.0693) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.069) = 0.0714) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*100*0.071/300= 340mm25) 验算最小配筋率ρ = As/(b*h) = 340/(1000*120) = 0.283%ρ≥ρmin = 0.214% 满足最小配筋要求用户选择了支座放大系数,系数值为:1.00所以最后面积As = 340*1.00 = 340 mm2采取方案 12@200, 实配面积565 mm2八、跨中挠度计算:Mk -------- 按荷载效应的标准组合计算的弯矩值Mq -------- 按荷载效应的准永久组合计算的弯矩值1.计算荷载效应Mk = Mgk + Mqk= (0.0236+0.0178*0.200)*(5.000+2.000)*4.52 = 3.845 kN*mMq = Mgk+ψq*Mqk= (0.0236+0.0178*0.200)*(5.000+0.5*2.000)*4.52 = 3.296 kN*m2.计算受弯构件的短期刚度 Bs1) 计算按荷载荷载效应的标准组合及准永久组合作用下,构件纵向受拉钢筋应力σsk = Mk/(0.87*ho*As) 混规(7.1.4-3)= 3.845×106/(0.87*100*565) = 78.225 N/mmσsq = Mq/(0.87*ho*As) 混规(7.1.4-3)= 3.296×106/(0.87*100*565) = 67.050 N/mm2) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积: Ate = 0.5*b*h = 0.5*1000*120= 60000mm2ρte = As/Ate 混规(7.1.2-4)= 565/60000 = 0.942%3) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψk = 1.1-0.65*ftk/(ρte*σsk) 混规(7.1.2-2)= 1.1-0.65*2.01/(0.942%*78.225) = -0.674ψq = 1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)= 1.1-0.65*2.01/(0.942%*78.225) = -0.969因为ψ不能小于最小值0.2,所以取ψk = 0.2因为ψ不能小于最小值0.2,所以取ψq = 0.24) 计算钢筋弹性模量与混凝土模量的比值αEαE = Es/Ec = 2.0×105/3.00×104 = 6.6675) 计算受压翼缘面积与腹板有效面积的比值γ f矩形截面,γf=06) 计算纵向受拉钢筋配筋率ρρ = As/(b*ho)= 565/(1000*100) = 0.565%7) 计算受弯构件的短期刚度 BsBsk = Es*As*ho2/[1.15ψk+0.2+6*αE*ρ/(1+ 3.5γf')] 混规(7.2.3-1) = 2.0×105*565*1002/[1.15*0.200+0.2+6*6.667*0.565%/(1+3.5*0.0)]= 1.723×103 kN*m2Bsq = Es*As*ho2/[1.15ψq+0.2+6*αE*ρ/(1+ 3.5γf')] 混规(7.2.3-1) = 2.0×105*565*1002/[1.15*0.200+0.2+6*6.667*0.565%/(1+3.5*0.0)]= 1.723×103 kN*m23.计算受弯构件的长期刚度B1) 确定考虑荷载长期效应组合对挠度影响增大影响系数θ当ρ'=0时,θ=2.0 混规(7.2.5)2) 计算受弯构件的长期刚度 BBk = Mk/(Mq*(θ-1)+Mk)*Bsk (混规(7.2.2-1))= 3.845/(3.296*(2.0-1)+3.845)*1.723×103= 9.275×102 kN*m2Bq = Bsq/θ (混规(7.2.2-2))= 1.723×103/2.0= 8.613×102 kN*m2B = min(Bk,Bq)= min(927.533,861.280)= 861.2804.计算受弯构件挠度fmax = f*(qgk+qqk)*Lo4/B= 0.00163*(5.000+2.000)*4.54/8.613×102 = 5.420mm5.验算挠度挠度限值fo=Lo/200=4500/200=22.500mmfmax=5.420mm≤fo=22.500mm,满足规范要求!九、裂缝宽度验算:1.跨中X方向裂缝1) 计算荷载效应Mx = 表中系数*(qgk+ψq*qqk)*Lo2= (0.0236+0.0178*0.200)*(5.000+0.5*2.000)*4.52= 3.296 kN*m2) 光面钢筋,所以取值vi=0.73) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=3.296×106/(0.87*100*565)=67.050N/mm4) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4)=565/60000 = 0.0094因为ρte=0.0094 < 0.01,所以让ρte=0.015) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*67.050)=-0.849因为ψ=-0.849 < 0.2,所以让ψ=0.26) 计算单位面积钢筋根数nn=1000/dist = 1000/200=57) 计算受拉区纵向钢筋的等效直径deqdeq = (∑ni*di2)/(∑ni*vi*di)=5*12*12/(5*0.7*12)=17 mm8) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.200*67.050/2.0×105*(1.9*20+0.08*17/0.0100)=0.0223mm ≤ 0.20 mm, 满足规范要求2.跨中Y方向裂缝1) 计算荷载效应My = 表中系数(qgk+ψq*qqk)*Lo2= (0.0178+0.0236*0.200)*(5.000+0.5*2.000)*4.52= 2.738 kN*m2) 光面钢筋,所以取值vi=0.73) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=2.738×106/(0.87*100*565)=55.705N/mm4) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4)=565/60000 = 0.0094因为ρte=0.0094 < 0.01,所以让ρte=0.015) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2) =1.1-0.65*2.010/(0.0100*55.705)=-1.245因为ψ=-1.245 < 0.2,所以让ψ=0.26) 计算单位面积钢筋根数nn=1000/dist = 1000/200=57) 计算受拉区纵向钢筋的等效直径deqdeq = (∑ni*di2)/(∑ni*vi*di)=5*12*12/(5*0.7*12)=17 mm8) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.200*55.705/2.0×105*(1.9*20+0.08*17/0.0100)=0.0185mm ≤ 0.20 mm, 满足规范要求3.支座上方向裂缝1) 计算荷载效应M o y = 表中系数(qgk+ψq*qqk)*Lo2= 0.0552*(5.000+0.5*2.000)*4.52= 6.704 kN*m2) 光面钢筋,所以取值vi=0.73) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=6.704×106/(0.87*100*565)=136.382N/mm4) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4)=565/60000 = 0.0094因为ρte=0.0094 < 0.01,所以让ρte=0.015) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*136.382)=0.142因为ψ=0.142 < 0.2,所以让ψ=0.26) 计算单位面积钢筋根数nn=1000/dist = 1000/200=57) 计算受拉区纵向钢筋的等效直径deqdeq = (∑ni*di2)/(∑ni*vi*di)=5*12*12/(5*0.7*12)=17 mm8) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.200*136.382/2.0×105*(1.9*20+0.08*17/0.0100)=0.0454mm ≤ 0.20 mm, 满足规范要求4.支座左方向裂缝1) 计算荷载效应M o x = 表中系数(qgk+ψq*qqk)*Lo2= 0.0607*(5.000+0.5*2.000)*4.52= 7.373 kN*m2) 光面钢筋,所以取值vi=0.73) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=7.373×106/(0.87*100*565)=149.990N/mm4) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4)=565/60000 = 0.0094因为ρte=0.0094 < 0.01,所以让ρte=0.015) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*149.990)=0.2296) 计算单位面积钢筋根数nn=1000/dist = 1000/200=57) 计算受拉区纵向钢筋的等效直径deqdeq = (∑ni*di2)/(∑ni*vi*di)=5*12*12/(5*0.7*12)=17 mm8) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.229*149.990/2.0×105*(1.9*20+0.08*17/0.0100)=0.0571mm ≤ 0.20 mm, 满足规范要求5.支座右方向裂缝1) 计算荷载效应M o x = 表中系数(qgk+qqk)*Lo2= 0.0607*(5.000+0.5*2.000)*4.52= 7.373 kN*m2) 光面钢筋,所以取值vi=0.73) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=7.373×106/(0.87*100*565)=149.990N/mm4) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4)=565/60000 = 0.0094因为ρte=0.0094 < 0.01,所以让ρte=0.015) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*149.990)=0.2296) 计算单位面积钢筋根数nn=1000/dist = 1000/200=57) 计算受拉区纵向钢筋的等效直径deqdeq = (∑ni*di2)/(∑ni*vi*di)=5*12*12/(5*0.7*12)=17 mm8) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.229*149.990/2.0×105*(1.9*20+0.08*17/0.0100)=0.0571mm ≤ 0.20 mm, 满足规范要求LB22矩形板计算项目名称_____________日期_____________设计者_____________校对者_____________一、构件编号: LB22二、示意图三、依据规范《建筑结构荷载规范》 GB50009-2001《混凝土结构设计规范》 GB50010-2010四、计算信息1.几何参数计算跨度: Lx = 4500 mm; Ly = 4500 mm板厚: h = 120 mm2.材料信息混凝土等级: C30 fc=14.3N/mm2 ft=1.43N/mm2 ftk=2.01N/mm2 Ec=3.00×104N/mm2钢筋种类: HRB335 fy = 300 N/mm2Es = 2.0×105 N/mm2最小配筋率: ρ= 0.214%纵向受拉钢筋合力点至近边距离: as = 20mm保护层厚度: c = 10mm3.荷载信息(均布荷载)= 1.200永久荷载分项系数: γG= 1.400可变荷载分项系数: γQ准永久值系数: ψq = 0.500永久荷载标准值: qgk = 5.000kN/m2可变荷载标准值: qqk = 2.000kN/m24.计算方法:弹性板5.边界条件(上端/下端/左端/右端):固定/固定/固定/固定6.设计参数结构重要性系数: γo = 1.00泊松比:μ = 0.200五、计算参数:1.计算板的跨度: Lo = 4500 mm2.计算板的有效高度: ho = h-as=120-20=100 mm六、荷载组合可变荷载控制组合:q = γG*qgk+γQ*qqk= 1.200*5.000+1.400*2.000= 8.800 KN/m2永久荷载控制组合:q = γG*qgk+γQ*qqk= 1.35*qgk+0.7*γQ*qqk= 1.35*5.000+0.7*1.400*2.000= 8.710 KN/m2取较大值荷载控制组合为:q = 8.800 KN/m2七、配筋计算(lx/ly=4500/4500=1.000<2.000 所以按双向板计算):1.X向底板钢筋1) 确定X向板底弯矩Mx = 表中系数q*Lo2= (0.0176+0.0176*0.200)*8.800*4.52= 3.764 kN*m2) 确定计算系数αs = γo*M/(α1*fc*b*ho*ho)= 1.00*3.764×106/(1.00*14.3*1000*100*100)= 0.0263) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.026) = 0.0274) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*100*0.027/300 = 127mm25) 验算最小配筋率ρ = As/(b*h) = 127/(1000*120) = 0.106%ρ<ρmin = 0.214% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.214%*1000*120 = 257 mm2用户选择了底板放大系数,系数值为:1.00所以最后面积As = 257*1.00 = 257 mm2采取方案 12@200, 实配面积565 mm22.Y向底板钢筋1) 确定Y向板底弯矩My = 表中系数q*Lo2= (0.0176+0.0176*0.200)*8.800*4.52= 3.764 kN*m2) 确定计算系数αs = γo*M/(α1*fc*b*ho*ho)= 1.00*3.764×106/(1.00*14.3*1000*100*100)= 0.0263) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.026) = 0.0274) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*100*0.027/300 = 127mm25) 验算最小配筋率ρ = As/(b*h) = 127/(1000*120) = 0.106%ρ<ρmin = 0.214% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.214%*1000*120 = 257 mm2用户选择了底板放大系数,系数值为:1.00所以最后面积As = 257*1.00 = 257 mm2采取方案 12@200, 实配面积565 mm23.X向支座左边钢筋1) 确定左边支座弯矩M o x = 表中系数q*Lo2= 0.0513*8.800*4.52= 9.142 kN*m2) 确定计算系数αs = γo*M/(α1*fc*b*ho*ho)= 1.00*9.142×106/(1.00*14.3*1000*100*100)= 0.0643) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.064) = 0.0664) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*100*0.066/300 = 315mm25) 验算最小配筋率ρ = As/(b*h) = 315/(1000*120) = 0.263%ρ≥ρmin = 0.214% 满足最小配筋要求用户选择了支座放大系数,系数值为:1.00所以最后面积As = 315*1.00 = 315 mm2采取方案 12@200, 实配面积565 mm24.X向支座右边钢筋1) 确定右边支座弯矩M o x = 表中系数q*Lo2= 0.0513*8.800*4.52= 9.142 kN*m2) 确定计算系数αs = γo*M/(α1*fc*b*ho*ho)= 1.00*9.142×106/(1.00*14.3*1000*100*100)= 0.0643) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.064) = 0.0664) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*100*0.066/300 = 315mm25) 验算最小配筋率ρ = As/(b*h) = 315/(1000*120) = 0.263%ρ≥ρmin = 0.214% 满足最小配筋要求用户选择了支座放大系数,系数值为:1.00所以最后面积As = 315*1.00 = 315 mm2采取方案 12@200, 实配面积565 mm25.Y向上边支座钢筋1) 确定上边支座弯矩M o y = 表中系数q*Lo2= 0.0513*8.800*4.52= 9.142 kN*m2) 确定计算系数αs = γo*M/(α1*fc*b*ho*ho)= 1.00*9.142×106/(1.00*14.3*1000*100*100)= 0.0643) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.064) = 0.0664) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*100*0.066/300 = 315mm25) 验算最小配筋率ρ = As/(b*h) = 315/(1000*120) = 0.263%ρ≥ρmin = 0.214% 满足最小配筋要求用户选择了支座放大系数,系数值为:1.00所以最后面积As = 315*1.00 = 315 mm2采取方案 12@200, 实配面积565 mm26.Y向下边支座钢筋1) 确定下边支座弯矩M o y = 表中系数q*Lo2= 0.0513*8.800*4.52= 9.142 kN*m2) 确定计算系数αs = γo*M/(α1*fc*b*ho*ho)= 1.00*9.142×106/(1.00*14.3*1000*100*100)= 0.0643) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.064) = 0.0664) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*100*0.066/300= 315mm25) 验算最小配筋率ρ = As/(b*h) = 315/(1000*120) = 0.263%ρ≥ρmin = 0.214% 满足最小配筋要求用户选择了支座放大系数,系数值为:1.00所以最后面积As = 315*1.00 = 315 mm2采取方案 12@200, 实配面积565 mm2八、跨中挠度计算:Mk -------- 按荷载效应的标准组合计算的弯矩值Mq -------- 按荷载效应的准永久组合计算的弯矩值1.计算荷载效应Mk = Mgk + Mqk= (0.0176+0.0176*0.200)*(5.000+2.000)*4.52 = 2.994 kN*mMq = Mgk+ψq*Mqk= (0.0176+0.0176*0.200)*(5.000+0.5*2.000)*4.52 = 2.566 kN*m2.计算受弯构件的短期刚度 Bs1) 计算按荷载荷载效应的标准组合及准永久组合作用下,构件纵向受拉钢筋应力σsk = Mk/(0.87*ho*As) 混规(7.1.4-3)= 2.994×106/(0.87*100*565) = 60.904 N/mmσsq = Mq/(0.87*ho*As) 混规(7.1.4-3)= 2.566×106/(0.87*100*565) = 52.204 N/mm2) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积: Ate = 0.5*b*h = 0.5*1000*120= 60000mm2ρte = As/Ate 混规(7.1.2-4)= 565/60000 = 0.942%3) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψk = 1.1-0.65*ftk/(ρte*σsk) 混规(7.1.2-2)= 1.1-0.65*2.01/(0.942%*60.904) = -1.178ψq = 1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)= 1.1-0.65*2.01/(0.942%*60.904) = -1.558因为ψ不能小于最小值0.2,所以取ψk = 0.2因为ψ不能小于最小值0.2,所以取ψq = 0.24) 计算钢筋弹性模量与混凝土模量的比值αEαE = Es/Ec = 2.0×105/3.00×104 = 6.6675) 计算受压翼缘面积与腹板有效面积的比值γ f矩形截面,γf=06) 计算纵向受拉钢筋配筋率ρρ = As/(b*ho)= 565/(1000*100) = 0.565%7) 计算受弯构件的短期刚度 BsBsk = Es*As*ho2/[1.15ψk+0.2+6*αE*ρ/(1+ 3.5γf')] 混规(7.2.3-1) = 2.0×105*565*1002/[1.15*0.200+0.2+6*6.667*0.565%/(1+3.5*0.0)]= 1.723×103 kN*m2Bsq = Es*As*ho2/[1.15ψq+0.2+6*αE*ρ/(1+ 3.5γf')] 混规(7.2.3-1)= 2.0×105*565*1002/[1.15*0.200+0.2+6*6.667*0.565%/(1+3.5*0.0)]= 1.723×103 kN*m23.计算受弯构件的长期刚度B1) 确定考虑荷载长期效应组合对挠度影响增大影响系数θ当ρ'=0时,θ=2.0 混规(7.2.5)2) 计算受弯构件的长期刚度 BBk = Mk/(Mq*(θ-1)+Mk)*Bsk (混规(7.2.2-1))= 2.994/(2.566*(2.0-1)+2.994)*1.723×103= 9.275×102 kN*m2Bq = Bsq/θ (混规(7.2.2-2))= 1.723×103/2.0= 8.613×102 kN*m2B = min(Bk,Bq)= min(927.533,861.280)= 861.2804.计算受弯构件挠度fmax = f*(qgk+qqk)*Lo4/B= 0.00127*(5.000+2.000)*4.54/8.613×102= 4.233mm5.验算挠度挠度限值fo=Lo/200=4500/200=22.500mmfmax=4.233mm≤fo=22.500mm,满足规范要求!九、裂缝宽度验算:1.跨中X方向裂缝1) 计算荷载效应Mx = 表中系数(qgk+ψq*qqk)*Lo2= (0.0176+0.0176*0.200)*(5.000+0.5*2.000)*4.52= 2.566 kN*m2) 光面钢筋,所以取值vi=0.73) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=2.566×106/(0.87*100*565)=52.204N/mm4) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4)=565/60000 = 0.0094因为ρte=0.0094 < 0.01,所以让ρte=0.015) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*52.204)=-1.403因为ψ=-1.403 < 0.2,所以让ψ=0.26) 计算单位面积钢筋根数nn=1000/dist = 1000/200=57) 计算受拉区纵向钢筋的等效直径deqdeq = (∑ni*di2)/(∑ni*vi*di)=5*12*12/(5*0.7*12)=17 mm8) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.200*52.204/2.0×105*(1.9*20+0.08*17/0.0100)=0.0174mm ≤ 0.20 mm, 满足规范要求2.跨中Y方向裂缝1) 计算荷载效应My = 表中系数(qgk+ψq*qqk)*Lo2= (0.0176+0.0176*0.200)*(5.000+0.5*2.000)*4.52= 2.566 kN*m2) 光面钢筋,所以取值vi=0.73) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=2.566×106/(0.87*100*565)=52.204N/mm4) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4)=565/60000 = 0.0094因为ρte=0.0094 < 0.01,所以让ρte=0.015) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*52.204)=-1.403因为ψ=-1.403 < 0.2,所以让ψ=0.26) 计算单位面积钢筋根数nn=1000/dist = 1000/200=57) 计算受拉区纵向钢筋的等效直径deqdeq = (∑ni*di2)/(∑ni*vi*di)=5*12*12/(5*0.7*12)=17 mm8) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.200*52.204/2.0×105*(1.9*20+0.08*17/0.0100)=0.0174mm ≤ 0.20 mm, 满足规范要求3.支座上方向裂缝1) 计算荷载效应M o y = 表中系数(qgk+ψq*qqk)*Lo2= 0.0513*(5.000+0.5*2.000)*4.52= 6.233 kN*m2) 光面钢筋,所以取值vi=0.73) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=6.233×106/(0.87*100*565)=126.802N/mm4) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4)=565/60000 = 0.0094因为ρte=0.0094 < 0.01,所以让ρte=0.015) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*126.802)=0.070因为ψ=0.070 < 0.2,所以让ψ=0.26) 计算单位面积钢筋根数nn=1000/dist = 1000/200=57) 计算受拉区纵向钢筋的等效直径deqdeq = (∑ni*di2)/(∑ni*vi*di)=5*12*12/(5*0.7*12)=17 mm8) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.200*126.802/2.0×105*(1.9*20+0.08*17/0.0100)=0.0422mm ≤ 0.20 mm, 满足规范要求4.支座下方向裂缝1) 计算荷载效应M o y = 表中系数(qgk+ψq*qqk)*Lo2= 0.0513*(5.000+0.5*2.000)*4.52= 6.233 kN*m2) 光面钢筋,所以取值vi=0.73) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=6.233×106/(0.87*100*565)=126.802N/mm4) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4)=565/60000 = 0.0094因为ρte=0.0094 < 0.01,所以让ρte=0.015) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*126.802)=0.070因为ψ=0.070 < 0.2,所以让ψ=0.2 6) 计算单位面积钢筋根数nn=1000/dist = 1000/200=57) 计算受拉区纵向钢筋的等效直径deqdeq = (∑ni*di2)/(∑ni*vi*di)=5*12*12/(5*0.7*12)=17 mm8) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.200*126.802/2.0×105*(1.9*20+0.08*17/0.0100)=0.0422mm ≤ 0.20 mm, 满足规范要求5.支座左方向裂缝1) 计算荷载效应M o x = 表中系数(qgk+ψq*qqk)*Lo2= 0.0513*(5.000+0.5*2.000)*4.52= 6.233 kN*m2) 光面钢筋,所以取值vi=0.73) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=6.233×106/(0.87*100*565)=126.802N/mm4) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4)=565/60000 = 0.0094因为ρte=0.0094 < 0.01,所以让ρte=0.015) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*126.802)=0.070因为ψ=0.070 < 0.2,所以让ψ=0.26) 计算单位面积钢筋根数nn=1000/dist = 1000/200=57) 计算受拉区纵向钢筋的等效直径deqdeq = (∑ni*di2)/(∑ni*vi*di)=5*12*12/(5*0.7*12)=17 mm8) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.200*126.802/2.0×105*(1.9*20+0.08*17/0.0100)=0.0422mm ≤ 0.20 mm, 满足规范要求6.支座右方向裂缝1) 计算荷载效应M o x = 表中系数(qgk+qqk)*Lo2= 0.0513*(5.000+0.5*2.000)*4.52= 6.233 kN*m2) 光面钢筋,所以取值vi=0.73) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=6.233×106/(0.87*100*565)=126.802N/mm4) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4)=565/60000 = 0.0094因为ρte=0.0094 < 0.01,所以让ρte=0.015) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*126.802)=0.070因为ψ=0.070 < 0.2,所以让ψ=0.26) 计算单位面积钢筋根数nn=1000/dist = 1000/200=57) 计算受拉区纵向钢筋的等效直径deqdeq = (∑ni*di2)/(∑ni*vi*di)=5*12*12/(5*0.7*12)=17 mm8) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.200*126.802/2.0×105*(1.9*20+0.08*17/0.0100)=0.0422mm ≤ 0.20 mm, 满足规范要求LB31矩形板计算项目名称_____________日期_____________设计者_____________校对者_____________一、构件编号: LB31二、示意图三、依据规范《建筑结构荷载规范》 GB50009-2001《混凝土结构设计规范》 GB50010-2010四、计算信息1.几何参数计算跨度: Lx = 4550 mm; Ly = 4550 mm板厚: h = 120 mm2.材料信息混凝土等级: C30 fc=14.3N/mm2 ft=1.43N/mm2 ftk=2.01N/mm2 Ec=3.00×104N/mm2钢筋种类: HRB335 fy = 300 N/mm2Es = 2.0×105 N/mm2最小配筋率: ρ= 0.214%纵向受拉钢筋合力点至近边距离: as = 20mm保护层厚度: c = 10mm3.荷载信息(均布荷载)= 1.200永久荷载分项系数: γG= 1.400可变荷载分项系数: γQ准永久值系数: ψq = 0.500永久荷载标准值: qgk = 5.000kN/m2可变荷载标准值: qqk = 2.000kN/m24.计算方法:弹性板5.边界条件(上端/下端/左端/右端):简支/固定/固定/简支6.设计参数结构重要性系数: γo = 1.00泊松比:μ = 0.200五、计算参数:1.计算板的跨度: Lo = 4550 mm2.计算板的有效高度: ho = h-as=120-20=100 mm六、荷载组合可变荷载控制组合:q = γG*qgk+γQ*qqk= 1.200*5.000+1.400*2.000= 8.800 KN/m2永久荷载控制组合:q = γG*qgk+γQ*qqk= 1.35*qgk+0.7*γQ*qqk= 1.35*5.000+0.7*1.400*2.000= 8.710 KN/m2取较大值荷载控制组合为:q = 8.800 KN/m2七、配筋计算(lx/ly=4550/4550=1.000<2.000 所以按双向板计算):1.X向底板钢筋1) 确定X向板底弯矩Mx = 表中系数q*Lo2= (0.0249+0.0249*0.200)*8.800*4.552= 5.444 kN*m2) 确定计算系数αs = γo*M/(α1*fc*b*ho*ho)= 1.00*5.444×106/(1.00*14.3*1000*100*100)= 0.0383) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.038) = 0.0394) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*100*0.039/300 = 185mm25) 验算最小配筋率ρ = As/(b*h) = 185/(1000*120) = 0.154%ρ<ρmin = 0.214% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.214%*1000*120 = 257 mm2用户选择了底板放大系数,系数值为:1.00所以最后面积As = 257*1.00 = 257 mm2采取方案 12@200, 实配面积565 mm22.Y向底板钢筋1) 确定Y向板底弯矩My = 表中系数q*Lo2= (0.0249+0.0249*0.200)*8.800*4.552= 5.444 kN*m2) 确定计算系数αs = γo*M/(α1*fc*b*ho*ho)= 1.00*5.444×106/(1.00*14.3*1000*100*100)= 0.0383) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.038) = 0.0394) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*100*0.039/300 = 185mm25) 验算最小配筋率ρ = As/(b*h) = 185/(1000*120) = 0.154%ρ<ρmin = 0.214% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.214%*1000*120 = 257 mm2用户选择了底板放大系数,系数值为:1.00所以最后面积As = 257*1.00 = 257 mm2采取方案 12@200, 实配面积565 mm23.X向支座左边钢筋1) 确定左边支座弯矩M o x = 表中系数q*Lo2= 0.0677*8.800*4.552= 12.334 kN*m2) 确定计算系数αs = γo*M/(α1*fc*b*ho*ho)= 1.00*12.334×106/(1.00*14.3*1000*100*100)= 0.0863) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.086) = 0.0904) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*100*0.090/300 = 431mm25) 验算最小配筋率ρ = As/(b*h) = 431/(1000*120) = 0.359%ρ≥ρmin = 0.214% 满足最小配筋要求用户选择了支座放大系数,系数值为:1.00所以最后面积As = 431*1.00 = 431 mm2采取方案 12@200, 实配面积565 mm24.Y向下边支座钢筋1) 确定下边支座弯矩M o y = 表中系数q*Lo2= 0.0677*8.800*4.552= 12.334 kN*m2) 确定计算系数αs = γo*M/(α1*fc*b*ho*ho)= 1.00*12.334×106/(1.00*14.3*1000*100*100)= 0.0863) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.086) = 0.0904) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*100*0.090/300= 431mm25) 验算最小配筋率ρ = As/(b*h) = 431/(1000*120) = 0.359%ρ≥ρmin = 0.214% 满足最小配筋要求用户选择了支座放大系数,系数值为:1.00所以最后面积As = 431*1.00 = 431 mm2采取方案 12@200, 实配面积565 mm2八、跨中挠度计算:Mk -------- 按荷载效应的标准组合计算的弯矩值Mq -------- 按荷载效应的准永久组合计算的弯矩值1.计算荷载效应Mk = Mgk + Mqk= (0.0249+0.0249*0.200)*(5.000+2.000)*4.552 = 4.330 kN*mMq = Mgk+ψq*Mqk= (0.0249+0.0249*0.200)*(5.000+0.5*2.000)*4.552 = 3.712 kN*m2.计算受弯构件的短期刚度 Bs1) 计算按荷载荷载效应的标准组合及准永久组合作用下,构件纵向受拉钢筋应力σsk = Mk/(0.87*ho*As) 混规(7.1.4-3)= 4.330×106/(0.87*100*565) = 88.091 N/mmσsq = Mq/(0.87*ho*As) 混规(7.1.4-3)= 3.712×106/(0.87*100*565) = 75.507 N/mm2) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积: Ate = 0.5*b*h = 0.5*1000*120= 60000mm2ρte = As/Ate 混规(7.1.2-4)= 565/60000 = 0.942%3) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψk = 1.1-0.65*ftk/(ρte*σsk) 混规(7.1.2-2)= 1.1-0.65*2.01/(0.942%*88.091) = -0.475ψq = 1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)= 1.1-0.65*2.01/(0.942%*88.091) = -0.737因为ψ不能小于最小值0.2,所以取ψk = 0.2因为ψ不能小于最小值0.2,所以取ψq = 0.24) 计算钢筋弹性模量与混凝土模量的比值αEαE = Es/Ec = 2.0×105/3.00×104 = 6.6675) 计算受压翼缘面积与腹板有效面积的比值γ f矩形截面,γf=06) 计算纵向受拉钢筋配筋率ρρ = As/(b*ho)= 565/(1000*100) = 0.565%7) 计算受弯构件的短期刚度 BsBsk = Es*As*ho2/[1.15ψk+0.2+6*αE*ρ/(1+ 3.5γf')] 混规(7.2.3-1) = 2.0×105*565*1002/[1.15*0.200+0.2+6*6.667*0.565%/(1+3.5*0.0)]= 1.723×103 kN*m2Bsq = Es*As*ho2/[1.15ψq+0.2+6*αE*ρ/(1+ 3.5γf')] 混规(7.2.3-1) = 2.0×105*565*1002/[1.15*0.200+0.2+6*6.667*0.565%/(1+3.5*0.0)]= 1.723×103 kN*m23.计算受弯构件的长期刚度B1) 确定考虑荷载长期效应组合对挠度影响增大影响系数θ当ρ'=0时,θ=2.0 混规(7.2.5)2) 计算受弯构件的长期刚度 BBk = Mk/(Mq*(θ-1)+Mk)*Bsk (混规(7.2.2-1))= 4.330/(3.712*(2.0-1)+4.330)*1.723×103= 9.275×102 kN*m2Bq = Bsq/θ (混规(7.2.2-2))= 1.723×103/2.0= 8.613×102 kN*m2B = min(Bk,Bq)= min(927.533,861.280)= 861.2804.计算受弯构件挠度fmax = f*(qgk+qqk)*Lo4/B= 0.00215*(5.000+2.000)*4.554/8.613×102= 7.489mm5.验算挠度挠度限值fo=Lo/200=4550/200=22.750mmfmax=7.489mm≤fo=22.750mm,满足规范要求!九、裂缝宽度验算:1.跨中X方向裂缝1) 计算荷载效应Mx = 表中系数(qgk+ψq*qqk)*Lo2= (0.0249+0.0249*0.200)*(5.000+0.5*2.000)*4.552= 3.712 kN*m2) 光面钢筋,所以取值vi=0.73) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=3.712×106/(0.87*100*565)=75.507N/mm4) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4)=565/60000 = 0.0094因为ρte=0.0094 < 0.01,所以让ρte=0.015) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*75.507) =-0.630因为ψ=-0.630 < 0.2,所以让ψ=0.2 6) 计算单位面积钢筋根数nn=1000/dist = 1000/200=57) 计算受拉区纵向钢筋的等效直径deqdeq = (∑ni*di2)/(∑ni*vi*di)=5*12*12/(5*0.7*12)=17 mm8) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.200*75.507/2.0×105*(1.9*20+0.08*17/0.0100)=0.0251mm ≤ 0.20 mm, 满足规范要求2.跨中Y方向裂缝1) 计算荷载效应My = 表中系数(qgk+ψq*qqk)*Lo2= (0.0249+0.0249*0.200)*(5.000+0.5*2.000)*4.552= 3.712 kN*m2) 光面钢筋,所以取值vi=0.73) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=3.712×106/(0.87*100*565)=75.507N/mm4) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4)=565/60000 = 0.0094因为ρte=0.0094 < 0.01,所以让ρte=0.015) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*75.507)=-0.630因为ψ=-0.630 < 0.2,所以让ψ=0.26) 计算单位面积钢筋根数nn=1000/dist = 1000/200=57) 计算受拉区纵向钢筋的等效直径deqdeq = (∑ni*di2)/(∑ni*vi*di)=5*12*12/(5*0.7*12)=17 mm8) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.200*75.507/2.0×105*(1.9*20+0.08*17/0.0100)=0.0251mm ≤ 0.20 mm, 满足规范要求3.支座下方向裂缝。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
百度文库 - 让每个人平等地提升自我 1 四边简支矩形板计算 项目名称_____________日 期_____________ 设 计 者_____________校对者_____________ 一、构件编号: LB-1 二、示意图
三、依据规范 《建筑结构荷载规范》 GB50009-2001 《混凝土结构设计规范》 GB50010-2010 四、计算信息 1.几何参数 计算跨度: Lx = 11000 mm; Ly = 7500 mm 板厚: h = 400 mm 2.材料信息 混凝土等级: C30 fc=mm2 ft=mm2 ftk=mm2 Ec=×104N/mm2 钢筋种类: HRB400 fy = 360 N/mm2 Es = ×105 N/mm2 最小配筋率: ρ= % 纵向受拉钢筋合力点至近边距离: as = 55mm 保护层厚度: c = 40mm 3.荷载信息(均布荷载) 永久荷载分项系数: γG = 可变荷载分项系数: γQ = 准永久值系数: ψq = 永久荷载标准值: qgk = m2 可变荷载标准值: qqk = m2 4.计算方法:弹性板 5.边界条件(上端/下端/左端/右端):简支/简支/简支/简支 6.设计参数 结构重要性系数: γo = 泊松比:μ = 五、计算参数: 1.计算板的跨度: Lo = 7500 mm 百度文库 - 让每个人平等地提升自我 2 2.计算板的有效高度: ho = h-as=400-55=345 mm 六、配筋计算(lx/ly=11000/7500=< 所以按双向板计算): 向底板钢筋 1) 确定X向板底弯矩 Mx = 表中系数(γG*qgk+γQ*qqk)*Lo2 = +***+** = kN*m 2) 确定计算系数 αs = γo*Mx/(α1*fc*b*ho*ho) = *×106/**1000*345*345) = 3) 计算相对受压区高度 ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2* = 4) 计算受拉钢筋面积 As = α1*fc*b*ho*ξ/fy = **1000*345*360 = 354mm2 5) 验算最小配筋率 ρ = As/(b*h) = 354/(1000*400) = % ρ 所以取面积为As = ρmin*b*h = %*1000*400 = 800 mm2 采取方案⌲12@140, 实配面积807 mm2
向底板钢筋 1) 确定Y向板底弯矩 My = 表中系数(γG*qgk+γQ*qqk)*Lo2 = +***+** = kN*m 2) 确定计算系数 αs = γo*My/(α1*fc*b*ho*ho) = *×106/**1000*345*345) = 3) 计算相对受压区高度 ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2* = 4) 计算受拉钢筋面积 As = α1*fc*b*ho*ξ/fy = **1000*345*360 = 638mm2 5) 验算最小配筋率 ρ = As/(b*h) = 638/(1000*400) = % ρ 所以取面积为As = ρmin*b*h = %*1000*400 = 800 mm2 采取方案⌲12@100, 实配面积1131 mm2
七、跨中挠度计算: Mk -------- 按荷载效应的标准组合计算的弯矩值 Mq -------- 按荷载效应的准永久组合计算的弯矩值 1.计算荷载效应 百度文库 - 让每个人平等地提升自我 3 Mk = Mgk + Mqk = +**+* = kN*m Mq = Mgk+ψq*Mqk = +**+** = kN*m 2.计算受弯构件的短期刚度 Bs 1) 计算按荷载荷载效应的两种组合作用下,构件纵向受拉钢筋应力 σsk = Mk/*ho*As) 混规(7.1.4-3) = ×106/*345*1131) = N/mm σsq = Mq/*ho*As) 混规(7.1.4-3) = ×106/*345*1131) = N/mm 2) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率 矩形截面积: Ate = *b*h = *1000*400= 200000mm2 ρte = As/Ate 混规(7.1.2-4) = 1131/200000 = % 3) 计算裂缝间纵向受拉钢筋应变不均匀系数ψ ψk = 混规(7.1.2-2) = = 因为ψ不能小于最小值,所以取ψk = ψq = 混规(7.1.2-2) = = 因为ψ不能小于最小值,所以取ψq = 4) 计算钢筋弹性模量与混凝土模量的比值 αE αE = Es/Ec = ×105/×104 = 5) 计算受压翼缘面积与腹板有效面积的比值 γf 矩形截面,γf=0 6) 计算纵向受拉钢筋配筋率ρ ρ = As/(b*ho)= 1131/(1000*345) = % 7) 计算受弯构件的短期刚度 Bs Bsk = Es*As*ho2/[ψk++6*αE*ρ/(1+ γf')](混规(7.2.3-1)) = ×105*1131*3452/[*++6**%/(1+*] = ×104 kN*m2 Bsq = Es*As*ho2/[ψq++6*αE*ρ/(1+ γf')](混规(7.2.3-1)) = ×105*1131*3452/[*++6**%/(1+*] = ×104 kN*m2 3.计算受弯构件的长期刚度B 1) 确定考虑荷载长期效应组合对挠度影响增大影响系数θ 当ρ'=0时,θ= 混规(7.2.5) 2) 计算受弯构件的长期刚度 B Bk = Mk/(Mq*(θ-1)+Mk)*Bs (混规(7.2.2-1)) = *+*×104 = ×104 kN*m2 Bq = Bsq/θ (混规(7.2.2-2)) = ×104/ = ×104 kN*m2 百度文库 - 让每个人平等地提升自我 4 B = min(Bk,Bq) = min, = 4.计算受弯构件挠度 fmax = f*(qgk+qqk)*Lo4/B = *+*×104 = 5.验算挠度 挠度限值fo=Lo/250=7500/250= fmax=≤fo=,满足规范要求! 八、裂缝宽度验算: 1.跨中X方向裂缝 1) 计算荷载效应 Mx = 表中系数(qgk+ψqqk)*Lo2 = +**+** = kN*m 2) 带肋钢筋,所以取值vi= 3) 因为C > 65,所以取C = 65 4) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力 σsq=Mq/*ho*As) 混规(7.1.4-3) =×106/*345*807) =mm 5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率 矩形截面积,Ate=*b*h=*1000*400=200000 mm2 ρte=As/Ate 混规(7.1.2-4) =807/200000 = 因为ρte= < ,所以让ρte= 6) 计算裂缝间纵向受拉钢筋应变不均匀系数ψ ψ= 混规(7.1.2-2) = = 7) 计算单位面积钢筋根数n n=1000/dist = 1000/140 =7 8) 计算受拉区纵向钢筋的等效直径deq deq= (∑ni*di2)/(∑ni*vi*di) =7*12*12/(7**12)=12 9) 计算最大裂缝宽度 ωmax=αcr*ψ*σsq/Es**C+*Deq/ρte) (混规(7.1.2-1) =**×105**40+*12/ = ≤ , 满足规范要求 2.跨中Y方向裂缝 1) 计算荷载效应 My = 表中系数(qgk+ψqqk)*Lo2 = +**+** 百度文库 - 让每个人平等地提升自我 5 = kN*m 2) 带肋钢筋,所以取值vi= 3) 因为C > 65,所以取C = 65 4) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力 σsq=Mq/*ho*As) 混规(7.1.4-3) =×106/*345*1131) =mm 5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率 矩形截面积,Ate=*b*h=*1000*400=200000 mm2 ρte=As/Ate 混规(7.1.2-4) =1131/200000 = 因为ρte= < ,所以让ρte= 6) 计算裂缝间纵向受拉钢筋应变不均匀系数ψ ψ= 混规(7.1.2-2) = = 7) 计算单位面积钢筋根数n n=1000/dist = 1000/100 =10 8) 计算受拉区纵向钢筋的等效直径deq deq= (∑ni*di2)/(∑ni*vi*di) =10*12*12/(10**12)=12 9) 计算最大裂缝宽度 ωmax=αcr*ψ*σsq/Es**C+*Deq/ρte) (混规(7.1.2-1) =**×105**40+*12/ = ≤ , 满足规范要求
