广东省揭阳市2018年高考第二次模拟考试数学(文)试题含答案
广东省揭阳市2018年高三高考第二次模拟考试理科数学试题(解析版)

揭阳市2018年高中毕业班高考第二次模拟考试数学(理科)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合,,则()A. B. C. D.【答案】B【解析】分析:首先由题意求得集合A,B,然后结合所给的选项逐一考查其真假即可,需注意集合运算的准确性.详解:求解函数的定义域可得:,求解指数不等式可得:,据此可得:,,,,结合选项可知只有选项B正确.本题选择B选项.点睛:本题主要考查集合的表示方法,集合的交并运算等知识,意在考查学生的转化能力和计算求解能力.2. 已知复数满足,则的共轭复数在复平面内对应的点在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】A【解析】分析:首先求得复数z,然后求解器共轭复数,随后确定共轭复数所在的象限即可.详解:由题意可得:,则,即的共轭复数对应的点为,位于第一象限.本题选择A选项.点睛:本题主要考查复数的运算,共轭复数的定义等知识,意在考查学生的转化能力和计算求解能力.3. 平面直角坐标系中,分别是与轴、轴正方向同向的单位向量,向量,以下说法正确的是()A. B. C. D.【答案】C【解析】分析:首先利用向量的坐标表示方法写出的坐标表示,然后结合选项逐一考查其是否正确即可.详解:由题意可设,则:,考查所给的选项:,选项A错误;,故,选项B错误;,故,即,选项C正确;不存在实数满足,则不成立,选项D错误.本题选择C选项.点睛:本题主要考查平面向量的坐标运算,平面向量的垂直、平行的判定方法等知识,意在考查学生的转化能力和计算求解能力.4. 已知直线、,平面、、,下列命题正确的是()A. 若,,,则B. 若,,,则C. 若,,则D. 若,,,则【答案】A【解析】分析:由题意利用线面关系的判定定理和性质定理逐一考查所给命题是否正确即可,注意定理运用的准确性.详解:逐一考查所给的选项:A.若,,,则,该说法正确;B.若,,,在三棱锥中,令平面分别为平面,交线为,不满足,该说法错误;C.若,,有可能,不满足,该说法错误;D.若,,,正方体中,取平面为平面,直线为,满足,不满足,该说法错误.本题选择A选项.点睛:本题主要考查线面关系相关命题真假的判定等知识,意在考查学生的转化能力和计算求解能力.5. 已知直线与相交于、两点,且,则实数的值为()A. B. C. 或 D. 或【答案】D【解析】分析:首先将圆的方程整理为标准方程,结合等腰三角形的性质和点到直线距离公式得到关于实数a的方程,解方程即可求得最终结果.详解:圆的方程整理为标准方程即:,作于点,由圆的性质可知△ABO为等腰三角形,其中,则,即圆心到直线的距离为,据此可得:,即,解得:或.本题选择D选项.点睛:本题主要考查圆的方程的应用,点到直线距离公式等知识,意在考查学生的转化能力和计算求解能力.6. 已知的展开式中常数项为,则的值为()A. B. C. D.【答案】C【解析】分析:首先写出展开式的通项公式,然后结合题意得到关于实数a的方程,解方程即可求得最终结果.详解:展开式的通项公式为:,令可得:,结合题意可得:,即.本题选择C选项.点睛:本题主要考查二项式定理的通项公式及其应用等知识,意在考查学生的转化能力和计算求解能力.7. 已知函数的部分图象如图所示,则的值为()A. 或B.C.D. 或【答案】C【解析】分析:首先由函数的周期求得的值,然后结合函数的对称中心求得的值即可,注意合理应用题中所给的的范围.详解:由题意可得函数的周期,则,当时,,则,令可得:.本题选择C选项.点睛:本题主要考查三角函数图像的性质,三角函数解析式的确定等知识,意在考查学生的转化能力和计算求解能力.8. 在如图的程序框图中,输出的值为()A. B. C. D.【答案】D【解析】分析:首先确定该流程图的功能,然后结合选项考查所给的数值是否满足流程图的输出即可.详解:由流程图可知该流程图输出大于的最小正整数,且满足,观察选项:不是3的倍数,选项C错误;,,,而,,选项AB错误;,,则53满足题意.本题选择D选项.点睛:识别、运行程序框图和完善程序框图的思路:(1)要明确程序框图的顺序结构、条件结构和循环结构.(2)要识别、运行程序框图,理解框图所解决的实际问题.(3)按照题目的要求完成解答并验证.9. 已知双曲线的焦距为,、是其左、右焦点,点在双曲线右支上,的周长为,则的取值范围是()A. B. C. D.【答案】C【解析】分析:由题意结合焦点三角形的性质求得左焦半径的表达形式,结合双曲线的性质和题意求解的取值范围即可.详解:设,由双曲线的定义可得:,①由题意可得:,②联立①②可得:,在双曲线中:,则:,即的取值范围是.本题选择C选项.点睛:双曲线上一点与两焦点构成的三角形,称为双曲线的焦点三角形,与焦点三角形有关的计算或证明常利用正弦定理、余弦定理、||PF1|-|PF2||=2a,得到a,c的关系.10. 如图是某几何体的三视图,图中每个小正方形的边长为,则此几何体的体积为()A. B. C. D.【答案】B【解析】分析:由题意首先确定该三视图对应的几何体,然后结合几何体的空间结构求解该组合体的体积即可.详解:由已知中的三视图可得:该几何体是棱长为2的正方体截去两个角所得的组合体,其直观图如下图所示:故组合体的体积.本题选择B选项.点睛:(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解;(2)若所给几何体的体积不能直接利用公式得出,则常用等积法、分割法、补形法等方法进行求解.11. 过抛物线上两点、分别作切线,若两条切线互相垂直,则线段的中点到抛物线准线的距离的最小值为()A. B. C. D.【答案】B【解析】分析:首先求得抛物线的斜率,然后结合直线垂直的充要条件得到横坐标的关系,最后利用均值不等式求解最值即可,注意等号成立的条件.详解:抛物线的方程即:,则,设,则过A,B两点切线的斜率为:,由题意可得:,由题意可知抛物线的直线方程为,则线段的中点到抛物线准线的距离为:,当且仅当时等号成立.据此可得线段的中点到抛物线准线的距离的最小值为1.本题选择B选项.点睛:本题的实质是在考查基本不等式求最值.在应用基本不等式求最值时,要把握不等式成立的三个条件,就是“一正——各项均为正;二定——积或和为定值;三相等——等号能否取得”,若忽略了某个条件,就会出现错误.12. 把函数的图象向右平移一个单位,所得图象与函数的图象关于直线对称;已知偶函数满足,当时,;若函数有五个零点,则的取值范围是()A. B. C. D.【答案】C【解析】分析:由题意分别确定函数f(x)的图象性质和函数h(x)图象的性质,然后数形结合得到关于k的不等式组,求解不等式组即可求得最终结果.详解:曲线右移一个单位,得,所以g(x)=2x,h(x-1)=h(-x-1)=h(x+1),则函数h(x)的周期为2.当x∈[0,1]时,,y=kf(x)-h(x)有五个零点,等价于函数y=kf(x)与函数y=h(x)的图象有五个公共点.绘制函数图像如图所示,由图像知kf(3)<1且kf(5)>1,即:,求解不等式组可得:.即的取值范围是。
广东省揭阳市2018届高三第二次模拟考试试题(理)数学试题及答案解析
广东省揭阳市2018届高三第二次模拟考试数学试题(理)第Ⅰ卷一、选择题1. 已知集合,,则()A. B. C. D.2. 已知复数满足,则的共轭复数在复平面内对应的点在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 平面直角坐标系中,分别是与轴、轴正方向同向的单位向量,向量,以下说法正确的是()A. B. C. D.4. 已知直线、,平面、、,下列命题正确的是()A. 若,,,则B. 若,,,则C. 若,,则D. 若,,,则5. 已知直线与相交于、两点,且,则实数的值为()A. B. C. 或 D. 或6. 已知的展开式中常数项为,则的值为()A. B. C. D.7. 已知函数的部分图象如图所示,则的值为()..............................A. 或B.C.D. 或8. 在如图的程序框图中,输出的值为()A. B. C. D.9. 已知双曲线的焦距为,、是其左、右焦点,点在双曲线右支上,的周长为,则的取值范围是()A. B. C. D.10. 如图是某几何体的三视图,图中每个小正方形的边长为,则此几何体的体积为()A. B. C. D.11. 过抛物线上两点、分别作切线,若两条切线互相垂直,则线段的中点到抛物线准线的距离的最小值为()A. B. C. D.12. 把函数的图象向右平移一个单位,所得图象与函数的图象关于直线对称;已知偶函数满足,当时,;若函数有五个零点,则的取值范围是()A. B. C. D.第Ⅱ卷二、填空题13. 曲线在点处的切线方程为__________.14. 题库中有道题,考生从中随机抽取道,至少做对道算通过考试.某考生会做其中道,有道不会做,则此考生能通过考试的概率为__________.15. 已知等差数列中,,、、成等比数列,把各项如下图排列:则从上到下第行,从左到右的第个数值为__________.16. 平面四边形中,,,,,则的最小长度为__________.三、解答题17. 已知数列的前项的和为,满足,.(Ⅰ)求数列的通项公式;(Ⅱ)设,数列的前项和与积分别为与,求与.18. 如图,在四面体中,,.(Ⅰ)求证:;(Ⅱ)若与平面所成的角为,点是的中点,求二面角的大小.19. 甲、乙、丙三人去某地务工,其工作受天气影响,雨天不能出工,晴天才能出工.其计酬方式有两种,方式一:雨天没收入,晴天出工每天元;方式而:雨天每天元,晴天出工每天元;三人要选择其中一种计酬方式,并打算在下个月(天)内的晴天都出工,为此三人作了一些调查,甲以去年此月的下雨天数(天)为依据作出选择;乙和丙在分析了当地近年此月的下雨天数()的频数分布表(见下表)后,乙以频率最大的值为依据作出选择,丙以的平均值为依据作出选择.8(Ⅰ)试判断甲、乙、丙选择的计酬方式,并说明理由;(Ⅱ)根据统计范围的大小,你觉得三人中谁的依据更有指导意义?(Ⅲ)以频率作为概率,求未来三年中恰有两年,此月下雨不超过天的概率.20. 已知椭圆的左、右焦点分别为、,圆经过椭圆的两个焦点和两个顶点,点在椭圆上,且,.(Ⅰ)求椭圆的方程和点的坐标;(Ⅱ)过点的直线与圆相交于、两点,过点与垂直的直线与椭圆相交于另一点,求的面积的取值范围.21. 已知函数,(Ⅰ)若,且是函数的一个极值,求函数的最小值;(Ⅱ)若,求证:,.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22. 在直角坐标系中,圆的圆心为,半径为,现以原点为极点,轴的正半轴为极轴建立极坐标系,(Ⅰ)求圆的极坐标方程;(Ⅱ)设,是圆上两个动点,满足,求的最小值.23. 已知函数,,(Ⅰ)若不等式恒成立,求实数的取值范围;(Ⅱ)求不等式的解集.【参考答案】第Ⅰ卷一、选择题1. 【答案】B【解析】首先由题意求得集合A,B,然后结合所给的选项逐一考查其真假即可,需注意集合运算的准确性.详解:求解函数的定义域可得:,求解指数不等式可得:,据此可得:,,,,结合选项可知只有选项B正确.本题选择B选项.2. 【答案】A【解析】首先求得复数z,然后求解器共轭复数,随后确定共轭复数所在的象限即可.详解:由题意可得:,则,即的共轭复数对应的点为,位于第一象限.本题选择A选项.3. 【答案】C【解析】首先利用向量的坐标表示方法写出的坐标表示,然后结合选项逐一考查其是否正确即可.详解:由题意可设,则:,考查所给的选项:,选项A错误;,故,选项B错误;,故,即,选项C正确;不存在实数满足,则不成立,选项D错误.本题选择C选项.4. 【答案】A【解析】由题意利用线面关系的判定定理和性质定理逐一考查所给命题是否正确即可,注意定理运用的准确性.详解:逐一考查所给的选项:A.若,,,则,该说法正确;B.若,,,在三棱锥中,令平面分别为平面,交线为,不满足,该说法错误;C.若,,有可能,不满足,该说法错误;D.若,,,正方体中,取平面为平面,直线为,满足,不满足,该说法错误.本题选择A选项.5. 【答案】D【解析】首先将圆的方程整理为标准方程,结合等腰三角形的性质和点到直线距离公式得到关于实数a的方程,解方程即可求得最终结果.详解:圆的方程整理为标准方程即:,作于点,由圆的性质可知△ABO为等腰三角形,其中,则,即圆心到直线的距离为,据此可得:,即,解得:或.本题选择D选项.6.【答案】C【解析】首先写出展开式的通项公式,然后结合题意得到关于实数a的方程,解方程即可求得最终结果.详解:展开式的通项公式为:,令可得:,结合题意可得:,即.本题选择C选项.7.【答案】C【解析】首先由函数的周期求得的值,然后结合函数的对称中心求得的值即可,注意合理应用题中所给的的范围.详解:由题意可得函数的周期,则,当时,,则,令可得:.本题选择C选项.8. 【答案】D【解析】首先确定该流程图的功能,然后结合选项考查所给的数值是否满足流程图的输出即可.详解:由流程图可知该流程图输出大于的最小正整数,且满足,观察选项:不是3的倍数,选项C错误;,,,而,,选项AB错误;,,则53满足题意.本题选择D选项.9. 【答案】C【解析】由题意结合焦点三角形的性质求得左焦半径的表达形式,结合双曲线的性质和题意求解的取值范围即可.详解:设,由双曲线的定义可得:,①由题意可得:,②联立①②可得:,在双曲线中:,则:,即的取值范围是.本题选择C选项.10. 【答案】B【解析】由题意首先确定该三视图对应的几何体,然后结合几何体的空间结构求解该组合体的体积即可.详解:由已知中的三视图可得:该几何体是棱长为2的正方体截去两个角所得的组合体,其直观图如下图所示:故组合体的体积.本题选择B选项.11. 【答案】B【解析】首先求得抛物线的斜率,然后结合直线垂直的充要条件得到横坐标的关系,最后利用均值不等式求解最值即可,注意等号成立的条件.详解:抛物线的方程即:,则,设,则过A,B两点切线的斜率为:,由题意可得:,由题意可知抛物线的直线方程为,则线段的中点到抛物线准线的距离为:,当且仅当时等号成立.据此可得线段的中点到抛物线准线的距离的最小值为1.本题选择B选项.12. 【答案】C【解析】由题意分别确定函数f(x)的图象性质和函数h(x)图象的性质,然后数形结合得到关于k的不等式组,求解不等式组即可求得最终结果.详解:曲线右移一个单位,得,所以g(x)=2x,h(x-1)=h(-x-1)=h(x+1),则函数h(x)的周期为2.当x∈[0,1]时,,y=kf(x)-h(x)有五个零点,等价于函数y=kf(x)与函数y=h(x)的图象有五个公共点.绘制函数图像如图所示,由图像知kf(3)<1且kf(5)>1,即:,求解不等式组可得:.即的取值范围是。
广东省揭阳市惠来一中2018学年高二上学期第二次段考数

2018-2018学年广东省揭阳市惠来一中高二(上)第二次段考数学试卷(文科)一、选择题:本大题共有12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.请把它选出后填在答题卡的相应位置上.1.已知命题p:对任意x∈R,有cosx≤1,则()A.¬p:存在x∈R,使cosx>1 B.¬p:对任意x∈R,有cosx>1C.¬p:存在x∈R,使cosx≥1 D.¬p:对任意x∈R,有cosx≥12.在△ABC中,若b=2asinB,则A等于()A.30°或60°B.45°或60°C.120°或60°D.30°或150°3.双曲线=1的实轴长是()A.3 B.4 C.6 D.84.已知命题①若a>b,则<,②若﹣2≤x≤0,则(x+2)(x﹣3)≤0,则下列说法正确的是()A.①的逆命题为真 B.②的逆命题为真C.①的逆否命题为真D.②的逆否命题为真5.等差数列{a n}的前n项和为S n,若a1=2,S3=12,则a6等于()A.8 B.10 C.12 D.146.椭圆x2+4y2=1的离心率为()A.B.C.D.7.若x>1,则的最小值是()A.B. C.2 D.38.条件p:x<﹣1或x>1,条件q:x<﹣2,则p是q的()A.充分但不必要条件B.充分且必要条件C.必要但不充分条件D.既不充分也不必要条件9.已知双曲线C:(a>0,b>0)的离心率为,则C的渐近线方程为()A.y= B.y= C.y=±x D.y=10.已知双曲线9y2﹣m2x2=1(m>0)的一个顶点到它的一条渐近线的距离为,则m=()A.1 B.2 C.3 D.411.各项均为正数的等比数列中:a5a6+a4a7=18,则log3a1+log3a2+…+log3a10=()A.12 B.10 C.1+log35 D.2+log3512.已知F1,F2是双曲线﹣=1(a>0,b>0)的左右焦点,若双曲线右支上存在一点(,﹣)与点F1关于直线y=﹣对称,则该双曲线的离心率为()A.B.C.2 D.二、填空题:本大题共4小题,每小题5分,满分20分13.经过点P(4,﹣2)的抛物线的标准方程是.14.已知等差数列{a n}的公差d≠0,且a1、a3、a9成等比数列,则的值是.15.已知命题p:∃x∈R,x2+2x+a≤0,若命题p是假命题,则实数a的取值范围是.(用区间表示)16.如图,F1,F2是椭圆C1: +y2=1与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是.三、解答题(本大题共6小题,共70分,解答应写出必要的文字说明、证明过程或演算步骤)17.已知命题p:方程+=1表示焦点在x轴上的椭圆,命题q:(k﹣1)x2+(k﹣3)y2=1表示双曲线.若p∨q为真命题,求实数k的取值范围.18.在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且(Ⅰ)确定角C的大小;(Ⅱ)若c=,且△ABC的面积为,求a2+b2的值.19.如图,已知斜三棱柱ABC﹣A1B1C1中,AB=AC,D为BC的中点.(1)若AA1⊥AD,求证:AD⊥DC1;(2)求证:A1B∥平面ADC1.20.已知双曲线C的方程为x2﹣15y2=15.(1)求其渐近线方程;(2)求与双曲线C焦点相同,且过点(0,3)的椭圆的标准方程.21.数列{a n}的前n项的和为S n,对于任意的自然数a n>0,(Ⅰ)求证:数列{a n}是等差数列,并求通项公式(Ⅱ)设,求和T n=b1+b2+…+b n.22.如图,已知椭圆+=1(a>b>0)的离心率为,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为.一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.(Ⅰ)求椭圆和双曲线的标准方程;(Ⅱ)设直线PF1、PF2的斜率分别为k1、k2,证明k1•k2=1;(Ⅲ)探究是否是个定值,若是,求出这个定值;若不是,请说明理由.2018-2018学年广东省揭阳市惠来一中高二(上)第二次段考数学试卷(文科)参考答案与试题解析一、选择题:本大题共有12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.请把它选出后填在答题卡的相应位置上.1.已知命题p:对任意x∈R,有cosx≤1,则()A.¬p:存在x∈R,使cosx>1 B.¬p:对任意x∈R,有cosx>1C.¬p:存在x∈R,使cosx≥1 D.¬p:对任意x∈R,有cosx≥1【考点】命题的否定.【分析】利用全称命题的否定是特称命题写出结果即可.【解答】解:因为全称命题的否定是特称命题,所以,命题p:对任意x∈R,有cosx≤1,则¬p:存在x∈R,使cosx>1.故选:A.2.在△ABC中,若b=2asinB,则A等于()A.30°或60°B.45°或60°C.120°或60°D.30°或150°【考点】正弦定理的应用.【分析】结合已知及正弦定理可求sinA,进而可根据特殊角的三角形函数值可求A【解答】解:∵b=2asinB,由正弦定理可得,sinB=2sinAsinB∵sinB≠0∴sinA=∴A=30°或150°故选D3.双曲线=1的实轴长是()A.3 B.4 C.6 D.8【考点】双曲线的简单性质.【分析】利用双曲线的定义、性质直接求解.【解答】解:双曲线=1中,a2=9,∴a=3,∴双曲线=1的实轴长是2a=6.故选:C.4.已知命题①若a>b,则<,②若﹣2≤x≤0,则(x+2)(x﹣3)≤0,则下列说法正确的是()A.①的逆命题为真 B.②的逆命题为真C.①的逆否命题为真D.②的逆否命题为真【考点】四种命题的真假关系;四种命题.【分析】分别求出①②的逆命题和逆否命题,再判断其真假即可【解答】解:①若a>b,则<的逆命题为“若<,则a>b”当a=﹣1,b=1,不成立,故为假命题,逆否命题为“若≥,则a≤b””当a=1,b=2,不成立,故为假命题②若﹣2≤x≤0,则(x+2)(x﹣3)≤0逆命题为“若(x+2)(x﹣3)≤0,则﹣2≤x≤0”,因为(x+2)(x﹣3)≤0,则﹣2≤x≤3,故为假命题,若﹣2≤x≤0,则(x+2)(x﹣3)≤0逆否命题为“若(x+2)(x﹣3)>0,则x<﹣2,或x>0”,故为真命题故选:D5.等差数列{a n}的前n项和为S n,若a1=2,S3=12,则a6等于()A.8 B.10 C.12 D.14【考点】等差数列的前n项和.【分析】由等差数列的性质和已知可得a2,进而可得公差,可得a6【解答】解:由题意可得S3=a1+a2+a3=3a2=12,解得a2=4,∴公差d=a2﹣a1=4﹣2=2,∴a6=a1+5d=2+5×2=12,故选:C.6.椭圆x2+4y2=1的离心率为()A.B.C.D.【考点】椭圆的简单性质.【分析】把椭圆的方程化为标准方程后,找出a与b的值,然后根据a2=b2+c2求出c的值,利用离心率公式e=,把a与c的值代入即可求出值.【解答】解:把椭圆方程化为标准方程得:x2+=1,得到a=1,b=,则c==,所以椭圆的离心率e==.故选A7.若x>1,则的最小值是()A.B. C.2 D.3【考点】基本不等式.【分析】由基本不等式可得=≥2+1=3.【解答】解:∵x>1,∴得=≥2+1=3,当且仅当x﹣1=1时,即x=2时,等号成立,答案为:3.故选D.8.条件p:x<﹣1或x>1,条件q:x<﹣2,则p是q的()A.充分但不必要条件B.充分且必要条件C.必要但不充分条件D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】由q⇒p,反之不成立,即可判断出结论.【解答】解:x<﹣2,⇒x<﹣1或x>1,但是x<﹣1或x>1不能推出x<﹣2,所以p是q的必要不充分条件.故选:C.9.已知双曲线C:(a>0,b>0)的离心率为,则C的渐近线方程为()A.y= B.y= C.y=±x D.y=【考点】双曲线的简单性质.【分析】由离心率和abc的关系可得b2=4a2,而渐近线方程为y=±x,代入可得答案.【解答】解:由双曲线C:(a>0,b>0),则离心率e===,即4b2=a2,故渐近线方程为y=±x=x,故选:D.10.已知双曲线9y2﹣m2x2=1(m>0)的一个顶点到它的一条渐近线的距离为,则m=()A.1 B.2 C.3 D.4【分析】由双曲线9y2﹣m2x2=1(m>0)可得,顶点,一条渐近线为mx﹣3y=0,再由点到直线的距离公式根据一个顶点到它的一条渐近线的距离为可以求出m.【解答】解:,取顶点,一条渐近线为mx﹣3y=0,∵故选D.11.各项均为正数的等比数列中:a5a6+a4a7=18,则log3a1+log3a2+…+log3a10=()A.12 B.10 C.1+log35 D.2+log35【考点】等比数列的性质.【分析】先根据等比中项的性质可知a5a6=a4a7,进而根据a5a6+a4a7=18,求得a5a6的值,最后根据等比数列的性质求得log3a1+log3a2+…+log3a10=log3(a5a6)5答案可得.【解答】解:∵a5a6=a4a7,∴a5a6+a4a7=2a5a6=18∴a5a6=9∴log3a1+log3a2+…+log3a10=log3(a5a6)5=5log39=10故选B.12.已知F1,F2是双曲线﹣=1(a>0,b>0)的左右焦点,若双曲线右支上存在一点(,﹣)与点F1关于直线y=﹣对称,则该双曲线的离心率为()A.B.C.2 D.【分析】求出过F1(c,0)且垂直于的直线方程,求出它与的交点坐标,求出点P的坐标,代入双曲线方程化简求解即可.【解答】解:由题意过F1(c,0)且垂直于的直线方程为,它与的交点坐标为,所以点P的坐标为,因为点P在双曲线上,,∵a2+b2=c2,可得c2=5a2,∴,∴,故选:A.二、填空题:本大题共4小题,每小题5分,满分20分13.经过点P(4,﹣2)的抛物线的标准方程是y2=x或x2=﹣8y.【考点】抛物线的标准方程.【分析】先设处抛物线的标准方程,把点P坐标代入,即可求得p,则抛物线方程可得.【解答】解:设抛物线方程为y2=2px或x2=2py(p>0),∵抛物线过点(4,﹣2)∴2p×4=4或2p×(﹣2)=16∴2p=1或﹣8∴抛物线的标准方程为y2=x或x2=﹣8y故答案为:y2=x或x2=﹣8y.14.已知等差数列{a n}的公差d≠0,且a1、a3、a9成等比数列,则的值是.【考点】等差数列的性质.【分析】因为{a n}是等差数列,故a1、a3、a9都可用d表达,又因为a1、a3、a9恰好是等比数列,所以有a32=a1a9,即可求出d,即可求比值.【解答】解:等差数列{a n}中,a1=a1,a3=a1+2d,a9=a1+8d,因为a1、a3、a9恰好是某等比数列,所以有a32=a1a9,即(a1+2d)2=a1(a1+8d),解得d=a1,则===.故答案是:.15.已知命题p:∃x∈R,x2+2x+a≤0,若命题p是假命题,则实数a的取值范围是(1,+∞).(用区间表示)【考点】特称命题.【分析】根据题意,写出命题p的否定命题,利用p与¬p真假相反得到¬p为真命题,再应用判别式求出a的取值范围.【解答】解:∵命题p:∃x∈R,x2+2x+a≤0,当命题p是假命题时,命题¬p:∀x∈R,x2+2x+a>0是真命题;即△=4﹣4a<0,∴a>1;∴实数a的取值范围是(1,+∞).故答案为:(1,+∞).16.如图,F1,F2是椭圆C1: +y2=1与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是.【考点】双曲线的简单性质.【分析】设|AF1|=x,|AF2|=y,利用椭圆的定义,四边形AF1BF2为矩形,可求出x,y的值,进而可得双曲线的几何量,即可求出双曲线的离心率.【解答】解:设|AF1|=x,|AF2|=y,∵点A为椭圆上的点,∴2a=4,b=1,c=;∴|AF1|+|AF2|=2a=4,即x+y=4;①又四边形AF1BF2为矩形,∴,即x2+y2=(2c)2=12,②由①②得,解得x=2﹣,y=2+,设双曲线C2的实轴长为2a′,焦距为2c′,则2a′=|AF2|﹣|AF1|=y﹣x=2,2c′=2,∴C2的离心率是e==.故答案为:.三、解答题(本大题共6小题,共70分,解答应写出必要的文字说明、证明过程或演算步骤)17.已知命题p:方程+=1表示焦点在x轴上的椭圆,命题q:(k﹣1)x2+(k﹣3)y2=1表示双曲线.若p∨q为真命题,求实数k的取值范围.【考点】复合命题的真假.【分析】分别求出p,q为真时的k的范围,根据若p∨q为真命题,取并集即可.【解答】解:当p为真时,k>4﹣k>0,即2<k<4;…当q为真时,(k﹣1)(k﹣3)<0,即1<k<3;…由题设,p∨q为真命题,知p和q中至少有一个为真命题,∴2<k<4或1<k<3,即1<k<4从而k的取值范围是1<k<4.…18.在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且(Ⅰ)确定角C的大小;(Ⅱ)若c=,且△ABC的面积为,求a2+b2的值.【考点】解三角形.【分析】(Ⅰ)根据,利用正弦定理得,从而可求C的大小;(Ⅱ)由面积公式得=,从而可得ab=6,由余弦定理,可得结论.【解答】解:(Ⅰ)∵,∴由正弦定理得…∴sinC=…∵△ABC是锐角三角形,∴C=…(Ⅱ)∵c=,C=,△ABC的面积为,∴由面积公式得=…∴ab=6 …由余弦定理得a2+b2﹣2abcos=7 …∴a2+b2=13 …19.如图,已知斜三棱柱ABC﹣A1B1C1中,AB=AC,D为BC的中点.(1)若AA1⊥AD,求证:AD⊥DC1;(2)求证:A1B∥平面ADC1.【考点】直线与平面平行的判定;空间中直线与直线之间的位置关系.【分析】(1)证明AD⊥BC,AD⊥CC1,利用线面垂直的判定定理,可得AD⊥平面BCC1B1,即可证明AD⊥DC1;(2)连结A1C,交AC1于点O,连结OD,则O为A1C的中点,证明OD∥A1B,可得A1B∥平面ADC1.【解答】证明:(1)因为AB=AC,D为BC的中点,所以AD⊥BC.…因为AA1⊥AD,AA1∥CC1,所以AD⊥CC1,…因为CC1∩BC=C,所以AD⊥平面BCC1B1,…因为DC1⊂平面BCC1B1,所以AD⊥DC1…(2)连结A1C,交AC1于点O,连结OD,则O为A1C的中点.因为D为BC的中点,所以OD∥A1B …因为OD⊂平面ADC1,A1B⊄平面ADC1,…所以A1B∥平面ADC1…20.已知双曲线C的方程为x2﹣15y2=15.(1)求其渐近线方程;(2)求与双曲线C焦点相同,且过点(0,3)的椭圆的标准方程.【考点】双曲线的简单性质;椭圆的标准方程.【分析】(1)双曲线方程化为标准方程,由双曲线的标准方程可求得a、b,可得渐近线方程.(2)求出抛物线的焦点坐标,求出双曲线的两焦点坐标,即为椭圆的焦点坐标,即可得到c的值,然后根据椭圆的定义得到a,最后利用a,b,c的关系即可求出b的值,得到椭圆方程.【解答】解:(1)双曲线方程化为,由此得,所以渐近线方程为,即.(2)双曲线中,,焦点为(﹣4,0),(4,0).椭圆中,,则a=5,b2=a2﹣c2=52﹣42=9.所以,所求椭圆的标准方程为.21.数列{a n}的前n项的和为S n,对于任意的自然数a n>0,(Ⅰ)求证:数列{a n}是等差数列,并求通项公式(Ⅱ)设,求和T n=b1+b2+…+b n.【考点】数列的求和;等差关系的确定.【分析】(Ⅰ)令n=1求出首项,然后根据4a n=4S n﹣4S n﹣1进行化简得a n﹣a n﹣1=2,从而得到数列{a n}是等差数列,直接求出通项公式即可;(Ⅱ)确定数列通项,利用错位相减法,可求数列的和.【解答】(Ⅰ)证明:∵4S1=4a1=(a1+1)2,∴a1=1.当n≥2时,4a n=4S n﹣4S n﹣1=(a n+1)2﹣(a n﹣1+1)2,∴2(a n+a n﹣1)=a n2﹣a n﹣12,又{a n}各项均为正数,∴a n﹣a n﹣1=2,∴数列{a n}是等差数列,∴a n=2n﹣1;(Ⅱ)解:=∴T n=b1+b2+…+b n=++…+﹣﹣﹣①∴T n=++…++﹣﹣﹣②①﹣②T n=+2(++…+)﹣=∴T n=1﹣.22.如图,已知椭圆+=1(a>b>0)的离心率为,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为.一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.(Ⅰ)求椭圆和双曲线的标准方程;(Ⅱ)设直线PF1、PF2的斜率分别为k1、k2,证明k1•k2=1;(Ⅲ)探究是否是个定值,若是,求出这个定值;若不是,请说明理由.【考点】直线与圆锥曲线的综合问题.【分析】(Ⅰ)由椭离心率为,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为,求出a,b,从而能求出椭圆的标准方程,设等轴双曲线的标准方程为,由等轴双曲线的顶点是椭圆的焦点,求出m,从而能求出双曲线的标准方程.(Ⅱ)设P(x0,y0),F1(﹣2,0),F2(2,0),则k1=,,由此能证明k1k2=1.(Ⅲ)PF1的方程为y=k1(x+2),将其代入椭圆方程得,由此利用韦达定理、弦长公式,结合已知条件能推导出是定值.【解答】解:(Ⅰ)设椭圆的半焦距为c,由题意知:,2a+2c=4(+1)解得a=2,c=2,又a2=b2+c2,解得b=2.故椭圆的标准方程为由题意设等轴双曲线的标准方程为(m>0),因为等轴双曲线的顶点是椭圆的焦点.所以m=2,因此双曲线的标准方程为证明:(Ⅱ)设P(x0,y0),F1(﹣2,0),F2(2,0)则k1=,.因为点P在双曲线x2﹣y2=4上,所以.因此,故k1k2=1.解:(Ⅲ)设A(x1,y1),B(x2,y2),由于PF1的方程为y=k1(x+2),将其代入椭圆方程得所以,所以==同理可得.则,又k1k2=1,所以=.故恒成立,即是定值.2018年2月11日。
广东省揭阳市第一中学2018学年高二上学期第二次段考考

揭阳第一中学2018---2018学年度第一学期高二级(96届)第二次阶段考试数学(文)科试题命题:高二文科数学备课组校对:吴奕锋班级:姓名:座号:一.选择题(每小题5分,每小题只有一个正确答案,请将正确答案填在答题卡上)1.设集合A={1,2,3},B={4,5},M={x|x=a+b,a∈A,b∈B},则M中元素的个数为()A.3 B.4 C.5 D.62.直线的倾斜角α=()A.30°B.60°C.120°D.150°3.在等差数列{a n}中,a20l5=a2018+6,则公差d等于()A.2 B.3 C.4 D.64.已知向量=(1,2),=(x,4),若向量∥,则x=()A.2 B.﹣2 C.8 D.﹣85.△ABC中,AB=2,AC=3,∠B=60°,则cosC=()A.B.C.D.6.已知等差数列{a n}中,|a3|=|a9|,公差d<0;S n是数列{a n}的前n项和,则()A.S5>S6B.S5<S6C.S6=0 D.S5=S67.已知直线l⊥平面α,直线m⊂平面β,给出下列命题①α∥β⇒l⊥m;②α⊥β⇒l∥m;③l∥m⇒α⊥β;④l⊥m⇒α∥β.其中正确命题的序号是()A.①②③B.②③④C.①③D.②④8.设p:实数x,y满足x>1且y>1,q:实数x,y满足x+y>2,则p是q的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件9.当时,函数f(x)=sinx+cosx的()A.最大值是1,最小值是﹣1 B.最大值是1,最小值是﹣C.最大值是2,最小值是﹣2 D.最大值是2,最小值是﹣110.函数f(x)=a x-1﹣2(a>0,a≠1)的图象恒过定点A,若点A在直线mx﹣ny﹣1=0上,其中m>0,n>0,则的最小值为()A.4 B.5 C.6 D.11.若实数x,y满足不等式组目标函数t=x﹣2y的最大值为2,则实数a的值是()A.﹣2 B.0 C.1 D.212.已知数列{a n}中,a n+1=3S n,则下列关于{a n}的说法正确的是()A.一定为等差数列B.一定为等比数列C.可能为等差数列,但不会为等比数列D.可能为等比数列,但不会为等差数列二.填空题(共4小题,每小题5分,请将正确答案填在答题卡上)13.不等式|x+1|+|x﹣2|≤5的解集为.14.已知正项等比数列{a n}的公比q=2,若存在两项a m,a n,使得=4a1,则+的最小值为.15.已知变量x,y满足,则的取值范围是.16.等比数列{a n}的前n项和为S n,且a3=2S2+1,a4=2S3+1,则公比q为.三.解答题(共6小题,共70分,解答过程必须写出正确计算、推理过程)17.(10分)设命题p:实数x满足x2﹣4ax+3a2<0(a>0),命题q:实数x满足≤0,P ;(1)若命题p的解集为P、命题q的解集为Q,当a=1时,求Q(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.18.(10分)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知asin2B=bsinA.(1)求B;(2)已知cosA=,求sinC的值.19.(12分)等差数列{a n}中,a2=8,S6=66(1)求数列{a n}的通项公式a n;(2)设b n=,T n=b1+b2+b3+…+b n,求T n20.(12分)设数列{a n}的前n项和为S n,且首项a1≠3,a n+1=S n+3n(n∈N*).(1)求证:{S n﹣3n}是等比数列;(2)若{a n}为递增数列,求a1的取值范围.21.(12分)已知向量=(,cos2ωx ),=(sin2ωx ,1),(ω>0),令f (x )=,且f(x )的周期为π.(1)求函数f (x )的解析式; (2)若时f (x )+ m ≤3,求实数m 的取值范围.22.(14分)已知函数f (x )=x 2+(3﹣a )x +2+2a +b ,a ,b ∈R .(1)若关于x 的不等式f (x )>0的解集为{x |x <﹣4或x >2},求实数a ,b 的值; (2)若关于x 的不等式f (x )≤b 在x ∈[1,3]上有解,求实数a 的取值范围;(3)若关于x 的不等式f (x )<12+b 的解集中恰有3个整数,求实数a 的取值范围.揭阳第一中学2018—2018学年度第一学期高二级(96届)第二次阶段考试数学(文)试题参考答案一.选择题(每小题5分,每小题只有一个正确答案,请将正确答案填在答题卡二.填空题(共4小题,每小题5分,请将正确答案填在答题卡上)[]31625,451523143,213⎥⎦⎤⎢⎣⎡-三.解答题(共6小题,共70分, 解答过程必须写出正确计算、推理过程)17.(10分)解:解:(1)若a=1,由x 2﹣4x +3<0得:1<x <3,)3,1(=∴P -----------------------2分 由得:2<x ≤3;(]3,2=∴Q -----------------------------------------------------------------------4分∴ =⋂Q P (2,3)---------------------------------------------------------------------------------------------------5分(2)¬q 为:实数x 满足x ≤2,或x >3;¬p 为:实数x 满足x 2﹣4ax +3a 2≥0,并解x 2﹣4ax +3a 2≥0得x ≤a ,或x ≥3a--------------------------7分¬p 是¬q 的充分不必要条件,所以a 应满足:a ≤2,且3a >3,解得1<a ≤2--------------------------9分∴a 的取值范围为:(1,2]------------------------------------------------------------------------------------------10分18.(10分)解:(1)∵asin2B=bsinA ,∴2sinAsinBcosB=sinBsinA ,-------------------------------------------------------------------------------------2分 ∴cosB=,∴B=.----------------------------------------------------------------------------------------------5分(2)∵cosA=,∴sinA=-------------------------------------------------------------------------------------7分∴sinC=sin (A +B )=sinAcosB +cosAsinB==.-----------------------------10分.19.(12分)解:(1)设等差数列{a n }的公差为d ,则有----------------------2分 解得:a 1=6,d=2,--------------------------------------------------------------------------------------------------- 4分∴a n =a 1+d (n ﹣1)=6+2(n ﹣1)=2n +4 -----------------------------------------------------6分(2)b n ===﹣--------------------------------------------------9分123111111112334122224n n n T b b b b n n n n ⎛⎫⎛⎫⎛⎫∴=++++=-+-++-=-= ⎪ ⎪ ⎪++++⎝⎭⎝⎭⎝⎭ --12分20.(12分)证明:(1)∵a n +1=S n +3n (n ∈N *),∴S n +1=2S n +3n------------------------------------------------------------------------------------------------------------1分∴S n +1﹣3n +1=2(S n ﹣3n)---------------------------------------------------------------------------------------------3分 ∵a 1≠3,∴数列{S n﹣3n}是公比为2,首项为a1﹣3的等比数列;----------------------------------------------------5分(2)由(1)得S n﹣3n=(a1﹣3)×2n﹣1,∴S n=(a1﹣3)×2n﹣1+3n,------------------------------------------------------------------------------------------6分n≥2时,a n=S n﹣S n﹣1=(a1﹣3)×2n﹣2+2×3n﹣1,------------------------------------------------------------8分∵{a n}为递增数列,∴n≥2时,(a1﹣3)×2n﹣1+2×3n>(a1﹣3)×2n﹣2+2×3n﹣1,------------------------------------------9分∴n≥2时,,∴a1>﹣9,-------------------------------------------------------------------------------------------------------------11分∵a2=a1+3>a1,∴a1的取值范围是a1>﹣9.---------------------------------------------------------------------------------------12分21.(12分)解:(1)∵向量=(,cos2ωx),=(sin2ωx,1),(ω>0)∴=sin2ωx+cos2ωx=2sin(2ωx+)----------------------------------------------------------3分∵函数的周期T==π,∴ω=1----------------------------------------------------------------------------------5分即函数f(x)的解析式是f(x)=2sin(2x+);----------------------------------------------------------6分(2)当时,2x+∈[,]-----------------------------------------8分∴﹣≤sin(2ωx+)≤1-----------------------------------------------------------------------------------------9分因此,若时,f(x)∈[﹣1,2]∴f(x)+m≤3恒成立,即2+m≤3,解之得m≤1----------------------------------------------------------11分即实数m的取值范围是(﹣∞,1].----------------------------------------------------------------------------12分22.(14分)解:(1)因为函数f(x)=x2+(3﹣a)x+2+2a+b,a,b∈R,又f(x)>0的解集为{x|x<﹣4或x>2},所以﹣4,2方程x2+(3﹣a)x+2+2a+b=0的两根,由,解得a=1,b=﹣12;----------------------------------------------------------------3分(2)因为函数f(x)=x2+(3﹣a)x+2+2a+b,a,b∈R,由f(x)≤b在x∈[1,3]上有解,知x2+(3﹣a)x+2+2a≤0在x∈[1,3]上有解,令g(x)=x2+(3﹣a)x+2+2a,则在x∈[1,3]上,g(x)min≤0;①,即得a≤﹣6;------------------------------------------------------4分②,即;---------------------------------------------5分有,解得a∈ ;------------------------------------------------------------6分③,即,解得a≥20;--------------------------------------------------7分综上,由①②③知,实数a的取值范围是a≤﹣6或a≥20.---------------------------------------8分(3)由f(x)<12+b得x2+(3﹣a)x+2a﹣10<0,令h(x)=x2+(3﹣a)x+2a﹣10,则h(x)=(x﹣2)[x﹣(a﹣5)],知h(2)=0,----------------------------------------------------10分故h(x)<0解集中的3个整数只能是3,4,5或﹣1,0,1;-------------------------------------11分①若解集中的3个整数是3,4,5,则5<a﹣5≤6,得10<a≤11;----------------------------- 12分②解集中的3个整数是﹣1,0,1;则﹣2≤a﹣5<﹣1,得3≤a<4;--------------------------- 13分综上,由①②知,实数a的取值范围为3≤a<4或10<a≤11.---------------------------------- 14分。
2018届广东省揭阳市普通高中学校高考高三数学4月月考模拟试题 01 Word版含答案
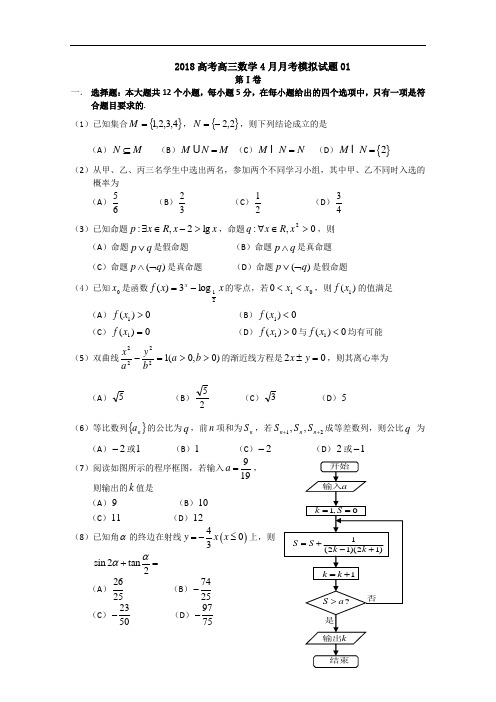
2018高考高三数学4月月考模拟试题01第Ⅰ卷一. 选择题:本大题共12个小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)已知集合{}4,3,2,1=M ,{}2,2-=N ,则下列结论成立的是(A )M N ⊆ (B )MN M = (C )M N N = (D ){}2MN =(2)从甲、乙、丙三名学生中选出两名,参加两个不同学习小组,其中甲、乙不同时入选的概率为(A )56 (B )23 (C )12 (D )34(3)已知命题x x R x p lg 2,:>-∈∃,命题0,:2>∈∀x R x q ,则(A )命题q p ∨是假命题 (B )命题q p ∧是真命题 (C )命题)(q p ⌝∧是真命题 (D )命题)(q p ⌝∨是假命题(4)已知0x 是函数x x f x 21log 3)(-=的零点,若010x x <<,则)(1x f 的值满足(A )0)(1>x f (B )0)(1<x f(C )0)(1=x f (D )0)(1>x f 与0)(1<x f 均有可能(5)双曲线)0,0(12222>>=-b a by a x 的渐近线方程是02=±y x ,则其离心率为(A )5(B )25(C )3 (D )5 (6)等比数列{}n a 的公比为q ,前n 项和为n S ,若21,,++n n n S S S 成等差数列,则公比q 为(A )2-或1 (B )1 (C )2- (D )2或1- (7)阅读如图所示的程序框图,若输入919a =, 则输出的k 值是(A )9 (B )10 (C )11 (D )12 (8)已知角α的终边在射线()403y x x =-≤上,则 sin 2tan2αα+=(A )2625 (B )7425- (C )2350- (D )9775-(9)一个几何体的三视图如图所示,则该几何体的表面积为(A )224+(B )244+ (C )8 (D )10522+++(10)已知P 是抛物线x y 42=上的一个动点,Q 是圆()()22311x y -+-=上的一个动点,)0,1(N 是一个定点,则PQ PN +的最小值为(A )3 (B )4 (C ) 5 (D )1(11)函数),0()0,(,sin ππ⋃-∈=x xxy 的图象可能是下列图象中的(A ) (B ) (C ) (D )(12)已知定义在R 上的函数)(x f 满足)(x f =223,([0,1))3,([1,0))x x x x ⎧∈⎪⎨∈⎪⎩+--,且)()2(x f x f =+,273)(++=x x x g ,则方程)()(x f x g =在区间]3,8[-上的所有实数根之和为 (A )0 (B )10- (C )11- (D ) 12-第Ⅱ卷本卷包括必考题和选考题两部分.第(13)题~(21)题为必考题,每个试题考生都必须做答.第(22)题~第(24)题为选考题,考生根据要求做答. 二.填空题:本大题共4小题,每小题5分.(13)若复数z 满足)1(2i i z +=-(i 为虚数单位),则=z .(14)在数列{}n a 中,11,a =当n N *∈时,1120n n n n a a a a ++-+=,则{}n a 的通项公式为_____________.2 222正视图 侧视图俯视图C 1B 1A 1DE CBA(151=,OB k =,0=⋅,点C 在AOB ∠内,且 30=∠AOC ,设2()OC OA OB R λλλ=+∈,则k 等于__________.(16)正方体1111D C B A ABCD -的各顶点都在球O 的球面上,若三棱锥11D AB O -的体积为32,则球O 的体积为____________.三. 解答题:解答应写出文字说明,证明过程或演算步骤. (17)(本小题满分12分)在ABC ∆中,角,,A B C 所对的边分别为,,a b c,已知S ABC =∆2.(I )求角B ;(II )若2b =,求a c +的取值范围.(18)(本小题满分12分)已知侧棱垂直于底面的三棱柱111C B A ABC -的所有棱长都相等,D 为棱1AA 中点. (I )证明:11DB BC ⊥;(II )在线段BC 上是否存在点E ,使DE ∥平面11C BA ,若存在,确定点E 的位置;若不存在,请说明理由.(19)(本小题满分12分)某校有1400名考生参加市模拟考试,现采取分层抽样的方法从文、理考生中分别抽取20份和50份数学试卷,进行成绩分析,得到下面的成绩频数分布表:(I )估计文科数学平均分及理科考生的及格人数(90分为及格分数线); (II )在试卷分析中,发现概念性失分非常严重,统计结果如下:问是否有90%的把握认为概念失分与文、理考生的不同有关? 附:))()()(()(22d b c a d c b a bc ad n K ++++-=(20)(本小题满分12分)已知直线01:1=-+y x l 与椭圆)0(12222>>=+b a b y a x 相交于B A ,两点,M 是线段AB 上的一点,BM AM -=,且点M 在直线x y l 21:2=上. (I )求椭圆的离心率;(II )设椭圆左焦点为1F ,若1AF B ∠为钝角,求椭圆长轴长的取值范围. (21)(本小题满分12分)已知函数21()ln (0)2f x x ax x a =-->. (I )当2=a 时,求)(x f y =的单调区间和极值;(II )若存在12,(0,)x x ∈+∞,且12x x ≠,使12()()f x f x =,证明:0)2(21<+'x x f .请考生在第(22)~(24)三题中任选一题做答,如果多做,则按所做的第一题计分.做答时,用2B 铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中. (22)(本小题满分10分)选修4-1:几何证明选讲如图,圆O 的直径10=AB ,P 是AB 延长线上一点,2=BP ,割线PCD 交圆O 于点C 、D ,过点P 作AP 的垂线,交直线AC 于点E ,交直线AD 于点F .(I )求证:PDF PEC ∠=∠; (II )求PF PE ⋅的值.(23)(本小题满分10分)选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,已知曲线1C : 122=+y x ,在极坐标系(与平面直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,直线l 的极坐标方程为6)sin cos 2(=-θθρ.(I )将曲线1C 上的所有点的横坐标、纵坐标分别伸长为原来的3倍、2倍后得到曲线2C ,试写出直线l 的直角坐标方程和曲线2C 的参数方程;(II )在曲线2C 上求一点P ,使点P 到直线l 的距离最大,并求出此最大值. (24)(本小题满分10分)选修4-5:不等式选讲已知函数a x x x f 212)(-+-=. (I )当1=a 时,求3)(≤x f 的解集;(II )当[]2,1∈x 时,3)(≤x f 恒成立,求实数a 的集合.参考答案二.填空题(13)i -1; (14)121n a n =-; (15)3; (16)π34 三. 解答题(17)(本小题满分12分)解:(I )由已知得sin cos ac B B =, ……………………………………2分 ∴3tan =B ,∵π<<B 0,∴3π=B . …………………………………4分(II )法一:由余弦定理得2242cos3a c ac π=+-, ……………………………6分∴()()2224332a c a c ac a c +⎛⎫=+-≥+- ⎪⎝⎭(当且仅当a c =时取等号), …………9分 解得04a c <+≤. ………………………………11分FC 1B 1A 1DEC BA又b c a >+,∴42≤+<c a ,∴a c +的取值范围是(]2,4. …………………………………12分 法二:由正弦定理得C c A a sin 34,sin 34==, ……………………………6分又32π=+C A ,∴)]sin([sin 34)sin (sin 34B A A C A c a ++=+=+, …………7分 )]3sin([sin 34π++=A A )cos 23sin 21(sin 34A A A ++=, ……………8分)6sin(4)cos 21sin 23(4π+=+=A A A . ………………………………………10分 ∵320π<<A ,∴6566πππ<+<A ,∴1)6sin(21≤+<πA ∴a c +的取值范围是(]2,4. …………………………………………………12分 (18)(本小题满分12分) 解:(I )连结CB 1,设11BC B C F =,连结1,,DC DB DF ,∵四边形11B BCC 是正方形,∴C B BC 11⊥且F 为1BC 的中点. …………2分 由题意知DAB Rt C DA Rt ∆≅∆11,∴1DC DB =,∴DF BC ⊥1. …………4分又∵⊂C B DF 1,平面DC B 1,F C B DF =⋂1,∴⊥1BC 平面DC B 1. …………6分 ∵⊂1DB 平面DC B 1,∴11DB BC ⊥. ……………………………………7分 (II )存在点E 为BC 的中点,使//DE 平面11BAC . …………………………8分 连接F A EF 1,,EF121CC ,D A1121CC ,∴EF ∥D A 1, ∴四边形D EFA 1为平行四边形,∴F A 1∥DE . ………………………………10分 ∵⊂F A 1平面11C BA ,⊄DE 平面11C BA ,∴DE ∥平面11C BA . ………………12分 (19)(本小题满分12分)解: (I )∵1524547581053135376.520⨯+⨯+⨯+⨯+⨯=∴估计文科数学平均分为76.5. ……………………………………………………3分∵501400100070⨯= , 208100056050+⨯=, ∴理科考生有560人及格. ………………………………………………………6分(II )706.24.145255020)3052015(7022<=⨯⨯⨯⨯-⨯=K . ……………………………10分 故没有90%的把握认为概念失分与文、理考生的不同有关. ……………………12分 (20)(本小题满分12分) 解:设B A ,两点的坐标分别为),().,(2211y x B y x A .(I )由BM AM -=知M 是AB 的中点, ……………………1分由⎪⎩⎪⎨⎧=+=-+,1,012222b y ax y x 得:02)(2222222=-+-+b a a x a x b a , ∴222212b a a x x +=+,222212122)(b a b x x y y +=++-=+, …………………3分 ∴点M 的坐标为),(222222b a b b a a ++. ………………………4分 又点M 在直线2l 上,∴02222222=+-+ba b b a a , ∴)(222222c a b a -==,∴222c a =,∴22=e . …………………6分 (II )由(I )知c b =,方程化为2234220x x c -+-=()2162410,c c ∆=-->>………………………7分 ∴3421=+x x ,212223c x x -=,31321)(2212121+-=++-=c x x x x y y .………8分 由已知知011<⋅B F A F ,即0)(),(),(21221212211<++++=+⋅+y y c x x c x x y c x y c x代入得0342>--c c ,解得72+>c 或72-<c ,综上得72+>c . …………………11分又a = , ∴a 2的取值范围是),14224(+∞+. ……………………12分 (21)(本小题满分12分)解:(I )当2=a 时,2()ln (0)f x x x x x =-->,∴2121(1)(21)()21x x x x f x x x x x +-+-'=--=-=-,………………………………2分令0)(>'x f ,则210<<x ;令()0f x '<,则21>x ,∴)21,0(是)(x f 的单调递增区间,),21(+∞是)(x f 的单调减区间. …………………5分当21=x 时,)(x f 取极大值为2ln 43--. ………………………………………………6分(II )解法1: 不妨设012>>x x ,由已知,得)21(ln )21(ln )()(1211222212x ax x x ax x x f x f -----=- )]()(21[ln ln 12212212x x x x a x x -+---=,0)](1)(21[ln ln 121212=-++--=x x x x a x x∴1)(21ln ln 121212++=--x x a x x x x . ……………………………………………………8分∵11)(--='ax xx f , ∴121221212121ln ln 21)(22)2(x x x x x x x x a x x x x f ---+=-+-+=+' ]ln 1)1(2[112121212x x x x x x x x -+--=. …………………………………………9分 设12x x t =,)1(ln 1)1(2)(>-+-=t t t t t g . ………………………………………………10分 ∵0)1()1()(22<+--='t t t t g ,∴)(t g 在(1,)+∞上是减函数,∴0)1()(=<g t g ,即0ln 1)1(2121212<-+-x x x x x x ,又∵0112>-x x , ∴0)2(21<+'x x f . ………………………………………………12分解法2:不妨设012>>x x ,由已知,得)21(ln )21(ln )()(1211222212x ax x x ax x x f x f -----=- )]()(21[ln ln 12212212x x x x a x x -+---=,0)](1)(21[ln ln 121212=-++--=x x x x a x x∴1)(21ln ln 121212++=--x x a x x x x . ………………………………………8分∵11)(--='ax xx f , ∴121221212121ln ln 21)(22)2(x x x x x x x x a x x x x f ---+=-+-+=+' 21122121221(ln ln )x x x x x x x x -=+--+. ……………………………………9分令222222()ln ln ((0,))x xg x x x x x x x-=+-∈+. ………………………………………10分∴2222()()0()x x g x x x x -'=>+,∴()g x 在2(0,)x 单调递增,∴12()()0g x g x <=,又2110x x >-,∴0)2(21<+'x x f . ………………………………………12分(22)(本小题满分10分)选修4-1:几何证明选讲 解法1:(I )连接BC ,则90=∠=∠APE ACB , 即B 、P 、E 、C 四点共圆.∴CBA PEC ∠=∠. …………………………3分 又A 、B 、C 、D 四点共圆, ∴PDF CBA ∠=∠∴PDF PEC ∠=∠. ………………………5分 (II )∵PDF PEC ∠=∠,∴F 、E 、C 、D 四点共圆,………………7分∴PD PC PF PE ⋅=⋅,又24)102(2=+⨯=⋅=⋅PA PB PD PC , ………9分24=⋅PF PE . ………………………………………10分解法2:(I )连接BD ,则AD BD ⊥,又AP EP ⊥ ∴ 90=∠+∠=∠+∠EAP PEA PDB PDF , ∵EAP PDB ∠=∠,∴PDF PEC ∠=∠. ………5分 (II )∵PDF PEC ∠=∠,DPF EPC ∠=∠, ∴PEC ∆∽PDF ∆,∴PDPEPF PC =, 即PD PC PF PE ⋅=⋅, ………………………………7分 又∵24)102(2=+=⋅=⋅PA PB PD PC , ………………………………………9分 ∴24=⋅PF PE . ………………………………………10分 (23)(本小题满分10分)选修4-4:坐标系与参数方程 解:(I )由题意知,直线l 的直角坐标方程为062=--y x , …………………2分 由题意知曲线2C 的直角坐标方程为1)2()3(22=+yx,…………………………………4分∴曲线2C的参数方程为,2sin .x y ϕϕ⎧=⎪⎨=⎪⎩(ϕ为参数). …………………………6分(II )设)sin 2,cos 3(ϕϕP ,则点P 到直线l 的距离56)3sin(456sin 2cos 32--=--=ϕπϕϕd , …………………………8分 当1)3sin(-=-ϕπ时,即点P 的坐标为)1,23(-时,点P 到直线l 的距离最大,此时52564max =+=d . …………………………10分(24)(本小题满分10分)选修4-5:不等式选讲 解:(I )解:原不等式可化为3212≤-+-x x ,当2>x 时,333≤-x ,则2≤x ,无解; …………………………1分 当221≤≤x 时,31≤+x ,则2≤x ,∴221≤≤x ; ………………………3分 当21<x 时,333≤-x ,则0≥x ,∴210<≤x , ………………………5分 综上所述:原不等式的解集为[]2,0. …………………………6分 (II )原不等式可化为1232--≤-x a x ,∵[]2,1∈x ,∴x a x 242-≤-, ……………………………7分 即x x a x 24242-≤-≤-,故x a x -≤≤-4243对[]2,1∈x 恒成立,当21≤≤x 时,43-x 的最大值为2,x -4的最小值为2,∴实数a 的集合为{}1. …………………10分。
广东省揭阳市2018年高考第二次模拟考试数学(理)试题-有答案

揭阳市2018年高中毕业班高考第二次模拟考试数学(理科)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|A x y ==,{}|31x B x =≥,则( )A .AB = B .A B ⊆C .A B R =D .A B φ=2.已知复数z 满足()123i z i +⋅=+,则z 的共轭复数z 在复平面内对应的点在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限3.平面直角坐标系xOy 中,i ,j 分别是与x 轴、y 轴正方向同向的单位向量,向量2a i =,b i j =+,以下说法正确的是( )A .1a b ⋅=B .a b =C .()a b b -⊥ D .//a b 4.已知直线a 、b ,平面α、β、γ,下列命题正确的是( ) A .若αγ⊥,βγ⊥,a αβ=,则a γ⊥ B .若a αβ=,b αγ=,c βγ=,则////a b cC.若a αβ=,//b a ,则//b α D .若αβ⊥,a αβ=,//b α,则//b a5.已知直线430x y a -+=与22:40C x y x ++=相交于A 、B 两点,且120AOB ∠=,则实数a 的值为( )A .3B .10 C. 11或21 D .3或136.已知()511x ax x ⎛⎫+- ⎪⎝⎭的展开式中常数项为40-,则a 的值为( )A .2B .2- C. 2± D .47.已知函数()()()sin 0,0,02f x A x A ωϕωϕπ=+>>≤<的部分图象如图所示,则ϕ的值为( )A .3π或23π B .23π C. 43π D .3π或43π8.在如图的程序框图中,输出的n 值为( )A .14B . 32 C. 46 D .539.已知双曲线的焦距为4,A 、B 是其左、右焦点,点C 在双曲线右支上,ABC △的周长为10,则AC 的取值范围是( )A .()2,5B .()2,6 C. ()3,5 D .()3,610.如图是某几何体的三视图,图中每个小正方形的边长为1,则此几何体的体积为( )A .83 B .163 C.4 D .20311.过抛物线22x y =上两点A 、B 分别作切线,若两条切线互相垂直,则线段AB 的中点到抛物线准线的距离的最小值为( ) A .12 B .1 C.32D .2 12.把函数()()2log 1f x x =+的图象向右平移一个单位,所得图象与函数()g x 的图象关于直线y x =对称;已知偶函数()h x 满足()()11h x h x -=--,当[]0,1x ∈时,()()1h x g x =-;若函数()()y k f x h x =⋅-有五个零点,则k 的取值范围是( )A .()3log 2,1B .[)3log 2,1 C.61log 2,2⎛⎫ ⎪⎝⎭ D .61log 2,2⎛⎤ ⎥⎝⎦第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.曲线1y x=在点()1,1处的切线方程为 . 14.题库中有10道题,考生从中随机抽取3道,至少做对2道算通过考试.某考生会做其中8道,有2道不会做,则此考生能通过考试的概率为 .15.已知等差数列{}n a 中,2416a a +=,11a +、21a +、41a +成等比数列,把各项如下图排列:则从上到下第10行,从左到右的第11个数值为 .16.平面四边形ABCD 中,60A ∠=,AD DC ⊥,3AB =2BD =,则BC 的最小长度为 . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 已知数列{}n a 的前n 项的和为n S ,满足21a =,1631n n S a +=-. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设2n n b a =,数列{}n b 的前n 项和与积分别为n R 与n T ,求n R 与n T .18. 如图,在四面体ABCD 中,90ABC ADC ∠=∠=,BC BD ==. (Ⅰ)求证:AD BD ⊥;(Ⅱ)若AB 与平面BCD 所成的角为60,点E 是AC 的中点,求二面角C BD E --的大小.19. 甲、乙、丙三人去某地务工,其工作受天气影响,雨天不能出工,晴天才能出工.其计酬方式有两种,方式一:雨天没收入,晴天出工每天250元;方式而:雨天每天120元,晴天出工每天200元;三人要选择其中一种计酬方式,并打算在下个月(30天)内的晴天都出工,为此三人作了一些调查,甲以去年此月的下雨天数(10天)为依据作出选择;乙和丙在分析了当地近9年此月的下雨天数(n )的频数分布表(见下表)后,乙以频率最大的n 值为依据作出选择,丙以n 的平均值为依据作出选择.(Ⅱ)根据统计范围的大小,你觉得三人中谁的依据更有指导意义?(Ⅲ)以频率作为概率,求未来三年中恰有两年,此月下雨不超过11天的概率.20. 已知椭圆()22122:10x y C a b a b+=>>的左、右焦点分别为1F 、2F ,圆2C 经过椭圆1C 的两个焦点和两个顶点,点P 在椭圆1C 上,且12PF =22PF =(Ⅰ)求椭圆1C 的方程和点P 的坐标;(Ⅱ)过点P 的直线1l 与圆2C 相交于A 、B 两点,过点P 与1l 垂直的直线2l 与椭圆1C 相交于另一点C ,求ABC △的面积的取值范围. 21. 已知函数()()()ln 22x mf x ex ax x m +=-+++-,(Ⅰ)若0a >,且()1f -是函数的一个极值,求函数()f x 的最小值; (Ⅱ)若0a =,求证:[]1,0x ∀∈-,()0f x ≥.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,圆C 的圆心为10,2⎛⎫ ⎪⎝⎭,半径为12,现以原点为极点,x 轴的正半轴为极轴建立极坐标系, (Ⅰ)求圆C 的极坐标方程;(Ⅱ)设M ,N 是圆C 上两个动点,满足23MON π∠=,求OM ON +的最小值. 23.选修4-5:不等式选讲已知函数()11f x x x m =++++,m R ∈,(Ⅰ)若不等式()2f x m ≥-恒成立,求实数m 的取值范围; (Ⅱ)求不等式()2f x m -<的解集.试卷答案一、选择题1-5:BACAD 6-10:CCDCB 11、12:B C 二、填空题13.20x y +-= 14.141515.275三、解答题(17)解:(Ⅰ)1361-=+n n a S ,1361-=∴-n n a S )2(≥n , 两式相减,得n n n a a a 3361-=+)2(≥n ,n n a a 31=∴+)2(≥n ,又12=a ,所以当2≥n 时,}{n a 是首项为1,公比为3的等比数列,22233--=⋅=n n n a a ,由13621-=a a 得311=a ,满足上式, 所以通项公式为23-=n n a *)(N n ∈;(Ⅱ)122293--===n n n n a b ,得11=b ,公比为9, 8199191-=--=n n n R ,1213219991-⋅⋅⋅⋅=⋅⋅⋅⋅=n n n b b b b T)1(2)1(121399---+++===n n n n n .(18)解:(Ⅰ)由已知得222CD BD BC =+,BC BD ⊥∴,又BC AB ⊥,B AB BD = ,ABD BC 平面⊥∴,AD BC ⊥∴,又AD CD ⊥,C CD BC = ,BCD AD 平面⊥∴,BD AD ⊥∴.(Ⅱ)解法1:由(Ⅰ)知,AB 与平面BCD 所成的角为ABD ∠,即︒=∠60ABD , 设BD =2,则BC =2,在ADB Rt ∆中,AB =4,由(Ⅰ)中ABD BC 平面⊥,得平面ABC ⊥平面ABD ,在平面ABD 内,过点B 作AB Bz ⊥,则Bz ⊥平面ABC ,以B 为原点,建立空间直角坐标系xyz B -,则)0,0,0(B ,)0,0,4(A ,)0,2,0(C ,)0,1,2(E ,由160cos ||=︒=BD x D , 360sin ||=︒=BD z D ,得)3,0,1(D ,∴)0,1,2(=,)3,0,1(=, 设平面BDE 的法向量为),,(z y x m =,则⎪⎩⎪⎨⎧=+=⋅=+=⋅0302z x BD m y x BE m ,取1=z ,解得⎪⎩⎪⎨⎧=-=323y x ,∴)1,32,3(-=m是平面BDE 的一个法向量,又)3,0,3(-=是平面CBD 的一个法向量. 设二面角E BD A --的大小为θ,易知θ为锐角,则2132434|||||,cos |cos =⨯==><=AD m mθ,∴60θ=,即二面角C BD E --的大小为60.【解法2:由(Ⅰ)知,AB 与平面BCD 所成的角为ABD ∠,即60ABD ∠=, 分别取CD 、BD 的中点F 、G ,连EG 、FG ,在Rt ABC ∆和Rt ADC ∆中,E 为斜边AC 中点,故12BE DE AC ==, ∴EG BD ⊥;又∵BC ⊥平面ABD ,∴BC BD ⊥, 又∵//BC FG ∴FG BD ⊥; ∴EGF ∠为二面角C BD E --的平面角, 由(Ⅰ)知AD ⊥平面BCD ,又//AD EF , 故EF ⊥平面BCD ,从而EF FG ⊥,∴12tan 12ADEF EGF FG BCBC ∠====,60EGF ∴∠=,即二面角C BD E --的大小为60.(19)解:(Ⅰ)按计酬方式一、二的收入分别记为)(n f 、)(n g ,(10)250(3010)5000f =⨯-=, 52002020010120)10(=⨯+⨯=g ,所以甲选择计酬方式二; 由频数分布表知频率最大的n=8,5500)830(250)8(=-⨯=f , 5360222008120)8(=⨯+⨯=g ,所以乙选择计酬方式一;n 的平均值为10)1132122101938(91=⨯+⨯+⨯+⨯+⨯⨯,所以丙选择计酬方式二;(Ⅱ)甲统计了1个月的情况,乙和丙统计了9个月的情况, 但乙只利用了部分数据,丙利用了所有数据, 所以丙的统计范围最大, 三人中丙的依据更有指导意义;(Ⅲ)任选一年,此月下雨不超过11天的频率为3296=,以此作为概率,则未来三年中恰有两年,此月下雨不超过11天的概率为94)321()32(223=-⨯C . (20)解:(I )设)0,(1c F -,)0,(2c F , 可知圆2C 经过椭圆焦点和上下顶点,得c b =, 由题意知4||||221=+=PF PF a ,得2=a , 由222a c b =+,得2==c b ,所以椭圆1C 的方程为12422=+y x , 点P 的坐标为)0,2(.(II )由过点P 的直线l 2与椭圆1C 相交于两点,知直线l 2的斜率存在, 设l 2的方程为)2(-=x k y ,由题意可知0≠k , 联立椭圆方程,得0488)12(2222=-+-+k x k x k ,设),(22y x C ,则12482222+-=⋅k k x ,得1224222+-=k k x ,所以1214|2|1||2222++=-+=k k x k PC ; 由直线l 1与l 2垂直,可设l 1的方程为)2(1--=x ky ,即02=-+ky x 圆心)0,0(到l 1的距离212kd +=,又圆的半径2=r ,所以1)1(2142)2||(222222+-=+-=-=k k k d r AB , 1122||22+-⋅=k k AB , 由r d <即2122<+k ,得12>k ,112||||2122+-⋅==∆k k PC AB S ABC1212412142222+-⋅=++⋅k k k k ,设12-=k t ,则0>t ,23233262ABC S t t t∆==≤=++ 当且仅当6t =10k =±,所以△ABC 的面积的取值范围是23(0,3. (21)解:(I )m ax ax x ex f mx -+++-=+2)2ln()(2,定义域为),2(∞+-,a ax x e x f m x 2221)('+++-=+. 由题意知0)1('=-f ,即011=--m e ,解得1=m , 所以1)2()2ln()(1-+++-=+x ax x e x f x ,a ax x e x f x 2221)('1+++-=+, 又1+=x ey 、21+-=x y 、a ax y 22+=(0>a )在),2(∞+-上单调递增, 可知)('x f 在),2(∞+-上单调递增,又0)1('=-f ,所以当)1,2(--∈x 时,0)('<x f ;当),1(∞+-∈x 时,0)('>x f . 得)(x f 在)1,2(--上单调递减,)(x f 在),1(∞+-上单调递增, 所以函数)(x f 的最小值为a a f -=--=-11)1(. (II )若0=a ,得m x ex f mx -+-=+)2ln()(,21)('+-=+x e x f m x 由)('x f 在]0,1[-上单调递增,可知)(x f 在]0,1[-上的单调性有如下三种情形:①当)(x f 在]0,1[-上单调递增时,可知0)('≥x f ,即0)1('≥-f ,即011≥--m e ,解得1≥m ,m e f m -=--1)1(,令m e m g m -=-1)(,则01)('1≥-=-m e m g ,所以)(m g 单调递增,0)1()(=≥g m g ,所以0)()1()(≥=-≥m g f x f ; ②当)(x f 在]0,1[-上单调递减时, 可知0)('≤x f ,即0)0('≤f ,即021≤-m e ,解得2ln -≤m , 得02ln 2ln 2ln )0(>=+-≥--=mmmee m ef ,所以0)0()(>≥f x f ;[或:令2ln )(--=m e m h m,则0211)('<-≤-=m e m h , 所以)(m h 单调递减,021)2ln ()(>=-≥h m h ,所以0)()0()(>=≥m h f x f ;] ③当)(x f 在]0,1[-上先减后增时,得)('x f 在]0,1[-上先负后正,所以)0,1(0-∈∃x ,0)('0=x f ,即2100+=+x e mx ,取对数得)2ln(00+-=+x m x , 可知)()(0min x f x f =m x e mx -+-=+)2ln(0002)1(2102000>++=++=x x x x ,所以0)(>x f ;综上①②③得:]0,1[-∈∀x ,0)(≥x f . 【或:若0=a ,得m x ex f mx -+-=+)2ln()(,21)('+-=+x e x f m x 由)('x f 在]0,1[-上单调递增,分如下三种情形:①当0)('≥x f 恒成立时,只需0)1('≥-f ,即011≥--m e ,解得1≥m , 可知)(x f 在]0,1[-上单调递增,m e f m -=--1)1(,令m e m g m -=-1)(,则01)('1≥-=-m em g ,所以)(m g 单调递增,0)1()(=≥g m g ,所以0)()1()(≥=-≥m g f x f ;②当0)('≤x f 恒成立时,只需0)0('≤f ,即021≤-m e ,解得2ln -≤m , 可知)(x f 在]0,1[-上单调递减时,02ln 2ln 2ln )0(>=+-≥--=mmme e m ef ,所以0)0()(>≥f x f ;③当)('x f 在]0,1[-上先负后正时,)(x f 在]0,1[-上先减后增,所以)0,1(0-∈∃x ,0)('0=x f ,即2100+=+x e mx ,取对数得)2ln(00+-=+x m x , 可知)()(0min x f x f =m x emx -+-=+)2ln(0002)1(2102000>++=++=x x x x ,所以0)(>x f ;综上①②③得:]0,1[-∈∀x ,0)(≥x f . 】(22)解:(I )圆C 的直角坐标方程为221124x y ⎛⎫+-= ⎪⎝⎭,化为极坐标方程为sin ρθ=; (II )设()122,,,3M N πρθρθ⎛⎫+⎪⎝⎭, 122sin sin 3OM ON πρρθθ⎛⎫+=+=++⎪⎝⎭1sin sin 23πθθθ⎛⎫==+ ⎪⎝⎭, 由0203θππθπ≤≤⎧⎪⎨≤+≤⎪⎩,得03πθ≤≤,2333πππθ≤+≤,故sin 123πθ⎛⎫≤+≤ ⎪⎝⎭,即OM ON +的最小值为2. (23)解:(I )|||)1(1||1||1|)(m m x x m x x x f =++-+≥++++=, 由题意知|2|||-≥m m ,得22)2(-≥m m ,解得1≥m ;(II )不等式为m x m x 2|1||1|<-++-,即m m x x 2|)1(||1|<+-+- 若0≤m ,显然不等式无解; 若0>m ,则11>+m .①当1≤x 时,不等式为m x m x 211<-++-,解得21mx ->, 所以121≤<-x m; ②当11+<<m x 时,不等式为m x m x 211<-++-,恒成立, 所以11+<<m x ;③当1+≥m x 时,不等式为m m x x 2)1(1<+-+-,解得123+<mx , 所以1231+<≤+mx m ; 综上所述,当0≤m 时,不等式的解集为空集, 当0>m 时,解集为}12321|{+<<-m x m x .。
广东省揭阳市高三第二次模拟考试数学(文)试题Word版含答案
绝密★启用前揭阳市2017年高中毕业班第二次高考模拟考试题数学(文科)本试卷共4页,满分150分.考试用时120分钟.注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答题前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第Ⅰ卷时,选出每个小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,写在本试卷上无效.3.回答第Ⅱ卷时,将答案写在答题卡上,答在本试卷上无效.4.考试结束,将本试卷和答题卡一并交回.第Ⅰ卷一、选择题:共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合}1,0,1{-=A ,}032|{2<--=x x x B ,则=B A(A )}1,0,1{- (B )}0{(C ))1,1(-(D ))3,1(-(2)已知复数2a iz i+=(其中i 为虚数单位)的虚部与实部相等,则实数a 的值为 (A )1 (B )12 (C )1- (D )12- (3)“p q ∧为真”是“p q ∨为真”的(A )充分不必要条件 (B )必要不充分条件 (C )充要条件(D )既不充分也不必要条件(4)甲乙两人下棋,已知两人下成和棋的概率为12,甲赢棋的概率为13,则甲输棋的概率为 (A )56 (B )23 (C )16 (D )12(5)图1是一个算法流程图,则输出的x 值为侧视图图2图3图4(A )95 (B )47 (C )23 (D )11 (6)某棱柱的三视图如图2示,则该棱柱的体积为 (A )3 (B )4 (C )6 (D )12 (7)已知等比数列{}n a 满足132410,5a a a a +=+=,则5a =(A )1 (B )12 (C )14(D )4(8)已知01a b c <<<<,则(A )b a a a > (B )a b c c > (C )log log a b c c > (D )log log b b c a >(9)已知双曲线22221(0,0)x y a b a b-=>>,点A 、F 分别为其右顶点和右焦点12(0,),(0,)B b B b -,若12B F B A ⊥,则该双曲线的离心率为(A)1 (B(C(D1 (10)已知实数,x y 满足不等式组⎪⎩⎪⎨⎧≤≤≤-+≥+-a y y x y x 003202,若 2z x y =-+的最大值为3,则a 的值为(A )1 (B )23(C )2 (D )37 (11)中国古代数学家赵爽设计的弦图(图3)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图4所示的菱形,已知弦图中, 大正方形的面积为100,小正方形的面积为4,则图4中菱形的一个锐 角的正弦值为 (A )2425(B )35(C )45(D )725(12)已知函数21352,(1)4()1log .(1)4x x x f x x x ⎧-+-≤⎪⎪=⎨⎪->⎪⎩()|2|sin g x A x =-⋅()x R ∈,若对任意的1x 、2x R ∈,都有12()()f x g x ≤,则实数A 的取值范围为(A )9(,]4-∞ (B )7[,)4+∞ (C )79[,]44 (D )7(,]4-∞9[,)4+∞第Ⅱ卷本卷包括必考题和选考题两部分.第(13)题第(21)题为必考题,每个试题考生都必须做答.第(22)题第(23)题为选考题,考生根据要求做答. 二、填空题(本大题共4小题,每小题5分,共20分,请把正确的答案填写在答题卡相应的横线上.(13)已知向量(1,2),(2,1)a x b x =-=-满足||||a b a b ⋅=-⋅,则x = .(14)设n S 为等差数列{}n a 的前n 项和,且35a =,642S =,则9S = . (15)已知直线3460x y --=与圆2220()x y y m m R +-+=∈相切,则m 的值为 . (16)已知一长方体的体对角线的长为10,这条对角线在长方体一个面上的正投影长为8,则这 个长方体体积的最大值为 .三、解答题:解答应写出文字说明,证明过程或演算步骤.(17)(本小题满分12分)ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ,已知ABC ∆的面积为B ac cos ,BC的中点为D .(Ⅰ) 求B cos 的值;(Ⅱ) 若2=c ,C c A a sin 5sin =,求AD 的长. (18)(本小题满分12分)某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n *)(N n ∈关者奖励12-n 件小奖品(奖品都一样).图5是小明在10次过关游戏中过关数的条形图,以此频率估计概率.(Ⅰ)求小明在这十次游戏中所得奖品数的均值;(Ⅱ)规定过三关者才能玩另一个高级别的游戏,估计小明一次游戏后能玩另一个游戏的概率;(Ⅲ)已知小明在某四次游戏中所过关数为{2,2,3,4},小聪在某四次游戏中所过关数为{3,3,4,5},现从中各选一次游戏,求小明和小聪所得奖品总数超过10的概率.(19)(本小题满分12)已知图6中,四边形 ABCD 是等腰梯形,CD AB //, CD EF //,AB DM ⊥于M 、交EF 于点N,DN =MN =现将梯形ABCD 沿EF 折起,记折起后C 、D 为'C 、'D 且使62'=M D ,如图7示.(Ⅰ)证明:M D '⊥平面ABFE ;,(Ⅱ)若图6中,60A ∠= ,求点M 到平面'AED 的距离.(20)(本小题满分12分)已知椭圆()012222>>=+b a by a x 与抛物线)0(22>=p px y 共焦点2F ,抛物线上的点M 到y 轴的距离等于1||2-MF ,且椭圆与抛物线的交点Q 满足25||2=QF . (I )求抛物线的方程和椭圆的方程;(II )过抛物线上的点P 作抛物线的切线=+y kx m 交椭圆于A 、B 两点,求此切线在x 轴上的截距的取值范围.(21)(本小题满分12分)已知0<a ,曲线c bx ax x f ++=22)(与曲线x a x x g ln )(2+=在公共点))1(,1(f 处的切线相同.(Ⅰ)试求a c -的值;(Ⅱ)若1)()(++≤a x g x f 恒成立,求实数a 的取值范围.请考生在第(22)、(23)题中任选一题作答,如果多做,则按所做的第一个题目计分. (22) (本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,已知直线l 1:x y ⋅=αtan (πα<≤0,2πα≠),抛物线C :⎩⎨⎧-==t y t x 22(t 为参数).以原点O 为极点,x 轴的非负半轴为极轴建立极坐标系. ABDCFE ABC ´D ´EF MMN图6图7(Ⅰ)求直线l 1 和抛物线C 的极坐标方程;(Ⅱ)若直线l 1 和抛物线C 相交于点A (异于原点O ),过原点作与l 1垂直的直线l 2,l 2和抛物线C 相交于点B (异于原点O ),求△OAB 的面积的最小值.(23) (本小题满分10分)选修4-5:不等式选讲已知函数()21f x x =-. (Ⅰ)求不等式()1f x ≤的解集A ;(Ⅱ)当,m n A ∈时,证明:1m n mn +≤+.揭阳市2017年高中毕业班第二次高考模拟考试题数学(文科)参考答案及评分说明一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数.一、选择题:(10) 如右图,当直线y x z 2+-=即221zx y +=过点(2,)A a a -时,截距2z最大,z 取得最大值3,即a a 223++-=,得1=a .(11)设围成弦图的直角三角形的三边长分别为,,a b c ,c a b >>,依题意10c =,22100a b +=,2()4a b -=,解得8,6a b ==,设小边b 所对的角为θ,则63sin 105θ==,4cos 5θ=,24sin 22sin cos 25θθθ==. (12)对任意的1x 、2x R ∈,都有12()()f x g x ≤max min ()()f x g x ⇔≤,注意到max1()(1)4f x f ==-,又()|2|sin |2|g x A x A =-≥--,故1179|2||2|4444A A A --≥-⇒-≤⇒≤≤ 二、填空题:(166=,设长方体底面边长分别为,a b ,则2264a b +=,6V ab =223()192a b ≤+=.三、解答题:(17)解:(Ⅰ) 由B ac B ac S ABC cos sin 21==∆,------------------------1分得B B cos 2sin =,----------------------------------①------------2分 ∵0B π<< ∴sin 0B > 故0cos >B ,--------------------3分 又1cos sin 22=+B B ,----------------------------②①代入②得51cos 2=B ,∴51cos =B=5;-----------------5分 (Ⅱ)由C c A a sin 5sin =及正弦定理得225c a =,---------------------7分∵2=c ,∴52=a ,521==a BD ,------------------------9分 在△ABD 中,由余弦定理得:55125254cos 2222=⨯⨯-+=⋅⋅-+=B c BD BD c AD ,------11分∴5=AD .----------------------------------------------12分 (18)解:(Ⅰ)小明的过关数与奖品数如下表:------------2分小明在这十次游戏中所得奖品数的均值为4)11618243221(101=⨯+⨯+⨯+⨯+⨯;------------------------------------4分 (Ⅱ)小明一次游戏后能玩另一个游戏的概率约为4.010112=++;---------------6分 (Ⅲ)小明在四次游戏中所得奖品数为{2,2,4,8},--------------------------------------7分小聪在四次游戏中所得奖品数为{4,4,8,16},-------------------------------------8分 现从中各选一次游戏,奖品总数如下表: ---------10分共16个基本事件,总数超过10的有8个基本事件,故所求的概率为21168=.----12分 (19)解:(Ⅰ) 可知AB EF //,∴N D '⊥EF 、MN ⊥EF ,-------------------1分ABDCFE ABC ´D ´EF MMNN又N MN N D = ',得EF ⊥平面'MND ,--------------------3分 得M D EF '⊥,--------------------4分∵222'27'D M MN D N +== ∴MN M D ⊥',--------------------------5分 又MNEF N =,∴M D '⊥平面ABFE .--------------------------------------6分(Ⅱ) 设点M 到平面'AED 的距离为h ,由AEM D AED M V V --='',得M D S h S AEM AED '3131'⋅=⋅∆∆,① ∵2sin 60MN AE ==,6sin 60DNDE ==,------------------------7分∴8AD =,4AM =,-------------------------------------------8分 在MA D Rt '∆中,40''222=+=AM M D A D ,又6'=E D ,2=AE ,得222''AE E D A D +=,∴AE E D ⊥',-----------------------------------------------10分'1'62AED S AE D E ∆=⋅=,又3221=⋅=∆MN AM S AEM ,代入①式,得123h =⨯h =∴点M 到平面'AED 的距离为---------------------------------12分 (20)解:(I )∵抛物线上的点M 到y 轴的距离等于2||1MF -,∴点M 到直线1-=x 的距离等于点M 到焦点2F 的距离,---------------1分 得1-=x 是抛物线px y 22=的准线,即12-=-p, 解得2=p ,∴抛物线的方程为x y 42=;-----------------------------------3分 可知椭圆的右焦点)0,1(2F ,左焦点)0,1(1-F , 由抛物线的定义及25||2=QF ,得251=+Q x , 又Q Q x y 42=,解得)6,23(±Q ,-----------------------------------4分由椭圆的定义得||||221QF QF a +=62527=+=,----------------------5分 ∴3=a ,又1=c ,得8222=-=c a b ,∴椭圆的方程为18922=+y x .-------------------------------------------------6分(II )显然0≠k ,0≠m ,由⎩⎨⎧=+=xy m kx y 42,消去x ,得0442=+-m y ky , 由题意知01616=-=∆km ,得1=km ,-----------------------------------7分由⎪⎩⎪⎨⎧=++=18922y x m kx y ,消去y ,得072918)89(222=-+++m kmx x k , 其中4)18(22-=∆km 0)729)(89(22>-+m k ,化简得08922>+-m k ,-------------------------------------------------------9分又mk 1=,得09824<--m m ,解得902<<m ,--------------------10分 切线在x 轴上的截距为k m x -=,又92->-=-m km, ∴切线在x 轴上的截距的取值范围是)0,9(-.----------------------------------12分 (21)解:(Ⅰ) b ax x f +=4)(',xax x g +=2)(',--------------------------1分 由已知得)1()1(g f =,且)1(')1('g f =, 即12=++c b a ,且a b a +=+24,所以23=+b a ,1-=-a c ;-------------------------------------------------4分 (Ⅱ)设1)()()(---=a x g x f x h ,则0>∀x ,0)(≤x h 恒成立,∵2ln )32()12()(2---+-=x a x a x a x h ,------------------------------5分 ∴xaa x a x h --+-=32)12(2)(',-------------------------------------------6分 法一:由0<a ,知x a y )12(2-=和xa-在),0(∞+上单调递减, 得xaa x a x h --+-=32)12(2)('在),0(∞+上单调递减,----------------7分 又032)12(2)1('=--+-=a a a h ,得当)1,0(∈x 时,0)('>x h ,当),1(∞+∈x 时,0)('<x h ,所以)(x h 在)1,0(上单调递增,在),1(∞+上单调递减,----------------------9分 得a h x h --==1)1()(max ,由题意知0)(max ≤x h ,得1-≥a ,----------11分 所以)0,1[-∈a .---------------------------------------------------------------------------12分【法二:xa x a x a x h --+-=)32()24()('2[(42)](1)a x a x x -+-=,-------8分由0<a ,0>x ,知(42)0a x a -+<,得当)1,0(∈x 时,0)('>x h ,当),1(∞+∈x 时,0)('<x h ,所以)(x h 在)1,0(上单调递增,在),1(∞+上单调递减,-----------------------10分 得a h x h --==1)1()(max ,由题意知0)(max ≤x h ,得1-≥a ,所以)0,1[-∈a .----------------------------------------------------12分】选做题:(22)解:(Ⅰ)可知l 1是过原点且倾斜角为α的直线,其极坐标方程为αθ=(,)2R παρ≠∈-----------------------------------------------------------------2分抛物线C 的普通方程为x y 42=,-------------------------------------------3分 其极坐标方程为θρθρcos 4)sin (2=,化简得θθρcos 4sin 2=.-----------------------------------------------------5分 (Ⅱ)解法1:由直线l 1 和抛物线C 有两个交点知0α≠,把αθ=代入θθρcos 4sin 2=,得ααρ2sin cos 4=A ,-----------------6分可知直线l 2的极坐标方程为2παθ+=)(R ∈ρ,-----------------------7分代入θθρcos 4sin 2=,得ααρsin 4cos 2-=B ,所以ααρ2cos sin 4-=B ,----8分 ||||21||||21B A OAB OB OA S ρρ⋅=⋅=∆|cos sin 2|16αα=16|2sin |16≥=α,∴△OAB 的面积的最小值为16.----------------------------------------------------------10分【解法2:设1l 的方程为(0)y kx k =≠,由24,.y x y kx ⎧=⎨=⎩得点244(,)A k k ,------6分依题意得直线2l 的方程为1y x k=-,同理可得点2(4,4)B k k -,-------------7分故1||||2OAB S OA OB ∆=⋅=分21816||k k +==⋅≥,(当且仅当1k =±时,等号成立) ∴△OAB 的面积的最小值为16.----------------------------------------------------------10分】 (23)解:(Ⅰ)由211x -≤,得1211x -≤-≤,即||1x ≤,--------------3分解得11x -≤≤,所以[]1,1A =-;----------------------------------------------5分(Ⅱ)法一:()22222211m n mn m n m n +-+=+--()()2211m n =--------------------------------------7分 因为,m n A ∈,故11m -≤≤,11n -≤≤,210m -≤,210n -≤,--------8分故()()22110m n ---≤,()221m n mn +≤+ 又显然10mn +≥,故1m n mn +≤+.-------------------------------------------------1 0分【法二:因为,m n A ∈,故11m -≤≤,11n -≤≤,----------------6分而()()()1110m n mn m n +-+=--≤------------------------------7分()()()1110m n mn m n +--+=++≥⎡⎤⎣⎦,-------------------------8分即()11mn m n mn -+≤+≤+, 故1m n mn +≤+.------------------------------------------------------------------10分】。
2018年广东省揭阳市高考一模数学试卷(文科)【解析版】
2018年广东省揭阳市高考数学一模试卷(文科)一、选择题:共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={x|x<0},B={x||x|≤1},则A∩B=()A.(0,1]B.[﹣1,1]C.[﹣1,0)D.[﹣1,0] 2.(5分)已知复数z=(3+i)2,则||=()A.4B.6C.8D.103.(5分)已知向量=(x,1),=(1,﹣2),若,则=()A.(2,0)B.(3,﹣1)C.(3,1)D.(﹣1,3)4.(5分)某地铁站有A、B、C三个自动检票口,甲乙两人一同进站,则他们选择同一检票口检票的概率为()A.B.C.D.5.(5分)为了规定工时定额,需要确定加工某种零件所需的时间,为此进行了5次试验,得到5组数据:(x1,y1),(x2,y2),(x3,y3),(x4,y4),(x5,y5),+x2+x3+x4+x5=由最小二乘法求得回归直线方程为=0.67x+54.9.若已知x150,则y1+y2+y3+y4+y5=()A.75B.155.4C.375D.466.26.(5分)若直线l1:x﹣3y+2=0与直线l2:mx﹣y+b=0关于x轴对称,则m+b =()A.B.﹣1C.D.17.(5分)已知△ABC中,角A、B、C的对边分别为a、b、c,且a=4,b=4,B=,则角A的大小为()A.B.或C.D.8.(5分)已知函数f(x)=sin(2x﹣),则要得到函数g(x)=sin2x的图象,只需将函数f(x)的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位9.(5分)已知一个正方体的所有顶点在一个球面上,若球的体积为,则这个正方体的体积为()A.3B.27C.D.910.(5分)函数y=xln|x|的部分图象大致为()A.B.C.D.11.(5分)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为()A.3B.3C.D.312.(5分)已知x∈(0,),函数y=f(x)满足:tan xf(x)>f′(x)恒成立,其中f′(x)是f(x)的导函数,则下列不等式中成立的是()A.f()>f()B.2f(1)cos1<f()C.f()>f()D.f()<f()二、填空题:本大题共4小题,每小题5分,共20分,请把正确的答案填写在答题卡相应的横线上.13.(5分)如图是一个算法流程图,若输入x的值为log23,则输出的y的值是.14.(5分)已知实数x,y满足约束条件,则3x+y的取值范围为是.15.(5分)中心在坐标原点的双曲线的一条渐近线被圆(x﹣2)2+y2=3截得的弦长为2,则该双曲线的离心率为.16.(5分)已知f(x)=sin()cos(),则f(1)+f(2)+…+f(2018)=.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(12分)已知递增等比数列{b n}的b1、b3二项为方程x2﹣20x+64=0的两根,}满足=b n.数列{a(Ⅰ)求数列{a n}的通项公式;(Ⅱ)求数列{a n}的前n项和S n.18.(12分)如图,在三棱锥P﹣ABC中,△ABC和△P AC都是正三角形,AC =2,E、F分别是AC、BC的中点,且PD⊥AB于D,平面P AC⊥平面ABC.(Ⅰ)证明:EF⊥ED;(Ⅱ)求点F到平面P AB的距离.19.(12分)甲、乙两人参加一个投掷飞镖的中奖游戏,从中随机选取50次所命中环数(整数),统计得下列频数分布表,游戏中规定命中环数为1、2、3、4时获奖一元,命中环数为5、6、7时获奖二元,命中环数为8、9时获奖三元,命中10环时获奖四元,没命中则无奖.(Ⅰ)根据上表,在答题卡给定的坐标系内画出甲50次获奖金额(单位:元)的条形图;(Ⅱ)估计甲投掷飞镖一次所获奖金不小于三元的概率;(Ⅲ)分别计算甲、乙各50次获奖金额的平均数和方差,若有一次投掷飞镖比赛的机会,你觉得从甲、乙两人选谁参赛比较好?20.(12分)设A,B为曲线C:x2=y上两点,A与B的横坐标之积为﹣1.(Ⅰ)试判断直线AB是否恒过定点,并说明理由;(Ⅱ)设曲线C在点A、B处的两条切线相交于点M,求点M的纵坐标.21.(12分)已知a≠0,函数f(x)=|e x﹣e|+e x+ax.(I)讨论f(x)的单调性;(II)已知当a<﹣e时,函数f(x)有两个零点x1和x2(x1<x2),求证:x1x2<1.请考生在第(22)、(23)题中任选一题作答,如果多做,则按所做的第一个题目计分.[选修44:坐标系与参数方程]22.(10分)在直角坐标系xOy中,直线l1的参数方程为(t为参数),直线l2的参数方程为(m为参数),当k变化时,设l1与l2的交点的轨迹为曲线C.(I)以原点为极点,x轴的非负半轴为极轴建立极坐标系,求曲线C的极坐标方程;(II)设曲线C上的点A的极角为,射线OA与直线l3:ρsin(θ+φ)﹣2=0 (0<φ<)的交点为B,且|OB|=|OA|,求φ的值.[选修45:不等式选讲]23.已知函数f(x)=|a+|+|a﹣|,a为实数.(I)当a=1时,求不等式f(x)>3的解集;(II)求f(a)的最小值.2018年广东省揭阳市高考数学一模试卷(文科)参考答案与试题解析一、选择题:共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={x|x<0},B={x||x|≤1},则A∩B=()A.(0,1]B.[﹣1,1]C.[﹣1,0)D.[﹣1,0]【解答】解:B={x||x|≤1}={x|﹣1≤x≤1},则A∩B={x|﹣1≤x<0},故选:C.2.(5分)已知复数z=(3+i)2,则||=()A.4B.6C.8D.10【解答】解:z=(3+i)2=9+6i﹣1=8+6i,则=8﹣6i,则||==10,故选:D.3.(5分)已知向量=(x,1),=(1,﹣2),若,则=()A.(2,0)B.(3,﹣1)C.(3,1)D.(﹣1,3)【解答】解:∵=(x,1),=(1,﹣2),∴,则•=x+1×(﹣2)=x﹣2=0,则x=2,则=(2,1),则=(3,﹣1),故选:B.4.(5分)某地铁站有A、B、C三个自动检票口,甲乙两人一同进站,则他们选择同一检票口检票的概率为()A.B.C.D.【解答】解:某地铁站有A、B、C三个自动检票口,甲乙两人一同进站,他们选择检票口检票的种数有n=3×3=9,他们选择同一检票口检票的种数有m=3,∴他们选择同一检票口检票的概率p==.故选:C.5.(5分)为了规定工时定额,需要确定加工某种零件所需的时间,为此进行了5次试验,得到5组数据:(x1,y1),(x2,y2),(x3,y3),(x4,y4),(x5,y5),由最小二乘法求得回归直线方程为=0.67x+54.9.若已知x+x2+x3+x4+x5=150,则y1+y2+y3+y4+y5=()A.75B.155.4C.375D.466.2【解答】解:(1)=,回归直线方程为=0.67x+54.9.可得:=0.67×30+54.8≈75.则y 1+y2+y3+y4+y5=•n=75×5=375.故选:C.6.(5分)若直线l1:x﹣3y+2=0与直线l2:mx﹣y+b=0关于x轴对称,则m+b =()A.B.﹣1C.D.1【解答】解:直线l1:x﹣3y+2=0与直线l2:mx﹣y+b=0关于x轴对称,可得:m=﹣,y=0时,x=﹣2,代入mx﹣y+b=0,所以b=﹣,则m+b=﹣1.故选:B.7.(5分)已知△ABC中,角A、B、C的对边分别为a、b、c,且a=4,b=4,B=,则角A的大小为()A.B.或C.D.【解答】解:△ABC中,角A、B、C的对边分别为a、b、c,且a=4,b=4,B=,a<b则,A<B,A+B<π,,sin A==,所以:A=.故选:D.8.(5分)已知函数f(x)=sin(2x﹣),则要得到函数g(x)=sin2x的图象,只需将函数f(x)的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位【解答】解:g(x)=sin2x=sin[2(x+)﹣],要得到函数g(x)=sin2x的图象,只需将函数f(x)的图象向左平移个单位即可,故选:C.9.(5分)已知一个正方体的所有顶点在一个球面上,若球的体积为,则这个正方体的体积为()A.3B.27C.D.9【解答】解:若正方体的所有顶点在一个球面上,则正方体的体对角线等于球的直径,设正方体的棱长为a,则体对角线为a,若球的体积为,则πR3=,即R3=,则R=,则a=2R=3,则a==,则正方体的条件V=a3=()3=3,故选:A.10.(5分)函数y=xln|x|的部分图象大致为()A.B.C.D.【解答】解:函数y=xln|x|是奇函数,排除选项B,当x>0时,函数y=xlnx的导数为:y′=lnx+1,可得函数的极值点x=.并且x∈(0,),y′<0,函数是减函数,x,y′>0,函数是增函数,所以函数的图象是C.故选:C.11.(5分)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为()A.3B.3C.D.3【解答】解:由三视图还原原几何体如图,四棱锥A﹣BCDE,其中AB⊥平面BCDE,底面BCDE为正方形,则BC=AB=BE=3,AC==3.∴该四棱锥的最长棱为AD,AD的长度为===3.故选:B.12.(5分)已知x∈(0,),函数y=f(x)满足:tan xf(x)>f′(x)恒成立,其中f′(x)是f(x)的导函数,则下列不等式中成立的是()A.f()>f()B.2f(1)cos1<f()C.f()>f()D.f()<f()【解答】解:因x∈(0,),故tan xf(x)>f′(x)⇔sin xf(x)>f′(x)cos x⇔sin xf (x)﹣cos xf′(x)>0,令g(x)=cos xf(x),则g′(x)=cos xf′(x)﹣sin xf(x)<0,所以函数g(x)在(0,)为减函数,∴cos f()>cos f(),∴f()>f().故选:A.二、填空题:本大题共4小题,每小题5分,共20分,请把正确的答案填写在答题卡相应的横线上.13.(5分)如图是一个算法流程图,若输入x的值为log23,则输出的y的值是2.【解答】解:根据程序框图得:x=log23>1,则程序执行右边的循环,所以:y=log23•log32+1=.故输出y=2.故答案为:214.(5分)已知实数x,y满足约束条件,则3x+y的取值范围为是(﹣∞,3].【解答】解:作出约束条件对应的平面区域如图:由z=3x+y得y=﹣3x+z,平移直线y=﹣3x+z,由图象可知当直线y=﹣3x+z,经过点A时,直线的截距最大,此时z最大.由,解得即A(1,0),此时z max=3×1+0=3,当直线y=﹣3x+z,z没有最小值,∴z∈(﹣∞,3].故答案为:(﹣∞,3].15.(5分)中心在坐标原点的双曲线的一条渐近线被圆(x﹣2)2+y2=3截得的弦长为2,则该双曲线的离心率为.【解答】解:双曲线的一条渐近线方程为bx+ay=0,圆(x﹣2)2+y2=3的圆心(2,0)到双曲线的渐近线的距离为:,∵渐近线被圆(x﹣2)2+y2=3截得的弦长为2,∴=,可得:∴2b2=c2,即c2=2a2,∴e==.故答案为:.16.(5分)已知f(x)=sin()cos(),则f(1)+f(2)+…+f(2018)=.【解答】解:∵f(x)=sin()cos()=,最小正周期T=6,f(1)+f(2)+f(3)+f(4)+f(5)+f(6)=0.∴f(1)+f(2)+…+f(2018),=336×6+f(2017)+f(2018)=f(1)+f(2)=.故答案为:.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(12分)已知递增等比数列{b n}的b1、b3二项为方程x2﹣20x+64=0的两根,}满足=b n.数列{a(Ⅰ)求数列{a n}的通项公式;(Ⅱ)求数列{a n}的前n项和S n.【解答】解:(Ⅰ)解方程x2﹣20x+64=0得x1=4,x2=16,依题意得b1=4,b3=16,设数列{b n}的公比为q,则q2==4,∵q>0,∴q=2,∴b n=b1q n﹣1=4×2n﹣1=2n+1,由+…+=b,①,②当n≥2时+…+=b①﹣②得=b n﹣b n﹣1=2n+1﹣2n=2n,∴a n=4n(n≥2),当n=1时,由①得a1=16,∴a n=,n∈N*;(Ⅱ)当n≥2时,前n项和S n=a1+a2+...+a n=16+42+43+ (4)=16+=,当n=1时,S1=16满足上式,∴S n=,18.(12分)如图,在三棱锥P﹣ABC中,△ABC和△P AC都是正三角形,AC =2,E、F分别是AC、BC的中点,且PD⊥AB于D,平面P AC⊥平面ABC.(Ⅰ)证明:EF⊥ED;(Ⅱ)求点F到平面P AB的距离.【解答】证明:(Ⅰ)∵E、F分别是AC、BC的中点,∴EF∥AB,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)在正三角形P AC中,PE⊥AC,又平面P AC⊥平面ABC,平面P AC∩平面ABC=AC,∴PE⊥平面ABC,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)∴PE⊥AB,又PD⊥AB,PE∩PD=P,∴AB⊥平面PED,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)∴AB⊥ED,又EF∥AB,∴EF⊥ED;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)解:(Ⅱ)设点F到平面P AB的距离为d,∵V F﹣P AB =V P﹣ABF,∴,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(7分)解得PE=BE=,由AB⊥ED,可知AB•ED=AE•BE,得ED=,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)∴PD==,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(9分)∴=,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)由EF∥AB,可知S△ABF==,∴点F到平面P AB的距离d===.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)19.(12分)甲、乙两人参加一个投掷飞镖的中奖游戏,从中随机选取50次所命中环数(整数),统计得下列频数分布表,游戏中规定命中环数为1、2、3、4时获奖一元,命中环数为5、6、7时获奖二元,命中环数为8、9时获奖三元,命中10环时获奖四元,没命中则无奖.(Ⅰ)根据上表,在答题卡给定的坐标系内画出甲50次获奖金额(单位:元)的条形图;(Ⅱ)估计甲投掷飞镖一次所获奖金不小于三元的概率;(Ⅲ)分别计算甲、乙各50次获奖金额的平均数和方差,若有一次投掷飞镖比赛的机会,你觉得从甲、乙两人选谁参赛比较好?【解答】解:(Ⅰ)依题意知甲50次获奖金额(单位:元)的频数分布为:其获奖金额的条形图如下图示:﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(4分)(Ⅱ)甲投掷飞镖一次所获奖金数不小于3,即甲投掷飞镖一次所命中的环数不小于8,因甲50次投掷中环数不小于8的有15+9+2=26(次),所以估计甲投掷一次所获奖金数不小于3的概率为:=;﹣﹣﹣﹣﹣﹣﹣﹣(7分)【或甲投掷飞镖一次所获奖金数不小于3,即所得的奖金为3元或4元,由(Ⅰ)的条形图知所求的概率为=,(Ⅲ)甲50次获奖金额的平均数为×(1×3+2×21+3×24+4×2)=,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)乙50次获奖金额的平均数为×(1×1+2×25+3×22+4×2)=,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(9分)甲50次获奖金额的方差为:×[×3+×21+×24+×2]=×=;﹣﹣(10分)乙50次获奖金额的方差为:×[×1+×25+×22+×2]=×=,﹣﹣﹣﹣﹣﹣(11分)甲、乙的平均数相等,乙的方差小,故选乙参赛比较好.﹣﹣﹣﹣﹣﹣﹣﹣(12分)20.(12分)设A,B为曲线C:x2=y上两点,A与B的横坐标之积为﹣1.(Ⅰ)试判断直线AB是否恒过定点,并说明理由;(Ⅱ)设曲线C在点A、B处的两条切线相交于点M,求点M的纵坐标.【解答】解:(Ⅰ)直线AB恒过定点(0,1),﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)设A(x1,y1),B(x2,y2),显然直线AB的斜率存在,设AB的方程为y=kx+m,联立x2=y,得x2﹣kx﹣m=0,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)则x1•x2=﹣m,又x1•x2=﹣1,得m=1,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)故直线AB的方程为y=kx+1,直线过定点(0,1).﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)(Ⅱ)设M(x0,y0),y′=2x,则曲线C在点A处的切线方程为y﹣y1=2x1(x﹣x1),又=y1,得切线为y=2x1x﹣,①﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(7分)同理得曲线C在点B处的切线为y=2x2x﹣,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)又x1•x2=﹣1,即x2=﹣,得切线为y=﹣x﹣,即y=﹣2x1x﹣1,②﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)①+②,得(1+)y=﹣﹣1,得y=﹣1,所以点M的纵坐标为﹣1.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)21.(12分)已知a≠0,函数f(x)=|e x﹣e|+e x+ax.(I)讨论f(x)的单调性;(II)已知当a<﹣e时,函数f(x)有两个零点x1和x2(x1<x2),求证:x1x2<1.【解答】(I)解:f(x)=,f′(x)=,①若a>0,显然f′(x)>0恒成立,f(x)在(﹣∞,+∞)上单调递增;②若﹣2e≤a<0,当x<1时,f′(x)=a<0,当x≥1时,f′(x)=2e x+a≥0,故f(x)在(﹣∞,1)上单调递减,在(1,+∞)上单调递增.③若a<﹣2e,当x<1时,f′(x)=a<0,当x≥1时,由2e x+a<0,得,由2e x+a>0,得x>,故f(x)在上单调递减,在上单调递增.(Ⅱ)证明:∵a<﹣e,故f(1)=a+e<0,结合f(x)的单调性知,f(x)的两个零点x1和x2满足:ax1+e=0,及+ax2﹣e=0,且x1<1<x2,∴a=,x1=﹣=,于是x1x2=,令g(x)=,(x>1).则g′(x)==,记h(x)=2e x﹣e﹣xe x,x>1,则h′(x)=e x﹣xe x<0,∴h(x)在(1,+∞)上单调递减,h(x)<h(1)=0,故g′(x)<0,即函数g(x)在(1,+∞)上单调递减,∴g(x)<g(1)=1,∴x1x2<1.请考生在第(22)、(23)题中任选一题作答,如果多做,则按所做的第一个题目计分.[选修44:坐标系与参数方程]22.(10分)在直角坐标系xOy中,直线l1的参数方程为(t为参数),直线l2的参数方程为(m为参数),当k变化时,设l1与l2的交点的轨迹为曲线C.(I)以原点为极点,x轴的非负半轴为极轴建立极坐标系,求曲线C的极坐标方程;(II)设曲线C上的点A的极角为,射线OA与直线l3:ρsin(θ+φ)﹣2=0 (0<φ<)的交点为B,且|OB|=|OA|,求φ的值.【解答】解:(Ⅰ)直线l1的参数方程为(t为参数),转换为:直线l1的普通方程为﹣4y=k(x﹣2).直线l2的普通方程为y=,联立两方程消去k,得:﹣4y2=x2﹣4,即曲线C的普通方程为:x2+4y2=4.由得曲线C的极坐标方程为:ρ2(cos2θ+4sin2θ)=4;化简得:ρ2(1+3sin2θ)=4.(Ⅱ)把代入ρ2(1+3sin2θ)=4,得,∴,得,由已知得:,把,ρ=4代入方程l3得φ)=,又,∴,∴,解得:φ=.[选修45:不等式选讲]23.已知函数f(x)=|a+|+|a﹣|,a为实数.(I)当a=1时,求不等式f(x)>3的解集;(II)求f(a)的最小值.【解答】解:(Ⅰ)当a=1时,不等式f(x)>3,即f(x)=>3,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)①当x<﹣1时,得f(x)=2>3,无解;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2分)②当﹣1≤x≤1时,得f(x)=>3,解得|x|<,得﹣<x<0或0<x<;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)③当x>1时,得f(x)=2>3,无解;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(4分)综上知,不等式的解集为(﹣,0)∪(0,).﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)(Ⅱ)f(a)==,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)①当a<﹣1或a>1时,f(a)==2|a|>2,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)②当﹣1≤a≤1时,f(a)=≥2,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(9分)综上知,f(a)的最小值为2.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)。
广东省揭阳市2018年高考第二次模拟考试数学(理)试题-有答案
揭阳市2018年高中毕业班高考第二次模拟考试数学(理科)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|A x y ==,{}|31x B x =≥,则( )A .AB = B .A B ⊆C .AB R = D .A B φ=2.已知复数z 满足()123i z i +⋅=+,则z 的共轭复数z 在复平面内对应的点在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限3.平面直角坐标系xOy 中,i ,j 分别是与x 轴、y 轴正方向同向的单位向量,向量2a i =,b i j =+,以下说法正确的是( )A .1a b ⋅=B .a b =C .()a b b -⊥ D .//a b 4.已知直线a 、b ,平面α、β、γ,下列命题正确的是( ) A .若αγ⊥,βγ⊥,a αβ=,则a γ⊥ B .若a αβ=,b αγ=,c βγ=,则////a b cC.若a αβ=,//b a ,则//b α D .若αβ⊥,a αβ=,//b α,则//b a5.已知直线430x y a -+=与22:40C x y x ++=相交于A 、B 两点,且120AOB ∠=,则实数a 的值为( )A .3B .10 C. 11或21 D .3或136.已知()511x ax x ⎛⎫+- ⎪⎝⎭的展开式中常数项为40-,则a 的值为( )A .2B .2- C. 2± D .47.已知函数()()()sin 0,0,02f x A x A ωϕωϕπ=+>>≤<的部分图象如图所示,则ϕ的值为( )A .3π或23π B .23π C. 43π D .3π或43π8.在如图的程序框图中,输出的n 值为( )A .14B . 32 C. 46 D .539.已知双曲线的焦距为4,A 、B 是其左、右焦点,点C 在双曲线右支上,ABC △的周长为10,则AC 的取值范围是( )A .()2,5B .()2,6 C. ()3,5 D .()3,610.如图是某几何体的三视图,图中每个小正方形的边长为1,则此几何体的体积为( )A .83 B .163 C.4 D .20311.过抛物线22x y =上两点A 、B 分别作切线,若两条切线互相垂直,则线段AB 的中点到抛物线准线的距离的最小值为( ) A .12 B .1 C.32D .2 12.把函数()()2log 1f x x =+的图象向右平移一个单位,所得图象与函数()g x 的图象关于直线y x =对称;已知偶函数()h x 满足()()11h x h x -=--,当[]0,1x ∈时,()()1h x g x =-;若函数()()y k f x h x =⋅-有五个零点,则k 的取值范围是( )A .()3log 2,1B .[)3log 2,1 C.61log 2,2⎛⎫ ⎪⎝⎭ D .61log 2,2⎛⎤ ⎥⎝⎦第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.曲线1y x=在点()1,1处的切线方程为 . 14.题库中有10道题,考生从中随机抽取3道,至少做对2道算通过考试.某考生会做其中8道,有2道不会做,则此考生能通过考试的概率为 .15.已知等差数列{}n a 中,2416a a +=,11a +、21a +、41a +成等比数列,把各项如下图排列:则从上到下第10行,从左到右的第11个数值为 .16.平面四边形ABCD 中,60A ∠=,AD DC ⊥,3AB =2BD =,则BC 的最小长度为 . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 已知数列{}n a 的前n 项的和为n S ,满足21a =,1631n n S a +=-. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设2n n b a =,数列{}n b 的前n 项和与积分别为n R 与n T ,求n R 与n T .18. 如图,在四面体ABCD 中,90ABC ADC ∠=∠=,BC BD ==. (Ⅰ)求证:AD BD ⊥;(Ⅱ)若AB 与平面BCD 所成的角为60,点E 是AC 的中点,求二面角C BD E --的大小.19. 甲、乙、丙三人去某地务工,其工作受天气影响,雨天不能出工,晴天才能出工.其计酬方式有两种,方式一:雨天没收入,晴天出工每天250元;方式而:雨天每天120元,晴天出工每天200元;三人要选择其中一种计酬方式,并打算在下个月(30天)内的晴天都出工,为此三人作了一些调查,甲以去年此月的下雨天数(10天)为依据作出选择;乙和丙在分析了当地近9年此月的下雨天数(n )的频数分布表(见下表)后,乙以频率最大的n 值为依据作出选择,丙以n 的平均值为依据作出选择.(Ⅱ)根据统计范围的大小,你觉得三人中谁的依据更有指导意义?(Ⅲ)以频率作为概率,求未来三年中恰有两年,此月下雨不超过11天的概率.20. 已知椭圆()22122:10x y C a b a b+=>>的左、右焦点分别为1F 、2F ,圆2C 经过椭圆1C 的两个焦点和两个顶点,点P 在椭圆1C 上,且12PF =22PF =(Ⅰ)求椭圆1C 的方程和点P 的坐标;(Ⅱ)过点P 的直线1l 与圆2C 相交于A 、B 两点,过点P 与1l 垂直的直线2l 与椭圆1C 相交于另一点C ,求ABC △的面积的取值范围. 21. 已知函数()()()ln 22x mf x ex ax x m +=-+++-,(Ⅰ)若0a >,且()1f -是函数的一个极值,求函数()f x 的最小值; (Ⅱ)若0a =,求证:[]1,0x ∀∈-,()0f x ≥.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,圆C 的圆心为10,2⎛⎫ ⎪⎝⎭,半径为12,现以原点为极点,x 轴的正半轴为极轴建立极坐标系, (Ⅰ)求圆C 的极坐标方程;(Ⅱ)设M ,N 是圆C 上两个动点,满足23MON π∠=,求OM ON +的最小值. 23.选修4-5:不等式选讲已知函数()11f x x x m =++++,m R ∈,(Ⅰ)若不等式()2f x m ≥-恒成立,求实数m 的取值范围; (Ⅱ)求不等式()2f x m -<的解集.试卷答案一、选择题1-5:BACAD 6-10:CCDCB 11、12:B C 二、填空题13.20x y +-= 14.1415 15.275 16.2三、解答题(17)解:(Ⅰ)1361-=+n n a S ,1361-=∴-n n a S )2(≥n , 两式相减,得n n n a a a 3361-=+)2(≥n ,n n a a 31=∴+)2(≥n ,又12=a ,所以当2≥n 时,}{n a 是首项为1,公比为3的等比数列,22233--=⋅=n n n a a ,由13621-=a a 得311=a ,满足上式, 所以通项公式为23-=n n a *)(N n ∈;(Ⅱ)122293--===n n n n a b ,得11=b ,公比为9,8199191-=--=n n n R ,1213219991-⋅⋅⋅⋅=⋅⋅⋅⋅=n n n b b b b T )1(2)1(121399---+++===n n n n n .(18)解:(Ⅰ)由已知得222CD BD BC =+,BC BD ⊥∴,又BC AB ⊥,B AB BD = ,ABD BC 平面⊥∴,AD BC ⊥∴,又AD CD ⊥,C CD BC = ,BCD AD 平面⊥∴,BD AD ⊥∴.(Ⅱ)解法1:由(Ⅰ)知,AB 与平面BCD 所成的角为ABD ∠,即︒=∠60ABD , 设BD =2,则BC =2,在ADB Rt ∆中,AB =4,由(Ⅰ)中ABD BC 平面⊥,得平面ABC ⊥平面ABD ,在平面ABD 内,过点B 作AB Bz ⊥,则Bz ⊥平面ABC ,以B 为原点,建立空间直角坐标系xyz B -,则)0,0,0(B ,)0,0,4(A ,)0,2,0(C ,)0,1,2(E ,由160cos ||=︒=BD x D ,360sin ||=︒=BD z D ,得)3,0,1(D ,∴)0,1,2(=,)3,0,1(=, 设平面BDE 的法向量为),,(z y x m =,则⎪⎩⎪⎨⎧=+=⋅=+=⋅0302z x BD m y x BE m ,取1=z ,解得⎪⎩⎪⎨⎧=-=323y x ,∴)1,32,3(-=m是平面BDE 的一个法向量,又)3,0,3(-=是平面CBD 的一个法向量. 设二面角E BD A --的大小为θ,易知θ为锐角,则2132434|||||,cos |cos =⨯==><=AD m mθ,∴60θ=,即二面角C BD E --的大小为60.【解法2:由(Ⅰ)知,AB 与平面BCD 所成的角为ABD ∠,即60ABD ∠=, 分别取CD 、BD 的中点F 、G ,连EG 、FG ,在Rt ABC ∆和Rt ADC ∆中,E 为斜边AC 中点,故12BE DE AC ==, ∴EG BD ⊥;又∵BC ⊥平面ABD ,∴BC BD ⊥, 又∵//BC FG ∴FG BD ⊥; ∴EGF ∠为二面角C BD E --的平面角, 由(Ⅰ)知AD ⊥平面BCD ,又//AD EF , 故EF ⊥平面BCD ,从而EF FG ⊥,∴12tan 12ADEF EGF FG BC ∠====60EGF ∴∠=,即二面角C BD E --的大小为60.(19)解:(Ⅰ)按计酬方式一、二的收入分别记为)(n f 、)(n g ,(10)250(3010)5000f =⨯-=, 52002020010120)10(=⨯+⨯=g ,所以甲选择计酬方式二; 由频数分布表知频率最大的n=8,5500)830(250)8(=-⨯=f , 5360222008120)8(=⨯+⨯=g ,所以乙选择计酬方式一;n 的平均值为10)1132122101938(91=⨯+⨯+⨯+⨯+⨯⨯,所以丙选择计酬方式二;(Ⅱ)甲统计了1个月的情况,乙和丙统计了9个月的情况, 但乙只利用了部分数据,丙利用了所有数据, 所以丙的统计范围最大, 三人中丙的依据更有指导意义;(Ⅲ)任选一年,此月下雨不超过11天的频率为3296=,以此作为概率,则未来三年中恰有两年,此月下雨不超过11天的概率为94)321()32(223=-⨯C . (20)解:(I )设)0,(1c F -,)0,(2c F , 可知圆2C 经过椭圆焦点和上下顶点,得c b =, 由题意知4||||221=+=PF PF a ,得2=a , 由222a c b =+,得2==c b ,所以椭圆1C 的方程为12422=+y x , 点P 的坐标为)0,2(.(II )由过点P 的直线l 2与椭圆1C 相交于两点,知直线l 2的斜率存在, 设l 2的方程为)2(-=x k y ,由题意可知0≠k , 联立椭圆方程,得0488)12(2222=-+-+k x k x k ,设),(22y x C ,则12482222+-=⋅k k x ,得1224222+-=k k x ,所以1214|2|1||2222++=-+=k k x k PC ; 由直线l 1与l 2垂直,可设l 1的方程为)2(1--=x ky ,即02=-+ky x 圆心)0,0(到l 1的距离212kd +=,又圆的半径2=r ,所以1)1(2142)2||(222222+-=+-=-=k k k d r AB , 1122||22+-⋅=k k AB , 由r d <即2122<+k ,得12>k ,112||||2122+-⋅==∆k k PC AB S ABC1212412142222+-⋅=++⋅k k k k ,设12-=k t ,则0>t ,3233262ABC S t t t∆==≤=++, 当且仅当6t =10k =,所以△ABC 的面积的取值范围是23(0,. (21)解:(I )m ax ax x e x f m x -+++-=+2)2ln()(2,定义域为),2(∞+-,a ax x e x f m x 2221)('+++-=+. 由题意知0)1('=-f ,即011=--m e ,解得1=m , 所以1)2()2ln()(1-+++-=+x ax x e x f x ,a ax x e x f x 2221)('1+++-=+, 又1+=x ey 、21+-=x y 、a ax y 22+=(0>a )在),2(∞+-上单调递增, 可知)('x f 在),2(∞+-上单调递增,又0)1('=-f ,所以当)1,2(--∈x 时,0)('<x f ;当),1(∞+-∈x 时,0)('>x f . 得)(x f 在)1,2(--上单调递减,)(x f 在),1(∞+-上单调递增, 所以函数)(x f 的最小值为a a f -=--=-11)1(.(II )若0=a ,得m x e x f mx -+-=+)2ln()(,21)('+-=+x e x f m x 由)('x f 在]0,1[-上单调递增,可知)(x f 在]0,1[-上的单调性有如下三种情形:①当)(x f 在]0,1[-上单调递增时,可知0)('≥x f ,即0)1('≥-f ,即011≥--m e ,解得1≥m ,m e f m -=--1)1(,令m e m g m -=-1)(,则01)('1≥-=-m e m g ,所以)(m g 单调递增,0)1()(=≥g m g ,所以0)()1()(≥=-≥m g f x f ; ②当)(x f 在]0,1[-上单调递减时,可知0)('≤x f ,即0)0('≤f ,即021≤-me ,解得2ln -≤m , 得02ln 2ln 2ln )0(>=+-≥--=m m m e e m ef ,所以0)0()(>≥f x f ; [或:令2ln )(--=m e m h m ,则0211)('<-≤-=m e m h , 所以)(m h 单调递减,021)2ln ()(>=-≥h m h ,所以0)()0()(>=≥m h f x f ;] ③当)(x f 在]0,1[-上先减后增时,得)('x f 在]0,1[-上先负后正, 所以)0,1(0-∈∃x ,0)('0=x f ,即2100+=+x emx ,取对数得)2ln(00+-=+x m x , 可知)()(0min x f x f =m x e mx -+-=+)2ln(0002)1(2102000>++=++=x x x x , 所以0)(>x f ;综上①②③得:]0,1[-∈∀x ,0)(≥x f .【或:若0=a ,得m x e x f mx -+-=+)2ln()(,21)('+-=+x e x f m x 由)('x f 在]0,1[-上单调递增,分如下三种情形:①当0)('≥x f 恒成立时,只需0)1('≥-f ,即011≥--m e ,解得1≥m , 可知)(x f 在]0,1[-上单调递增,m e f m -=--1)1(,令m e m g m -=-1)(,则01)('1≥-=-m em g ,所以)(m g 单调递增,0)1()(=≥g m g ,所以0)()1()(≥=-≥m g f x f ;②当0)('≤x f 恒成立时,只需0)0('≤f ,即021≤-me ,解得2ln -≤m , 可知)(xf 在]0,1[-上单调递减时,02ln 2ln 2ln )0(>=+-≥--=mmme e m ef , 所以0)0()(>≥f x f ;③当)('x f 在]0,1[-上先负后正时,)(x f 在]0,1[-上先减后增, 所以)0,1(0-∈∃x ,0)('0=x f ,即2100+=+x emx ,取对数得)2ln(00+-=+x m x , 可知)()(0min x f x f =m x emx -+-=+)2ln(0002)1(2102000>++=++=x x x x ,所以0)(>x f ;综上①②③得:]0,1[-∈∀x ,0)(≥x f . 】(22)解:(I )圆C 的直角坐标方程为221124x y ⎛⎫+-= ⎪⎝⎭,化为极坐标方程为sin ρθ=; (II )设()122,,,3M N πρθρθ⎛⎫+⎪⎝⎭, 122sin sin 3OM ON πρρθθ⎛⎫+=+=++⎪⎝⎭1sin sin 23πθθθ⎛⎫==+ ⎪⎝⎭, 由0203θππθπ≤≤⎧⎪⎨≤+≤⎪⎩,得03πθ≤≤,2333πππθ≤+≤,sin 13πθ⎛⎫≤+≤ ⎪⎝⎭,即OM ON +2 (23)解:(I )|||)1(1||1||1|)(m m x x m x x x f =++-+≥++++=,由题意知|2|||-≥m m ,得22)2(-≥m m ,解得1≥m ;(II )不等式为m x m x 2|1||1|<-++-,即m m x x 2|)1(||1|<+-+- 若0≤m ,显然不等式无解; 若0>m ,则11>+m .①当1≤x 时,不等式为m x m x 211<-++-,解得21m x ->, 所以121≤<-x m; ②当11+<<m x 时,不等式为m x m x 211<-++-,恒成立, 所以11+<<m x ;③当1+≥m x 时,不等式为m m x x 2)1(1<+-+-,解得123+<mx , 所以1231+<≤+mx m ; 综上所述,当0≤m 时,不等式的解集为空集, 当0>m 时,解集为}12321|{+<<-m x m x .。
广东省揭阳市2018年高考第二次模拟考试数学(理)试题有答案AlUlln
揭阳市2018年高中毕业班高考第二次模拟考试数学(理科) 第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}|2A x y x ==-,{}|31x B x =≥,则( )A .AB = B .A B ⊆C .A B R =UD .A B φ=I2.已知复数z 满足()123i z i +⋅=+,则z 的共轭复数z 在复平面内对应的点在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限3.平面直角坐标系xOy 中,i r ,j r 分别是与x 轴、y 轴正方向同向的单位向量,向量2a i =r r ,b i j =+r r r,以下说法正确的是( )A .1a b ⋅=r rB .a b =r rC .()a b b -⊥r r rD .//a b r r4.已知直线a 、b ,平面α、β、γ,下列命题正确的是( )A .若αγ⊥,βγ⊥,a αβ=I ,则a γ⊥B .若a αβ=I ,b αγ=I ,c βγ=I ,则////a b c C.若a αβ=I ,//b a ,则//b α D .若αβ⊥,a αβ=I ,//b α,则//b a 5.已知直线430x y a -+=与22:40C x y x ++=e 相交于A 、B 两点,且120AOB ∠=o ,则实数a 的值为( )A .3B .10 C. 11或21 D .3或136.已知()511x ax x ⎛⎫+- ⎪⎝⎭的展开式中常数项为40-,则a 的值为( )A .2B .2- C. 2± D .47.已知函数()()()sin 0,0,02f x A x A ωϕωϕπ=+>>≤<的部分图象如图所示,则ϕ的值为( )A .3π或23π B .23π C. 43π D .3π或43π8.在如图的程序框图中,输出的n 值为( )A .14B . 32 C. 46 D .539.已知双曲线的焦距为4,A 、B 是其左、右焦点,点C 在双曲线右支上,ABC △的周长为10,则AC 的取值范围是( )A .()2,5B .()2,6 C. ()3,5 D .()3,610.如图是某几何体的三视图,图中每个小正方形的边长为1,则此几何体的体积为( )A .83 B .163 C.4 D .20311.过抛物线22x y =上两点A 、B 分别作切线,若两条切线互相垂直,则线段AB 的中点到抛物线准线的距离的最小值为( ) A .12 B .1 C.32D .2 12.把函数()()2log 1f x x =+的图象向右平移一个单位,所得图象与函数()g x 的图象关于直线y x =对称;已知偶函数()h x 满足()()11h x h x -=--,当[]0,1x ∈时,()()1h x g x =-;若函数()()y k f x h x =⋅-有五个零点,则k 的取值范围是( )A .()3log 2,1B .[)3log 2,1 C.61log 2,2⎛⎫ ⎪⎝⎭ D .61log 2,2⎛⎤ ⎥⎝⎦ 第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.曲线1y x=在点()1,1处的切线方程为 . 14.题库中有10道题,考生从中随机抽取3道,至少做对2道算通过考试.某考生会做其中8道,有2道不会做,则此考生能通过考试的概率为 .15.已知等差数列{}n a 中,2416a a +=,11a +、21a +、41a +成等比数列,把各项如下图排列:则从上到下第10行,从左到右的第11个数值为 .16.平面四边形ABCD 中,60A ∠=o ,AD DC ⊥,3AB =2BD =,则BC 的最小长度为 . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 已知数列{}n a 的前n 项的和为n S ,满足21a =,1631n n S a +=-. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设2n n b a =,数列{}n b 的前n 项和与积分别为n R 与n T ,求n R 与n T . 18. 如图,在四面体ABCD 中,90ABC ADC ∠=∠=o ,22BC BD ==. (Ⅰ)求证:AD BD ⊥;(Ⅱ)若AB 与平面BCD 所成的角为60o,点E 是AC 的中点,求二面角C BD E --的大小.19. 甲、乙、丙三人去某地务工,其工作受天气影响,雨天不能出工,晴天才能出工.其计酬方式有两种,方式一:雨天没收入,晴天出工每天250元;方式而:雨天每天120元,晴天出工每天200元;三人要选择其中一种计酬方式,并打算在下个月(30天)内的晴天都出工,为此三人作了一些调查,甲以去年此月的下雨天数(10天)为依据作出选择;乙和丙在分析了当地近9年此月的下雨天数(n )的频数分布表(见下表)后,乙以频率最大的n 值为依据作出选择,丙以n 的平均值为依据作出选择.n8 9 10 11 12 13 频数31221(Ⅱ)根据统计范围的大小,你觉得三人中谁的依据更有指导意义?(Ⅲ)以频率作为概率,求未来三年中恰有两年,此月下雨不超过11天的概率.20. 已知椭圆()22122:10x y C a b a b+=>>的左、右焦点分别为1F 、2F ,圆2C 经过椭圆1C 的两个焦点和两个顶点,点P 在椭圆1C 上,且122PF =222PF =(Ⅰ)求椭圆1C 的方程和点P 的坐标;(Ⅱ)过点P 的直线1l 与圆2C 相交于A 、B 两点,过点P 与1l 垂直的直线2l 与椭圆1C 相交于另一点C ,求ABC △的面积的取值范围. 21. 已知函数()()()ln 22x mf x ex ax x m +=-+++-,(Ⅰ)若0a >,且()1f -是函数的一个极值,求函数()f x 的最小值; (Ⅱ)若0a =,求证:[]1,0x ∀∈-,()0f x ≥.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,圆C 的圆心为10,2⎛⎫ ⎪⎝⎭,半径为12,现以原点为极点,x 轴的正半轴为极轴建立极坐标系,(Ⅰ)求圆C 的极坐标方程;(Ⅱ)设M ,N 是圆C 上两个动点,满足23MON π∠=,求OM ON +的最小值.23.选修4-5:不等式选讲已知函数()11f x x x m =++++,m R ∈,(Ⅰ)若不等式()2f x m ≥-恒成立,求实数m 的取值范围; (Ⅱ)求不等式()2f x m -<的解集.试卷答案一、选择题1-5:BACAD 6-10:CCDCB 11、12:B C 二、填空题13.20x y +-= 14.141515.275 16.2三、解答题(17)解:(Ⅰ)1361-=+n n a S Θ,1361-=∴-n n a S )2(≥n , 两式相减,得n n n a a a 3361-=+)2(≥n ,n n a a 31=∴+)2(≥n ,又12=a ,所以当2≥n 时,}{n a 是首项为1,公比为3的等比数列,22233--=⋅=n n n a a ,由13621-=a a 得311=a ,满足上式, 所以通项公式为23-=n n a *)(N n ∈;(Ⅱ)122293--===n n n n a b ,得11=b ,公比为9, 8199191-=--=n n n R ,1213219991-⋅⋅⋅⋅=⋅⋅⋅⋅=n n n b b b b T ΛΛ)1(2)1(121399---+++===n n n n n Λ.(18)解:(Ⅰ)由已知得222CD BD BC =+,BC BD ⊥∴,又BC AB ⊥,B AB BD =I ,ABD BC 平面⊥∴,AD BC ⊥∴,又AD CD ⊥,C CD BC =I ,BCD AD 平面⊥∴,BD AD ⊥∴.(Ⅱ)解法1:由(Ⅰ)知,AB 与平面BCD 所成的角为ABD ∠,即︒=∠60ABD , 设BD =2,则BC =2,在ADB Rt ∆中,AB =4,由(Ⅰ)中ABD BC 平面⊥,得平面ABC ⊥平面ABD ,在平面ABD 内,过点B 作AB Bz ⊥,则Bz ⊥平面ABC ,以B 为原点,建立空间直角坐标系xyz B -,则)0,0,0(B ,)0,0,4(A ,)0,2,0(C ,)0,1,2(E ,由160cos ||=︒=BD x D , 360sin ||=︒=BD z D ,得)3,0,1(D ,∴)0,1,2(=BE ,)3,0,1(=BD , 设平面BDE 的法向量为),,(z y x m =ρ,则⎪⎩⎪⎨⎧=+=⋅=+=⋅0302z x m y x BE m ρρ,取1=z ,解得⎪⎩⎪⎨⎧=-=323y x ,∴)1,32,3(-=m ρ是平面BDE 的一个法向量,又)3,0,3(-=是平面CBD 的一个法向量. 设二面角E BD A --的大小为θ,易知θ为锐角,则2132434|||||,cos |cos =⨯==><=AD m m ρρρθ,∴60θ=o ,即二面角C BD E --的大小为60o .【解法2:由(Ⅰ)知,AB 与平面BCD 所成的角为ABD ∠,即60ABD ∠=o, 分别取CD 、BD 的中点F 、G ,连EG 、FG ,在Rt ABC ∆和Rt ADC ∆中,E 为斜边AC 中点,故12BE DE AC ==, ∴EG BD ⊥;又∵BC ⊥平面ABD ,∴BC BD ⊥,又∵//BC FG ∴FG BD ⊥; ∴EGF ∠为二面角C BD E --的平面角, 由(Ⅰ)知AD ⊥平面BCD ,又//AD EF , 故EF ⊥平面BCD ,从而EF FG ⊥,∴12tan 12ADEF EGF FG BC ∠====60EGF ∴∠=o ,即二面角C BD E --的大小为60o .(19)解:(Ⅰ)按计酬方式一、二的收入分别记为)(n f 、)(n g ,(10)250(3010)5000f =⨯-=,52002020010120)10(=⨯+⨯=g ,所以甲选择计酬方式二; 由频数分布表知频率最大的n=8,5500)830(250)8(=-⨯=f , 5360222008120)8(=⨯+⨯=g ,所以乙选择计酬方式一;n 的平均值为10)1132122101938(91=⨯+⨯+⨯+⨯+⨯⨯,所以丙选择计酬方式二;(Ⅱ)甲统计了1个月的情况,乙和丙统计了9个月的情况, 但乙只利用了部分数据,丙利用了所有数据, 所以丙的统计范围最大, 三人中丙的依据更有指导意义;(Ⅲ)任选一年,此月下雨不超过11天的频率为3296=,以此作为概率,则未来三年中恰有两年,此月下雨不超过11天的概率为94)321()32(223=-⨯C . (20)解:(I )设)0,(1c F -,)0,(2c F , 可知圆2C 经过椭圆焦点和上下顶点,得c b =, 由题意知4||||221=+=PF PF a ,得2=a ,由222a c b =+,得2==c b ,所以椭圆1C 的方程为12422=+y x , 点P 的坐标为)0,2(.(II )由过点P 的直线l 2与椭圆1C 相交于两点,知直线l 2的斜率存在, 设l 2的方程为)2(-=x k y ,由题意可知0≠k , 联立椭圆方程,得0488)12(2222=-+-+k x k x k ,设),(22y x C ,则12482222+-=⋅k k x ,得1224222+-=k k x ,所以1214|2|1||2222++=-+=k k x k PC ; 由直线l 1与l 2垂直,可设l 1的方程为)2(1--=x ky ,即02=-+ky x 圆心)0,0(到l 1的距离212kd +=,又圆的半径2=r ,所以1)1(2142)2||(222222+-=+-=-=k k k d r AB , 1122||22+-⋅=k k AB , 由r d <即2122<+k ,得12>k ,112||||2122+-⋅==∆k k PC AB S ABC1212412142222+-⋅=++⋅k k k k ,设12-=k t ,则0>t ,2ABC S t t∆==≤=+当且仅当2t =2k =±时,取“=”,所以△ABC 的面积的取值范围是(0,. (21)解:(I )m ax ax x ex f mx -+++-=+2)2ln()(2,定义域为),2(∞+-,a ax x e x f m x 2221)('+++-=+. 由题意知0)1('=-f ,即011=--m e ,解得1=m ,所以1)2()2ln()(1-+++-=+x ax x e x f x ,a ax x e x f x 2221)('1+++-=+, 又1+=x ey 、21+-=x y 、a ax y 22+=(0>a )在),2(∞+-上单调递增, 可知)('x f 在),2(∞+-上单调递增,又0)1('=-f ,所以当)1,2(--∈x 时,0)('<x f ;当),1(∞+-∈x 时,0)('>x f . 得)(x f 在)1,2(--上单调递减,)(x f 在),1(∞+-上单调递增, 所以函数)(x f 的最小值为a a f -=--=-11)1(. (II )若0=a ,得m x ex f mx -+-=+)2ln()(,21)('+-=+x e x f m x 由)('x f 在]0,1[-上单调递增,可知)(x f 在]0,1[-上的单调性有如下三种情形: ①当)(x f 在]0,1[-上单调递增时,可知0)('≥x f ,即0)1('≥-f ,即011≥--m e ,解得1≥m ,m e f m -=--1)1(,令m e m g m -=-1)(,则01)('1≥-=-m e m g ,所以)(m g 单调递增,0)1()(=≥g m g ,所以0)()1()(≥=-≥m g f x f ; ②当)(x f 在]0,1[-上单调递减时, 可知0)('≤x f ,即0)0('≤f ,即021≤-m e ,解得2ln -≤m , 得02ln 2ln 2ln )0(>=+-≥--=mmmee m ef ,所以0)0()(>≥f x f ;[或:令2ln )(--=m e m h m,则0211)('<-≤-=m e m h , 所以)(m h 单调递减,021)2ln ()(>=-≥h m h ,所以0)()0()(>=≥m h f x f ;] ③当)(x f 在]0,1[-上先减后增时,得)('x f 在]0,1[-上先负后正, 所以)0,1(0-∈∃x ,0)('0=x f ,即2100+=+x emx ,取对数得)2ln(00+-=+x m x , 可知)()(0min x f x f =m x e mx -+-=+)2ln(0002)1(2102000>++=++=x x x x ,所以0)(>x f ;综上①②③得:]0,1[-∈∀x ,0)(≥x f . 【或:若0=a ,得m x ex f mx -+-=+)2ln()(,21)('+-=+x e x f m x 由)('x f 在]0,1[-上单调递增,分如下三种情形: ①当0)('≥x f 恒成立时,只需0)1('≥-f ,即011≥--m e ,解得1≥m ,可知)(x f 在]0,1[-上单调递增,m e f m -=--1)1(,令m e m g m -=-1)(,则01)('1≥-=-m em g ,所以)(m g 单调递增,0)1()(=≥g m g ,所以0)()1()(≥=-≥m g f x f ;②当0)('≤x f 恒成立时,只需0)0('≤f ,即021≤-m e ,解得2ln -≤m ,可知)(x f 在]0,1[-上单调递减时,02ln 2ln 2ln )0(>=+-≥--=mm m e e m e f ,所以0)0()(>≥f x f ;③当)('x f 在]0,1[-上先负后正时,)(x f 在]0,1[-上先减后增, 所以)0,1(0-∈∃x ,0)('0=x f ,即2100+=+x emx ,取对数得)2ln(00+-=+x m x , 可知)()(0min x f x f =m x e mx -+-=+)2ln(0002)1(2102000>++=++=x x x x ,所以0)(>x f ;综上①②③得:]0,1[-∈∀x ,0)(≥x f . 】(22)解:(I )圆C 的直角坐标方程为221124x y ⎛⎫+-= ⎪⎝⎭,化为极坐标方程为sin ρθ=; (II )设()122,,,3M N πρθρθ⎛⎫+⎪⎝⎭, 122sin sin 3OM ON πρρθθ⎛⎫+=+=++⎪⎝⎭1sin sin 223πθθθ⎛⎫=+=+ ⎪⎝⎭, 由0203θππθπ≤≤⎧⎪⎨≤+≤⎪⎩,得03πθ≤≤,2333πππθ≤+≤,故sin 123πθ⎛⎫≤+≤ ⎪⎝⎭,即OM ON +的最小值为2. (23)解:(I )|||)1(1||1||1|)(m m x x m x x x f =++-+≥++++=, 由题意知|2|||-≥m m ,得22)2(-≥m m ,解得1≥m ;(II )不等式为m x m x 2|1||1|<-++-,即m m x x 2|)1(||1|<+-+- 若0≤m ,显然不等式无解; 若0>m ,则11>+m .①当1≤x 时,不等式为m x m x 211<-++-,解得21mx ->, 所以121≤<-x m; ②当11+<<m x 时,不等式为m x m x 211<-++-,恒成立, 所以11+<<m x ;③当1+≥m x 时,不等式为m m x x 2)1(1<+-+-,解得123+<m x , 所以1231+<≤+m x m ; 综上所述,当0≤m 时,不等式的解集为空集, 当0>m 时,解集为}12321|{+<<-m x m x .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
揭阳市2018年高中毕业班高考第二次模拟考试 数学(文科);; 第Ⅰ卷(共60分); 一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设复数11zi,234zi,则12zz在复平面内对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.设集合230Axxx,1Bxyx,则AB( ) A.31xx B.31xx C.1xx D.3xx 3.函数xfxex的零点所在的区间为( )
A.11,2 B.1,02 C.10,2 D.1,12 4.执行如图所示的程序框图,若输入x的值为9,输出y的值为2,则空白判断框中的条件可能为( ); A.9x B.10x C. 8x D.9x 5.平面直角坐标系xOy中,i、j分别是与x轴、y轴正方向同向的单位向量,向量2ai,bij,以下说法正确的是( ) A.ab B.abb C.1ab D.//ab
6.已知511xaxx的展开式中常数项为40,则a的值为( ) A.2 B.2 C. 2 D.4 7.已知函数sin0,0,02fxAxA的部分图象如图所示,则的值为( )
A. 3或23 B.23 C. 43 D.3或43 8.在如图的程序框图中,输出的n值为( ) A.14 B. 32 C. 46 D.53 9.已知双曲线的焦距为4,A、B是其左、右焦点,点C在双曲线右支上,ABC△的周长为10,则AC的取值范围是( ) A.2,5 B.2,6 C. 3,5 D.3,6 10.如图是某几何体的三视图,图中每个小正方形的边长为1,则此几何体的体积为( )
A. 83 B.163 C.4 D.203 11.过抛物线22xy上两点A、B分别作切线,若两条切线互相垂直,则线段AB的中点到抛物线准线的距离的最小值为( ) A.12 B.1 C.32 D.2 12.把函数2log1fxx的图象向右平移一个单位,所得图象与函数gx的图象关于直线yx对称;已知偶函数hx满足11hxhx,
当0,1x时,1hxgx;若函数ykfxhx有五个零点,则k的取值范围是( ) A.3log2,1 B.3log2,1 C.61log2,2
D.61log2,2 第Ⅱ卷(共90分) 二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.曲线1yx在点1,1处的切线方程为 . 14.题库中有10道题,考生从中随机抽取3道,至少做对2道算通过考试.某考生会做其中8道,有2道不会做,则此考生能通过考试的概率为 . 15.已知等差数列na中,2416aa,11a、21a、41a成等比数列,把各项如下图排列: 则从上到下第10行,从左到右的第11个数值为 . 16.平面四边形ABCD中,60A,ADDC,3AB,2BD,则BC
的最小长度为 . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 已知数列na的前n项的和为nS,满足21a,1631nnSa. (Ⅰ)求数列na的通项公式; (Ⅱ)设2nnba,数列nb的前n项和与积分别为nR与nT,求nR与nT.
18. 如图,在四面体ABCD中,90ABCADC,22BCBDCD. (Ⅰ)求证:ADBD; (Ⅱ)若AB与平面BCD所成的角为60,点E是AC的中点,求二面角CBDE的大小.
19. 甲、乙、丙三人去某地务工,其工作受天气影响,雨天不能出工,晴天才能出工.其计酬方式有两种,方式一:雨天没收入,晴天出工每天250元;方式而:雨天每天120元,晴天出工每天200元;三人要选择其中一种计酬方式,并打算在下个月(30天)内的晴天都出工,为此三人作了一些调查,甲以去年此月的下雨天数(10天)为依据作出选择;乙和丙在分析了当地近9年此月的下雨天数(n)的频数分布表(见下表)后,乙以频率最大的n值为依据作出选择,丙以n的平均值为依据作出选择. n 8 9 10 11 12 13
频数 3 1 2 0 2 1 (Ⅰ)试判断甲、乙、丙选择的计酬方式,并说明理由; (Ⅱ)根据统计范围的大小,你觉得三人中谁的依据更有指导意义? (Ⅲ)以频率作为概率,求未来三年中恰有两年,此月下雨不超过11天的概率.
20. 已知椭圆22122:10xyCabab的左、右焦点分别为1F、2F,圆2C经过椭圆1C的两个焦点和两个顶点,点P在椭圆1C上,且122PF,222PF. (Ⅰ)求椭圆1C的方程和点P的坐标; (Ⅱ)过点P的直线1l与圆2C相交于A、B两点,过点P与1l垂直的直线
2l与椭圆1C相交于另一点C,求ABC△的面积的取值范围. 21. 已知函数ln22xmfxexaxxm, (Ⅰ)若0a,且1f是函数的一个极值,求函数fx的最小值; (Ⅱ)若0a,求证:1,0x,0fx. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程 在直角坐标系xOy中,圆C的圆心为10,2,半径为12,现以原点为极点,x轴的正半轴为极轴建立极坐标系, (Ⅰ)求圆C的极坐标方程; (Ⅱ)设M,N是圆C上两个动点,满足23MON,求OMON的最小值. 23.选修4-5:不等式选讲 已知函数11fxxxm,mR, (Ⅰ)若不等式2fxm恒成立,求实数m的取值范围; (Ⅱ)求不等式2fxm的解集. 试卷答案 一、选择题 1-5:CADDB 6-10:ADBCB 11、12:CD 二、填空题
13.8349 14.3或13 15.23 16.2 三、解答题: (17)解:(Ⅰ)1361nnaS,1361nnaS)2(n, 两式相减,得nnnaaa3361)2(n,
nnaa31)2(n,又12a, 所以当2n时,}{na是首项为1,公比为3的等比数列, 22233nnnaa
,
由13621aa得311a,满足上式, 所以通项公式为23nna*)(Nn; (Ⅱ)122293nnnnab,得11b,公比为9,
8199191nnnR,
1213219991nnnbbbbT
)1(2)1(121399nnnnn. (18)解:(Ⅰ)由已知得222CDBDBC, BCBD, 又BCAB,BABBD, ABDBC平面, ADBC, 又ADCD,CCDBC, BCDAD平面, BDAD. (Ⅱ)解法1:由(Ⅰ)知,AB与平面BCD所成的角为ABD,即60ABD, 设BD=2,则BC=2,在ADBRt中,AB=4, 由(Ⅰ)中ABDBC平面,得平面ABC⊥平面ABD,在平面ABD内,过点B作ABBz,则Bz平面ABC,以B为原点,建立空间直角坐标系xyzB, 则)0,0,0(B,)0,0,4(A,)0,2,0(C, )0,1,2(E,由160cos||BDxD, 360sin||BDzD
,
得)3,0,1(D, ∴)0,1,2(BE,)3,0,1(BD, 设平面BDE的法向量为),,(zyxm,
则0302zxBDmyxBEm,取1z,解得323yx, ∴)1,32,3(m是平面BDE的一个法向量, 又)3,0,3(AD是平面CBD的一个法向量. 设二面角EBDA的大小为,易知为锐角,
则2132434|||||||,cos|cosADmADmADm, ∴60,即二面角CBDE的大小为60. 【解法2:由(Ⅰ)知,AB与平面BCD所成的角为ABD,即60ABD, 分别取CD、BD的中点F、G,连EG、FG, 在RtABC和RtADC中,E为斜边AC中点,故12BEDEAC, ∴EGBD; 又∵BC平面ABD,∴BCBD, 又∵//BCFG ∴FGBD; ∴EGF为二面角CBDE的平面角, 由(Ⅰ)知AD平面BCD,又//ADEF, 故EF平面BCD,从而EFFG,
