第一章 线性规划及单纯形法3-单纯形法计算步骤
运筹学单纯形法
只要取 x5=min{-,8/2,12}=4 就有上式成立。 x5=4时, x4=0,故决定用x5换x4 x1 =4- 1/4 x4 x5 =4-1/2 x4 +2 x3 x2 =2+1/8 x4–1/2 x3 代入得 z=14-3/2 x3 –1/8 x4 ,令x3 ,x4=0得z=14。新基可 行解为 X(3) =(4,2,0,0,4) T –为最优解,新顶点Q2 最优目标值z=14 。
§3.4 最优性检验和判别定理
线性规划解的四种可能: 1、有唯一解; 2、无穷多最优解; 3、无界解; 4、无可行解。 何时达最优解, 何种最优解?
将基本可行解X(0)和X(1)分别代入目标函数得
z z
(0)
= ∑ ci xi0
i =1 m
mቤተ መጻሕፍቲ ባይዱ
(1)
= ∑ ci [ xi0 − θ aij ] + θ ci
§3.3 从初始基可行解转换为另一基可行解
0 0 记初始基可行解为X(0),有 X ( 0 ) = (x10 x 2 L x m 0 L 0
)
Pi xi0 = b 该解满足约束方程, 即 ∑
i =1
m
(1)
非基向量可以用基向量的线性组合表示
Pj = ∑ aij Pj
i =1 m
m
(2) (3)
Pj − ∑ aij Pj = 0
从实际例子中分析单纯形法原理的基本框架为 •第一步:将LP线性规划变标准型,确定一个初始可行解 (顶点)。 •第二步:对初始基可行解最优性判别,若最优,停止;否 则转下一步。 •第三步:从初始基可行解向相邻的基可行解(顶点)转 换,且使目标值有所改善—目标函数值增加,重复第二和 第三步直到找到最优解。
单纯形法求解过程

单纯形法求解过程单纯形法是一种经典的线性规划求解方法,它是由乔治·达竞士等人在1947年提出的。
该方法的基本思想是,通过在单纯形空间内不断移动顶点的位置来寻找最优解。
单纯形法是目前广泛应用的线性规划求解方法之一,它求解线性规划问题可大大地简化计算过程。
单纯形法的求解过程包括以下几个步骤:1. 将线性规划问题转化为标准形式线性规划问题的标准形式为:$ \max_{x} \ \ c^T x $$s.t. \ Ax=b$$x\geq 0$其中,$x$是要求解的向量;$b$是一个常数向量;$A$是一个$m\times n$的矩阵;$c$是一个常数向量。
2. 初始化单纯形表因为单纯形法是通过移动顶点来寻找最优解的方法,因此需要初始化单纯形表。
单纯形表是将原始的约束条件表示为不等式形式时形成的。
例如,对于一个带有3个变量的线性规划问题,其单纯形表的形式如下:CB | X1 | X2 | X3 | X4 | RHS----|-----|-----|-----|-----|----0 | a11| a12| a13| 0 | b10 | a21| a22| a23| 0 | b20 | a31| a32| a33| 0 | b31 | z1 | z2 | z3 | 0 | 0其中,CB代表成本系数,X1、X2、X3、X4分别代表变量。
a11、a12、a13等代表矩阵A中的元素,b1、b2、b3代表矩阵b中的元素。
3. 选择进入变量和离开变量在单纯形表中,规定最后一列为等式右边的常数(RHS),即b。
在单纯形法的求解过程中,首先需要选择一个“进入变量”,即在单纯形表的第一行中,寻找一个系数为正的变量,使得将其加入目标函数后,目标函数值可以上升。
这里以X1为例,X1为进入变量。
接着,需要选择一个“离开变量”,即在单纯形表中,寻找一个使得添加X1变量后,约束条件不改变且取得约束条件中系数最小的一个变量离开。
运筹学第1章-线性规划

下一页 返回
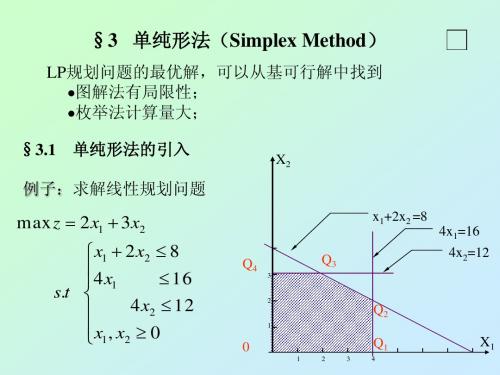
图解法步骤:
(1)建立坐标系; (2)将约束条件在图上表示; (3)确立满足约束条件的解的范围; (4)绘制出目标函数的图形 (5)确定最优解
用图解法求解下列线性规划问题
max z 2x1 3x2
4x1 0x2 16
s.t
10xx11
4x2 2x2
12 8
x1, x2 0
1. 1.1问题举例
(1)生产计划问题。 生产计划问题是典型的已知资源求利润最大化的问题,对于此类
问题通常有三个假设:①在某一计划期内对生产做出的安排;②生产 过程的损失忽略不计;③市场需求无限制,即假设生产的产品全部 卖出。
下一页 返回
1.一般线性规划问题的数学模型
例1 用一块连长为a的正方形铁皮做一个容 器,应如何裁剪,使做成的窗口的容积为最 大?
解:设 x1, x2分别表示从A,B两处采购的原油量(单
位:吨),则所有的采购方案的最优方案为:
min z 200x1 290x2
0.15x1 0.50x2 150000
s.t
0.20x1 0.50x1
0.30x2 0.15x2
120000 120000
x1 0, x2 0
1. 1线性规划问题与模型
也可以写成模型(1-6)和模型(1-7)的形式,其中模型(1-7)较为常用。
运筹学

2013-12-16 安徽工程大学 12
如果表中所有的检验数都小于等于零,且基变量中不含有人工变量时,表中 的基可行解即为最优解,计算结束。若果表中检验数存在大于零的数,需转 向下一步。
3、从一个基转换到相邻的目标函数值更大的基可行解,列出新的单纯形表。 A、确定转入基的变量。 确定检验数最大的一个,对应的变量就可以作为换 入基的变量。 B、确定换出基的变量。 用b除检验数最大的一列的数就可以确定 ,取其 最小的数,其对应的变量就可以作为换出变量。则该列对应的的那个数即为 主元素。 C、用换入变量替换基变量中的换出变量,得到一个新基。对应的可以却确 定表的前三列。
3、线性规划问题的基可行解X对应线性规划问题可行域的顶点。
4、若线性规划问题有最优解,一定存在一个基可行解是最优解。
四、单纯形法迭代原理 1、确定初始基可行解
2、从一个基可行解转换为相邻的基可行解
3、最优性检验和解的判别
第四节
对标准型的线性规划问题
单纯形法计算步骤
1、求初始基可行解,列出初始单纯形表。 n
2013-12-16
max z cjxj
j 1
ij j i
a x b , (i 1,2,3...... m)
j 1
n
xj 0, ( j 1,2,...... n)
安徽工程大学 11
在约束条件式的变量系数矩阵中总会存在一个单位矩阵
1 0 ... 0 0 1 ... 0 P1, P 2, P 3,...... Pm : : : 0 0 ... 1
物流运筹学单纯形法

如何确定出基变量(可以按照下述方法来理解) 当x2定为入基变量后,必须从x3 、 x4 、 x5中换出来一个,并保 证其余的变量在新可行解中还都是非负,即: x3≥0 、 x4 ≥0 、 x5 ≥0
因为x1 仍为基变量, 所以将x1=0,带入约 束条件,得到:
4 x2 x3 360 5 x2 x4 200 s.t . 10x2 x5 300 x , x , x , x , x 0 1 2 3 4 5
需要解决的问题: (1)为了使目标函数逐步变优,怎么转移? (2)目标函数何时达到最优?判断标准是什么?
1.5.1单纯形法原理
单纯形法步骤
确定初始基本可行解
检验其 是否为最优
是
停
主要工作: 最优性检验
否 寻找更好的 基本可行解
主要工作: 1、基变换(将原来的基换成新的基) 2、修正单纯形表,得到新的基本可行解
基变量的 价值系数 基变量
基本 可行解
CB
0 0 0
XB
X3 X4 X5 机会成本行 σj
7 B b 360 200 300
-1
12 X2 4 5 10 0 12
0 X3 1 0 0 0 0
0 X4 0 1 0 0 0
0 X5 0 0 1 0 0
X1 9 4 3 0 7
θ
90 40 30
因为基变量的检验数σ1和σ2都大于0,所以当前解不是最优。需要变换可行 基,寻找新的解。即原来的非基变量x1 、x2,要有一个被换为基变量,基变 量中也要有一个被换为非基变量,以确定新的基、新的解。
0
0
0
主元列 (确定入基变量)
主元行 (确定 出基变 量)
主元素
单纯形法的计算步骤

函数变化值
的净利润变化值
最小比值 θj
2019/11/26
确保在迭代过程中所有 确保在增加产品产量的 变量的值非负,即每步 过程中,不超过现在的 得到的解均为基可行解。资源限量。
单纯形法的计算步骤
Page 5
将3化为1
cj
cB
基变量
0
x3
0
x4
j
乘
0
x3
以
4
x2
3/5 后
j
得
3
x1
到
4
x2
j
Page 6
例1.11 用单纯形法求解
max Z x1 2 x2 x3
2x1 3x2 2x3 15
s.t
1 3 x1 x2 x1、x2、x3
5x3 0
20
解:将数学模型化为标准形式:
max Z x1 2 x2 x3
2x1 3x2 2x3 x4 15
4)解的判断同单纯形法
2019/11/26
例4.2 用两阶段法求解线性规划问题
minΖ =-3x1+x2+x3
s.t.
x1-2x2+x3 ≤11
-4x1+x2+2x3 ≥3
-2x1 +x3
=1
x1,x2,x3, ≥0
解:先在约束条件中加入人工变量,写出辅助规划问
题。
s.t.
2019/11/26
Min W=x6+x7
最优解:
2019/11/26
换入列
bi /ai2,ai2>0
3
4
0
b
单纯形法求最小值的计算步骤例题
单纯形法求最小值的计算步骤例题《用单纯形法求线性规划问题最小值的详细计算步骤及例题讲解》。
今天咱们一起来学习一下怎么用单纯形法求最小值。
这个方法在数学里可是很有用的哦,特别是在解决一些资源分配、成本优化之类的问题时,经常能派上大用场。
下面我就给大家详细讲讲它的计算步骤,再通过一个具体的例题让大家更清楚地明白怎么操作。
一、单纯形法求最小值的基本思路。
单纯形法呢,简单来说,就是从一个初始的可行解出发,然后通过不断地调整这个解,让目标函数的值越来越小,直到找到最小值为止。
就好比你要找一条下山的路,一开始你在某个位置,然后一步一步朝着更低的地方走,最后走到山脚下,那个山脚下就是咱们要找的最小值啦。
二、计算步骤。
1. 将线性规划问题化为标准形式。
- 目标函数要是求最小值的形式,所有的约束条件都得是等式,而且右边的常数项都得是非负的。
比如说,有个线性规划问题是这样的:- 目标函数:Z = 3x_1 + 2x_2(求最小值)。
- 约束条件:x_1 + x_2 ≥ 5,2x_1 - x_2 ≤ 8,x_1 ≥ 0,x_2 ≥ 0- 那咱们就得把它化成标准形式。
对于x_1 + x_2 ≥ 5这个不等式,我们可以引入一个松弛变量x_3,把它变成等式x_1 + x_2 - x_3 = 5;对于2x_1 - x_2 ≤ 8,引入松弛变量x_4,变成2x_1 - x_2 + x_4 = 8。
这样,标准形式就是:- 目标函数:Z = 3x_1 + 2x_2 + 0x_3 + 0x_4(求最小值)。
- 约束条件:x_1 + x_2 - x_3 = 5,2x_1 - x_2 + x_4 = 8,x_1 ≥ 0,x_2 ≥ 0,x_3 ≥ 0,x_4 ≥ 02. 找出初始可行基和初始基本可行解。
- 一般来说,我们可以从标准形式的约束条件里,找那些系数矩阵中能构成单位矩阵的列对应的变量作为基变量。
比如说上面这个例子里,x_3和x_4对应的系数构成了单位矩阵,那它们就是基变量,x_1和x_2就是非基变量。
单纯形法
四、单纯形法的实现——单纯形表
例1:煤电油例 Max Z=7 x1 +12x2 9 x1 +4x2≤360 化为标准型 s.t. 4x1 +5x2 ≤200 3 x1 +10x2 ≤300 x1 , x2≥0 s.t. Max Z=7 x1 +12x2 9 x1 +4x2 +x3 4x1 +5x2 3 x1 +10x2 x1 ,…,x5≥0 +x4 =360 = 200
•
“≥”型约束,减松弛变量;
练习1.3 请将例1.1的约束化为标准型
Maxz = 7 x1 + 12 x 2 ⎧9 x1 + 4 x 2 ≤ 360 ⎪4 x1 + 5 x 2 ≤ 200 s.t.⎨ 3x1 + 10 x 2 ≤ 300 ⎪x , x ≥ 0 ⎩ 1 2
则约束化为
= 360 ⎧9 x1 + 4 x 2 + x3 ⎪4 x + 5 x 2 + x4 = 200 s.t.⎨ 1 3 x1 + 10 x 2 + x5 = 300 ⎪x , x , x , x , x ≥ 0 ⎩ 1 2 3 4 5
例4 下面为某线性规划的约束
=1 ⎧ x1 + 2 x2 + x3 ⎪ + x4 = 3 ⎨2 x1 − x2 ⎪ x1 , , x4 ≥ 0 ⎩ 请例举出其基矩阵和相应的基向量、基变量。
解:
本例中, A = ⎡1 2 1 0⎤,A中的2阶可逆子阵有 ⎢ 2 − 1 0 1⎥ ⎦ ⎣
问题:本例的A中一共有几个基?—— 6个。
易见,增加的松弛变量的系数恰构成一个单位阵I。
一般地,记松弛变量的向量为 X s,则
单纯形法文档
单纯形法1. 什么是单纯形法单纯形法(Simplex Method)是一种数学优化方法,用于在线性规划问题中寻找最优解。
其基本思想是通过不断地在可行解空间中移动,逐步优化目标函数的值,直到找到最优解。
单纯形法是由美国数学家乔治·达内策在20世纪40年代开发的,成为线性规划问题求解的一种经典方法。
2. 单纯形法的基本原理单纯形法的基本原理是通过构造一系列的顶点组合,这些顶点组合构成了可行解空间的一个多面体,称为单纯形。
每次移动都是在单纯形的边界上进行,直到找到最优解。
2.1 线性规划问题的标准形式在使用单纯形法求解线性规划问题之前,首先需要将问题转化为标准形式。
线性规划问题的标准形式包括以下特征:•最大化目标函数或最小化目标函数•约束条件为等式或不等式•决策变量为非负数2.2 单纯形法的步骤单纯形法的求解步骤如下:1.初始化:将线性规划问题转化为标准形式,并找到初始可行解。
2.检验最优性:计算当前基可行解对应的目标函数值,判断是否达到最优解。
3.寻找进入变量:通过计算目标函数的系数与约束条件中的系数之比,找到使目标函数值最大(或最小)增长的变量。
4.寻找离开变量:从进入变量所属列中选择合适的变量离开基,使得新的基可行解依然满足约束条件。
5.更新基:将进入变量换入基,将离开变量换出基,得到新的基可行解。
6.重复步骤 2-5,直到找到最优解或判断无界。
2.3 单纯形表在单纯形法的求解过程中,通过使用单纯形表(Simplex Table)来记录每一步的计算结果和变量的取值。
单纯形表是一个矩阵,包含基变量、非基变量、目标函数系数、约束条件左边的系数等信息,方便进行计算和调整。
3. 单纯形法的优缺点3.1 优点•单纯形法是一种简单直观的求解线性规划问题的方法,容易理解和实现。
•单纯形法对于规模较小的问题,可以得到精确的最优解。
•单纯形法可以处理带有不等式约束的问题,适用范围广。
3.2 缺点•单纯形法在解决大规模问题时,计算复杂度较高,效率较低。
单纯形法的计算步骤及应用
(4-16)
(4-17)
bi' bi
bl ai ,k ( i 1,2, , n; i l ) al ,k
这样经过变换以后就得到了新的增广矩阵 p1 … pl pm pm+1 pk pn b
a1,k 1 a l ,k 1 0 al ,k a m ,k 0 a l ,k 0 a
单纯形法介绍及相关问题
标准型线性规划问题 max s=c1x1+c2x2+…+cnxn s.t. a11x1+a12x2+…+a1nxn=b1 a21x1+a22x2+…+a2nxn=b2
an1x1+an2x2+…+annxn=bn xj≥0(j=1,2,…,n)
单纯形法介绍及相关问题
例1 已知约束如下
(4-11)
单纯形法介绍及相关问题
2、基本可行解之间的迭代
在讨论中我们假设对方程组(4-10)的系数增广矩阵 p1 … pl pm pm+1 pk pn b
a1,m1 1 1 al ,m1 1 am ,m1
a1,m1 a1,n al ,m1 al ,n am ,m1 am ,n
' a1 ,m 1 ' 0 a1 ,n
' l ,m 1
0
1 al' ,n
1 a'm ,m 1 0 a'm ,n
' b1 bl' ' bm
