05粗糙面电磁散射的小斜率近似方法研究05
粗糙面电磁散射的小斜率近似方法研究

粗糙面电磁散射的小斜率近似方法研究粗糙面电磁散射的小斜率近似方法研究电磁波在遇到任意粗糙表面时都会发生散射,这种散射现象是一种常见的自然现象。
由于自然界中存在着大量粗糙表面,因此了解这种现象并准确预测其行为对于许多领域都有着重要的意义。
粗糙面散射的主要特点是随机性和多次反射。
通常采用小斜率近似方法来描述这种现象。
该方法简单易用,可以用于大多数不同类型的粗糙表面散射情况。
本文将探讨粗糙面电磁散射的小斜率近似方法的研究进展。
一般来说,小斜率指的是平行于入射波矢的平面内表面的斜率非常小。
基于这个条件,可以在表面上任意一点假设有一个微观平面,该平面是和表面斜率相同的水平面。
因此,当电磁波遇到这个微观平面时,只有非常小的部分会被反射。
那么我们就可以对表面每个微观平面的反射完全相加,得到表面的整体反射率。
在研究粗糙表面电磁散射时,一个核心问题是如何计算散射幅度随角度变化的关系。
典型的情况下,我们要计算反射系数或散射系数。
因此,我们需要研究不同粗糙度下反射系数的变化情况,以便充分利用这种方法。
目前,粗糙面散射问题研究的主要方法有精确解法、小斜率近似方法和数值计算法。
其中,精确解法和数值计算法都要求表面的形状以及其它参数可以明确地表达出来。
然而,通常情况下,由于表面形状过于复杂,很难得到相对精确的解析解。
因此,小斜率近似方法成为研究粗糙表面散射的一种标准方法。
小斜率近似方法的基本思路是,在局部微观区域内,表面斜率可以被近似为常数。
这种近似条件使得入射波只会被少数表面微观平面反射。
而反射波浸透到下层表面后又会继续被反射。
整个过程可以看作一系列相同的逐渐递减的反射事件。
粗糙表面散射的研究在军事、制造和通信等领域有着重要的应用。
例如,研究铁路与地面的电磁散射问题对于确保交通安全和实现无线通信至关重要。
同样地,粗糙表面散射也对于雷达系统的性能造成了影响。
粗糙表面的电磁散射也对于天体测量的准确性产生影响。
了解粗糙表面散射现象以及采用小斜率近似方法进行研究能够为这些领域提供有力的支持。
随机粗糙表面电磁散射特性的双尺度法

应用电子技术
随机粗糙表面电磁散射特性的双尺度法
郑 帆,代泽洋,刘宝泉 中国电子科技集团公司第三十八研究所,安徽 合肥 230000
摘要:介绍了双尺度法计算随机粗糙表面后向散射系数的方法,同时采用蒙特卡洛法仿真了单尺度和双尺度的 二维随机粗糙表面。利用基尔霍夫近似、微扰法和双尺度法分别计算了粗糙面的后向散射系数,并且比较了这 三种方法计算的结果,显示出了双尺度法在研究粗糙面电磁散射特性的优越性。 关键词:双尺度法;随机粗糙面;后向散射系数 中图分类号:TN011
式中的集平均仅是针对大尺度粗糙度,其中
对于大小尺度同时具有高斯型谱密度函数的粗 糙面,在散射系数计算中总的谱密度函数以及斜率概 率密度函数分别为
式
中,cosθ′i=-(n^ ·n^ i)=(cosθi+fx
sinθi)(1+f
2x+f
) 2 -1/2
y
,
δ是小尺度粗糙面的均方根高度。W 为粗糙面谱密度
函数。
在式(8)和式(11)中对大尺度粗糙度求集平
均时,需要引入关于表面斜率 fx 和 fy 的概率密度函 数 P(fx,fy),由于入射发生在 x-z 平面内,fy 的积 分极限由 - ∞到∞,为避免照射到倾斜面的背面去,
fx 的积分极限从 -cot θi 到∞,所以散射系数最终可 以写为
其中,t=k[sinθ2 ′s+sinθ2 ′i-2 sinθ′ssinθ′i cos(φ′s-φ′i)], φ′i 和 φ′s 为分别为本地坐标系中的入射方位角和散 射方位角,s 为均方根斜率。
大粗糙大粗度糙度
φs′φs′ φφs s
y′′ yy
x
xx′′
图 1 双尺度粗糙面的电磁散射示意图
双尺度方法在粗糙海面中的电磁散射分析和应用

双尺度方法在粗糙海面中的电磁散射分析和应用张凯【摘要】给出双尺度方法的粗糙海面散射理论。
并给出了双尺度粗糙面的电磁散射示意图,以示意图分析和推导了用双尺度法计算海面粗糙面的散射系数和概率密度函数。
并基于双尺度方法与粗糙海面的散射理论,研究了不同方法计算随入射角变化的后向散射系数、双站散射系数,以及不同方法得到随方位角变化的双站散射系数、双尺度方法与实测数据的比较。
最后进行了结果分析,验证了该方法的有效性。
【期刊名称】《电子世界》【年(卷),期】2015(000)024【总页数】2页(P69-70)【关键词】双尺度方法;粗糙海面;双站散射系数;后向散射系数【作者】张凯【作者单位】贵州航天计量测试技术研究所【正文语种】中文自然界中的某些粗糙面同时含有大、小粗糙度或者粗糙度是连续分布的,即有多个尺度的粗糙度。
对于这类粗糙面的电磁散射计算,其粗糙度既不在微扰法适用区域又不在基尔霍夫近似方法的适用范围,根据文献[1]单独使用微扰法或基尔霍夫近似方法均不能较客观地反映粗糙面的电磁散射特性。
此时可以将表面粗糙度视为大小两种粗糙度的叠加,将微扰法用于小粗糙度,基尔霍夫近似用于大粗糙度,将小粗糙度计算的散射系数在大粗糙度的斜率分布上作集平均,得到总散射系数,即双尺度方法(Two Scal e Met hod,TSM)。
图1 双尺度粗糙面的电磁散射示意图如图1所示,根据文献[2]假设平面波入射到粗糙面上,粗糙面高度用f(x,y)来表示,fx和fy分别代表粗糙面沿x和y方向的导数,表面单位法矢,坐标系(x,y,z)为主坐标系,坐标系为本地坐标系。
设入射方向与成角,与成角,若方位角等于,则入射波矢,本地坐标系中,与切平面法线重合,本地单位坐标矢量定义为:所以:其中,当表面斜率为零时,主坐标系与本地坐标系一致。
类似地定义水平极化矢量和垂直极化矢量分别为:一般情况下,主坐标系中的一个水平极化入射波E0在本地坐标系中可以看成一个水平和一个垂直入射波的叠加,即:在主坐标系与本地坐标系中,分别定义入射波的水平和垂直极化分量。
第五章电磁散射 _简版

第五章 电磁散射 5.1 雷达散射截面雷达散射截面(Radar Cross section,缩写RCS )是雷达隐身技术中最关键的概念,它表征了目标在雷达波照射下所产生回波强度的一种物理量。
RCS 是一个假想的量,我们将RCS 等效为一个截面,将其放置在一个与电磁波传播方向垂直的平面上,它可以无损耗地把入射功率全部地、均匀地向各个方向传播出去,并且,在接收处的回波功率密度与实际目标产生的功率密度相等。
将RCS 定义为目标在单位立体角内向接收机处散射功率与入射波在目标上的功率密度之比的4π倍。
假设入射波,r k j i i ie E E ∙-=0,则有ii i E k H ⨯=η1入射波平均功率密度21Re()22ii i i i E S E H k η=⨯= 目标截取的总功率为入射波功率密度与目标“等效面积”σ 的乘积,即:202i i E S P ησσ==假设目标功率是各向同性均匀地向四周散射,则在距离目标R 处的目标散射功率密度为:220284RE R PS i s πησπ ==散射功率密度亦可用散射场强表示:η22s s E S=由上可得:222R 4,s is c i iE R E E S E S σπ===∝∝接收天线处目标散射总功率距离目标处散射总功率目标处入射总功率目标处入射总功率另外:1. σ与R 无关;2. 符合远场条件:R 远大于目标特征尺寸 ;3. σ与入射波方向,散射波方向,散射体形状,表面粗糙度以及介电特性等相关。
雷达散射系数是指单位照射面积上的雷达散射截面,是归一化处理的结果,它是入射电磁波与地面目标相互作用结果的度量,定义为,为照射面积为入射角,或者A A Ai io o θθσσσσ,cos ,==雷达散射的三个特征区域若目标的特征尺寸为a ,则ka 为其电尺寸。
其中λπ2=k 为雷达波数。
目标RCS 随电尺寸的变化分为三个区域。
以金属球为例,令02=rσσπ,其中r 是金属球的半径,λ 为入射波波长。
关于终值微分方程的解

2005 年12 月J O U RN AL O F XI′A N J IA O TO N G U N IV ER SI T Y Dec .2005关于终值微分方程的解朱传喜, 叶梅燕, 郭玲(南昌大学数学系, 330047 , 南昌)摘要: 为了解决满足一个微分方程且已知终值物体运动轨迹的存在性的问题,首先证明了一个重要定理,即在一定条件下,定义于实Ba n ach 空间 E 中的凝聚算子在E 的某个闭球中有不动点,其次研究了一类终值微分方程的解.关键词: 凝聚算子;不动点;终值微分方程中图分类号: O1751 1 文献标识码: A文章编号: 0253Ο987 X (2005) 12Ο1384Ο03On Sol u t i ons of T erminal V al u e Diff e rent i al Equat i onsZ h u C h u a n x i , Ye M ei y a n , Guo L i n g( D ep a r t ment of Mat he mati cs , Nancha ng U ni ver s it y , Na ncha ng 330047 ,Chi na)Abstract : To re s ol v e t h e e xi s t e n ce of a mo v ed o b ject loc u s go v e r n ed by a diff e re n tial equatio n wit h a k no w n t e r mi nal val ue , t h e t h eo re m , t h at u nde r ce rt ai n co n ditio n s t h e co nde n s i ng op e rato r defi n ed i n real Ba nac h sp ace E ha s a f i xe d poi nt i n a clo sed sp he re of E , i s p ro ved ; t h u s t he sol utio n s of a ki nd of t e r m i n al val u e diff e re n tial equatio n s a r e i n ve s ti g at e d.K ey w ords : con de n s i n g o p e r a t o r ; f i x e d p o i nt ; t e r m i n a l v al ue d i f f e r e n t i al eq u a t i o n微分方程初值问题在物理中的应用非常广泛,但是对于满足一个微分方程且已知末端值的物体( 导弹/ 飞机) 运动轨迹是否存在这个问题的解决是非常重要的. 由于微分方程终值问题存在一定的难度, 过去研究的人比较少, 本文主要研究该问题的理论基础和应用.为了解决上述满足一个微分方程且已知末端值的物体(导弹/ 飞机) 运动轨迹是否存在的问题, 我们研究该类终值微分方程,首先证明下面的定理.定理1 设A : E →E 是一个凝聚算子,且 E 是一个实Ba n ac h空间, 如果集合{ x | x ∈E , x =λA x , 0 < λ< 1}是有界的,则A 在E 的闭球T 中必有不动点, 这里T = { x| x ∈E , ‖x ‖≤R} , R = s up { ‖x ‖| x = λA x ,0 <λ< 1 .设E1 、E2 是两个实Ba n ach 空间, D < E1 ,又设A : D →E2 是一个连续的有界算子. 一个算子A 称为D 上的凝聚算子, 如果对任何非紧的有界集S < D , 满足α[ A ( S) ] <α( S) , 其中α表示非紧性测度[ 1Ο5 ] . C1 [ a , b]表示从定义域[ a , b]到值域[ a , b]上具有一阶连续导函数的全体所成集合.在上述物理问题或信息科学理论中得到了一类终值微分方程如下x| x ∈E , ‖x ‖< R + 1证明令T = . 假设AKK在5 T K 上没有不动点(否则存在x K ∈5 T K , 使得x K = A x K , 定理已经获证) .令h t ( x)= x - t A x , 于是在5 T K 上, ‖x ‖=R + 1 , Πx ∈5 T K ,即在5 T K 上, x ≠λA x ,λ∈( 0 ,1) .K由R 的定义,θ|d xx ∈R n , t ∈[ a , b]= f ( t , x)h 5 T , Π0 ≤t ≤1 , 否则, θ= x -t ( K )d tt A x, Πx ∈5 T K, t ∈[0 ,1 ].若t = 0 ,则x =θ,矛盾于x ( b) =x1收稿日期: 2005Ο04Ο14 .作者简介: 朱传喜( 1956~) , 男, 教授. 基金项目: 国家自然科学基金资助项目( 10461007) ; 江西省自然科学基金资助项目( 0411043) .第 12 期朱传喜 ,等 :关于终值微分方程的解1385θ∈5 T K . 若 t = 1 , 则有θ= x - A x , Π x ∈5 T K , 即A x = x , 矛盾于上面的假设 ( A 在5 T K 上没有不动 点) . 因此 , x = t A x , t ∈( 0 , 1) , Π x ∈5 T K . 由 R 的定义 , 在5 T K 上 , x ≠t A x , t ∈( 0 , 1) , 矛盾.于是 , 根据凝聚算子拓扑度的同伦不变性可知de g ( I - A , T K ,θ) = de g ( h 1 , T K ,θ) = deg ( h 0 , T K ,θ) = de g ( I , T K ,θ) = 1 ≠0 其中 M 1 = [ ‖x 1 ‖+ M ( b - a ) ] e M b - a . 设 x ( t ) ∈()C n [ a , b]满足 x ( t ) =λA x ( t ) , 0 <λ< 1 , 于是由已知条件 ‖f ( t , x ) ‖≤M ( 1 + ‖x ‖) , Π t ∈[ a , b ] , x ∈ R n , 可知‖x ( t ) ‖ = ‖λA x ( t ) ‖ ≤ ‖A x ( t ) ‖ ≤ b‖x 1 ‖+∫‖f ( s , x ( s ) ) ‖d s ≤t b 因此 , 由凝聚算子拓扑度的可解性可知 , 存在 x 3 ∈‖x 1‖ + M ∫( 1 +‖x ( s ) ‖) d s ≤ tT K , 使得( I - A ) x 3 = 0 , 即 A x 3 = x 3 , 即 A 在 T K 中具有不动点. b a ) + M ∫‖x ( s ) ‖d s‖x 1‖+ M ( b - ( 2)t综上所述 , 在任何情形下 , A 在 T K 中都有不动 点 x K , 即 令b∫tφ( t ) = ‖x 1 ‖ + M ( b - a ) + M ‖x ( s ) ‖d s( K = 1 , 2 , 3 , ) , x K ∈ T K ( 1)x K = A x K由式 ( 2) 可知 ‖x ( t ) ‖≤φ( t ) . 又显然 令 S = { x 1 , x 2 , } , A S = { A x 1 , A x 2 , , x K , ,φ′( t ) = - M ‖x ( t ) ‖ ≥- M φ( t )A x K , } . 由式( 1) 可知 S = A S . 根据 A 的凝聚性 可知α( S ) = 0 ( 其中α为非紧性测度) , 否则 ,α( S ) = α( A S ) <α( S ) , 矛盾. 由α( S ) = 0 可知 S 为紧集. 于 即φ′( t ) + M φ( t ) > 0 即是 , 在 S 中 , 存在子列 x K , 使 A x K →x 3 ∈E , 于是 i iφ′( t ) e M t + Mφ( t ) e M t > 0 由 ‖x K ‖≤R + 1得 ‖x 3 →x 3. ‖≤R .x K = A x K iiK即根据 A 的连续性 , 得 x 3 = A x 3 .注 1 与定理 1 相关的不动点问题参见文献[ 6Ο12 ] 定理 2 考察常微分方程的终值问题[φ( t ) eM t ]′t > 0 , Πt ∈[ a , b] 故φ( t ) e M t 是一个增函数 , φ( t ) e M t ≤φ( b ) e M b , a ≤ t ≤b. 所以 d x‖x ( t ) ‖ ≤φ( t )≤φ( b ) e M ( b- t ) ≤φ( b ) e M ( b- a ) =x ∈ R n , t ∈[ a , b]= f ( t , x ) d t( H 1 )a ) ]e M ( b- a ) [ ‖x 1 ‖+ M (b - = M 1x ( b ) = x 1若 f : [ a , b ] ×R n→R n连续 , 并且满足‖f ( t , x ) ‖ ≤M ( 1 + ‖x ‖) Π t ∈[ a , b] , x ∈ R n其中 M 是某正数 , 则问题 ( H 1 ) 必具有属于 C 1 [ a , b ] 的解 x ( t ) , 满足即 ‖x ‖≤M 成立 , 其中1 a ) ]e M ( b- a )M 1 = [ ‖x 1 ‖+ M ( b - 即‖x ‖ = ma x ‖x ( t ) ‖ ≤M 1a ≤t ≤b显然 M 1 有界. 从定理 1 可知 , A 在 C n [ a , b ]中有一 个不动点.因此 , 终值微分方程问题 ( H 1 ) 有一个解 x ∈ a ) ]e M ( b- a )‖x ( t ) ‖ ≤[ ‖x 1 ‖ + M ( b - Π t ∈[ a , b]1 C [ a , b]满足 ‖x ( t ) ‖≤[ ‖x 1 ‖+ M ( b - a ) ] ·e M ( b - a) , Π t ∈[ a , b ] .参考文献 :证明 显然 , 问题 ( H 1 ) 属于 C 1 [ a , b ]的解等价于积 b分方程 x ( t ) = x 1 - ∫f ( s , x ( s ) ) d s 的连续解 , 亦即t b - ∫f ( s , x ( s ) ) d s 在连续函数空间算子 A x ( t ) = x 1郭大均. 非线性泛函分析[ M ] . 济南 : 山东科学技术出版社 , 1985 .Elo e P W , R affo u l Y , Reid D T , et al . Po s itives so l u 2 tio n s of no n li n ea r f u nct io n al diff e rence equatio n s [ J ] . C o m p u t er s and Mat h ematic s wit h Ap p licatio n s , 2001 , 42 (5) :639Ο646 .Cho u ik ha A R. Rema r k o n p erio d ic sol u tio n s of no n 2 linea r o s cillato r s [ J ] . App lied Mat h ematic s L e t t er , 2001 ,14 (8) :963Ο968 .[ 1 ] tC n [ a , b] = { x ( t ) | x ( ·) : [ a , b] → R n 连续} 中的不[ 2 ]动点 ( 注 意 , C n [ a , b] 是 Ba n ac h 空 间 , 其 中 范 数‖x ‖ = ma x ‖x ( t ) ‖) . 易知 , A : C n [ a , b] →C n [ a ,a ≤t ≤bb]是凝聚的.我们证明x ( t) ∈C n [ a , b] , x ( t) = λA x ( t)[ 3 ]0 < λ < 1 ]‖x ‖ ≤M 1西安交通大学学报第39 卷1386[ 4 ]Lo u Ben d o n g. Fixed poi n t s fo r op erato r s in a sp ace of co ntin u o us f unctio n s a nd app licatio n s [ J ] . Pro ceedings of t h e A m erica n Mat h ematical S o ciet y , 1999 ,127 ( 8) :2 259Ο2 264 .Gu o Daj un. Bo unda r y val ue p ro blems fo r i mp ul sive in2 tegro2diff erent ial equatio n s o n un b o unded d o main s in a Ba nach sp ace [ J ] . App lied Mat hematic s a nd Co mp u ta2 tio n ,1999 , 99 (1) :1Ο15 .朱传喜. 随机半闭1Ο集压缩算子的几个定理[J ] .数学学报, 1999 , 42 (3) :501Ο504 .朱传喜,徐宗本. Hil b er t 空间中的一类随机算子方程[J ] .数学学报, 2004 , 47 (4) :641Ο646 .[ 8 ]朱传喜. 关于随机算子方程的随机解[ J ] .数学进展, 1997 , 26 (5) :429Ο434 .Zh u Ch ua n xi , Xu Z o n gben. S o m e t h eo r ems of ra n d o mop erato r equat io n s [ J ] . Inter J Mat h a n d Mat h S ci , 2002 ,30 (9) :511Ο514 .Zh u Ch ua n xi .S o m e t h eo r em s in t h e XΟMΟPN sp ace[J ] . Ap p l Mat h a n d Mech , 2000 , 21 (2) :181Ο184 .Zh u Ch ua n xi . S o m e p r o b lem s in t h e ZΟCΟX sp a ce [ J ] .Ap p l Mat h and Mech , 2002 ,23 (8) :942Ο947 .[ 9 ][ 5 ][ 10 ][ 11 ][ 6 ][ 12 ]朱传喜. 1Ο集压缩型随机算子方程若干定理[ J ] .数学进展, 1998 , 27 (5) :464Ο468 .(编辑杜秀杰) [ 7 ]《西安电子科技大学学报》2005 年第3 期目次大型星载天线展开机构中同步齿轮系防卡滞研究基于凸集模型的多学科耦合系统不确定性分析以改进影像逼真度为约束条件的变换域水印嵌入强度一种结合ML 检测的高性能VΟBL A S T系统基于MO S F E T 失配分析的低压高精度CMO S 带隙基准源镁在钙钛矿型氧敏材料中的作用直扩分层空时结构在下行衰落相关M I MO 中的应用接收端驱动的流媒体组播拥塞控制协议基于衬底驱动技术的亚1V 与温度成正比基准源基于小波变换的多分辨率高维图像检索方法基于四阶累积量的多参数联合估计算法基于分数迟延估计的外辐射源雷达杂波相消算法一种多目标情况下的单脉冲测角方法利用码元约束技术消除O F DM 系统中的限幅噪声基于微扫描的焦平面阵列成像特性研究碳化硅CMO S倒相器温度特性一种基于DΟS 理论的P2 P 网络信任模型基于F P G A 的红外图像目标检测粗糙面电磁散射的小斜率近似方法研究大型目标RCS 的快速计算及分析利用有效的求逆算法快速计算超椭圆曲线标量乘基于有限域的最佳周期交织方法mΟ挠群上一种基于身份的聚合签名方案基于自对准和空气桥工艺的SiG e HB T 研究跟踪及数据中继卫星系统瞄准式干扰的最佳干扰波形基于B P 神经网络的车型分类器彩色电视信号的旁瓣抑制一种针对复值信号的独立分量分析方法基于表单译码的软G MD 算法陈建军,张建国,段宝岩,等(329)曹鸿钧,段宝岩(335) 尹忠海,简剑峰,周利华,等(339) 苏昕,孙永军,易克初(344) 刘帘曦,杨银堂,朱樟明(348) 曹全喜,邓亮雄,杨鹏,等(353) 李勇朝,廖桂生,王峰(357)张冰,徐雅嫣,刘增基,等(362)朱樟明,杨银堂(367) 崔江涛,孙君顶,周利华(370)王兰美,王洪洋,廖桂生(374)俊,水鹏朗,保铮,等(378)赵永波,谷泓,张守宏(383)杨刚,陈媛媛,李玉山(387)王王晓蕊,胡方明,张建奇,等(392)王平,杨银堂,王旭(396)温浩宇,任小龙,徐国华(400) 王艳,鲍建跃,林晓春,等(403) 郭立新,陈建军,韦国晖,等(408) 李建瀛,唐松,刘其中(414) 郝艳华,姜正涛,王育民(418)王莹,王育民(423) 程相国,刘景美,王新梅(427) 刘道广,郝跃,徐世六,等(432)李鹏,姬红兵(435)胡方明,简琴,张秀君(439)孙晓闻,刘立东,吴顺君(443)李小军,楼顺天,张贤达(447)徐朝军,王新梅(452)。
第四章 海面微波散射

n 介质边界面的法向单位矢量, E(r),H(r)
s 介质的本质阻抗,
边界面上的总电磁场强度。
只要求出边界面上的电场和磁场,就能求出散射场。
基尔霍夫近似方法的基本假设是:在表面的任何一 点都产生平面界面的反射。也就是说,将某一局部 区域的表面看成是一个平面。因此,当粗糙面任意 点曲率半径远大于入射波长和粗糙面高度起伏的相 关长度时,采用基尔霍夫近似方法是有效的。
hs xsinsycoss v s h s n s x c o ss c o ss y c o ss s i n s z s i n s
• 求解基尔霍夫方法的矢量表达式的依据是格林
矢量第二定理,该定理表述如下:以封闭面为
边界的无源区内任意一点的散射场,可以用与
表面相切的场来表示,数学表达式如下
对于平面分界面,入射波被反射到镜像方向,因此,对于单 站雷达系统,即用同一个天线进行收、发,则除非是垂直方 向,否则接收不到任何反射波。
海面是不平坦的,其粗糙度谱跨越5个数量级,涌浪swell波长 达几百米,风生的海浪波长从几十米到1厘米左右,而短毛细 波的波长只有几个毫米。
然而,海面的均方根斜率通常是较小的,因此大多数入射波 仍被反射到镜像方向,而海面粗糙度的出现,使得小部分的 入射波散射到其它所有方向,我们尤其关注后向散射方向的 散射波。
另散射场也可以用多个幅度未知的平面波叠加来表示(即傅里叶 变换)。
微扰法的解分为0阶,1阶,2阶,…..
(0)(1 )(2)...
其中0阶解对应平面反射(相干反射),1阶解即Bragg反射机制 (非相干反射),2阶解是对相干反射的最低阶矫正,它是能量守 恒的重要保证。
• 在入射介质中的双基地散射系数是
3.1 经典的粗糙面散射法之一-KA
电磁散射特性研究

方案,并用时域有限差分(FDTD)方法[6]对等离子体隐 身翼面结构进行了优化设计。
1 FDTD迭代公式
各向同性媒质中麦克斯韦旋度方程为:
荦 × 軖H = ε0εr鄣E軑/鄣t + σE軑
(1a)
荦 × E軑 = - μ0 μr鄣軖H/鄣t - σm軖H
(1b)
式中:μ0和ε0分别为真空中的磁导率和介电常数;εr、μr、
第 22 卷 第 4 期 2012 年 12 月
天津职业技术师范大学学报 JOURNAL OF TIANJIN UNIVERSITY OF TECHNOLOGY AND EDUCATION
Vol.22 No.4 Dec. 2012
等离子体隐身翼面的电磁散射特性研究
成 丹,郑宏兴
(天津职业技术师范大学天线与微波技术研究所,天津 300222)
电磁散射计算模型
导读:复合网格法在电磁散射问题中的应用研究,电磁散射问题中的频域有限元算法,电
磁散射的高效混合计算方法,电磁散射问题的有限元分析,电磁散射特性仿真研究,电磁散 射计算模型。
中国学术期刊文辑(2013)
目录
一、理论篇 等离子体隐身翼面的电磁散射特性研究 1 电磁散射问题中的频域有限元算法 5 短切碳纤维电磁散射特性仿真研究 8 二维改进分形海面微波电磁散射计算模型 13 非高斯海面后向电磁散射的小斜率近似方法 19 复合目标电磁散射的高效混合计算方法 24 复合网格法在电磁散射问题中的应用研究 31 基于 POEEC 的各向同性介质薄层涂覆目标电磁散射 34 基于 SIBC 的等离子体薄涂层电磁散射的 FDTD 分析 39 基于基尔霍夫近似的改进分形海面电磁散射特性 48 基于矩量法的机身截面电磁散射特性分析 54 介质粗糙面及其与上方目标的复合电磁散射 60 二、发展篇 介质涂层金属圆柱体有限元法电磁散射特性的分析 63 金属介质涂覆的 S 形扩压器电磁散射特性 64 均匀介质中衍射光栅的电磁散射 73 雷达目标电磁散射特性仿真与测量 78 某型轮式自行突击炮电磁散射场特性与表面电流分布 83 偏心介质柱电磁散射 87 三维时变等离子体目标的电磁散射特性研究 92 双尺度法下改进分形海面电磁散射特性研究 98 水面目标复合电磁散射的并行迭代快速计算 104 指数型分布粗糙地面电磁散射的 FDTD 研究 110
【国家自然科学基金】_高斯粗糙面_基金支持热词逐年推荐_【万方软件创新助手】_20140802
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年 序号 1 2 3 4
2014年 科研热词 粗糙目标 相关函数 平均强度 大气湍流 推荐指数 1 1 1 1
科研热词 高斯粗糙面 高斯介质粗糙面 随机粗糙面 透射系数 脉冲波散射 聚酯薄膜 电磁散射 激光散射 散射系数 微扰法 小斜率近似 基尔霍夫学近似 四阶矩统计特征 双频互相关散射截面 双频互相关函数 双点双频互相关函数 功率展宽 分层介质 光透射
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13
科研热词 粗糙面 矩量法 电磁散射 高斯粗糙面 遮蔽效应 透射电磁波 电磁波散射 无线电物理 并行计算 分形粗糙面 分层介质 信息传递接口 pc集群
推荐指数 2 2 2 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9
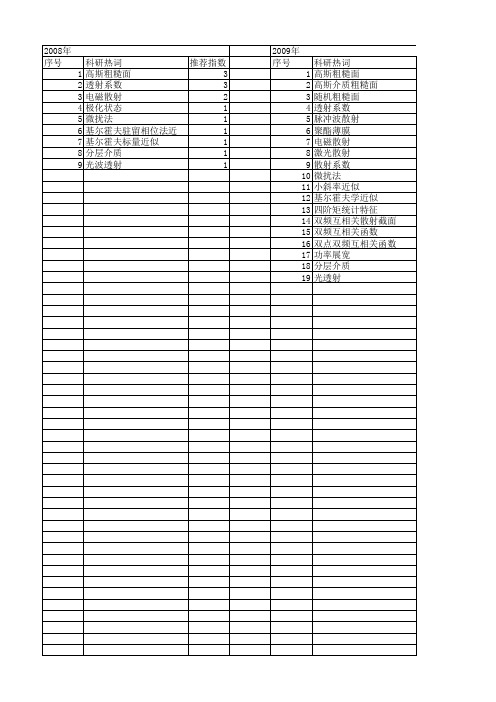
2008年 序号 1 2 3 4 5 6 7 8 9
科研热词 推荐指数 高斯粗糙面 3 透射系数 3 电磁散射 2 极化状态 1 微扰法 1 基尔霍夫驻留相位法近似 1 基尔霍夫标量近似 1 分层介质 1 光波透射 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
科研热词 随机粗糙面 透射系数 退相干 蒙特卡罗方法 粗糙面 粗糙表面 矩量法 相关函数 电磁波透射 激光波束散射 斯托克斯矢量 散射 指数型粗糙面 均方值 合成孔径激光雷达 偏振特性 偏振双向反射分布函数 二阶统计特征
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( ! !% ) ! 1!% ) # &’
’& (" ! ! !% )# ( ! (% , ! 1!% ) *). # ( ’ (% , ! !% ) * . # ( ! (% , ! 1!% ) * ! ] ) & )[ . # ( ! (% , ’ & # &’’ 2 &’% 2 &%% 2 …) ,
-’(
!" 小斜率近似下粗糙面散射截面公式的推导
考虑一单位平面电磁波 !"# [ $! ! ・"]入射到某一维随机粗糙面 " #( $ %)上, 如图 % 所示& 这里的 " # ( %,
& ") , !! # ( ’% % , ’ !" ) , !( # ( ’ (% , ’ (" ) , ’ !" # [ ’& ’ ! # ! + , 是 入 射 波 数& 图 中 入 射 角 为 " ( ) (’ - . ! ! ) ’ !% ] * ’ , , 散射角为 "( &设# " ! . (’ - ) ( ) (’ - . " ( . (’ - ) [ *, +] 是入射场, 散射场 # ( 可用 # 传播矩阵表示
2 &’% ) ,
( &) # & 2 &%% ) &
关于式 ( + )< (() 的计算方法跟扰动理论式一样的, 然而由于包含了变量 8 ( 7) , 而8 ( 7) 是( $ %) 的傅里叶变
" #( $ %)
中, 下面给出 3’ 和 3% 的均值表达式
& % " (%
[ $4 %] . !"# [ . $4 ( $ %) ] * # ) !"# [ ) ( + & ]( ’ ! % ,% !"#
在一般粗糙 面 电 磁 散 射 计 算 当 中, 基尔霍夫近似法 ( Q2 ) 和小扰动近似法 ( 3RS ) 是常用的近似方 法
[ &, !]
. 这两种计算方法都是基于粗糙面统计结构模型, 有各自的适用范围, 因而都有很大局限性, 尤其对掠
[ (] 入射而言这些散射计算方法就更不准确了 . 因此需要寻求不用考虑粗糙面结构也能精确地解决粗糙面电 [ #] 磁散射的理论. 对于这个问题的研究早期有 T>5>E 的全波法 , 近年来还出现了有关数值算法, 如扩展边界
& %+& $ #[ ) $1 $ 2$ $・ , 粗糙面单位法向数由 % ( %) +(% 2 [ $1 ( %) ] ) 来决定, 矩阵 # # 3’ 2 3% 2 这里的 + + +0 # % & ’] [ +] 3& 2 3/ 2 …, 式 (& ) 中的前两项可以表示为
#( ! !% ) # ) ’ ! (% ,
1 !% 1 ’ ! !% ) ! !% ) # &’% (
’& (" ! ! !% )#( ! 1!% ) * ) . #( ! !% ) * . #( ! 1!% ) * ! ] , (7) & ;! [ . #( ’ ! (% , % ! (% , ’ ! (% , % ! (% , ’ ’& (" ! ! !% )#( ! 1!% ) * ) . #( ! !% ) * . #( ! 1!% ) * ! ] ) & [ . #( % ! (% , % ! (% , % ! (% , % ! (% , ’ &
" $( "# $# ! ! ! [ !] 函数的傅里叶变换 4当1 ( *! )满足高斯谱分布的形式时, 式 ( !* )中的积分
收稿日期: !""#$"%$&’ 基金项目: 国家部委预研基金资助项目 ( %&#"("!"("#)*"&&& , %&#++"’"&"#)*"&"& ) ; 高等学校博士点专项基金资助项目 作者简介: 郭立新 ( &’,-$) , 男, 教授.
第 / 期) ) ) ) ) ) ) ) ) ) ) ) ) ) 郭立新等: 粗糙面电磁散射的小斜率近似方法研究
’ !% ) # #( ( ",
% ,’
(%
!"# [ $ ! ( ・"] ・ (%)
(
) , # ( ! (% ,! !% ) # ( ! (% ,! !% ) # ) $ - !’ ("
[ . $ ! ・"] ・ % ,/ !"# (&)
图 %) 一维粗糙面电磁散射示意图
( ", ! !% ) +# ) , +0 " #( $ %) $
( %) ( &) ( /)
1 ’ ! !% ) ! !% ) # &%% (
(()
) ) 通常可以把小斜率近似下粗糙面散射的一阶、 二阶和三阶散射截面写成如下形式 # &’’ ) , # &
( %)
( %’ ) ( %% ) ( %& )
& & 换, ( $ %)存在于指数函数 !"# [ $(・"]5 ! !% ) * # ) . #( ’ ! (% , & ’ !" % 4" & !
& ’ !" % 4" & !
[ $(・"]5 % ,%{!"#
" #( $ %)
} ) ,
(/)
!’ !" % ! !% ) # ,% !"# #( [ $(・"]5 " #( ,7 !"# [ $7%]8 ( 7) [ ’% ! 2% 2 ’% ( )% ) 4 " ] ) , ( - ) % ! (% , $ %) 6 4" & ! 万方数据 & %+& , 其中 4 % # ! !% ) ’ (% , 4 " # ’ !" 2 ’ (" , ’%% 2! #[ ’& ) ( 7 2’ !% ) ) , 01 [ %% 2! ] * ’ ; 这里的 ( # ! ! ) ! ( #( 4 % ,) 4 " )
H:E9:H 9; D5: G:;:E>79O:= HIE8>4: H76J:,L9D5 D5: N9HD>D94 H4>DD:E9;G 4E6HH H:4D96;H 86E D5: P>IHH9>; 46;=I4D9;G E6IG5 HIE8>4: I;=:E D5: 89EHD,H:46;= >;= D59E=$6E=:E HF>77 H76J: >JJE6K9F>D96; 6ND>9;:=. 05: E:HI7DH NM D5: HF>77 H76J: >JJE6K9F>D96; >E: >7H6 46FJ>E:= L9D5 D56H: 68 D5: Q9E455688 >JJE6K9F>D96; L9D5 D5: H5>=6L9;G :88:4D 46;H9=:E:= >;= D5: :KJ:E9F;:D>7 =>D>,L5945 H56LH D5>D D5: HF>77 H76J: >JJE6K9F>D96; 9H F6E: >44IE>D: 86E D5: L567: E:G96; 68 D5: 9;49=:;D >;G7: >;= D5: ;IF:E94>7 E:HI7DH >7H6 H56L G66= >GE::F:;D L9D5 D5: :KJ:E9F:;D>7 =>D> 86E D5: 7>EG: H4>DD:E9;G >;G7:. 7(% 8&+$1: / HF>77 H76J: >JJE6K9F>D96;; Q9E455688 >JJE6K9F>D96;; H5>=6L9;G :88:4D; :7:4DE6F>G;:D94 H4>DD:E9;G
% {
%
}
& %+& ’% ( )% #[ ’& )( ’ (% )7) ] , 01 [ % ( )! ] * ’ , 8 ( 7 )为粗糙表面轮廓 ( $ %)的傅里叶变换& 3’ 可以认为是一阶斜
3& 是三阶斜率函数, 依此类推& 为了简化, 把 3 0 认为是 0 2 % 阶斜率函数2 3!4156 率函数, 3% 是二阶斜率函数,
万方数据
561"+-*": /
C7:4DE6F>G;:D94 H4>DD:E9;G 8E6F D5: E6IG5 HIE8>4: IH9;G D5: HF>77 H76J: >JJE6K9F>D96; 9H
9;@:HD9G>D:=,L5945 G9@:H > HMHD:F>D94 :KJ>;H96; 68 D5: H4>DD:E9;G 4E6HH H:4D96; D5>D 4>; N: 9;D:EJE:D:= >H >
