画法几何_两立体相交
画法几何立体表面的交线

1’
4’
5’
2’
3’
解题步骤
1 分析 截交线的水平投影和 侧面投影已知,正面投影为 双曲线并反映实形;
2 求出截交线上的特殊点Ⅰ
1” 、ⅡⅢ;
3 求出一般点ⅣⅤ ;
4”(5”) 4 光滑且顺次地连接各点,
作出截交线,并且判别可见 性;
5 整理轮廓线。
2”(3”)
24
1 53
点击动画
点击动画
例10 求带缺口圆锥的水平投影和侧面投影。
4 整理轮廓线。
y
a1
4
s
y
2 b
例3 求立体截切后的投影
6
(5)4
1
2 (3)
35
1
6
24
6
5
4
3 1 2 Ⅵ
Ⅴ Ⅳ
Ⅲ
ⅠⅡ
5.1.2 平面与曲面立体相交
曲面立体截交线通常是封闭的平面曲线,或是由曲线和直 线所围成的平面图形或多边形。
截交线
点击动画
截交线
点击动画
1. 平面与圆柱相交
截平面平行于轴线, 交线为平行于轴线的 两条平行直线
1. 表面取点法
表面取点法求作相贯线的一般步骤
(1)分析 首先分析两曲面立体的几何形状、相对大小和 相对位置,进一步分析相贯线是空间曲线,还是处于特殊情况 (平面曲线或直线)。分析两曲面立体对投影面的相对位置, 两曲面立体的投影是否有积聚性,哪个投影有积聚性。分析相 贯线哪个投影是已知的,哪个投影是要求作的。
1’ 6’
2’(3’) 4’(5’)
1”
3” 5” 6”
2” 4”
6 1
5 3
2 4
例11 已知正垂面所截切球的正面投影,求其余两面投影。
画法几何第10章 相贯线

当直线或立体表面的某投影具有积聚性时,则在 具有积聚性的投影上,可得到贯穿点的第一个投影, 再用面上或线上取点法,求作贯穿点的第二投影。
[例1] 求作直线与圆柱的贯穿点。
b' n' (m') a'
a m
n b
[例2] 求垂直线AB,CD与圆锥的贯穿点。
2.利用辅助平面法求贯穿点
1”
பைடு நூலகம்
Pw
6”
2”
Qw
5”
3”
4”
Ⅰ 56
1 4
32
Ⅳ
求圆柱与半球的相贯线
10.5.2 相贯线的特殊情况
特殊情况下,相贯线为平面曲线或直线。
相贯线为圆
相贯线为直线
当两个回转体具有公共轴线时,其表面的相贯线为圆
外切于同一球面的圆锥、圆柱相交时,其相贯线为两条平面曲线—椭圆
特殊位置和形状的相贯线 ----等径正交两圆柱的相贯线
1.相贯线的性质及形状
• 相贯线是两立体表面的共有线;也是相交两立体表面的分界线;相贯 线上的点是两立体表面的共有点;
• 由于立体都有一定的范围,所以相贯线都是封闭的线,一般为封闭的 空间折线或空间曲线;
• 不同的立体以及不同的相贯位置,相贯线的形状也不同--全贯和互贯。
2.求相贯线的方法
求相贯线实质上是求两立体表面一系列共有点,然后依次光滑连接, 并判可性。一般地说这些共有点是一个立体的素线与另一立体表面的交 点,也称为贯穿点。
求曲面立体相贯线的方法有:
1.表面取点法 2.辅助平面法 3.辅助球面法
四、求相贯线的一般步骤
2.求作相贯线上的特殊点。 3.根据需要求出若干个一般点。 4.光滑且顺次地连接各点,作出相贯线,并判别可见性。 5.整理轮廓线。
第十一章 相贯线

画 法 几 何 及 机 械 制 图 . 北 京 航 空 航 天 大 学
例7:求圆柱与圆锥斜交的相贯线
分析 圆柱与圆 锥轴线斜 交,相贯 线的三个 投影均未 知,可利 用辅助球 面法求共 有点; 有点;
画 法 几 何 及 机 械 制 图 . 北 京 航 空 航 天 大 学
2 ' 3 ' 1 '
2 " 3 " 1 "
特殊情况
画 7、组合相贯 、 法 几 何 及 机 械 制 图 . 北 京 航 空 航 天 三个或三个以上的立体相交在一起,称为组合相贯。 三个或三个以上的立体相交在一起,称为组合相贯 组合相贯。 大 相贯线由若干条相贯线组合而成,结合处的点称为结合点 结合点。 学 相贯线由若干条相贯线组合而成,结合处的点称为结合点。
画 法 几 何 及 机 械 制 图 . 北 京 航 空 航 天 大 学
画 法 几 何 及 机 械 制 图 . 北 京 航 空 航 天 大 学
6、两曲面立体的相贯线 、
不同的立体以及不同的相贯位置、相贯线的形状不同。 不同的立体以及不同的相贯位置、相贯线的形状不同。
画 法 几 何 及 机 械 制 图 . 北 京 航 空 航 天 大 学
1) 求两曲面立体的相贯线的方法: 求两曲面立体的相贯线的方法: 表面取点法 辅助平面法 辅助球面法(同心、异心) 辅助球面法(同心、异心) 回转平面法 作图实质是找出相贯的两立体表面的若 实质是找出相贯的两立体表面的 作图实质是找出相贯的两立体表面的若 干共有点的投影 的投影。 干共有点的投影。
画 法 几 何 及 机 械 制 图 . 北 京 航 空 航 天 大 学
画 法 几 何 及 机 械 制 图 . 北 京 航 空 航 天 大 学
画法几何与机械制图第章立体的投影平面与立体表面相交(截交线)
倾斜于轴线
椭圆
例4:求左视图
● ● ●
截交线的 截交线的已知投影? 空间形状? 截交线的侧面投 影是什么形状?
●
● ● ● ●
●
●
●
●
★找特殊点 ★补充中间点 ★光滑连接各点 ★分析轮廓素线的投影
例4:求左视图
★找特殊点 ★找中间点 ★光滑连接各点 ★分析轮廓素线的投影
椭圆的长、短 轴随截平面与圆 柱轴线夹角的变 化而改变。
图3-30
㈢ 圆球表面的截交线
例:求半球体截切后的俯视图和左视图。
两个侧平面与圆球面的 水平面与圆球面的交 交线的投影,在侧视上为 线的投影,在俯视图上 部分圆弧,在俯视图上积 为部分圆弧,在侧视图 聚为直线。 上积聚为直线。
y
二、平面立体的切割与穿孔
例:已知缺口三棱锥的正面投 影,补全它的水平投影和侧面 投影。P55
y
y
★ 空间分析 ★ 投影分析 两个截平面一个是水平面,一个是正垂 ★ 求截交线 注意: 面,都在正面投影中积聚。 ★ 分析棱线的投影 要逐个截平面分析和绘制截交线和 水平截面在水平投影中反映实形,在侧 ★ 检查 尤其注意检查截 截平面之间的交线。 面投影中积聚。 交线投影的类似性
当平面立体只有局部被截切时,先 假想为整体被截切,求出截交线后再
y
y
二. 平面立体的切割与穿孔
已知一个具有正垂的三棱柱穿孔的正六棱 柱的正面投影,补全穿孔六棱柱的水平投 影,作出它的侧面投影。P56
y
y 分析:正垂的三棱柱孔在正投影面上积 聚,三个截面的交线积聚成三角形的三 个顶点。 找到各截面与棱边的交点的正面投影。
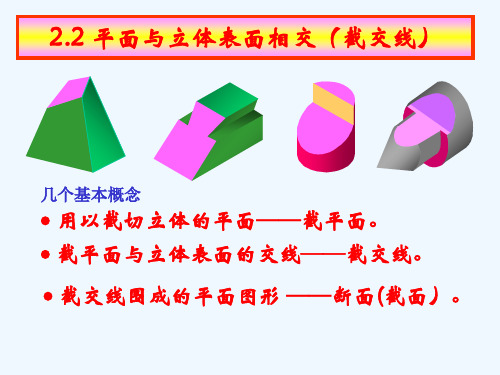
2.2 平面与立体表面相交(截交线)
几个基本概念
画法几何 立体的相贯线

相贯线是立体相交 的公共线投影在平 面上形成交点
相贯线的投影是立 体相交的投影线投 影在平面上形成交 点
相贯线的投影是立 体相交的投影线投 影在平面上形成交 点
相贯线的投影是立 体相交的投影线投 影在平面上形成交 点
相贯线与截面法的联系
相贯线是立体几何中的重要概念表示两个立体相交时产生的公共线。 截面法是研究立体几何的重要方法通过截面可以直观地看到立体的形状和结构。 相贯线与截面法密切相关截面法可以帮助我们更好地理解和分析相贯线。 相贯线与截面法的结合可以更好地解决立体几何中的问题如立体的体积、表面积等。
立体相贯线的应用实例
第四章
圆柱与圆柱的相贯线
相贯线:两个圆柱体相交时其公共 部分的边界线
相贯线的性质:相贯线是圆柱体的 公共边界线也是圆柱体的截面线
添加标题
添加标题
添加标题
添加ห้องสมุดไป่ตู้题
应用实例:两个圆柱体相贯时相贯 线是它们的公共边界线
相贯线的计算:通过计算两个圆柱 体的半径和角度可以计算出相贯线 的长度和位置
投影法需要掌握立体投影的基 本原理和技巧
截面法
截面法原理:通过截面将立体 相贯线转化为平面问题
截面选择:选择合适的截面如 垂直于相贯线的平面
截面求解:在截面上求解相贯 线的投影得到相贯线的方程
相贯线求解:根据截面求解的 结果求解立体相贯线的方程
辅助面法
辅助面法的定义: 通过添加辅助平 面使立体相贯线 在辅助平面上投 影从而求解立体 相贯线
平面相贯线:两个 平面相交形成的相 贯线
曲面相贯线:两个 曲面相交形成的相 贯线
空间相贯线:两个 空间相交形成的相 贯线
组合相贯线:多个 立体相交形成的相 贯线
画法几何及机械制图-两曲面立体表面的交线

b' a' 1'6' 4'
5' 2' 3'
6” (4”)
1” 5”
2”
3”
1
a 5b 6 4
P4H
(3)
2
作图: (1)选辅助面(正平面); (2)求斜圆柱轮廓线与半 球的交点; (3)求中间点;
§8-3 两曲面立体表面的交线
二、辅助平面法
例3 求圆球与斜圆柱偏交时的相贯线。
d'
c'
1'6' 4' 5' 2' 8'
最小球面半径球心或者是
球心到两回转面轮廓交点中较
近的一个交点的距离,或者是
O
内切于较大的回转面的球面半
径,如图中的R2。
§8-3 两曲面立体表面的交线
三、辅助球面法
辅助球面法求立体表面的相贯线的适用条件:
1.参与相贯的必须都是回转体,一般要求轴线相交; 2.两轴线同时平行于某一投影面。
例4 用球面法求相交两圆柱的相贯线。
圆柱体上 的交线
§8-3 两曲面立体表面的交线
共有点
圆台上 的交线
二、辅助平面法
辅助平面的选择:应使该平面与两立体表面交线的投影简 单易画(如投影为圆或多边形),而且两条交线要相交。
§8-3 两曲面立体表面的交线
二、辅助平面法
基本回转体上的辅助平面选择:
1.圆柱体:
平行或垂直于轴线;
2.圆锥体:
d'
c'
1'6' 4' 5' 2' 8'
3'7'
6” (4”8)”
画法几何之直线与曲面立体相交基本知识
本节提要: (1)直线或曲面立体表面的投影有积聚性时相交
(2)直线或曲面立体表面的投影都无积聚性时相交
1、直线与曲面立体相交 (1)直线或曲面立体表面的投影有积聚性时相交 如图所示,求作直线AB与轴线垂直于侧面的圆柱的 贯穿点,并表明直线的投影及其可见性。
a' c' d' d" c"
a' a' c'
d' b'
b'
a
b
aPH
c
d
b
如图所示,求作正平线AB与球的贯穿点,并表明直 线AB的投影及其可见性。
a' a' c'
d' b'
b'
a
b
aPH
c
d
b
a'b' c'd' b d
a'b' c'd' b d
b
s
a
c a
s
c a
s
用纬圆法解题
用素线法解题
如图所示,求作直线AB与圆锥的贯穿点,并表明直 线的投影及其可见性。
s' s' s'
Байду номын сангаас
a'b'
a'b' c'd' b d
a'b' c'd' b d
b
s
a
c a
s
c a
s
用纬圆法解题
用素线法解题
(2) 直线和曲面立体表面的投影都无积聚性时相交 常用通过该直线的辅助截平面截切曲面立体,则直线
20春学期《画法几何及土木建筑制图X》在线平时作业3【100分答案】
20春学期《画法几何及土木建筑制图X》在线平时作业3------------------------1.图样上标注尺寸的起止符号( )形式。
A.只有箭头一种B.只有短斜线C.<p>有箭头和斜短线两种</p>D.没有规定的正确答案:["C"]2.当平面在某两个投影面的投影具有积聚性时,该平面一定是()。
A.那个投影面的垂直面B.那个投影面的平行面C.一般位置平面D.某个投影面的垂直面,或某个投影面的平行面。
正确答案:"[B]"3.在投影图上,直线的投影画(),投影连线画()。
A.细实线,细实线B.细实线,粗实线C.粗实线,粗实线D.粗实线,细实线正确答案:["D"]4.画剖面图时,图上应标注出:A.剖切位置B.剖切符号C.剖面图名称D.ABC正确答案:["D"]5.点的直角坐标(X,Y,Z),分别代表空间点到投影面()的距离。
A.V,H,WB.H,V,WC.W,H,VD.W,V,H正确答案:["D"]6.工程图样上所注的尺寸,如没注明计量单位时,一定是以()为单位的。
A.㎜B.㎝C.㎡D.㎞正确答案:["A"]7.房屋工程图按专业不同,一般包括()。
A.建筑施工图、结构施工图、总平面图B.建筑施工图、结构施工图、设备施工图C.建筑施工图、水电施工图、设备施工图D.建筑施工图、装修施工图、水电施工图正确答案:["B"]8.国家标准中规定绘制工程图样时,图框画()。
A.粗实线B.细实线C.中实线D.没有要求正确答案:["A"]9.绘制结构平面布置图的常用比例为()。
A.1:5、1:10B.1:10、1:20C.1:50、1:100D.1:200、1:500正确答案:["C"]10.楼梯平面图上应该用()表示表示剖切位置。
画法几何_同济大学中国大学mooc课后章节答案期末考试题库2023年
画法几何_同济大学中国大学mooc课后章节答案期末考试题库2023年1.若两条直线空间垂直,且其中有一条直线平行于某一投影面,则两直线在该投影面上的投影一定相互垂直。
参考答案:正确2.在辅助投影面法中,新的投影面选择可以是任意位置。
参考答案:错误3.用辅助投影面法,一般位置平面变成投影面平行面需要几次变换?参考答案:24.工程上常用的投影图类型包括:参考答案:透视投影_轴测投影_标高投影_多面正投影5.要判断两平面平行,必须作两对相交直线对应平行,如所作第一对直线即不平行,即可断定两平面不平行。
参考答案:正确6.平面将三棱柱截断后的截断面形状,可能为:参考答案:五边形_三角形_四边形7.的平面,其W面投影反映其实形。
参考答案:平行W面8.两平面立体相交,在全贯的情况下,应该将被贯的立体作为被动体,找出主动体的穿过被动体的棱线相贯点,即可用同面相连的方法求出交线。
参考答案:错误9.两平面相交,平面边界转折点的可见性一定相反。
参考答案:错误10.平面截切棱柱,截切方式若是全部穿透棱线,则截平面多边形的边数与棱线数相一致。
参考答案:正确11.用辅助投影面法,一般位置直线经过一次变换就可以变成投影面垂直线。
参考答案:错误12.任意位置的截平面与球面交得的截交线形状为:参考答案:圆或圆弧13.直线与平面相交,直线于交点两侧的可见性一定相反。
参考答案:正确14.两特殊位置平面相交,其交线可能是()参考答案:垂直线、平行线或一般位置线15.过一已知点可以作多少个平面垂直于一已知直线?参考答案:116.直线与平面及平面与平面相交共有___ __种情况。
参考答案:617.投影变换的目的是什么?参考答案:有利于图示和图解18.一直线垂直于平面中的任意一条H面平行线,则直线就垂直于该平面。
参考答案:错误19.点的Y坐标,即点到的距离。
参考答案:V面20.投影面上的特殊点,有两个坐标值为0。
参考答案:错误21.圆、椭圆、抛物线、双曲线都可以从正圆锥面上截得,因此它们统称为圆锥曲线。
《画法几何》课程教学大纲
《画法几何》课程教学大纲课程名称:画法几何Descriptive Geometry课程编码:6311Z002 学分:2 总学时:36说 明【课程简介】本课程是土木类专业学生必修的专业核心课程。
它研究解决空间几何问题以及绘制和阅读工程图样的理论和方法。
由于生产和科学研究对计算机图形技术提出了日益迫切的多方面的要求,本课程在适应这一新形势方面更加成为重要的基础。
它的任务主要是(1)研究在平面上表达空间形体的图示法;(2)研究在平面上解答空间形体的图解法。
画法几何是具有系统理论、抽象性较强的一门学科。
学习时要注意理论联系实际,而且必须完成一定数量的习题。
【课程性质】专业核心课【适用专业】土木类专业【教学目标】培养学生的绘图和读图能力,并通过实践,培养他们的空间想象能力。
【先修课程要求】无【能力培养要求】培养学生的绘图和读图能力,空间想象能力。
解决空间几何元素本身及其相互的定位问题和度量问题。
【学习总量】总学时36学时,其中理论36学时。
【教学方法与环境要求】课堂讲授、辅导课、习题课,多媒体课件与网络教学,组织讨论、辅导答疑,课外作业和考试等计划安排。
(1)课堂讲授36学时;(2)课堂针对相关问题进行讨论。
(随教学进程);(3)课内、课外做练习;(4)课下辅导答疑,包括作业总结辅导、相关专题辅导;(5)配合课堂讲授,配有模型;(6)本课程教学内容应适当结合实际,以提高学生对本课程理论联系实际的认识。
【学时分配】学 时 安 排序号 内 容 理论课时 实验课时实践课时习题课时小计1 投影的基础知识2 22 点、直线和平面投影 6 63直线与平面、平面和平面的相对位置6 64 投影变换 4 45 立体的投影14 146 轴测投影 4 4总 计 36 36【教材与主要参考书】教 材:《土木工程制图》,贾洪斌,高等教育出版社,2005,第四版参考书:【1】《画法几何及土木工程制图》,唐人为,东南大学出版社,2002【2】《画法几何》,同济大学教研室,同济大学出版社,1996大纲内容第一章 投影的基本知识【教学目的和要求】了解:投影的概念及投影法的分类;理解:三面投影图的形成;掌握:正投影的几何性质;运用:正投影的绘制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相贯线的分类
平 —— 平相贯
按立体形状
平 —— 曲相贯
曲 —— 曲相贯
相贯线的分类
按相对位置
全贯
互贯
全贯 —— 一立体完全穿入另一立体,相贯线有两条。
互贯 —— 两立体互相贯穿,相贯线只有一条。
求相贯线的一般步骤
分析两立体(形状、大小、相对位置) 定性判别相贯线的形状 求特殊点
例
求两三棱柱的相贯线。
l m 1 3 4 r 2 6 2 (6) r 5 n l(n) m
q
q (5) 1
3 p 4
p
k
l q(r) 1 (2) 5 (6)
n
3 m (4) p k
例
求两三棱柱的相贯线。
l m 1 3 4 r 2 6 2 (6) r 5 n l(n) m
工程实例
2.8.4 两曲面立体表面相交
封闭的空间曲线
相贯线的形状
平面曲线 直线
2.8.4 两曲面立体表面相交
求出两曲面立体表面上的 一系列共有点,依次连成光滑 的曲线,并判别可见性。
2.8.4 两曲面立体表面相交
表面取点法
相贯线的求法
辅助平面法 辅助球面法
表面取点法(积聚性法)
2.8 两立体相交
2.8.1 2.8.2 2.8.3 2.8.4
概述 两平面立体表面相交 平面立体和曲面立体表面相交 两曲面立体表面相交
2.8.1 概述
两立体相交,通常称两立体相贯。它 们表面产生的交线称为相贯线。
相贯线的一般性质
相贯线在立体的表面上 —— 表面性
相贯线是两立体表面的共有线 —— 共有性 相贯线通常是封闭的 —— 封闭性
相贯线的变化趋势
◆相交二立体的大小变化时,相贯线将发生变化。
◆相交二立体的相对位置变化时,相贯线也将发生变化。
例 画出两圆柱相贯线,并补画侧面投影。
例 画出两圆柱相贯线,并补画侧面投影。
例 画出两圆柱相贯线,并补画侧面投影。
几种常见的相贯形式
几种常见的相贯形式
多立体表面相交
多立体表面相交又称组合相贯。
q
q (5) 1
3 p 4
p
l q(r) 1 (2) 5 (6)
n
3 m (4) p
例
求房屋表面的交线。
例
求房屋表面的交线。
2.8.3 平面立体和曲面立体表面相交
相贯线的形状
平面曲线段或 直线段的集合
相贯线的求法
截交线法
2.8.3 平面立体和曲面立体表面相交
解题前应先分析平面立 体有哪些棱面参与了相贯, 以避免作图的盲目性。
分析: ◇该立体由哪些简单形体组合 而成?它们的表面是什么面? ◇哪些面之间产生交线?交线形 状如何?如何求出?
分别求出各段相贯线或截交 线以及它们的结合点,组合起来 即为所求的相贯线。
例 求作物体表面的相贯线
1
1
4 1
6 2
5
3
例 求圆柱和圆锥的相贯线。
2 5
(2) (6) 4 1 3 (5)
3 (4)
1
(6)
4 1
6 2 5
3
相贯线的特殊情况
◆两柱面轴线平行,相贯线是一对平行直线;
两锥面共顶,相贯线是一对相交直线。
◆两回转面共轴线,相贯线为垂直于回转轴线的圆。
◆两曲面立体同时外切于一球面时,相贯线为平面曲线。
例
求三棱柱与圆锥的相贯线。
s s
a
a b c
c
b
s
c
a b
例
求四棱柱与圆锥的相贯线。
4 2 (5)
1 3 5
4
1 2 (3)
5 4 1 2 3
圆锥薄壳基础
c a b
c a (b)
c a b
圆锥薄壳基础
c a b
c a (b)
c a b
轮廓线上的点
曲线的特征点 极限位置点
转折点
求一般点 判别可见性,连线 整理轮廓线
2.8.2 两平面立体表面相交
相贯线的形状
封闭的空间折线
平面多边形
2.8.2 两平面立体表面相交
相贯线的求法
截交线法
贯穿点法
2.8.2 两平面立体表面相交
解题前应先分析两立体共有哪些棱面、棱线 及底边参与了相贯,以避免作图的盲目性。
两曲面立体相交,如果其中一个立体的某投影 有积聚性,则相贯线的该投影是已知的,其它投影 可以用曲面立体表面上取点的方法求出。
例
求作两圆柱的相贯线。
1
5
(7)
3 (4)
6
(8)
2 4
7 (8)
1
(2) (6) 3
5
4
7
1
实实相贯 —— 两外表面相交
实空相贯 —— 外表面和内表面相交
空空相贯 —— 两内表面相交
工程实例
例
求两圆柱的相贯线。
3 (5)
7
4 (6)
3 (4) 5 (6)
7
(1)
(2)
1 (2)
1
2
5
6
3
7
4
例
求两圆柱的相贯线。
4 (6)
3 (5)
7
4 (6)
3 (4) 5 (6)
求交线的交点,即为相贯线上的点
例
求圆柱和圆锥的相贯线。
1
1
3 (4)
2
4 2
3
4 (2) 1
3
例
求圆柱和圆锥的相贯线。
1
1
3 (4)
2
4 2
3
4 (2) 1
3
圆锥穿圆柱孔
例 求圆柱和半球的相贯线。
3
5 (6) (4)
2 4
(6) (2) (5) 3
例
求三棱柱与三棱锥的相贯线。
l 1 s 3 2 6 c m 4 n
a
5
b
连线规则:
只有位于甲立体同一表
n b
l
2 s 1 3 m 4 6 c
5 a
面上,同时又位于乙立体 同一表面上的两点才能相 连。
同一棱线上的两点不能
相连。
例
求三棱柱与三棱锥的相贯线。
l 1 s 3 2 6 c m 4 n
a
5
b
可见性判别:
n b
l
2 s 1 3 m 4 6 c
5 a
只有既在甲立体表面上 可见,同时又在乙立体表面 上可见,交线才可见。即只 有两立体的可见表面相交, 交线才可见。
例
求三棱柱与三棱锥的相贯线。
l 1 s 2 3 4 m 5 c n
a
k
6 b n
l b 2 s 1 m 3(4) k c 5 6 a
7
(1)
(2)
1 (2)
1
2
5
6
3
7
4
辅助平面法
辅助平面法的基本出发点 —— 三面共点原理
选择辅助平面的原则:应使辅助平面与两个曲面立 体表面交线的投影都为最简单的线条(直线或圆)。
辅助平面法作图步骤:
作辅助平面
—— 一般为投影面平行面或投影面垂直面。
分别求辅助平面与两曲面立体表面的交线
