河南省洛阳市第八中学2015-2016学年高一数学下学期第二次段考(5月)试题(无答案)
2015-2016学年度洛阳市第八中学高一上学期第二次段考
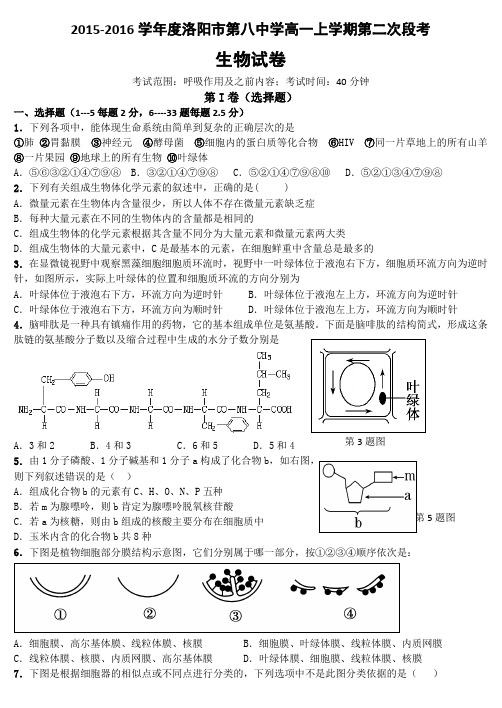
2015-2016学年度洛阳市第八中学高一上学期第二次段考生物试卷考试范围:呼吸作用及之前内容;考试时间:40分钟第I 卷(选择题)一、选择题(1---5每题2分,6----33题每题2.5分)1.下列各项中,能体现生命系统由简单到复杂的正确层次的是①肺 ②胃黏膜 ③神经元 ④酵母菌 ⑤细胞内的蛋白质等化合物 ⑥HIV ⑦同一片草地上的所有山羊 ⑧一片果园 ⑨地球上的所有生物 ⑩叶绿体A .⑤⑥③②①④⑦⑨⑧B .③②①④⑦⑨⑧C .⑤②①④⑦⑨⑧⑩D .⑤②①③④⑦⑨⑧2.下列有关组成生物体化学元素的叙述中,正确的是( )A .微量元素在生物体内含量很少,所以人体不存在微量元素缺乏症B .每种大量元素在不同的生物体内的含量都是相同的C .组成生物体的化学元素根据其含量不同分为大量元素和微量元素两大类D .组成生物体的大量元素中,C 是最基本的元素,在细胞鲜重中含量总是最多的3.在显微镜视野中观察黑藻细胞细胞质环流时,视野中一叶绿体位于液泡右下方,细胞质环流方向为逆时针,如图所示,实际上叶绿体的位置和细胞质环流的方向分别为A .叶绿体位于液泡右下方,环流方向为逆时针B .叶绿体位于液泡左上方,环流方向为逆时针C .叶绿体位于液泡右下方,环流方向为顺时针D .叶绿体位于液泡左上方,环流方向为顺时针4.脑啡肽是一种具有镇痛作用的药物,它的基本组成单位是氨基酸。
下面是脑啡肽的结构简式,形成这条肽链的氨基酸分子数以及缩合过程中生成的水分子数分别是A .3和2B .4和3C .6和5D .5和45.由1分子磷酸、1分子碱基和1分子a 构成了化合物b,如右图,则下列叙述错误的是( )A .组成化合物b 的元素有C 、H 、O 、N 、P 五种B .若m 为腺嘌呤,则b 肯定为腺嘌呤脱氧核苷酸C .若a 为核糖,则由b 组成的核酸主要分布在细胞质中D .玉米内含的化合物b 共8种6.下图是植物细胞部分膜结构示意图,它们分别属于哪一部分,按①②③④顺序依次是:A .细胞膜、高尔基体膜、线粒体膜、核膜B .细胞膜、叶绿体膜、线粒体膜、内质网膜C .线粒体膜、核膜、内质网膜、高尔基体膜D .叶绿体膜、细胞膜、线粒体膜、核膜7.下图是根据细胞器的相似点或不同点进行分类的,下列选项中不是此图分类依据的是( ) 第第3题图A.是否与能量转换有关B.有无膜结构C.是否含有色素D.是否普遍存在于动植物细胞中8.对染色体和染色质的描述错误的是A.染色质是细胞核内易被碱性染料染成深色的物质B.染色质和染色体的形态结构、化学成分完全相同C.染色体或染色质的主要成分是DNA和蛋白质D.染色体或染色质存在于真核细胞的细胞核中9.紫色洋葱外表皮细胞的色素存在于细胞的A.细胞膜B.细胞质基质C.液泡D.细胞核10.浸泡在一定浓度KNO3溶液中的洋葱表皮细胞,发生了质壁分离后又出现质壁分离复原,与质壁分离复原相关的细胞器有 ( )A.液泡和细胞膜B.细胞核和核糖体C.液泡和线粒体D.叶绿体和细胞核11.下列关于细胞膜的流动性和选择透过性的叙述,不正确的是( )A.流动性的基础是组成细胞膜的磷脂分子和蛋白质分子大多可以运动B.选择透过性的基础是细胞膜上的载体蛋白和磷脂分子具有特异性C.细胞的胞吞和胞吐体现了细胞膜的流动性D.钾离子通过主动运输的形式进入细胞体现了细胞膜的选择透过性12.下列有关细胞中“一定”的说法正确的是①光合作用一定在叶绿体中进行②有氧呼吸一定在线粒体中进行③没有细胞结构的生物一定是原核生物④以RNA为遗传物质的生物一定是原核生物⑤所有生物的多肽一定是在核糖体上合成⑥有中心体的生物一定不是高等植物A.①③⑤⑥ B.②④⑥ C.④⑤ D.⑤⑥13.下列能够正确表示细胞膜结构的是()14.下面能发生质壁分离作用的一组细胞是()①食用的糖醋蒜的细胞②蚕豆叶的表皮细胞③洋葱鳞片叶外表皮细胞④人的口腔上皮细胞⑤蓝藻细胞A.①⑤ B.②③⑤ C.①②③④⑤ D.②③15.单纯的磷脂分子在水中可以形成双层脂分子的球形脂质体(如图),它载入药物后可以将药物送入靶细胞内部,下列关于脂质体的叙述正确的是A.在a处嵌入脂溶性药物,利用它的流动性将药物送入细胞B.在b处嵌入脂溶性药物,利用它的流动性将药物送入细胞C.在a处嵌入水溶性药物,利用它与细胞膜融合的特点将药物送入细胞D.在b处嵌入水溶性药物,利用它与细胞膜融合的特点将药物送入细胞16.下列说法中,与生物膜发现史不一致的是()A.欧文顿在实验基础上提出膜是由脂质组成的B.荷兰科学家用丙酮从人的红细胞中提取脂质,在空气—水界面上铺展成单分子层,测得单分子层面积为红细胞表面积的2倍。
河南省洛阳市第八中学学高一历史下学期第二次段考(月)试题(无答案)-课件

河南省洛阳市第八中学2015-2016学年高一历史下学期第二次段考(5月)试题(无答案)一、选择题 (每小题2分,32小题,共64分)1.英国著名历史学家汤因比在1932年出版的《国际事务概览》第一页就提出了这样一个问题:“这个伟大、古老、一直是成功的社会的成员们正在自问:西方生命及其成长的长期历程,是不是在他们的时代很可能将到终点?”这主要是他对当时什么状况的担忧()A.1929~1933年经济危机B.经济“滞胀”局面C.苏联的日益壮大D.法西斯主义盛行2.下图改编自保罗·肯尼迪《大国的兴衰》。
据此判断,下列说法正确的是()A.德国开始步入欧洲强国之列 B.经济危机使英国丧失了世界霸主地位C.苏联成功渡过经济危机实现了工业化 D.美国在世界经济中仍占据着关键地位3.1929~1933年,首先发生在美国的经济危机迅速席卷了整个资本主义世界,主要资本主义国家工业生产迅速大幅度下降,如下表所示。
出现这一现象的关键因素是()1929~1933A.美国是资本主义世界的经济霸主 B.资本主义的基本矛盾激化C.殖民地人民的抵制 D.资本主义世界市场已经最终形成4..富兰克林·罗斯福是美国历史上第一位利用“炉边谈话”向人民阐释其施政方针的总统。
在“新政”期间,罗斯福“炉边谈话”的内容最有可能的是()A.主张推行计划经济模式 B.阐释福利国家所带来的弊端C.解读《全国劳工关系法》 D.展望“新经济”时代的奇迹5.罗斯福曾说:“低收入的工人是我们人数最多的消费集团,可是今天他们却无法维持像样的生活水准,不能购买食品、衣服和其他必需品以保持我们的工厂和农场充分运转。
”为此,他采取的直接措施是()A.整顿银行,恢复银行正常信贷活动 B.调整工业生产,争取供需平衡C.实行社会救济和以工代赈 D.调节农业生产,稳定农产品价格6.1933年底,一位国会议员在纪念林肯诞辰124周年的演说中说:“我已经看到一位独裁者正在成长,他已使希特勒、墨索里尼十分嫉妒,私营企业的独立已成为往事,个人自由不过是记忆而已。
河南省洛阳市第八中学高一数学3月段考试题

河南省洛阳市第八中学2015-2016学年高一数学3月段考试题一、选择题:(本大题共10小题,每小题4分,共40分。
) 1、 化简0sin 600的值是( )A .0.5B .0.5-C .32 D .32- 2、若角α的终边过点(sin30o,-cos30o),则sin α等于( ) A .21 B .-21C .-23D .-333、若点(sin cos ,tan )P ααα-在第一象限,则在[0,2)π内α的取值范围是( )A .35(,)(,)244ππππU B.5(,)(,)424ππππUC.353(,)(,)2442ππππUD.33(,)(,)244ππππU4、方程1sin 4x x π=的解的个数是( )A.5B.6C.7D.8 5、下列不等式中,正确的是( ) A .tan513tan 413ππ<,B .sin )7cos(5ππ->,C .sin(π-1)<sin1o,D .cos )52cos(57ππ-<6、函数cos tan y x x = (22π<<π-x )的大致图象是( )7、已知ABC ∆是锐角三角形,sin sin ,cos cos ,P A B Q A B =+=+则( ) A.P Q < B.P Q > C.P Q = D.P 与Q 的大小不能确定 8、函数|tan |x y =的周期和对称轴分别为( ) A. )(2,Z k k x ∈=ππ, B. )(,2Z k k x ∈=ππ,C. )(,Z k k x ∈=ππ,D. )(2,2Z k k x ∈=ππ 9、设()f x 是定义域为R ,最小正周期为32π的函数,若cos (0)()2sin (0)x x f x x x ππ⎧-≤<⎪=⎨⎪≤≤⎩,则15()4f π-的值等于( ) A.1 B .2 C.0 D.2- x x o A 2π-2π x x o B 2π-2π x xo D 2π-2π x x oC2π-2π 1 -1 1 -1 -1 1 -1 110、设函数()sin ()3f x x x π⎛⎫=+∈ ⎪⎝⎭R ,则()f x ( ) A .在区间2736ππ⎡⎤⎢⎥⎣⎦,上是增函数B .在区间2π⎡⎤-π-⎢⎥⎣⎦,上是减函数 C .在区间84ππ⎡⎤⎢⎥⎣⎦,上是增函数D .在区间536ππ⎡⎤⎢⎥⎣⎦,上是减函数二、填空题:(本大题共4小题,每小题4分,共16分。
河南省洛阳八中11-12学年高一数学上学期第二次段考【会员独享】

河南省洛阳八中高一上学期第二次段考(数学)一、选择题:(10*4=40)1. 设有两条直线α、b 和两个平面α、β,则下列命题中错误的是A .若α//α,且a //b ,则b α⊂或//b aB .若//a b ,且//,a b αβ⊥,则//αβC .若//αβ,且,,a b αβ⊥⊥则//a bD .若a b ⊥,且//,a α则b α⊥2.有一个几何体的三视图如下图所示,这个几何体应是一个A .棱台B .棱锥C .棱柱D .都不对3.正三棱锥S ABC -的侧棱长和地面边长相等,如果E 、F 分别为SC ,AB 的中点,那么异面直线EF 与SA 所成角为 A .90° B .60°C .45°D .30°4.右图是正方体的平面展开图,在这个正方体中:①BM 与DE 平行 ②CN 与BE 是异面直线 ③CN 与BM 成60°角 ④DM 与BN 垂直以上四个命题中,正确的是 A .①②③ B .②④C .②③④D .③④5.一个水平放置的平面图形的斜二测直观图是一个底角为45°腰和上底边卫1的等腰梯形的面积是A .122 B .22 C .2D .21+6.给出下列关于互不相同的直线,,m n l 和平面,αβ的四个命题:(1),,m l αα⊂I 点A m ∉,则l 与m 不共面;(2)l 、m 是异面直线,//,//l m αα,且,n l n m ⊥⊥,则n α⊥;(3)若//,//,//l m αβαβ,则//l m ;(4)若,,l m a l m α⊂⊂=I 点A ,//,//l m ββ,则//αβ,则//εβ,其中为错误的命题是( )个A .1个B .2个C .3个D .4个7.设a 、b 是两条不同的直线,αβ、是两个不同的平面,则下列四个命题:①若,,,a b a b αα⊥⊥⊄则//b α; ②若//,,a ααβ⊥则a β⊥; ③若,,a a ββ⊥⊥则//a α或a α⊂ ④若,,a b a b αβ⊥⊥⊥,则αβ⊥ 其中正确命题的个数为 A .0B .1C .2D .38.定点P 不再ABC ∆所在平面内,过P 作平面a ,使ABC ∆的三个顶点到a 的距离相等,这样的平面共有A .1个B .2个C .3个D .4个9.下列各图是正方体或正四面体,P ,Q ,R ,S 分别是所在棱的中点,这四个中不共面得一个图是10.(天津卷10)如图,在长方体1111ABCD A B C D -中,16,4,3AB AD AA ===,分别过BC ,11A D 的两个平行截面将长方体分成三部分,其体积分别记为11111113AEA DFD B E B C F C V V V V -===g若123::1:4:1V V V =,则截面11A EFD 的面积为A .410B .83C .413D .16二、填空题:(4*4=16)11.已知a 、b 为不垂直的异面直线,α是一个平面,则a、b在α上的射影有可能是:①两条平行直线②两条互相垂直的直线③同一条直线④一条直线及其外一点在一面结论中,正确结论的编号是 (写出所有正确结论的编号) 12.[06山东·理]如图,在等腰梯形ABCD 中,AB=2DC=2,60oDAB ∠=,E 为AB 的中点,将ADE ∆与BEC ∆分别沿ED 、EC 向上折起,使A 、B 重合于点P ,则三棱锥P-DCE 的外接球的体积为 。
河南省洛阳市第八中学1516学年度高一下学期第二次段考

河南省洛阳市第八中学2015—2016学年度下学期第二次段考高一物理试题一、选择题(每题4分,选对但不全得2分)1.关于元电荷的理解,下列说法正确的是( )A.元电荷就是电子B.元电荷是表示跟一个电子所带电荷量数值相等的电荷量C.元电荷就是质子D.物体所带电量只能是元电荷的整数倍2.关于摩擦起电和感应起电的实质,下列说法中正确的是( )A.摩擦起电现象说明机械能可以转化为电能,也说明通过做功可以创造出电荷B.摩擦起电说明电荷可以从一个物体转移到另一个物体C.感应起电说明电荷可以从物体的一部分转移到另一个部分D.感应起电说明电荷可以从带电的物体转移到原来不带电的物体3.关于点电荷的说法,正确的是()A.只有体积很小的带电体才能看作点电荷B.体积很大的带电体一定不能看成点电荷C.当两个带电体的大小及形状对它们之间的相互作用力的影响可忽略时,这两个带电体可看作点电荷D.一切带电体都可以看成是点电荷4、.真空中两个相同的金属小球A和B,带电荷量分别为Q A=2×10-8C和Q B=4×10-8C,相互作用力为F.若将两球接触后再放回原处,则它们之间的作用力将变为()A.9F/8B.FC.8F/9D.2F/35. 关于库仑定律的公式F=kQ1Q2/r2,下列说法中正确的是()A.当真空中两个电荷间距离r→∞时,它们间的静电力F→0B.当真空中两个电荷间距离r→0时,它们间的静电力F→∞C.当两个电荷间的距离r→∞时,库仑定律的公式就不适用了D.当两个电荷间的距离r→0时,电荷不能看成是点电荷,库仑定律的公式就不适用了6、一平行板电容器中存在匀强电场,电场沿竖直方向。
两个比荷(即粒子的电荷量与质量之比)不同的带正电的粒子a和b,从电容器边缘的P点(如图)以相同的水平速度射入两平行板之间。
测得a和b与电容器的撞击点到入射点之间的水平距离之比为1∶2。
若不计重力,则a和b的比荷之比是A.1∶2 B.1∶1C.2∶1 D.4∶17、如图所示,实线是一簇未标明方向的由点电荷Q产生的电场线,若带电粒子q(|Q|>>|q|)由a运动到b ,电场力做正功。
河南省洛阳八中2013-高一下学期第一次月考数学试题

INPUT XIF X>=0 THEN Y=X^2-1 ELSEY=2*X^2-5 END IF PRINT Y END第3题图一、选择题(每题5分)1.下列给出的赋值语句中正确的是: ( ) A 、3=A B 、M=-M C 、B=A=2 D 、x+y=02.用二分法求方程的近似根,精确度为,则当型循环的终止条件是()A .B.C.D.3.三位七进制的数表示的最大的十进制的数是 ( )A.322B.332C.342D.3524.若右图程序输出的y=3,则输入的x 为()A .2B. -2 C .2或-2D. 85.右图给出的是计算0101614121+⋅⋅⋅+++的值的一个程序框图,其中判断框内应填入的条件是()A .i<=100B .i>100C .i>50D .i<=506.我校高中生共有2700人,其中高一级900人,高二级1200人,高三级600人,现采取分层抽样法抽取容量为135的样本,则高一、高二、高三各级抽 取的人数分别为 ()A.45,75,15B. 45,45,45C.30,90,15D. 45,60,307.用秦九韶算法计算多项式654323567983512)(x x x x x x x f ++++-+=在4-=x 时的值时,3V 的值为()A. -845B. 220C. -57D. 348.100个个体分成10组,编号后分别为第1组:00,01,02,…,09;第2组:10,11,12,…,19;…;第10组:90,91,92,…,99.现在从第k 组中抽取其号码的个位数与()1k m +-的个位数相同的个体,其中m 是第1组随机抽取的号码的个位数,则当5m =时,从第7组中抽取的号码是()第5题图甲 乙 8 0 8 5 6 0 1 2 4 7 8 9 7 6 5 3 2 2 1 7 8 9 2 3 A .71 B .61 C .75 D .659.若样本,,21x x …,n x 的平均数、方差分别为x 、2s ,则样本531+x ,532+x ,…,53+n x 的平均数、方差分别为()A .x 、2s B .53+x 、2s C .53+x 、29s D .53+x 、2)53(+s 10.某大学随机取30名学生参加环保知识测试得分(十分制)如图所示,假设得分值的中位数为,众数,平均值,则()A . B.C.D.二、填空题(每题5分)11.某学校有教师200人,男学生1200人,女生1000人,用分层抽样的方法从全体学生中抽取一个容量为n 的样本,若女生抽取80人,则n=_____________12.程序框图如下:第12题图第13题图如果上述程序运行的结果为S =132,那么判断框中应填入13.下图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则平均得分高的运动员是_____________14.5280和2155的最大公约数是__________________________. 答题卡:11:__________________________________ 12: ___________________________________ 13:___________________________________ 14:___________________________________ 三、解答题(最后一题14分,其余12分)15.求和1!2!3!...20!s =++++(n !=1*2*3*…*(n-1)*n )(1)________________(2)________________(3)________________16.求100991431321211⨯+⋅⋅⋅+⨯+⨯+⨯的值.将程序补充完整并将与其功能相同的当型程序框图画出来! 程序: S = 0 I = 1 DOS=______(1)______是否5 5 85 4 4 0 41 42 44 AB35937 36 38 39 40 43 459 5 4 47 3 3 3 53 11 2 4 4 5 7 0 1 1 3 0 2 5 2 0________(2)_________ LOOP UNTIL ___(3)____ PRINT S END(1)________________(2)________________(3)________________17.某良种培育基地正在培育一种小麦新品种A ,将其与原有的一个优良品种B 进行对照 试验,两种小麦共种植了34亩,所得亩产数据(单位:千克)如下 (I )用茎叶图处理现有的数据,有什么优点?(II )通过观察茎叶图,对品种A 与B 的亩产量及其稳定性进行比较,写出统计结论。
河南省洛阳八中2012-2013学年高一12月段考数学试题 Word版含答案
洛阳市第八中学高一年级2012-2013学年第二次月考(考试时间:90分钟,满分100分)一、选择题(本大题共10小题,每小题5分,共50分)1、已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.则该几何体的体积为( )(A )48 (B )64 (C )96 (D )192 2.棱长都是1的三棱锥的表面积为( )B.3.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( )A .25πB .50πC .125πD .都不对4、已知正方体外接球的体积是323π,那么正方体的棱长等于 ( )(A) (B)3 (C)3 (D)35、若l 、m 、n 是互不相同的空间直线,α、β是不重合的平面,则下列命题中为真命题的是( )A .若//,,l n αβαβ⊂⊂,则//l nB .若,l αβα⊥⊂,则l β⊥ C. 若,//l l αβ⊥,则αβ⊥ D .若,l n m n ⊥⊥,则//l m 6、如图,在正方体1111ABCD A BCD -中,EFGH ,,,分别为1AA ,AB ,1BB ,11B C 的中点,则异面直线EF 与GH 所成的角等于( ) A.45° B.60° C.90° D.120° 7.已知两个平面垂直,下列命题 ①一个平面内的已知直线必垂直于另一个平面的任意一条直线; ②一个平面内的已知直线必垂直于另一个平面的无数条直线;③一个平面内的任一条直线必垂直于另一个平面;④过一个平面内任意一点作交线的垂线,则垂线必垂直于另一个平面. 其中正确的个数是( ) A.3 B.2 C.1 D.0 8、如图长方体中,AB=AD=23,CC 1=2,则二面角C 1—BD —C 的大小为( )A.30° B .45° C .60° D .90°9、平面α与平面β平行的条件可以是( )A.α内有无穷多条直线与β平行;B.直线a//α,a//βA F DBC GE 1BH 1C1D 1AA BC D A 1B 1C 1D 1C.直线a α⊂,直线b β⊂,且a//β,b//αD.α内的任何直线都与β平行 10、在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是A 、23 B 、76 C 、45D 、56二、填空题(本大题共4小题,每小题5分,共20分)11.已知直线b//平面α,平面α//平面β,则直线b 与β的位置关系为 . 12.正方体的内切球和外接球的半径之比为____________.13如图,△ABC 是直角三角形,∠ACB=︒90,PA ⊥平面ABC ,此图形中有 个直角三角形14. 将正方形ABCD 沿对角线BD 折成直二面角A -BD -C ,有如下四个结论:(1)AC ⊥BD ;(2)△ACD 是等边三角形 (3)AB 与平面BCD 所成的角为60°;(4)AB 与CD 所成的角为60°。
河南省洛阳八中高一数学上学期12月月考试题(含解析)
2015-2016学年河南省洛阳八中高一(上)12月月考数学试卷一、选择题(60分)1.直线l:ax+y﹣2﹣a=0在x轴和y轴上的截距相等,则a的值是()A.1 B.﹣1 C.﹣2或﹣1 D.﹣2或12.M,N在圆C:x2+y2+2x﹣4y=0上,且点M,N关于直线3x+y+a=0对称,则a=()A.﹣1 B.﹣3 C.3 D.13.将长方体截去一个四棱锥后,得到的几何体的直观图如图所示,则该几何体的俯视图为()A.B.C.D.4.已知直线l的倾斜角为135°,直线l1经过点A(3,2)和B(a,﹣1),且直线l1与直线l垂直,直线l2的方程为2x+by+1=0,且直线l2与直线l1平行,则a+b等于()A.﹣4 B.﹣2 C.0 D.25.等腰梯形ABCD,上底CD=1,腰AD=CB=,下底AB=3,以下底所在直线为x轴,则由斜二侧画法画出的直观图A′B′C′D′的面积为()A.B.C.D.26.已知圆C经过点A(5,1),B(1,3)两点,圆心在x轴上,则C的方程是()A.(x﹣2)2+y2=50 B.(x+2)2+y2=10 C.(x+2)2+y2=50 D.(x﹣2)2+y2=107.已知正方体的棱长为2,则该正方体外接球的体积为()A.B.4πC.4πD.8.设点A(﹣2,3),B(3,2),若直线ax+y+2=0与线段AB没有交点,则a的取值范围是()A.(﹣∞,﹣]∪[,+∞) B.(﹣,)C.[﹣,] D.(﹣∞,﹣]∪[,+∞)9.若a,b,c是直角三角形的三边(c为斜边),则圆x2+y2=4被直线ax+by+c=0所截得的弦长等于()A.1 B.2 C.3 D.210.设曲线C的方程为(x﹣2)2+(y+1)2=9,直线l的方程x﹣3y+2=0,则曲线上的点到直线l的距离为的点的个数为()A.1 B.2 C.3 D.4二、填空题(30分)11.已知点P(3,2)与点Q(1,4)关于直线l对称,则直线l的方程为.12.若直线(m+2)x+3my+1=0与直线(m﹣2)x+(m+2)y﹣3=0互相垂直,则m的值为.13.已知圆C:(x﹣a)2+(y﹣2)2=4(a>0)及直线l:x﹣y+3=0,当直线l被C截得弦长为时,则a= .14.直线y=x+b与曲线有且有一个公共点,则b的取值范围是.15.有下列命题:①有两个面平行,其余各面都是平行四边形的几何体为棱柱;②有一个面为多边形,其余各面都是三角形的几何体为棱锥;③用一个平面去截棱锥,底面和截面之间的部分组成的几何体叫棱台;④若球的直径为2a,则球的表面积为4πa2;⑤各侧面都是正方形的四棱柱一定是正方体.正确的命题序号为.三、解答题(60分)16.已知点A(3,3)、B(5,2)到直线l的距离相等,且直线l经过两直线l1:3x﹣y﹣1=0和l2:x+y﹣3=0的交点,求直线l的方程.17.过点(4,﹣3)作圆C:(x﹣3)2+(y﹣1)2=1的切线,求此切线的方程.18.已知直线l平行于直线3x+4y﹣7=0,并且与两坐标轴围成的三角形的面积为24,求直线l的方程.19.设定点M(﹣3,4),动点N在圆x2+y2=4上运动,以OM,ON为两边作平行四边形MONP (O为坐标原点),求点P的轨迹.2015-2016学年河南省洛阳八中高一(上)12月月考数学试卷参考答案与试题解析一、选择题(60分)1.直线l:ax+y﹣2﹣a=0在x轴和y轴上的截距相等,则a的值是()A.1 B.﹣1 C.﹣2或﹣1 D.﹣2或1【考点】直线的截距式方程.【专题】计算题.【分析】先求出直线在两个坐标轴上的截距,由在两个坐标轴上的截距相等解方程求得a 的值.【解答】解:由直线的方程:ax+y﹣2﹣a=0得,此直线在x轴和y轴上的截距分别为和2+a,由=2+a,得a=1 或 a=﹣2,故选 D.【点评】本题考查直线在两坐标轴上的截距的定义,待定系数法求参数的值.2.M,N在圆C:x2+y2+2x﹣4y=0上,且点M,N关于直线3x+y+a=0对称,则a=()A.﹣1 B.﹣3 C.3 D.1【考点】直线与圆的位置关系.【专题】直线与圆.【分析】由题意可得,圆心(﹣1,2)在直线3x+y+a=0上,从而解得a的值.【解答】解:由于M,N在圆C:x2+y2+2x﹣4y=0上,且点M,N关于直线3x+y+a=0对称,则圆心(﹣1,2)在直线3x+y+a=0上,故有﹣3+2+a=0,解得a=1,故选:D.【点评】本题主要考查直线和圆的位置关系,判断圆心(﹣1,2)在直线3x+y+a=0上,是解题的关键,属于基础题.3.将长方体截去一个四棱锥后,得到的几何体的直观图如图所示,则该几何体的俯视图为()A.B.C.D.【考点】简单空间图形的三视图.【专题】计算题.【分析】根据三视图的特点,知道俯视图从图形的上边向下边看,看到一个正方形的底面,在底面上有一条对角线,对角线是由左上角都右下角的线,得到结果.【解答】解:俯视图从图形的上边向下边看,看到一个正方形的底面,在度面上有一条对角线,对角线是由左上角到右下角的线,故选C.【点评】本题考查空间图形的三视图,考查俯视图的做法,本题是一个基础题,考查的内容比较简单,可能出现的错误是对角线的方向可能出错.4.已知直线l的倾斜角为135°,直线l1经过点A(3,2)和B(a,﹣1),且直线l1与直线l垂直,直线l2的方程为2x+by+1=0,且直线l2与直线l1平行,则a+b等于()A.﹣4 B.﹣2 C.0 D.2【考点】直线的倾斜角;直线的一般式方程与直线的平行关系.【专题】计算题;方程思想;定义法;直线与圆.【分析】先求出l的斜率,利用垂直关系可得l1的斜率,由斜率公式求出a 的值,由l1∥l2 得,﹣ =1,解得b值,可得结果.【解答】解:∵直线l的斜率为tan135°=﹣1,l1⊥l,∴l1的斜率为1,∴,∴a=0,∵l1∥l2,∴l2的斜率为1,∴,∴b=﹣2,∴a+b=﹣2,故选:B.【点评】本题考查两直线平行、垂直的性质,斜率公式的应用.5.等腰梯形ABCD,上底CD=1,腰AD=CB=,下底AB=3,以下底所在直线为x轴,则由斜二侧画法画出的直观图A′B′C′D′的面积为()A.B.C.D.2【考点】斜二测法画直观图.【专题】转化思想;数形结合法;空间位置关系与距离.【分析】根据题意,求出原图形的面积,再求出它的直观图的面积即可.【解答】解:如图所示,,梯形ABCD的高为1,面积为,∴它的直观图的面积为2×=.故选:A.【点评】本题考查了斜二测画法直观图的面积与原图形面积的应用问题,是基础题目.6.已知圆C经过点A(5,1),B(1,3)两点,圆心在x轴上,则C的方程是()A.(x﹣2)2+y2=50 B.(x+2)2+y2=10 C.(x+2)2+y2=50 D.(x﹣2)2+y2=10 【考点】圆的标准方程.【专题】计算题.【分析】根据垂径定理可得弦AB的垂直平分线必然过圆心,故利用线段中点坐标公式求出AB的中点坐标,由A和B的坐标求出直线AB的斜率,根据两直线垂直时斜率的乘积为﹣1求出线段AB垂直平分线的斜率,由求出的斜率与AB的中点坐标得出线段AB的垂直平分线方程,又圆心在x轴上,令求出的直线方程中y=0,求出x的值,可确定出圆心C的坐标,再由A和C的坐标,利用两点间的距离公式求出|AC|的长,即为圆C的半径,由圆心和半径写出圆C的标准方程即可.【解答】解:∵A(5,1),B(1,3),∴线段AB的中点坐标为(,),即(3,2),直线AB的斜率k AB==﹣,∴线段AB垂直平分线的方程为y﹣2=2(x﹣3),即y=2x﹣4,又圆心在x轴上,∴令y=0,得到2x﹣4=0,即x=2,∴圆心C坐标为(2,0),∴圆的半径r=|AC|==,则圆C的方程为(x﹣2)2+y2=10.故选D【点评】此题考查了圆的标准方程,涉及的知识有:线段的中点坐标公式,两直线垂直时斜率满足的关系,直线的点斜式方程,一次函数与坐标轴的交点,两点间的距离公式,以及垂径定理的运用,根据题意确定出圆心C的坐标是解本题的关键.7.已知正方体的棱长为2,则该正方体外接球的体积为()A.B.4πC.4πD.【考点】球的体积和表面积;球内接多面体.【专题】规律型;函数思想;空间位置关系与距离.【分析】求出外接球的半径,然后求解球的体积.【解答】解:正方体的外接球直径为正方体的体对角线,∴2R=a=2∴R=.∴.故选:C.【点评】本题考查正方体的外接球的体积的求法,考查计算能力.8.设点A(﹣2,3),B(3,2),若直线ax+y+2=0与线段AB没有交点,则a的取值范围是()A.(﹣∞,﹣]∪[,+∞) B.(﹣,)C.[﹣,] D.(﹣∞,﹣]∪[,+∞)【考点】两条直线的交点坐标.【专题】作图题;转化思想;数形结合法.【分析】直线ax+y+2=0过定点(0,﹣2),直线ax+y+2=0与线段AB没有交点转化为过定点(0,﹣2)的直线与线段AB无公共点,作出图象,由图求解即可.【解答】解:直线ax+y+2=0恒过点M(0,﹣2),且斜率为﹣a,∵k MA==﹣,k MB==,由图可知:﹣a>﹣且﹣a<,∴a∈(﹣,),故选B.【点评】本题考点是两直线的交点坐标,考查直线与线段无公共点时参数的范围,此题常采用的技巧是借助图象求参数的取值范围,本题直线ax+y+2=0形式简单,作答时易想不到这也是一个直线系方程,从而解不出定点致使题目无从下手.9.若a,b,c是直角三角形的三边(c为斜边),则圆x2+y2=4被直线ax+by+c=0所截得的弦长等于()A.1 B.2 C.3 D.2【考点】直线与圆的位置关系.【专题】方程思想;数形结合法;直线与圆.【分析】由题意可得圆心和半径,结合勾股定理和点到直线的距离和圆的弦长公式可得.【解答】解:∵x2+y2=4的圆心为(0,0),半径为2,又由勾股定理可得a2+b2=c2,即c=,∴圆心(0,0)到直线ax+by+c=0的距离,∴弦长=,故选:D.【点评】本题考查直线和圆的位置关系,涉及点到直线的距离公式和圆的弦长公式,属基础题.10.设曲线C的方程为(x﹣2)2+(y+1)2=9,直线l的方程x﹣3y+2=0,则曲线上的点到直线l的距离为的点的个数为()A.1 B.2 C.3 D.4【考点】圆与圆的位置关系及其判定.【专题】直线与圆.【分析】求出圆心坐标,利用圆心到直线的距离与条件之间的关系即可得到结论.【解答】解:由(x﹣2)2+(y+1)2=9,得圆心坐标为C(2,﹣1),半径r=3,圆心到直线l的距离d=.∴要使曲线上的点到直线l的距离为,∴此时对应的点位于过圆心C的直径上,故有两个点.故选:B.【点评】本题主要考查直线和圆的位置关系的应用,利用点到直线的距离公式是解决本题的关键.二、填空题(30分)11.已知点P(3,2)与点Q(1,4)关于直线l对称,则直线l的方程为x﹣y+1=0 .【考点】与直线关于点、直线对称的直线方程.【专题】计算题.【分析】求出PQ的中点,PQ的斜率,推出对称轴的斜率,利用点斜式方程求出对称轴方程.【解答】解:点P(3,2)与点Q(1,4)关于直线l对称,所以PQ的中点坐标为:(2,3),PQ的斜率为:,所以对称轴的斜率为:1,所以对称轴方程为:y﹣3=x﹣2,即:x﹣y+1=0.故答案为:x﹣y+1=0.【点评】本题是基础题,考查对称问题,直线方程的求法,考查计算能力.12.若直线(m+2)x+3my+1=0与直线(m﹣2)x+(m+2)y﹣3=0互相垂直,则m的值为或﹣2..【考点】直线的一般式方程与直线的垂直关系.【专题】直线与圆.【分析】由垂直关系可得(m+2)(m﹣2)+3m(m+2)=0,解方程可得.【解答】解:∵直线(m+2)x+3my+1=0与直线(m﹣2)x+(m+2)y﹣3=0互相垂直,∴(m+2)(m﹣2)+3m(m+2)=0,即(m+2)(m﹣2+3m)=0,解得m=或﹣2故答案为:或﹣2【点评】本题考查直线的一般式方程与直线的垂直关系,属基础题.13.已知圆C:(x﹣a)2+(y﹣2)2=4(a>0)及直线l:x﹣y+3=0,当直线l被C截得弦长为时,则a= .【考点】直线与圆相交的性质.【专题】计算题.【分析】由题意可得圆心C(a,2)半径r=2,则圆心(a,2)到直线x﹣y+3=0得距离d==,在Rt△CBM中由勾股定理可得,d2+BM2=BC2结合a>0可求【解答】解:由题意可得圆心C(a,2)半径r=2则圆心(a,2)到直线x﹣y+3=0的距离d==Rt△CBM中由勾股定理可得,d2+BM2=BC2∵a>0∴或a=(舍去)故答案为:【点评】本题主要考查了直线与圆相交的弦的应用,出了此类问题一般有两个方法:①直接利用弦长公式求解,该方法思路清晰但需要一定的计算②利用本题中的解法,结合弦长及弦心距及半径三者之间的关系进行求解.14.直线y=x+b与曲线有且有一个公共点,则b的取值范围是.【考点】直线和圆的方程的应用.【专题】数形结合;解题方法.【分析】直线y=x+b是一条斜率为1,截距为b的直线;曲线是一个圆心为(0,0),半径为1的右半圆.它们有且有一个公共点,做出它们的图形,则易得b的取值范围.【解答】解:直线y=x+b是一条斜率为1,截距为b的直线;曲线变形为x2+y2=1且x≥0显然是一个圆心为(0,0),半径为1的右半圆.根据题意,直线y=x+b与曲线有且有一个公共点做出它们的图形,则易得b的取值范围是.【点评】(1)要注意曲线是一个圆心为(0,0),半径为1的右半圆.始终要注意曲线方程的纯粹性和完备性.(2)它们有且有一个公共点,做出它们的图形,还要注意直线和曲线相切的特殊情况.15.有下列命题:①有两个面平行,其余各面都是平行四边形的几何体为棱柱;②有一个面为多边形,其余各面都是三角形的几何体为棱锥;③用一个平面去截棱锥,底面和截面之间的部分组成的几何体叫棱台;④若球的直径为2a,则球的表面积为4πa2;⑤各侧面都是正方形的四棱柱一定是正方体.正确的命题序号为④.【考点】命题的真假判断与应用.【专题】综合题;转化思想;综合法;简易逻辑.【分析】对5个命题分别进行判断,即可得出结论.【解答】解:有两个面平行,其余各面是相邻的公共边都相互平行的平行四边形的几何体叫棱柱,故①错误;有一个面是多边形,其余各面都是有公共顶点三角形的几何体叫棱锥,故②错误用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台,故③错误;若球的直径为2a,半径为a,则球的表面积为4πa2,故④正确;所有侧面都是正方形的四棱柱不一定是正方体,如底面是菱形时,此时的四棱柱不是正方体,∴⑤错误.故答案为:④.【点评】本题考查命题的真假判断,考查学生分析解决问题的能力,知识综合性强.三、解答题(60分)16.已知点A(3,3)、B(5,2)到直线l的距离相等,且直线l经过两直线l1:3x﹣y﹣1=0和l2:x+y﹣3=0的交点,求直线l的方程.【考点】直线的一般式方程与直线的平行关系;两条直线平行的判定;直线的点斜式方程;直线的两点式方程.【专题】规律型;直线与圆.【分析】根据A、B在直线的同侧与异侧两种情况求解,在同侧时,利用直线平行则斜率相等求直线的斜率,从而求出直线方程;在异侧时,判定直线过线段的中点,利用两点式求直线方程.【解答】解:解方程组得交点P(1,2).(1)若A、B在直线L的同侧,则L∥AB,K AB==﹣,∴直线的方程是:y﹣2=﹣(x﹣1),即x+2y﹣5=0.(2)若A、B分别在直线L的异侧,则直线L过线段AB的中点(4,),∴直线L的两点式方程是,即x﹣6y+11=0.综(1)(2)知直线L的方程是x+2y﹣5=0或x﹣6y+11=0.【点评】本题考查直线方程的点斜式、两点式、一般式及直线平行的条件.17.过点(4,﹣3)作圆C:(x﹣3)2+(y﹣1)2=1的切线,求此切线的方程.【考点】圆的切线方程.【专题】直线与圆.【分析】设过P点的圆的切线为y+3=k(x﹣4),它与圆心(3,1)的距离等于半径,建立方程,求出k,即可求过P点的圆的切线方程.【解答】解:设过P点的圆的切线为y+3=k(x﹣4),即kx﹣y﹣4k﹣3=0它与圆心(3,1)的距离等于半径,故=1.解得,k=,过P点的圆的切线方程:15x+8y﹣36=0当k不存在即过(4,﹣3)与x轴垂直的直线方程:x=4.故过P点的圆的切线方程为15x+8y﹣36=0或x=4.【点评】本题给出圆方程,求圆在P点处的切线方程,着重考查了圆的标准方程和直线与圆的位置关系等知识点,属于基础题.18.已知直线l平行于直线3x+4y﹣7=0,并且与两坐标轴围成的三角形的面积为24,求直线l的方程.【考点】直线的一般式方程与直线的平行关系.【专题】直线与圆.【分析】设直线l的方程为:3x+4y+m=0,分别令x=0,解得y=﹣;y=0,x=﹣.利用l 与两坐标轴围成的三角形的面积为24,可得=24,解得m即可.【解答】解:设直线l的方程为:3x+4y+m=0,分别令x=0,解得y=﹣;y=0,x=﹣.∵l与两坐标轴围成的三角形的面积为24,∴=24,解得m=±24.∴直线l的方程为3x+4y±24=0.【点评】本题考查了相互平行的直线斜率之间的关系、直线的截距意义,考查了计算能力,属于基础题.19.设定点M(﹣3,4),动点N在圆x2+y2=4上运动,以OM,ON为两边作平行四边形MONP (O为坐标原点),求点P的轨迹.【考点】轨迹方程.【专题】计算题.【分析】先假设点P,N的坐标,利用向量的加法,找出两点坐标之间的关系,再利用动点N在圆x2+y2=4上,即可求得点P的轨迹方程,从而可得点P的轨迹【解答】解:设P(x,y),N(x0,y0)则=(﹣3,4),=(x0,y0),=(x,y)∵∴(x,y)=(x0﹣3,y0+4)∴x=x0﹣3,y=y0+4∴x0=x+3,y0=y﹣4∵点N(x0,y0)在圆x2+y2=4上,∴(x+3)2+(y﹣4)2=4由O,M,N三点共线时,N()或N()∴x≠﹣且x≠﹣∴P的轨迹是以(﹣3,4)为圆心,2为半径的圆(去掉两个点).【点评】本题重点考查代入法求轨迹方程,解题的关键是寻找动点坐标之间的关系,区分轨迹与轨迹方程.。
数学-高一-河南省洛阳八中高一(下)3月段考数学试卷
2015-2016学年河南省洛阳八中高一(下)3月段考数学试卷一、选择题:(本大题共10小题,每小题4分,共40分.)1.化简sin600°的值是()A.0.5 B.﹣0.5 C.D.﹣2.若角α的终边过点(sin30°,﹣cos30°),则sinα等于()A.B.﹣C.﹣D.﹣3.若点P(sinα﹣cosα,tanα)在第一象限,则在2kπ﹣,2kπ0,2π)内α的取值范围是()A.* B.C. D.【考点】正弦函数的单调性;象限角、轴线角;正切函数的单调性.【分析】先根据点P(sinα﹣cosα,tanα)在第一象限,得到sinα﹣cosα>0,tanα>0,进而可解出α的范围,确定答案.【解答】解:∵故选B.4.方程的解的个数是()A.5 B.6 C.7 D.8【考点】正弦函数的图象;根的存在性及根的个数判断.【分析】先在同一坐标系中分别作出函数的图象,根据函数y1=sinπx,的周期性和对称性,数形结合即可得图象交点个数,即方程的根的个数【解答】解:在同一坐标系中分别作出函数的图象如图,当x=±4.5时,>1,故由图可知函数的图象的交点在y轴左边三个交点,右边三个交点,再加上原点,共计7个即方程的解的个数是7故选C5.下列不等式中,正确的是()A.tan<tam B.sin>cos(﹣)C.sin(π﹣1)<sin1°D.cos<cos(﹣)【考点】正切函数的单调性.【分析】A利用诱导公式化简>0,==﹣tan<0,即可比较B:利用诱导公式对函数化简,然后结合y=sinx在(0,)上单调递增即可比较C:先利用诱导公式化简已知函数,然后结合y=sinx在(0,)上单调性可比较D:由诱导公式可得,,,即可比较【解答】解:A:>0,==﹣tan<0则,故A错误∵=,而y=sinx在(0,)上单调递增,且∴sin即,故B错误C:由于y=sinx在(0,)上单调递增,且,则sin(π﹣1)=sin1>sin1°,故C错误D:,∴,故D正确故选D6.函数y=cosx|tanx|(﹣<x<)的大致图象是()A. B.C.D.【考点】函数的图象.【分析】化简函数的解析式,然后判断函数的图象即可.【解答】解:﹣<x<⇒cosx>0,故函数y=cosx|tanx|=|sinx|,函数y=cosx|tanx|(﹣<x<)的大致图象是:B.故选:B.7.已知△ABC是锐角三角形,P=sinA+sinB,Q=cosA+cosB,则()A.P>Q B.P<QC.P=Q D.P与Q的大小不能确定【考点】两角和与差的正弦函数;正弦函数的单调性.【分析】先化简P﹣Q=(sinA+sinB)﹣(cosA+cosB)=2cos(sin﹣2cos),然后根据锐角三角形得出sin>2cos,cos>0从而得出结论.【解答】解:P﹣Q=(sinA+sinB)﹣(cosA+cosB)=2sin cos﹣2cos cos=2cos(sin﹣cos)由于是锐角三角形A+B=180°﹣C>90°所以>45°sin>2cos0<A,B<90°所以﹣45°<<45°cos>0综上,知P﹣Q>0.P>Q故选:A.8.函数y=|tanx|的周期和对称轴分别为()A.π,x=(k∈Z)B.,x=kπ(k∈Z)C.π,x=kπ(k∈Z)D.,x=(k∈Z)【考点】正切函数的图象.【分析】利用正切函数的周期性以及它的图象的对称性,得出结论.【解答】解:对于函数y=|tanx|,它的周期和y=tanx的周期一样,也是π.它的图象的对称轴方程为x=,k∈Z.故选:A.9.设f(x)是定义域为R,最小正周期为的函数,若,则等于()A.B.1 C.0 D.【考点】三角函数的化简求值.【分析】先根据函数的周期性可以得到=f()=f(),再代入到函数解析式中即可求出答案.【解答】解:∵,最小正周期为=f()=f()=sin =故选A.10.设函数,则f(x)()A.在区间上是增函数B.在区间上是减函数C.在区间上是增函数D.在区间上是减函数【考点】函数的图象与图象变化;正弦函数的图象.【分析】结合正弦型函数和对折变换的性质,我们画出函数的图象,数形结合分析出函数的单调性,然后逐一分析四个答案,即可得到结论.【解答】解:函数图象如图所示:由图可知函数在区间上是增函数故选A二、填空题:(本大题共4小题,每小题4分,共16分.)11.设扇形的周长为8cm,面积为4cm2,则扇形的圆心角的弧度数是2.【考点】扇形面积公式.【分析】设扇形的圆心角的弧度数为α,半径为r,弧长为l,面积为S,由面积公式和周长可得到关于l和r的方程组,求出l和r,由弧度的定义求α即可.【解答】解:S=(8﹣2r)r=4,r2﹣4r+4=0,r=2,l=4,|α|==2.故答案为:2.12.函数y=f(cosx)的定义域为(k∈Z),则函数y=f(x)的定义域为.【考点】函数的定义域及其求法.【分析】复合函数y=f(cosx)中,自变量为x,(k∈Z)是指x的取值范围.复合函数y=f (cosx)中,令cosx=u,则函数为y=f(u),u的值域为复合函数的定义域.【解答】解:令u=cosx,则函数为y=f(u)∵x∈(k∈Z)∴cosx∈∴u∈∴函数y=f(x)的定义域为故答案为:13.已知f(x)是以π为周期的偶函数,且时,f(x)=1﹣sinx,则当时,f(x)=1﹣sinx.【考点】函数解析式的求解及常用方法.【分析】先由偶函数求出x∈时f(x)的解析式,再利用函数是以π为周期的函数得到x∈hslx3y3h,3π﹣,00,0,﹣,0,3π﹣,0﹣﹣,2(x﹣)+0,﹣3+2kπ, +2kπ+4kπ, +4kπhslx3y3h.(k ∈Z)2016年10月21日。
河南省洛阳市强基联盟2023-2024学年高一下学期5月联考数学试题(含解析)
洛阳强基联盟高一5月联考数学一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.工人师傅在检测椅子的四个“脚”是否在同一个平面上时,只需连接对“脚”的两条线段,看它们是否相交,就知道它们是否合格.工人师傅运用的数学原理是( )A.两条相交直线确定一个平面B.两条平行直线确定一个平面C.四点确定一个平面D.直线及直线外一点确定一个平面2.已知直线与平面没有公共点,直线,则a 与b 的位置关系是( )A.平行B.异面C.相交D.平行或异面3.下列说法中错误的是()A.棱台的上、下底面是相似且对应边平行的多边形B.用一个平行于圆锥底面的平面去截圆锥可得到圆台C.直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥D.在圆柱的上、下底面的圆周上各取一点,则这两点的连线不一定是圆柱的母线4.某城市有学校700所,其中大学20所,中学200所,小学480所,现用分层抽样方法从中抽取一个容量为70的样本进行某项调查,则应抽取中学数为( )A.70B.20C.48D.25.如图所示,在直角坐标系中,已知,,,,则四边形的直观图面积为()A. B. C.6.在长方体中,为的中点,在中,,,,则( )A.1B.2C.3D.47.某商业集团董事长想了解集团旗下五个超市的销售情况,通知五个超市经理把最近一周每天的销售金额统计上报,要求既要反映一周内每天销售金额的多少,又能反映一周内每天销售金额的变化情况和趋势,则最好选用的统计图表为()a αb α⊂()1,0A ()1,2B -()1,0C -()1,2D -ABCD 1111ABCD A B C D -M AB 1CMD △1CM MD ⊥4CD =13DD =AD =A.频率分布直方图B.统计表C.扇形统计图D.折线统计图8.图1是唐朝著名的风鸟花卉纹浮雕银杯,它的盛酒部分可以近似地看作半球与圆柱的组合体(如图2).设这种酒杯内壁的表面积为,半球的半径为3cm ,若半球的体积不小于圆柱体积,则S 的取值范围是()A. B. C. D.二、选择题:本题共3小题,每小题6分,共18分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
洛阳市第八中学高一段考数学试卷
一、选择题:本大题共10个小题,每小题4分,共40分.
1、下列程序语句正确的是( )
A.输出语句PRINT 4A =
B.输入语句 INPUT 3x =
C.赋值语句 *3A A A A =+-
D.赋值语句 55a =
2、为支援西部教育事业,从某校118名教师中随机抽取16名教师组成暑期西部讲师团.若先用简单随机抽样从118名教师中剔除6名,剩下的112名再按系统抽样的方法进行,则每人入选的可能性( )
A .不全相等
B .都相等,且为859
C .均不相等
D .都相等,且为17
3、下列说法正确的是( ).
A .甲、乙两人做游戏;甲、乙两人各写一个数字,若是同奇数或同偶数则甲胜,否则乙胜,这个游戏
公平
B .做n 次随机试验,事件A 发生的频率就是事件A 发生的概率
C .某地发行福利彩票,回报率为47%,某人花了100元买该福利彩票,一定会有47元的回报
D .试验:某人射击中靶或不中靶,这个试验是古典概型
4、在一次随机试验中,三个事件A 1,A 2,A 3的概率分别为0.2,0.3,0.5,则下列说法正确的个数是( ).
①12A A +与3A 是互斥事件,也是对立事件;②123A A A ++是必然事件;
③23()0.8P A A +=; ④12()0.5P A A +≤.
A .0
B .1
C .2
D .3
5、甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表,123,,s s s 分别为甲、乙、丙三名运动员这次测试成绩的标准差,则有( )
A.312s s s >>
B.213s s s >>
C.123s s s >>
D.321s s s >>
6、如图所示程序框图描述的算法,若输入m =2010,n=1541,
则输出的m 值为( ).
A .2010
B .1541
C .134
D .67
7、某中学高三(2)班甲、乙两名同学自高中以来每次考试成
绩的茎叶图如图,下列说法正确的是( ).
A .乙同学比甲同学发挥稳定,且平均成绩也比甲同学高
B .乙同学比甲同学发挥稳定,但平均成绩不如甲同学高
C .甲同学比乙同学发挥稳定,且平均成绩比乙同学高
D .甲同学比乙同学发挥稳定,但平均成绩不如乙同学高
8、执行如图所示的程序框图,若输出结果是8,
则判断框内m 的取值范围是( ).
A .(30,42] B.(42,56]
C.(56,72] D .(30,72)
9、为得到函数y=cos(2x+3
π)的图像, 只需将函数y=sin2x 的图象( )
A.向左平移512
π个长度单位
B.向右平移
512
π个长度单位 C.向左平移56
π个长度单位 D.向右平移56π个长度单位 10.函数f(x)=cos x( >0)的图象关于点M(
34π,0)对称,且在区间[0,2π]上是单调函数,则 值为( )
A .23
B .12
C .23或12
D .23
或2 二、填空题(每题4分,满分16分,将答案填在答题纸上)
11、将二进制101101(2)化为十进制数,结果为__________.
12、某工厂生产的A 、B 、C 三种不同型号的产品,产品数量之比依次为2:3:5,现用分层抽样方法,抽出一
个容量为n 的样本,样本中A 种型号产品有16件,那么此样本的容量为n=__________.
13、已知向量→AB 与→AC 的夹角为120°,且|→AB |=3,|→AC |=2.若→AP = →AB +→AC ,
且→AP ⊥→BC ,则实数 的值为________.
14、设f(x)=asin2x+bcos2x ,其中a ,b ∈R ,ab ≠0,
若f(x)≤|f(
6
π)|对一切x ∈R 恒成立, 则①f(1112π)=0 ②|f(710π)|<|f(5π)| ③f(x)既不是奇函数也不是偶函数 ④f(x)的单调递增区间是[k + 6,k +2 3
](k ∈Z) ⑤存在经过点(a,b)的直线与函数f(x)的图像不相交,
以上结论正确的是__________(写出所有正确结论的编号).
洛阳市第八中学高一段考数学答题卷
二、填空题:11.______ 12.______ 13._______ 14._________
三、解答题(共4小题,共44分.写出文字说明、证明过程或演算步骤)
15、(8分)一只口袋内装有形状、大小都相同的6只小球,其中4只白球,2只红球,从袋中随机摸出2只
球.
(1)求2只球都是红球的概率;(2)求至少有1只球是红球的概率.
16、(12分)某校从高一年级学生中随机抽取40名学生,将他
们的期中考试物理成绩(满分100分,成绩均不低于40分的整数)分成六段[40,50),[50,60),…,
[90,100]后得到如图的频率分布直方图.
(1)求图中实数a 的值及估算中位数m 的值.
(2)若该校高一年级共有学生640人,试估计该校高一年级期中考试物理成绩不低于60分的人数;
(3)若从物理成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的物理成绩之差的绝对值不大于10的概率.
17、(12分)为了探究车流量与PM2.5的浓度是否相关,现采集到北方某城市2015年12月份星期一到星期日
(1)(2)求y 关于x 的线性回归方程; (3)①利用所求回归方程,预测该市车流量为8万辆时,PM2.5的浓度;
②规定当一天内PM2.5的浓度平均值在(0,50]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(50,100]内,空气质量等级为良,为使该市某日空气质量等级为优或良,则应控制当天车流量在多少万辆以内(结果以万辆为单位,保留整数
) 参考公式:回归直线的方程是 y bx
a =+ ,其中 1122211()()()n n i i i i i i n n i i i i x x y y x y nx y b
x x x nx ====---==--∑∑∑∑ , a
y bx =-
18、(12分)已知函数 x+ )-cos( x+ )(0< < , >0)为偶函数,且函数y=f(x)
图象的两相邻对称轴之间的距离为 2
, (1)求f( 8)的值,(2)求函数y=f(x)+f(x+ 4
)的最大值及对应的x 的值,。
