概率试卷06-07
06-07(二)概率论与数理统计浙江工商大学试卷B

3.设X和Y方差存在且大于0,则X和Y 相互独立是X和Y不相关的
()
A、充分必要条件 B、充分但非必要条件 C、必要但非充分条件 D、既非充分也非必要条件 4.若,则下列表达式中不是统计量的为( ) A、; B、; C、; D、 5.: A、 B、 C、 D、 三、(10分)一批产品分别由甲、乙、丙三车床加工,其中甲 车床加工的占产品总数的25%,乙车床加工的产品占35%,其 余的是丙车床加工的。又甲、乙、丙三车床加工时出现次品的 概率分别为0.05,0.04,0.02。今从中任取一件,试求 (1)任取一件是次品的概率; (2)若已知取的一件是次品,则该次品是由甲车床加工的概 率是多少? 四、(10分)设随机变量的密度函数为 求 :(1)常数A; (2) (3)分布函数F(x);(4); 五、(10分)若(X,Y)的分布律由下表给出: X
得到估计量为:-----------------------10分 九、(12分)解: 在下检验 1.(1) ----------------1分 构造检验统计量 ----------------------3分 从而拒绝域-----------4分 而; 所以拒绝域 由样本观测值,得;---------------5分 因为, 所以接受,即认为两总体的方差无显著差异。-------------------6分 2. --------------------7分 其中 -------------------9分 在显著性水平下,查自由度为34的分布,, 拒绝域--------------------
七、(8分)设二维连续型随机变量(X,Y)的联合概率密度为: 求:(1) 常数k;(2)求边缘密度函数 (3)X与Y是否独立 八、(10分)设总体X的概率密度为,其中是未知参数,是已 知常数,求的极大似然估计。 九、(12分)某种零件的椭圆度服从正态分布,改变工艺前抽 取16件,测得数据,改变工艺后抽取20件,测得问(1).改变工艺前 后,方差有无明显的差异? (2)改变工艺前后,均值有无显著的差 异? (均取0.05,) 10、 证明题(4分)若;X与Y相互独立,分布是X和Y的样 本。证明:是的无偏估计。
山东省诸诚一中06-07年上学期高三摸底考试数学理(附答案)

山东省诸诚一中2006—2007学年高三摸底考试数 学 试 卷(理)本试题分为选择题和非选择题两部分,满分150分。
参考公式:如果事件A 、B 互斥,那么 正棱锥、圆锥的侧面积公式P(A+B)=P(A)+P(B) cl S 21=侧面如果事件A 、B 相互独立,那么P(A·B)=P(A)·P(B) 其中c 表示底面周长,l 表示斜高或母线长 如果事件A 在一次试验中发生的概率是 球的体积公式 P ,那么n 次独立重复试验中恰好发生k 334R V π=球次的概率k n kk n n P P C k P --=)1()( 其中R 表示球的半径第I 卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分。
下列各小题所给出的四个答案中只有一个是正确的。
1.已知全集I=R ,集合 A B x xy x A 则},4,3{},24|{=--==( U B )等于 ( )A .(2,3)∪(3,4)B .(2,4)C .(2,3)∪(3,4]D .(2,4]2.与圆(x -3)2+(y+1)2=2相切,且在两坐标轴上有相等截距的切线有 ( )A .1条B .2条C .3条D .4条 3.已知数列{a n }是等差数列,且a 3+a 11=50,a 4=13,则a 2等于 ( )A .1B .4C .5D .64.复数Bi A imi+=+-212(m 、A 、B ∈R ),且A+B=0,则m 的值是( )A .2B .32C .-32D .25.下列说法正确的是( )A .定义在R 上的函数f(x)满足f(2)>f(1),则f(x)在R 上是增函数B .定义在R 上的函数f(x)满足f(2)>f(1),则f(x)在R 上不是减函数C .y=tanx 在定义域上是增函数D .若f(x+1)是奇函数,则f(-x -1)=-f(x+1)6.若不等式|2x -3|>4与不等式x 2+px+q>0的解集相同,则p: q 等于( )A .12:7B .7:12C .-12:7D .-3:47.设F 1和F 2为双曲线1422=-y x 的两个焦点,点P 在双曲线上,若021=⋅PF ,则 △F 1PF 2的面积是 ( )A .1B .25C .2D .58.已知函数y=f -1(x)的图象过点(1,0),则y=f(21x -1)的反函数的图象一定过点( )A .(0,2)B .(2,0)C .(2,1)D .(1,2)9.在120°的二面角内,放置一个半径为3的球,该球切二面角的两个半平面于A 、B 两点,那么这两个切点在球面上的最短距离为 ( )A .3πB .πC .2πD .310.某班由24名女生和36名男生组成,现要组织20名学生外出参观,若这20名学生按性别分层抽样产生,则参观团的组成方法共有( )A .2060C 种B .1236824C A 种 C .10361024C C 种D .1236824C C 种 11.已知函数axx f πsin3)(=的图象上相邻的一个最大值点与一个最小值点恰好在圆x 2+y 2=a 2上,则正数a 的值是( )A .1B .2C .3D .412.给出如下4个命题:①对于任意一条直线a ,平面α内必有无数条直线与a 垂直;②若α、β是两个不重合的平面,l 、m 是两条不重合的直线,则α//β的一个充分而不必要条件是l ⊥α,m ⊥β,且l //m ;③已知a 、b 、c 、d 是四条不重合的直线,如果a ⊥c ,a ⊥d,b ⊥c,b ⊥d ,则 “a //b” 与 “c//d” 不可能都不成立;④已知命题P :若四点不共面,那么这四点中任何三点都不共线.则命题P 的逆否命题是假命题. 以上命题中,正确命题的个数是 ( )A .1B .2C .3D .4第Ⅱ卷(非选择题,共90分)二、填空题:本大题4小题,每小题4分,共16分,把答案填在题中的横线上。
东北林业大学06-07(2)概率论与数理统计期末试卷
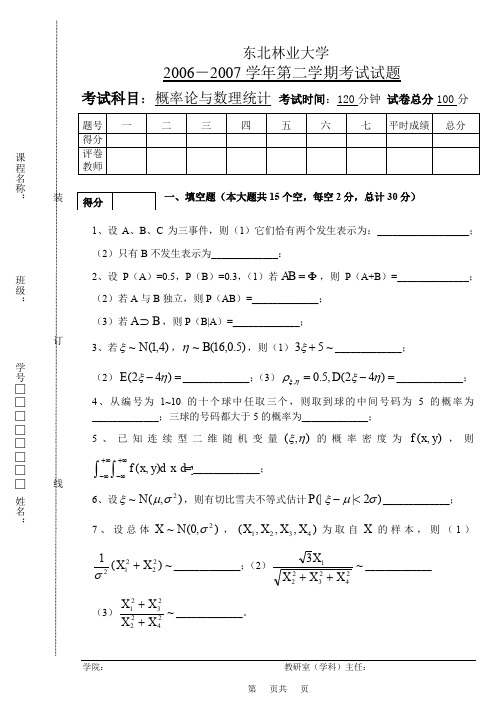
东北林业大学2006-2007学年第二学期考试试题考试科目:概率论与数理统计 考试时间:120分钟 试卷总分100分一、填空题(本大题共15个空,每空2分,总计30分)1、设A 、B 、C 为三事件,则(1)它们恰有两个发生表示为:__________________;(2)只有B 不发生表示为_____________:2、设P (A )=0.5,P (B )=0.3,(1)若Φ=AB ,则P (A+B )=______________;(2)若A 与B 独立,则P (AB )=_____________; (3)若B A ⊃,则P (B|A )=_____________;3、若)4,1(~N ξ,)5.0,16(~B η,则(1)~53+ξ_____________;(2)=-)42(ηξE _____________;(3)=-=)42(,5.0,ηξρηξD _____________; 4、从编号为1~10的十个球中任取三个,则取到球的中间号码为5的概率为_____________;三球的号码都大于5的概率为_____________;5、已知连续型二维随机变量),(ηξ的概率密度为),(y x f ,则=⎰⎰∞+∞-∞+∞-d x d yy x f ),(_____________; 6、设),(~2σμξN ,则有切比雪夫不等式估计)2|(|σμξ<-P _____________; 7、设总体),0(~2σN X ,),,,(4321X X X X 为取自X 的样本,则(1)~)(122212X X +σ_____________;(2)~32423221XX X X ++_____________(3)~24222321X X X X ++_____________。
二、(本题10分)设总体⎩⎨⎧<<=-其他10);(~1x x x f X θθθ,),,,(21n X X X 为取自X 的样本,求参数)0(>θθ的矩估计和最大似然估计。
概率试题及答案解析

概率试题及答案解析1. 某次考试中,学生A和学生B通过考试的概率分别为0.6和0.7。
求学生A和学生B至少有一人通过考试的概率。
答案:设事件A为学生A通过考试,事件B为学生B通过考试。
则至少有一人通过考试的概率为P(A∪B)。
根据概率的加法公式,P(A∪B) = P(A) + P(B) - P(A∩B)。
由于A和B是相互独立的事件,所以P(A∩B) = P(A)P(B)。
将已知概率代入公式,得到P(A∪B) = 0.6 + 0.7 - 0.6×0.7 = 0.86。
2. 一个袋子里有5个红球和3个蓝球,随机抽取3个球,求至少抽到一个红球的概率。
答案:设事件C为抽到至少一个红球。
首先计算对立事件C',即抽到的3个球都是蓝球的概率。
由于袋子里有5个红球和3个蓝球,总共8个球,所以抽到3个蓝球的概率为P(C') = (3/8)×(2/7)×(1/6) = 1/56。
根据对立事件的概率公式,P(C) = 1 - P(C') = 1 - 1/56 = 55/56。
3. 一个工厂生产某种零件,合格率为95%。
求连续生产5个零件,至少有3个合格的概率。
答案:设事件D为连续生产5个零件,至少有3个合格。
这是一个二项分布问题,其中n=5,p=0.95。
根据二项分布的概率公式,P(D) = C(5,3)×(0.95)^3×(0.05)^2 + C(5,4)×(0.95)^4×(0.05)^1 +C(5,5)×(0.95)^5×(0.05)^0。
计算得到P(D) = 0.98375。
4. 抛一枚硬币3次,求恰好出现2次正面的概率。
答案:设事件E为抛硬币3次,恰好出现2次正面。
这是一个二项分布问题,其中n=3,p=0.5。
根据二项分布的概率公式,P(E) =C(3,2)×(0.5)^2×(0.5)^1 = 3/8。
海师概率论与数理统计06--07(A)
○ 装
六. (15 分)设总体 服从指数分布,密度函数为:
f x;
解:
e
1
x
,
x 0 , 0 .试求参数 的极大似然估计量.
解:
○ 订
○ 线
○
第 5 页(共 6 页) 第 6 页(共 6 页)
P ( A B) a b 1 .
○ 密
求: (1) 的特征函数 (t ) ; (2) E ( ) 及 D ( ) . 解:
(2)已知 P( A B) 1/ 8 , P( A B) 1/ 3 , P( B A) 1/ 4 ,求:------------------------------------------------------------------------------------------------
A3 ,它们的产品分别占全部产品的
10%,40%,
○ 密
50%,并且它们的废品率分别为 7%,2%,1%.令 B 表示“从产品中任 取一件,并发现是废品”这一事件,求: (1)
------------------------------------------------
P(B) ;
1
(2) 今从全部产品中任取一件,发现是废品,问它是 A 制造的概率.
七. (10 分)某工厂生产的电灯泡的使用时数用 表示, 假定 服从正态分布 N a, ,其中 a 及 都是未知参 数,现在观察 n 17 个灯泡,测得 17 个灯泡的使用时数
○ 封
x1, x2 ,, x17 ,并由此算得 x 1800 , s 500 ,试问:给定显著性水平 0.05 ,该厂电灯泡的平均使用时数为“ a a0 2000 ” (小时)这个 结论是否成立? (注: t 分布的双侧临界值表中, 从 可查得 t16 0.05 2.12 )
概率统计考试试卷

概率统计考试试卷一、选择题(每题3分,共30分)1. 设随机变量X服从正态分布N(μ, σ^2),下列说法正确的是:A. X的期望值是μB. X的方差是σ^2C. X的取值范围是(-∞, +∞)D. 以上说法均正确答案:D2. 已知随机变量X的概率密度函数为f(x),下列关于X的分布函数F(x)的说法正确的是:A. F(x)是单调递增的B. F(x)是连续的C. F(x)在x=0处的值为0.5D. F(x)在x=0处的值为0答案:A3. 设随机变量X服从二项分布B(n, p),下列说法正确的是:A. X的期望值是npB. X的方差是np(1-p)C. X的取值范围是{0, 1, ..., n}D. 以上说法均正确答案:D4. 已知随机变量X和Y相互独立,下列说法正确的是:A. X和Y的期望值之和等于它们的期望值B. X和Y的方差之和等于它们的方差C. X和Y的协方差为0D. 以上说法均正确答案:C5. 设随机变量X服从泊松分布,下列说法正确的是:A. X的期望值等于其方差B. X的取值范围是{0, 1, 2, ...}C. X的概率质量函数为P(X=k) = λ^k / k! * e^(-λ)D. 以上说法均正确答案:D6. 已知随机变量X服从均匀分布U(a, b),下列说法正确的是:A. X的期望值是(a+b)/2B. X的方差是(b-a)^2/12C. X的概率密度函数为f(x) = 1/(b-a)D. 以上说法均正确答案:D7. 设随机变量X服从指数分布,下列说法正确的是:A. X的期望值是1/λB. X的方差是1/λ^2C. X的概率密度函数为f(x) = λe^(-λx)D. 以上说法均正确答案:D8. 已知随机变量X和Y的联合概率密度函数为f(x, y),下列说法正确的是:A. X和Y的边缘概率密度函数可以通过对f(x, y)积分得到B. X和Y的期望值可以通过对f(x, y)积分得到C. X和Y的协方差可以通过对f(x, y)积分得到D. 以上说法均正确答案:A9. 设随机变量X服从正态分布N(0, 1),下列说法正确的是:A. X的期望值是0B. X的方差是1C. X的概率密度函数为f(x) = 1/√(2π) * e^(-x^2/2)D. 以上说法均正确答案:D10. 已知随机变量X服从t分布,下列说法正确的是:A. X的期望值是0B. X的方差是1C. X的概率密度函数为f(x) = Γ((ν+1)/2) / (√(νπ) *Γ(ν/2) * (1+x^2/ν)^((ν+1)/2))D. 以上说法均正确答案:C二、填空题(每题2分,共20分)1. 设随机变量X服从正态分布N(μ, σ^2),则X的期望值E(X) = ________。
概率统计A试题 答案 06-07(秋)
θ1 = ( X 1 + X 2 + X 3 ) ,θ 2 =
有效.
1 3
1 1 1 X 1 + X 2 + X 3 ,都是期望 EX 的无偏估计,但 θ 1 比 θ 2 2 3 6
(是)
二、填空题:(每格 3 分,共计 15 分) 6、设 P ( A) = 0.5 , P( B )=0.4 , P ( B | A) = 0.8 ,则 P( A ∪ B) = 0.7 . 7、已知事件 A 与 B 满足条件 P( AB) = P( A B ) ,且 P( B) = p ,则 P ( A) = 1 − p .
(1) 置信区间 ( X −
评分参考 (1) 写出密度函数(5 分) ; 。 (2) 得到 P ( S ≤ s) (2×5=10 分)
s n
tα / 2 (n − 1), X +
s n
tα / 2 (n − 1)) (4 分) ;
(2) 计算正确(3 分) ; (3) 拒绝域 s > k =
2
σ 02
草
稿
纸
14、 X , Y 是独立同分布的随机变量, U = X + Y , = X − Y , 设 而 V 那么 U 和 V (A)一定不独立 (C)相关系数一定为零 四、计算题:(15 分×3=45 分) (B)一定独立 (D)相关系数一定不为零
15. 已知一批产品中 90%是合格品,检查时,一个合格品被误认为是次品的概率为 0.05,一个次品被误认为是合格品的概率为 0.02,求(1)一个产品经检查后被认为 是合格品的概率; (2)一个经检查后被认为是合格品的产品确是合格品的概率.
2 2 2 χ 0.05 (16) = 26.296, χ 0.05 (15) = 24.996, χ 0.025 (15) = 27.488.
概率期末考试试题及答案
概率期末考试试题及答案一、选择题(每题3分,共30分)1. 随机变量X服从标准正态分布,下列哪个选项是正确的?A. P(X > 1) = 0.3413B. P(X < 0) = 0.5C. P(-1 < X < 1) = 0.6826D. P(X = 0) = 0答案:C2. 已知随机变量X服从二项分布B(n, p),其中n=10,p=0.5,求E(X)。
A. 2B. 5C. 10D. 15答案:B3. 某次考试的及格率是0.6,如果随机抽取10名学生,求至少有6名学生及格的概率。
A. 0.05B. 0.25C. 0.5D. 0.75答案:D4. 随机变量X服从泊松分布,其参数λ=3,求P(X=2)。
A. 0.1494B. 0.2439C. 0.3439D. 0.1494*2答案:B5. 已知随机变量X和Y相互独立,且X服从参数为2的指数分布,Y服从参数为0.5的指数分布,求Z=X+Y的分布。
A. 指数分布,参数为2B. 指数分布,参数为0.5C. 指数分布,参数为2.5D. 非指数分布答案:C6. 某工厂生产的产品中,次品率为0.05,如果随机抽取100件产品,求恰好有5件次品的概率。
A. 0.05B. 0.25C. 0.0245D. 0.05^5答案:C7. 随机变量X服从正态分布N(μ, σ^2),若μ=10,σ=2,求P(X >12)。
A. 0.0228B. 0.1587C. 0.9772D. 0.8413答案:A8. 已知随机变量X服从均匀分布U(0,1),求P(0.5 < X < 0.7)。
A. 0.2B. 0.3C. 0.5D. 0.7答案:A9. 随机变量X服从标准正态分布,求P(X > 2)。
A. 0.0228B. 0.9772C. 0.1587D. 0.5答案:A10. 随机变量X服从参数为2的泊松分布,求E(X)和Var(X)。
概率论与数理统计考试试卷与答案
n05——06一.填空题(每空题2分,共计60分)1、A 、B 是两个随机事件,已知0.3)B (p ,5.0)(,4.0)A (p ===A B P ,则=)B A (p 0.6 ,=)B -A (p 0.1 ,)(B A P ⋅= 0.4 , =)B A (p 0.6。
2、一个袋子中有大小相同的红球6只、黑球4只。
(1)从中不放回地任取2只,则第一次、第二次取红色球的概率为: 1/3 。
(2)若有放回地任取2只,则第一次、第二次取红色球的概率为: 9/25 。
(3)若第一次取一只球观查球颜色后,追加一只与其颜色相同的球一并放入袋中后,再取第二只,则第一次、第二次取红色球的概率为: 21/55 。
3、设随机变量X 服从B (2,0.5)的二项分布,则{}=≥1X p 0.75, Y 服从二项分布B(98, 0.5), X 与Y 相互独立, 则X+Y 服从 B(100,0.5),E(X+Y)= 50 ,方差D(X+Y)= 25 。
4、甲、乙两个工厂生产同一种零件,设甲厂、乙厂的次品率分别为0.1、0.15.现从由甲厂、乙厂的产品分别占60%、40%的一批产品中随机抽取一件。
(1)抽到次品的概率为: 0.12 。
(2)若发现该件是次品,则该次品为甲厂生产的概率为: 0.5 . 5、设二维随机向量),(Y X 的分布律如右,则=a 0.1,=)(X E 0.4,Y X 与的协方差为: - 0.2 ,2Y X Z +=的分布律为:6、若随机变量X ~)4 ,2(N 且8413.0)1(=Φ,9772.0)2(=Φ,则=<<-}42{X P 0.8185 ,(~,12N Y X Y 则+= 5 , 16 )。
7、随机变量X 、Y 的数学期望E(X)= -1,E(Y)=2, 方差D(X)=1,D(Y)=2, 且X 、Y 相互独立,则:=-)2(Y X E - 4 ,=-)2(Y X D 6 。
概率试题大全及答案
概率试题大全及答案1. 单选题:如果一个事件的概率是0.3,那么它的对立事件的概率是多少?A. 0.7B. 0.3C. 0.6D. 0.4答案:A2. 多选题:下列哪些事件是独立事件?A. 抛一枚硬币,连续两次正面朝上B. 抛一枚硬币,第一次正面朝上,第二次反面朝上C. 抛一枚硬币,第一次正面朝上,第二次正面朝上D. 抛一枚硬币,第一次反面朝上,第二次正面朝上答案:B, D3. 判断题:如果事件A和事件B是互斥的,那么P(A∪B) = P(A) +P(B)。
答案:错误。
正确公式为P(A∪B) = P(A) + P(B) - P(A∩B)。
4. 填空题:如果一个袋子里有5个红球和3个蓝球,随机抽取一个球,抽到红球的概率是______。
答案:5/85. 简答题:请解释什么是条件概率,并给出一个例子。
答案:条件概率是指在某个事件已经发生的条件下,另一个事件发生的概率。
例如,已知一个班级有50%的学生是女生,那么在已知一个学生是女生的条件下,她数学成绩优秀的概率。
6. 计算题:一个袋子里有3个红球和2个蓝球,随机抽取2个球,求两个球都是红球的概率。
答案:首先计算抽取2个球的总组合数,即C(5,2) = 10种。
然后计算两个球都是红球的组合数,即C(3,2) = 3种。
所以两个球都是红球的概率为3/10。
7. 综合题:一个骰子掷两次,求至少出现一次6的概率。
答案:首先计算不出现6的概率,即每次掷骰子有5种可能不出现6,所以两次都不出现6的概率是(5/6) * (5/6) = 25/36。
那么至少出现一次6的概率就是1 - 25/36 = 11/36。
8. 应用题:一个工厂生产的产品合格率为90%,求连续生产3个产品至少有2个合格的概率。
答案:首先计算3个产品都合格的概率,即0.9 * 0.9 * 0.9 = 0.729。
然后计算3个产品中恰好有2个合格的概率,即C(3,2) * 0.9^2 *0.1 = 3 * 0.81 * 0.1 = 0.243。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
概率论与数理统计试卷
(06-07)各专业适用
二、选择题(每小题2分,共10分)
1. 设B A ,为两事件, 1)(0<<A P 且,1)|(=A B P 则以下 ( )成立
A. B A ,互斥
B. A B ⊂
C. 0)(=AB P
D.
0)(=B P
2.设随机变量),(Y X 有联合分布律
,则=),cov(Y X ( )
A. 16.0 B 。
22.0
C.
22.0-
D.
16.0-
3.设 X 和Y 都服从 )1,0(N ,则以下 ( ) 成立
A. X+Y 服从正态分布
B. X 2
和Y 2
都服从卡方分布 C. )2(~222χY X + D. 22/Y X 服从F 分布
4. 设总体
),(~2σμN X , n
X X X ,,21是来自总体的样本,
2
11)(1μ∑=-=n i i X n S ,21
2)(1X X n S n i i ∑=-= 则
以下( ) 是2σ的无偏估计量。
A.
2
21S n n - B. 211S n n - C. 221S n n - D. 2
11S n
n -
5. 设总体),(~2σμN X ,2σ未知,921,,X X X 为来自总体的样本,要检验 ,3:
0=μH ,3:
1>μH 时,
若采用统计量 3
/3
S X T -=, 则0H 的拒绝域 W 为 ( )
A. )8(95.0t T >,
B. )8(90.0t T -<
C. )8(95.0t T >
D. )8(90.0t T >
二、填空题(每小题2分,共10分)
1. 一袋中有4个红球3个白球,从中任意取出2个.则此两求颜色不同的概率为__________
2.若
X
有密度8
)1(2
221
)(--
=
x e x f π
,则数学期望
=+)32(2X X E _________________
3. 设)7.0,100(~B X ,由切比雪夫不等式,应有≥≤≤)8060(X P ________________
4. 设)2/1,2,2,1,1(~),(N Y X ,则=)(XY E ______________
5. 某公司职工年收入服从标准差为4单位:万元)的正态分布,今从该公司随机抽取16名职工,求得平均年收入为3.6万元,则该公司职工收入的置信度为
95%的置信区间为
___. (95.0)645.1(=Φ,975.0)96.1(=Φ)
三、解答题
1. (10分)
设区域G 由曲线x y cos =以及0,0==y x 围成(
x 轴正向)。
随
机点),(Y X M 在G 内 均匀随机游动(即),(Y X 在G 内服从二
维均匀分布),设 ]2.0,0[]2.0,0[⨯=D 为一矩形区域。
(1)求概率);(D M P ∈(2)对M 独立观察100次,用中心极限定理求M 在D 内的次数在2-6次的概率。
(正态分布表自己查书)
2 (10分)
设连续型随机变量
X
有分布函数
⎪⎩
⎪
⎨⎧>-≤≤-+-<=-0
2/1102,
2/12,0)(x e x Ax x x F x (1)求?=A (2)求E(X 2); (3) 令X e Y =,求Y 的概率密度函数
)(y f Y .
3(8分)
设有两个总体)36,15(~N X
,)51,10(~N Y ,从中分别随机抽取两个容
量为10,15 的样本,求两样本均值差的 绝对值小于6的概率。
正
态分布表查书。
4 (18分)
设平面区域G 由x y 2= ,0,2==x y 围成,二维随机变量),(Y X
有联合密度⎪⎩⎪⎨⎧∈=else G
y x y y x f 0
),(43
),(,
求(1)
Y
X ,的边缘密度函数;(2)边缘数字特征
);().(),(),(Y D X D Y E X E 及),cov(Y X 相关系数xy ρ; (3) Y X , 独立吗? 5. (12分)
设n X X X ,,21是来自总体X ,容量为n 的样本,若X 有密度
⎪⎩
⎪⎨
⎧≤≤+=+else
x x x f 010)2()(1
θθ,其中θ为未知参数, 求θ 的矩估计
量及极大似然估计量。
6. (12分)以前没有的题型
设设某种化肥用量与水稻产量之间有如下关系:
(1) 请拟合出y 对x 的一元线性回归方程。
(系数取到 小
数点后一位)
(2) 用相关系数检验法检验回归方程的显著性
)05.0(=α
相关系数临界值表略,自己查书。
7. (10分)
某批电子元件寿命)1
(~θ
e X
,(指数分布),其中θ
未知,从中任
取n 个元件组成一个串联系统。
(1) 证明:这个串联系统的寿命Y 仍
服从指数分布;(2)求常数C 使得CY Z =是θ的无偏估计;(3)指出Z 与X 作为θ的两个无偏估计量谁更有效。
