第24届全国中学生物理竞赛复赛试题参考解答
第19届全国中学生物理竞赛复赛试题(含解析)
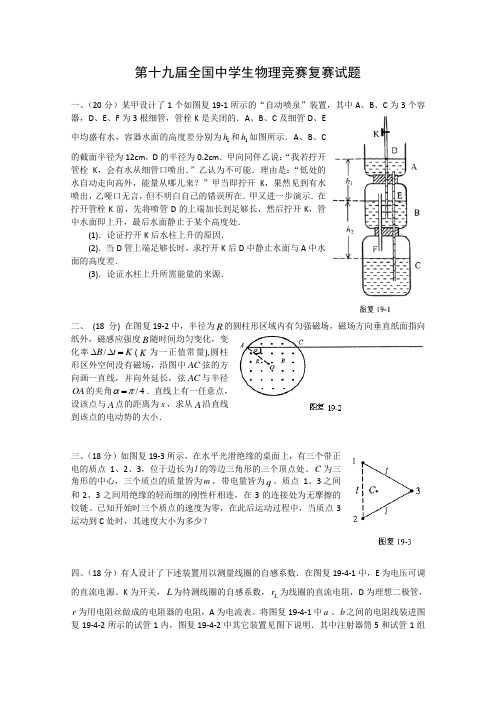
第十九届全国中学生物理竞赛复赛试题一、(20分)某甲设计了1个如图复19-1所示的“自动喷泉”装置,其中A 、B 、C 为3个容器,D 、E 、F 为3根细管,管栓K 是关闭的.A 、B 、C 及细管D 、E中均盛有水,容器水面的高度差分别为1h 和1h 如图所示.A 、B 、C 的截面半径为12cm ,D 的半径为0.2cm .甲向同伴乙说:“我若拧开管栓K ,会有水从细管口喷出.”乙认为不可能.理由是:“低处的水自动走向高外,能量从哪儿来?”甲当即拧开K ,果然见到有水喷出,乙哑口无言,但不明白自己的错误所在.甲又进一步演示.在拧开管栓K 前,先将喷管D 的上端加长到足够长,然后拧开K ,管中水面即上升,最后水面静止于某个高度处. (1).论证拧开K 后水柱上升的原因.(2).当D 管上端足够长时,求拧开K 后D 中静止水面与A 中水面的高度差.(3).论证水柱上升所需能量的来源.二、 (18 分) 在图复19-2中,半径为R 的圆柱形区域内有匀强磁场,磁场方向垂直纸面指向纸外,磁感应强度B 随时间均匀变化,变化率/B t K ∆∆=(K 为一正值常量),圆柱形区外空间没有磁场,沿图中AC 弦的方向画一直线,并向外延长,弦AC 与半径OA 的夹角/4απ=.直线上有一任意点,设该点与A 点的距离为x ,求从A 沿直线到该点的电动势的大小.三、(18分)如图复19-3所示,在水平光滑绝缘的桌面上,有三个带正电的质点1、2、3,位于边长为l 的等边三角形的三个顶点处。
C 为三角形的中心,三个质点的质量皆为m ,带电量皆为q 。
质点 1、3之间和2、3之间用绝缘的轻而细的刚性杆相连,在3的连接处为无摩擦的铰链。
已知开始时三个质点的速度为零,在此后运动过程中,当质点3运动到C 处时,其速度大小为多少? 四、(18分)有人设计了下述装置用以测量线圈的自感系数.在图复19-4-1中,E 为电压可调的直流电源。
第26届全国中学生物理竞赛复赛试题及答案

第26届全国中学生物理竞赛复赛试卷一、填空(问答)题(每题5分,共25分)有人假想了一种静电场:电场的方向都垂直于纸面并指向纸里,电场强度的大小自左向右慢慢增大,如下图。
这种散布的静电场是不是可能存在?试述理由。
2.海尔-波普彗星轨道是长轴超级大的椭圆,近日点到太阳中心的距离为天文单位(1天文单位等于地日间的平均距离),那么其近日点速度的上限与地球公转(轨道可视为圆周)速度之比约为(保留2位有效数字) 。
用测电笔接触市电相线,即便赤脚站在地上也可不能触电,缘故是;另一方面,即便穿绝缘性能良好的电工鞋操作,测电笔仍会发亮,缘故是 。
4.在图示的复杂网络中,所有电源的电动势均为E 0,所有电阻器的电阻值均为R 0,所有电容器的电容均为C 0,那么图示电容器A 极板上的电荷量为 。
5.如图,给静止在水平粗糙地面上的木块一初速度,使之开始运动。
一学生利用角动量定理来考察此木块以后的运动进程:“把参考点设于如下图的地面上一点O ,现在摩擦力f 的力矩为0,从而地面木块的角动量将守恒,如此木块将不减速而作匀速运动。
”请指出上述推理的错误,并给出正确的说明: 。
二、(20分)图示正方形轻质刚性水平桌面由四条完全相同的轻质细桌腿一、二、3、4支撑于桌角A 、B 、C 、D 处,桌腿竖直立在水平粗糙刚性地面上。
已知桌腿受力后将产生弹性微小形变。
现于桌面中心点O 至角A 的连线OA 上某点P 施加一竖直向下的力F ,令c OAOP,求桌面对桌腿1的压力F 1。
三、(15分)1.一质量为m 的小球与一劲度系数为k 的弹簧相连组成一体系,置于滑腻水平桌面上,弹簧的另一端与固定墙面相连,小球做一维自由振动。
试问在一沿此弹簧长度方向以速度u 作匀速运动的参考系里观看,此体系的机械能是不是守恒,并说明理由。
2.假设不考虑太阳和其他星体的作用,那么地球-月球系统可看成孤立系统。
假设把地球和月球都看做是质量均匀散布的球体,它们的质量别离为M 和m ,月心-地心间的距离为R ,万有引力恒量为G 。
第28届全国中学生物理竞赛复赛试题参考解答及评分标准

σ=
πab T
b
rP
S
由(9) 、 (13) 、 (14) 、 (15)式并代入有关数据可 得
θP
P0
ϕ
x
a
O
ϕ = 127D
(16) 图2
解法二 取极坐标,极点位于太阳 S 所在的焦点处,由 S 引向近日点的射线为极轴,极角为 θ ,取逆 时针为正向,用 r、 θ 表示彗星的椭圆轨道方程为
r=
p 1 + e cos θ
第 28 届全国中学生物理竞赛复赛试题参考解答及评分标准
一、参考解答: 解法一 取直角坐标系 Oxy,原点 O 位于椭圆的中心,则哈雷彗星的椭圆轨道方程为
x2 y 2 + =1 a 2 b2
a、b 分别为椭圆的半长轴和半短轴,太阳 S 位于椭圆的一个焦点处,如图 1 所示.
(1)
以 Te 表示地球绕太阳运动的周期,则 Te = 1.00年 ;以 ae 表示地球到太阳的距离(认为地球 绕太阳作圆周运动) ,则 ae = 1.00AU ,根据开普勒第三定律,有
取杆 CD 为研究对象,由平衡条件有
(4)
N 4 + N 2 cos θ − f 2 sin θ = 0 N 2 sin θ + f 2 cos θ − mg = 0
以及对 C 点的力矩
(5) (6)
1 N 4l cos α − mgl sin α = 0 2
解以上各式可得
(7)
N4 =
1 mg tan α 2
T
v
v1
P
v2
1 1 1 1 2 2 2 2 M ( Rω0 ) + m ( Rω0 ) = M ( Rω ) + m ( v12 + v 2 ) 2 2 2 2
第28届全国中学生物理竞赛复赛试卷(含答案)

第28届全国中学生物理竞赛复赛试题一、(20分)如图所示,哈雷彗星绕太阳S 沿椭圆轨道逆时针方向运动,其周期T 为76.1年,1986年它过近日点P 0时与太阳S 的距离r 0=0.590AU ,AU 是天文单位,它等于地球与太阳的平均距离,经过一段时间,彗星到达轨道上的P 点,SP 与SP 0的夹角θP =72.0°。
已知:1AU=1.50×1011m ,引力常量G=6.67×10-11Nm 2/kg 2,太阳质量m S =1.99×1030kg ,试求P 到太阳S 的距离r P 及彗星过P 点时速度的大小及方向(用速度方向与SP 0的夹角表示)。
二、(20分)质量均匀分布的刚性杆AB 、CD 如图放置,A 点与水平地面接触,与地面间的静摩擦系数为μA ,B 、D 两点与光滑竖直墙面接触,杆AB 和CD 接触处的静摩擦系数为μC ,两杆的质量均为m ,长度均为l 。
1、已知系统平衡时AB 杆与墙面夹角为θ,求CD 杆与墙面夹角α应该满足的条件(用α及已知量满足的方程式表示)。
2、若μA =1.00,μC =0.866,θ=60.0°。
求系统平衡时α的取值范围(用数值计算求出)。
三、(25分)在人造卫星绕星球运行的过程中,为了保持其对称转轴稳定在规定指向,一种最简单的办法就是让卫星在其运行过程中同时绕自身的对称轴转,但有时为了改变卫星的指向,又要求减慢或者消除卫星的旋转,减慢或者消除卫星旋转的一种方法就是所谓消旋法,其原理如图所示。
一半径为R ,质量为M 的薄壁圆筒,,其横截面如图所示,图中O 是圆筒的对称轴,两条足够长的不可伸长的结实的长度相等的轻绳的一端分别固定在圆筒表面上的Q 、Q ′(位于圆筒直径两端)处,另一端各拴有一个质量为2m的小球,正常情况下,绳绕在圆筒外表面上,两小球用插销分别锁定在圆筒表面上的P 0、P 0′处,与卫星形成一体,绕卫星的对称轴旋转,卫星自转的角速度为ω0。
2011全国物理竞赛复赛试题及答案

得分 评卷人
图1
1.当风速为 6.0m/s 时,风力发电机的输出功率将变为 50W,在这种情况下,将蓄电池的电量由 20%充 至 90%需多长时间? 2.如果当地垂直于太阳光的平面得到的太阳辐射最大强度约为 240W/m2,要想太阳能电池的最大功率 达到 36W,太阳能电池板的面积至少要多大? 3.若遇到阴天无风的天气,仅靠蓄电池供电,最多可供灯具正常发光多长时间?
1.图 6 为安装示意图,安装时要将 L 形挂钩用膨胀螺钉固定在承重墙上,上表是热水器的部分数据, 请估算 L 形挂钩受到的最大向下拉力 F 及 对应此时膨胀 F 承重墙 螺钉与承重墙体间的摩擦力 f。 悬挂孔 L 形挂钩 2.这台热水器共有三挡加热功率,销 售人员曾介绍 E 悬挂架 说:热水器内部有两个加热管。请你根据 销售人员的介 D 绍,猜测并画出内部加热电路的主要结构 (简化的等效 安全阀 出水管 B 进水管 电路图) 。然后依据你的猜想,计算出每个 加热管的电阻 C A 值。 图6 3.产品说明书上标明:当达到设定 温度,停止加 热后,如果水温降到低于设定温度 4℃时,热水器将自动以设置功率将桶内的水加热至设定温度,如此反复 直至手动停止加热。小芳想到了国家提倡的峰谷电价制度的有关规定:2011 年起,本地的分时电价为:峰 时段 (08: 00~ 22: 00)0.6 元 /度,谷时段 (22: 00~次日 08: 00)0.3 元 /度。她想,如果每天下午 6 点洗浴 时需要把 20℃的冷水加热至 50℃,可以下午直接加热,也可以早晨 8 点前加热好,让热水器自动保温至 下午 6 点,哪种方式更省钱呢?为此她利用热水器提供的测温功能测量了水温从 50℃降至 46℃需要 190 分钟,已知 c 水 =4.2× 103J/(kg•℃),请帮她通过计算做出哪种方式更省钱的判断。
2023年全国初中应用物理竞赛试题及参考答案版

2023年全国初中应用物理竞赛试题一、本题共10小题,毎小题2分,共20分。
以下各小题给出的四个选项中只有一个选项中只有一个是对的的,把对的选项前面的字母填在题后的括号内。
1.我国有句谚语说:“下雪不冷化雪冷”。
你认为以下几个说法中一定错误....的是()A.冷与不冷是将下雪过程中与下雪过后的温度进行对比来说的B.冷气流的北上导致气温的减少C.雪的熔化、熔化后水的蒸发以及雪的升华都需要吸热导致气温的减少D.人们感觉的“冷”与“不冷”除与温度有关之外,还受空气湿度的影响2.公路交通标志由基板和附着其上的反光膜组成,夜晚它可以反射汽车射来的灯光,使司机看清交通标志。
图1所示的反光膜横截面的结构示意图中,设计最合理的是()3.如图2所示,生活中有很多方法都可以将斧头安紧在斧柄上,下面四种方法能更好地运用斧头惯性的是( )图2 4.将一根直木棒放在一装有水的长方体形状的玻璃水槽中的偏左侧的位置,直木棒静止后从其正前方观测到的现象是下面四种情况中的哪一种()5.用手提起如图4甲所示长细金属链的一端,使金属链的另一端接触玻璃杯底部,然后逐渐将长金属链顺序地盘入玻璃杯中,直到金属链几乎能装满玻璃杯。
将玻璃杯放置在水平桌面的最左端,使金属链的另一端伸出玻璃杯外,然后用手指按住金属链,如图4乙所示。
若将手指放开,将会出现下列哪种现象()A.没有变化B.金属链会回到玻璃杯中C.金属链会下落一段距离后停止滑出杯子D.金属链会下落直到玻璃杯清空6.如图5所示为双金属片温度计的内部结构示意图,双金属片一般是由形状相同的铜片和铁片铆合在一起制成的,其中铜的热膨胀限度比铁的大。
当温度变化时,由于内外两层金属片的膨胀限度不同样而引起指针偏转,同时在弹力的平衡下,指针便指在刻度盘上相应的温度值位置上,从而显示出被测的温度。
下面关于双金属片温度计的结识中,错误的是( )A.双金属片温度计是根据固体热胀冷缩的原理制成的B.被测温度越高,双金属片温度计内弹簧的弹力越大C.双金属片温度计的指针做得比较长,是为了能起到将微小形变放大的作用D.要使温度升高时指针顺时针偏转,双金属片的外层(图中较粗线所示)应是铁,内层(图中较细线所示)应是铜7.有经验的面点师傅在用手从蒸笼里拿刚蒸熟的馒头之前,总是先用手蘸上少许凉水。
第28届全国中学生物理竞赛复赛试题及答案
第28届全国中学生物理竞赛复赛试题(2011)一、(20分)如图所示,哈雷彗星绕太阳S 沿椭圆轨道逆时针方向运动,其周期T 为76.1年,1986年它过近日点P 0时与太阳S 的距离r 0=0.590AU ,AU 是天文单位,它等于地球与太阳的平均距离,经过一段时间,彗星到达轨道上的P 点,SP 与SP 0的夹角θP =72.0°。
已知:1AU=1.50×1011m ,引力常量G=6.67×10-11Nm 2/kg 2,太阳质量m S =1.99×1030kg ,试求P 到太阳S 的距离r P 及彗星过P 点时速度的大小及方向(用速度方向与SP 0的夹角表示)。
二、(20分)质量均匀分布的刚性杆AB 、CD如图放置,A 点与水平地面接触,与地面间的静摩擦系数为μA ,B 、D 两点与光滑竖直墙面接触,杆AB 和CD 接触处的静摩擦系数为μC ,两杆的质量均为m ,长度均为l 。
1、已知系统平衡时AB 杆与墙面夹角为θ,求CD 杆与墙面夹角α应该满足的条件(用α及已知量满足的方程式表示)。
2、若μA =1.00,μC =0.866,θ=60.0°。
求系统平衡时α的取值范围(用数值计算求出)。
三、(25分)在人造卫星绕星球运行的过程中,为了保持其对称转轴稳定在规定指向,一种最简单的办法就是让卫星在其运行过程中同时绕自身的对称轴转,但有时为了改变卫星的指向,又要求减慢或者消除卫星的旋转,减慢或者消除卫星旋转的一种方法就是所谓消旋法,其原理如图所示。
一半径为R ,质量为M 的薄壁圆筒,,其横截面如图所示,图中O 是圆筒的对称轴,两条足够长的不可伸长的结实的长度相等的轻绳的一端分别固定在圆筒表面上的Q 、Q ′(位于圆筒直径两端)处,另一端各拴有一个质量为2m的小球,正常情况下,绳绕在圆筒外表面上,两小球用插销分别锁定在圆筒表面上的P 0、P 0′处,与卫星形成一体,绕卫星的对称轴旋转,卫星自转的角速度为ω0。
2005年第22届全国中学生物理竞赛预赛和复赛试题(附标准答案)
九、 (30 分)如图所示,水平放置的金属细圆环半径为 a,竖直放置的 金属细圆柱(其半径比 a 小得多)的端面与金属圆环的上表面在同一平 面内,圆柱的细轴通过圆环的中心 O. 一质量为 m, 电阻为 R 的均匀导 体细棒被圆环和细圆柱端面支撑,棒的一端有一小孔套在细轴 O 上, 另一端 A 可绕轴线沿圆环作圆周运动,棒与圆环的摩擦系数为.圆环 处于磁感应强度大小为 B Kr 、方向竖直向上的恒定磁场中,式中 K 为大于零的常量,r 为场点到轴线的距离.金属细圆柱与圆环用导线 ed 连接.不计棒与轴及与细圆柱端面的摩擦,也不计细圆柱、圆环及导线 的电阻和感应电流产生的磁场. 问沿垂直于棒的方向以多大的水平外力 作用于棒的 A 端才能使棒以角速度 匀速转动. 注: x Δx x 3 3x 2 Δx 3xΔx Δx
(4)
评分标准:本题 17 分. 正确画出装置示意图给 5 分.(1)式、(2)式各 4 分,(3)式、(4)式各 2 分.
三、
S
M r S O N
S
M S
2R
2R
R
r O O N
图1
图2
自 S 作球的切线 S,并画出 S 经管壁反射形成的虚像点 S ,及由 S 画出球面的切线 S N,如图 1 所示, 由图可看出,只要 S M 和 S N 之间有一夹角,则筒壁对从 S 向右的光线的反射光线就有一部分进入球的右方, 不会完全落在球上被吸收. 由图可看出,如果 r 的大小恰能使 S N 与 S M 重合,如图 2,则 r就是题所要求的筒的内半径的最大值.这 时 SM 与 MN 的交点到球心的距离 MO 就是所要求的筒的半径 r.由图 2 可得
(2)
在温度升高T 的同时,气体体积膨胀,推动液柱克服大气压力做功.设液柱的位移为 Δl ,则气体对外做功
第35届全国中学生物理竞赛复赛理论考试试题解答
1 r2
1 2GM
r1
r1v12
1
③
显然, r2 R ,且有限,故有
0 1 1
④
r2 R
由③④式得,当 r1 给定时, v1 必须满足
2GMR
r1 r1 R
v1
2GM .
r1
由题意知
r1 R h , v1 v0
故有
R
2GMR
h2R
h
v0
2GM Rh
⑤
(2)如果
v0
2GMR
R h2R h
‐A0
O
x
弹簧相对于其原长的伸长记为 A0 ( A0 0 ,但 A0 并不是已知量)。重力加速度大小为 g ,
假设最大静摩擦力等于滑动摩擦力。
(1)如果小球至多只能向右运动,求小球最终静止的位置,和此种情形下 A0 应满足的条件; (2)如果小球完成第一次向右运动至原点右边后,至多只能向左运动,求小球最终静止的
r2
d dt
2
G
Mm r
1 2
mv02
G
Mm Rh
⑫
消去 d 得 dt
dr dt
R h2
r2
v02
2GM r
v02
2GM Rh
⑬
物体从开始发射直至落地需要的时间为
Rh
t R
dr
R h2
r2
v02
2GM r
v02
2GM Rh
⑭
Rh
R
rdr
v02
2GM Rh
r
2
2GMr
R
h2
v 02
a bx cx2 c
b
2 c 3/ 2
第28届全国中学生物理竞赛复赛试题及答案解析(纯word版)
第28届全国中学生物理竞赛复赛试题2011 一、(20分)如图所示,哈雷彗星绕太阳S沿椭圆轨道逆时针方向运动,其周期T为76.1年。
1986年它过近日点P0时,与太阳S的距离r0=0.590AU,AU是天文单位,它等于地球与太阳的平均距离。
经过一段时间,彗星到达轨道上的P点,SP与SP0的夹角θP=72.0°.已知:1AU=1.50×1011m,引力常量G=6.67×10-11m3•kg-1•s-2,太阳质量m S=1.99×1030kg.试求P到太阳S的距离r P及彗星过P点时速度的大小及方向(用速度方向与SP0的夹角表示)。
二、(20分)质量均匀分布的刚性杆AB、CD如图放置,A点与水平地面接触,与地面间的静摩擦因数为μA,B、D两点与光滑竖直墙面接触,杆A B和CD接触处的静摩擦因数为μC,两杆的质量均为m,长度均为l.(1)已知系统平衡时AB杆与墙面夹角θ,求CD杆与墙面的夹角α应满足的条件(用α及已知量满足的方程式表示)。
(2)若μA=1.00,μC=0.866,θ=60.0°,求系统平衡时α的取值范围(用数值计算求出)。
三、(25分)人造卫星绕星球运行的过程中,为了保持其对称轴稳定在规定指向,一种最简单的办法就是让卫星在其运行过程中同时绕自身的对称轴旋转。
但有时为了改变卫星的指向,又要求减慢或者消除卫星的旋转。
减慢或者消除卫星旋转的一种方法是所谓的“YO—YO”消旋法,其原理如图。
设卫星是一半径为R、质量为M的薄壁圆筒,其横截面如图所示。
图中O是圆筒的对称轴。
两条足够长的不可伸长的结实的长度相等的轻绳的一端分别固定在圆筒表面上的Q、Q'(位于圆筒直径两端)处,另一端各拴有一质量为m/2的小球。
正常情况下,绳绕在圆筒外表面上,两小球用插销分别锁定在圆筒表面上的P0、P0'处,与卫星形成一体,绕卫星的对称轴旋转。
卫星自转的角速度为ω0.若要使卫星减慢或停止旋转(消旋),可瞬间撤去插销释放小球,让小球从圆筒表面甩开,在甩开的整个过程中,从绳与圆筒表面相切点到小球的那段绳都是拉直的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第24届全国中学生物理竞赛复赛试题参考解答 一、参考解答: 如果小球的水平速度比较大,它与平板的第一次碰撞正好发生在平板的边缘Q处,这时0u的值便是满足题中条件的最大值;如果小球的水平速度0u较小,在它与平板发生第一次碰撞后再次接近平板时,刚好从平板的边缘Q处越过而不与平板接触,这时
0u的值便是满足题中条件的最小值.
设小球从台面水平抛出到与平板发生第一次碰撞经历的时间为1t,有 21
1
2hgt (1)
若碰撞正好发生在Q处,则有 01Lut (2)
从(1)、(2)两式解得的0u值便是满足题中条件的最大值,即
0max2guLh
(3)
代入有关数据得 0max0.71m/su (4)
如果00maxuu,小球与平板的碰撞处将不在Q点.设小球第一次刚要与平板碰撞时在竖直方向的速度为1v,则有
12ghv (5)
以1v、1V分别表示碰撞结束时刻小球和平板沿竖直方向的速度,由于碰撞时间极短,在碰撞过程中,小球和平板在竖直方向的动量守恒.设小球和平板的质量都是m,则有
111mVmv=mv (6)
因为碰撞是弹性的,且平板是光滑的,由能量守恒可得
2222210110
11111
22222mVmvmu=mvmu (7)
解(6)、(7)两式,得 10v (8)
112Vgh=v (9)
碰撞后,平板从其平衡位置以1V为初速度开始作简谐振动.取固定坐标,其原点O与平板处于平衡位置时板的上表面中点重合,x轴的方向竖直向下,若以小球和平板发生碰撞的时刻作为0t,则平板在t时刻离开平衡位置的位移 PQcosxAt (10)
h P Q
B u
0
式中 2πT (11)
A和是两个待定的常量,利用参考圆方法,在t时刻平板振动的速度 PQsinAtv (12)
因0t时,PQ0x.PQVv,由(9)、(11)、(12)式可求得 22ghAT (13)
π2 (14)
把(13)、(14)式代入(10)式,得
PQ22ππcos2π2ghxTtT
(15)
碰撞后,小球开始作平抛运动.如果第一次碰撞后,小球再经过时间2t与平板发生第二次碰撞且发生在Q处,则在发生第二次碰撞时,小球的x座标为 2
B22
1
2xtgt (16)
平板的x座标为 PQ22
22ππcos2π2gh
xtTtT
(17)
在碰撞时,有 B2PQ2xtxt (18)
由(16)、(17)、(18)式,代入有关数据得 222
π4.904.41cosπ2tt
(19)
这便是2t满足的方程式,通过数值计算法求解方程可得(参见数值列表) 20.771st (20)
如果第二次碰撞正好发生在平板的边缘Q处,则有 012Lutt (21)
由(1)、(20)和(21)式得
012
0.46m/sLutt
(22)
而满足题中要求的0u的最小值应大于(22)式给出的值.综合以上讨论,0u的取值范围是
00.46m/s0.71m/su (23)
附:(19)式的数值求解 用数值解法则要代入2t不同数值,逐步逼近所求值,列表如下:
2t 0.730 0.750 0.760 0.765 0.770 0.771 0.772 0.775 0.780 0.790 0.810
2π4.41cosπ2PQxt 3.31 3.12 3.02 2.96 2.91 2.91 2.90 2.86 2.81 2.70 2.48
224.90Bxt 2.61 2.76 2.83 2.87 2.91 2.91 2.91 2.94 2.98 3.06 3.21
PQBxx 0.70 0.36 0.19 0.09 0 0 -0.01 -0.08 -0.17 -0.36 -0.73
二、参考解答: 解法一 因为B点绕A轴作圆周运动,其速度的大小为
Blv (1)
B点的向心加速度的大小为 2Bal (2)
因为是匀角速转动,B点的切向加速度为0,故Ba也是B点的加速度,其方向沿BA方向.因为C点绕D轴作圆周运动,其速度的大小用Cv表示,方向垂直于杆CD,在考察的时刻,由图可知,其方向沿杆BC
方向.因BC是刚性杆,所以B点和C点沿BC方向的速度必相等,故有
Cπ2cos42lBvv (3)
此时杆CD绕D轴按顺时针方向转动,C点的法向加速度 2CCnaCD
v (4)
由图可知22CDl,由(3)、(4)式得 228Cnal (5)
其方向沿CD方向. 下面来分析C点沿垂直于杆CD方向的加速度,即切向加速度Cta.因为BC是刚性杆,所以C点相对B点的运动只能是绕B的转动,C点相对B点的速度方向必垂直于杆BC.令CBv表示其速度的大小,根据速度合成公式有
CBCBvvv
由几何关系得
222222CBBCBlvvvv (6)
由于C点绕B作圆周运动,相对B的向心加速度
CBv
A C
D B Bv
Cv
aCn aC t
aC
2CBCBaCB
v (7)
因为2CBl,故有
224CBal (8)
其方向垂直杆CD. 由(2)式及图可知,B点的加速度沿BC杆的分量为
πcos4BBBCaa (9)
所以C点相对A点(或D点)的加速度沿垂直于杆CD方向的分量 2324CtCBBBCaaal (10)
C点的总加速度为C点绕D点作圆周运动的法向加速度Cna与切向加速度Cta的合加速度,即 222748CCnCtaaal (11)
Ca的方向与杆CD间的夹角
arctanarctan680.54CtCnaa (12)
解法二:通过微商求C点加速度 以固定点A为原点作一直角坐标系Axy,Ax轴与AD重合,Ay与AD垂直.任意时刻t,连杆的位形如图所示,此时各杆的位置分别用,和表示,且已知ABl,
2BCl,22CDl,3ADl,ddt,C点坐
标表示为 cos2cosCxll (1)
sin2sinCyll (2)
A
B C D
x
y
将(1)、(2)式对时间t求一阶微商,得 dddsin2sindddCxlttt
(3)
dddcos2cosdddCylttt
(4)
把(3)、(4)式对时间t求一阶微商,得 22222
222dddddcossin2cos2sindddddCx
lttttt
(5)
22222
222dddddsincos2sin2cosdddddCy
lttttt
(6)
根据几何关系,有 sinsinsinCDABBC coscoscos3CDABBCl 即
22sinsin2sin (7)
22cos3cos2cos (8)
将(7)、(8)式平方后相加且化简,得 2sinsin2coscos3cos32cos20 (9)
对(9)式对时间t求一阶微商,代入π2,π4,ddt,得 d1d2t
(10)
对(9)式对时间t求二阶微商,并代入上述数据,得 22
2
d3
d8t
(11)
将(10)、(11)式以及,,ddt的数值代入(5)、(6)式,得 22
2
d5d8Cxlt
22
2
d7d8Cylt
所以 2222
2
22
dd74dd8CCCxyaltt
(12)
由图知,Ca与x轴的夹角为
