2019-2020年中考数学总复习第二编中档题型突破专项训练篇中档题型训练七网格中的图形变换试题

合集下载

2019-2020学年中考复习：人教版九下数学平面直角坐标系专题突破精讲精练(含答案)

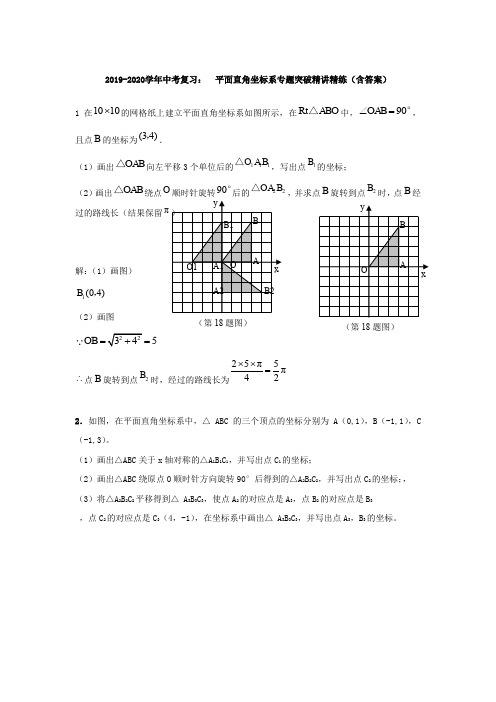
2019-2020学年中考复习：平面直角坐标系专题突破精讲精练（含答案）1在1010⨯的网格纸上建立平面直角坐标系如图所示，在Rt ABO △中，90OAB ∠=°，且点B 的坐标为(34)，．（1）画出OAB △向左平移3个单位后的111O A B △，写出点1B 的坐标；（2）画出OAB △绕点O 顺时针旋转90°后的22OA B △，并求点B 旋转到点2B 时，点B 经过的路线长（结果保留π解：（1）画图）1(04)B ，（2）画图22345OB =+=∴点B 旋转到点2B 时，经过的路线长为25π5π42⨯⨯=2．如图，在平面直角坐标系中，△ ABC 的三个顶点的坐标分别为A （0,1），B （-1,1），C （-1,3）。

（1）画出△ABC 关于x 轴对称的△A 1B 1C 1，并写出点C 1的坐标；（2）画出△ABC 绕原点O 顺时针方向旋转90°后得到的△A 2B 2C 2，并写出点C 2的坐标；，（3）将△A 2B 2C 2平移得到△ A 3B 3C 3，使点A 2的对应点是A 3，点B 2的对应点是B 3 ，点C 2的对应点是C 3（4，-1），在坐标系中画出△ A 3B 3C 3，并写出点A 3，B 3的坐标。

（第18题图）（第18题图）【答案】（1）C1(-1,-3) (2)C2(3,1) (3)A3(2,-2),B3(2,-1)3．常用的确定物体位置的方法有两种.如图，在4×4个边长为1的正方形组成的方格中，标有A，B两点. 请你用两种不同方法表述点B相对点A的位置.【答案】方法1．用有序实数对(a，b)表示.比如：以点A为原点，水平方向为x轴，建立直角坐标系，则B(3，3). --- 3分方法2. 用方向和距离表示.比如: B点位于A点的东北方向（北偏东45°等均可），距离Ａ点32处． --- 3分4.一动点沿着数轴向右平移3个单位，再向左平移2个单位，相当于向右平移1个单位．用实数加法表示为 3+（2）=1．若坐标平面上的点作如下平移：沿x轴方向平移的数量为a（向右为正，向左为负，平移a 个单位），沿y 轴方向平移的数量为b （向上为正，向下为负，平移b 个单位），则把有序数对{a ，b }叫做这一平移的“平移量”；“平移量”{a ，b }与“平移量”{c ，d }的加法运算法则为}{}{}{d b c a d c b a ++=+，，，．解决问题：（1）计算：{3，1}+{1，2}；{1，2}+{3，1}．（2）①动点P 从坐标原点O 出发，先按照“平移量”{3，1}平移到A ，再按照“平移量”{1，2}平移到B ；若先把动点P 按照“平移量”{1，2}平移到C ，再按照“平移量” {3，1}平移，最后的位置还是点B 吗? 在图1中画出四边形OABC . ②证明四边形OABC 是平行四边形.（3）如图2，一艘船从码头O 出发，先航行到湖心岛码头P （2，3），再从码头P 航行到码头Q （5，5），最后回到出发点O . 请用“平移量”加法算式表示它的航行过程．【答案】（1）{3，1}+{1，2}={4，3}． ………………………………………………2分{1，2}+{3，1}={4，3}． (2)分（2）①画图 …………………………………………………2分最后的位置仍是B ．……………………………………1分 ② 证明：由①知，A （3，1），B(4，3)，C （1，2） ∴OC=AB =2221+=5，OA=BC =2213+=10，∴四边形OABC 是平行四边形．…………………………3分（3）{2，3}+{3，2}+{-5，-5}={0, 0}．……………………2分5．△ABC 在平面直角坐标系中的位置如图所示，A 、B 、C 三点在格点上．（１）作出 △ABC 关于ｙ轴对称的△111A B C ，并写出点1C 的坐标；（第22图1（２）作出△ABC 关于原点O 对称的△222A B C ，并写出点2C 的坐标．【答案】解：（１）（２）如图，点1C 的坐标（－3，2）；点2C 的坐标（－3，－2）．A 1B 22C 1B 1A 26．如图，在平面直角坐标系中，O 为原点，每个小方格的边长为1个单位长度．在第一象限内有横、纵坐标均为整数的A 、B 两点，且OA = OB （1）写出A 、B 两点的坐标；（2）画出线段AB 绕点O 旋转一周所形成的图形，并求其面积（结果保留π）．【答案】解：（1）A 、B 两点坐标分别为A ()1,3、B ()3,1或A ()3,1、B ()1,3 （2）画图(如图)，COB由题意得:大圆半径10=OA ,小圆半径22=OC∴πππ2221022=-=）（）（圆环S7．（2010福建福州）如图,在矩形OABC 中，点B 的坐标为(－2，3)．画出矩形OABC绕点O 顺时针旋转90°后的矩形OA 1B 1C 1，并直接写出点A 1、B 1、C 1的坐标．A第24题BCDO【答案】如图所示，矩形OA 1B 1C 1就是所求作的． A 1(0，2)，B l (3，2)，C 1(3，0)．7．如图，正方形网格中的每一个小正方形的边长都是1，四边形ABCD 的四个顶点都在格点上，O 为AD 边的中点，若把四边形ABCD 绕着点O 顺时针旋转，试解决下列问题：（1）画出四边形ABCD 旋转后的图形；（2）求点C 旋转过程事所经过的路径长；（3）设点B 旋转后的对应点为B ’，求tan ∠DAB ’的值．【答案】8某同学从家里出发，骑自行车上学时，速度v（米/秒）与时间t（秒）的关系如图a，A （10，5），B（130，5），C（135，0）.（1）求该同学骑自行车上学途中的速度v与时间t的函数关系式；（2）计算该同学从家到学校的路程（提示：在OA和BC段的运动过程中的平均速度分别等于它们中点时刻的速度，路程＝平均速度×时间）；（3）如图b，直线x＝t（0≤t≤135），与图a的图象相交于P、Q，用字母S表示图中阴影部分面积，试求S与t的函数关系式；（4）由（2）（3），直接猜出在t时刻，该同学离开家所超过的路程与此时S的数量关系.图a 图b【答案】（1）1(010)25(10130)135(130135)v t t v t v t t ⎧=≤<⎪⎪=≤<⎨⎪=-≤≤⎪⎩ （2）2.5×10+5×120+2×5＝635（米）（3）221(010)4525(10130)1(130135)2S t t S t t S t t ⎧=≤<⎪⎪=-≤<⎨⎪⎪=-≤≤⎩ +135t-8475 (4) 相等的关系9（1）在平面直角坐标系中，将点A （-3，4）向右平移5个单位到点1A ，再将点1A 绕坐标原点顺时针旋转90到点2A ，直接写出点1A ，2A 的坐标；（2）在平面直角坐标系中，将第二象限内的点(),B a b 向右平移m 个单位到点1B ，再将点1B 绕坐标原点顺时针旋转90到点2B ，直接写出点1B ，2B 的坐标；（3）在平面直角坐标系中，将点(),P c d 沿水平方向平移n 个单位到点1P ，再将点1P 绕坐标原点顺时针旋转90到点2P ，直接写出点2P 的坐标；【答案】（解：（1）点A 1的坐标为（2，4），点A 2的坐标为（4，－2）；（2）点B 1的坐标为（a+m ， b ），点A 2的坐标为（b ，－a －m ）；（3）点P 1的坐标为（d ，－c －n ）或（d ，－c ＋n ）；10小明在研究苏教版《有趣的坐标系》后，得到启发，针对正六边形OABCDE ，自己设计了一个坐标系如图，该坐标系以O 为原点，直线OA 为x 轴，直线OE 为y 轴，以正六边形OABCDE 的边长为一个单位长。

2020年中考数学二轮专项冲刺复习——几何综合、压轴题(含详细解答)

2020年中考数学二轮专项冲刺复习——几何综合、压轴题1、（2019河南•中考第22题•10分）在△ABC中，CA＝CB，∠ACB＝α．点P是平面内不与点A，C重合的任意一点．连接AP，将线段AP绕点P逆时针旋转α得到线段DP，连接AD，BD，CP．（1）观察猜想如图1，当α＝60°时，的值是1，直线BD与直线CP相交所成的较小角的度数是60°．（2）类比探究如图2，当α＝90°时，请写出的值及直线BD与直线CP相交所成的小角的度数，并就图2的情形说明理由．（3）解决问题当α＝90°时，若点E，F分别是CA，CB的中点，点P在直线EF上，请直接写出点C，P，D在同一直线上时的值．【考点】相似形综合题．【分析】（1）如图1中，延长CP交BD的延长线于E，设AB交EC于点O．证明△CAP≌△BAD（SAS），即可解决问题．（2）如图2中，设BD交AC于点O，BD交PC于点E．证明△DAB∽△P AC，即可解决问题．（3）分两种情形：①如图3﹣1中，当点D在线段PC上时，延长AD交BC的延长线于H．证明AD＝DC即可解决问题．②如图3﹣2中，当点P在线段CD上时，同法可证：DA＝DC解决问题．【解答】解：（1）如图1中，延长CP交BD的延长线于E，设AB交EC于点O．∵∠P AD＝∠CAB＝60°，∴∠CAP＝∠BAD，∵CA＝BA，P A＝DA，∴△CAP≌△BAD（SAS），∴PC＝BD，∠ACP＝∠ABD，∵∠AOC＝∠BOE，∴∠BEO＝∠CAO＝60°，∴＝1，线BD与直线CP相交所成的较小角的度数是60°，故答案为1，60°．（2）如图2中，设BD交AC于点O，BD交PC于点E．∵∠P AD＝∠CAB＝45°，∴∠P AC＝∠DAB，∵＝＝，∴△DAB∽△P AC，∴∠PCA＝∠DBA，＝＝，∵∠EOC＝∠AOB，∴∠CEO＝∠OABB＝45°，∴直线BD与直线CP相交所成的小角的度数为45°．（3）如图3﹣1中，当点D在线段PC上时，延长AD交BC的延长线于H．∵CE＝EA，CF＝FB，∴EF∥AB，∴∠EFC＝∠ABC＝45°，∵∠P AO＝45°，∴∠P AO＝∠OFH，∵∠POA＝∠FOH，∴∠H＝∠APO，∵∠APC＝90°，EA＝EC，∴PE＝EA＝EC，∴∠EP A＝∠EAP＝∠BAH，∴∠H＝∠BAH，∴BH＝BA，∵∠ADP＝∠BDC＝45°，∴∠ADB＝90°，∴BD⊥AH，∴∠DBA＝∠DBC＝22.5°，∵∠ADB＝∠ACB＝90°，∴A，D，C，B四点共圆，∠DAC＝∠DBC＝22.5°，∠DCA＝∠ABD＝22.5°，∴∠DAC＝∠DCA＝22.5°，∴DA＝DC，设AD＝a，则DC＝AD＝a，PD＝a，∴＝＝2﹣．如图3﹣2中，当点P在线段CD上时，同法可证：DA＝DC，设AD＝a，则CD＝AD＝a，PD＝a，∴PC＝a﹣a，∴＝＝2+．2、（2019陕西•中考第22题•9分）在图1，2，3中，已知ABCDY，120ABC∠=︒，点E为线段BC上的动点，连接AE，以AE为边向上作菱形AEFG，且120EAG∠=︒．（1）如图1，当点E与点B重合时，CEF∠=60︒；（2）如图2，连接AF．①填空：FAD∠EAB∠（填“>”，“<“，“=”)；②求证：点F在ABC∠的平分线上；（3）如图3，连接EG，DG，并延长DG交BA的延长线于点H，当四边形AEGH是平行四边形时，求BCAB的值．【考点】相似形综合题【分析】（1）根据菱形的性质计算；（2）①证明60DAB FAE∠=∠=︒，根据角的运算解答；②作FM BC⊥于M，FN BA⊥交BA的延长线于N，证明AFN EFM∆≅∆，根据全等三角形的性质得到FN FM=，根据角平分线的判定定理证明结论；（3）根据直角三角形的性质得到2GH AH=，证明四边形ABEH为菱形，根据菱形的性质计算，得到答案．【解答】解：（1）Q四边形AEFG是菱形，18060AEF EAG∴∠=︒-∠=︒，60CEF AEC AEF∴∠=∠-∠=︒，故答案为：60︒；（2）①Q四边形ABCD是平行四边形，18060DAB ABC ∴∠=︒-∠=︒，Q 四边形AEFG 是菱形，120EAG ∠=︒，60FAE ∴∠=︒，FAD EAB ∴∠=∠，故答案为：=；②作FM BC ⊥于M ，FN BA ⊥交BA 的延长线于N ，则90FNB FMB ∠=∠=︒，60NFM ∴∠=︒，又60AFE ∠=︒，AFN EFM ∴∠=∠，EF EA =Q ，60FAE ∠=︒，AEF ∴∆为等边三角形，FA FE ∴=，在AFN ∆和EFM ∆中，AFN EFM FNA FME FA FE ∠=∠⎧⎪∠=∠⎨⎪=⎩，()AFN EFM AAS ∴∆≅∆，FN FM ∴=，又FM BC ⊥，FN BA ⊥，∴点F 在ABC ∠的平分线上；（3）Q 四边形AEFG 是菱形，120EAG ∠=︒，60AGF ∴∠=︒，30FGE AGE ∴∠=∠=︒，Q 四边形AEGH 为平行四边形，//GE AH ∴，30GAH AGE ∴∠=∠=︒，30H FGE ∠=∠=︒，90GAH ∴∠=︒，又30AGE ∠=︒，2GH AH ∴=，60DAB ∠=︒Q ，30H ∠=︒，30ADH ∴∠=︒，AD AH GE ∴==，Q 四边形ABEH 为平行四边形，BC AD ∴=，BC GE ∴=，Q 四边形ABEH 为平行四边形，30HAE EAB ∠=∠=︒，∴平行四边形ABEH 为菱形，AB AH HE ∴==，3GE AB ∴=， ∴3BC AB=．3、（2019上海•中考第22题•10分）图1是某小型汽车的侧面示意图，其中矩形ABCD 表示该车的后备箱，在打开后备箱的过程中，箱盖ADE 可以绕点A 逆时针方向旋转，当旋转角为60︒时，箱盖ADE 落在AD E ''的位置（如图2所示）．已知90AD =厘米，30DE =厘米，40EC =厘米．（1）求点D '到BC 的距离；（2）求E 、E '两点的距离．【考点】解直角三角形的应用；矩形的性质【分析】（1）过点D '作D H BC '⊥，垂足为点H ，交AD 于点F ，利用旋转的性质可得出90AD AD '==厘米，60DAD ∠'=︒，利用矩形的性质可得出90AFD BHD ∠'=∠'=︒，在Rt △AD F '中，通过解直角三角形可求出D F '的长，结合FH DC DE CE ==+及D H D F FH '='+可求出点D '到BC 的距离；（2）连接AE ，AE '，EE '，利用旋转的性质可得出AE AE '=，60EAE ∠'=︒，进而可得出AEE ∆'是等边三角形，利用等边三角形的性质可得出EE AE '=，在Rt ADE ∆中，利用勾股定理可求出AE 的长度，结合EE AE '=可得出E 、E '两点的距离．【解答】解：（1）过点D '作D H BC '⊥，垂足为点H ，交AD 于点F ，如图3所示．由题意，得：90AD AD '==厘米，60DAD ∠'=︒．Q 四边形ABCD 是矩形，//AD BC ∴，90∴∠'=∠'=︒．AFD BHD在Rt△AD F'中，sin90sin60453g厘米．D F AD DAD'='∠'=⨯︒=又40Q厘米，30DE=厘米，CE=∴==+=厘米，FH DC DE CE70∴'='+=+厘米．D H D F FH(45370)答：点D'到BC的距离为(45370)+厘米．（2）连接AE，AE'，EE'，如图4所示．由题意，得：AE AE'=，60∠'=︒，EAE∴∆'是等边三角形，AEE∴'=．EE AEQ四边形ABCD是矩形，90∴∠=︒．ADE在Rt ADEDE=厘米，AD=厘米，30∆中，90223010∴=+=厘米，AE AD DE∴'=厘米．EE3010答：E、E'两点的距离是3010厘米．4、（2019河南•中考第17题•9分）如图，在△ABC中，BA＝BC，∠ABC＝90°，以AB为直径的半圆O交AC于点D，点E是上不与点B，D重合的任意一点，连接AE交BD于点F，连接BE并延长交AC于点G．（1）求证：△ADF≌△BDG；（2）填空：①若AB＝4，且点E是的中点，则DF的长为4﹣2；②取的中点H，当∠EAB的度数为30°时，四边形OBEH为菱形．【考点】圆的综合题．【分析】（1）利用直径所对的圆周角是直角，可得∠ADB＝∠AEB＝90°，再应用同角的余角相等可得∠DAF＝∠DBG，易得AD＝BD，△ADF≌△BDG得证；（2）作FH⊥AB，应用等弧所对的圆周角相等得∠BAE＝∠DAE，再应用角平分线性质可得结论；由菱形的性质可得BE＝OB，结合三角函数特殊值可得∠EAB＝30°．【解答】解：（1）证明：如图1，∵BA＝BC，∠ABC＝90°，∴∠BAC＝45°∵AB是⊙O的直径，∴∠ADB＝∠AEB＝90°，∴∠DAF+∠BGD＝∠DBG+∠BGD＝90°∴∠DAF＝∠DBG∵∠ABD+∠BAC＝90°∴∠ABD＝∠BAC＝45°∴AD＝BD∴△ADF≌△BDG（ASA）；（2）①如图2，过F作FH⊥AB于H，∵点E是的中点，∴∠BAE＝∠DAE∵FD⊥AD，FH⊥AB∴FH＝FD∵＝sin∠ABD＝sin45°＝，∴，即BF＝FD∵AB＝4，∴BD＝4cos45°＝2，即BF+FD＝2，（+1）FD＝2∴FD＝＝4﹣2故答案为．②连接OE，EH，∵点H是的中点，∴OH⊥AE，∵∠AEB＝90°∴BE⊥AE∴BE∥OH∵四边形OBEH为菱形，∴BE＝OH＝OB＝AB∴sin∠EAB＝＝∴∠EAB＝30°．故答案为：30°5、（2019河北•中考第23题•9分）如图，△ABC和△ADE中，AB＝AD＝6，BC＝DE，∠B＝∠D＝30°，边AD与边BC交于点P（不与点B，C重合），点B，E在AD异侧，I为△APC的内心．（1）求证：∠BAD＝∠CAE；（2）设AP＝x，请用含x的式子表示PD，并求PD的最大值；（3）当AB⊥AC时，∠AIC的取值范围为m°＜∠AIC＜n°，分别直接写出m，n的值．【考点】圆的综合题．【分析】（1）由条件易证△ABC≌△ADE，得∠BAC＝∠DAE，∴∠BAD＝∠CAE．（2）PD＝AD﹣AP＝6﹣x，∵点P在线段BC上且不与B、C重合，∴AP的最小值即AP⊥BC时AP的长度，此时PD可得最大值．（3）I为△APC的内心，即I为△APC角平分线的交点，应用“三角形内角和等于180°“及角平分线定义即可表示出∠AIC，从而得到m，n的值．【解答】解：（1）在△ABC和△ADE中，（如图1）∴△ABC≌△ADE（SAS）∴∠BAC＝∠DAE即∠BAD+∠DAC＝∠DAC+∠CAE∴∠BAD＝∠CAE．（2）∵AD＝6，AP＝x，∴PD＝6﹣x当AD⊥BC时，AP＝AB＝3最小，即PD＝6﹣3＝3为PD的最大值．（3）如图2，设∠BAP＝α，则∠APC＝α+30°，∵AB⊥AC∴∠BAC＝90°，∠PCA＝60°，∠P AC＝90°﹣α，∵I为△APC的内心∴AI、CI分别平分∠P AC，∠PCA，∴∠IAC＝∠P AC，∠ICA＝∠PCA∴∠AIC＝180°﹣（∠IAC+∠ICA）＝180°﹣（∠P AC+∠PCA）＝180°﹣（90°﹣α+60°）＝α+105°∵0＜α＜90°，∴105°＜α+105°＜150°，即105°＜∠AIC＜150°，∴m＝105，n＝150．6、（2019海南•中考第21题•13分）如图，在边长为1的正方形ABCD中，E是边CD的中点，点P是边AD上一点（与点A、D不重合），射线PE与BC的延长线交于点Q．（1）求证：△PDE≌△QCE；（2）过点E作EF∥BC交PB于点F，连结AF，当PB＝PQ时，①求证：四边形AFEP是平行四边形；②请判断四边形AFEP是否为菱形，并说明理由．【考点】四边形综合题．【分析】（1）由四边形ABCD是正方形知∠D＝∠ECQ＝90°，由E是CD的中点知DE＝CE，结合∠DEP＝∠CEQ即可得证；（2）①由PB＝PQ知∠PBQ＝∠Q，结合AD∥BC得∠APB＝∠PBQ＝∠Q＝∠EPD，由△PDE≌△QCE知PE ＝QE，再由EF∥BQ知PF＝BF，根据Rt△P AB中AF＝PF＝BF知∠APF＝∠P AF，从而得∠P AF＝∠EPD，据此即可证得PE∥AF，从而得证；②设AP＝x，则PD＝1﹣x，若四边形AFEP是菱形，则PE＝P A＝x，由PD2+DE2＝PE2得关于x的方程，解之求得x的值，从而得出四边形AFEP为菱形的情况．【解答】解：（1）∵四边形ABCD是正方形，∴∠D＝∠ECQ＝90°，∵E是CD的中点，∴DE＝CE，又∵∠DEP＝∠CEQ，∴△PDE≌△QCE（ASA）；（2）①∵PB＝PQ，∴∠PBQ＝∠Q，∵AD∥BC，∴∠APB＝∠PBQ＝∠Q＝∠EPD，∵△PDE≌△QCE，∴PE＝QE，∵EF∥BQ，∴PF＝BF，∴在Rt△P AB中，AF＝PF＝BF，∴∠APF＝∠P AF，∴∠P AF＝∠EPD，∴PE∥AF，∵EF∥BQ∥AD，∴四边形AFEP是平行四边形；②当AP＝时，四边形AFEP是菱形．设AP＝x，则PD＝1﹣x，若四边形AFEP是菱形，则PE＝P A＝x，∵CD＝1，E是CD中点，∴DE＝，在Rt△PDE中，由PD2+DE2＝PE2得（1﹣x）2+（）2＝x2，解得x＝，即当AP＝时，四边形AFEP是菱形．7、（2019福建•中考第21题•8分）在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，将△ABC绕点A顺时针旋转一定的角度α得到△DEC，点A、B的对应点分别是D、E．（1）当点E恰好在AC上时，如图1，求∠ADE的大小；（2）若α＝60°时，点F是边AC中点，如图2，求证：四边形BEDF是平行四边形．【考点】平行四边形的判定；旋转的性质．【分析】（1）如图1，利用旋转的性质得CA＝CD，∠ECD＝∠BCA＝30°，∠DEC＝∠ABC＝90°，再根据等腰三角形的性质和三角形内角和计算出∠CAD，从而利用互余和计算出∠ADE的度数；（2）如图2，利用直角三角形斜边上的中线性质得到BF＝AC，利用含30度的直角三角形三边的关系得到AB ＝AC，则BF＝AB，再根据旋转的性质得到∠BCE＝∠ACD＝60°，CB＝CE，DE＝AB，从而得到DE＝BF，△ACD和△BCE为等边三角形，接着证明△CFD≌△ABC得到DF＝BC，然后根据平行四边形的判定方法得到结论．【解答】（1）解：如图1，∵△ABC绕点A顺时针旋转α得到△DEC，点E恰好在AC上，∴CA＝CD，∠ECD＝∠BCA＝30°，∠DEC＝∠ABC＝90°，∵CA＝CD，∴∠CAD＝∠CDA＝（180°﹣30°）＝75°，∴∠ADE＝90°﹣75°＝15°；（2）证明：如图2，∵点F是边AC中点，∴BF＝AC，∵∠ACB＝30°，∴AB＝AC，∴BF＝AB，∵△ABC绕点A顺时针旋转60得到△DEC，∴∠BCE＝∠ACD＝60°，CB＝CE，DE＝AB，∴DE＝BF，△ACD和△BCE为等边三角形，∴BE＝CB，∵点F为△ACD的边AC的中点，∴DF⊥AC，易证得△CFD≌△ABC，∴DF＝BC，∴DF＝BE，而BF＝DE，∴四边形BEDF是平行四边形．8、（2019北京•中考第20题•5分）如图，在菱形ABCD中，AC为对角线，点E，F分别在AB，AD上，BE＝DF，连接EF．（1）求证：AC⊥EF；（2）延长EF交CD的延长线于点G，连接BD交AC于点O．若BD＝4，tan G＝，求AO的长．【考点】全等三角形的判定与性质；菱形的性质；解直角三角形．【分析】（1）由菱形的性质得出AB＝AD，AC⊥BD，OB＝OD，得出AB：BE＝AD：DF，证出EF∥BD即可得出结论；（2）由平行线的性质得出∠G＝∠ADO，由三角函数得出tan G＝tan∠ADO＝＝，得出OA＝OD，由BD ＝4，得出OD＝2，得出OA＝1．【解答】（1）证明：连接BD，如图1所示：∵四边形ABCD是菱形，∴AB＝AD，AC⊥BD，OB＝OD，∵BE＝DF，∴AB：BE＝AD：DF，∴EF∥BD，∴AC⊥EF；（2）解：如图2所示：∵由（1）得：EF∥BD，∴∠G＝∠ADO，∴tan G＝tan∠ADO＝＝，∴OA＝OD，∵BD＝4，∴OD＝2，∴OA＝1．10、（2019北京•中考第27题•7分）已知∠AOB＝30°，H为射线OA上一定点，OH＝+1，P为射线OB上一点，M为线段OH上一动点，连接PM，满足∠OMP为钝角，以点P为中心，将线段PM顺时针旋转150°，得到线段PN，连接ON．（1）依题意补全图1；（2）求证：∠OMP＝∠OPN；（3）点M关于点H的对称点为Q，连接QP．写出一个OP的值，使得对于任意的点M总有ON＝QP，并证明．【考点】三角形综合题．【分析】（1）根据题意画出图形．（2）由旋转可得∠MPN＝150°，故∠OPN＝150°﹣∠OPM；由∠AOB＝30°和三角形内角和180°可得∠OMP ＝180°﹣30°﹣∠OPM＝150°﹣∠OPM，得证．（3）根据题意画出图形，以ON＝QP为已知条件反推OP的长度．由（2）的结论∠OMP＝∠OPN联想到其补角相等，又因为旋转有PM＝PN，已具备一边一角相等，过点N作NC⊥OB于点C，过点P作PD⊥OA于点D，即可构造出△PDM≌△NCP，进而得PD＝NC，DM＝CP．此时加上ON＝QP，则易证得△OCN≌△QDP，所以OC＝QD．利用∠AOB＝30°，设PD＝NC＝a，则OP＝2a，OD＝a．再设DM＝CP＝x，所以QD＝OC＝OP+PC ＝2a+x，MQ＝DM+QD＝2a+2x．由于点M、Q关于点H对称，即点H为MQ中点，故MH＝MQ＝a+x，DH ＝MH﹣DM＝a，所以OH＝OD+DH＝a+a＝+1，求得a＝1，故OP＝2．证明过程则把推理过程反过来，以OP＝2为条件，利用构造全等证得ON＝QP．【解答】解：（1）如图1所示为所求．（2）设∠OPM＝α，∵线段PM绕点P顺时针旋转150°得到线段PN∴∠MPN＝150°，PM＝PN∴∠OPN＝∠MPN﹣∠OPM＝150°﹣α∵∠AOB＝30°∴∠OMP＝180°﹣∠AOB﹣∠OPM＝180°﹣30°﹣α＝150°﹣α∴∠OMP＝∠OPN（3）OP＝2时，总有ON＝QP，证明如下：过点N作NC⊥OB于点C，过点P作PD⊥OA于点D，如图2∴∠NCP＝∠PDM＝∠PDQ＝90°∵∠AOB＝30°，OP＝2∴PD＝OP＝1∴OD＝∵OH＝+1∴DH＝OH﹣OD＝1∵∠OMP＝∠OPN∴180°﹣∠OMP＝180°﹣∠OPN即∠PMD＝∠NPC在△PDM与△NCP中∴△PDM≌△NCP（AAS）∴PD＝NC，DM＝CP设DM＝CP＝x，则OC＝OP+PC＝2+x，MH＝MD+DH＝x+1∵点M关于点H的对称点为Q∴HQ＝MH＝x+1∴DQ＝DH+HQ＝1+x+1＝2+x∴OC＝DQ在△OCN与△QDP中∴△OCN≌△QDP（SAS）∴ON＝QP11、（2019北京•中考第28题•7分）在△ABC中，D，E分别是△ABC两边的中点，如果上的所有点都在△ABC的内部或边上，则称为△ABC的中内弧．例如，图1中是△ABC的一条中内弧．（1）如图2，在Rt△ABC中，AB＝AC＝，D，E分别是AB，AC的中点，画出△ABC的最长的中内弧，并直接写出此时的长；（2）在平面直角坐标系中，已知点A（0，2），B（0，0），C（4t，0）（t＞0），在△ABC中，D，E分别是AB，AC的中点．①若t＝，求△ABC的中内弧所在圆的圆心P的纵坐标的取值范围；②若在△ABC中存在一条中内弧，使得所在圆的圆心P在△ABC的内部或边上，直接写出t的取值范围．【考点】圆的综合题．【分析】（1）由三角函数值及等腰直角三角形性质可求得DE＝2，最长中内弧即以DE为直径的半圆，的长即以DE为直径的圆周长的一半；（2）根据三角形中内弧定义可知，圆心一定在DE的中垂线上，①当t＝时，要注意圆心P在DE上方的中垂线上均符合要求，在DE下方时必须AC与半径PE的夹角∠AEP满足90°≤∠AEP＜135°；②根据题意，t的最大值即圆心P在AC上时求得的t值．【解答】解：（1）如图2，以DE为直径的半圆弧，就是△ABC的最长的中内弧，连接DE，∵∠A＝90°，AB＝AC＝，D，E分别是AB，AC的中点，∴BC＝＝＝4，DE＝BC＝×4＝2，∴弧＝×2π＝π；（2）如图3，由垂径定理可知，圆心一定在线段DE的垂直平分线上，连接DE，作DE垂直平分线FP，作EG ⊥AC交FP于G，①当t＝时，C（2，0），∴D（0，1），E（1，1），F（，1），设P（，m）由三角形中内弧定义可知，圆心线段DE上方射线FP上均可，∴m≥1，∵OA＝OC，∠AOC＝90°∴∠ACO＝45°，∵DE∥OC∴∠AED＝∠ACO＝45°作EG⊥AC交直线FP于G，FG＝EF＝根据三角形中内弧的定义可知，圆心在点G的下方（含点G）直线FP上时也符合要求；∴m≤综上所述，m≤或m≥1．②如图4，设圆心P在AC上，∵P在DE中垂线上，∴P为AE中点，作PM⊥OC于M，则PM＝，∴P（t，），∵DE∥BC∴∠ADE＝∠AOB＝90°∴AE＝＝＝，∵PD＝PE，∴∠AED＝∠PDE∵∠AED+∠DAE＝∠PDE+∠ADP＝90°，∴∠DAE＝∠ADP∴AP＝PD＝PE＝AE由三角形中内弧定义知，PD≤PM∴AE≤，AE≤3，即≤3，解得：t≤，∵t＞0∴0＜t≤．12、（2019安徽•中考第20题•10分）如图，点E在ABCDY内部，//AF BE，//DF CE．（1）求证：BCE ADF∆≅∆；（2）设ABCDY的面积为S，四边形AEDF的面积为T，求ST的值．【考点】全等三角形的判定与性质；平行四边形的性质【分析】（1）根据ASA 证明：BCE ADF ∆≅∆；（2）根据点E 在ABCD Y 内部，可知：12BEC AED ABCD S S S ∆∆+=Y ，可得结论．【解答】解：（1）Q 四边形ABCD 是平行四边形，AD BC ∴=，//AD BC ，180ABC BAD ∴∠+∠=︒，//AF BE Q ，180EAB BAF ∴∠+∠=︒，CBE DAF ∴∠=∠，同理得BCE ADF ∠=∠，在BCE ∆和ADF ∆中，Q CBE DAF BC AD BCE ADF ∠=∠⎧⎪=⎨⎪∠=∠⎩，()BCE ADF ASA ∴∆≅∆；（2）Q 点E 在ABCD Y 内部，12BEC AED ABCD S S S ∆∆∴+=Y ，由（1）知：BCE ADF ∆≅∆，BCE ADF S S ∆∆∴=，12ADF AED BEC AED ABCD AEDF S S S S S S ∆∆∆∆∴=+=+=Y 四边形， ABCD QY 的面积为S ，四边形AEDF 的面积为T ， ∴212S S T S ==． 13、如图，矩形ABCD 中，点E 在边CD 上，将BCE ∆沿BE 折叠，点C 落在AD 边上的点F 处，过点F 作//FG CD 交BE 于点G ，连接CG ．（1）求证：四边形CEFG 是菱形；（2）若6AB =，10AD =，求四边形CEFG 的面积．【考点】LA：菱形的判定与性质；PB：翻折变换（折叠问题）；LB：矩形的性质【分析】（1）根据题意和翻着的性质，可以得到BCE BFE∆≅∆，再根据全等三角形的性质和菱形的判定方法即可证明结论成立；（2）根据题意和勾股定理，可以求得AF的长，进而求得EF和DF的值，从而可以得到四边形CEFG的面积．【解答】（1）证明：由题意可得，BCE BFE∆≅∆，BEC BEF∴∠=∠，FE CE=，//FG CEQ，FGE CEB∴∠=∠，FGE FEG∴∠=∠，FG FE∴=，FG EC∴=，∴四边形CEFG是平行四边形，又CE FE=Q，∴四边形CEFG是菱形；（2）Q矩形ABCD中，6AB=，10AD=，BC BF=，90BAF∴∠=︒，10AD BC BF===，8AF∴=，2DF∴=，设EF x=，则CE x=，6DE x=-，90FDE=︒Q，2222(6)x x∴+-=，解得，103x=，103CE∴=，∴四边形CEFG的面积是：1020233 CE DF=⨯=g．14、（2019成都•中考第27题•10分）如图1，在ABC∆中，20AB AC==，3tan4B=，点D为BC边上的动点（点D 不与点B ，C 重合）．以D 为顶点作ADE B ∠=∠，射线DE 交AC 边于点E ，过点A 作AF AD ⊥交射线DE 于点F ，连接CF ．（1）求证：ABD DCE ∆∆∽；（2）当//DE AB 时（如图2)，求AE 的长；（3）点D 在BC 边上运动的过程中，是否存在某个位置，使得DF CF =？若存在，求出此时BD 的长；若不存在，请说明理由．【考点】SO ：相似形综合题【分析】（1）根据两角对应相等的两个三角形相似证明即可．（2）解直角三角形求出BC ，由ABD CBA ∆∆∽，推出AB DB CB AB =，可得222025322AB DB CB ===，由//DE AB ，推出AE BD AC BC=，求出AE 即可．（3）点D 在BC 边上运动的过程中，存在某个位置，使得DF CF =．作FH BC ⊥于H ，AM BC ⊥于M ，AN FH ⊥于N ．则90NHM AMH ANH ∠=∠=∠=︒，由AFN ADM ∆∆∽，可得3tan tan 4AN AF ADF B AM AD ==∠==，推出3312944AN AM ==⨯=，推出1697CH CM MH CM AN =-=-=-=，再利用等腰三角形的性质，求出CD 即可解决问题．【解答】（1）证明：AB AC =Q ，B ACB ∴∠=∠，ADE CDE B BAD ∠+∠=∠+∠Q ，ADE B ∠=∠，BAD CDE ∴∠=∠，BAD DCE ∴∆∆∽．（2）解：如图2中，作AM BC ⊥于M ．在Rt ABM∆中，设4BM k=，则3tan434AM BM B k k ==⨯=g，由勾股定理，得到222AB AM BM=+，22220(3)(4)k k∴=+，4k∴=或4-（舍弃），AB AC=Q，AM BC⊥，22432BC BM k∴===g，//DE ABQ，BAD ADE∴∠=∠，ADE B∠=∠Q，B ACB∠=∠，BAD ACB∴∠=∠，ABD CBA∠=∠Q，ABD CBA∴∆∆∽，∴AB DBCB AB=，222025322ABDBCB∴===，//DE ABQ，∴AE BDAC BC=，252012523216AC BDAEBC⨯∴===g．（3）点D在BC边上运动的过程中，存在某个位置，使得DF CF=．理由：作FH BC⊥于H，AM BC⊥于M，AN FH⊥于N．则90NHM AMH ANH∠=∠=∠=︒，∴四边形AMHN为矩形，90MAN∴∠=︒，MH AN=，AB AC=Q，AM BC⊥，11321622BM CM BC∴===⨯=，在Rt ABM ∆中，由勾股定理，得12AM ==， AN FH ⊥Q ，AM BC ⊥，90ANF AMD ∴∠=︒=∠，90DAF MAN ∠=︒=∠Q ，NAF MAD ∴∠=∠，AFN ADM ∴∆∆∽， ∴3tan tan 4AN AF ADF B AM AD ==∠==， 3312944AN AM ∴==⨯=， 1697CH CM MH CM AN ∴=-=-=-=，当DF CF =时，由点D 不与点C 重合，可知DFC ∆为等腰三角形， FH DC ⊥Q ，214CD CH ∴==，321418BD BC CD ∴=-=-=，∴点D 在BC 边上运动的过程中，存在某个位置，使得DF CF =，此时18BD =．。

2019-2020年中考数学二轮复习-化归思想(附答案)

2019-2020年中考数学二轮复习-化归思想（附答案）Ⅰ、专题精讲：数学思想是数学内容的进一步提炼和概括，是对数学内容的种本质认识，数学方法是实施有关数学思想的一种方式、途径、手段，数学思想方法是数学发现、发明的关键和动力．抓住数学思想方法，善于迅速调用数学思想方法，更是提高解题能力根本之所在．因此，在复习时要注意体会教材例题、习题以及中考试题中所体现的数学思想和方法，培养用数学思想方法解决问题的意识．初中数学的主要数学思想是化归思想、分类讨论思想、数形结合思想等．本专题专门复习化归思想．所谓化归思想就是化未知为已知、化繁为简、化难为易．如将分式方程化为整式方程，将代数问题化为几何问题，将四边形问题转化为三角形问题等．实现这种转化的方法有：待定系数法、配方法、整体代人法以及化动为静、由抽象到具体等． Ⅱ、典型例题剖析【例1】（嘉峪关，8 分）如图3－1－1，反比例函数y=－8x 与一次函数y=－x+2的图象交于A 、B 两点．（1）求 A 、B 两点的坐标；（2）求△AOB 的面积．解：⑴解方程组82y x y x ⎧=-⎪⎨⎪=-+⎩ 得121242;24x x y y ==-⎧⎧⎨⎨=-=⎩⎩ 所以A 、B 两点的坐标分别为A （－2，4）B(4，－2（2）因为直线y=－x+2与y 轴交点D 坐标是(0， 2），所以11222,24422AOD BOD S S ∆∆=⨯⨯==⨯⨯= 所以246AOB S ∆=+=点拨：两个函数的图象相交，说明交点处的横坐标和纵坐标，既适合于第一个函数，又适合于第二个函数，所以根据题意可以将函数问题转化为方程组的问题，从而求出交点坐标．【例2】（自贡，5分）解方程：22(1)5(1)20x x ---+=解：令y= x —1，则2 y 2—5 y +2=0．所以y 1=2或y 2=12 ，即x —1＝2或x —1=12 ．所以x ＝3或x=32 故原方程的解为x ＝3或x=32点拨：很显然，此为解关于x －1的一元二次方程．如果把方程展开化简后再求解会非常麻烦，所以可根据方程的特点，含未·知项的都是含有（x —1）所以可将设为y ，这样原方程就可以利用换元法转化为含有y 的一元二次方程，问题就简单化了．【例3】（达川模拟，6分）如图 3－1－2，梯形 ABCD 中，AD ∥BC ，AB=CD ，对角线AC 、BD 相交于O 点，且AC ⊥BD ，AD=3,BC=5，求AC 的长．解：过 D 作DE ⊥AC 交BC 的延长线于E ，则得AD=CE 、AC=DE ．所以BE=BC+CE=8．因为 AC ⊥BD ，所以BD ⊥DE ．因为 AB=CD ，所以AC ＝BD ．所以GD=DE ．在Rt △BDE 中，BD 2＋DE 2=BE 2所以BD BE=4 2 ，即AC=4 2 . 点拨：此题是根据梯形对角线互相垂直的特点通过平移对角线将等腰梯形转化为直角三角形和平行四边形，使问题得以解决．【例4】（新泰模拟，5分）已知△ABC 的三边为a ，b ，c ，且222a b c ab ac bc ++=++，试判断△ABC 的形状．解：因为222a b c ab ac bc ++=++，所以222222222a b c ab ac bc ++=++，即：222()()()0a b b c a c -+-+-= 所以a=b ，a=c ， b=c 所以△ABC 为等边三角形．点拨：此题将几何问题转化为代数问题，利用凑完全平方式解决问题．【例5】（临沂，10分）△ABC 中，BC ＝a ，AC ＝b ，AB ＝c ．若90C ∠=︒，如图l ，根据勾股定理，则222a b c +=。

2019-2020年中考数学总复习(浙江地区 )考点跟踪突破29 图形的平移

2019-2020年中考数学总复习（浙江地区）考点跟踪突破29 图形的平移一、选择题1．(xx·贵港)在平面直角坐标系中，将点A(1，－2)向上平移3个单位长度，再向左平移2个单位长度，得到点A′，则点A′的坐标是( A )A．(－1，1) B．(1，－2)C．(－1，2) D．(1，2)2．(xx·青岛)如图，线段AB经过平移得到线段A′B′，其中A，B的对应点分别为点A′，B′，这四个点都在格点上．若线段AB上有一个点P(a，b)，则点P在A′B′上对应点P′的坐标为( A )A．(a－2，b＋3) B．(a－2，b－3)C．(a＋2，b＋3) D．(a＋2，b－3)3．某数学兴趣小组开展动手操作活动，设计了如图所示的三种图形，现计划用铁丝按照图形制作相应的造型，则所用铁丝的长度关系是( D )A．甲种方案所用铁丝最长B．乙种方案所用铁丝最长C．丙种方案所用铁丝最长D．三种方案所用铁丝一样长4．(xx·丽水)如图，在方格纸中，线段a，b，c，d的端点在格点上，通过平移其中两条线段，使得和第三条线段首尾相接组成三角形，则能组成三角形的不同平移方法有( B ) A．3种B．6种C．8种D．12种,第4题图),第5题图) 5．如图，等边△ABC沿射线BC向右平移到△DCE的位置，连结AD，BD，则下列结论：①AD＝BC；②BD，AC互相平分；③四边形ACED是菱形．其中正确的个数有( D ) A．0个B．1个C．2个D．3个二、填空题[来源:]6．(xx·莆田)在平面直角坐标系中，点P(－1，2)向右平移3个单位长度得到的点的坐标是__(2，2)__． 7．(xx ·泰州)如图，△ABC 中，BC ＝5 cm ，将△ABC 沿BC 方向平移至△A ′B ′C ′的对应位置时，A ′B ′恰好经过AC 的中点O ，则△ABC 平移的距离为__2.5__cm.[来源:][来源:学+科+网Z+X+X+K],第7题图) ,第8题图)8．如图，△ABC 中，∠ACB ＝90°，AB ＝8 cm ，D 是AB 的中点．现将△BCD 沿BA 方向平移1 cm ，得到△EFG ，FG 交AC 于点H ，则GH 的长等于__3__ cm.点拨：∵△ABC 中，∠ACB ＝90°，AB ＝8 cm ，D 是AB 的中点，∴AD ＝BD ＝CD ＝12AB ＝4 cm ；又∵△EFG 由△BCD 沿BA 方向平移1 cm 得到的，∴GH ∥CD ，GD ＝1 cm ，∴GH DC ＝AG AD ，即GH 4＝4－14，解得GH ＝3 cm 三、解答题9. (xx ·安徽)如图，在边长为1个单位长度的小正方形组成的12×12网格中，给出了四边形ABCD 的两条边AB 与BC ，且四边形ABCD 是一个轴对称图形，其对称轴为直线AC.(1)试在图中标出点D ，并画出该四边形的另两条边；(2)将四边形ABCD 向下平移5个单位，画出平移后得到的四边形A ′B ′C ′D ′.解：(1)点D 以及四边形ABCD 另两条边如图所示．(2)得到的四边形A ′B ′C ′D ′如图所示．10．(xx ·锦州)如图，在平面直角坐标系中，线段AB 的两个端点是A(－5，1)，B(－2，3)，线段CD 的两个端点是C(－5，－1)，D(－2，－3)．(1)线段AB 与线段CD 关于某直线对称，则对称轴是__x 轴__；(2)平移线段AB 得到线段A 1B 1，若点A 的对应点A 1的坐标为(1，2)，画出平移后的线段A 1B 1，并写出点B 1的坐标为__(4，4)__．解：(1)x 轴 (2)图略：B (4，4)．B 组能力提升11．(xx ·济南)如图，将边长为12的正方形ABCD 沿其对角线AC 剪开，再把△ABC 沿着AD 方向平移，得到△A ′B ′C ′，当两个三角形重叠部分的面积为32时，它移动的距离AA ′等于__4或8__．12．如图①，两个等边△ABD ，△CBD 的边长均为1，将△ABD 沿AC 方向向右平移到△A ′B ′D ′的位置得到图②，则阴影部分的周长为__2__．[来源:][来源:Z+xx+k]点拨：∵两个等边△ABD ，△CBD 的边长均为1，将△ABD 沿AC 方向向右平移到△A ′B ′D ′的位置，∴A ′M ＝A ′N ＝MN ，MO ＝DM ＝DO ，OD ′＝D ′E ＝OE ，EG ＝EC ＝GC ，B ′G ＝RG ＝RB ′，∴OE ＋OM ＋MN ＋NR ＋GR ＋EG ＝A ′D ′＋BC ＝1＋1＝2.13．如图，在Rt △ABC 中，∠BAC ＝90°，AB ＝4，AC ＝3，线段AB 为半圆O 的直径，将Rt △ABC 沿射线AB 方向平移，使斜边与半圆O 相切于点G ，得到△DEF ，DF 与BC 交于点H.(1)求BE 的长；(2)求Rt △ABC 与△DEF 重叠(阴影)部分的面积．[来源:Z §xx §k]解：(1)连结OG (图略)，∵∠BAC ＝90°，AB ＝4，AC ＝3，∴BC ＝AB 2＋AC 2＝5，∵Rt △ABC 沿射线AB 方向平移，使斜边与半圆O 相切于点G ，得△DEF ，∴AD ＝BE ，DF ＝AC ＝3，EF ＝BC ＝5，∠EDF ＝∠BAC ＝90°，∵EF 与半圆O 相切于点G ，∴OG ⊥EF ，∵AB ＝4，线段AB 为半圆O 的直径，∴OB ＝OG ＝2，∵∠GEO ＝∠DEF ，∴Rt△EOG ∽Rt △EFD ，∴OE EF ＝OG DF ，即OE 5＝23，解得OE ＝103，∴BE ＝OE －OB ＝103－2＝43. (2)BD ＝DE －BE ＝4－43＝83.∵DF ∥AC ，∴DH AC ＝BD AB ，即DH 3＝834，解得DH ＝2.∴S 阴影＝S △BDH ＝12BD ·DH ＝12×83×2＝83，即Rt △ABC 与△DEF 重叠(阴影)部分的面积为83C 组拓展培优[来源:学§科§网]14．如图，矩形ABCD 中，AB ＝6，第1次平移将矩形ABCD 沿AB 的方向向右平移5个单位，得到矩形A 1B 1C 1D 1，第2次平移将矩形A 1B 1C 1D 1沿A 1B 1的方向向右平移5个单位，得到矩形A2B2C2D2，…，第n次平移将矩形A n－1B n－1C n－1D n－1沿A n－1B n－1的方向平移5个单位，得到矩形A n B n C n D n(n＞2)．[来源:](1)求AB1和AB2的长；(2)若AB n的长为56，求n.[来源:学,科,网Z,X,X,K]解：(1)∵AB＝6，第1次平移将矩形ABCD沿AB的方向向右平移5个单位，得到矩形A1B1C1D1，第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位，得到矩形A2B2C2D2…∴AA1＝5，A1A2＝5，A2B1＝A1B1－A1A2＝6－5＝1，∴AB1＝AA1＋A1A2＋A2B1＝5＋5＋1＝11，∴AB2的长为5＋5＋6＝16.[来源:](2)∵AB1＝2×5＋1＝11，AB2＝3×5＋1＝16，∴AB n＝(n＋1)×5＋1＝56，解得n＝10.。

2019-2020年中考数学专项训练：统计概率和圆(二,word版)

2016 年中考数学专项训练统计概率和圆（二）日期：月日做题时间：至耗时共分钟学校：姓名：得分：草稿区1. （2015 年浙江湖州 8 分）为了深化课程改革，某校积极开展校本课程建设，计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团，要求每位学生都自主选择其中一个社团，为此，随机调查了本校各年级部分学生选择社团的意向，并将调查结果绘制成如下统计图表(不完整)：某校被调查学生选择社团意向统计表根据统计图表中的信息，解答下列问题：（1）求本次调查的学生总人数及 a ，b ，c 的值；（2）将条形统计图补充完整(温馨提示：请画在答题卷相对应的图上)；（3）若该校共有 1200 名学生，试估计全校选择“科学实验”社团的学生人数.2. （2015 年浙江金华 8 分）小明随机调查了若干市民租用公共自行车的骑车时间 t （单位：分），将获得的数据分成四组，绘制了如下统计图. 请根据图中信息，解答下列问题：（1）这次被调查的总人数是多少？（2）试求表示A组的扇形圆心角的度数，并补全条形统计图；（3）如果骑自行车的平均速度为12km/h，请估算，在租用公共自行车的市民中，骑车路程不超过6km 的人数所占的百分比.3.（2015 年浙江丽水 10 分）如图，在△ABC 中，AB=AC ，以 A B 为直径的⊙O 分别与 BC ，AC 交于点 D ，E ，过点 D 作⊙O 的切线 D F ，交 A C 于点 F . （1）求证：DF ⊥AC ；（2）若⊙O 的半径为 4，∠CDF=22.5°，求阴影部分的面积.4.（2015 年浙江宁波 12 分）如图，在平面直角坐标系中，点 M 是第一象限内一点，过 M 的直线分别交 x 轴， y轴的正半轴于 A ，B 两点，且 M 是 A B 的中点. 以 O M 为直径的⊙P 分别交x 轴， y 轴于 C ，D 两点，交直线 A B 于点 E （位于点 M 右下方），连结 D E 交 O M 于点 K .（1）若点 M 的坐标为（3，4），①求 A ，B 两点的坐标； ②求 M E 的长；OK（2）若MK 3，求∠OBA 的度数；OKy（3）设tanOBA x （0< x <1），MK ，直接写出 y关于x 的函数解析式.5.（2015 年浙江台州12 分）如图，四边形A BCD 内接于⊙O，点E在对角线A C 上，EC=BC=DC.（1）若∠CBD=39°，求∠BAD 的度数；（2）求证：∠1=∠2.2016 年中考数学专项训练统计概率和圆（二）参考答案1.【答案】解：（1）本次调查的学生总人数： 70 35%200 （人），b 40 200 20%,c 10 200 5%, a1 35% 20% 10%5%30%.（2）条形统计图补充完整如答图：（3）全校选择“科学实验”社团的学生人数约为120035%420 （人）【考点】条形统计图和频率统计表；频数、频率和总量的关系；用样本估计总体. 2.【答案】解：（1）被调查总人数为 19÷38％=50（人）.2019-2020年中考数学专项训练：统计概率和圆（二，word 版）（2）表示 A 组的扇形圆心角的度数为 50 .∵C 组的人数为 50 1519412 （人），∴补全条形统计图如答图：12t6（3）设骑车时间为t分，则60，解得t≤30，∴被调查的50 人中，骑公共自行车的路程不超过6km 的人数为50－4＝46（人），∴在租用公共自行车的市民中，骑车路程不超过6km 的人数所占的百分比为46÷50＝92％.（1）【考点】条形统计图和扇形统计图；频数、频率和总量的关系；用样本估计总体. 3. 【答案】解：证明：如答图，连接O D，∵OB=OD，∴∠ABC=∠ODB.∴AB=AC，∴∠ABC=∠ACB.∴∠ODB=∠ACB.∴OD∥AC.∵DF 是⊙O 的切线，∴DF⊥OD∴DF⊥AC.（2）如答图，连接O E，∵DF⊥AC，∠CDF=22.5°，∴∠ABC=∠ACB=67.5°. ∴∠BAC=45°. ∵OA=OB，∴∠AOE=90°.S SS90 4 144 8∵⊙O 的半径为4，∴阴影扇形OAEAOC360 2 .【考点】等腰三角形的性质；平行的判定；切线的性质；三角形内角和定理；扇形和三角形面积的计算；转换思想的应用.5.【答案】解：（1）①如答图，连接DM ,MC ，∵OM 是⊙P 的直径，∴MDO MCO 90.∵AOB 90，∴M D ∥OA ，MC ∥OB .∵点M是A B 的中点，∴点D是A B 的中点，点C是O A 的中点.∵点M的坐标为（3，4），∴OB 2MC8,OA 2MD 6 .∴点B的坐标为（0，8），点A的坐标为（6，0）.②在Rt AOB 中，∵OA6,OB 8 ，∴由勾股定理，得AB 10 .BM1AB 5∵点 M 是 A B 的中点，∴ 2.BMBO∵BOM BED ，OBM EBD ，∴ OBM ∽EBD .∴ BD BE .BEBOBD4 86.4∴BM5.∴ME BE BM 6.4 51.4 .（2）如答图，连接 D P ，OK∵ MK3，∴OK 3MK,OM4MK .∴ P K MK .∵ OP PM ,BDDO ，∴ D P 是 BOM 的中位线. ∴ D P ∥ B M .∴PDKMEK又∵PKDMKE .∴ DPK ≌EMKAAS.∴ D K KE .∵ OM 是⊙P 的直径，∴OM DE . ∴cosDPK1cosDPKPKPD .∵DPPM 2ME，∴ 2 .∴DPK 60,DOM 30.∵在Rt AOB 中，点 M 是 A B 的中点，∴BM MO . ∴OBADOM 30.（3） y 关于 x 的函数解析式为y 21x 2 .【考点】圆的综合题；圆周角定理；平行的性质；点的坐标；勾股定理；相似三角形的判定和性质；三角形中位线定理；全等三角形的判定和性质；锐角三角函数定义；特殊角的三角函数值；等腰三角形的性质；由实际问题列函数关系式；方程思想的应用.6. 【答案】解：（1）∵BC=DC，∠CBD=39°，∴∠BDC=∠CBD=39°.∵四边形A BCD 内接于⊙O，∴∠BAC=∠BDC，∠CAD=∠CBD.∴∠BAD=∠BAC+∠CAD=∠BDC+∠CBD=78°.（2）证明：∵BC=DC，∴∠BDC=∠CBD.∵EC=BC，∴∠CBE=∠CEB.∵四边形A BCD 内接于⊙O，∴∠BAC=∠BDC.∴∠1=∠CBE ∠CBD=∠CEB ∠CBD=∠2+∠BAC ∠CBD=∠2+∠BDC ∠CBD=∠2. 【考点】圆周角定理；等腰三角形的性质；三角形外角性质.。

(名师整理)最新数学中考专题复习《网格题》精讲精练

解法二:选取E、F，连接EF与AC交于点Q，连接PQ.
2020河西一模在每个小正方形边长为1的网格中，有等腰三角形ABC，点A,B,C都在格点上，点D 为线段BC上的动点. (Ⅰ)AC的长等于__5___; (Ⅱ)当 AD 3 DC最短时，请用无刻度的直尺，画出点D，并简要说明点D的位置是如何
2020北辰二模 18.如图，在每个小正方形的边长为1的网格中，点A,B,C,D都在格点上.
(Ⅰ)AC的长是__2_5__; (Ⅱ)将四边形ABCD折叠,使点C与点A重合,折痕EF交BC于点E,交AD于点F,点D
的对应点为Q,得五边形ABEFQ,请用无刻度的直尺在网格中画出折叠后的五边形,并简要说明点E,F,Q的位置是如何找到：如图所示,取格点O,H,M,N,连接HO并延长分别交AD,BC于点F,E,连接BN,DM 相交于点Q,则E,F,G即为所求.
取格点D,F,E,连接DE,DF分别交AB,AC于点M,N,再取格点S,T,G,K,连接GK,ST交于点Q, 连接MQ并延长交BC于点P,同理得到点R,四边形MPRN即为所求的正方形.
理由是：设正方形的边长为x, ∵MN//BC , ∴△AMN∽ABC,
解得:x=
20 则有
9
AM AN 4 ,即 AM AN 4 AB AC 9 MB NC 5
2020河北二模 18. 如图，在每个小正方形的边长为1的网格中，点A,B均在格点上，l1,l2是一条小河平行的两岸.
(Ⅰ)AB距离等于___41__; (Ⅱ)现要在小可上修一座垂直于两岸的桥MN(点M在l1 上,点N在 l2 上,桥的宽度忽略),
使AM+MN+NB最短,请在如图所示的网格中,用无刻度的直尺,画出MN,并简要说明点M,N的位置是如何找到的(不要求证明). 如图,取格点C,连接AC,(使AC⊥ l1 ),取格点E、F，连接EF(使EF// l1),与AC交于点A’;同理作点B’;连接AB’与 l1交于点M,连接A’B与 l2交于点N,连接MN即为所求.

2020年中考数学二轮专项冲刺复习——填空题、压轴题型(含详细解答)

2020年中考数学二轮专项冲刺复习——填空题、压轴题型1、（2019天津•中考第17题•3分）如图，正方形纸片ABCD 的边长为12，E 是边CD 上一点，连接AE 、折叠该纸片，使点A 落在AE 上的G 点，并使折痕经过点B ，得到折痕BF ，点F 在AD 上，若5DE =，则GE 的长为 4913．【考点】正方形的性质；PB ：翻折变换（折叠问题）【分析】由折叠及轴对称的性质可知，ABF GBF ∆≅∆，BF 垂直平分AG ，先证ABF DAE ∆≅∆，推出AF 的长，再利用勾股定理求出BF 的长，最后在Rt ADF ∆中利用面积法可求出AH 的长，可进一步求出AG 的长，GE 的长．【解答】解：Q 四边形ABCD 为正方形，12AB AD ∴==，90BAD D ∠=∠=︒，由折叠及轴对称的性质可知，ABF GBF ∆≅∆，BF 垂直平分AG ，BF AE ∴⊥，AH GH =，90FAH AFH ∴∠+∠=︒，又90FAH BAH ∠+∠=︒Q ，AFH BAH ∴∠=∠，()ABF DAE AAS ∴∆≅∆，5AF DE ∴==，在Rt ADF ∆中，222212513BF AB AF =++，1122ABF S AB AF BF AH ∆==g g ， 12513AH ∴⨯=，6013AH ∴=， 120213AG AH ∴==， 13AE BF ==Q ，12049131313GE AE AG ∴=-=-=，故答案为：4913．2、（2019陕西•中考第14题•3分）如图，在正方形ABCD 中，8AB =，AC 与BD 交于点O ，N 是AO 的中点，点M 在BC 边上，且6BM =．P 为对角线BD 上一点，则PM PN -的最大值为 2 ．【考点】轴对称-最短路线问题；正方形的性质【分析】作以BD 为对称轴作N 的对称点N '，连接PN '，MN '，依据PM PN PM PN MN ''-=-…，可得当P ，M ，N '三点共线时，取“=”，再求得13CM CN BM AN '=='，即可得出////PM AB CD ，90CMN '∠=︒，再根据△N CM '为等腰直角三角形，即可得到2CM MN '==．【解答】解：如图所示，作以BD 为对称轴作N 的对称点N '，连接PN '，MN '，根据轴对称性质可知，PN PN '=，PM PN PM PN MN ''∴-=-…，当P ，M ，N '三点共线时，取“=”，Q 正方形边长为8，282AC AB ∴==O Q 为AC 中点，42AO OC ∴==N Q 为OA 中点，22ON ∴=，22ON CN ''∴==62AN '∴=6BM =Q ，862CM AB BM ∴=-=-=，∴13CM CN BM AN '==' ////PM AB CD ∴，90CMN '∠=︒，45N CM '∠=︒Q ，∴△N CM '为等腰直角三角形， 2CM MN '∴==，即PM PN -的最大值为2，故答案为：2．3、（2019上海•中考第17题•4分）如图，在正方形ABCD 中，E 是边AD 的中点．将ABE ∆沿直线BE 翻折，点A 落在点F 处，联结DF ，那么EDF ∠的正切值是 2 ．【考点】翻折变换（折叠问题）；正方形的性质；解直角三角形【分析】由折叠可得AE FE =，AEB FEB ∠=∠，由折叠的性质以及三角形外角性质，即可得到AEB EDF ∠=∠，进而得到tan tan 2AB EDF AEB AE∠=∠==．【解答】解：如图所示，由折叠可得AE FE =，12AEB FEB AEF ∠=∠=∠， Q 正方形ABCD 中，E 是AD 的中点，1122AE DE AD AB ∴===， DE FE ∴=，EDF EFD ∴∠=∠，又AEF ∠Q 是DEF ∆的外角，AEF EDF EFD ∴∠=∠+∠，12EDF AEF ∴∠=∠，AEB EDF ∴∠=∠，tan tan 2AB EDF AEB AE∴∠=∠==．故答案为：2．4、（2019成都•中考第24题•4分）如图，在边长为1的菱形ABCD 中，60ABC ∠=︒，将ABD ∆沿射线BD 的方向平移得到△A B D '''，分别连接A C '，A D '，B C '，则A C B C ''+的最小值为 3 ．【考点】PA ：轴对称-最短路线问题；KM ：等边三角形的判定与性质；8L ：菱形的性质；2Q ：平移的性质【分析】根据菱形的性质得到1AB =，30ABD ∠=︒，根据平移的性质得到1A B AB ''==，30A B D ∠''=︒，当B C A B '⊥''时，A C B C ''+的值最小，推出四边形A B CD ''是矩形，30B AC ∠''=︒，解直角三角形即可得到结论．【解答】解：Q 在边长为1的菱形ABCD 中，60ABC ∠=︒，1AB ∴=，30ABD ∠=︒，Q 将ABD ∆沿射线BD 的方向平移得到△A B D '''，1A B AB ∴''==，30A B D ∠''=︒，当B C A B '⊥''时，A C B C ''+的值最小，//AB A B ''Q ，AB A B =''，AB CD =，//AB CD ，A B CD ∴''=，//A B CD ''，∴四边形A B CD ''是矩形，30B AC ∠''=︒，3B C ∴'=，23A C '=， A C B C ''∴+335、（2019宁夏•中考第16题•3分）你知道吗，对于一元二次方程，我国古代数学家还研究过其几何解法呢！以方程25140x x +-=即(5)14x x +=为例加以说明．数学家赵爽（公元3~4世纪）在其所著的《勾股圆方图注》中记载的方法是：构造图（如下面左图）中大正方形的面积是2(5)x x ++，其中它又等于四个矩形的面积加上中间小正方形的面积，即24145⨯+，据此易得2x =．那么在下面右边三个构图（矩形的顶点均落在边长为1的小正方形网格格点上）中，能够说明方程24120x x --=的正确构图是 ② ．（只填序号）【考点】一元二次方程的应用【分析】仿造案例，构造面积是2(4)x x +-的大正方形，由它的面积为24124⨯+，可求出6x =，此题得解．【解答】解：24120x x --=Q 即(4)12x x -=，∴构造如图②中大正方形的面积是2(4)x x +-，其中它又等于四个矩形的面积加上中间小正方形的面积，即24124⨯+，据此易得6x =．故答案为：②．6、（2019江西•中考第12题•3分）在平面直角坐标系中，A ，B ，C 三点的坐标分别为(4,0)，(4,4)，(0,4)，点P 在x 轴上，点D 在直线AB 上，若1DA =，CP DP ⊥于点P ，则点P 的坐标为 (2,0)或(222-，或(22+，0) ．【考点】一次函数图象上点的坐标特征【分析】先由已知得出1(4,1)D ，2(4,1)D -，然后分类讨论D 点的位置从而依次求出每种情况下点P 的坐标．【解答】解：A Q ，B 两点的坐标分别为(4,0)，(4,4)//AB y ∴轴Q 点D 在直线AB 上，1DA =1(4,1)D ∴，2(4,1)D -如图：（Ⅰ）当点D 在1D 处时，要使CP DP ⊥，即使1COP ∆≅△11P AD ∴111OP CO P AAD = 即441OP OP =- 解得：12OP =1(2,0)P ∴（Ⅱ）当点D 在2D 处时，(0,4)C Q ，2(4,1)D -2CD ∴的中点3(2,)2E CP DP ⊥Q∴点P 为以E 为圆心，CE 长为半径的圆与x 轴的交点设(,0)P x ，则PE CE = 222233(2)(0)2(4)22x -+-+-解得：222x =±2(222P ∴-0)，3(222P +0)综上所述：点P 的坐标为(2,0)或(222-，0)或(22+0)．7、（2019重庆•中考 A 卷第18题•4分）在精准扶贫的过程中，某驻村服务队结合当地高山地形，决定在该村种植中药材川香、贝母、黄连增加经济收入．经过一段时间，该村已种植的川香、贝母、黄连面积之比4:3:5，是根据中药材市场对川香、贝母、黄连的需求量，将在该村余下土地上继续种植这三种中药材，经测算需将余下土地面积的916种植黄连，则黄连种植总面积将达到这三种中药材种植总面积的1940．为使川香种植总面积与贝母种植总面积之比达到3:4，则该村还需种植贝母的面积与该村种植这三种中药材的总面积之比是 3:20 ．【分析】设该村已种药材面积x ，余下土地面积为y ，还需种植贝母的面积为z，则总面积为()x y +，川香已种植面积13x 、贝母已种植面积14x ，黄连已种植面积512x 依题意列出方程组，用y 的代数式分别表示x 、y ，然后进行计算即可．【解答】解：设该村已种药材面积x ，余下土地面积为y ，还需种植贝母的面积为z ，则总面积为()x y +，川香已种植面积13x 、贝母已种植面积14x ，黄连已种植面积512x 依题意可得，()5919121640191:3:43164x y x y x y y z x z ⎧+=+⎪⎪⎨⎡⎤⎛⎫⎛⎫⎪+--+= ⎪ ⎪⎢⎥⎪⎝⎭⎝⎭⎣⎦⎩①② 由①得32x y =③，将③代入②，38z y =， ∴贝母的面积与该村种植这三种中药材的总面积之比3383202y z x y y y ===++，故答案为3:20．8、（2019河南•中考第15题•3分）如图，在矩形ABCD 中，AB ＝1，BC ＝a ，点E 在边BC 上，且BE ＝a ．连接AE ，将△ABE 沿AE 折叠，若点B 的对应点B ′落在矩形ABCD 的边上，则a 的值为或．【考点】矩形的性质；翻折变换（折叠问题）．【分析】分两种情况：①点B ′落在AD 边上，根据矩形与折叠的性质易得AB ＝BE ，即可求出a 的值；②点B ′落在CD 边上，证明△ADB ′∽△B ′CE ，根据相似三角形对应边成比例即可求出a 的值．【解答】解：分两种情况：①当点B ′落在AD 边上时，如图1．∵四边形ABCD 是矩形，∴∠BAD＝∠B＝90°，∵将△ABE沿AE折叠，点B的对应点B′落在AD边上，∴∠BAE＝∠B′AE＝∠BAD＝45°，∴AB＝BE，∴a＝1，∴a＝；②当点B′落在CD边上时，如图2．∵四边形ABCD是矩形，∴∠BAD＝∠B＝∠C＝∠D＝90°，AD＝BC＝a．∵将△ABE沿AE折叠，点B的对应点B′落在CD边上，∴∠B＝∠AB′E＝90°，AB＝AB′＝1，EB＝EB′＝a，∴DB′＝＝，EC＝BC﹣BE＝a﹣a＝a．在△ADB′与△B′CE中，，∴△ADB′∽△B′CE，∴＝，即＝，解得a1＝，a2＝0（舍去）．综上，所求a的值为或．故答案为或．9、（2019福建•中考第16题•4分）如图，菱形ABCD顶点A在函数y＝（x＞0）的图象上，函数y＝（k＞3，x＞0）的图象关于直线AC对称，且经过点B、D两点，若AB＝2，∠BAD＝30°，则k＝6+2．【考点】反比例函数与一次函数的交点问题．【分析】连接OC，AC过A作AE⊥x轴于点E，延长DA与x轴交于点F，过点D作DG⊥x轴于点G，得O、A、C在第一象限的角平分线上，求得A点坐标，进而求得D点坐标，便可求得结果．【解答】解：连接OC，AC过A作AE⊥x轴于点E，延长DA与x轴交于点F，过点D作DG⊥x轴于点G，∵函数y＝（k＞3，x＞0）的图象关于直线AC对称，∴O、A、C三点在同直线上，且∠COE＝45°，∴OE＝AE，不妨设OE＝AE＝a，则A（a，a），∵点A在在反比例函数y＝（x＞0）的图象上，∴a2＝3，∴a＝，∴AE＝OE＝，∵∠BAD＝30°，∴∠OAF＝∠CAD＝∠BAD＝15°，∵∠OAE＝∠AOE＝45°，∴∠EAF＝30°，∴AF＝，EF＝AE tan30°＝1，∵AB＝AD＝2，AE∥DG，∴EF＝EG＝1，DG＝2AE＝2，∴OG＝OE+EG＝+1，∴D（+1，2），故答案为：6+2．10、（2019北京•中考第10题•2分）在矩形ABCD中，M，N，P，Q分别为边AB，BC，CD，DA上的点（不与端点重合），对于任意矩形ABCD，下面四个结论中，①存在无数个四边形MNPQ是平行四边形；②存在无数个四边形MNPQ是矩形；③存在无数个四边形MNPQ是菱形；④至少存在一个四边形MNPQ是正方形．所有正确结论的序号是①②③．【考点】平行四边形的判定与性质；菱形的判定与性质；矩形的判定与性质；正方形的判定．【分析】根据矩形的判定和性质，菱形的判定，正方形的判定，平行四边形的判定定理即可得到结论．【解答】解：①如图，∵四边形ABCD是矩形，连接AC，BD交于O，过点O直线MP和QN，分别交AB，BC，CD，AD于M，N，P，Q，则四边形MNPQ是平行四边形，故当MQ∥PN，PQ∥MN，四边形MNPQ是平行四边形，故存在无数个四边形MNPQ是平行四边形；故正确；②如图，当PM＝QN时，四边形MNPQ是矩形，故存在无数个四边形MNPQ是矩形；故正确；③如图，当PM⊥QN时，存在无数个四边形MNPQ是菱形；故正确；④当四边形MNPQ是正方形时，MQ＝PQ，则△AMQ≌△DQP，∴AM＝QD，AQ＝PD，∵PD＝BM，∴AB＝AD，∴四边形ABCD是正方形与任意矩形ABCD矛盾，故错误；故答案为：①②③．11、（3分）如图，在平面直角坐标系中，已知(1,0)A -，(0,2)B ，将ABO ∆沿直线AB 翻折后得到ABC ∆，若反比例函数(0)k y x x =<的图象经过点C ，则k = 3225- ．【分析】由(1,0)A -，(0,2)B ，可知OA ，OB ，由折叠得1OA AC ==，2OB BC ==，要求k 的值只要求出点C 的坐标即可，因此过点C 作垂线，构造相似三角形，得出线段之间的关系，设合适的未知数，在直角三角形中由勾股定理，解出未知数，进而确定点C 的坐标，最终求出k 的值．【解答】解：过点C 作CD x ⊥轴，过点B 作BE y ⊥轴，与DC 的延长线相交于点E ，由折叠得：1OA AC ==，2OB BC ==，易证，ACD BCE ∆∆∽，∴12CD AC BE BC ==，设CD m =，则2BE m =，2CE m =-，21AD m =-在Rt ACD ∆中，由勾股定理得：222AD CD AC +=，即：222(21)1m m +-=，解得：145m =，20m =（舍去）； 45CD ∴=，85BE OA ==， 8(5C ∴-，4)5代入k y x =得，84325525k =-⨯=-，故答案为：3225-12、（3分）如图，在Rt ABC ∆中，90ABC ∠=︒，3BC =，D 为斜边AC 的中点，连接BD ，点F 是BC 边上的动点（不与点B 、C 重合），过点B 作BE BD ⊥交DF 延长线交于点E ，连接CE ，下列结论：①若BF CF =，则222CE AD DE +=；②若BDE BAC ∠=∠，4AB =，则158CE =； ③ABD ∆和CBE ∆一定相似；④若30A ∠=︒，90BCE ∠=︒，则21DE =．其中正确的是 ①②④ ．（填写所有正确结论的序号）【分析】①由直角三角形斜边上的中线等于斜边的一半，得AD BD =，由BF CF =，BD CD =得DE 是BC 的垂直平分线，得BE CE =，再由勾股定理便可得结论，由此判断结论的正误；②证明ABC DBE ∆∆∽，求得BE ，再证明//DE AB ，得DE 垂直平分BC ，得CE BE =，便可判断结论的正误； ③证明ABD CBE ∠=∠，再证明BE 与BC 或BC 与BE 两边的比不一定等于AB 与BD 的比，便可判断结论正误； ④先求出AC ，进而得BD ，再在Rt BCE ∆中，求得BE ，进而由勾股定理求得结果，便可判断正误．【解答】解：①90ABC ∠=︒Q ，D 为斜边AC 的中点，AD BD CD ∴==，AF CF =Q ，BF CF ∴=，DE BC ∴⊥，BE CE ∴=，QBE BD ⊥Q ，222BD BE DE ∴+=，222CE AD DE ∴+=，故①正确；②4AB =Q ，3BC =，225AC AB BC ∴=+=，∴52BD AD CD ===， A BDE ∠=∠Q ，90ABC DBE ∠=∠=︒，ABC DBE ∴∆∆∽，∴AB BC DB BE=，即4352BE=． 158BE ∴=， AD BD =Q ，A ABD ∴∠=∠，A BDE ∠=∠Q ，BDC A ABD ∠=∠+∠，A CDE ∴∠=∠，//DE AB ∴，DE BC ∴⊥，BD CD =Q ，DE ∴垂直平分BC ，BE CE ∴=，158CE ∴=，故②正确；③90ABC DBE ∠=∠=︒Q ，ABD CBE ∴∠=∠， Q 55248BD AB ==，但随着F 点运动，BE 的长度会改变，而3BC =，3BE ∴3BE 或3BE 不一定等于58， ABD ∴∆和CBE ∆不一定相似，故③错误；④30A ∠=︒Q ，3BC =，30A ABD CBE ∴∠=∠=∠=︒，26AC BC ==，132BD AC ∴==， 3BC =Q ，90BCE ∠=︒，cos30BC BE ∴==︒，DE ∴==Q ，故④正确；故答案为：①②④．13、（2019菏泽•中考第14题•3分）如图，直线334y x =--交x 轴于点A ，交y 轴于点B ，点P 是x 轴上一动点，以点P 为圆心，以1个单位长度为半径作P e ，当P e 与直线AB 相切时，点P 的坐标是 7(3-，0) ．【考点】8F ：一次函数图象上点的坐标特征；ME ：切线的判定与性质【分析】根据函数解析式求得(4,0)A -，(0B ．3)-，得到4OA =，3OB =，根据勾股定理得到5AB =，设P e 与直线AB 相切于D ，连接PD ，则PD AB ⊥，1PD =，根据相似三角形的性质即可得到结论．【解答】解：Q 直线334y x =--交x 轴于点A ，交y 轴于点B ， ∴令0x =，得3y =-，令0y =，得4x =-，(4,0)A ∴-，(0B ．3)-，4OA ∴=，3OB =，5AB ∴=，设P e 与直线AB 相切于D ，连接PD ，则PD AB ⊥，1PD =， 90ADP AOB ∠=∠=︒Q ，PAD BAO ∠=∠，APD ABO ∴∆∆∽，∴PD AP OB AB =， ∴135AP =， 53AP ∴=， 73OP ∴=， 7(3P ∴-，0)，故答案为：7(3-，0)．14、（2019成都•中考第14题•4分）如图，ABCD Y 的对角线AC 与BD 相交于点O ，按以下步骤作图：①以点A 为圆心，以任意长为半径作弧，分别交AO ，AB 于点M ，N ；②以点O 为圆心，以AM 长为半径作弧，交OC 于点M '；③以点M '为圆心，以MN 长为半径作弧，在COB ∠内部交前面的弧于点N '；④过点N '作射线ON '交BC 于点E ．若8AB =，则线段OE 的长为 4 ．【考点】5L ：平行四边形的性质；3N ：作图-复杂作图【分析】利用作法得到COE OAB ∠=∠，则//OE AB ，利用平行四边形的性质判断OE 为ABC ∆的中位线，从而得到OE 的长．【解答】解：由作法得COE OAB ∠=∠，//OE AB ∴，Q 四边形ABCD 为平行四边形，OC OA ∴=，CE BE ∴=， OE ∴为ABC ∆的中位线，118422OE AB ∴==⨯=．故答案为4．15、（2019遂宁•中考第15题•4分）如图，在平面直角坐标系中，矩形OABC 的顶点O 落在坐标原点，点A 、点C 分别位于x 轴，y 轴的正半轴，G 为线段OA 上一点，将OCG ∆沿CG 翻折，O 点恰好落在对角线AC 上的点P 处，反比例函数12y x =经过点B ．二次函数2(0)y ax bx c a =++≠的图象经过(0,3)C 、G 、A 三点，则该二次函数的解析式为 2111324y x x =-+ ．（填一般式）【考点】3H ：二次函数的性质；LB ：矩形的性质；5H ：二次函数图象上点的坐标特征；8H ：待定系数法求二次函数解析式；9H ：二次函数的三种形式；6G ：反比例函数图象上点的坐标特征；PB ：翻折变换（折叠问题）【分析】点(0,3)C ，反比例函数12y x=经过点B ，则点(4,3)B ，由勾股定理得：22(4)4x x -=+，故点3(2G ，0)，将点C 、G 、A 坐标代入二次函数表达式，即可求解．【解答】解：点(0,3)C ，反比例函数12y x =经过点B ，则点(4,3)B ，则3OC =，4OA =，5AC ∴=，设OG PG x ==，则4GA x =-，532PA AC CP AC OC =-=-=-=，由勾股定理得：22(4)4x x -=+，解得：32x =，故点3(2G ，0)，将点C 、G 、A 坐标代入二次函数表达式得：3930421440c a b c a b c =⎧⎪⎪++=⎨⎪++=⎪⎩，解得：121143a b c ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩，故答案为：2111324y x x =-+．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2019-2020年中考数学总复习第二编中档题型突破专项训练篇中档题型训练七网格中
年怀化中考试题，图形的轴对称、平移、旋转是中考的热
网格中的平移、旋转
【例1】如图，方格纸中每个小正方形的边长都是1个单位长度，Rt △ABC 的三个顶点A(－2，2)，B(0，
5)，C(0，2)．
(1)将△ABC 以点C 为旋转中心旋转180°，得到△A 1B 1C ，请画出△A 1B 1C 的图形；
(2)平移△ABC，使点A 的对应点A 2坐标为(－2，－6)，请画出平移后对应的△A 2B 2C 2的图形；
(3)若将△A 1B 1C 绕某一点旋转可得到△A 2B 2C 2，请直接写出旋转中心的坐标．
【解析】(1)分别画出点A ，B 以点C 为旋转中心的对称点A 1，B 1，再顺次连接A 1，B 1，C 即得到所求△A 1B 1C ；
(2)根据平移后点A 对应的点A 2坐标确定出△ABC 平移的距离和方向，按此画出B ，C 平移后的对应点B 2，C 2，顺次连接
A 2，
B 2，
C 2即可；(3)由图可知，△A 1B 1C 绕点(0，－2)旋转180°得到△A 2B 2C 2.
【学生解答】解：(1)、(2)如图所示；(3)旋转中心坐标为(0，－2)．
1．如图，在平面直角坐标系中，△ABC 的三个顶点的坐标分别是A(－3，2)，B(
－1，4)，C(0，2)．
(1)将△ABC 以点C 为旋转中心旋转180°，画出旋转后对应的△A 1B 1C ；
(2)平移△ABC，若A 的对应点A 2的坐标为(－5，－2)，画出平移后的△A 2B 2C
2；
(3)若将△A 2B 2C 2绕某一点旋转可以得到△A 1B 1C ，请直接写出旋转中心的坐标．
解：(1)△A 1B 1C 如图所示；(2)△A 2B 2C 2如图所示；(3)如图所示，旋转中心的坐标为P(－1，0)．
网格中的位似
【例2】如图，在平面直角坐标系中，△ABC 的三个顶点均在格点上，A(－1，3)，B(－3，1)，C(0，1)．
(1)画出在网格内把△ABC 向右平移3个单位，再向上平移1个单位所得到的图形△A 1B 1C 1；
(2)在网格内把△ABC 以原点O 为位似中心放大，使放大前后对应边的比为1∶2，请在网格中画出放大后的图形△A 2B 2C 2.
【解析】(1)把△ABC 的三个顶点分别向右平移3个单位，再向上平移1个单位，找到对应的点，即可画出平移后的三角形；(2)把△ABC 以原点O 为位似中心放大，使放大前后对应边的比为1∶2，连接AO 并延长到A 2，使OA 2＝2OA ，得到A 的对应点A 2，同理得到B 2与C 2，然后顺次连接即得△A 2B 2C 2.
【学生解答】解：(1)作出△A 1B 1C 1如图所示；(2)作出△A 2B 2C 2如图所示．
2．如图，在边长为1个单位长度的小正方形网格中：
(1)画出△ABC 向上平移6个单位，再向右平移5个单位后的△A 1B 1C 1；
(2)以点B 为位似中心，将△ABC 放大为原来的2倍，得到△A 2BC 2，请在网格中画出△A 2BC 2；
(3)求△CC 1C 2的面积．
解：(1)、(2)如图所示；(3)9.
网格中的对称
【例3】如图，在边长为1的正方形组成的网格中，△AOB 的顶点均在格点上，点A ，B 的坐标分别是A(3，
2)，B(1，3)．△AOB 绕点O 逆时针旋转90°后得到△A 1OB 1.(直接填写答案)
(1)点A 关于点O 中心对称的点的坐标为________；
(2)点A 1的坐标为________；
(3)在旋转过程中，点B 经过的路径为BB 1︵，那么BB 1︵的长为________．
【解析】(1)根据关于中心对称坐标特点解答；(2)运用勾股定理先求出OB ，再根据弧长公式求．
【学生解答】解：(1)(－3，－2)；(2)(－2，3)；(3)102
π
3．(2016原创)如图，在平面直角坐标系中，已知△ABC 的三个顶点的坐标分别为A(－1，1)，B(－3，1)，C(－1，4)．
(1)画出△ABC 关于y 轴对称的△A 1B 1C 1；
(2)将△ABC 绕着点B 顺时针旋转90°后得到△A 2B 2C 2，请在图中画出△A 2B 2C 2，并求出线段BC 旋转过程中所
扫过的面积．(结果保留π)
解：(1)如图所示，△A 1B 1C 1即为所求；
(2)如图所示，△A 2B 2C 2即为所求．BC ＝22＋32＝13，∠CB 2C 2＝90°，线段BC 旋转过程中所扫过的部分是
一个扇形，因此扇形面积是S ＝90π×（13）2360＝134
π.
4．(2015聊城中考)在如图所示的直角坐标系中，每个小方格都是边长为1的正方形，△ABC 的顶点均在格点上，点A 的坐标是(－3，－1)．
(1)将△ABC 沿y 轴正方向平移3个单位得到△A 1B 1C 1，画出△A 1B 1C 1，并写出点B 1的坐标；
(2)画出△A 1B 1C 1关于y 轴对称的△A 2B 2C 2，并写出点C 2的坐标．
解：(1)△A 1BC 1的位置如图所示，点B 1的坐标是(－2，－1)；(2)△A 2B 2C 2的位置如图所示，点C 2的坐标是(1，1)．。