湖南专版2019年中考数学一轮复习第六章空间与图形6.4视图与投影试卷部分
(湖南专版)2019年中考数学一轮复习第六章空间与图形6.1图形的轴对称、平移与旋转(讲解部分)素材(pdf)

������������������������������������������������������������������������������������������������������������������������������������
移后新旧两图形全等.
考点三㊀ 图形的旋转
1 1 øABAᶄ = ( øOBAᶄ+øOBC) = 60ʎ. 2 2
①探究三条线段 AB,CE,CF 之间的数量关系,并说明理由; ②若 CE = 4,CF = 2,求 DN 的长. 解析㊀ (1) 证明:ȵ øACB = 90ʎ ,AC = BC,AD = BD, ʑ øBCD = øACD = 45ʎ ,øBCE = øACF = 90ʎ , ʑ øDCE = øDCF = 135ʎ ,在әDCE 与әDCF 中, ȵ CE = CF,øDCE = øDCF,CD = CD, ʑ әDCEɸәDCF,ʑ DE = DF. (2) ①AB 2 = 4CE㊃CF. ȵ øCDF +øCDE = 45ʎ , 理由:ȵ øDCF = øDCE = 135ʎ , ʑ øCDF +øF = 180ʎ -135ʎ = 45ʎ , ʑ øF = øCDE,ʑ әCDFʐәCED,ʑ 即 CD 2 = CE㊃CF, ȵ øACB = 90ʎ ,AC = BC,AD = BD, ʑ CD = 1 AB,ʑ AB 2 = 4CE㊃CF. 2 CD CF = , CE CD
考点二㊀ 图形的平移
㊀ ㊀ 1. 定义: 在平面内, 将某 个图 形沿 某个 方向 移动一 定的 距 离,这样的图形运动称为平移. 所连的线段平行( 或共线) 且相等. 2. 特征:(1) 平移后,对应线段相等且平行 ( 或共线 ) . 对应点
2019年中考数学题投影与三视图
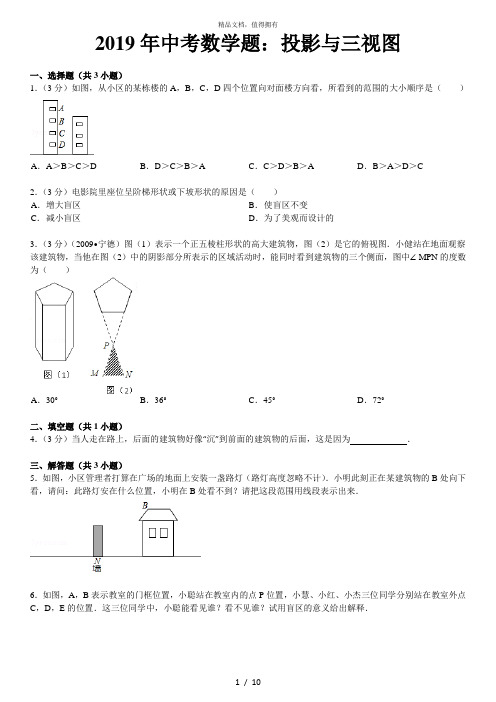
2019年中考数学题:投影与三视图一、选择题(共3小题)1.(3分)如图,从小区的某栋楼的A,B,C,D四个位置向对面楼方向看,所看到的范围的大小顺序是()3.(3分)(2009•宁德)图(1)表示一个正五棱柱形状的高大建筑物,图(2)是它的俯视图.小健站在地面观察该建筑物,当他在图(2)中的阴影部分所表示的区域活动时,能同时看到建筑物的三个侧面,图中∠MPN的度数为()二、填空题(共1小题)4.(3分)当人走在路上,后面的建筑物好像“沉”到前面的建筑物的后面,这是因为_________.三、解答题(共3小题)5.如图,小区管理者打算在广场的地面上安装一盏路灯(路灯高度忽略不计).小明此刻正在某建筑物的B处向下看,请问:此路灯安在什么位置,小明在B处看不到?请把这段范围用线段表示出来.6.如图,A,B表示教室的门框位置,小聪站在教室内的点P位置,小慧、小红、小杰三位同学分别站在教室外点C,D,E的位置.这三位同学中,小聪能看见谁?看不见谁?试用盲区的意义给出解释.7.如图,在一间黑暗的屋子里用一盏白炽灯照一个球.(1)球在地面上的阴影是什么形状?(2)当把白炽灯向高处移时,阴影的大小怎样变化?(3)若自炽灯到球心的距离是1m,到地面的距离是3m,球的半径是0.2m,问:球在地面上阴影的面积是多少?四、选择题8.(3分)(2006•镇江)图1表示正六棱柱形状的高大建筑物,图2中的阴影部分表示该建筑物的俯视图,P、Q、M、N表示小明在地面上的活动区域.小明想同时看到该建筑物的三个侧面,他应在()五、解答题(共4小题)9.如图,有一种动画程序,屏幕上正方形ABCD是黑色区域(含边界),其中A(1,1),B(2,1),C(2,2),D(1,2).用信号枪沿直线y=kx(k>0)发射信号.当信号遇到黑色区域时,区域便由黑变白,若没遇到黑色区域,则无变化,无变化的区域即为信号枪使用的盲区,则使信号枪成为盲区的k的取值范围是_________.10.如图,在房子外的屋檐E处装有一台监视器,房子前面有一面落地的广告牌.(1)监视器的盲区在哪一部分?(2)已知房子上的监视器离地面高12m,广告牌高6m,广告牌距离房子5m,求盲区在地面上的长度.11.(2003•常州)当你进入博物馆的展览厅时,你知道站在何处观赏最理想?如图,设墙壁上的展品最高处点P距离地面a米,最低处点Q距离地面b米,观赏者的眼睛点E距离地面m米,当过P、Q、E三点的圆与过点E的水平线相切于点E时,视角∠PEQ最大,站在此处观赏最理想.(1)设点E到墙壁的距离为x米,求a、b、m、x的关系式;(2)当a=2.5,b=2,m=1.6,求:(ⅰ)点E和墙壁距离x;(ⅱ)最大视角∠PEQ的度数.(精确到1度)12.如图所示的网格图均是20×20的等距网格图(每个小方格的边长均为1个单位长).侦察兵王凯在点P处观察区域MNCD内的活动情况,当5个单位长的列车AB(图中的﹣)以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).请针对图①,②,③中列车位于不同位置的情形分别画出相应的盲区,并在盲区内涂上阴影.2019年中考数学题:投影与三视图参考答案与试题解析一、选择题(共3小题)1.(3分)如图,从小区的某栋楼的A,B,C,D四个位置向对面楼方向看,所看到的范围的大小顺序是()3.(3分)(2009•宁德)图(1)表示一个正五棱柱形状的高大建筑物,图(2)是它的俯视图.小健站在地面观察该建筑物,当他在图(2)中的阴影部分所表示的区域活动时,能同时看到建筑物的三个侧面,图中∠MPN的度数为()二、填空题(共1小题)4.(3分)当人走在路上,后面的建筑物好像“沉”到前面的建筑物的后面,这是因为到了自己的盲区的范围内.三、解答题(共3小题)5.如图,小区管理者打算在广场的地面上安装一盏路灯(路灯高度忽略不计).小明此刻正在某建筑物的B处向下看,请问:此路灯安在什么位置,小明在B处看不到?请把这段范围用线段表示出来.6.如图,A,B表示教室的门框位置,小聪站在教室内的点P位置,小慧、小红、小杰三位同学分别站在教室外点C,D,E的位置.这三位同学中,小聪能看见谁?看不见谁?试用盲区的意义给出解释.7.如图,在一间黑暗的屋子里用一盏白炽灯照一个球.(1)球在地面上的阴影是什么形状?(2)当把白炽灯向高处移时,阴影的大小怎样变化?(3)若自炽灯到球心的距离是1m,到地面的距离是3m,球的半径是0.2m,问:球在地面上阴影的面积是多少?==π四、选择题8.(3分)(2006•镇江)图1表示正六棱柱形状的高大建筑物,图2中的阴影部分表示该建筑物的俯视图,P、Q、M、N表示小明在地面上的活动区域.小明想同时看到该建筑物的三个侧面,他应在()五、解答题(共4小题)9.如图,有一种动画程序,屏幕上正方形ABCD是黑色区域(含边界),其中A(1,1),B(2,1),C(2,2),D(1,2).用信号枪沿直线y=kx(k>0)发射信号.当信号遇到黑色区域时,区域便由黑变白,若没遇到黑色区域,则无变化,无变化的区域即为信号枪使用的盲区,则使信号枪成为盲区的k的取值范围是0<k<或k>2.k=时,使信号枪成为盲区,或<10.如图,在房子外的屋檐E处装有一台监视器,房子前面有一面落地的广告牌.(1)监视器的盲区在哪一部分?(2)已知房子上的监视器离地面高12m,广告牌高6m,广告牌距离房子5m,求盲区在地面上的长度.=11.(2003•常州)当你进入博物馆的展览厅时,你知道站在何处观赏最理想?如图,设墙壁上的展品最高处点P距离地面a米,最低处点Q距离地面b米,观赏者的眼睛点E距离地面m米,当过P、Q、E三点的圆与过点E的水平线相切于点E时,视角∠PEQ最大,站在此处观赏最理想.(1)设点E到墙壁的距离为x米,求a、b、m、x的关系式;(2)当a=2.5,b=2,m=1.6,求:(ⅰ)点E和墙壁距离x;(ⅱ)最大视角∠PEQ的度数.(精确到1度)=,HEQ=,12.如图所示的网格图均是20×20的等距网格图(每个小方格的边长均为1个单位长).侦察兵王凯在点P处观察区域MNCD内的活动情况,当5个单位长的列车AB(图中的﹣)以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).请针对图①,②,③中列车位于不同位置的情形分别画出相应的盲区,并在盲区内涂上阴影.。
2019年中考数学复习第六章空间与图形6.4视图与投影试卷部分课件

10.(2017河北,8,3分)如图是由相同的小正方体木块粘在一起的几何体,它的主视图是 ( )
答案 A 从正面看易得共有两层,下层有3个正方形,上层有两个小正方形.故选A.
11.(2017安徽,3,4分)如图,一个放置在水平实验台上的锥形瓶,它的俯视图为 ( )
答案 B 从上往下看只有B符合.
A.3 B.4 C.5 D.6 答案 C 易得这个几何体共有2层,结合主视图和俯视图可知,左边下层有2个正方体,左边上 层最多有2个正方体;右边只有1层,且只有1个正方体.所以这个几何体中的正方体最多有5个. 故选C.
3.(2018云南,8,4分)下列图形是某几何体的三视图(其中主视图也称正视图,左视图也称侧视 图),则这个几何体是 ( )
2.(2018新疆乌鲁木齐,2,4分)如图是某个几何体的三视图,该几何体是 ( )
A.长方体 B.正方体 C.三棱柱 D.圆柱 答案 C 由俯视图可判断只有C符合.
3.(2018云南昆明,7,4分)下列几何体的左视图为长方形的是 ( )
答案 C 选项A、B、D中的几何体的左视图分别是圆、等腰梯形、等腰三角形,只有选项C 中的几何体的左视图为长方形,故选C.
6.(2017吉林,2,2分)下图是一个正六棱柱的茶叶盒,其俯视图为( )
答案 B 正六棱柱的俯视图为正六边形,故选B.
7.(2017湖北武汉,7,3分)某物体的主视图如图所示,则该物体可能为 ( )
答案 A 只有选项A中物体的主视图是圆,故选A.
8.(2017四川绵阳,4,3分)如图所示的几何体的主视图正确的是 ( )
A.全 B.国 C.明 D.城 答案 D 根据动手操作可知,与“文”字所在的面相对的面上标的字是“城”.故选D.
考点三 投影
(湖南专版)2019年中考数学一轮复习第六章空间与图形6.2图形的相似(讲解部分)素材(pdf)

又 E,F 分别为线段 AO,DO 的中点, ʑ ʑ 又ȵ ADʊBC,ʑ әAEGʐәCEB,әHDFʐәCBF, AG AE 1 HD DF 1 = = , = = , CB CE 3 CB BF 3 AE 1 DF 1 = , = . CE 3 BF 3
第六章㊀ 空间与图形 易得 G,H 为 AD 的三等分点,即 AG = GH = HD, GH 1 = ,又ȵ GHʊBC,ʑ әMGHʐәMBC, ʑ BC 3 GM MH GH 1 = = = , BM MC BC 3 ʑ MB = 3GM,MC = 3MH. ʑ ʑ EF������ 1 AD, 2 ʑ EF������ 1 BC, 2
㊀ ㊀ 1. 在同一单位长度下,①㊀ 两条线段的长度之比 ㊀ 叫做两条线 段的比,那么这四条线段叫做成比例线段,简称比例线段. 3. 比例的基本性质: a c = ⇔②㊀ ad = bc㊀ ( bdʂ0) . b d 2. 在四条线段中, 如果其中两条线段的比等于另外两条线
这两个三角形叫做相似三角形.
4. 如果两个三角形的对应角相等,③㊀ 对应边成比例 ㊀ , 那么 5. 如果两个图形相似, 并且它们的对应点所在直线交于一
点,那么这两个图形叫做位似图形. 这一点叫做 ④㊀ 位似中心 ㊀ , 对 应边的比叫做位似比,位似比等于相似比. ㊀ ㊀ 1. 相似三角形的判定
������������������������������������������������������������������������������������������������������������������������
第六章㊀ 空间与图形
41 ㊀
ɦ 6. 2㊀ 图的比.
和一条直角边与另一个直角三角形的斜边和一条直角边对应成 比例,那么这两个直角三角形相似. 2. 相似三角形的性质 (2) 对应边成比例; (1) ⑦㊀ 对应角相等㊀ ; (3) 对应线段之比 ( 高线㊁ 中线㊁ 角平分线 ) 与 ⑧㊀ 周长之比㊀ (4) 面积之比等于相似比的平方. (1) 如图①. 若 DEʊBC,则әADEʐәABC. (2) 如图②. 若 EDʊBC,则әEADʐәCAB. (3) 如图③. 若øAED = øB,则әADEʐәACB.
(湖南专版)2019年中考数学一轮复习 第六章 空间与图形 6.3 解直角三角形(试卷部分)课件

A.6 B.5 C.4 D.3 3
h
7
答案 D ∵ED是BC的垂直平分线, ∴DB=DC, ∴∠C=∠DBC, ∵BD是△ABC的角平分线, ∴∠ABD=∠DBC,∵∠BAC=90°, ∴∠C=∠DBC=∠ABD=30°, ∴BD=2AD=6, ∴CE=CD×cos C=3 .3 故选D.
h
8
2.(2017湖南益阳,7,3分)如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉 线BC的长度为(A、D、B在同一条直线上) ( )
3
在Rt△ACD中,∵∠CAD=60°, ∴CD=AD·tan∠CAD=120·tan 60°=120× =3 120 (m3 ). ∴BC=BD+CD=40 +3 120 =3160 (m3),故选A. 评析 本题考查了解直角三角形,解答本题的关键h是构造直角三角形,利用锐角三角函数求解. 12
6.(2015湖南长沙,11,3分)如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的 B处,测得树顶A的仰角∠ABO为α,则树OA的高度为 ( )
A. 3 0米
B.30sin α米
tan α
C.30tan α米 D.30cos α米
答案 C 根据题意可得BO=30米,tan∠ABO= A O,则AO=BO·tan∠ABO=30tan α(米). BO
x
1 sin α
h
11
5.(2016湖南长沙,11,3分)如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为3 0°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为120 m,则这栋楼的高度为 ()
A.160 3 m B.120 m3 C.300 m D.160 m 2 答案 A 设AD⊥BC于点D,由题意得AD=120 m, 在Rt△ABD中,∵∠BAD=30°, ∴BD=AD·tan∠BAD=120·tan 30°=120× 3 =40 (3m).
(湖南专版)2019年中考数学一轮复习第六章空间与图形6.4视图与投影(讲解部分)素材(pdf)

考点二㊀ 几何体的平面展开图
形的平面展开图.
������������������������������������������������������������������������
㊀ ㊀ 有些立体图形是由一些平面图形围成的, 将它们的表面适 当剪开可以展开成平面图形, 这样的平面图形称为相应立体图
46 ㊀
5 年中考 3 年模拟
ɦ 6. 4㊀ 视图与投影
156
考点一㊀ 三视图
㊀ ㊀ 1. 当我们从某一方向观察一个物体时, 所看到的平面图形 叫做物体的一个①㊀ 视图㊀ . 的由前向后观察物体的视图, 叫做 ②㊀ 主视图 ㊀ ; 在水平面内得到 的由上向下观察物体的视图,叫做俯视图; 在侧面内得到的由左 向右观察物体的视图,叫做③㊀ 左视图㊀ . 图,左视图在主视图的右边, 画三视图时, 三个视图要放在正确 的位置,并且使主视图与俯视图的长对正, 主视图与左视图的高 平齐,左视图与俯视图的宽相等. 3. 三视图位置有规定,主视图要在左上方, 它下方应是俯视 2. 对一个物体在三个投影面内进行正投影, 在正面内得到
球
㊀ ㊀ 例㊀ ( 2016 湖南郴州, 6, 3 分 ) 下列四个立体图形中, 它们 各自的三视图都相同的是 (㊀ ㊀ )
正方体
形,俯视图是带圆心的圆;圆柱的主视图和左视图是矩形,俯视图是 圆;三棱柱的主视图和左视图是矩形,俯视图是三角形.故选 A. 答案㊀ A 体的三视图,根据图中数据,求得该几ห้องสมุดไป่ตู้体的体积为 ㊀ ㊀ 变式训练㊀ ( 2014 内蒙古呼和浩特,4,3 分 ) 下图是某几何 (㊀ ㊀ )
考点三㊀ 投影
做⑤㊀ 投影面㊀ .
㊀ ㊀ 1. 一般地,用光线照射物体, 在某个平面上得到的影子叫做 物体的投影, 照 射 光 线 叫 做 ④ ㊀ 投 影 线 ㊀ , 投 影 所 在 的 平 面 叫 的光线形成的投影叫做中心投影. 投影线垂直于投影面产生的投 影叫做⑦㊀ 正投影㊀ . 2. 由平行光线形成的投影叫做 ⑥㊀ 平行投影 ㊀ . 由同一点发出
(完整版)2019全国各地中考数学试题分类汇编-投影与视图,推荐文档
2019全国各地中考数学试题分类汇编-投影与视图注意事项:认真阅读理解,结合历年的真题,总结经验,查找不足!重在审题,多思考,多理解!一.选择题1、〔2018柳州〕李师傅做了一个零件,如图,请你告诉他这个零件的主视图是〔A〕A、B、C、D、【考点】简单组合体的三视图、【专题】推理填空题、【分析】根据主视图的定义,从前面看即可得出答案、【解答】解:根据主视图的定义,从前面看,得出的图形是一个正六边形和一个圆,应选A、【点评】此题考查了简单组合体的三视图的应用,通过做此题培养了学生的理解能力和观察图形的能力,同时也培养了学生的空间想象能力2、〔2018十堰〕如图是某体育馆内的颁奖台,其主视图是〔A〕A、B、C、D、【考点】简单组合体的三视图、【专题】【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中、【解答】解:从颁奖台正面看所得到的图形为A、应选A、【点评】此题考查了三视图的知识,主视图是从物体的正面看得到的视图、3、〔2018义乌市〕以下四个立体图形中,主视图为圆的是〔〕A、B、C、D、考点:简单几何体的三视图。
解答:解:A、主视图是正方形,故此选项错误;B、主视图是圆,故此选项正确;C、主视图是三角形,故此选项错误;D、主视图是长方形,故此选项错误;应选:B、4、〔2018•广州〕一个几何体的三视图如下图,那么这个几何体是〔〕A、四棱锥B、四棱柱C、三棱锥D、三棱柱考点:由三视图判断几何体。
分析:主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形、解答:解:由于主视图和左视图为长方形可得此几何体为柱体,由俯视图为三角形,可得为棱柱体,所以这个几何体是三棱柱;应选D、点评:此题考查了由三视图来判断几何体,还考查学生对三视图掌握程度和灵活运用能力,同时也表达了对空间想象能力、5、〔2018•烟台〕如图是几个小正方体组成的一个几何体,这个几何体的俯视图是〔〕A、B、C、D、考点:简单组合体的三视图。
2019年全国各地中考数学试题分类汇编:投影与视图(含答案)
一、选择题1.(2015·兰州)由五个同样大小的立方体组成如图的几何体,则关于此几何体三种视图叙述正确的是A. 左视图与俯视图相同B. 左视图与主视图相同C. 主视图与俯视图相同D. 三种视图都相同2.(2015·广东梅州)下图所示几何体的左视图为()DCBA第2题图考点:简单组合体的三视图..分析:根据从左边看得到的图形是左视图,可得答案.解答:解:从左边看第一层一个小正方形,第二层一个小正方形,第三层一个小正方形,故选:A.点评:本题考查了简单组合体的三视图,从左边看看得到的图形是左视图.3.(2015·广东汕尾)下图所示几何体的左视图为()ADCBA第2题图4.(2015·贵州安顺)A B C D5.(2015·河南)如图所示的几何体的俯视图是()D6.(2015·孝感)如图是一个几何体的三视图,则这个几何体是A.正方体B.长方体C.三棱柱D.三棱锥C DBA正面第2题)4(题第7.(2015·湖南衡阳)如下左图的几何体是由一个圆柱体和一个长方体组成的,则这个几何体的俯视图是( C ).A .B .C .D .8. (2015•益阳)一个几何体的三视图如图所示,则这个几何体是( )10(2015·南昌)如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为( ).(第4题)DCBA解析:选C. ∵根据光的正投影可知,几何体的左视图是图C. ∴选C.11.(2015·呼和浩特).如图是某几何体的三视图,根据图中所标的数据求得该几何体的体积为A. 236πB. 136πC. 132πD. 120π12.(2015·黔西南州)下面几个几何体,主视图是圆的是A13.(2015·菏泽)如图是由6个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体A.主视图改变,左视图改变B.俯视图不变,左视图不变C.俯视图改变,左视图改变D.主视图改变,左视图不变14(2015·青岛).如图,在一次数学活动课上,张明用17个边长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭的几何体拼成一个大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要个小正方体,王亮所搭几何体表面积为________________.19,4815(2015·东营)由六个小正方体搭成的几何体如图所示,则它的主视图是()A. B. C. D.16.(2015·临沂)如图所示,该几何体的主视图是(A) (B) (C) (D)17(2015·深圳)下列主视图正确的是()【答案】A.【解析】由前面往后面看,主视图为A。
2023年中考数学一轮复习:投影与视图(含解析)
2023年中考数学一轮复习:投影与视图一、单选题1.如图,用一个平面去截正方体,截掉了正方形的一个角,且截面经过原正方体三条棱的中点,剩下几何体的展开图应该是()A.B.C.D.2.如图是由5个相同小正方形搭成的几何体,若将小正方体A放到小正方体B的正上方,则关于该几何体变化前后的三视图,下列说法正确的是()A.主视图不变B.俯视图改变C.左视图不变D.以上三种视图都改变3.两个完全相同的长方体,按如图方式摆放,其主视图为()A.B.C.D.二、填空题4.一个几何体是由许多规格相同的小正方体堆积而成的,其主视图、左视图如图所示,要摆成这样的几何体,至少需用个正方体,最多需用个正方体;5.如图,是正方体的一种平面展开图,各面都标有数字,则数字为-4的面与它对面的数字之积是.6.如图所示,水平放置的长方体的底面是长为4 cm、宽为2 cm的长方形,它的主视图的面积为12 2cm,则长方体的体积等于3cm.三、综合题7.下面图(1),图(2)分别是两种不同情形下旗杆和木杆的影子.(1)哪个图反映了阳光下的情形?(2)若同一时刻阳光下,木杆的影子长为0.8米,旗杆的影子长为7.2米,木杆的高为1.5米,求旗杆的高度.8.如图是由10个同样大小的小正方体搭成的物体,(1)请分别画出它的主视图和俯视图.(2)在主视图和俯视图不变的情况下,你认为最多还可以添加个小正方体.9.如图是小明用10块棱长都为3cm的正方体搭成的几何体.(1)分别画出从正面、从左面、从上面看到的所搭几何体的形状图;(2)小明所搭几何体的表面积(包括与桌面接触的部分)是.10.李明同学设计了某个产品的正方体包装盒如图所示,由于粗心少设计了其中一个顶盖,请你把它补上,使其成为一个两面均有盖的正方体盒子.(1)共有种弥补方法;(2)任意画出一种成功的设计图(在图中补充);(3)在你帮忙设计成功的图中,要把-6,8,10,-10,-8,6这些数字分别填入六个小正方形,使得折成的正方体相对面上的两个数相加得0.(直接在图中填上)11.如图是一个正方体纸盒的表面展开图,纸盒中相对两个面上的数互为倒数.(1)填空:a=,b=;(2)先化简,再求值:()()2223252ab a b ab a ab⎡⎤------⎣⎦.12.有若干个完全相同的小正方体堆成一个如图所示几何体.(1)图中共有个小正方体.(2)画出该几何体的主视图、左视图、俯视图.(3)若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加个小正方体.13.我们知道,将一个正方体或长方体的表面沿某些棱剪开,可以展成一个平面图形.(1)下列图形中,是正方体的表面展开图的是.(2)如图所示的长方体,长、宽、高分别为4、3、6,若将它的表面沿某些棱剪开,展成一个平面图形.则下列图形中,可能是该长方体表面展开图的有(填序号)(3)下列图是题(2)中长方体的一种表面展开图,它的外围周长为52,事实上,题(2)中长方体的表面展开图还有不少,聪明的你能画出一个使外围周长最大的表面展开图吗?请画出这个表面展开图,并求出它的外围周长.14.小彬做了探究物体投影规律的实验,并提出了一些数学问题请你解答:(1)如图1,白天在阳光下,小彬将木杆AB水平放置,此时木杆在水平地面上的影子为线段A B''.①若木杆AB的长为1m,则其影子A B''的长为m;②在同一时刻同一地点,将另一根木杆CD直立于地面,请画出表示此时木杆CD在地面上影子的线段DM;(2)如图2,夜晚在路灯下,小彬将木杆EF水平放置,此时木杆在水平地面上的影子为线段E F''.①请在图中画出表示路灯灯泡位置的点P;②若木杆EF的长为1m,经测量木杆EF距离地面1m,其影子E F''的长为1.5m,则路灯P距离地面的高度为m.15.如图,在平整的地面上,用10个棱长都为2cm的小正方体堆成一个几何体.(1)画出这个几何体的三视图;(2)求这个几何体的表面积;(3)如果现在你还有一些棱长都为2cm的小正方体,要求保持俯视图和左视图都不变,最多可以再添加个小正方体.16.用若干个完全相同的小正方体搭成一个几何体,使它从正面和左面看到的形状图如图所示.(1)搭这样一个几何体最多需要多少个小正方体?(2)画出(1)中所搭几何体从上面看到的形状图,并标出各个小正方形所在位置的小正方体的个数. 17.如图,是由6个大小相同的小正方体块搭建的几何体,其中每个小正方体的棱长为l厘米.(1)如果在这个几何体上再添加一些小立方体块,并保持俯视图和左视图不变,最多可以再添加个小立方块.(2)请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.18.晚上,小亮在广场乘凉,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯.(1)请你在图中画出小亮在照明灯P照射下的影子BC(请保留作图痕迹,并把影子描成粗线);(2)如果小亮的身高 1.6AB m=,测得小亮影长2BC m=,小亮与灯杆的距离13BO m=,请求出灯杆的高PO.19.综合实践问题情景:某综合实践小组进行废物再利用的环保小卫士行动. 他们准备用废弃的宣传单制作装垃圾的无.盖.纸盒.操作探究:(1)若准备制作一个无盖..的正方体形纸盒,如图1,下面的哪个图形经过折叠能围成无盖..正方体形纸盒?(2)如图2是小明的设计图,把它折成无盖..正方体形纸盒后与“保”字相对的是哪个字?(3)如图3,有一张边长为20cm的正方形废弃宣传单,小华准备将其四角各剪去一个小正方形,折成无.盖.长方体形纸盒.①请你在图3中画出示意图,用实线表示剪切线,虚线表示折痕.②若四角各剪去了一个边长为xcm的小正方形,用含x的代数式表示这个纸盒的高以及底面积,当小正方形边长为4cm时,求纸盒的容积.20.如图所示,一透明的敞口正方体容器ABCD﹣A'B'C'D'装有一些液体,棱AB始终在水平桌面上,液面刚好过棱CD,并与棱BB'交于点Q.此时液体的形状为直三棱柱,其三视图及尺寸见下图所示请解决下列问题:(1)CQ与BE的位置关系是,BQ的长是dm:(2)求液体的体积;(提示:直棱柱体积=底面积×高)(3)若容器底部的倾斜角∠CBE=α,求α的度数.(参考数据:sin49°=cos41°=34,tan37°=34)21.【问题情境】小圣所在的综合实践小组准备制作一些无盖纸盒收纳班级讲台上的粉笔.【操作探究】(1)图1中的哪些图形经过折叠能围成无盖正方体纸盒?(填序号).(2)小圣所在的综合实践小组把折叠成6个棱长都为2dm的无盖正方体纸盒摆成如图2所示的几何体.①请计算出这个几何体的体积;②如果在这个几何体上再添加一些相同的正方体纸盒,并保持从上面看到的形状和从左面看到的形状不变,最多可以再添加个正方体纸盒.22.阅读以下文字并解答问题:在“物体的高度”活动中,某数学兴趣小组的4名同学选择了测量学校里的四棵树的高度.在同一时刻的阳光下,他们分别做了以下工作:小芳:测得一根长为1米的竹竿的影长为0.8米,甲树的影长为4.08米(如图1).小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图2),墙壁上的影长为1.2米,落在地面上的影长为2.4米.小丽:测量的丙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上(如图3),测得此影子长为0.2米,一级台阶高为0.3米,落在地面上的影长为4.4米.小明:测得丁树落在地面上的影长为2.4米,落在坡面上影长为3.2米(如图4).身高是1.6m的小明站在坡面上,影子也都落坡面上,小芳测得他的影长为2m.(1)在横线上直接填写甲树的高度为米.(2)求出乙树的高度(画出示意图).(3)请选择丙树的高度为()A.6.5米B.5.75米C.6.05米D.7.25米(4)你能计算出丁树的高度吗?试试看.23.如图1是边长为20cm的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).(1)设剪去的小正方形的边长为 (cm)x ,折成的长方体盒子的容积为 ()3cm V ,直接写出用只含字母x 的式子表示这个盒子的高为 cm ,底面积为 2cm ,盒子的容积 V 为3cm ,(2)为探究盒子的体积与剪去的小正方形的边长 x 之间的关系,小明列表分析:填空:①m = , n = ;②由表格中的数据观察可知当 x 的值逐渐增大时, V 的值 .(从“逐渐增大”,“逐渐减小”“先增大后减小”,“先减小后增大”中选一个进行填空)24.如图,A 、B 、C 分别表示甲、乙、丙三个物体的顶端,甲物体高3米,影长2米,乙物体高2米,影长3米,甲乙两物体相距4米.(1)请在图中画出光源灯的位置及灯杆,并画出物体丙的影子.(2)若甲、乙、丙及灯杆都与地面垂直,且在同一直线上,求灯杆的高度.25.测量金字塔高度:如图1,金字塔是正四棱锥 S ABCD -,点O是正方形 ABCD 的中心 SO 垂直于地面,是正四棱锥 S ABCD - 的高,泰勒斯借助太阳光.测量金字塔影子 PBC 的相关数据,利用平行投影测算出了金字塔的高度,受此启发,人们对甲、乙、丙三个金字塔高度也进行了测量.甲、乙、丙三个金字塔都用图1的正四棱锥 S ABCD - 表示.(1)测量甲金字塔高度:如图2,是甲金字塔的俯视图,测得底座正方形 ABCD 的边长为 80m ,金字塔甲的影子是 50m PBC PC PB ==, ,此刻,1米的标杆影长为0.7米,则甲金字塔的高度为m.(2)测量乙金字塔高度:如图1,乙金字塔底座正方形 ABCD 边长为 80m ,金字塔乙的影子是PBC , 75PCB PC ∠=︒=, ,此刻1米的标杆影长为0.8米,请利用已测出的数据,计算乙金字塔的高度.答案解析部分1.【答案】B【解析】【解答】将A、C、D折叠,发现都不能合成切口,只有B选项折叠后两个剪去的三角形与另一个剪去的三角形交于一点,与题目中的题设一致,故答案为:B.【分析】利用正方体的展开图定义和特征逐项判断即可。
湖南专版2019年中考数学一轮复习第六章空间与图形6.2图形的相似试卷部分课件
A.2 B.1 C.4 D.2.5 答案 A ∵点A(2,4),过点A作AB⊥x轴于点B,将△AOB以坐标原点O为位似中心缩小为原图
形的 1 ,得到△COD,∴C(1,2),则CD的长度是2.故选A.
2
2.(2014湖南张家界,7,3分)下列关于位似图形的表述: ①相似图形一定是位似图形,位似图形一定是相似图形; ②位似图形一定有位似中心; ③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图 形是位似图形; ④位似图形上任意两点与位似中心的距离之比等于位似比. 其中正确的序号是 ( ) A.②③ B.①② C.③④ D.②③④
中考数学 (湖南专用)
§6.2 图形的相似
五年中考
A组 2014—2018年湖南中考题组
考点一 相似与位似
1.(2018湖南邵阳,8,3分)如图所示,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.
将△AOB以坐标原点O为位似中心缩小为原图形的 1 ,得到△COD,则CD的长度是( )
AB BC
6.(2018湖南邵阳,12,3分)如图所示,点E是平行四边形ABCD的边BC延长线上一点,连接AE,交
CD于点F,连接BF,写出图中任意一对相似三角形
.
答案 △ADF∽△ECF(答案不唯一)
解析 ∵四边形ABCD为平行四边形, ∴AD∥CE,∴∠DAF=∠E,∠D=∠FCE, ∴△ADF∽△ECF.
∴ AC = AD ,
AB AC
∴AC2=AD·AB=2×(2+6)=16, ∵AC>0,∴AC=4. 故选B.
思路分析 先证明△ADC∽△ACB,可得 AC = AD ,即AC2=AD·AB,由此即可解决问题.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
)
答案 B 从正面看是矩形,能看见的棱用实线表示,故选B. 思路分析 根据三视图的含义及主视图观察的角度来解决此题.
易错警示 此题易错选A或C.
10.(2014湖南株洲,5,3分)下列几何体中,有一个几何体的主视图与俯视图的形状不一样,这个 几何体是 ( )
答案 C A项,主视图、俯视图都是正方形,故A不符合题意;B项,主视图、俯视图都是矩形,
6.(2017湖南长沙,7,3分)某几何体的三视图如图所示,则此几何体是 (
)
A.长方体
C.球
B.圆柱
D.正三棱柱
答案 B
因为俯视图是圆,故可排除A、D,又主视图和左视图都是矩形,可排除C.故选B.
7.(2016湖南长沙,6,3分)下图是由六个相同的小正方体搭成的几何体,这个几何体的主视图是
(
3.(2017河北,8,3分)如图是由相同的小正方体木块粘在一起的几何体,它的主视图是 (
)
答案 A 从正面看易得共有两层,下层有3个小正方形,上层有两个小正方形.故选A.
4.(2017湖北武汉,7,3分)某物体的主视图如图所示,则该物体可能为 (
)
答案 A 只有选项A中物体的主视图是圆,故选A.
5.(2017四川绵阳,4,3分)如图所示的几何体的主视图正确的是(
)
答案 D 由主视图的定义知选D.
6.(2016山东潍坊,3,3分)如图,几何体是由底面圆心在同一条竖直线上的三个圆柱构成的,其俯 视图是 ( )
答案 C 从上往下看,最上面的圆柱体是能被看到的,在俯视图中应画成实线,最下面的圆柱 体是被遮挡的,在俯视图中应画成虚线,故选C.
故选D.
11.(2015内蒙古呼和浩特,9,3分)如图是某几何体的三视图,根据图中所标的数据求得该几何体 的体积为 ( )
A.236π B.136π C.132π D.120π 答案 B 从题中三视图可看出,该几何体是由两个圆柱组成的,其体积为π×22×2+π×42×8=136
π,故选B.
12.(2015甘肃兰州,2,4分)由五个同样大小的立方体组成如图的几何体,则关于此几何体的三种 视图叙述正确的是( )
(
)
答案 C 选项C中几何体的主视图和左视图均为 .故选C.
9.(2016安徽,4,4分)如图,一个放置在水平桌面上的圆柱,它的主(正)视图是 (
)
答案 C 该圆柱的主(正)视图为矩形,故选C.
10.(2016北京,5,3分)下图是某个几何体的三视图,该几何体是(
)
A.圆锥 B.三棱锥 C.圆柱 D.三棱柱 答案 D 由主视图是矩形,知选项A,B不符合题意;由俯视图是三角形,知选项C不符合题意.
答案 A 根据主视图的定义可知选A.
3.(2018湖南湘潭,2,3分)如图所示的几何体的主视图是 (
)
答案 C
4.(2018湖南永州,4,4分)如图,几何体的主视图是 (
)
答案 B
5.(2017湖南湘潭,2,3分)如图所示的几何体的主视图是 (
)
答案 D 从正面看,从下往上数,第一层有三个小正方形,第二层最左边有一个小正方形,故选 D.
B.0.288π m2
C.1.08π m2
D.0.72π m2
答案 D 如图所示,∵AC⊥OB,BD⊥OB,
∴△AOC∽△BOD,
AC 2 0.6 OA = ∴ ,即 = ,
OB
BD
3
BD
解得BD=0.9 m,
同理可得BD'=0.3 m, ∴S圆环形阴影=0.92π-0.32π=0.72π(m2),故选D.
B组
考点一 三视图
2014—2018年全国中考题组
)
1.(2018安徽,4,4分)一个由圆柱和圆锥组成的几何体如图水平放置,其主(正)视图为 (
答案 A 由主(正)视图的定义可知A正确.
2.(2018四川成都,3,3分)如图所示的正六棱柱的主视图是 (
)
答案 A 主视图是从正面看得到的图形,从正面看是左右相邻的3个矩形,中间的矩形面积较 大,两边相同,故选A.
7.(2016湖北十堰,2,3分)下列几何体中,其主视图与俯视图相同的是 (
)
答案 C A.圆柱的主视图是矩形,俯视图是圆; B.圆锥的主视图是三角形,俯视图是带圆心的圆; C.正方体的主视图与俯视图都是正方形;
D.三棱柱的主视图是矩形(中间有1条竖实线),俯视图是三角形.故选C.
8.(2016河南,3,3分)下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是
故B不符合题意;C项,主视图是三角形、俯视图是圆(含圆心),故C符合题意;D项,主视图、俯视
图都是圆,故D不符合题意.故选C.
考点二
几何体的平面展开图
)
(2013湖南岳阳,3,3分)一个正方体的平面展开图如图所示,将它折成正方体后,与汉字“岳”相
对的面上的汉字是 (
A.建 B.设 C.和 D.谐 答案 C 正方体的平面展开图中,相对的两个面之间相隔一个正方形,根据这一特点,可知与 “岳”字相对的是“和”字,故选C.
中考数学
(湖南专用)
§6.4 视图与投影
五年中考 A组
考点一 三视图
)
2014—2018年湖南中考题组
1.(2018湖南常德,7,3分)把图1中的正方体的一角切下后摆在图2所示的位置,则图2中的几何体 的主视图为 (
答案 D 从正面看是一个等腰三角形,且底边上的高线是虚线,故选D.
2.(2018湖南衡阳,4,3分)如图是由5个大小相同的小正方体摆成的立体图形,它的主视图是 ( )
)
答案 B 根据主视图的定义,可知选B.
8.(2015湖南益阳,4,5分)一个几何体的三视图如图所示,则这个几何体是 (
)
A.三棱锥 C.圆柱 答案 B B.三棱柱 D.长方体 根据题图中三视图的形状,符合条件的只有直三棱柱,因此这个几何体的名称是三 棱柱.故选B.
9.(2015湖南娄底,8,3分)如图,正三棱柱的主视图为 (
考点三
投影
(2016湖南永州,10,4分)圆桌面(桌面中间有一个直径为0.4 m的圆洞)正上方的灯泡(看作一个
点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直
径为1.2 m,桌面离地面1 m,若灯泡离地面3 m,则地面圆环形阴影的面积是 ( )
A.0.324π m2
