学年高中数学第一章立体几何初步1.1.4投影与直观图课后作业新人教B版必修2
人教B版高中数学必修二《第一章 立体几何初步 1.1 空间几何体 1.1.4 投影与直观图》_1

课题:投影与直观图教学目标1. 知识与技能目标: 会画出和看懂一些几何体的直观图,了解平行投影、正投影和中心投影的概念及主要特征,能够运用斜二测画法的画图规则正确的画图和看图,并可以根据直观图进行简单的计算。
2. 过程与方法目标: 使用现代信息技术展示空间图形,帮助学生利用平行投影和中心投影,进一步掌握在平面上表示空间图形的方法和技能具有重要的意义。
3. 情感态度与价值观目标: 在学习的过程中体现立体图形和平面图形的转化关系,培养学生认真参与,积极交流的主体意识和乐于探索、勇于创新的科学态度。
教学重点和难点重点: 平行投影的性质与斜二测画法难点: 正确的把握斜二测画法的要点以及 选择放置直观图的角度启发、讨论、探究教学手段利用多媒体辅助教学教学环节一 、平行投影与中心投影1、 平行投影在立体几何中,一般都是根据平行投影的性质,用平面图形来表示空间图形,给出平行投影的概念和性质。
概念:已知图形F ,直线l 与平面α相交,过F 上任意一点M 作直线/MM 平行于l ,交平面α于点/M ,则点/M 叫做M 在平面α内关于直线l 的平行投影(或象),如果图形F 上的所有点在平面α内关于直线l 的平行投影构成图形/F ,则/F 叫做图形F 在α内关于直线l 的平行投影。
平面α叫做投射面,l 叫做投射线。
容易观察到,当图形中的直线或线段不平行于投射线时,平行投影都具有下述性质: ① 直线或线段的平行投影仍是直线或线段;② 平行直线的平行投影是平行或重合的直线;③ 平行于投射面的线段,它的投影与这条线段平行且等长;④ 与投射面平行的平面图形,它的平行投影与这个图形全等;⑤ 在同一直线或平行直线上,两条线段平行投影的比等于这两条线段的比。
当投射线和投射面成适当的角度或改变图形相对于投诉面的位置时,一个空间图形在投射面上的平行投影可以形象地表示这个空间图形。
2、 中心投影结合图形让学生了解二、直观图1、 直观图定义:用来表示空间图形的平面图形2、 直观图画法:斜二测画法规则(1)在已知图形所在的空间中取水平平面,作互相垂直的轴Ox,Oy,再作Oz 轴,使9090o o xOz yOz ∠=∠=,且(2)画直观图时,把Ox Oy Oz ,,,画成对应////O x ,O y ,O z ,使///o o x O y 45135∠=或(),///o ///x O z 90,x O y ∠=所确定的平面表示水平平面。
2019版高中人版B版数学必修二练习:1.1.4 投影与直观图 含答案

1.1.4 投影与直观图1。
利用斜二测画法得到的①三角形的直观图一定是三角形;②正方形的直观图一定是菱形;③等腰梯形的直观图可以是平行四边形;④菱形的直观图一定是菱形.以上结论正确的是( B )(A)①②(B)①(C)③④(D)①②③④解析:①正确.②正方形的直观图是平行四边形.③等腰梯形的直观图是梯形.④菱形的直观图是平行四边形.选B。
2。
用斜二测画法画水平放置的平面图形的直观图,对其中两条线段结论错误的是( B )(A)原来相交的仍相交(B)原来垂直的仍垂直(C)原来平行的仍平行 (D)原来共点的仍共点解析:斜二测画法保平行,保相交,保平行线段的比,但不保垂直.选B.3。
如图所示为一个平面图形的直观图,则此平面图形可能是( C )解析:由直观图知,平面图形中靠右侧一边与y轴平行,满足这一特征的只有C。
4.△A′B′C′是水平放置的△ABC的直观图,则在△ABC的三边及中线AD中,最长的线段是( D )(A)AB (B)AD (C)BC (D)AC解析:由于直观图中,∠x′O′y′=45°,所以∠A′B′C′=45°,故∠ABC=90°,所以AC最长.故选D.5.如图,△A′O′B′为水平放置的△AOB的直观图,且O′A′=2,O′B′=3,则△AOB的周长为( A )(A)12 (B)10 (C)8 (D)7解析:根据斜二测画法得到三角形OAB为直角三角形,底面边长OB=3,高OA=2O′A′=4,AB=5,所以直角三角形OAB的周长为3+4+5=12.6。
如图所示,正方形O′A′B′C′的边长为1 cm,它是一个水平放置的平面图形的直观图,则原图形的周长为.解析:由于平行性不变,O′A′∥B′C′,故在原图形中,OA BC,所以四边形OABC为平行四边形,且对角线OB⊥OA,对角线OB=2,则AB==3。
所以原图形的周长为l=3×2+1×2=8.答案:8 cm7.已知正三角形AOB的边长为a,如图所示,把它放在平面直角坐标系中,则它的水平放置的平面直观图的面积为( B )(A)a2(B)a2(C)a2(D)a2解析:在直观图△A′B′O′中,O′A′=a,O′A′边上的高为××a=a,故△A′B′O′的面积为S=×a×a=a2。
高中数学 1.1 空间几何体 1.1.4 投影与直观图课后训练
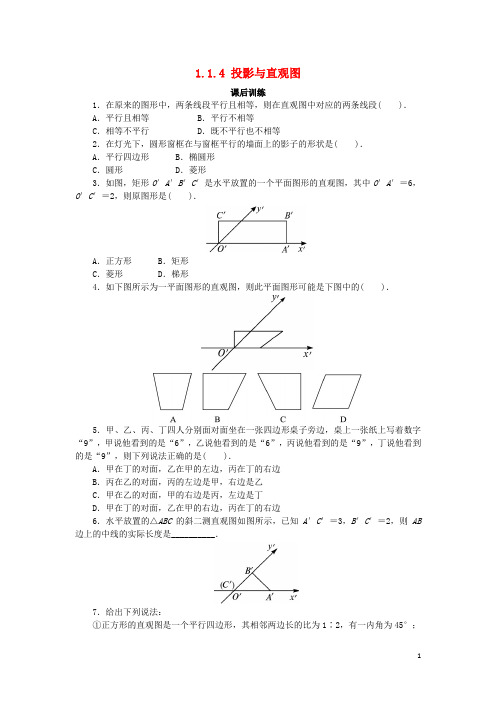
1.1.4 投影与直观图课后训练1.在原来的图形中,两条线段平行且相等,则在直观图中对应的两条线段( ).A.平行且相等 B.平行不相等C.相等不平行 D.既不平行也不相等2.在灯光下,圆形窗框在与窗框平行的墙面上的影子的形状是( ).A.平行四边形 B.椭圆形C.圆形 D.菱形3.如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6,O′C′=2,则原图形是( ).A.正方形 B.矩形C.菱形 D.梯形4.如下图所示为一平面图形的直观图,则此平面图形可能是下图中的( ).5.甲、乙、丙、丁四人分别面对面坐在一张四边形桌子旁边,桌上一张纸上写着数字“9”,甲说他看到的是“6”,乙说他看到的是“6”,丙说他看到的是“9”,丁说他看到的是“9”,则下列说法正确的是( ).A.甲在丁的对面,乙在甲的左边,丙在丁的右边B.丙在乙的对面,丙的左边是甲,右边是乙C.甲在乙的对面,甲的右边是丙,左边是丁D.甲在丁的对面,乙在甲的右边,丙在丁的右边6.水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB 边上的中线的实际长度是__________.7.给出下列说法:①正方形的直观图是一个平行四边形,其相邻两边长的比为1∶2,有一内角为45°;②水平放置的正三角形的直观图是一个底边长不变,高为原三角形高的一半的三角形;③不等边三角形水平放置的直观图是不等边三角形;④水平放置的平面图形的直观图是平面图形.写出其中正确说法的序号__________.8.如图所示,已知用斜二测画法画出的△ABC的直观图△A′B′C′是边长为a的正三角形,那么原△ABC的面积为__________.9.画出一个正三棱台的直观图(尺寸:上、下底面边长分别为1 cm,2 cm,高2 cm).10.在水平放置的平面α内有一边长为2的正方形A′B′C′D′(如图),其中对角线A′C′位于水平位置.已知该正方形是某个平行四边形用斜二测画法画出的直观图,试画出原平行四边形,并求其面积.参考答案1. 答案:A2. 答案:C 由点光源的中心投影的性质可知影子应是圆形.3. 答案:C4. 答案:C 根据斜二测画法的规则:平行于x 轴或在x 轴上的线段的长度在新坐标系中不变,在y 轴上或平行于y 轴的线段的长度在新坐标系中变为原来的12,并注意到∠xOy =90°,∠x ′O ′y ′=45°,因此由直观图还原成原图形为选项C.5. 答案:D 可以从每个人观察的角度进行分析.6. 答案:52在直观图中,∠A ′C ′B ′=45°,则在原图形中∠ACB =90°,AC =3,BC =4,则斜边AB =5,故斜边上的中线长为52. 7. 答案:④ 对于①,若以该正方形的一组邻边所在的直线为x 轴、y 轴,则结论正确;但若以该正方形的两条对角线所在的直线为x 轴、y 轴,由于此时该正方形的各边均不在坐标轴上或与坐标轴平行,则其直观图中相邻两边长不一定符合“横不变,纵减半”的规则;对于②,水平放置的正三角形的直观图是一个底边长不变,高比原三角形高的一半还要短的三角形;对于③,只要坐标系选取的恰当,不等边三角形水平放置的直观图可以是等边三角形.8.答案:22a 过C ′作y ′轴的平行线C ′D ′与x ′轴交于D ′,则2sin 45a C'D'==︒. 又∵C ′D ′是原△ABC 的高CD 的直观图,∴CD =.∴211222ABC S AB CD a ∆=⋅==. 9. 答案:解:(1)画轴,以底面△ABC 的垂心O 为原点,OC 所在直线为y 轴,平行于AB 的直线为x 轴,建立平面直角坐标系,以上底面△A ′B ′C ′的垂心O ′与O 的连线为z 轴,建立空间坐标系.(2)画下底面,在xOy 平面上画△ABC 的直观图,在y轴上量取OC =cm,OD =cm.过D 作AB ∥x 轴,且AB =2 cm ,以D 为中点,则△ABC 为下底面三角形的直观图.(3)画上底面,在z 轴上截取OO ′=2 cm ,过O ′作x ′轴∥x 轴,y ′轴∥y 轴,在y ′轴上量取6O'C'=,12O'D'=cm ,过D ′作A ′B ′∥x ′轴,A ′B ′=1 cm ,且以D ′为中点,则△A ′B ′C ′为上底面三角形的直观图.(4)连线成图,连接AA ′,BB ′,CC ′,并擦去辅助线,则三棱台ABC -A ′B ′C ′即为所要画的正三棱台的直观图.10. 答案:解:平行四边形ABCD 如图所示.∵A ′C ′在水平位置,A ′B ′C ′D ′为正方形,∴在四边形ABCD 中,DA ⊥AC ,AC ⊥CB .又∵DA =2D ′A ′=4,AC =A ′C ′=,BC =2B ′C ′=4,∴S 四边形ABCD =AC ·AD =。
高中数学第一章立体几何初步1.1.4投影与直观图同步练习含解析新人教B版必修2

1.下列关于直观图画法的说法不正确的是( ).A .原图中平行于x 轴的线段,其对应线段仍平行于x 轴,且长度不变B .原图中平行于y 轴的线段,其对应线段仍平行于y 轴,且长度不变C .画与坐标系xOy 对应的坐标系x ′O ′y ′时,∠x ′O ′y ′可等于135°D .作直观图时,由于选轴不同,所画直观图可能不同2.如果一个三角形的平行投影仍是一个三角形,则下列说法中正确的是( ).A .内心的平行投影还是内心B .重心的平行投影还是重心C .垂心的平行投影还是垂心D .外心的平行投影还是外心3.下晚自习后,小华走路回家,在经过一盏路灯时,他发现自己的影子( ).A .变长B .变短C .先变长后变短D .先变短后变长4.对于一条底边在x 轴上的三角形,采用斜二测画法作出其直观图,其直观图面积是原三角形面积的( ).A .2倍B .2倍C .2倍D .12倍 5.若线段AB 平行于投射面,O 是AB 上一点,且AO ∶OB =m ∶n ,则点O 的平行投影O ′分线段AB 的平行投影A ′B ′的长度之比是______.6.小明想利用树影测树高,他在某一时刻测得长为1 m 的竹竿影长0.9 m ,但当他马上测树高时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子上了墙,如图所示.他测得留在地面部分的影子长2.7 m ,留在墙壁部分的影高1.2 m ,则树的高度为(太阳光线可看作为平行光线)______.7.如图所示,在水平放置的平面α内有一边长为1的正方形A ′B ′C ′D ′,其中对角线A ′C ′处于水平位置.已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.8.小迪身高1.6 m,一天晚上放学回家,走到两路灯之间,她发现自己的身影的顶部正好在A 路灯的底部,她又向前走了5 m,又发现身影的顶部正好在B路灯的底部,已知两路灯之间的距离为10 m.(两路灯的高度是一样的)求:(1)路灯的高度;(2)当小迪走到B路灯下,她在A路灯下的身影有多长?9.某地夏季中午,当太阳移到屋顶上方偏南时,光线与地面成60°角,房屋向南的窗户AB高1.6米,现要在窗子外面的上方安装一个水平遮阳篷AC,如图所示.求:(1)当遮阳篷AC的宽度在什么范围内,太阳光线能直接射入室内?(2)当遮阳篷AC的宽度在什么范围时,太阳光线不能直接射入室内?(精确到0.01米)参考答案1. 答案:B2. 答案:C3. 答案:D4. 答案:B解析:底边上的高变为原来的2倍. 5. 答案:m ∶n6. 答案:4.2 m解析:树高为AB ,影长为BE ,CD 为树留在墙上的影高, ∴ 1.210.9CD CE CE ==,CE =1.08 m ,树影长BE =2.7+1.08=3.78 m ,树高1 4.2m 0.9AB BE ==. 7. 解:四边形ABCD 的图形如图所示.∵A ′C ′在水平位置,A ′B ′C ′D ′为正方形,∴在四边形ABCD 中,DA ⊥AC .∵DA =2D ′A ′=2,AC A C =''=∴·ABCD S AC AD ==四边形8. 解:如图所示,设A 、B 为两路灯,小迪从MN 移到PQ ,并设C 、D 分别为A 、B 路灯的底部.由题目已知得MN =PQ =1.6 m ,NQ =5 m ,CD =10 m.(1)设CN =x ,则QD =5-x ,路灯高BD 为h .∵△CMN ∽△CBD , 即 1.610CN MN x CD BD h=⇒=.① 又∵△PQD ∽△ACD , 即1.6510PQ QD x AC CD h -=⇒=② 由①②式得x =2.5 m ,h =6.4 m ,即路灯高为6.4 m.(2)当小迪移到BD所在线上(设为DH)时,连接AH交地面于E,则DE长即为所求的影长.∵1.66.410DH DE DE DEH CEAAC CE DE∆∆⇒=⇒=+∽,解得10m3DE=,即影长为10m3.9.解:(1)在Rt△ABC中,∠ACB=60°,AB=1.6 m,则AC2=BC2-AB2,BC=2AC,∴AC2=4AC2-1.62,∴AC0.92(m).当0≤A C≤0.92米时,太阳光线可直接射入室内.。
高中数学 第一章 立体几何初步 1.1.4 投影与直观图练习(含解析)新人教B版必修2-新人教B版高

1.1.4 投影与直观图对应学生用书P11知识点一平行投影与中心投影1.下列说法正确的是( )A.矩形的平行投影一定是矩形B.正方形的平行投影一定是矩形C.正方形的平行投影一定是菱形D.梯形的平行投影一定是梯形或线段答案 D解析矩形的平行投影可能是矩形,也可能是线段;正方形的平行投影可能是线段,也可能是正方形;梯形的平行投影一定是梯形或线段.2.下列命题:①空间图形在平行投影和中心投影后有不同的图形;②正方形的直观图可能是平行四边形;③空间图形经过中心投影后,直线变成直线,但平行直线有可能变成相交直线;④互相垂直的两条直线的直观图一定是互相垂直的两条直线.其中正确命题的个数为( )A.1 B.2 C.3 D.4答案 C解析由平行投影、中心投影的概念与性质知,命题①②③正确;命题④中假设这两条直线为共面垂直,则当投射线平行于这两条直线所确定的平面时,得到的直观图是一条直线,故④错误.知识点二斜二测画法解(1)如图①,画x′轴、y′轴和z′轴,使∠x′O′y′=45°(或135°),∠x′O′z′=90°.(2)以点O′为EF的中点,在y′轴上截取EF=1.5 cm,以点E为CD的中点画CD∥O′x′,并使CD=3 cm;再以点F为AB的中点画AB∥O′x′,并使AB=3 cm.连接AD,BC.(3)过点A,B,C,D分别作z′轴的平行线,并在这些平行线上分别截取长为4 cm的线段AA′,BB′,CC′,DD′.(4)顺次连接A′,B′,C′,D′,A′,并擦去作为辅助线的坐标轴及点E,F,就得到正四棱柱的直观图,如图②所示.知识点三与直观图有关的问题4.如图所示是水平放置的三角形的直观图,A′B′∥y′轴,则原图形中△ABC是( )A.等边三角形B.等腰三角形C.直角三角形D.等腰直角三角形答案 C解析本题主要考查由直观图还原为原图,将斜二测画法逆用,即与x′O′y′坐标轴平行的线在xOy 系中与坐标轴垂直,且AB =2A′B′,AC =A′C′.如图.故选C .5.已知正△ABC 的边长为a ,以它的一边为x 轴,对应的高线为y 轴,画出它的水平放置的直观图△A′B′C′,则△A′B′C′的面积是( )A .34a 2 B .38a 2 C .68a 2 D .616a 2 答案 D解析 本题考查水平放置的平面图形的直观图,因此要正确作出直观图,如图.则有A′B′=AB =a ,O′C′=12OC =12·32a =34a ,∠B′O′C′=45°,∴S △A′B′C′=12A′B′·O′C′·sin45°=12a×34a×22=616a 2,故选D .对应学生用书P11一、选择题1.当图形中的直线或线段不平行于投影线时,关于平行投影的性质,下列说法中不正确的是( )A .直线或线段的平行投影仍是直线或线段B.平行直线的平行投影仍是平行的直线C.与投射面平行的平面图形,它的投影与这个图形全等D.在同一直线或平行直线上,两条线段平行投影的比等于这两条线段的比答案 B解析根据平行投影的意义可知,平行直线的平行投影是平行或重合的直线,故选B.2.水平放置的△ABC有一边在水平线上,它的直观图是正△A1B1C1,则△ABC是( ) A.锐角三角形 B.直角三角形C.钝角三角形 D.任意三角形答案 C解析如图,原图中∠BAC>90°,故选C.3.如果一个三角形的平行投影仍是一个三角形,则下列结论正确的是( )A.内心的平行投影还是内心B.重心的平行投影还是重心C.垂心的平行投影还是垂心D.外心的平行投影还是外心答案 B解析三角形的重心是三条中线的交点,三角形平行投影后各边的中点位置不会变,故其中线的交点,即重心仍是三角形的重心.4.如图在正方体ABCD-A1B1C1D1中,M,N分别是BB1,BC的中点,则图中阴影部分在平面ADD1A1上的正投影(投射线垂直于投射面所得的平行投影)是( )答案 A解析 过△DMN 三个顶点D ,M ,N 分别在投影面ADD 1A 1上作正投影即得.故选A . 5.已知两个圆锥底面重合在一起(底面平行于水平面),若其中一个圆锥顶点到底面的距离为 2 cm ,另一个圆锥顶点到底面的距离为 3 cm ,则其直观图中这两个顶点之间的距离为( )A .2 cmB .3 cmC .2.5 cmD .5 cm 答案 D解析 圆锥顶点到底面的距离即圆锥的高,故两顶点间的距离为2+3=5(cm),因为在直观图中与z 轴平行的线段长度不变,所以仍为5 cm .二、填空题6.水平放置的△ABC 的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB 边上的中线的实际长度为________.答案 52解析 原图是AC =3,BC =4的直角三角形,故斜边上的中线长为1232+42=52.7.如图所示为一个水平放置的正方形ABCO ,在直角坐标系xOy 中,点B 的坐标为(2,2),则在用斜二测画法画出的正方形的直观图中,顶点B′到x′轴的距离为________.答案22解析 点B′到x′轴的距离等于点A′到x′轴的距离d ,而O′A′=12OA =1,∠C′O′A′=45°(或135°),所以d =22O′A′=22. 8.在等腰梯形ABCD 中,上底边CD =1,AD =CB =2,下底边AB =3,按平行于上、下底边取x 轴,则直观图A′B′C′D′的面积为________.答案22解析 等腰梯形ABCD 的高为1,而直观图A′B′C′D′仍为梯形,其高为12sin45°=24,故面积为12×(1+3)×24=22.三、解答题9.用斜二测画法画边长为4 cm 的水平放置的正三角形的直观图.解 解法一:(1)如图①所示,以BC 边所在的直线为x 轴,以BC 边上的高线AO 所在的直线为y 轴.(2)画对应的x′轴、y′轴,使∠x′O′y′=45°. 在x′轴上截取O′B′=O′C′=2 cm , 在y′轴上截取O′A′=12OA = 3 cm ,连接A′B′,A′C′,则三角形A′B′C′即为正三角形ABC 的直观图,如图②所示. 解法二:(1)如图③所示,以BC 边所在的直线为y 轴,以BC 边上的高AO 所在的直线为x 轴.(2)画对应的x′轴、y′轴,使∠x′O′y′=45°. 在x′轴上截取O′A′=OA ,在y′轴上截取O′B′=O′C′=12OC =1 cm ,连接A′B′,A′C′,则三角形A′B′C′即为正三角形ABC 的直观图,如图④所示.10.水平放置的平面α内有一个边长为1的正方形A′B′C′D′,如图所示,其中对角线A′C′在水平位置,已知该正方形是一个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形,并求出其面积.解四边形ABCD的真实图形如图.因为A′C′在水平位置,且四边形A′B′C′D′ 为正方形,所以四边形ABCD中,DA⊥AC,BC⊥AC.由DA=2D′A′=2,AC=A′C′=2,得S四边形ABCD=AC·AD=22.。
人教B版数学必修二讲义:第1章 1.1 1.1.4 投影与直观图 Word版含答案

1.1.4投影与直观图1.平行投影(1)投影①定义:由于光的照射,在不透明物体后面的屏幕上可以留下这个物体的影子,这种现象叫做投影.②投射线:光线.③投射面:留下影子的屏幕.(2)平行投影当投射光线为一束平行线时,该投影称为平行投影.(3)平行投影的性质①直线或线段的平行投影仍是直线或线段;②平行直线的平行投影是平行或重合的直线;③平行于投射面的线段,它的投影与这条线段平行且等长;④与投射面平行的平面图形,它的投影与这个图形全等;⑤在同一直线或平行直线上,两条线段平行投影的比等于这两条线段的比.2.直观图的概念(1)定义:把空间图形(平面图形和立体图形的统称)画在平面内,使得既富有立体感,又能表达出主要部分的位置关系和度量关系的图形叫做直观图.(2)说明:在立体几何中,空间几何体的直观图是在平行投影下画出的空间图形.3.用斜二测画法画水平放置的平面图形的直观图的步骤(1)画轴:在已知图形中取互相垂直的x轴和y轴,两轴相交于点O,画直观图时,把它们画成对应的x′轴和y′轴,两轴交于点O′,且使∠x′O′y′=45°(或135°),它们确定的平面表示水平面.(2)画线:已知图形中平行于或在x轴、y轴的线段,在直观图中分别画成平行于或在x′轴、y′轴的线段.(3)取长度:已知图形中在x轴上或平行于x轴的线段,在直观图中长度不变,在y轴上或平行于y轴的线段,长度为原来的一半.4.立体图形直观图的画法画立体图形的直观图,在画轴时,要多画一条与平面x′O′y′垂直的轴O′z′,且平行于O′z′的线段长度不变.其他同平面图形的画法.1.利用斜二测画法画出边长为3 cm的正方形的直观图,正确的是图中的()C[正方形的直观图是平行四边形,且平行于x轴的边长为3 cm,平行于y 轴的边长为1.5 cm.]2.如图,△A′B′C′是△ABC的直观图,其中A′B′=A′C′,那么△ABC 是()A.等腰三角形B.直角三角形C.等腰直角三角形D.钝角三角形B[由斜二测画法的规则可知△ABC为直角三角形,且直角边的长度关系为AC=2AB.]3.一图形的投影是一条线段,这个图形不可能是________.①线段;②直线;③圆;④梯形;⑤长方体.②⑤[线段、圆、梯形都是平面图形,且在有限范围内,投影都可能为线段;长方体是三维空间图形,其投影不可能是线段;直线的投影,只能是直线或点.]【例1】按图的建系方法,画水平放置的正五边形ABCDE的直观图.[思路探究]按照斜二测画法画水平放置的平面图形的步骤画直观图.[解]画法:(1)在图①中作AG⊥x轴于点G,作DH⊥x轴于点H.(2)在图②中画相应的x′轴与y′轴,两轴相交于点O′,使∠x′O′y′=45°.(3)在图②中的x′轴上取O′B′=OB,O′G′=OG,O′C′=OC,O′H′=OH,y′轴上取O′E′=12OE,分别过G′和H′作y′轴的平行线,并在相应的平行线上取G′A′=12GA,H′D′=12HD.(4)连接A′B′,A′E′,E′D′,D′C′,并擦去辅助线G′A′,H′D′,x′轴与y′轴,便得到水平放置的正五边形ABCDE的直观图A′B′C′D′E′(如图③).1.在画水平放置的平面图形的直观图时,选取恰当的坐标系是关键,一般要使得平面多边形尽可能多的顶点在坐标轴上,以便于画点.2.画平面图形的直观图,首先画与坐标轴平行的线段(平行性不变),与坐标轴不平行的线段通过与坐标轴平行的线段确定它的两个端点,然后连接成线段.1.用斜二测画法画水平放置的等腰梯形ABCD的直观图,如图所示.[解]画法:(1)如图①所示,取AB所在直线为x轴,AB中点O为原点,建立直角坐标系,画对应的坐标系x′O′y′,使∠x′O′y′=45°(如图②).①(2)以O′为中点在x′轴上取A′B′=AB,在y′轴上取O′E′=12OE,以E′为中点画C′D′∥x′轴,并使C′D′=CD.②(3)连接B′C′,D′A′,所得的四边形A′B′C′D′就是水平放置的等腰梯形ABCD的直观图.【例2】画出底面是正方形,侧棱均相等的四棱锥的直观图.[思路探究]画轴→画底面→画顶点→成图[解]画法:(1)画轴:①②画Ox轴、Oy轴、Oz轴,∠xOy=45°(或135°),∠xOz=90°,如图①.(2)画底面:以O为中心,在xOy平面内,画出正方形水平放置的直观图ABCD.(3)画顶点:在Oz轴上截取OP,使OP的长度是原四棱锥的高.(4)成图:顺次连接P A、PB、PC、PD,并擦去辅助线,将被遮挡的部分改为虚线,得四棱锥的直观图,如图②.1.画空间图形的直观图,一般先用斜二测画法画出水平放置的平面图形,再画z轴,并确定竖直方向上的相关的点,最后连点成图便可.2.直观图画法口诀可以总结为:“横长不变,纵长减半,竖长不变,平行关系不变.”2.用斜二测画法画正六棱柱(底面是正六边形,侧棱垂直于底面)的直观图.[解](1)画轴:画x′轴、y′轴、z′轴,使∠x′O′y′=45°(或135°),∠x ′O ′z ′=90°.(2)画底面:在面x ′O ′y ′内,画出正六边形的直观图ABCDEF .(3)画侧棱:过A 、B 、C 、D 、E 、F 分别作z ′轴的平行线,在这些平行线上分别截取AA ′、BB ′、CC ′、DD ′、EE ′、FF ′都等于侧棱长.(4)成图:顺次连线A ′、B ′、C ′、D ′、E ′、F ′,并加以整理就得到正六棱柱的直观图,如图所示.1.如图,△A ′B ′C ′是水平放置的△ABC 斜二测画法的直观图,能否判断△ABC 的形状?[提示] 根据斜二测画法规则知:∠ACB =90°,故△ABC 为直角三角形.2.若探究1中△A ′B ′C ′的A ′C ′=6,B ′C ′=4,则AB 边的实际长度是多少? [提示] 由已知得△ABC 中,AC =6,BC =8,故AB =AC 2+BC 2=10.3.若已知一个三角形的面积为S ,它的直观图面积是多少?[提示] 原三角形面积为S =12a ·h (a 为三角形的底,h 为三角形的高),画直观图后,a ′=a ,h ′=12h ·sin 45°=24h ,S ′=12a ′·h ′=12a ·24h =24×12a ·h =24S .【例3】如图所示,△A′B′C′是水平放置的平面图形的斜二测直观图,将其还原成平面图形.[思路探究]由直观图还原平面图形的关键(1)平行于x′轴的线段长度不变,平行于y′轴的线段扩大为原来的2倍.(2)对于相邻两边不与x′、y′轴平行的顶点可通过作x′轴,y′轴平行线变换确定其在xOy中的位置.[解]①画出直角坐标系xOy,在x轴的正方向上取OA=O′A′,即CA=C′A′;②过B′作B′D′∥y′轴,交x′轴于点D′,在OA上取OD=O′D′,过D作DB∥y轴,且使DB=2D′B′;③连接AB,BC,得△ABC.则△ABC即为△A′B′C′对应的平面图形,如图所示.如图所示,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6 cm,C′D′=2 cm,则原图形的形状是________.菱形[如图所示,在原图形OABC中,应有OA BC,OD=2O′D′=2×22=42(cm),CD=C′D′=2(cm),∴OC=OD2+CD2=(42)2+22=6(cm),∴OA=OC,故四边形OABC是菱形.]1.由原图形求直观图的面积,关键是掌握斜二测画法,明确原来实际图形中的高,在直观图中变为与水平直线成45°角且长度为原来一半的线段,这样可得出所求图形相应的高.2.若一个平面多边形的面积为S,它的直观图面积为S′,则S′=2 4S.1.本节课的重点是了解中心投影与平行投影,难点是画几何体的直观图.2.本节课掌握的规律方法(1)判断几何体投影形状及画投影的方法.(2)画出空间几何体的直观图.(3)直观图的还原与计算.3.本节课的易错点是混淆中心投影和平行投影.1.判断(正确的打“√”,错误的打“×”)(1)两条平行线段在直观图中对应的两条线段仍然平行.()(2)平行于坐标轴的线段在直观图中仍然平行于坐标轴.()(3)平行于坐标轴的线段长度在直观图中仍然保持不变.()(4)斜二测坐标系取的角可能是135°. ()[答案](1)√(2)√(3)×(4)√[提示]平行于y轴的线段在直观图中变为原来的一半,故(3)错误;由斜二测画法的基本要求可知(1)(2)(4)正确.2.关于斜二测画法所得直观图的说法正确的是()A.直角三角形的直观图仍是直角三角形B.梯形的直观图是平行四边形C.正方形的直观图是菱形D.平行四边形的直观图仍是平行四边形D[由斜二测画法规则可知,平行于y轴的线段长度减半,直角坐标系变成斜坐标系,而平行性没有改变,故只有选项D正确.]3.如图所示为水平放置的正方形ABCO,它在直角坐标系xOy中,点B的坐标为(2,2),则在用斜二测画法画出的它的直观图中,顶点B′到x′轴的距离为________.22[画出直观图,BC对应B′C′,且B′C′=1,∠B′C′x′=45°,故顶点B′到x′轴的距离为2 2.]4.画边长为1 cm的正三角形的水平放置的直观图.[解](1)如图所示,以BC边所在直线为x轴,以BC边上的高线AO所在直线为y轴,再画对应的x′轴与y′轴,两轴相交于点O′,使∠x′O′y′=45°.(2)在x′轴上截取O′B′=O′C′=0.5 cm,在y′轴上截取O′A′=12AO=34cm,连接A′B′,A′C′,则△A′B′C′即为正三角形ABC的直观图.。
人教新课标版数学高一B版必修2课时作业 1.1.4 投影与直观图
一、选择题1.关于斜二测画法所得直观图的说法正确的是()A.直角三角形的直观图仍是直角三角形B.梯形的直观图是平行四边形C.正方形的直观图是菱形D.平行四边形的直观图仍是平行四边形【解析】由斜二测画法规则可知,平行于y轴的线段长度减半,直角坐标系变成斜坐标系,而平行性没有改变,故只有选项D正确.【答案】 D图1-1-382.(2013·泉州高一检测)利用斜二测画法画一个水平放置的平行四边形的直观图,得到的直观图是一个边长为1的正方形(如图1-1-38所示),则原图形的形状是()【解析】直观图中正方形的对角线为2,故在平面图形中平行四边形的高为22,只有A项满足条件,故A正确.【答案】 A3.已知△ABC,选定的投影面与△ABC所在平面平行,则经过中心投影后得到的△A′B′C′与△ABC()A.全等B.相似C.不相似D.以上都不对【解析】本题主要考查对中心投影的理解,根据题意画出图形如图所示.由图易得ABA′B′=OBOB′=BCB′C′=OCOC′=ACA′C′,则△ABC∽△A′B′C′.故正确答案为B.【答案】 B4.一个建筑物上部为四棱锥,下部为长方体,且四棱锥的底面与长方体的上底面尺寸一样,已知长方体的长、宽、高分别为20 m、5 m、10 m,四棱锥的高为8 m,若按1∶1 000的比例画出它的直观图,那么直观图中,长方体的长、宽、高和棱锥的高应分别为()A.4 cm,1 cm,2 cm,1.6 cmB.4 cm,0.5 cm,2 cm,0.8 cmC.4 cm,0.5 cm,2 cm,1.6 cmD.2 cm,0.25 cm,1 cm,0.8 cm【解析】由比例尺可知长方体的长、宽、高和锥高分别为2 cm,0.5 cm,1 cm 和0.8 cm,再结合直观图的画法可知,直观图中相应尺寸分别为2 cm,0.25 cm,1 cm和0.8 cm.【答案】 D5.(2013·威海高一检测)如果一个水平放置的图形的斜二测直观图是一个边长为2的正三角形,那么原平面图形的面积是()A.3B.26C.64D.2 3【解析】如图所示,过△O′B′C′的顶点C′,作C′D′∥y′轴,C′A′⊥x′轴,在△O′C′B′中易知C′A′= 3.又在Rt△C′D′B′中,C′D′=2C′A′= 6.故原平面图形的面积S=12O′B′×2C′D′=2×6=2 6.【答案】 B二、填空题图1-1-396.如图1-1-39所示,△A′B′C′是水平放置的△ABC的直观图,则在△ABC的三边及中线AD中,最长线段是________.【解析】画出原图形如图,△ABC为直角三角形,显然,AC边为最长.【答案】AC图1-1-407.如图1-1-40所示为一个水平放置的矩形ABCO,在直角坐标系xOy 中,点B的坐标为(4,2),则用斜二测画法画出的该矩形的直观图中,顶点B′到x ′轴的距离为________.【解析】 直观图如图所示,则O ′A ′=B ′C ′=1,∠B ′C ′x ′=45°,故B ′到x ′轴的距离为22.【答案】 228.(2013·信阳高一检测)已知用斜二测画法,画得的正方形的直观图面积为182,则原正方形的面积为________.【解析】 如图所示,正方形OABC 的直观图O ′A ′B ′C ′的面积为18 2.S 直观图=O ′A ′×C ′D ′.又S 正方形=OC ×OA .∴S 正方形S 直观图=OC ×OA O ′A ′×C ′D ′. 又在Rt △O ′D ′C ′中O ′C ′=2C ′D ′,即C ′D ′=22O ′C ′,结合平面图与直观图间的关系可知OA =O ′A ′,OC =2O ′C ′,∴S 正方形S 直观图=OC ×OA OA ×22O ′C ′=2O ′C ′22O ′C ′=2 2. 又S 直观图=182,∴S 正方形=22×182=72.【答案】 72三、解答题9.画出水平放置的四边形OBCD(如图1-1-41)的直观图.图1-1-41【解】(1)过点C作CE⊥x轴,垂足为E,如图①所示,画出对应的x′轴、y′轴,使∠x′O′y′=45°,如图②所示.(2)如图②所示,在x′轴上取点B′,E′,使得O′B′=OB,O′E′=OE;在y′轴上取一点D,使得O′D′=12OD;过E′作E′C′∥y′轴,使E′C′=12EC.(3)连接B′C′,C′D′,并擦去x′轴与y′轴及其他一些辅助线,如图③所示,四边形O′B′C′D′就是所求的直观图.10.用斜二测画法画出六棱锥P-ABCDEF的直观图,其中底面ABCDEF 为正六边形,点P在底面的投影是正六边形的中心O.(尺寸自定) 【解】(1)画出六棱锥P-ABCDEF的底面.如图①所示,在正六边形ABCDEF中,取AD所在的直线为x轴,对称轴MN所在的直线为y轴,两轴相交于O.(2)画相应的x′轴、y′轴和z′轴,三轴相交于O′,使∠x′O′y′=45°,∠x′O′z′=90°;在图②中,以O′为中点,在x′轴上取A′D′=AD,以O′为中点,在y′轴上取M′N′=12MN,以N′点为中点画B′C′平行于x′轴,并且等于BC;再以M′为中点画E′F′平行于x′轴,并且等于EF;连接A′B′,C′D′,D′E′,F′A′,得正六边形ABCDEF水平放置的直观图A′B′C′D′E′F′.(3)画正六棱锥P-ABCDEF的顶点.在O′z′轴上取点P′,使P′O′=PO.(4)成图.连接P′A′,P′B′,P′C′,P′D′,P′E′,P′F′,并进行整理,便得到六棱锥P-ABCDEF的直观图P′—A′B′C′D′E′F′.如图③所示.图1-1-4211.一个水平放置的平面图形的斜二测直观图是直角梯形ABCD,如图1-1-42所示,∠ABC=45°,AB=AD=1,DC⊥BC,求原平面图形的面积.【解】过A作AE⊥BC,垂足为E,又∵DC⊥BC且AD∥BC,∴四边形ADCE是矩形,∴EC=AD=1,由∠ABC=45°,AB=AD=1知BE=2,2,高为2,∴原平面∴原平面图形是梯形且上下两底边长分别为1和1+22图形的面积为12×(1+1+22)×2=2+22.。
2019版高中数学第一章立体几何初步1.1空间几何体1.1.4投影与直观图练习新人教B版必修2
1.1.4 投影与直观图1.利用斜二测画法得到的①三角形的直观图一定是三角形;②正方形的直观图一定是菱形;③等腰梯形的直观图可以是平行四边形;④菱形的直观图一定是菱形.以上结论正确的是( B )(A)①② (B)①(C)③④ (D)①②③④解析:①正确.②正方形的直观图是平行四边形.③等腰梯形的直观图是梯形.④菱形的直观图是平行四边形.选B.2.用斜二测画法画水平放置的平面图形的直观图,对其中两条线段结论错误的是( B )(A)原来相交的仍相交 (B)原来垂直的仍垂直(C)原来平行的仍平行 (D)原来共点的仍共点解析:斜二测画法保平行,保相交,保平行线段的比,但不保垂直.选B.3.如图所示为一个平面图形的直观图,则此平面图形可能是( C )解析:由直观图知,平面图形中靠右侧一边与y轴平行,满足这一特征的只有 C.4.△A′B′C′是水平放置的△ABC的直观图,则在△ABC的三边及中线AD中,最长的线段是( D )(A)AB (B)AD (C)BC (D)AC解析:由于直观图中,∠x′O′y′=45°,所以∠A′B′C′=45°,故∠ABC=90°,所以AC最长.故选D.5.如图,△A′O′B′为水平放置的△AOB的直观图,且O′A′=2,O′B′=3,则△AOB的周长为( A )(A)12 (B)10 (C)8 (D)7解析:根据斜二测画法得到三角形OAB为直角三角形,底面边长OB=3,高OA=2O′A′=4,AB=5, 所以直角三角形OAB的周长为3+4+5=12.6.如图所示,正方形O′A′B′C′的边长为 1 cm,它是一个水平放置的平面图形的直观图,则原图形的周长为.解析:由于平行性不变,O′A′∥B′C′,故在原图形中,OABC,所以四边形OABC为平行四边形,且对角线OB⊥OA,对角线OB=2,则AB==3.所以原图形的周长为l=3×2+1×2=8.答案:8 cm7.已知正三角形AOB的边长为a,如图所示,把它放在平面直角坐标系中,则它的水平放置的平面直观图的面积为( B )(A)a2 (B)a2 (C)a2 (D)a2解析:在直观图△A′B′O′中,O′A′=a,O′A′边上的高为××a=a,故△A′B′O′的面积为S=×a×a=a2.8.如图所示是水平放置的正方形ABCO,在平面直角坐标系xOy中,点B的坐标为(2,2),则由斜二测画法画出的正方形的直观图中,顶点B′到x′轴的距离为( A )(A)(B)1 (C) (D)2解析:由斜二测画法规则画出直观图如图所示,作B′E⊥x′轴于点E,在Rt△B′EC′中,B′C′=1,∠B′C′E=45°,B′E=B′C′sin 45°=1×=.9.一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底长均为1的等腰梯形,则这个平面图形的面积为.解析:由图形知,原图形是一个直角梯形,上底BC=1,下底OA=×2+1=1+,高h=OC=2,故S=×(1+1+)×2=2+.答案:2+10.如图,画水平放置的等腰梯形ABCD的直观图.解:画法:如图.(1)在等腰梯形ABCD中,以AB所在的直线为x轴,AB的中点O为坐标原点建立直角坐标系xOy,并画相应的坐标系x′O′y′,使∠x′O′y′=45°.(2)以O′为中点在x′轴上取A′B′=AB,在y′轴上取O′E′=OE,以E′为中点,过E′作D′C′平行于x′轴,并使D′C′=DC,连接A′D′,B′C′,所得梯形A′B′C′D′即为水平放置的等腰梯形ABCD的直观图.11.已知△ABC的面积为a2,它的水平放置的直观图为△A′B′C′是一个正三角形,根据给定的条件作出△A′B′C′的原图形,并计算△A′B′C′的面积.解:(1)取B′C′所在的直线为x′轴,过B′C′中点O′与O′x′成45°的直线为y′轴,建立坐标系x′O′y′;(2)过A′点作A′M′∥y′轴交x′轴于M′点.在△A′B′C′中,设它的边长为x,因为O′A′=x,∠A′M′O′=45°,所以O′A′=O′M′=x,故A′M′=x;(3)在直角坐标系xOy中,在x轴上O点左右两侧,取到点O距离为的点B,C,在x轴O点左侧取到原点O距离为x的点M,过M在x轴上方作y轴的平行线并截取MA=x,连接AB,AC,则△ABC为△A′B′C′的原图形,由S△ABC=a2,得x×x=a2,所以x=a,故△A′B′C′的面积为a2.。
2019_2020学年高中数学第一章立体几何初步1.1.4投影与直观图应用案巩固提升课件新人教B版必修2
第一章 立体几何初步
2.下列说法正确的是( ) A.相等的线段在直观图中仍然相等 B.若两条线段平行,则在直观图中对应的两条线段仍然平行 C.两个全等三角形的直观图一定也全等 D.两个图形的直观图是全等的三角形,则这两个图形一定 是全等三角形 解析:选 B.直角坐标系的选取不同时,图形的直观图也会 不同,所以选项 A,C,D 错误,但平行关系不会发生变化.
第一章 立体几何初步
解析:对于①,若以该正方形的一组邻边所在的直线为 x 轴、 y 轴,则结论正确;但若以该正方形的两条对角线所在的直 线为 x 轴、y 轴,由于此时该正方形的各边均不在坐标轴上 或与坐标轴平行,则其直观图中相邻两边长不一定符合“横 不变,纵减半”的规则;对于②,水平放置的正三角形的直 观图是一个底边长不变,高比原三角形高的一半还要短的三 角形;对于③,只要坐标系选取的恰当,不等边三角形的水 平放置的直观图可以是等边三角形. 答案:④
第一章 立体几何初步
8.如图所示的是一个水平放置的正方形 ABCO, 它在直角坐标系 xOy 中,点 B 的坐标为(2,2), 则用斜二测画法画出的正方形的直观图中,顶 点 B′到 x′轴的距离为________.
第一章 立体几何初步
解析:在直观图中四边形 A′B′C′O′是有一个角为 45°且长边
第一章 立体几何初步
法二:梯形 ABCD 的面积 S=12(DC+AB)×OD =12(1+2)×1=32. 所以梯形 ABCD 直观图的面积为 S′= 42S= 42×32=382.
第一章 立体几何初步
[B 能力提升]
11.已知一水平放置的三角形的平面直观图是边长为 1 的正
三角形,那么原三角形的面积为( )
第一章 立体几何初步
高中数学第一章立体几何初步1.1.4投影与直观图学案新人教B版必修2(2021学年)
2017-2018学年高中数学第一章立体几何初步1.1.4 投影与直观图学案新人教B版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017-2018学年高中数学第一章立体几何初步 1.1.4 投影与直观图学案新人教B版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017-2018学年高中数学第一章立体几何初步 1.1.4 投影与直观图学案新人教B版必修2的全部内容。
1。
1.4投影与直观图[学习目标] 1。
了解中心投影与平行投影.2.用斜二测画法画水平放置的平面图形的直观图.3.用斜二测画法画常见的柱、锥、台以及简单组合体的直观图.[知识链接]1。
三角形的面积S=12ah(其中a为底边长,h为底边上的高)。
2。
梯形的面积S=12(a+b)h(其中a、b为两底长,h为高).[预习导引]1。
平行投影已知图形F,直线l与平面α相交。
过F上任意一点M作直线MM′平行于l,交平面α于点M′,则点M′叫做点M在平面α内关于直线l的平行投影(或象)。
如果图形F上的所有点在平面α内关于直线l的平行投影构成图形F′,则F′叫做图形F在α内关于直线l的平行投影. 2.平行投影的性质当图形中的直线或线段不平行于投射线时,平行投影都具有下述性质:(1)直线或线段的平行投影仍是直线或线段;(2)平行直线的平行投影是平行或重合的直线;(3)平行于投射面的线段,它的投影与这条线段平行且等长;(4)与投射面平行的平面图形,它的投影与这个图形全等;(5)在同一直线或平行直线上,两条线段平行投影的比等于这两条线段的比。
3.中心投影一个点光源把一个图形照射到一个平面上,这个图形的影子就是它在这个平面上的中心投影。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1.4 投影与直观图
一、非标准
1.晚上放学后,当你走路回家经过一盏路灯时,你会发现自己的身影是( )
A.变长
B.变短
C.先变长再变短
D.先变短再变长
解析:由中心投影的性质知,身影先变短后变长.
答案:D
2.如果图形所在的平面不平行于投射线,那么下列说法正确的是( )
A.矩形的平行投影一定是矩形
B.梯形的平行投影一定是梯形
C.正方形的平行投影一定是矩形
D.正方形的平行投影一定是菱形
解析:结合平行投影的性质去判断.
答案:B
3.如图所示,用斜二测画法画一个水平放置的平面图形为一个正方形,则原来图形的形状是( )
答案:A
4.利用斜二测画法,作出直线AB的直观图如图所示,若O'A'=O'B'=1,则直线AB在平面直角坐标系中对应的函数表达式是( )
A.y=-x+1
B.y=x-1
C.y=-2x+2
D.y=2x-2
解析:由直观图还原规律可得A,B在平面直角坐标系中的位置如图所示.
令函数表达式为y=kx+b,
将A(1,0),B(0,-2)代入上式得解得
故函数表达式为y=2x-2.
答案:D
5.如图所示,是水平放置的三角形的直观图,D为△ABC中BC边上的中点,则AB,AD,AC三条线段中( )
A.最长的是AB,最短的是AC
B.最长的是AC,最短的是AB
C.最长的是AB,最短的是AD
D.最长的是AC,最短的是AD
解析:逆用斜二测画法把直观图还原,原图还原后为∠B是直角的直角三角形,如图,则AB为一条直角边,从图上可以看出,AC>AD>AB.
答案:B
6.一个水平放置的平面图形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,则该平面图形的面积等于( )
A. B.1+
C.1+
D.2+
解析:建立如图所示的坐标系x'O'y',梯形为A'B'C'D'.
所以梯形A'B'C'D'的底A'B'=1+,
对应还原到xOy中图形为下图.
梯形为直角梯形ABCD,
所以AB=A'B'=1+,AD=2A'D'=2,DC=D'C'=1.
所以S=(CD+AB)×AD=(1+1+)×2=2+,故选D.
答案:D
7.如图所示,矩形A'B'C'D'是水平放置的图形ABCD的直观图,其中A'B'=6,A'D'=2,则图形ABCD的形状为.
答案:菱形
8.已知正三角形ABC的边长为a,那么△ABC的平面直观图的面积为.
解法一:实际图形和直观图如图所示,
根据斜二测画法规则可知,
A'B'=AB=a,O'C'=OC=a,
作C'D'⊥A'B'于点D',
则C'D'=O'C'=a.
所以△A'B'C'的面积=A'B'·C'D'=×a×a=a2.
解法二:由于该正三角形面积为S=a2,
所以由公式S'=S可得其平面直观图面积S'=a2·a2.
答案:a2
9.给出下列说法:
①正方形的直观图是一个平行四边形,其相邻两边长的比为1∶2,有一内角为45°;
②水平放置的正三角形的直观图是一个底边长不变,高为原三角形高的一半的三角形;
③水平放置的不等边三角形的直观图是不等边三角形;
④水平放置的平面图形的直观图是平面图形.
写出其中正确说法的序号.
解析:对于①,若以该正方形的一组邻边所在的直线为x轴、y轴,则结论正确;但若以该正方形的两条对角线所在的直线为x轴、y轴,由于此时该正方形的各边均不在坐标轴上且不与坐标轴平行,则其直观图中相邻两边长的比不为1∶2;对于②,水平放置的正三角形的直观图是一个底边长不变,高比原三角形高的一半还要短的三角形;对于③,只要坐标系选取的恰当,水平放置的不等边三角形的直观图可以是等边三角形.
答案:④
10.用斜二测画法画出图中水平放置的四边形OABC的直观图.
解:如图所示.(1)画x'轴,y'轴,两轴相交于点O',使∠x'O'y'=45°,x'轴,y'轴与xOy坐标系中对应轴的单位长度相同.
(2)在x'轴上取点H,使O'H=3,作HA'∥y'轴,并取A'H=1,在y'轴上取C',使O'C'=1,在x'轴上取B',使O'B'=4.
(3)顺次连接O',A',B',C',便得到四边形OABC的直观图O'A'B'C'.
11.用斜二测画法画出底面边长为4cm,高为3cm的正四棱锥(底面是正方形,并且顶点在底面的正投影是底面中心的棱锥)的直观图.
解:(1)作水平放置的正方形的直观图ABCD,使∠BAD=45°,AB=4cm,AD=2cm.
(2)过O'作z'轴,使∠x'O'z'=90°,在z'轴上截取O'S=3cm.
(3)连接SA,SB,SC,SD,得到如图②的图形就是所求的正四棱锥的直观图.
12.如图所示,在水平放置的平面α内有一个边长为1的正方形A'B'C'D',其中对角线A'C'在水平位置.已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.
解:四边形A'B'C'D'的真实图形如图所示,
因为A'C'在水平位置,A'B'C'D'为正方形,
所以在四边形ABCD中,DA⊥AC.
因为DA=2D'A'=2,AC=A'C'=,
所以S四边形ABCD=AC·AD=2.。
