沪教版九年级数学第二学期专题复习三 动点产生的相似三角形问题
上海市中考数学综合复习专题动点产生的相似三角形3星(教师版)

专题-动点产生的相似三角形1.掌握相似基本图形中的相似三角形和各种比例式;2.通过观察了解因动点产生的相似三角形问题的特点,熟悉对应的解题方法, 掌握“动中取静,以静窥动”的解题策略;3.学习对图形的直觉能力以及从变化中看到不变实质的数学洞察力;4.学会挖掘题目中的隐藏条件,从未知到已知的一个转变;5.掌握动点产生的相似三角形的分类讨论情况,并能根据题目中的条件进行求解。
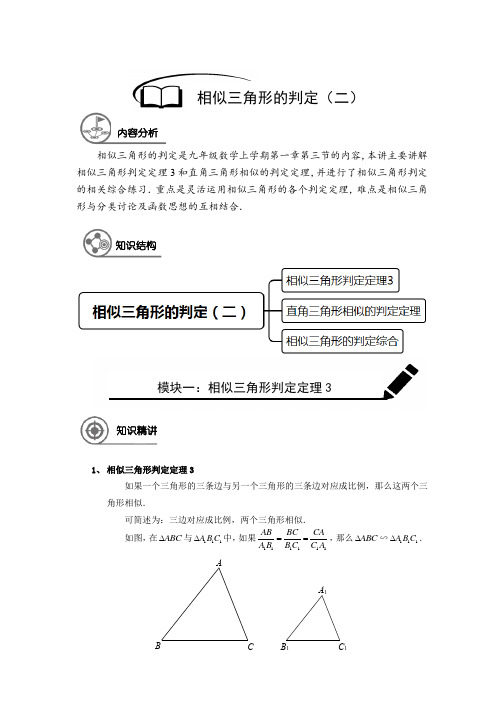
知识结构1、相似基本图形:2、相似三角形的基本图形产生的结论: (1)、A 字型:①正A 字型 ②斜A 字型 ③其它A 字型ABCD EABC DEABCEA B C ∽∆∆A D E ACB ∽∆∆ADE ACB ∽∆∆ABEAC AE AB AD = AB AE AC AD = ACABAB AE =AB AE AC AD ⋅=⋅ AC AE AB AD ⋅=⋅ AC AE AB ⋅=2(2)、X 型:①正X 字型 ②斜X 字型ADEBCADEBCA E D ∽∆∆ABC 相似三角形:_________________ABAEAC AD =比例式:_________________ AC AE AB AD ⋅=⋅ 乘积式:_________________ (3)、直角三角形:DCABCDB ∽ACB ∽∆∆∆ADC ①AB AD AC AB ACADC ⋅=⇒=⇒∆∆2AC AD ACB ∽ ②AB BD BC BC BDBDC ⋅=⇒=⇒∆∆2AB BC BCA ∽ ③BD AD CD BDCDADC ⋅=⇒=⇒∆∆2CD AD CDB ∽(4)、直线型(一线三角): (5)、其他基本型:A BCDEFEDABC相似三角形:_________________ 相似三角形:_________________比例式:_________________ 比例式:_________________乘积式:_________________ 乘积式:_________________3、相似三角形方法的选择:(1)已知有一角相等时,可选择方法两角相等和方法两边对应成比例且夹角相等; (2)已知有二边对应成比例时,可选择方法三边对应成比例和方法两边对应成比例且夹角相等;(3)若有平行条件时,可考虑方法基本图形“A 字型和X 型”; (4)有直角三角形时,可考虑方法直角三角形判定方法; (5)不管选择用哪一个方法,先找角度,再根据题目选择。
上海中考数学压轴题专题09 动点产生的相似三角形(原卷版)

上海中考数学压轴题专题09 动点产生的相似三角形教学重难点1.掌握相似基本图形中的相似三角形和各种比例式;2.通过观察了解因动点产生的相似三角形问题的特点,熟悉对应的解题方法, 掌握“动中取静,以静窥动”的解题策略;3.培养学生对图形的直觉能力以及从变化中看到不变实质的数学洞察力;4.培养学生学会挖掘题目中的隐藏条件,从未知到已知的一个转变;5.掌握动点产生的相似三角形的分类讨论情况,并能根据题目中的条件进行求解。
【注意】:1.此部分知识点梳理,先提问学生学过的基本图形,并且画出来,再结合讲义讲解;2.部分基本图形的比例式,可以在白板上先画出基本图形再让学生找相似三角形,并写出比比例式,尤其是第四、五个基本图形一定要让学生写,部分地方让学生填写完,建议8分钟左右完成。
相似三角形的基本图形产生的结论结论: A 字型:① 正A 字型 ②斜A 字型 ③其它A 字型ABC ∽∆∆ADE ACB ∽∆∆ADE ACB ∽∆∆ABEAC AE AB AD = AB AE AC AD = ACABAB AE = AB AE AC AD ⋅=⋅ AC AE AB AD ⋅=⋅ AC AE AB ⋅=2X 型:①正X 字型 ②斜X 字型CCCAED ∽∆∆ABC ADE ∽∆∆ABCAB AE AC AD = ACAEAB AD = AC AE AB AD ⋅=⋅ AB AE AC AD ⋅=⋅直角三角形:CDB ∽ACB ∽∆∆∆ADC①AB AD AC AB ACADC ⋅=⇒=⇒∆∆2AC AD ACB ∽ ②AB BD BC BC BDBDC ⋅=⇒=⇒∆∆2AB BC BCA ∽BD AD CD BDCDADC ⋅=⇒=⇒∆∆2CD AD CDB ∽直线型(一线三角): 其他基本型:CEF ∽∆∆BDE AEB ∽∆∆ADC 和ACB ∽∆∆ADECF BE CE BD = ABAEAC AD = BE CE CF BD ⋅=⋅ AC AE AB AD ⋅=⋅CCCB相似三角形方法的选择:(1)已知有一角相等时,可选择方法两角相等和方法两边对应成比例且夹角相等;(2)已知有二边对应成比例时,可选择方法三边对应成比例和方法两边对应成比例且夹角相等;(3)若有平行条件时,可考虑方法基本图形“A字型和X型”;(4)有直角三角形时,可考虑方法直角三角形判定方法;(5)不管选择用哪一个方法,先找角度,再根据题目选择。
上海初三相似三角形总结

相似三角形知识点1 相似图形形状相同的图形叫相似图形,在相似多边形中,最简单的是相似三角形. 知识点2 比例线段的相关概念如果选用同一单位量得两条线段b a ,的长度分别为n m ,,那么就说这两条线段的比是nmb a =,或写成n m b a ::=. 注意:在求线段比时,线段单位要统一,单位不统一应先化成同一单位.在四条线段d c b a ,,,中,如果b a 和的比等于d c 和的比,那么这四条线段d c b a ,,,叫做成比例线段,简称比例线段.注意:(1)当两个比例式的每一项都对应相同,两个比例式才是同一比例式.(2)比例线段是有顺序的,如果说a 是d c b ,,的第四比例项,那么应得比例式为:adc b =.知识点3 比例的性质基本性质:(1)bc ad d c b a =⇔=::;(2)b a c b c c a ⋅=⇔=2::. 注意:由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,如bc ad =,除 了可化为d c b a ::=,还可化为d b c a ::=,b a d c ::=,c a d b ::=,c d a b ::=,b d a c ::=,a b c d ::=,a c b d ::=.更比性质(交换比例的内项或外项):()()()a bc d a c d cb d b ad bc a ⎧=⎪⎪⎪=⇒=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项 反比性质(把比的前项、后项交换):cd a b d c b a =⇒=. 合比性质:dd c b b a d c b a ±=±⇒=. 注意:实际上,比例的合比性质可扩展为:比例式中等号左右两个比的前项,后项之间发生同样和差变化比例仍成立.如:⎪⎪⎩⎪⎪⎨⎧+-=+--=-⇒=d c d c b a b a ccd a a b d c b a 等等.等比性质:如果)0(≠++++====n f d b nmf e d c b a ,那么b a n f d b m ec a =++++++++ . 注意:(1)此性质的证明运用了“设k 法” ,这种方法是有关比例计算,变形中一种常用方法. (2)应用等比性质时,要考虑到分母是否为零.(3)可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.如:baf d b e c a f e d c b a f e d c b a =+-+-⇒=--=⇒==32323322;其中032≠+-f d b . 知识点4 比例线段的有关定理平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例. 推论:(1)平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例. (2)平行于三角形一边并且和其它两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例.定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形第三边. 知识点5 黄金分割把线段AB 分成两条线段)(,BC AC BC AC >,且使AC 是BC AB 和的比例中项,叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点,其中AB AC 215-=≈0.618AB . 知识点6 相似三角形的概念对应角相等,对应边成比例的三角形,叫做相似三角形. 相似用符号“∽”表示,读作“相似于” .相似三角形对应边的比叫做相似比(或相似系数). 相似三角形对应角相等,对应边成比例. 注意:①对应性:即两个三角形相似时,通常把表示对应顶点的字母写在对应位置上,这样写比较容易找到相似三角形的对应角和对应边. ②顺序性:相似三角形的相似比是有顺序的. ③两个三角形形状一样,但大小不一定一样.④全等三角形是相似比为1的相似三角形.二者的区别在于全等要求对应边相等,而相似要求对应边成比例.知识点7 相似三角形的基本定理定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原 三角形相似. 定理的基本图形:用数学语言表述是: BC DE // ,ADE ∆∴∽ABC ∆.知识点8 相似三角形的等价关系(1)反身性:对于任一ABC ∆有ABC ∆∽ABC ∆.(2)对称性:若ABC ∆∽'''C B A ∆,则'''C B A ∆∽ABC ∆.(3)传递性:若ABC ∆∽C B A '∆'',且C B A '∆''∽C B A ''''''∆,则ABC ∆∽C B A ''''''∆. 知识点9 三角形相似的判定方法1、定义法:对应角相等,对应边成比例的两个三角形相似.2、平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角 形与原三角形相似.3、判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两 个三角形相似.简述为:两角对应相等,两三角形相似.4、判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹 角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似.5、判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这 两个三角形相似.简述为:三边对应成比例,两三角形相似.6、判定直角三角形相似的方法: (1)以上各种判定均适用.(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.(3)直角三角形被斜边上的高分成的两个直角三角形与原三角形相似.直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
九年级数学动点问题之相似三角形

因动点产生的相似三角形问题(一)例1、直线113y x =-+分别交x 轴、y 轴于A 、B 两点,△AOB 绕点O 按逆时针方向旋转90°后得到△COD ,抛物线y =ax 2+bx +c 经过A 、C 、D 三点.三点.(1) 写出点A 、B 、C 、D 的坐标;的坐标;(2) 求经过A 、C 、D 三点的抛物线表达式,并求抛物线顶点G 的坐标;的坐标;(3) 在直线BG 上是否存在点Q ,使得以点A 、B 、Q 为顶点的三角形与△COD 相似?若存在,请求出点Q 的坐标;若不存在,请说明理由.的坐标;若不存在,请说明理由.图1 思路点拨1.图形在旋转过程中,对应线段相等,对应角相等,对应线段的夹角等于旋转角..图形在旋转过程中,对应线段相等,对应角相等,对应线段的夹角等于旋转角. 2.用待定系数法求抛物线的解析式,用配方法求顶点坐标..用待定系数法求抛物线的解析式,用配方法求顶点坐标.3.第(3)题判断∠ABQ =90°是解题的前提.°是解题的前提.4.△ABQ 与△COD 相似,相似,按照直角边的比分两种情况,按照直角边的比分两种情况,按照直角边的比分两种情况,每种情况又按照点每种情况又按照点Q 与点B 的位置关系分上下两种情形,点Q 共有4个.个. 例2、Rt △ABC 在直角坐标系内的位置如图1所示,反比例函数(0)ky k x =¹在第一象限内的图像与BC 边交于点D (4,m ),与AB 边交于点E (2,n ),△BDE 的面积为2.(1)求m 与n 的数量关系;的数量关系;(2)当tan ∠A =12时,求反比例函数的解析式和直线AB 的表达式;的表达式; (3)设直线AB 与y 轴交于点F ,点P 在射线FD 上,在(2)的条件下,如果△AEO与△EFP 相似,求点P 的坐标.的坐标.图1 思路点拨1.探求m 与n 的数量关系,用m 表示点B 、D 、E 的坐标,是解题的突破口.的坐标,是解题的突破口. 2.第(2)题留给第(3)题的隐含条件是FD //x 轴.轴.3.如果△AEO 与△EFP 相似,因为夹角相等,根据对应边成比例,分两种情况.相似,因为夹角相等,根据对应边成比例,分两种情况. 例3、如图1,已知梯形OABC ,抛物线分别过点O (0,0)、A (2,0)、B (6,3).(1)直接写出抛物线的对称轴、解析式及顶点M 的坐标;的坐标;(2)将图1中梯形OABC 的上下底边所在的直线OA 、CB 以相同的速度同时向上平移,分别交抛物线于点O1、A1、C1、B1,得到如图2的梯形O1A1B1C1.设梯形O1A1B1C1的面积的坐标分别为 (x1,y1)、(x2,y2).用含S的代数式表示x2-x1,并求出当S=36为S,A1、B1的坐标分别为的坐标;时点A1的坐标;(3)在图1中,设点D的坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、的值;若不存在,请说明理由.抛物线的对称轴围成的三角形相似?若存在,请求出t的值;若不存在,请说明理由.图1 图2 思路点拨1.第(2)题用含S的代数式表示x2-x1,我们反其道而行之,用x1,x2表示S.再注.通过代数变形就可以了.意平移过程中梯形的高保持不变,即y2-y1=3.通过代数变形就可以了.2.第(3)题最大的障碍在于画示意图,在没有计算结果的情况下,无法画出准确的位置关系,因此本题的策略是先假设,再说理计算,后验证.置关系,因此本题的策略是先假设,再说理计算,后验证.3.第(3)题的示意图,不变的关系是:直线AB与x轴的夹角不变,直线AB与抛物线的对称轴的夹角不变.变化的直线PQ的斜率,因此假设直线PQ与AB的交点G在x轴轴的上方.的下方,或者假设交点G在x轴的上方.例4、如图1,已知点A (-2,4) 和点B (1,0)都在抛物线22y mx mx n上.=++上.(1)求m、n;(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边为菱形,求平移后抛物线的表达式;形A A′B′B为菱形,求平移后抛物线的表达式;(3)记平移后抛物线的对称轴与直线AB′的交点为C,试在x轴上找一个点D,使得以点B′、C、D为顶点的三角形与△ABC相似.图1 思路点拨1.点A与点B的坐标在3个题目中处处用到,各具特色.第(1)题用在待定系数法的长. 中;第(2)题用来计算平移的距离;第(3)题用来求点B′的坐标、AC和B′C的长.2.抛物线左右平移,变化的是对称轴,开口和形状都不变..抛物线左右平移,变化的是对称轴,开口和形状都不变.3.探求△ABC与△B′CD相似,根据菱形的性质,∠BAC=∠CB′D,因此按照夹角的两边对应成比例,分两种情况讨论.两边对应成比例,分两种情况讨论.例5、如图1,抛物线经过点A (4,0)、B (1,0)、C (0,-2)三点.)三点.(1)求此抛物线的解析式;)求此抛物线的解析式;(2)P 是抛物线上的一个动点,过P 作PM ⊥x 轴,垂足为M ,是否存在点P ,使得以A 、P 、M 为顶点的三角形与△OAC 相似?若存在,请求出符合条件的相似?若存在,请求出符合条件的 点P 的坐标;若不存在,请说明理由;存在,请说明理由; (3)在直线AC 上方的抛物线是有一点D ,使得△DCA 的面积最大,求出点D 的坐标.,思路点拨1.已知抛物线与x 轴的两个交点,用待定系数法求解析式时,设交点式比较简便.轴的两个交点,用待定系数法求解析式时,设交点式比较简便. 2.数形结合,用解析式表示图象上点的坐标,用点的坐标表示线段的长..数形结合,用解析式表示图象上点的坐标,用点的坐标表示线段的长.3.按照两条直角边对应成比例,分两种情况列方程..按照两条直角边对应成比例,分两种情况列方程.4.把△DCA 可以分割为共底的两个三角形,高的和等于OA .例6、如图1,△ABC 中,AB =5,AC =3,cos A =310.D 为射线BA 上的点(点D 不与点B 重合),作DE //BC 交射线CA 于点E ..(1) 若CE =x ,BD =y ,求y 与x 的函数关系式,并写出函数的定义域;的函数关系式,并写出函数的定义域;(2) 当分别以线段BD ,CE 为直径的两圆相切时,求DE 的长度;的长度;(3) 当点D 在AB 边上时,BC 边上是否存在点F ,使△ABC 与△DEF 相似?若存在,请求出线段BF 的长;若不存在,请说明理由.的长;若不存在,请说明理由.图1 备用图备用图 备用图备用图思路点拨 1.先解读背景图,△ABC 是等腰三角形,那么第(3)题中符合条件的△DEF 也是等腰三角形.腰三角形.2.用含有x 的式子表示BD 、DE 、MN 是解答第(2)题的先决条件,注意点E 的位置不同,DE 、MN 表示的形式分两种情况.表示的形式分两种情况.3.求两圆相切的问题时,先罗列三要素,再列方程,最后检验方程的解的位置是否符合题意.合题意.4.第(3)题按照DE 为腰和底边两种情况分类讨论,运用典型题目的结论可以帮助我们轻松解题.们轻松解题.。
中考—动点产生的相似三角形、等腰三角形、直角三角形、平行四边形问题-含答案

一、动点产生的相似三角形问题1、 满分解答(1)因为抛物线与x 轴交于A (4,0)、B (1,0)两点,设抛物线的解析式为)4)(1(--=x x a y ,代入点C 的 坐标(0,-2),解得21-=a .所以抛物线的解析式为22521)4)(1(212-+-=---=x x x x y .(2)设点P 的坐标为))4)(1(21,(---x x x .①如图2,当点P 在x 轴上方时,1<x <4,)4)(1(21---=x x PM,x AM -=4.如果2==CO AOPM AM ,那么24)4)(1(21=----x x x .解得5=x 不合题意.如果21==COAOPM AM ,那么214)4)(1(21=----x x x .解得2=x . 此时点P 的坐标为(2,1).②如图3,当点P 在点A 的右侧时,x >4,)4)(1(21--=x x PM,4-=x AM . 解方程24)4)(1(21=---x x x ,得5=x .此时点P 的坐标为)2,5(-.解方程214)4)(1(21=---x x x ,得2=x 不合题意.③如图4,当点P 在点B 的左侧时,x <1,)4)(1(21--=x x PM ,x AM -=4.解方程24)4)(1(21=---x x x ,得3-=x .此时点P 的坐标为)14,3(--.解方程214)4)(1(21=---x x x ,得0=x .此时点P 与点O 重合,不合题意.综上所述,符合条件的 点P 的坐标为(2,1)或)14,3(--或)2,5(-.图2 图3 图4(3)如图5,过点D 作x 轴的垂线交AC 于E .直线AC 的解析式为221-=x y . 设点D 的横坐标为m )41(<<m ,那么点D 的坐标为)22521,(2-+-m m m ,点E 的坐标为)221,(-m m .所以)221()22521(2---+-=m m m DE m m 2212+-=.因此4)221(212⨯+-=∆m m S DAC m m 42+-=4)2(2+--=m .当2=m 时,△DCA 的面积最大,此时点D 的坐标为(2,1).图5 图6,2、 满分解答(1)将M (2, 2)代入1(2)()y x x m m =-+-,得124(2)m m =-⨯-.解得m =4. (2)当m =4时,2111(2)(4)2442y x x x x =-+-=-++.所以C (4, 0),E (0, 2).所以S △BCE =1162622BC OE ⋅=⨯⨯=.(3)如图2,抛物线的对称轴是直线x =1,当H 落在线段EC 上时,BH +EH 最小. 设对称轴与x 轴的交点为P ,那么HP EOCP CO=. 因此234HP =.解得32HP =.所以点H 的坐标为3(1,)2. (4)①如图3,过点B 作EC 的平行线交抛物线于F ,过点F 作FF ′⊥x 轴于F ′.由于∠BCE =∠FBC ,所以当CE BC CB BF=,即2BC CE BF =⋅时,△BCE ∽△FBC . 设点F 的坐标为1(,(2)())x x x m m -+-,由''FF EO BF CO =,得1(2)()22x x m m x m+-=+.解得x =m +2.所以F ′(m +2, 0).由'CO BF CE BF =4m BF +=.所以BF =. 由2BC CE BF =⋅,得2(2)m +=整理,得0=16.此方程无解.图2 图3 图4②如图4,作∠CBF =45°交抛物线于F ,过点F 作FF ′⊥x 轴于F ′,由于∠EBC =∠CBF ,所以BE BC BC BF=,即2BC BE BF =⋅时,△BCE ∽△BFC . 在Rt △BFF ′中,由FF ′=BF ′,得1(2)()2x x m x m+-=+.解得x =2m .所以F ′(2,0)m .所以BF ′=2m +2,2)BF m =+.由2BCBE BF =⋅,得2(2)2)m m +=+.解得2m =±综合①、②,符合题意的m为2+考点伸展第(4)题也可以这样求BF 的长:在求得点F ′、F 的坐标后,根据两点间的距离公式求BF 的长.二、因动点产生的等腰三角形问题 满分解答(1)因为抛物线与x 轴交于A (-1,0)、B (3, 0)两点,设y =a (x +1)(x -3), 代入点C (0 ,3),得-3a =3.解得a =-1.所以抛物线的函数关系式是y =-(x +1)(x -3)=-x 2+2x +3. (2)如图2,抛物线的对称轴是直线x =1.当点P 落在线段BC 上时,P A +PC 最小,△P AC 的周长最小. 设抛物线的对称轴与x 轴的交点为H . 由BH PHBO CO=,BO =CO ,得PH =BH =2. 所以点P 的坐标为(1, 2).(3)点M 的坐标为(1, 1)、、(1,)或(1,0).设点M 的坐标为(1,m ).在△MAC 中,AC 2=10,MC 2=1+(m -3)2,MA 2=4+m 2.①如图3,当MA =MC 时,MA 2=MC 2.解方程4+m 2=1+(m -3)2,得m =1. 此时点M 的坐标为(1, 1).②如图4,当AM =AC 时,AM 2=AC 2.解方程4+m 2=10,得m =此时点M 的坐标为或(1,.③如图5,当CM =CA 时,CM 2=CA 2.解方程1+(m -3)2=10,得m =0或6. 当M (1, 6)时,M 、A 、C 三点共线,所以此时符合条件的点M 的坐标为(1,0).图3 图4 图54.思路点拨1.用含m 的代数式表示表示△APD 的三边长,为解等腰三角形做好准备. 2.探求△APD 是等腰三角形,分三种情况列方程求解.3.猜想点H 的运动轨迹是一个难题.不变的是直角,会不会找到不变的线段长呢?Rt △OHM 的斜边长OM 是定值,以OM 为直径的圆过点H 、C . 满分解答(1)因为PC //DB ,所以1CP PM MCBD DM MB===.因此PM =DM ,CP =BD =2-m .所以AD =4-m .于是得到点D 的坐标为(2,4-m ).(2)在△APD 中,22(4)AD m =-,224AP m =+,222(2)44(2)PD PM m ==+-.①当AP =AD 时,2(4)m -24m =+.解得32m =(如图3).②当P A =PD 时,24m +244(2)m =+-.解得43m =(如图4)或4m =(不合题意,舍去).③当DA =DP 时,2(4)m -244(2)m =+-.解得23m =(如图5)或2m =(不合题意,舍去).综上所述,当△APD 为等腰三角形时,m 的值为32,43或23.图3 图4 图5(3)点H . 三、①因动点产生的直角三角形问题5、满分解答(1)设抛物线的函数表达式为2(1)y x n =-+,代入点C (0,-3),得4n =-.所以抛物线的函数表达式为22(1)423y x x x =--=--.(2)由223(1)(3)y x x x x =--=+-,知A (-1,0),B (3,0).设直线BC 的函数表达式为y kx b =+,代入点B (3,0)和点C (0,-3),得30,3.k b b +=⎧⎨=-⎩ 解得1k =,3b =-.所以直线BC 的函数表达式为3y x =-.(3)①因为AB =4,所以334PQ AB ==.因为P 、Q 关于直线x =1对称,所以点P 的横坐标为12-.于是得到点P 的坐标为17,24⎛⎫-- ⎪⎝⎭,点F 的坐标为70,4⎛⎫- ⎪⎝⎭.所以75344FC OC OF =-=-=,522EC FC ==.进而得到51322OE OC EC =-=-=,点E 的坐标为10,2⎛⎫- ⎪⎝⎭.直线BC:3y x =-与抛物线的对称轴x =1的交点D 的坐标为(1,-2).过点D 作DH ⊥y 轴,垂足为H .在Rt △EDH 中,DH =1,13222EH OH OE =-=-=,所以tan ∠CED 23DH EH ==.②1(12)P -,25(1)2P -.图2 图3 图4②动点产生的平行四边形问题 2 满分解答(1) 因为抛物线与x 轴交于A (-4,0)、C (2,0)两点,设y =a (x +4)(x -2).代入点B (0,-4),求得12a =.所以抛物线的解析式为211(4)(2)422y x x x x =+-=+-. (2)如图2,直线AB 的解析式为y =-x -4.过点M 作x 轴的垂线交AB 于D ,那么2211(4)(4)222MD m m m m m =---+-=--.所以2142MDA MDB S S S MD OA m m ∆∆=+=⋅=--2(2)4m =-++.因此当2m =-时,S 取得最大值,最大值为4.(3) 如果以点P 、Q 、B 、O 为顶点的四边形是平行四边形,那么PQ //OB ,PQ =OB =4. 设点Q 的坐标为(,)x x -,点P 的坐标为21(,4)2x x x +-.①当点P 在点Q 上方时,21(4)()42x x x +---=.解得2x =-±此时点Q 的坐标为(2-+-(如图3),或(2--+(如图4). ②当点Q 在点P 上方时,21()(4)42x x x --+-=. 解得4x=-或0x =(与点O 重合,舍去).此时点Q 的坐标为(-4,4) (如图5).。
上海中考数学--因动点产生的相似三角形问题
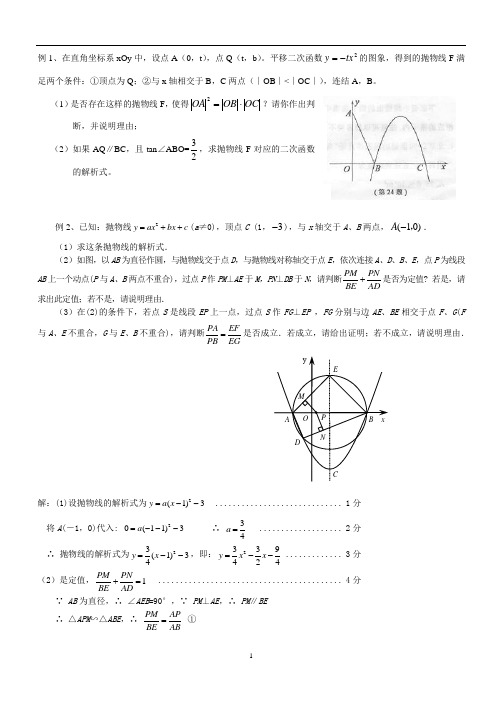
例1、在直角坐标系xOy 中,设点A (0,t ),点Q (t ,b )。
平移二次函数2tx y -=的图象,得到的抛物线F 满足两个条件:①顶点为Q ;②与x 轴相交于B ,C 两点(∣OB ∣<∣OC ∣),连结A ,B 。
(1)是否存在这样的抛物线F ,使得OC OB OA ⋅=2?请你作出判断,并说明理由;(2)如果AQ ∥BC ,且tan ∠ABO=23,求抛物线F 对应的二次函数的解析式。
例2、已知:抛物线2y ax bx c =++(a ≠0),顶点C (1,3-),与x 轴交于A 、B 两点,(10)A -,. (1)求这条抛物线的解析式.(2)如图,以AB 为直径作圆,与抛物线交于点D ,与抛物线对称轴交于点E ,依次连接A 、D 、B 、E ,点P 为线段AB 上一个动点(P 与A 、B 两点不重合),过点P 作PM ⊥AE 于M ,PN ⊥DB 于N ,请判断PM PNBE AD+是否为定值? 若是,请求出此定值;若不是,请说明理由.(3)在(2)的条件下,若点S 是线段EP 上一点,过点S 作FG ⊥EP ,FG 分别与边.AE 、BE 相交于点F 、G (F与A 、E 不重合,G 与E 、B 不重合),请判断PA EFPB EG=是否成立.若成立,请给出证明;若不成立,请说明理由.解:(1)设抛物线的解析式为2(1)3y a x =-- ............................. 1分 将A (-1,0)代入: 20(11)3a =--- ∴ 34a =................... 2分 ∴ 抛物线的解析式为23(1)34y x =--,即:2339424y x x =-- ............. 3分(2)是定值,1PM PNBE AD+= .......................................... 4分 ∵ AB 为直径,∴ ∠AEB =90°,∵ PM ⊥AE ,∴ PM ∥BE ∴ △APM ∽△ABE ,∴PM APBE AB=①CO xA D P M EB Ny同理:PN PBAD AB=② .............................................. 5分 ① + ②:1PM PN AP PBBE AD AB AB+=+= ....................................6分 (3)∵ 直线EC 为抛物线对称轴,∴ EC 垂直平分AB∴ EA =EB∵ ∠AEB =90°∴ △AEB 为等腰直角三角形.∴ ∠EAB =∠EBA =45° .......... 7分 如图,过点P 作PH ⊥BE 于H ,由已知及作法可知,四边形PHEM 是矩形, ∴PH =ME 且PH ∥ME 在△APM 和△PBH 中∵∠AMP =∠PHB =90°, ∠EAB =∠BPH =45° ∴ PH =BH且△APM ∽△PBH∴ PA PMPB BH=∴PA PM PMPB PH ME ==① ......... 8分 在△MEP 和△EGF 中,∵ PE ⊥FG , ∴ ∠FGE +∠SEG =90° ∵∠MEP +∠SEG =90° ∴ ∠FGE =∠MEP ∵ ∠PME =∠FEG =90° ∴△MEP ∽△EGF ∴PM EFME EG=② 由①、②知:PA EFPB EG=.............................................. 9分 (本题若按分类证明,只要合理,可给满分)例3、将一矩形纸片OABC 放在平面直角坐标系中,(00)O ,,(60)A ,,(03)C ,.动点Q 从点O 出发以每秒1个单位长的速度沿OC 向终点C 运动,运动23秒时,动点P 从点A 出发以相等的速度沿AO 向终点O 运动.当其中一点到达终点时,另一点也停止运动.设点P 的运动时间为t (秒).(1)用含t 的代数式表示OP OQ ,;(2)当1t =时,如图1,将OPQ △沿PQ 翻折,点O 恰好落在CB 边上的点D 处,求点D 的坐标;(3)连结AC ,将OPQ △沿PQ 翻折,得到EPQ △,如图2.问:PQ 与AC 能否平行?PE 与AC 能否垂直?若能,求出相应的t 值;若不能,说明理由.B DC QyBC yE解:(1)6OP t =-,23OQ t =+.(2)当1t =时,过D 点作1DD OA ⊥,交OA 于1D ,如图1, 则53DQ QO ==,43QC =, 1CD ∴=,(13)D ∴,. (3)①PQ 能与AC 平行. 若PQ AC ∥,如图2,则OP OAOQ OC=, 即66233t t -=+,149t ∴=,而703t ≤≤, 149t ∴=.②PE 不能与AC 垂直.若PE AC ⊥,延长QE 交OA 于F ,如图3,则23335t QF OQAC OC +==.23QF t ⎫∴=+⎪⎭.EFQF QE QF OQ ∴=-=- 2233t t ⎫⎛⎫=+-+⎪ ⎪⎭⎝⎭21)1)3t =+.又Rt Rt EPF OCA △∽△,PE OCEF OA∴=, 图163261)3t t -∴=⎛⎫+ ⎪⎝⎭,3.45t ∴≈,而703t ≤≤,t ∴不存在.例4、如图,抛物线(1)(5)y a x x =+-与x 轴的交点为M N ,.直线y kx b =+与x 轴交于(20)P -,,与y 轴交于C .若A B ,两点在直线y kx b =+上,且AO BO ==,AO BO ⊥.D 为线段MN 的中点,OH 为Rt OPC △斜边上的高.(1)OH 的长度等于 ;k = ,b = .(2)是否存在实数a ,使得抛物线(1)(5)y a x x =+-上有一点E ,满足以D N E ,,为顶点的三角形与AOB △相似?若不存在,说明理由;若存在,求所有符合条件的抛物线的解析式,同时探索所求得的抛物线上是否还有符合条件的E 点(简要说明理由);并进一步探索对符合条件的每一个E 点,直线NE 与直线AB 的交点G 是否总满足PG PB ⋅<,写出探索过程.解:(1)1OH =;k =b =. (2)设存在实数a ,使抛物线(1)(5)y a x x =+-上有一点E ,满足以D N E ,,为顶点的三角形与等腰直角AOB △相似.∴以D N E ,,为顶点的三角形为等腰直角三角形,且这样的三角形最多只有两类,一类是以DN 为直角边的等腰直角三角形,另一类是以DN 为斜边的等腰直角三角形. ①若DN 为等腰直角三角形的直角边,则ED DN ⊥.由抛物线(1)(5)y a x x =+-得:(10)M -,,(50)N ,.(20)D ∴,,3ED DN ∴==.E ∴的坐标为(23),. 把(23)E ,代入抛物线解析式,得13a =-. x∴抛物线解析式为1(1)(5)3y x x =-+-.即2145333y x x =-++.②若DN 为等腰直角三角形的斜边, 则DE EN ⊥,DE EN =.E ∴的坐标为(3.51.5),. 把(3.51.5)E ,代入抛物线解析式,得29a =-. ∴抛物线解析式为2(1)(5)9y x x =-+-,即22810999y x x =-++当13a =-时,在抛物线2145333y x x =-++上存在一点(23)E ,满足条件,如果此抛物线上还有满足条件的E 点,不妨设为E '点,那么只有可能DE N '△是以DN 为斜边的等腰直角三角形,由此得(3.51.5)E ',,显然E '不在抛物线2145333y x x =-++上,因此抛物线2145333y x x =-++上没有符合条件的其他的E 点. 当29a =-时,同理可得抛物线22810999y x x =-++上没有符合条件的其他的E 点.当E 的坐标为(23),,对应的抛物线解析式为2145333y x x =-++时,EDN △和ABO △都是等腰直角三角形,45GNP PBO ∴∠=∠=. 又NPG BPO ∠=∠,NPG BPO ∴△∽△.PG PNPO PB∴=,2714PB PG PO PN ∴==⨯=,∴总满足10PB PG <. 当E 的坐标为(3.51.5),,对应的抛物线解析式为22810999y x x =-++时,同理可证得:2714PB PG PO PN ==⨯=,∴总满足10PB PG <例5、在平面直角坐标系xOy 中,将抛物线22y x =沿y 轴向上平移1个单位,再沿x 轴向右平移两个单位,平移后抛物线的顶点坐标记作A ,直线3x =与平移后的抛物线相交于B ,与直线OA 相交于C .(1)求△ABC 面积;(2)点PP 点坐标.解:平移后抛物线的解析式为22(2)1y x =-+.……………………2分 ∴A 点坐标为(2,1),………………………………………………………1分 设直线OA 解析式为y kx =,将A (2,1)代入得12k =,直线OA 解析式为12y x =, 将3x =代入12y x =得32y =,∴C 点坐标为(3,32).…………………1分将3x =代入22(2)1y x =-+得3y =,∴B 点坐标为(3,3).………1分 ∴ABC34S=……………………………………………………………………2分(2)∵P A ∥BC ,∴∠P AB =∠ABC1°当∠PBA =∠BAC 时,PB ∥AC ,∴四边形P ACB 是平行四边形,∴32PA BC ==.………………………………………1分∴15(2,)2P2°当∠APB =∠BAC 时,AP AB AB BC=,∴2AB AP BC =. 又∵AB ==∴103AP =∴213(2,)3P 综上所述满足条件的P 点有5(2,)2,13(2,)3.……………………………1分例6、如图所示,抛物线()23m x y --=(m >0)的顶点为A ,直线l :m x y -=33与y 轴交点为B . (1)写出抛物线的对称轴及顶点A 的坐标(用含m 的代数式表示); (2)证明点A 在直线l 上,并求∠OAB 的度数; (3)动点Q 在抛物线对称轴上,问抛物线上是否存在点P ,使以点P 、Q 、A 为顶点的三角形与⊿OAB 全等?若存在,求出m 的值,并写出所有符合上述条件的P 点坐标;若不存在,请说明理由.- m解:(1)对称轴:m x 3= --------1分顶点:A(0,3m )--------1分(2)将 m x 3=代入函数m x y -=33,得 0333=-⨯=m m y --------1分 ∴点A (0,3m )在直线l 上. --------1分 当x =0时,y=- m ,∴B (0,-m ) --------1分 ta n ∠OAB =333=mm ,∴∠OAB=30°. --------1分 (3) 以点P 、Q 、A 为顶点的三角形与⊿OAB 全等共有以下四种情况:①当∠AQP =90°,PQ =m 3,AQ=m 时,如图1,此时点P 在y 轴上,与点B 重合,其坐标为(0,-m ),代入抛物线()23m x y --=得23m m -=-,∵m >0,∴m =31这时有⎪⎭⎫ ⎝⎛-31,01P --------1分 其关于对称轴的对称点⎪⎪⎭⎫⎝⎛-31,3322P 也满足条件. --------1分②当∠AQP =90°,PQ =m ,AQ=m 3时点P 坐标为(m m m 3,3--),代入抛物线()23m x y --=得23m m =,∵m >0,∴m =3这时有()3,333--P --------1分还有关于对称轴的对称点()3,334-+P .--------1分③当∠APQ =90°,AP =m 3,PQ=m 时图2点P 坐标为(m m 23,23-),代入抛物线()23m x y --=得 24323m m =,∵m >0,∴m =2 这时有()3,35-P --------1分还有关于对称轴的对称点()3,336-P .--------1分④当∠APQ =90°,AP =m , PQ =m 3时点P 坐标为(m m 21,23-),代入抛物线()23m x y --=得 24321m m =,∵m >0,∴m =32这时有⎪⎪⎭⎫⎝⎛-31,337P --------1分 还有关于对称轴对称的点⎪⎭⎫ ⎝⎛-31,38P .--------1分例7、如图,抛物线经过(40)(10)(02)A B C -,,,,,三点. (1)求出抛物线的解析式;(2)P 是抛物线上一动点,过P 作PM x ⊥轴,垂足为M ,是否存在P 点,使得以A ,P ,M 为顶点的三角形与OAC △相似?若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由; (3)在直线AC 上方的抛物线上有一点D ,使得DCA △的面积最大,求出点D 的坐标.解:(1)该抛物线过点(02)C -,,∴可设该抛物线的解析式为22y ax bx =+-.将(40)A ,,(10)B ,代入,图3图4得1642020a b a b .+-=⎧⎨+-=⎩,解得1252a b .⎧=-⎪⎪⎨⎪=⎪⎩, ∴此抛物线的解析式为215222y x x =-+-. ················································ (3分)(2)存在. ···························································································· (4分)如图,设P 点的横坐标为m ,则P 点的纵坐标为215222m m -+-,当14m <<时,4AM m =-,215222PM m m =-+-. 又90COA PMA ∠=∠=°,∴①当21AM AO PM OC ==时, APM ACO △∽△,即21542222m m m ⎛⎫-=-+- ⎪⎝⎭. 解得1224m m ==,(舍去),(21)P ∴,. ···················································· (6分)②当12AM OC PM OA ==时,APM CAO △∽△,即2152(4)222m m m -=-+-.解得14m =,25m =(均不合题意,舍去)∴当14m <<时,(21)P ,. ······································································ (7分)类似地可求出当4m >时,(52)P -,. ························································ (8分)当1m <时,(314)P --,. 综上所述,符合条件的点P 为(21),或(52)-,或(314)--,. ························· (9分)(3)如图,设D 点的横坐标为(04)t t <<,则D 点的纵坐标为215222t t -+-.过D 作y 轴的平行线交AC 于E .由题意可求得直线AC 的解析式为122y x =-. ··········································· (10分) E ∴点的坐标为122t t ⎛⎫- ⎪⎝⎭,. 2215112222222DE t t t t t⎛⎫∴=-+---=-+ ⎪⎝⎭. ········································ (11分) 22211244(2)422DAC S t t t t t ⎛⎫∴=⨯-+⨯=-+=--+ ⎪⎝⎭△.∴当2t =时,DAC △面积最大.(21)D ∴,. ·························································································· (13分)。
沪教版 九年级数学 暑假同步讲义 第5讲 相似三角形的判定(二)(全)
ABCA 1B 1C 1相似三角形的判定是九年级数学上学期第一章第三节的内容,本讲主要讲解相似三角形判定定理3和直角三角形相似的判定定理,并进行了相似三角形判定的相关综合练习.重点是灵活运用相似三角形的各个判定定理,难点是相似三角形与分类讨论及函数思想的互相结合.1、 相似三角形判定定理3如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.可简述为:三边对应成比例,两个三角形相似.如图,在ABC ∆与111A B C ∆中,如果111111AB BC CAA B B C C A ==,那么ABC ∆∽111A B C ∆.相似三角形的判定(二)内容分析知识结构模块一:相似三角形判定定理3知识精讲2 / 17ABCDEFABCDE F【例1】 根据下列条件判定ABC ∆与DEF ∆是否相似,如果是,那么用符号表示出来.(1)2AB cm =,3BC cm =,4CA cm =,10DE cm =,15EF cm =,20FD cm = (2)1AB cm =,2BC cm =, 1.5CA cm =,6DE cm =,4EF cm =,8FD cm =.【例2】 如图,在边长为1个单位的方格纸上,有ABC ∆与DEF ∆.求证:ABC ∆∽FDE ∆.【例3】 如图,D 、E 、F 分别是ABC ∆的边BC 、CA 、AB 的中点.求证:DEF ∆∽ABC ∆.【例4】 ABC ∆的边长分别为a 、b 、c ,111A B C ∆的边长分别为a 、b 、c ,则ABC∆与111A B C ∆(选填“一定”、“不一定”或“一定不”)相似.例题解析ABCD E FABCDEA BCDE ABCD【例5】 如图,点D 为ABC ∆内一点,点E 为ABC ∆外一点,且满足AB BC ACAD DE AE==. 求证:ABD ∆∽ACE ∆.【例6】 如图,在ABC ∆中,90ABC ∠=︒,30ACB ∠=︒,2AC =,23CD =,4AD =. 求证:ABC ∆∽ACD ∆【例7】 已知:如图,在t R ABC ∆中,90ACB ∠=︒,2AC =,4BC =,点D 在BC 边上,且CAD B ∠=∠. (1)求AD 的长;(2)取AD 、AB 的中点E 、F ,联结CE 、CF 、EF .求证:CEF ∆∽ADB ∆.【例8】 如图,在梯形ABCD 中,AB // CD ,90A ∠=︒,2AB =,3BC =,1CD =,点E 是AD 的中点.(1)求证:CDE ∆∽EAB ∆;(2)CDE ∆与CEB ∆有可能相似吗?若相似,请证明;若不相似,请说明理由.4 / 171、 直角三角形相似的判定定理如果一个直角三角形的斜边及一条直角边与另一个直角三角形的斜边及一条直角边对应成比例,那么这两个直角三角形相似.可简述为:斜边和直角边对应成比例,两个直角三角形相似.如图,在Rt ABC ∆和111Rt A B C ∆中,如果190C C ∠=∠=︒,1111AB BCA B B C =,那么ABC ∆∽111A B C ∆.【例9】 在Rt ABC ∆和Rt DEF ∆中,90C F ∠=∠=︒.依据下列各组条件判定这两个三角形是否相似,并说明理由. (1)55A ∠=︒,35D ∠=︒;(2)9AC =,12BC =,6DF =,8EF =; (3)3AC =,4BC =,6DF =,8DE =; (4)10AB =,8AC =,15DE =,9EF =.模块二:直角三角形相似的判定定理知识精讲例题解析ABCA 1B 1C 1ABC DA 1B 1C 1D 1AB CDABCD AB CDF G【例10】 如图,在ABC ∆和111A B C ∆中,AD BC ⊥,1111A D B C ⊥,垂足为D 和1D ,且111111AC AB ADAC A B A D ==. 求证:ABC ∆∽111A B C ∆.【例11】 如图,四边形ABCD 中,90BAC ADC ∠=∠=︒,AD a =,BC b =,AC ab求证:DC BC ⊥.【例12】 如图,AB AD ⊥,BD DC ⊥,且2BD AB BC =.求证:ABD DBC ∠=∠.【例13】 如图,在ABC ∆中,CD AB ⊥于D ,DF AC ⊥于F ,DG BC ⊥于G .求证:CF CA CG CB =.6 / 17ABCDE FA B CDEFMABCD EF【例14】 已知直角三角形斜边上的高为12,并且斜边上的高把斜边分成3:4两段,则斜边上的中线长是.【例15】 如图,直角梯形ABCD 中,90BCD ∠=︒,AD // BC ,BC CD =,E 为梯形内一点,且90BEC ∠=︒.将BEC ∆绕点C 旋转90°使BC 与DC 重合,得到DCF ∆,连接EF 交CD 于点M .已知5BC =,3CF =,求:DM MC 的值.【例16】 如图,在ABC ∆中,CD AB ⊥于D ,DE AC ⊥于E ,DF BC ⊥于F ,求证:CEF ∆∽CBA ∆.【例17】 在Rt ABC ∆中,90ACB ∠=︒,CD AB ⊥于点D ,E 是AC 边上的一个动点(不与A 、C 重合),CF BE ⊥于点F ,连接DF . (1)求证:2CB BF BE =; (2)求证:BF AE FD BA =.BCDE FGABCDEF【例18】 求证:如果一个三角形的两边和第三边的高与另一个三角形的对应线段成比例,那么这两个三角形相似.【例19】 如图,在Rt BDC ∆中,点E 在CD 上,DF BC ⊥于F ,DG BE ⊥于G .求证:FG BC CE BG =.【例20】 如图,90CAB ∠=︒,AD CB ⊥,ACE ∆、ABF ∆是正三角形.求证:DE DF ⊥.8 / 17ABC DEPAB CD1、 相似三角形判定定理1:两角对应相等,两个三角形相似.2、 相似三角形判定定理2:两边对应成比例且夹角相等,两个三角形相似.3、 相似三角形判定定理3:三边对应成比例,两个三角形相似.4、 直角三角形相似的判定定理:斜边和直角边对应成比例,两个直角三角形相似.【例21】 根据下列条件,能判定ABC ∆和DEF ∆相似的个数是().(1)35ABC ∠=︒,75ACB ∠=︒,80EDF ∠=︒,35DEF ∠=︒; (2)3AB =,2BC =,30ABC ∠=︒,6DE =,4EF =,30EDF ∠=︒;(3)2AB =,3BC =,4AC =,12DE =,13EF =,14DF =;(4)6AB =,2CB =,2AC =,3DE =,1EF =,2DF =. (A )1个(B )2个(C )3个(D )4个【例22】 如图,四边形ABCD 是正方形,E 是CD 的中点,P 是BC 边上的一点,下列条件中,不能推出ABP ∆与ECP ∆相似的是( ). (A )APB EPC ∠=∠ (B )90APE ∠=︒ (C )P 是BC 的中点 (D ):2:3BP BC =【例23】 已知ABC ∆中,AB AC =,36A ∠=︒,BD 是角平分线,求证:ABC ∆∽BCD ∆.模块三:相似三角形的判定综合知识精讲例题解析ABCDEFGH1 23ABCD EABCDENM【例24】 在ABC ∆中,12AB =,15AC =,D 为AB 上一点,3ABBD=,在AC 上取一点E ,得到ADE ∆,若ADE ∆与ABC ∆相似,则AE =.【例25】 如图,四边形ABDC 、CDFE 、EFGH 是三个正方形,则123∠+∠+∠的值为多少?【例26】 如图,正方形ABCD 的边长为2,AE EB =,1MN =,线段MN 的两端在CB 、CD 上滑动,当CM 为何值时,AED ∆与以M 、N 、C 为顶点的三角形相似.【例27】 如图,AB AC =,2AC AD AE =,求证:BC 平分DBE ∠.10 / 17AB C DE FAB CDEF A B CMACDEM【例28】 如图,在ABC ∆中,M 在AB 上,且8MB =,12AB =,16AC =,在AC 上求作一点N ,使AMN ∆与原三角形相似,并求AN 的长.【例29】 如图,EM AM ⊥,CE DE =.求证:2ED DM AD CD =.【例30】 如图,在ABC ∆和DEF ∆中,90A D ∠=∠=︒,3AB DE ==,24AC DF ==.(1)判断这两个三角形是否相似,并说明为什么;(2)能否分别过点A 、D 在这两个三角形中各作一条辅助线,使ABC ∆分割成的两个三角形与DEF ∆分割成的两个三角形分别对应相似?证明你的结论.【例31】 如图,在ABC ∆中,3AB AC ==,2BC =,点D 、E 、F 分别在AC 、AB 、BC边上,BEF ∆沿着直线EF 翻折后与DEF ∆重合,设CD x =,BF y =.试问DFC ∆是否有可能与ABC ∆相似,如有可能,求出CD 的长;如不可能,说明理由.ABCD EF【例32】 如图,ABC ∆是等边三角形,D 是AC 上的一点,BD 的垂直平分线交AB 于E ,交BC 于F .(1)当点D 在边AC 上移动时,DEF ∆中哪一个角的大小始终保持不变?并求出它的度数;(2)当点D 在边AC 上移动时,ADE ∆与哪一个三角形始终相似?并写出证明过程.又问:当点D 移动到什么位置时,这两个三角形的相似比为1? (3)若等边三角形ABC 的边长为6,2AD =,试求:BE BF 的值.12 / 17A BCD E FGHK AB CDEF【习题1】如图,网格里面有许多三角形.在下列所列出的各三角形之中,不能够与ABC ∆相似的是()(A )BCD ∆ (B )BDE ∆ (C )BFG ∆(D )FGH ∆【习题2】下列命题中,说法正确的个数是( )(1)有一个锐角相等的两个直角三角形一定相似;(2)斜边和一条直角边对应相等的两个直角三角形一定相似;(3)两个等腰三角形腰上的高和腰对应成比例,则这两个三角形必相似; (4)两边对应成比例的两个三角形相似. (A )1个(B )2个(C )3个(D )4个【习题3】如图,AC BD ⊥,DE AB ⊥,AC 与ED 交于点F ,3BC =,1FC =,5BD =,则AC =.【习题4】在ABC ∆中,点G 为重心,若BC 边上的高为6,求点G 到BC 的距离.随堂检测ABCDEF ABCDEA BCDEOA BCPQ【习题5】 如图,在ABC ∆中,90ACB ∠=︒,CD AB ⊥于D ,E 为AC 上一点,CF BE⊥于F ,联结DF . 求证:BD DFBE AE=.【习题6】已知梯形ABCD 中,AB // CD ,90B ∠=︒,3AB =,6CD =,12BC =,点E 在BC 边上自B 点向C 点移动,求使得ABE ∆与ECD ∆相似的BE 的值.【习题7】如图,梯形ABCD 中,AD //BC ,AC 与BD 相交于点O ,过点B 作BE //CD交CA 的延长线于点E ,求证:2OC OA OE =.【习题8】如图,在ABC ∆中,90C ∠=︒,8BC cm =,6AC cm =,点P 从B 出发,沿BC 方向以2cm/s 的速度移动到C 点,点Q 从C 出发,沿CA 方向以1cm/s 的速度移动到A 点.若点P 、Q 分别同时从B 、C 出发,经过多少时间CPQ ∆与CBA ∆相似?14 / 17ABCDEOABCPQN【习题9】如图,ABC ∆中,90C ∠=︒,2AC BC ==,O 是AB 的中点,将45°角的顶点置于点O ,并绕点O 旋转,使角的两边分别交边AC 、BC 于点D 、E ,连接点D 、E .(1)观察图形,在旋转过程中有无一定相似的三角形?若有,请找出,并证明; (2)设AD x =,BE y =,求y 关于x 的函数关系式,并写出它的定义域; (3)当x 为何值时,ODE ∆是等腰三角形?【习题10】 在ABC ∆中,90ACB ∠=︒,CQ 是斜边AB 上的中线,6AC =,10AB =,点P 是BC 边上的一个动点(与B 、C 不重合),经过点P 、Q 的直线与直线AC 交于点N ,若PNC ∆与ABC ∆相似,求BP 的值.ABCDEFAB CD EF【作业1】如图,ABC ∆与DEF ∆在边长为1个单位的方格纸中,它们的顶点在小正方形的顶点位置,试判定ABC ∆与DEF ∆是否相似,为什么?【作业2】下列每组中的两个三角形,相似的是() (A )ABC ∆中,35A ∠=︒,50B ∠=︒;'''A B C ∆中,'35A ∠=︒,'105B ∠=︒ (B )ABC ∆中, 1.5AB =, 1.25BC =,38B ∠=︒;'''A B C ∆中,''2A B =,'' 1.5B C =,'38B ∠=︒(C )ABC ∆中,12AB =,15BC =,26CA =;'''A B C ∆中,''20A B =,''25B C =,''40C A =(D )Rt ABC ∆中,斜边5AB =,直角边3BC =;'''Rt A B C ∆中,斜边''15A B =,直角边''12A C =【作业3】如图,AD BC ⊥于点D ,CE AB ⊥于点E ,交AD 于点F ,则图中相似三角形的对数是(). (A )3对(B )4对(C )5对(D )6对课后作业16 / 17ABCDE FGABCDE FABCDEFG【作业4】如图,在ABC ∆中,CD 垂直平分AB ,点E 在CD 上,DF AC ⊥于F ,DG BE ⊥于G .求证:AF AC BG BE =.【作业5】如图,D 是AC 上的点,BE 平行于AC ,BE AD =,AE 分别交BD 、BC于点F 、G ,CAE CBD ∠=∠. 求证:BF 是FG 和EF 的比例中项.【作业6】已知,E 、F 分别是正方形ABCD 的边AB 和AD 上的点,且13EB AF AB AD ==,求证:AEF FBD ∠=∠.ABCDEFABP QR12ABCDPQ 【作业7】 如图,正方形ABCD 中,2AB =,P 是BC 边上与B 、C 不重合的任意点,DQ AP ⊥于Q .(1)求证:DQA ∆∽ABP ∆;(2)当点P 在BC 上变化时,线段DQ 也随之变化.设PA x =,DQ y =,求y 与x 之间的函数关系式,并写出x 的取值范围.【作业8】如图,在Rt ABC ∆中,90ACB ∠=︒,CD AB ⊥于D ,DE AC ⊥于E ,DF BC ⊥于F . 求证:33AE AC BF BC =.【作业9】如图,A 是等边PQR ∆的边RQ 的延长线上的点,B 是QR 延长线上的点.(1)若1260∠+∠=︒,求证:2QR AQ BR =;(2)若12AQ QR =,当RB 与QR 满足什么条件时,BRP ∆∽PQA ∆?(3)BPQ ∆有可能与PQA ∆相似吗?若可能相似,说明应满足什么条件;若不可能相似,请说明理由.。
沪教版初三C专题(中考冲刺:因动点产生的相似三角形问题3星)巩固基础
-------------压轴题突破1:因动点产生的相似三角形问题(★★★)1. 掌握相似三角形的分类2. 学会利用几何方法快速计算知识结构1.本部分建议时长5分钟.2.请学生先试着自行补全上图,发现学生有遗忘时教师帮助学生完成.“知识结构”这一部分的教学,可采用下面的策略:“典例精讲”这一部分的教学,可采用下面的策略:相似三角形的分类按角分按边分 几何方法代数方法1.本部分建议时长20分钟.2.进行例题讲解时,教师宜先请学生试着自行解答.若学生能正确解答,则不必做过多的讲解;若学生不能正确解答,教师应对相关概念、公式进行进一步辨析后再讲解例题.3.在每一道例题之后设置了变式训练题,应在例题讲解后鼓励学生独立完成,以判断学生是否真正掌握了相关考点和题型.4.教师应正确处理好例题与变式训练题之间的关系,宜采用讲练结合的方式,切不可将所有例题都讲完后再让学生做变式训练题.如图1,已知抛物线211(1)444by x b x =-++(b 是实数且b >2)与x 轴的正半轴分别交于点A 、B (点A 位于点B 是左侧),与y 轴的正半轴交于点C .(1)点B 的坐标为______,点C 的坐标为__________(用含b 的代数式表示);(2)请你进一步探索在第一象限内是否存在点Q ,使得△QCO 、△QOA 和△QAB 中的任意两个三角形均相似(全等可看作相似的特殊情况)?如果存在,求出点Q 的坐标;如果不存在,请说明理由.(★★★)图1答案:(1)B 的坐标为(b, 0),点C 的坐标为(0, 4b).(2)由2111(1)(1)()4444b y x b x x x b =-++=--,得A(1, 0),OA =1.①如图4,以OA 、OC 为邻边构造矩形OAQC ,那么△OQC ≌△QOA .当BA QAQA OA =,即2QA BA OA =⋅时,△BQA ∽△QOA .所以2()14bb =-.解得843b =±.所以符合题意的点Q 为(1,23+). ②如图5,以OC 为直径的圆与直线x =1交于点Q ,那么∠OQC =90°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级专题复习三动点产生的相似三角形问题知识梳理
动点问题是中考卷压轴题中的常客.常见的动点有-个或者两个,动点运动的路线是线段、射线、直线或者折线,动点的速度也不尽相同.随着点的运动图形发生着巨大的变化,根据题目给出的条件结合常见的基本图形解题规律是解决此类问题常用的策略.
【典型例题】
[例1]如图,在▱ABCD中,∠C= 60°,BC=6cm,DC= 7cm。
点M是边AD上一点,且DM:AD=1:3.点E,F分别从A,C同时出发,以1cm/s的速度分别沿AB, CB向点B运动(当点F运动到点B时,点E随之停止运动),EM, CD的延长
线交于点P, FP交AD于点Q.设运动时间为xs,线段
PC的长为y cm.
(1)求y与x之间函数关系式,并写出自变量x的取值
范围;
(2)当x为何值时,PF⊥AD.
[思路分析]平行四边形中一般都有A字形或者8字形等基本图形,抓住这一规律,y 与x之间函数关系式便可轻松建立.
解
[点评]点E和F在运动过程中始终满足第(1)题的y与x的一般关系.而第(2)题中PF⊥AD这一条件下y 与工一定还存在一个特殊关系,将两种关系所对应的兩数解析式联立方程便可求得x的值.
[例2]如图,在矩形ABCD中, AB= 12cm, BC = 6cm,点P沿AB边从A向B以2 cm/s的速度移动点Q沿DA边从D向A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动时间(0≤1≤6),那么:
(1)当t为何值时,△QAP为等腰直角三角形?
(2)求四边形QAPC的面积;你有什么发现?
(3)当t为何值时,以点A, P, Q为顶点的三角形与△ABC相
似?
[思路分析]随着P、Q两点的移动,四边形QAPC的形状不断地发生变化.题中问四边形QAPC 的面积有什么发现,估计面积是一个定值.
解
[点评] 动中的不变性,动中取静是解题的巧妙之处.
[例3] 如图,已知△ABC是边长为6 cm的等边三角形,动点P, Q同时从A, B两点出发,分别沿AB, BC匀速运动,其中点P运动的速度是1 cm/s,点Q运动的速度是2 cm/s,当点Q到达点C,时,P, Q两点都停止运动,设运动时间为t(s),解答下列问题:
(1)当t= 2s时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR//BA交AC于点R.联结PR,当1为何值时,APR∼△PRQ. [思路分析]由t= 2求出BP与BQ的长度,从而可得△BPQ的形状;作
QE⊥BP于点E,将PB,QE用t表示,由S△BPQ =1
2
BP×QE可得S
与t的函数关系式;先证得四边形EPRQ为平行四边形,得PR = QE,
再由△APR∼△PRQ,对应边成比例列方程,求得t值.
[点评]本题是双动点问题.动态问题是近几年来中考数学的热点题型,这类试题信息量大,对同学们获取信息和处理信息的能力要求较高.解题时需要用运动和变化的眼光去观察和研究问题,挖掘运动、变化的全过程,并特别关注运动与变化中的不变量、不变关系或特殊关系,动中取静,静中求动..
【练习题】
1.已知:如图,等腰△ABC中,AB= AC=5cm. BC=6cm,动点P, Q分别从A, B两点同时出发,沿AB, BC方向匀速移动,它们的速度都是1 cm/s.当点P到达点B时,P,Q两点停止运动,设点p的运动时间为t(s).在P, Q运动中,△BPQ与△ABC能否相似?若能,请求出l的值;若不能,请说明理由.
2.如图,梯形ABCD中,AD // BC. AB= CD = 3 cm,∠C= 60°,BD⊥CD
(1)求BC, AD的长度;
(2)若点P从点B开始沿BC边向点C以2cm/s的速度运动,点Q从点C开始沿CD边向点D 以1 cm/s的速度运动.当P, Q分别从B, C同时出发,写出五边形ABPCQD的面积S 与运动时间t之间的两数关系式,并写出自变量t的取值范围(不包括点P在B,C两点的情况);
(3)在(2)的前提下,是否存在某一时刻t,使线段PQ把梯形ABCD分成两部分的面积比为1:5?若存在,求出t的值;若不存在.请说明理由.
3.如图, Rt△ABC中,∠C=90°, AB=50, AC=30,D, E, F分别是AC, AB,BC的中点,点P从点D出发沿折线DE - EF - FC - CD以每秒7个单位的速度匀速运动,点Q从点B出发沿BA方向以每秒4个单位的速度匀速运动,过点Q作射线QK⊥AB.交折线BC-CA于点G,点P, Q同时出发,当点P绕行一周回到点D时停止运动,点Q也随之停止运动,设点P, Q运动的时间为t(s) (t> 0)
(1) D, F两点之间的距离;
(2)射线QK能否把四边形CDEF分成面积相等的两部分?
若能,求出l的值.若不能,请说明理由;
(3)当点P运动到折线EF-FC上时,且点P又恰好落在射线QK上,求t的值;
(4)联结PG,PG//AB时,请直接写出t的值.
4.已知:如图,等边△ABC的边长为6,点D, E分别在AB, AC上,且AD =AE=2.若点F从点B 开始以每秒1个单位长度速度沿射线BC方向运动,设点F运动的时间为t(s).当t>0时,直线FD与过点A且平行于BC的直线相交于点G, GE的延长线与BC的延长线相交于点H, AB 与GH相交于点O.
(1)设△OGA的面积为S,写出S与t的函数关系式;
(2)当t为何值时, AB⊥GH;
(3)请你比较△ABC和△FGH的面积的大小;
(4)当t为何值时,点F和点C是线段BH的三等分点.
5.如图,在梯形ABCD中,AD// BC, AD=3, DC=5, AB=42,∠B=45°,动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动;设运动的时间为t(s)
(1)求BC的长;
(2)当MN//AB时,求t的值;
(3)试探究:t为何值时.△MNC为等腰:三角形.
6.在四边形ABCD中,∠D= 90°, BC // AD, BC= 20,DC=16,AD=30.动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发.在线段CB上以每秒1个单位长的速度向点B运动,点P, Q分别从点D,C同时出发.当点Q运动到点B时,点P随之停止运动,设运动时间为t(s).
(1)设△BPQ的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,以B, P, Q三点为顶点的三角形是等腰三角形;
(3)当线段PQ与线段AB相交于点O,且2AO = OB时,求∠BQP的正切值;
(4)是否存在时刻t,使得PQ⊥BD,若存在,求出t的值;若不存在,请说明理由.
7.如图,二次函数y=−1
4x2 +
5
2x −4的图像与x轴相交于点A, B,与y轴相交于点C,联结AC.
(1)求证:△AOC ∼△COB;
(2)过点C作CD // x轴,交二次函数y= y=−1
4x2 +
5
2x −4的图像于点D,若点M在线段AB上
以每秒1个单位的速度由A向B运动,同时点N在线段CD上也以每秒1个单位的速度由点D向点C运动,联结线段MN,设运动时间为t(s). (0<t≤6)
①是否存在时刻t,使MN = AC,若存在,求出t的值;若不存在,请说明理由..
②是否存在时刻t,使MN⊥BC,若存在,直接写出t的值;若不存在,请说明理由
8.如图,AB=16cm,AC=12cm,动点P,Q分别以每秒2cm和1cm的速度同时开始运动,其中点P 从点A出发沿AC边一直移到点C为止,点Q从点B出发沿BA边一直移动到点A为止
(1)写出AP的长y1和AQ的长y2关于时间t的函数;
(2)经过多少时间后,△APQ与△A BC相似?
(3)在整个过程中,是否存在使△APQ的面积恰好为△A BC面积一半的情况,若存在,请问此时点Q运动了多少时间?若不存在,请说明理由.
9.如图,在等腰梯形ABCD中,AD // BC,AB=DC=5,AD=6, BC= 12.
(1)求梯形ABCD的面积;
(2)设E在AD上,AE=2,F为AB上一个动点(不与A,B重合),过F作FG // EC,交BC于G.
①设BF =x,四边形EFGC的面积等于y,写出y与x之间的函数解析式,并求出这个函数的定义域。
②当△AEF与△CDE相似时,求四边形EFGC的面积.
10.如图,在直角梯形ABCD中,AD // BC,∠ADC =90°,AB=5, AD=8, CD=3,线段AD上有一动点E,以E点为圆心,作一个⊙E与线段AB相切与点F.
(1)求sinA的值;
(2)若设DE=x, EF=y,试写出y关于自变量x的函数关系式和x的取值范围;
(3)当△AEF与△CED相似时,求DE的长.
11.如图,已知在矩形ABCD中,AD=8cm, CD=4cm,点E从点D出发,沿线段DA以每秒1cm的速度向点A方向移动,同时点F从点C出发,沿射线CD方向以每秒2 cm的速度移动,当B, E, F三点共线时,两点同时停止运动.设点E移动的时间为t(s).
(1)求证:△BCF ∼ △CDE;
(2)求t的取值范围;
(3)联结BE,当t为何值时,∠BEC =∠BFC.
12.如图,△ABC中,AB=5,AC=3, cosA=3
10
,D为线段BA上的点(点D不与点B重合),作DE // BC交线段CA于点E.
(1)若CE=x, BD=y,求y与x的函数关系式,并写出函数的定义域;
(2)当点D在AB边上时,BC边上是否存在点F,使△ABC与△DEF相似?
若存在,请求出线段BF的长;若不存在,请说明理由.。
