流体力学例题总汇03-04
流体力学计算题及答案

3p = 13600kg /m,水的密度解:3p 二1000kg /该微压计是一个水平倾角为二P i — P2= Y Z3 —Z4)= Y sin9第二章例1用复式水银压差计测量密封容器内水面的相对压强,如图所示。
已知:水面高程z o=3m,压差计各水银面的高程分别为z i=0.03m, z2=0.18m, Z3=0.04m, Z4=0.20 m,水银密度P o Y z°—z i) - Y(Z2 - 乙)一Y(Z4 —Z3)= P aP0 二*(Z2 —Z i • Z4 — Z3)- YZ0 —Z i)例2:用如图所示的倾斜微压计测量两条同高程水管的压差。
B的n形管。
已知测压计两侧斜液柱读数的差值为L=30mm,倾角9=30 °,试求压强差p i解:;P i - Y Z3 — Z i) • Y Z4 —Z2)= P2例3:用复式压差计测量两条气体管道的压差(如图所示)。
两个U形管的工作液体为水银,密度为P 2,其连接管充以酒精,密度为P 1。
如果水银面的高度读数为z i、Z2、Z3、Z 4 ,试求压强差 p A —pB 。
解:点1的压强:P A 点2的压强:p 2二P A - Y (Z 2 -z 1)点3的 压强:P 3 = P A ~■ Y (z ^ ~■ z1)Y(z 2 ~'Z 3)p4= P A -Y( z2- z 1 )'Y (z 2- z3)- Y (Z4-z3)= p BP A - P B = Y (z2 -乙z 4 ~ z 3)~Y ( z2 - z 3)例4 :用离心铸造机铸造车轮。
求A-A 面上的液体总压力。
|h1 2 2r - gz 2 9P a 在界面A-A 上: Z = - hP ] 2『gh PaR 冷 I '[ L (p —P a )2nrdr =2兀P — co 2R 4十一ghR 2 |<8 2 ,/H = 500mm 的园柱形容器中注水至高度 h 1 = 300mm, 例5 :在一直径 d = 300mm 而高度 使容器绕垂直轴作等角速度旋转。
流体力学题库

流体的粘滞切应力:【例1-1】一平板距另一固定平板δ=0.5mm,二板水平放置,其间充满流体,上板在单位面积上为τ=2N/m2的力作用下,以μ=0.25m/s的速度移动,求该流体的动力黏度。
【解】由牛顿内摩擦定律由于两平板间隙很小,速度分布可认为是线性分布,可用增量来表示微分(pa.s)【例1-2】长度L=1m,直径D=200mm水平放置的圆柱体,置于内径D1=206mm的圆管中以u=1m/s的速度移动,已知间隙中油液的相对密度为d=0.92,运动黏度=5.6×10-4m2/s,求所需拉力F为多少?解】间隙中油的密度为(kg/m3)动力黏度为(Pa·s)由牛顿内摩擦定律由于间隙很小,速度可认为是线性分布如图所示,转轴直径=0.36m,轴承长度=1m,轴与轴承之间的缝隙=0.2mm,其中充满动力粘度=0.72 Pa.s的油,如果轴的转速200rpm,求克服油的粘性阻力所消耗的功率。
解:油层与轴承接触面上的速度为零,与轴接触面上的速度等于轴面上的线速度:设油层在缝隙内的速度分布为直线分布,即则轴表面上总的切向力为:克服摩擦所消耗的功率为:三、解题步骤1.判断形心位置;2.计算左边的总压力和作用点;3.计算右边的总压力和作用点;4.计算总压力F=F1-F2;5.由力矩平衡,计算总压力的作用点。
静水奇象 应用:对容器底部进行严密性检查一块平板矩形闸门可绕铰轴A 转动,如图示。
已知θ=60°,H=6 m ,h1=1.5 m ,h=2m ,不计闸门自重以及摩擦力,求开启单位宽度b=1 m (垂直于纸面)的闸门所需的提升力F ?四、静止液体作用在曲面上的总压力的计算程序 (1)将总压力分解为水平分力Fx 和垂直分力Fz (2)水平分力的计算(3)确定压力体的体积(4)垂直分力的计算,方向由虚、实压力体确 (5)总压力的计算, (6)总压力方向的确定,[例2-7]下图表示一个两边都承受水压的矩形水闸,如果两边的水深分别为h1=2m ,h2=4m ,试求每米宽度水闸上所承受的净总压力及其作用点的位置。
第四章 流体动力学例题

按照不可压连续方程,有:
lV l1V l2 V
由上两式得:
1 l1 (1 co s 0 )l 2 1 l 2 (1 co s 0 )l 2
设射流受到沿y方向的合力为Fy, 写出沿y方向的动量方程:
Fy V lsin0
2
平板受到的合力即为 R= -Fy
用文特利管测流量如下图所示流动为定常不可压流流体密度为用文特利管测流量如下图所示流动为定常不可压流流体密度为收缩段和出口截面的压强差收缩段和出口截面的压强差pp11p22
连续方程的应用 1) 证明下述不可压缩流体的运动不存在
u x,
v y,
w z
证明:不可压缩流应满足的连续方程为
v 0
v1 P , A 1 1
P2, A2 v2
5 p 27.58 10 Pa 下图中,水以 qV 5.663m / s , 1
3
进入弯头,弯头的进口与出口面积分别为
A1=0.1858m2, A2=0.0929m2, 忽略摩擦及重力影响。
试计算:
1)
v1 , v2 , p2
a
b
2)水对弯头内壁的作用力。
求合力的作用点:
t
r V dV (r V) (V n)dS r F
V S
(一般形式的动量矩方程 )
r 2 2
l r ctg 0 2
思考练习
1. 不可压定常流动中,速度随面积如何变化? 可压缩流动中变化又如何? 2. 写出不可压流的伯努利方程,质量力为重力, 并指出各项的物理意义。 3. 可压绝热流的温度随速度如何变化?不计质 量力的不可压流压力随速度如何变化?
流体力学复习题集整理版

1.一底面积为40 ×45cm2,高为1cm的木块,质量为5kg,沿着涂有润滑油的斜面向下作等速运动,如图1-4所示,已知木块运动速度u =1m/s,油层厚度d =1mm,由木块所带动的油层的运动速度呈直线分布,求油的粘度。
解:∵等速∴αs=0由牛顿定律:∑F s=mαs=0 m gsinθ-τ·A=0(呈直线分布)∵θ=tan-1(5/12)=22.62°2. 应用细管式粘度计测定油的粘度,已知细管直径d=6mm,测量段长l=2m ,如图6-5。
实测油的流量Q=77cm3/s,水银压差计的读值h p=30cm,油的密度ρ=900kg/m3。
试求油的运动粘度和动力粘度。
解: 列细管测量段前、后断面能量方程(4-15)设为层流图6-5校核状态,为层流。
3.如图2-14所示,一洒水车等加速度a=0.98m/s2向右行驶,求水车内自由表面与水平面间的夹角;若B点在运动前位于水面下深为h=1.0m,距z轴为x B=-1.5m,求洒水车加速运动后该点的静水压强。
解:考虑惯性力与重力在内的单位质量力为(取原液面中点为坐标原点)X= -a ;Y=0 ;Z= -g代入式(2-7)得:积分得:在自由液面上,有:x=z=0;p=p0得:C=p0=0代入上式得:B点的压强为:自由液面方程为(∵液面上p0=0)ax+gz=0即:4.如图2-15所示,有一盛水的开口容器以3.6m/s2的加速度沿与水平成30º夹角的倾斜平面向上运动,试求容器中水面的倾角θ,并分析p与水深的关系。
解:根据压强平衡微分方程式:单位质量力:在液面上为大气压强,代入由压强平衡微分方程式,得:p与水深成正比。
5. :一密封水箱如图所示,若水面上的相对压强p0=-44.5kN/m2,求:1)h值;(2)求水下0.3m处M点的压强,要求分别用绝对压强、相对压强、真空度、水柱高及大气压表示;(3)M点相对于基准面O—O的测压管水头。
流体力学考研复习题库

流体力学考研复习题库一、选择题1.如图所示,一平板在油面上作水平运动。
已知平板运动速度V=1m/s ,平板与固定边界的距离δ=5mm,油的动力粘度μ=0.1Pa·s,则作用在平板单位面积上的粘滞阻力为( ) A .10Pa ; B .15Pa ; C .20Pa ; D .25Pa ;2.动量方程( )A .仅适用于理想流体的流动B .仅适用于粘性流体的流动C .理想流体与粘性流体的流动均适用D .仅适用于紊流3. 实际流体总水头线的沿程变化是:A .保持水平;B .沿程上升;C .沿程下降;D .前三种情况都有可能。
4.圆管层流,实测管轴上流速为0.4m/s ,则断面平均流速为( ) A .0.4m/s B .0.32m/s C .0.2m/s D .0.1m/s5.绝对压强abs p ,相对压强p ,真空度v p ,当地大气压a p 之间的关系是: A .v abs p p p +=; B .abs a v p p p -=; C .a abs p p p +=;D .a v p p p +=。
6.下列说法正确的是: A .水一定从高处向低处流动;B .水一定从压强大的地方向压强小的地方流动;C .水总是从流速大的地方向流速小的地方流动;D .以上说法都错误。
7.长管串联管道各管段的( )A.水头损失相等; B .水力坡度相等; C .总能量损失相等; D .通过流量相等。
8. 并联管道1、2,两管的直径相同,沿程阻力系数相同,长度123l l =,通过的流量为( )A. 21Q Q =;B .215.1Q Q =;C .213Q Q =;D .2173.1Q Q =。
9. 圆柱形外管嘴的正常工作条件是A .()03~4,9m L d H =>B .()03~4,9m L d H =<C .()03~4,9m L d H >>L 〉 D. ()03~4,9m L d H <<L 10、静止液体中同一点各方向的压强 ( )A 、数值相等;B 、数值不等;C 、仅水平方向数值相等;D 、铅直方向数值最大11、如下图所示容器内有一放水孔,孔口设有面积为A 的阀门ab ,容器内水深为h ,阀门所受静水总压力为 ( )A 、0.5γhA;B 、γhA;C 、0.5γh 2A ; D 、γhA 212..某流体的运动粘度v =3×10-6m 2/s,密度ρ=800kg/m 3,其动力粘度μ为( ) A.3.75×10-9Pa·s ; B.2.4×10-3Pa·s; C.2.4×105Pa·s; D.2.4×109Pa·s 13. 理想流体是一种( )的假想流体。
(完整版)流体力学基本练习题

(完整版)流体力学基本练习题流体力学基本练习题一、名词解释流体质点、流体的体膨胀系数、流体的等温压缩率、流体的体积模量、流体的粘性、理想流体、牛顿流体、不可压缩流体、质量力、表面力、等压面、质点导数、定常场、均匀场、迹线、流线、流管、流束、流量、过流断面(有效截面)、层流、湍流、层流起始段、粘性底层、水力光滑管、水力粗糙管、沿程阻力、局部阻力二、简答题1. 流体在力学性能上的特点。
2. 流体质点的含义。
3. 非牛顿流体的定义、分类和各自特点。
4. 粘度的物理意义及单位。
5. 液体和气体的粘度变化规律。
6. 利用欧拉平衡方程式推导出等压面微分方程、重力场中平衡流体的微分方程。
7. 等压面的性质。
8. 不可压缩流体的静压强基本公式、物理意义及其分布规律。
9. 描述流体运动的方法及其各自特点10. 质点导数的数学表达式及其内容。
写出速度质点导数。
11. 流线和迹线的区别,流线的性质。
三、填空题、判断(一)流体的基本物理性质1. 水力学是研究液体静止和运动规律及其应用的一门科学。
()2. 当容器大于液体体积,液体不会充满整个容器,而且没有自由表面。
()3. 气体没有固定的形状,但有自由表面。
()4. 水力学中把液体视为内部无任何间隙,是由无数个液体质点组成的。
()5. 粘滞性是液体的固有物理属性,它只有在液体静止状态下才能显示出来,并且是引起液体能量损失的根源。
()6. 同一种液体的粘滞性具有随温度升高而降低的特性。
()7. 作层流运动的液体,相邻液层间单位面积上所作的内摩擦力,与流速梯度成正比,与液体性质无关。
()8. 惯性力属于质量力,而重力不属于质量力。
()9. 质量力是指通过所研究液体的每一部分重量而作用于液体的、其大小与液体的质量成比例的力. ()10. 所谓理想流体,就是把水看作绝对不可压缩、不能膨胀、有粘滞性、没有表面张力的连续介质。
()11. 表面力是作用于液体表面,与受力作用的表面面积大小无关。
流体力学习题解析

《流体力学》习题(三)3-1 已知速度场为k z x j y x i y x u )()()(2-+-++= (m/s),求(2,3,1)点的速度和加速度。
3-2 已知速度场为k z y j y i x u )34()(2)3(2-+-++=ττ (m/s),求τ=2秒时,位于(2,2,1)点的速度和加速度。
3-3 已知二维流场的速度分布为j x y i x y u ττ)96()64(-+-= (m/s)。
问:(1) 该流动是稳定流还是非稳定流?是均匀流还是非均匀流?(2) τ=1秒时,(2,4)点的加速度为多少?(3) τ=1秒时的流线方程?3-4 已知速度场为022z y 3x ==+=u x u y u ,,τττ。
求τ=1时,过(0,2)点的流线方程。
3-5 20℃的空气在大气压下流过0.5m 直径的管道,截面平均流速为30m/s 。
求其体积流量、质量流量和重量流量。
3-6 流体在两平行平板间流动的速度分布为 ])(1[2max b y u u -=式中u max 为两板中心线y =0处的最大速度,b 为平板距中心线的距离,均为常数。
求通过两平板间单位宽度的体积流量。
3-7 下列各组方程中哪些可用来描述不可压缩流体二维流动?(1) )2(223y 22x y y x x u y x u --=+=,(2) 22y 2x 22x y xy u y x xy u +-=+-=,(3) τττy x u y x u -=+=2y x 2,(4) ττy y x u x y x u )2()2(y x -=+=,3-8 下列两组方程中哪个可以用来描述不可压缩流体空间流动? (1) 22z 2y x )(21z y x u xyz u xyz u ττττ-=-==,, (2) 4322z 2y 2x 2122y x z x u yz yz x u xz y u +=-=+=,, 3-9 已知不可压缩流体二维流动在y 方向的速度分量为y x y u 222y +-=,求速度在x 方向的分量u x 。
流体力学例题
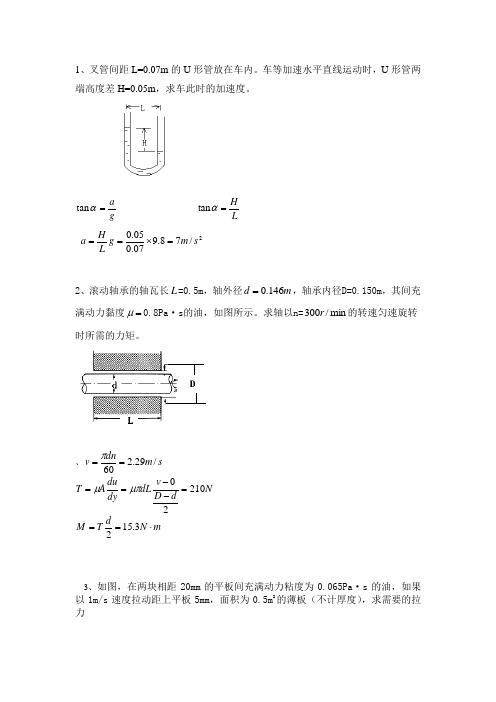
1、叉管间距L=0.07m 的U 形管放在车内。
车等加速水平直线运动时,U 形管两端高度差H=0.05m ,求车此时的加速度。
g a =αtan LH =αtan 2/78.907.005.0s m g L H a =⨯==2、滚动轴承的轴瓦长L =0.5m ,轴外径m d 146.0=,轴承内径D=0.150m ,其间充满动力黏度=μ0.8Pa ·s 的油,如图所示。
求轴以n=min /300r 的转速匀速旋转时所需的力矩。
、s m dnv /29.260==πN d D v dL dydu A T 2102=--==μπμm N dT M ⋅==3.1523、如图,在两块相距20mm 的平板间充满动力粘度为0.065Pa ·s 的油,如果以1m/s 速度拉动距上平板5mm ,面积为0.5m 2的薄板(不计厚度),求需要的拉力dy du AT μ= N huA dy du AT 5.61===μμ N hH u A dy du AT 17.22=-==μμ N T T T 67.821=+=4、用复式U 形管差压计测量A 、B 两点的压力差。
已知:mm h 3001=,mm h 5002=。
水31000m kg =ρ,水银内313600m kg m =ρ,3800m kg ='ρ。
求B A p p -。
A B p h h h g gh h h p =+∆++'-∆-)(211ρρρPa p p B A 32144-=-5、有一敞口容器,长=L 2米,高=H 1.5米,等加速水平直线运动,求当水深h 分别为1.3米和0.5米时,使容器中的液体开始溢出的最大加速度。
g a =αtan L h H )(2tan -=α 2/96.1)(2s m g Lh H a =-= xH hL 21=34=x x H g a ==αtan s m g a /11892==6、有一敞口容器,长2米,高1.3 米,宽B=1m ,等加速水平直线运动,水深0.5米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Chap 33-1已知流速场为U x二二L,U y二二也,U z =0其中C为常数,求流线方程。
x +y x + ydx dydz解:由式U?二叮二&得dx dyCx Cy~2 2 ~2 2x y x ydx dy" ____________ —x y积分得:In x ln G = In y则:y 二Gx此外,由U z=0得d z=0 :.'r Z — C2因此,流线为xoy平面上的一簇通过原点的直线,这种流动称为平面点源流动( 面点汇流动(C v 0时)3-2 已知平面流动u x = x • t, u y二-y • t, u z = 0。
试求:(1)t=0时,过点M (-1, -1)的流线;(2)求在t=0时刻位于x=-1,y=-1点处流体质点的迹线。
dx _ dy解:(1)由式U7 一石得dx dyx t -y tc>0时)或平(x 将:t)( -y t) =Ct=0,x=-1,y=-1代入得瞬时流线xy=1即流线是双曲线dxx tdy-y t-dtIn x t = -1 n :;:-y t InC(2)由式血二生=dt得U x U y 得由(1)式得:lnx = In ( 1+t ) +lnC= In[C ( 1+t )]x = C ( 1+t )X o当t= t o 时,x= x o 代入上式得C一 1,t o得:tx 二Ge t -1 J y =C 2e t -1最后可得迹线为:x+y+2-O3-3已知流动速度场为U x二 _xit试求: (1) 在t= t o 瞬间,过A(2) 在t= t o 瞬间,位于x o ,y o ,z o )点的流线方程; (x o ,y o ,Z o )点的迹线方程。
dxdy 解:(1)流线方程的一般表达式为_ dzUy = U7,将本题已知条件代入,则有:dxdy积分得:(i+t ) lnx = Iny + InClnyIn C x(1 t)当 t= t o 时,x= X o , y=y oyo 2 t o )=y °x 。
-(i t o )故过 A ( X o ,y o,z o )点的流线方程为y=y o xo-(1 t o )(1 t)x(2)求迹线方程迹线一般表达式为dxU xdy U ydt,代入本题已知条件有:dx dt(1)dy Vdt由 t=0 时,x=-1 , y=-1 得 C i =0, C 2=0,则有:X 0X =皿(1 t)由(2)式得:lny = t +lnC= Ine t+|nC=ln(Ce t) y = Ce t故液体流动是无旋流。
解:(1)s 叫 i 川角)q=0 0 = 0 excy cz ex 列符合不可压缩流体的连续性方程。
•••是不可压缩流体。
巴巴巴二血 -3)= 0 3x = 0:x :y :z :x 为当t= t 0时,y= y 0代入上式得C = y oe-toyfeZ故迹线方程为X ox (1+t ) (t 」0 )y =y °ez=z ot 是自变量,消t 后得到的轨迹方程为迹线方程:y o 普2) 八 e to e3-4已知流体流动的流速场为 试判断该流动是无旋流还是有旋流?解: --z-( zy ':z2 :y 1(■:Ux fu z 2(.z.x 1(- U y 辿)=0 2」^0 0" 3-5有两种二元流体,其流速可表示为:试问这两种流体是不可压缩流体吗?(1) U x = -2y, U y =3x ;( 2)U x =0, u y =3xy)=0 ■ -x■y.:U y不符合不可压缩流体的连续性方程。
•••不是不可压缩流体。
3-6 已知均匀流与点源流动叠加后的流动。
均匀流:u x二u0(常数)uy =0解:叠加后的流速势函数与流函数均匀流:d i =U x dx u d y o u dx. ^u0x Cd'-l 二q d x u d y= o u d 八 1 = u°y C该流网如图(a)所示点源流:d = u「dr u 丁d v - 2^7 dr :2 =守ln r Cd =ujd 丁u#r ‘一 2 =扌'丁C即流线是辐射线,等势线是一簇与流线正交的同心圆(图 b )。
叠加后的流速势函数与流函数(图c)点源流: u r = U .J - 01 ACk—►!<Pi<Ps_ J牡即誉I 二U o X 昙In r = u o rcos:头In r 二u°x 头1 n .、x2 y2=巧 1 =u°y 昇丁- u o rsin 丁 ~ 丁叠加后的流动流速场_ 汐_ q sin 日_ q _ yy_ :y _2二r _2「x2 y2通过滞止点的流线方程滞止点A u x =0,u =0则:卄二,r -x y2nu o通过滞止点的流线为:u o rsin v - q v - C2兀或u o y 头丁=C通过滞止点人(石冬,二)则有:c=q2 応U o 2通过滞止点的流线:u o rsin v '头严-二)=0 得「=蔬恭或y=2^(—)=氏(一tg钱)当x r ■'时,r“ ',v)o, y T绘得流网如图所示。
结论:通过滞止点的流线将流场分为两部分; 由均匀流引起的这部分流量皆在这条流线之外流动,而由点源引起的那部分流量皆在这条流线之内流动。
这样便可把通过滞止点的这一条流线视为固壁,并且仅考察其外部绕流,这就是所谓“二元半体绕流”。
(1) 冋是无旋流还是有旋流; (2)若是无旋流,求其速度势 ;(3 )求平面流动的流函数; (4)求压强分布。
• 'x = y = z= 0为无旋流。
3-7对于下面平面点源汇流动:U xCx~22 , uyx y鼻,u^0 x y解:(1)■U x2Cxy(X y):‘Uy 2Cyx:x (x 2 y 2)2:U y:z=0.zz-U(2 )对于点源汇流动,为方便起见采用极坐标示(如图 a ),此时:u 打0因: d 「= u x dx U y dyu x dx u y dy = u dr = u r dr u yd v=Cdr = Cln r C = Cln . x 2 y 2 C r '上式中积分常数可任意给定,现取积分常数 C/等于0,由该式可见,等势线是一簇以原点为圆心的同心圆(r=Co nst ) (3)因:d - -u y dx u x dy(4 )由平面势流流场的伯努里方程,若不计重力的影响,应 将u 二C 代入整理得r,P C 2 P 二C -()2 2 r2可设 r T 20 时 u=0,p=p^(则 C'= po3,于是 p = p^ — —(—)2 r所以p 沿r 方向按抛物线规律分布, 如图b 所示。
最后,上式中C 的确定:由单位深度(z=1) 的流量2兀2兀CQ u r rdrd r - 2 二C ‘0 ‘0 r称为平面点源(汇)强度。
U r =u = , u : u y=-u y dx u x dy =Cy x 2 y 2 dC) =C J 1(与xdx ~^dyx y=C tg -1 — Const = C J Const x从上式中可见,流线是 交。
簇通过原点的射线( q=Const )由此说明了等势线与流线互相正2P u cG2g 1Chap 44-1例1:如图所示的虹吸管泄水,已知断面1,2及2,3的损失分别为h .1,2=06 2/(2g ) 和h 洋,30.5『/(2g ),试求断面2的平均压强。
d=200mmCO)解:取0-0,列断面1,2的能量方程(取:-1=「2=1)而v2=v 3=v (因d 2=d 1=d )可对断面1, 3写出能量方程可得:毎询±".43m代入式(a )得P2- -4.29m 或p 2 - -9.8 4.29 - -42.04kPa可见虹吸管顶部,相对压强为负值,即出现真空。
为使之不产生空化, 应控制虹吸管顶高(即 吸出高),防止形成过大真空。
4-2水深1.5m 、水平截面积为3m x 3m 的水箱,箱底接一直径为200mm ,长为 2m 的竖直管,在水箱进水量等于出水量情况下作恒定出流,略去水头损失,试 求点2的压强。
1.5m 1,0m 1.0m解:根据题意和图示,水流为恒定流;水箱表面,管子出口,管中点 2所在断面,都是渐变流断面;水流不可压缩,只受重力作用。
符合总流能量方程应用条件。
0+0 十0 =2+卑+ 舊+0.62|(a )(b )4取渐变流断面1-1、2-2和3-3。
因为1-1断面为水箱水面,较竖直管大得多,故流速水头2a^g 0,取 &1 =&3 = 1。
将基准面0-0取在管子出口断面 3-3上,写出断面1-1和断面3-3的总流能量方程 p V?z12g =z 3采用相对压强 山=p 3 =0,z 1 = 3.5m,z 3 = 0。
将已知数据代入上式,3.5 0 000遵即得=3.5m由连续方程,因V 2二V 3,所以=3.5m取断面3-3为基准面,取a 2 =1再写出断面1-1和2-2的总流能量方程z1卫坛乂 ~2- Vg将已知数据代入上式可得3.5 =1 P 2- 3.5 所以 P2 = —1.0m上式说明点2压强小于大气压强,其真空度为1m 水柱,或绝对压强相当于 10-1=9m 水 柱。
其真空值为 9.8kPa ,或绝对值压强为4-3某一水库的溢流坝,如图所示。
已知坝下游河床高程为 105.0m,当水库水位为120.0m 时,坝址处过水断面C 处的水深hc=1.2m 。
设溢流坝的水头损失解:于溢流坝面水流为急变流,所以在距坝前一段距离处,取渐变流断面 流较平直的C 处取断面2-2。
由于水库的过水断面面积大,流速水头2g88.2kPa 。
h =0.1:g 。
求坝址处断面的平均流速。
105.0 01-1和在坝下游水誉0。
水库水位和下游河床高程都为已知,基准面 0-0取在下游河床底部。
取宀=2 = 1.0 ,写因为渐变流断面上各点的单位势能(z p )等于常数。
可选断面上任一点求得其 z 和p 值。
为了计算方便,可选水面上一点,故可用相对压强计算,该点动水压强为零,即P l = P 2 = 0,又 P l = P 2 = 0,令V 2 =Vc 。
由图可知乙=120 -105 =15m; z 2 二 h c =1.2mv 2h w =0.1g^将以上已知数据代入总流量方程,得解得坝址处的流速4-4如图所示为一流动系统,各种损失如图中所示。
AB 段直径d1=129mm , BC 段直径d2=150mm 。
试求:1) AB 段流速ul 、Q ; 2)绘制总水头线和测压管水 头线。
