流体力学典型例题
流体力学例题汇总
答案:D
例9. 某液体的容重为γ,在液体内部B点较A点低 1m,其B点的压强比A点的压强大_____Pa. A.γ; B.9800; C.10000; D.不能确定
答案:A
例10.仅在重力作用下,静止液体中任意点对 同一基准面的______为一常数。 A.单位位能;B.单位势能; C.单位压能;D.单位动能
整理后得A,B两点的压强差
9806 0.5 0.3 133400 0.3 7850 0.2 133400 0pB 1 g h5 h4 3 gh4 2 gh3 3 gh2 1 gh1
解
对于底盖,由于在水平方向上压强分布对称,所以流体静压强作 用在底盖上的总压力的水平分力为零。底盖上总压力的垂直分力
d 2 h d 3 Fpz1 gVp1 g H 4 2 12 0.52 0.53 9806 2.5 0.75 6579N 4 12
例2 5如图所示,两圆筒用管 子连接。第一个圆筒直 径d1 45cm,活塞上受力 F1 3197N,密封 气体的计示压强 pe 9810Pa;第二个圆筒 d 2 30cm,活塞上受力 F2 4945.5 N,上部通大气。若 不计活塞质量,求平衡 状态时两活塞的高度差 h。(已知水银的密度 13600kg m 3 )
答案:C
下一页
例6. 仅在重力作用下,静止液体的测压管水 头线必定________. A 水平 B 线形降低 C 线形升高 D 呈曲线
答案:A
例7. 某点压强为1.0kgf/cm^2,用国际单位表示 该处的压强为______kPa。 A.100; B.98; C.1000; D.980
答案:B
《流体力学》典型例题

《例题力学》典型例题例题1:如图所示,质量为m =5 kg 、底面积为S =40 cm ×60 cm 的矩形平板,以U =1 m/s 的速度沿着与水平面成倾角θ=30的斜面作等速下滑运动。
已知平板与斜面之间的油层厚度δ=1 mm ,假设由平板所带动的油层的运动速度呈线性分布。
求油的动力粘性系数。
解:由牛顿内摩擦定律,平板所受的剪切应力du Udy τμμδ== 又因等速运动,惯性力为零。
根据牛顿第二定律:0m ==∑F a ,即:gsin 0m S θτ-⋅=()324gsin 59.8sin 301100.1021N s m 1406010m U S θδμ--⋅⨯⨯⨯⨯==≈⋅⋅⨯⨯⨯ 例题2:如图所示,转轴的直径d =0.36 m 、轴承的长度l =1 m ,轴与轴承的缝隙宽度δ=0.23 mm ,缝隙中充满动力粘性系数0.73Pa s μ=⋅的油,若轴的转速200rpm n =。
求克服油的粘性阻力所消耗的功率。
解:由牛顿内摩擦定律,轴与轴承之间的剪切应力()60d d n d uy πτμμδ==粘性阻力(摩擦力):F S dl ττπ=⋅= 克服油的粘性阻力所消耗的功率:()()3223223230230603.140.360.732001600.231050938.83(W)d d n d n n lP M F dl πππμωτπδ-==⋅⋅=⨯⨯=⨯⨯⨯=⨯⨯=例题3:如图所示,直径为d 的两个圆盘相互平行,间隙中的液体动力黏度系数为μ,若下盘固定不动,上盘以恒定角速度ω旋转,此时所需力矩为T ,求间隙厚度δ的表达式。
解:根据牛顿黏性定律 d d 2d r r F A r r ωωμμπδδ== 2d d 2d r T F r r r ωμπδ=⋅=42420d d 232dd d T T r r πμωπμωδδ===⎰432d Tπμωδ=例题4:如图所示的双U 型管,用来测定比水小的液体的密度,试用液柱高差来确定未知液体的密度ρ(取管中水的密度ρ水=1000 kg/m 3)。
流体力学例题(动力学部分)

1000
q
49 7 m / s
d 2
4
v2
0 .12
4
7 55 10
3
m /s
3
2
6.一个100N的重物恰被一垂直水射 流所支承,其中d=6cm,出口速度 v=8m/s,不计沿程损失,求Y=? 解:水流接触重物后动量发生了变化
Fiy q ( 2 v y 2 1 v y 1 )
Fiy 100 N q v y2
d 2
4 0
v
0 . 06 2
z1 z 2 z
v2 q2
v1
q1
由伯努利方程: v1 v 2 v
v1 q1
令: 1 由动量方程:
v
A
F i 0 q1v q 2 v qv cos
q1 q 2 q cos v 2 q2 由连续性方程:q1 q 2 q
2 gH v
令: 2 1 1
带入动量方程: F q ( 2 v z 2 1v z1 )
F av ( v a A 2 gH v )
2
水流对水桶的作用为-F
W W 0 F W 0 av ( v a A 2 gH v )
4
8 0 . 0226 m / s
3
令: 2 1 1
则:
v y1
F
q
100 1000 0 . 0226
4 . 42 m / s
由出口和重物底面的伯努利方程:
z1 p
g
v1
流体力学例题
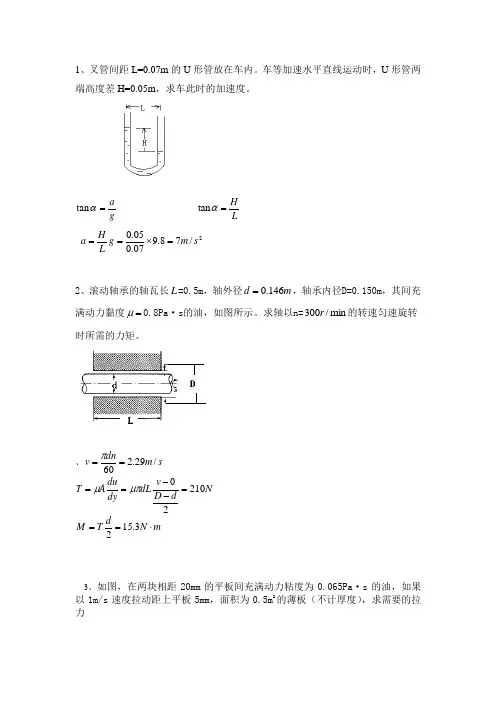
1、叉管间距L=0.07m 的U 形管放在车内。
车等加速水平直线运动时,U 形管两端高度差H=0.05m ,求车此时的加速度。
g a =αtan LH =αtan 2/78.907.005.0s m g L H a =⨯==2、滚动轴承的轴瓦长L =0.5m ,轴外径m d 146.0=,轴承内径D=0.150m ,其间充满动力黏度=μ0.8Pa ·s 的油,如图所示。
求轴以n=min /300r 的转速匀速旋转时所需的力矩。
、s m dnv /29.260==πN d D v dL dydu A T 2102=--==μπμm N dT M ⋅==3.1523、如图,在两块相距20mm 的平板间充满动力粘度为0.065Pa ·s 的油,如果以1m/s 速度拉动距上平板5mm ,面积为0.5m 2的薄板(不计厚度),求需要的拉力dy du AT μ= N huA dy du AT 5.61===μμ N hH u A dy du AT 17.22=-==μμ N T T T 67.821=+=4、用复式U 形管差压计测量A 、B 两点的压力差。
已知:mm h 3001=,mm h 5002=。
水31000m kg =ρ,水银内313600m kg m =ρ,3800m kg ='ρ。
求B A p p -。
A B p h h h g gh h h p =+∆++'-∆-)(211ρρρPa p p B A 32144-=-5、有一敞口容器,长=L 2米,高=H 1.5米,等加速水平直线运动,求当水深h 分别为1.3米和0.5米时,使容器中的液体开始溢出的最大加速度。
g a =αtan L h H )(2tan -=α 2/96.1)(2s m g Lh H a =-= xH hL 21=34=x x H g a ==αtan s m g a /11892==6、有一敞口容器,长2米,高1.3 米,宽B=1m ,等加速水平直线运动,水深0.5米。
流体力学例题ppt课件

F2p 1 hc Bo sv1 2h B 2co s3 2 2 7
【例题5】在水箱水面下H=3m处装有一个收缩 -扩张形的文丘里管嘴,其喉部直径d1=4cm, 喉部绝对压强为24.5kPa,大气压强为101.3kPa。 渐扩部分的损失假定是从d1突扩到d2时所产生 损失的20%,收缩部分的阻力可以不计,其他
已知:斜激波表(k=1.4)为:
【解】可以知道,气流在三角翼头部处将产生斜
激波。经过斜激波后,气流的参数如下变化: 由波前马赫数M1=4及气流偏转角 5 ,查表
得到气流的激波角 、对应的波后1:
17.26 ,M2=3.709,p2 p11.476
vh 5.8(cm)
ve
【例题6】在汽油发动机吸气过程中,如图所示的汽 化器喉部绝对压力为p=88kPa,已知喉部截面面积 A=4cm2,环境温度T0=27oC,环境压强为p0=105Pa, 试按不可压缩以及等熵绝热可压缩两种情况计算: (1)喉部空气速度; (2)发动机进口的质量流量。
[解]从外部大气中,引 一条流线至汽化器的喉 道。
故F=149.45N。
【例题4】混流器的横断面如图所示,两股水分别从 左边两口流入。混合后经右边流出。任何横断面 的流动情况与图示断面相同。
已知入口高度为h,入口夹角为θ ,水的密 度口为处平ρ 均,速混度流为器宽v1。度为B,入口处的表压为p1,入 出口处压力为大气压,
出口处的速度如图: 在中心两侧各为h的
所以,波后气流的静压为:p2=29.52kPa,总压
为
p2* p2121M221 =3017.52kPa。
因为波后仍然是超音速的,因此在翼弦最高点处,
将产生膨胀波。由于后翼面BC段的马赫数为4.45。
流体力学例题与解答

0.6 pa V22 H 00 0 g 2g
当阀门关闭时,根据压强计的读数,应用流体静力学基本
12
方程求出H值
2.8 pa 2.8 98060 28(mH2 O) 代入到上式 H g 9806
0.6 p a 0.6 98060 V2 2 g H 2 9 . 806 2 . 8 20.78 (m/s) g 9806
18
(3)将流段AB作为隔离体取出,规定 坐标正方向,假定弯管 反力 Rx 和 R y 的方向,写 x 和 y 两个坐标方向的动量方 程: Fx Q(VBx VAx ) Fy Q(VBy VAy ) 代入题中的外力和流速 ,注意力和流速的正负 性
2 2 p A d A pB d B cos Rx Q(VB cos VA ) 4 4 2 pB d B sin R y Q(VB sin 0) 4 代入已知数据可求得 Rx 0.538 KN , R y 0.598 KN
2
p
5
p4 (5 4 )
【例】 如图所示测量装置,活塞直径d=35㎜,油的相 对密度d油=0.92 ,水银的相对密度dHg=13.6,活塞与缸壁无 泄漏和摩擦。当活塞重为15N时,h=700㎜,试计算U形管 测压计的液面高差Δh值。 【解】 重力使活塞单位面积上承受的压强为
水
水
Fz1 gV1
1 98001 4 2 2 4 61500 N
9
合力
2 F1 Fx2 F 1 z1
78400 2 61500 2
99640 N
作用线通过中心与铅垂线成角度 1 。 右部:
流体力学例题大全
第一章:绪论例1-1 200 ºC体积为的2.5m3水,当温度升至800ºC时,其体积增加多少?解: 200 ºC时:ρ1=998.23kg/m3 800CºC时:ρ2=971.83kg/m3即:则:例1-2使水的体积减小0.1%及1%时,应增大压强各为多少?(K=2000MPa)d V/V =-0.1%=-2000×106×(-0.1%)=2×106Pa=2.0MPad V /V = -1%= -2000×106×(-1%)=20 MPa例1-3输水管l=200m,直径d=400mm,作水压试验。
使管中压强达到55at后停止加压,经历1小时,管中压强降到50at。
如不计管道变形,问在上述情况下,经管道漏缝流出的水量平均每秒是多少?水的体积压缩率κ =4.83×10-10m2 /N 。
解水经管道漏缝泄出后,管中压强下降,于是水体膨胀,其膨胀的水体积水体膨胀量5.95 l 即为经管道漏缝流出的水量,这是在1小时内流出的。
设经管道漏缝平均每秒流出的水体积以Q 表示,则例1-4:试绘制平板间液体的流速分布图与切应力分布图。
设平板间的液体流动为层流,且流速按直线分布,如图1-3所示。
解:设液层分界面上的流速为u,则:切应力分布:图1-3上层下层:在液层分界面上:--流速分布:上层:下层:例1-5:一底面积为40 ×45cm2,高为1cm的木块,质量为5kg,沿着涂有润滑油的斜面向下作等速运动,如图1-4所示,已知木块运动速度u =1m/s,油层厚度d =1mm,由木块所带动的油层的运动速度呈直线分布,求油的粘度。
解:∵等速∴αs =0由牛顿定律:∑F s=mαs=0m gsinθ-τ·A=0(呈直线分布)图1-4∵ θ=tan-1(5/12)=22.62°例1-6: 直径10cm的圆盘,由轴带动在一平台上旋转,圆盘与平台间充有厚度δ=1.5mm的油膜相隔,当圆盘以n =50r/min旋转时,测得扭矩M =2.94×10-4 N·m。
流体力学典型例题
典 型 例 题 1 基本概念及方程【1-1】底面积A =0.2m ×0.2m 的水容器,水面上有一块无重密封盖板,板上面放置一个重量为G 1=3000N 的铁块,测得水深h =0.5m ,如图所示。
如果将铁块加重为G 2=8000N ,试求盖板下降的高度Δh 。
【解】:利用体积弹性系数计算体积压缩率:E p v v //∆=∆ )/(00B p p np E +=p 为绝对压强。
当地大气压未知,用标准大气压 Pa p 501001325.1⨯=代替。
Pa A G p p 51011076325.1/⨯=+= Pa A G p p 52021001325.3/⨯=+=因 01/p p 和 02/p p 不是很大,可选用其中任何一个,例如,选用 02/p p 来计算体积弹性系数:Pa B p p np E 9020101299.2)/(⨯=+=在工程实际中,当压强不太高时,可取 Pa E 9101.2⨯=512104827.6/)(///-⨯=-=∆=∆=∆E p p E p v v h h m h h 55102413.310604827--⨯=⨯=∆【2-2】用如图所示的气压式液面计测量封闭油箱中液面高程h 。
打开阀门1,调整压缩空气的压强,使气泡开始在油箱中逸出,记下U 形水银压差计的读数Δh 1=150mm ,然后关闭阀门1,打开阀门2,同样操作,测得Δh 2=210mm 。
已知a =1m ,求深度h 及油的密度ρ。
【解】水银密度记为ρ1。
打开阀门1时,设压缩空气压强为p 1,考虑水银压差计两边液面的压差,以及油箱液面和排气口的压差,有同样,打开阀门2时,两式相减并化简得代入已知数据,得所以有2 基本概念及参数【1-3】测压管用玻璃管制成。
水的表面张力系数σ=m,接触角θ=8º,如果要求毛细水柱高度不超过5mm,玻璃管的内径应为多少【解】由于因此【1-4】高速水流的压强很低,水容易汽化成气泡,对水工建筑物产生气蚀。
流体力学流体动力学基础例题
5
2024/10/12
6
【例】 有一贮水装置如图所示,贮水池足够大,当阀 门关闭时,压强计读数为2.8个大气压强。而当将阀门全 开,水从管中流出时,压强计读数是0.6个大气压强,试 求当水管直径d=12cm时,通过出口的体积流量(不计流动 损失)。
【解】 当阀门全开时列1-l、2-2截面的伯努利方程
当阀门关闭时,根据压强计的读数,应用流体静力学基本
试求管中流量qv。
【解】 首先计算1-1断面管路中心的压强。因为A-B为
等压面,列等压面方程得: Hg gh p1 gh1
p1 Hg gh gh1
则
p1
g
Hg
h h1
13.6 0.2 0.72 2
(mH2O)
列1-1和2-2断面的伯努利方程
z1
p1
g
V12 2g
z2
p2
g
V22 2g
H pa 0 0 pa 0.6 pa V22
g
g
2g
2024/10/12
1
方程求出H值
pa gH pa 2.8 pa则H 2.8 pa
g
2.8 98060 9806
28(mH 2O)
代入到上式
V2
2g
H
0.6 pa g
29.8062.8 0.698060 20.78(m/s)
9806
所以管内流量
qV
4
d
2V2
0.785 0.122 20.78 0.235(m3/s)
2024/10/12
2
2024/10/12
3
【例】 水流通过如图所示管路流入大气,已知:U形
测压管中水银柱高差Δh=0.2m,h1=0.72m H2O,管径
流体力学 课堂例题
课堂例题第一章例1 使水的体积减小0.1%及1%时,应增大压强各为多少?(K =2000MPa )解: d V /V =-0.1%∆p =-2000×106×(-0.1%)=2×106Pa=2.0Mpad V /V = -1%∆p = -2000×106×(-1%)=20 Mpa例2 一平板距离另一固定平板0.5mm ,两板间充满液体,上板在每平方米上有2N 的力作用下以0.25m/s 的速度移动,求该流体的粘度?解: 第二章例1:测压装置。
A 中p e =2.45×104Pa, h=500mm,h 1=200mm, h 2=100mm, h 3=300mm, ρ2=800kg/m3,求B 中气体表压。
解:1、2、3、4四个等压面,1点忽略气体密度,得例2 求斜壁圆形闸门的总压力,已知d=0.5m,a=1m,α=60°解:由式 得总压力V dV dp K -=V dV K dp -=∴h U A F μ=0005.025.02μ=)(004.0s Pa ⋅=μ)(111h h g p p e e ++=ρ13111312)(gh h h g p gh p p e e e ρρρ-++=-=2213112223)(gh gh h h g p gh p p e e e ρρρρ+-++=+=332213113334)(gh gh gh h h g p gh p p e e e ρρρρρ-+-++=-=Pap p e Be 345384-==Ap A gh F ce c p ==ρ)(20834sin )2(2N d d a g F p =+=παρ例3:圆柱扇形闸门,已知H=5m,闸门宽B=10m,α=60°。
求曲面ab 上总压力解: 总压力大小和方向为第三章例1离心水泵吸水装置,d=200mm,q V =170m 3/h,泵入口前真空为330mmHg,如不计能量损失,求水泵的吸水高度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p 为绝对压强。
E np0 ( p / p0 B)
当地大气压未知,用标准大气压 p0 1.01325 10 5 Pa 代替。
p1 p0 G1 / A 1.76325 10 5 Pa p2 p0 G2 / A 3.01325 10 5 Pa
因 p1 / p0 和 p2 / p0 不是很大,可选用其中任何一个,例如,选用 p2 / p0 来计算体积弹
还可以算得大、小气泡的压强分布为
,
。
【1-5】一重 W=500N 的飞轮,其回转半径ρ=30cm,由于轴套间流体粘性的影响,当飞 轮以速度 ω=600 转/分旋转时,它的减速度 ε=0.02m/s2。已知轴套长 L=5cm,轴的直径
d=2cm,其间隙 t=0.05mm,求流体粘度。 【解】:由物理学中的转动定律知,造成飞轮减速的力矩 M=Jε,飞轮的转动惯量 J
【2-4】如图所示,圆形闸门的半径 R=0.1m,倾角α=45o,上端有铰轴,已知 H1=5m, H2=1m,不计闸门自重,求开启闸门所需的提升力 T。 【解】设 y 轴沿板面朝下,从铰轴起算。在闸门任一点,左侧受上游水位的压强 p1,右侧 受下游水位的压强 p2,其计算式为
平板上每一点的压强 p1-p2 是常数,合力为(p1-p2)A,作用点在圆心上,因此 代入已知数据,求得 T=871.34N。
【解】活塞盖具有重量,系统没有旋转时,盖子处在一个平衡位置。旋转时,盖子下降,竖 管液面上升。 设系统静止时,活塞盖如实线所示,其高度为 h1,竖管的液面高度设为 H1。此时,液体总 压力等于盖子重量,设为 G: 旋转时,活塞盖下降高度为 h,两支竖管的液面上升高度为 H。 液体压强分布的通式为 将坐标原点放在活塞盖下表面的中心,并根据竖管的液面参数确定上式的积分常数 C。当 r =R,z=H1-h1+H + h 时,p=pa, 因此,液体压强分布为 旋转时,液体压力、大气压力的合力应等于盖子重量, 即 因盖子下表面的相对压强为 代入 G 式并进行积分,得到
不妨设竖管中较低的液面到转盘的高度差为 h。现根据液面边界条件进行计算。 当 r=R1,z=h 及 r=R2,z=h+Δh 时
; 两式相减得
所以
【2-10】航标灯可用如图所示模型表示:灯座是一个浮 在水面的均质圆柱体,高度 H=0.5m,底半径 R=0.6m, 自重 G=1500N,航灯重 W=500N,用竖杆架在灯座上, 高度设为 z。若要求浮体稳定,z 的最大值应为多少? 【解】浮体稳定时要求倾半径 r 大于偏心距 e,即 r>e 先求定倾半径 r=J/V,浮体所排开的水的体积 V 可根据吃水深度 h 计算。
教育资料
.
将
,
,
代入,得
所以有:
在点(0,1)处, ,
算得 ,
【3-2】验证下列速度分布满足不可压缩流体的连续性方程: (1)
, (2)
,
(3)
,
【解】: (1)
,
,
(2)
(3)从速度分布的表达式看出,用极坐标比较方便。当然,使用直角坐标也可以进行有关 计算,但求导过程较为复杂。
,
【3-3】已知平面流场的速度分布为
【2-5】盛水容器底部有一个半径 r=2.5cm 的圆形孔口,该孔口用半径 R=4cm、自重 G =2.452N 的圆球封闭,如图所示。已知水深 H=20cm,试求升起球体所需的拉力 T。 【解】用压力体求铅直方向的静水总压力 Fz:
由于
,
因此
,
,
教育资料
.
,
【2-6】如图所示的挡水弧形闸门,已知 R=2m,θ=30o,h=5m,试求单位宽度所受到 的静水总压力的大小。 【解】水平方向的总压力等于面 EB 上的水压力。铅直方向的总压力对应的压力体为 CABEDC 。
利用连续方程,由上式得
教育资料
.
此外细管有液柱上升,说明 p1 低于大气压,即 式中,ρˊ是水的密度,因此
.
典型例题 1 基本概念及方程 【1-1】底面积 A=0.2m×0.2m 的水容器,水面上有一块无重密封盖板,板上面放置一个 重量为 G1=3000N 的铁块,测得水深 h=0.5m,如图所示。如果将铁块加重为 G2=8000N, 试求盖板下降的高度Δh。 【解】:利用体积弹性系数计算体积压缩率:
v / v p / E
教育资料
.
代入上式,化简得
由图中看出,活塞盖挤走的液体都进入两支竖管,因此
所以有
【2-9】如图所示,U 形管角速度测量仪,两竖管距离旋转轴为 R1 和 R2,其液面高差为Δh, 试求ω的表达式。如果 R1=0.08m,R2=0.20m,Δh=0.06m,求ω的值。 【解】两竖管的液面的压强都是 pa(当地大气压),因而它们都在同一等压面上,如图虚线 所示。设液面方程为
,
, 试求 t=1 时经过坐标原点的流线方程。
【解】对于固定时刻 to,流线的微分方程为
教育资料
.
积分得
这就是时刻 to 的流线方程的一般形式。 根据题意,to=1 时,x=0,y=0,因此 C=2
【3-4】如图所示的装置测量油管中某点的速度。已知油的密度为ρ =800kg/m3,水银密度为ρ’=13600 kg/m3,水银压差计的读数Δh =60mm,求该点的流速 u。 【解】我们分析管流中的一条流至测压管管口的流线,即如图中的流线 1-0。这条流线从 上游远处到达“L”形管口后发生弯曲,然后绕过管口,沿管壁面延伸至下游。流体沿这条流 线运动时,速度是发生变化的。在管口上游远处,流速为 u。当流体靠近管口时,流速逐渐 变小,在管口处的点 0,速度变为 0,压强为 po,流体在管口的速度虽然变化为 0,但流体 质点并不是停止不动,在压差作用下,流体从点 0 开始作加速运动,速度逐渐增大,绕过管 口之后,速度逐渐加大至 u。 综上分析,可以看到,流体沿流线运动,在点 1,速度为 u,压强为 p,在点 0,速度为 0, 压强为 po,忽略重力影响,沿流线的伯努利方程是
压力机柱塞上的总压力 静压力作用在密封圈上的总压力为 p∏Dh ,方向与柱塞垂直。所以密封圈上的摩擦力
故压力机对重物的压力为
4 流体运动的基本概念及方程 【3-1】已知平面流动的速度分布为
, 试计算点(0,1)处的加速度。 【解】先将极坐标的速度分量换算成直角坐标的速度,然后再求直角坐标中的加速度。
由此可见,只要测出压差为 po-p,就可以求出速度 u。 不妨设压差计的右侧水银面与流线的高差为 l。由于流线平直,其曲率半径很大,属缓变流, 沿管截面压强的变化服从静压公式,因此,
式中,ρ和ρˊ分别是油和水银的密度。将已知数据代入计算,Δh 的单位应该是用 m 表示, Δh=0.06m,得速度为 u=4.3391m/s。 【3-5】矿山排风管将井下废气派入大气。为了测量排风的流量,在排风管出口处装有一 个收缩、扩张的管嘴,其喉部处装有一个细管,下端插入水中,如图所示。喉部流速大,压 强低,细管中出现一段水柱。已知空气密度 ρ=1.25kg/m3,管径 d1=400mm,d2=600mm, 水柱 h=45mm,试计算体积流量 Q。 【解】截面 1-1 的管径小,速度大,压强低;截面 2-2 接触大气,可应用伯努利方程, 即
性系数:
E np0 ( p2 / p0 B) 2.1299 10 9 Pa 在工程实际中,当压强不太高时,可取 E 2.1109 Pa
h / h v / v p / E ( p2 p1) / E 6.4827 10 5 h 604827105 h 3.2413105 m
【2-2】用如图所示的气压式液面计测量封闭油箱中液面高程 h。打开阀门 1,调整压缩空 气的压强,使气泡开始在油箱中逸出,记下 U 形水银压差计的读数Δh1=150mm,然后关闭 阀门 1,打开阀门 2,同样操作,测得Δh2=210mm。已知 a=1m,求深度 h 及油的密度ρ。 【解】水银密度记为ρ1。打开阀门 1 时,设压缩空气压强为 p1,考虑水银压差计两边液面的 压差,以及油箱液面和排气口的压差,有
所以力矩 另一方面,从摩擦阻力 F 的等效力系看,造成飞轮减速的力矩为:
为线性分布。 则
摩擦阻力矩应等于 M,即 T=M 即
教育资料
.
所以 3 流体静力学 【2-1】试求解图中同高程的两条输水管道的压强差 p1-p2,已知液面高程读数 z1=18mm, z2=62mm,z3=32mm,z4=53mm,酒精密度为 800kg/m3。 【解】设管轴到水银面 4 的高程差为 ho,水密度为ρ,酒精密度为ρ1,水银密度为ρ2,则
同样,打开阀门 2 时,
两式相减并化简得
代入已知数据,得
所以有
2 基本概念及参数 【1-3】测压管用玻璃管制 成。水的表面张力系数σ= 0.0728N/m,接触角θ=8º,如 果要求毛细水柱高度不超过 5mm,玻育资料
.
【1-4】高速水流的压强很低,水容易汽化成气泡,对水工建筑物产生气蚀。拟将小气泡 合并在一起,减少气泡的危害。现将 10 个半径 R1=0.1mm 的气泡合成一个较大的气泡。已 知气泡周围的水压强 po=6000Pa,水的表面张力系数σ=0.072N/m。试求合成后的气泡半 径 R。 【解】小泡和大泡满足的拉普拉斯方程分别是
【2-7】如图所示,底面积为 b×b=0.2m×0.2m 的方口容器,自重 G=40N,静止时装水高 度 h=0.15m,设容器在荷重 W=200N 的作用下沿平面滑动,容器底与平面之间的摩擦系 数 f=0.3,试求保证水不能溢出的容器的最小高度。 【解】解题的关键在于求出加速度 a。如果已知加速度,就可以确定容器里水面的斜率。 考虑水、容器和重物的运动。系统的质量 M 和外力分别为
将 z 的单位换成 m,代入数据,得
【2-2】用如图所示的气压式液面计测量封闭油箱中液面高程 h。打开阀门 1,调整压缩空 气的压强,使气泡开始在油箱中逸出,记下 U 形水银压差计的读数Δh1=150mm,然后关闭 阀门 1,打开阀门 2,同样操作,测得Δh2=210mm。已知 a=1m,求深度 h 及油的密度ρ。 【解】水银密度记为ρ1。打开阀门 1 时,设压缩空气压强为 p1,考虑水银压差计两边液面的 压差,以及油箱液面和排气口的压差,有 同样,打开阀门 2 时, 两式相减并化简得 代入已知数据,得 所以有
