高中数学必修一全册图文
合集下载
人教A版(2019)高中数学选择性必修第一册课件(共50张PPT)

知 2.掌握空间直角坐标系中点的 的核心素养.
养
合
作 坐标的确定.(重点)
探
究 释
3.掌握空间向量的坐标表示
疑
难 (重点、难点)
2.通过空间向量的坐标表示,培
课 时
分
养学生直观想象和数学建模的核 层
作
心素养.业Leabharlann 返 首 页·3
·
情
课
景
堂
导
小
学
结
·
探
提
新 知
合
情景
导学
探新
知
素 养
作
课
探
时
究
分
层
释
作
疑
业
课
探
时
究
坐标系 向,以它们的长为单位长度建立三条数轴:x
分
层
释 疑
轴、y轴、z轴,这样就建立了空间直角坐标系
作 业
难
返 首 页
·
7
·
情
坐标轴 _x__轴、_y__轴、_z__轴
课
景
堂
导 学
坐标原点 点_O__
小 结
·
探 新
坐标向量 __i __,__j __,_k___
提 素
知
养
坐标平面 O__xy_平面、O__yz_平面和_O_x_z平面
课
探 究
点坐标 _a_=___(_x,__y_,__z_)_
时 分
层
释
作
疑
业
难
返 首 页
·
10
·
情
课
景 导
1.思考辨析(正确的打“√”,错误的打“×”)
人教版高中数学必修一章节思维导图全套
质》思维导图
《3.3 幂函数》思维导图
《4.1 指数的运算》思维导图
《4.2指数函数》思维导图
《4.3 对数的运算》思维导图
《4.4 对数函数》思维导图
《4.5 函数的应用(二)》思维导图
《5.1 任意角和弧度制》思维导图
《5.2 三角函数的概念》思维导图
《5.3 诱导公式》思维导图
《5.4 三角函数的图象与性质》思维导图
《5.5 三角恒等变换》思维导图
《5.6 函数 》思维导图
《5.7 三角函数的应用》思维导图
人教版高中数学必修一章节思维导图全套11集合的概念及特征思维导图12集合间的关系思维导图13集合的基本运算思维导图14充分必要条件思维导图15全称量词与存在量词思维导图21等式与不等式的性质思维导图22基本不等式思维导图23二次函数与一元二次方程不等式思维导图31函数的概念思维导图32函数的性质思维导图33幂函数思维导图41指数的运算思维导图42指数函数思维导图43对数的运算思维导图44对数函数思维导图45函数的应用二思维导图51任意角和弧度制思维导图52三角函数的概念思维导图53诱导公式思维导图54三角函数的图象与性质思维导图55三角恒等变换思维导图56函数思维导图57三角函数的应用思维导图
人教版高中数学必修一章节思维导图全套
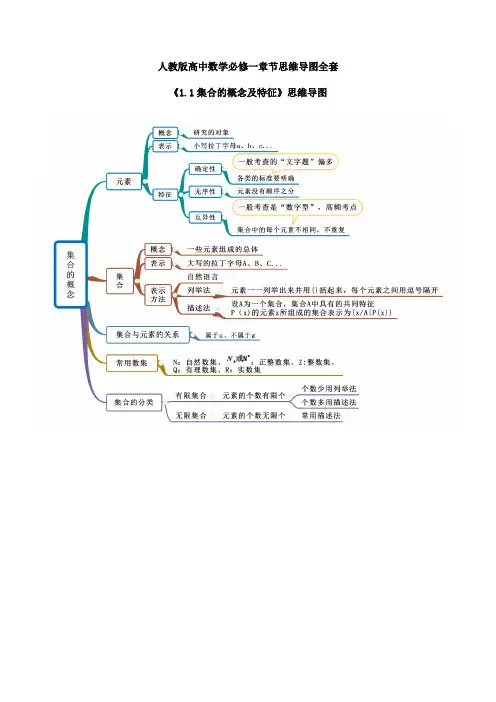
《1.1集合的概念及特征》思维导图
《1.2 集合间的关系》思维导图
《1.3 集合的基本运算》思维导图
《1.4 充分、必要条件》思维导图
《1.5 全称量词与存在量词》思维导图
《2.1 等式与不等式的性质》思维导图
《2.2 基本不等式》思维导图
《2.3 二次函数与一元二次方程、不等式》思维导图
《3.3 幂函数》思维导图
《4.1 指数的运算》思维导图
《4.2指数函数》思维导图
《4.3 对数的运算》思维导图
《4.4 对数函数》思维导图
《4.5 函数的应用(二)》思维导图
《5.1 任意角和弧度制》思维导图
《5.2 三角函数的概念》思维导图
《5.3 诱导公式》思维导图
《5.4 三角函数的图象与性质》思维导图
《5.5 三角恒等变换》思维导图
《5.6 函数 》思维导图
《5.7 三角函数的应用》思维导图
人教版高中数学必修一章节思维导图全套11集合的概念及特征思维导图12集合间的关系思维导图13集合的基本运算思维导图14充分必要条件思维导图15全称量词与存在量词思维导图21等式与不等式的性质思维导图22基本不等式思维导图23二次函数与一元二次方程不等式思维导图31函数的概念思维导图32函数的性质思维导图33幂函数思维导图41指数的运算思维导图42指数函数思维导图43对数的运算思维导图44对数函数思维导图45函数的应用二思维导图51任意角和弧度制思维导图52三角函数的概念思维导图53诱导公式思维导图54三角函数的图象与性质思维导图55三角恒等变换思维导图56函数思维导图57三角函数的应用思维导图
人教版高中数学必修一章节思维导图全套
《1.1集合的概念及特征》思维导图
《1.2 集合间的关系》思维导图
《1.3 集合的基本运算》思维导图
《1.4 充分、必要条件》思维导图
《1.5 全称量词与存在量词》思维导图
《2.1 等式与不等式的性质》思维导图
《2.2 基本不等式》思维导图
《2.3 二次函数与一元二次方程、不等式》思维导图
(共34套)人教版高中数学必修一(全册)配套教学课件汇总

二、数学为什么难学? 1.高度的抽象性 2.严密的逻辑性 3.应用的广泛性
三、高中学哪些数学?
1.必修课程:5个模块
2.选修课程:4个系列 系列1:2个模块(文科选修) 系列2:3个模块(理科选修) 系列3:6个专题(自主选修) 系列4:10个专题(自主选修)
四、高中数学要获多少学分?
文科学生:必修课程(10个学分); 选修系列1(4个学分); 选修系列3(2个学分); 共16个学分.
六、对数学学习有什么要求? 1.专注认真; 2.勤思多练; 3.常做笔记; 4.规范作业; 5.加强交流; 6.反思评价.
老师寄语 :
是花就要绽放,是树就要撑出绿荫,是 水手就要博击风浪,是雄鹰就要展翅飞翔。
很难说什么事情是难以办到的,昨天的 梦想就是今天的希望和明天的现实。我们要 以坚定的信心托起昨天的梦想,以顽强的斗 志,耕耘今天的希望,那我们一定能用我们 的智慧和汗水书写明天的辉煌。
高一年级 数学 第一章 1.1.1集合的含义与表示
课题: 集合的表示
问题提出
1.集合中的元素有哪些特征?确定性、无序性、互异性
2.元素与集合有哪几种关系? 属于、不属于
3.用自然语言描述一个集合往往是不简明的,如 “在平面直角坐标系中以原点为圆心,2 为半径的圆周 上的点”组成的集合,那么,我们可以用什么方式表示 集合呢?
例4 已知集合A={1,2,3},B={1,2},设集合
C=x | x a b, a A,b B ,试用列举法表示集合C.
C={-1,0,1,2}
高一年级 数学 第一章 1.1.1集合的含义与表示
课题: 集合的含义
问题提出
“集合”是日常生活中的一个常用词,现代汉语解释为: 许多的人或物聚在一起.
新人教版高中数学选择性必修第一册全套精品课件

·
情
课
景
堂
导
小
学
解答空间向量有关概念问题的关键点及注意点
结
·
探
提
新 知
(1)关键点:紧紧抓住向量的两个要素,即大小和方向.
素 养
合
(2)注意点:注意一些特殊向量的特性.
作
课
探 究
①零向量不是没有方向,而是它的方向是任意的,且与任何向
时 分
层
释 疑
量都共线,这一点说明了共线向量不具备传递性.
作 业
难
返 首 页
小 结
·
探
提
新
(2)√ 相等向量一定共线,但共线不一定相等.
素
知
养
(3)× 空间两个向量一定是共面向量,但三个空间向量可能是
合
作
课
探 共面的,也可以是不共面的.
时
究
分
层
释
(4)× 零向量有方向,它的方向是任意的.
作
疑
业
难
返 首 页
·
19
情
2.如图所示,在四棱柱 ABCD-A1B1C1D1 所有的棱中,可作为直 课
情
课
景
堂
导 学
B
[根据向量的定义,知长度相等、方向相同的两个向量是相等
小 结
·
探
提
新 向量,①正确;平行且模相等的两个向量可能是相等向量,也可能是 素
知
养
相反向量,②不正确;当 a=-b 时,也有|a|=|b|,③不正确;只要
合
作
课
探 模相等、方向相同,两个向量就是相等向量,与向量的起点与终点无 时
景
堂
导 学
高中数学新课标人教A版必修一:1.2.1 函数的概念 课件 (共16张PPT)

3 两个函数相同:当且仅当三要素相同。
例1 y= x 3 + 2 x 是函数吗?
——函数的定义域和值域均为非空的数集
例2 y=± x 是函数吗?
——对于函数定义域中每一个x,值域中都有 唯一确定的y和它对应。(不是函数)
练习:下列图形哪个可以表示函数的图象?
y
0x
A
y
0x
B
y
0x
C
四、如何求函数的定义域
想 f(1)表示什么意思? 一 想 f(1)与f(x)有什么区别?
一般地,f(a)表示当x=a时的函数值,是一个常量。 f(x)表示自变量x的函数,一般情况下是变量。 14
例:已知函数f(x)=3x2-5x+2.求f(0),f(a)和 f(a+1)
想一想 f[f(0)]等于多少?
练习:f(x)=|x+1|,则f(-1) +f(1)等于多少?
六、小结
1 函数的概念
2 定义域的求法 3 对函数符号y=f(x)的理解
七、布置作业
一、复习回顾
初中时学过函数的概念,它是怎样叙述的? 设在一个变化过程中,有两个变量x和y,
如果对于x的每一个值,y都有唯一的值与 它对应.那么就说y是x的函数. 其中x叫做 自变量,y是函数值。
想一想
y=1(x∈R)是函数吗?
Go to 13
研究函数y 1 x
为了研究的方便,取几组特殊的x值和对应的y值
当x=1时,y=1
当x=2时,y
1 2
当xБайду номын сангаас3时,y 1
3
A
B
y1
x
1
1
1
2
2
人教A版数学必修第一册【高清教材】

获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
获取更多精品资料,关注微信公众号"Hi数学派"
人教版A版高中数学必修一配套全册完整课件
答案
3.设集合 A={x|x≤ 13},a= 11,那么( D )
A.a A
B.a∉A
C.{a}∈A
D.{a} A
1 23 45
答案
1 23 45
4.设全集I={a,b,c,d,e},集合M={a,b,c},N={b,d,e},
那么(∁IM)∩(∁IN)等于( A ) A.∅
B.{d}
C.{b,e}
反思与感悟
解析答案
跟踪训练4 学校举办了排球赛,某班45名同学中有12名同学参赛,后 来又举办了田径赛,这个班有20名同学参赛,已知两项都参赛的有6名 同学,两项比赛中,这个班共有多少名同学没有参加过比赛? 解 设A={x|x为参加排球赛的同学},B={x|x为参加田径赛的同学}, 则A∩B={x|x为参加两项比赛的同学}.画出Venn图(如图),
第一章 集合与函数概念
习题课
集合
学习目标
1.系统和深化对集合基础知识的理解与掌握; 2.重点掌握好集合间的关系与集合的基本运算.
问题导学
题型探究
达标检测
问题导学
新知探究 点点落实
1.集合元素的三个特性:_确__定__性___,_互__异__性___,__无__序__性__. 2.元素与集合有且只有两种关系:__∈______,__∉______. 3. 已 经 学 过 的 集 合 表 示 方 法 有 _列__举__法___ , _描__述__法___ , _V_e_n_n_图___ , _常__用__数__集__字__母__代__号___.
返回
第一章 集合与函数概念
章末复习课
学习目标
1.构建知识网络,理解其内在联系; 2.盘点重要技能,提炼操作要点; 3.体会数学思想,培养严谨灵活的思维能力.
3.设集合 A={x|x≤ 13},a= 11,那么( D )
A.a A
B.a∉A
C.{a}∈A
D.{a} A
1 23 45
答案
1 23 45
4.设全集I={a,b,c,d,e},集合M={a,b,c},N={b,d,e},
那么(∁IM)∩(∁IN)等于( A ) A.∅
B.{d}
C.{b,e}
反思与感悟
解析答案
跟踪训练4 学校举办了排球赛,某班45名同学中有12名同学参赛,后 来又举办了田径赛,这个班有20名同学参赛,已知两项都参赛的有6名 同学,两项比赛中,这个班共有多少名同学没有参加过比赛? 解 设A={x|x为参加排球赛的同学},B={x|x为参加田径赛的同学}, 则A∩B={x|x为参加两项比赛的同学}.画出Venn图(如图),
第一章 集合与函数概念
习题课
集合
学习目标
1.系统和深化对集合基础知识的理解与掌握; 2.重点掌握好集合间的关系与集合的基本运算.
问题导学
题型探究
达标检测
问题导学
新知探究 点点落实
1.集合元素的三个特性:_确__定__性___,_互__异__性___,__无__序__性__. 2.元素与集合有且只有两种关系:__∈______,__∉______. 3. 已 经 学 过 的 集 合 表 示 方 法 有 _列__举__法___ , _描__述__法___ , _V_e_n_n_图___ , _常__用__数__集__字__母__代__号___.
返回
第一章 集合与函数概念
章末复习课
学习目标
1.构建知识网络,理解其内在联系; 2.盘点重要技能,提炼操作要点; 3.体会数学思想,培养严谨灵活的思维能力.
高中数学人教A版必修第一册第一章集合的含义课件
1867年在库默尔指导下以数论方面的论文获博士学位。1869年在哈雷大学通过讲师资格考 试,后即在该大学任讲师,1872年任副教授,1879年任教授。
大学期间康托尔主修数论,但受外尔斯特拉斯的影响,对数学推导的严格性和数学分析感兴趣。
哈雷大学教授H.E.海涅鼓励他研究函数论。他于1870、1871、1872年发表三篇关于三角级数 的论文。在1872年的论文中提出了以基本序列(即柯西序列)定义无理数的实数理论, 并初步提出以高阶导出集的性质作为对无穷集合的分类准则。函数论研究引起他进一 步探索无穷集和超穷序数的兴趣和要求。
① 高一级身高较高的同学,能否构成集合?
否
② 高一级身高160cm以上的同学,能否构成集合?
能
①确定性: 集合中的元素必须是确定的。即确定了一个集
合,任何一个元素是不是这个集合的元素也就
确定了。 (具有某种属性)
二、集合中元素的特性
先思考以下两个问题:
集合中的元素是互异的。
① 高一级身高较高的同学,能否构成集合? 1、集合中元素的三个特性:
在整数和实数两个不同的无穷集合之外,是否还有更大的无穷?从1874年初起,康托尔开 始考虑面上的点集和线上的点集有无一一对应。经过三年多的探索,1877
说,“我见到了,但我不相信。”这似乎抹煞了维数的区别。论文于1878年发表后引起了很 大的怀疑。P.D.G.杜布瓦-雷蒙和克罗内克都反对,而戴德金早在1877年7月就看到,不 同维数空间的点可以建立不连续的一一对应关系,而不能有连续的一一对应。此问题直到1910 年才由L.E.J.布劳威尔给出证明。
作 aA ; 如 果 a不 是 集 合 A 的 元 素 , 就 说 a不 属 于 1845年3月3日生于圣彼得堡(今苏联列宁格勒),1918年1月6日病逝于哈雷。
大学期间康托尔主修数论,但受外尔斯特拉斯的影响,对数学推导的严格性和数学分析感兴趣。
哈雷大学教授H.E.海涅鼓励他研究函数论。他于1870、1871、1872年发表三篇关于三角级数 的论文。在1872年的论文中提出了以基本序列(即柯西序列)定义无理数的实数理论, 并初步提出以高阶导出集的性质作为对无穷集合的分类准则。函数论研究引起他进一 步探索无穷集和超穷序数的兴趣和要求。
① 高一级身高较高的同学,能否构成集合?
否
② 高一级身高160cm以上的同学,能否构成集合?
能
①确定性: 集合中的元素必须是确定的。即确定了一个集
合,任何一个元素是不是这个集合的元素也就
确定了。 (具有某种属性)
二、集合中元素的特性
先思考以下两个问题:
集合中的元素是互异的。
① 高一级身高较高的同学,能否构成集合? 1、集合中元素的三个特性:
在整数和实数两个不同的无穷集合之外,是否还有更大的无穷?从1874年初起,康托尔开 始考虑面上的点集和线上的点集有无一一对应。经过三年多的探索,1877
说,“我见到了,但我不相信。”这似乎抹煞了维数的区别。论文于1878年发表后引起了很 大的怀疑。P.D.G.杜布瓦-雷蒙和克罗内克都反对,而戴德金早在1877年7月就看到,不 同维数空间的点可以建立不连续的一一对应关系,而不能有连续的一一对应。此问题直到1910 年才由L.E.J.布劳威尔给出证明。
作 aA ; 如 果 a不 是 集 合 A 的 元 素 , 就 说 a不 属 于 1845年3月3日生于圣彼得堡(今苏联列宁格勒),1918年1月6日病逝于哈雷。
人教版(新教材)高中数学第一册(必修1)优质课件:5.7三角函数的应用
解 (1)由题意可作图如图.过点O作地面平行线ON,过点B作ON的垂线BM交 ON于点M.
当π2<θ≤π 时,∠BOM=θ-π2. h=|OA|+0.8+|BM|=5.6+4.8 sinθ-π2; 当 0≤θ≤π2,π<θ≤2π 时,上述解析式也适合. 则 h 与 θ 间的函数解析式为 h=5.6+4.8sinθ-π2.
解析 设 y=Asin(ωt+φ)(A>0,ω>0),则从表中数据可以得到 A=4,ω=2Tπ =02.π8=52π,又由 4sin φ=-4.0,得 sin φ=-1,取 φ=-π2,则 y=4sin52πt-π2, 即 y=-4cos52πt. 答案 y=-4cos52πt
一、素养落地 1.通过本节课的学习,重点提升学生的数学抽象、数学运算、数学建模素养. 2.三角函数模型构建的步骤:
解 (1)由题图知 A=300,设 t1=-9100,t2=1180,
则周期 T=2(t2-t1)=21180+9100=715. ∴ω=2Tπ=150π. 又当 t=1180时,I=0,即 sin150π·1180+φ=0,而|φ|<π2,∴φ=π6.
故所求的解析式为 I=300sin150πt+π6.
【训练4】 一物体相对于某一固定位置的位移y(cm)和时间t(s)之间的一组
对应值如下表所示,则可近似地描述该物体的位置y和时间t之间的关系的一个
三角函数式为
.
t0
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
y -4.0 -2.8 0.0 2.8 4.0 2.8 0.0 -2.8 -4.0
1φ
(3)简谐运动的频率由公式___f=__T_=__2_π_给出,它是做简谐运动的物体在单位时间内
人教A版高一数学必修一第一章综合复习 PPT课件 图文
必修1 第一章 集合与函数的概念
栏目导引
2.函数及其表示
(1)本节是函数部分的起始部分,以考查函数的概念 、三要素及表示法为主,同时考查实际问题中的建 模能力.
(2)以多种题型出现在高考试题中,要求相对较低, 但很重要.特别是函数的表达式,对以后函数应用 起非常重要的作用.
必修1 第一章 集合与函数的概念
必修1 第一章 集合与函数的概念
栏目导引
(2)集合间的基本关系
①理解集合之间包含与相等的含义,能识别给定集合的 子集.
②在具体情境中,了解全集与空集的含义.
(3)集合的基本运算
①理解两个集合的并集与交集的含义,会求两个简单集 合的并集与交集.
②理解在给定集合中一个子集的补集的含义,会求给定 子集的补集.
B.{x|x≥0}
C.{x|x≥1 或 x≤0} D.{x|0≤x≤1}
解析:
1-x≥0, x≥0
⇔0≤x≤1.故选 D.
答案: D
必修1 第一章 集合与函数的概念
栏目导引
3.若定义在R上的函数f(x)满足:对任意x1,x2∈R 有f(x1+x2)=f(x1)+f(x2)+1,则下列说法一定正确 的是( )
当 x<0 时,函数 f(x)=(x+1)2-2 的最小值为-2,
最大值为 f(-3)=2.故函数 f(x)的值域为[-2,2].
必修1 第一章 集合与函数的概念
栏目导引
1.已知集合A={x|x<a},B={x|1<x<2},且
A∪(∁RB)=R,则实数a的取值范围是( )
A.a≥2
B.a<1
C.a≤2
解析: 假设存在x,使得B∪(∁AB)=A, 即B A.
①若x+2=3,则x=1,此时A={1,3,-1},B= {1,3},符合题意.
