07.角动量守恒定律
角动量守恒定律

角动量守恒定律角动量守恒定律,也称转动动量守恒定律,是描述旋转系统中物体角动量守恒的物理定律。
它是在伽利略与牛顿的基础上,由欧拉和拉格朗日等人发展起来的。
它表明,在无外力矩作用下,一个封闭系统的总角动量守恒。
在物理学中,角动量是描述物体旋转运动的物理量。
一个物体的角动量等于其自转角速度和惯性矩的乘积。
考虑一个刚性物体,其围绕某个轴心旋转。
此时,物体的角动量L等于其自转惯性矩I和角速度ω的积,即L=Iω。
这个公式可以用来描述物体的旋转状态。
在没有外力矩作用的情况下,物体的角动量守恒。
也就是说,在这种情况下,刚体自身的角速度和惯性矩不会发生改变。
这个定律可以由牛顿第二定律的角动量形式推导出来。
当一个刚体受到外部力矩时,他的角动量就会发生变化。
这个变化量等于力矩与旋转时间的积。
一个封闭系统中的物体,在没有外部力矩作用时,总角动量守恒,即所有物体的角动量的代数和不变。
如果物体中有某一个物体受到外部力矩,那么这个物体的角动量就会发生变化,但是,由于总系y运中的总力矩为零,所以其他物体的角动量将以相反的方式发生变化,以保证总角动量守恒。
一个典型的例子是一个旋转跳板启动一个跳跃者,高度和角速度的变化取决于跳板和跳跃者的质量和形状。
在这个过程中,跳板和跳跃者的角动量守恒,因为在计算角速度和角动量时,两个物体的总和是不变的。
总之,角动量守恒定律是一种重要的动力学基本定律。
它说明,封闭系统中的角动量总和保持不变。
在硬物体的运动中往往非常有用,可以帮助计算速度、加速度和其他涉及运动的数值。
在工程学和物理学中,它被广泛地应用于旋转系统、制药生产,以及其他需要涉及转动的领域。
角动量及其守恒定律

m r2 r1 J0
22
因为 1 2, 1 1 2 E k 1 J 1 1 ( J 1 1 ) 1 2 2 相 E k1 E k 2 等 1 1 2 E k 2 J 2 2 ( J 2 2 ) 2 2 2 即系统的机械能不守恒。
23
人双臂收回过程中,内力做功,
J 2
l/2
r dr
2
1 12
l
3
0
1 12
ml
2
如转轴过端点垂直于棒 l 1 2 J r d r ml 2 0 3
例3 一质量为 m 、半径为 R 的均匀圆盘,求通 过盘中心 O 并与盘面垂直的轴的转动惯量 .
解 设圆盘面密度为 , 在盘上取半径为 r ,宽为 d r 的圆环
v M (2 gh )
u l 2
1 2
M
h N
B
l 2 1 12
2
2
把M、N和跷板作为 一个系统, 角动量守恒
mvM l 2 J 2 mu
C l
m l 1 2 1 6 m ( 2 gh )
A l/2
ml
2
解得
mvMl 2 m l
2
2
12 ml
2
2 2 2
质量连续分布刚体的转动惯量
J
m
j
j j
r
2
r dm
2
d m :质量元
例2 一质量为 m 、长为 l 的均匀细长棒,求 通过棒中心并与棒垂直的轴的转动惯量 .
O
l 2
O
dr
l 2
r
dr
O´
角动量守恒

r
θ
p
y
质点对圆心的角动量(动量矩) 质点对圆心的角动量(动量矩)
大小 | L |= Pr⊥ = Pr sin θ 矢量式 L = r × P = mr × v
p
o m
r
行星在公转轨道上的角动量
p
p
r
d
O
d
r
L = pd = pr sin
定义:质点对点的角动量为 定义 质点对点的角动量为
L = r × P = r ×(mv ) 面积) 角动量大小 L= rmv sinα(面积)
dL mgR cos θ = dt mR 2 dt = dθ L
(1)
(2)
t = 0,θ0 = 0, L0 = 0, 对上式积分 ∫ LdL = ∫0 m gR cosθ dθ
L 0 2 3
θ
即 由
2 1/ L = mR3/(2 g sin θ)2 (3)
L = mR2ω 2g 1/ ω=( sin θ)2 R
∵ M = r × F; L = r × mv dL ∴ M= dt
dP 上式与牛顿第二定律F = 在形式上是相似的 dt 只是用M 代替了F,用L代替了P。
上式还可以写成
Mdt = dL
Mdt为力矩对时间的累积效应,仿照冲量的定义 我们称之为冲量矩
Mdt = dL
对此式左右积分得 ∫ Mdt = ∫ dL = L2 L1
大小不变
L
方向不变 方向不变
L
O
r
α m
v
α
r
v
质点对圆心O的角动量为恒量 质点对圆心 的角动量为恒量
2. 质点的角动量定理
设质量为m的质点,在合力F的作用下,其运动方程为
07. 质点角动量与角动量守恒定律
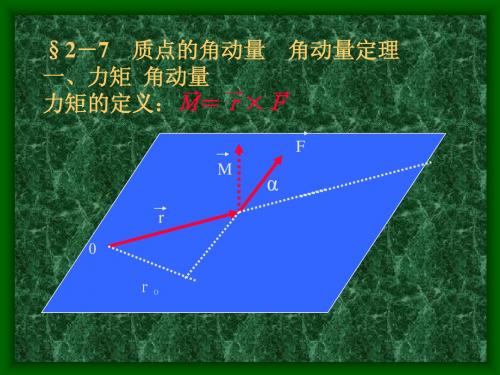
mv2r2 mv1r1
v2r2 v1r1
表明小球对圆心的 角动量保持不变。
例:行星运动的开普勒第二定律。
解:太阳作为力心,行星受到有心引力, 万有引力,行星相对力心(太阳)的角动 量守恒。行星作平面运动,其轨道是以太 阳为焦点的椭圆。
0
r α
L mvr sin r r sin dr mr sin m lim t 0 dt t 2s m lim t 0 t ds 2m dt
显然,上关系中的L,M是相对同一参考 点而言。 类似质点的动量定理的讨论,有
dL Mdt
t2 L 2 L 2 Mdt t1
(冲量矩)
上关系用的不多,但基本概念应清楚。 如已知t1~t2的L变化,求平均力矩。
三、 角动量守恒定律 对某一参考点,若质点受的合外力矩为零, 则质点相对此点的角动量不变, L=常矢 即质点相对此点的角动量守恒。 质点角动量守恒定律又表明了运动中存在 的一个不变量。 ∵L=mr×v 其方向也不变,决定了 质点在r与v确定的平面上运动。
§2-7 质点的角动量 角动量定理 一、力矩 角动量 力矩的定义:M=r×F
F M r 0 rO
α
M的大小:
M=rFsinα=r F r ,力臂,0到力作用线的垂直距离。 M的方向: 右手螺旋法则。右手四指由r向F方向 (小于π)转,拇指的方向,显然M垂直r, F构成的平面。
O O
SI:mN(量纲同功,物理量不同。) 力矩的定义与力的三要素(力的大小、方 向、力作用点的位置(坐标)有关。)
ds/dt行星对太阳的位矢在单位时间扫过的面 积,掠面速度。 ∵L大小不变,ds/dt不变。
行星与太阳的连线在相同时间内扫过相等的面积
力学-7-角动量守恒定律

注意:M=0,可以是r=0,也可以是F =0,
2
2.力矩作用效果
M rF
r
dp
d
(r
p)
dr
p
dr
v
dt
dt
p mv
dt
dr
p
dt
0
dt
3.角动量矢量
Lrp
积分形式
4.角动量定理
M
dL
dt
t
0 M dt L'L0
质点所受合外力矩等于它的角动量对时间的变化率。
3
二、角动量守恒定律
ቤተ መጻሕፍቲ ባይዱ
M
dL
dt
如果:M 0
则:dL 0
dt
角动量守恒定律
即L=常矢量
如果对于某一固定点,质点所受的合外力矩 为零,则此点对该固定点的角动量矢量保持不变。
5
三、质点系角动量守恒定律
1、定义:质点系各质点对该定点的角动量的矢量和。
Mi
dL dt
L
8
质点的角动量 角动量守恒定律
1
一、质点的角动量
1.rM 力是矩P点r相反对映F于力固的定大小点、O的方向位和矢作。用点M对 o物d 体r转动的p θ影F 响
大小:M=Frsin=Fd
方力向臂::右d=手rsi螺n旋定则判定力与M力 臂的r乘 F积 。
单位:N•m(不能写成功的单位J)
量纲:ML2T–2
dLi
dt
ri
i
i
Li Fi
ri
i M i ri
(ri
i
pi
(Fi
fi j )
j
fi j )
i j
角动量 角动量守恒定律
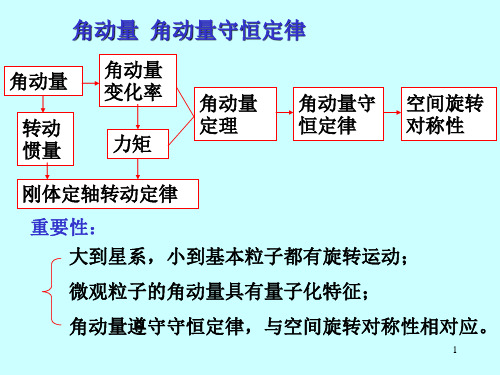
r为力的作用点到 参考点的位置矢量
20
2) 力对定轴的力矩
z
Mz
o
d
F F //
r
F
M r F r ( F// F ) r F// r F
第一项
力F对O点的力矩 (F不在转动平面内):
M1 r F//
dL 可得 M r F dt
对 N 个质点 m1, m2 ,, mN 组成的质点系,由
dL1 r1 F1外 F1内 M 1外 M 1内 dt 两边求和得 dL2 r2 F2外 F2内 M 2外 M 2内 dL总 d dt Li dt i dt M i 外 M i内 dLN i i 24 rN FN外 FN内 M N外 M N内 dt
z
vi
转轴与其转动平面交点
o
转动 平面
mi 对 o 的角动量: Lio ri mi vi
大小:Lio ri mi vi mi ri 2 Lio 方向:沿 2 即 Lio mi ri
o圆周运动半径为 ri
o ri
mi
6
定义:质点 mi 对其转动平面上圆心 o 点的角动 量的大小,称为质点对转轴的角动量。
11
m 1 L3 L3 1 2 m L 12 L 3 8 8
(2) 轴过一端端点
dm
o
x
J r dm x dm
2 2 L
L
x
2
若使用平行轴定理:
0
大学物理课件角动量守恒定律
只要整个系统受到的合外力矩为0,则系统 只要整个系统受到的合外力矩为 , 的总角动量守恒, 的总角动量守恒,即: 恒量 比如:当研究质点与刚体的碰撞问题 质点与刚体的碰撞问题时 比如:当研究质点与刚体的碰撞问题时,可以把质 点和刚体看成一个系统,在碰撞过程中, 点和刚体看成一个系统,在碰撞过程中,系统所受 的合外力矩为零,所以系统的角动量守恒 系统的角动量守恒。 的合外力矩为零,所以系统的角动量守恒。
刚体定轴转动的角动量定理 三、刚体定轴转动的角动量守恒定律 若 ,则
当刚体受到的合外力矩为0 时,其角动量保持不变。 其角动量保持不变。 当刚体受到的合外力矩为 讨论 Ø 内力矩不改变系统的角动量。 内力矩不改变系统的角动量。 Ø 在冲击等问题中 冲击等问题中 常量
Ø 角动量守恒定律是自然界的一个基本定律。 角动量守恒定律是自然界的一个基本定律。
可得:质点系的角动量守恒定律: 可得:质点系的角动量守恒定律: 若: 则: 或:
当质点系所受的合外力矩为零时,其角动量守恒。 当质点系所受的合外力矩为零时,其角动量守恒。
二、刚体定轴转动的角动量定理角动量守恒定律 刚体定轴转动的角动量定理角动量守恒定律 质点对点的角动量: 质点对点的角动量: 作圆周运动的质点的角动量: 作圆周运动的质点的角动量: 1、刚体定轴转动的角动量
( 海豚 Ⅱ )
(支奴干 CH47)
装置反向转动的双旋翼产生 反向角动量而相互抵消
用两个对转的顶浆
自然界中存在多种守恒定律 2 动量守恒定律 2 能量守恒定律 2 角动量守恒定律 2 电荷守恒定律 2 质量守恒定律 2 宇称守恒定律等
例:人与转盘的转动惯量J0,伸臂时 人与转盘的转动惯量 , 臂长为 l1,收臂时臂长为 l2。人站在 , 。 不计摩擦的自由转动的圆盘中心上, 不计摩擦的自由转动的圆盘中心上, 的哑铃。 每只手抓有质量为 m的哑铃。伸臂时 的哑铃 转动角速度为 1, , 求:收臂时的角速度 2 。 解:整个过程合外力矩为0, 整个过程合外力矩为 , 角动量守恒, 角动量守恒,
角动量角动量守恒定律
确定细杆受的摩擦力矩
0
细杆的质量密度为:
m /l
分割质量元dm
m ,l o dm l / 2
l/2
x dx x
dm dx
质元受的摩擦力矩 dM dmgx
细杆受的摩擦力矩
M
l /2 l / 2
dM
20l /2 gxdx
1 mgl
4
始末两态的角动量为:L0 J 0 , L 0
( 2g sin )1 2
R
4-3角动量 角动量守恒定律
二、刚体定轴转动的角动量定理和角动量守恒定律
1. 刚体定轴转动的动量矩
质点对 Z 轴的动量矩… LZ mvr mr 2
刚体上任一质点对 Z 轴的动量矩为
LZi Δmviri Δmri2
且刚体上任一质点对 Z 轴的动 量矩具有相同的方向
当 M 0,L 恒矢量
当质点所受对参考点O的合力矩为
零时,质点对该参考点O的角动量为一
恒矢量.——质点的角动量守恒定律
讨论
(1) 守恒条件
F 0 M 0F过O点
(2) 有心力的动量矩守恒。
4-3角动量 角动量守恒定律
物理学
第五版
第四章 刚体转动
例 一半径为 R 的 光滑圆环置于竖直平面 内. 一质量为 m 的小球 穿在圆环上, 并可在圆 环上滑动. 小球开始时 静止于圆环上的点 A (该点在通过环心 O 的 水平面上),然后从 A
4-3角动量 角动量守恒定律
物理学
第五版
第四章 刚体转动
例 一质点m,速度为v,如图所示,A、B、C 分别为三
个参考点,此时m 相对三个点的距离分别为d1 、d2 、 d3 求 此时刻质点对三个参考点的动量矩
什么是角动量守恒定律
什么是角动量守恒定律角动量守恒定律是物理学中的基本定律之一。
它描述了一个物体或系统的角动量在没有外力作用下的守恒性质。
本文将通过对角动量守恒定律的概念、应用和实例的探讨,详细阐述什么是角动量守恒定律。
角动量守恒定律是基于物体的转动性质而产生的定律。
角动量表示物体绕某个轴旋转时的运动状态,它与物体的质量、转动轴离轴距离和物体的角速度有关。
角动量守恒定律提出,当一个物体或一个系统不受外力矩作用时,其总角动量将保持不变。
具体而言,对于一个孤立系统或一个不受外部扰动的物体,其初始角动量与最终角动量相等。
也就是说,如果在没有外力作用下,物体的转动轴保持不变,那么它的角动量将始终保持不变。
这表明,物体在转动过程中,无论是改变转动速度还是转动轴的位置,总角动量都将保持恒定。
角动量守恒定律可以通过转动动力学原理来解释。
当一个物体受到作用力时,根据转动动力学原理,作用力和物体受力点之间的力矩将导致物体发生角加速度,从而改变物体的角动量。
然而,在不受外力的情况下,物体的角动量将保持不变,因为没有力矩可以改变物体的角动量。
角动量守恒定律在实际应用中有着广泛的意义。
首先,在天体物理学中,它可以用来解释和预测行星、卫星等天体的运动。
例如,当卫星绕地球旋转时,由于不受外力的作用,卫星的角动量保持恒定,这使得我们能够理解卫星的运动轨迹和速度变化。
此外,角动量守恒定律还可以应用于机械系统中,如陀螺仪的运动理论分析、转子动力学等等。
值得一提的是,角动量守恒定律与动量守恒定律密切相关。
动量守恒定律指出在没有外力作用下,物体的动量保持不变。
而角动量守恒定律可以被视为动量守恒定律在转动系统中的体现。
因为角动量等于动量与物体到转动轴距离的乘积,所以角动量守恒定律实际上是动量守恒定律在转动系统中的推论。
为了更好地理解角动量守恒定律,让我们通过一个实际的例子来具体说明。
考虑一个自行车车轮的旋转运动。
当骑手在自行车上进行转动操作时,车轮开始加速旋转。
-角动量定理角动量守恒定律
太原理工大学物理系
结论: 1)内力对定点的力矩之和为零。 2)只有外力矩才能改变系统的总角动量。 3.质点系的对轴的角动量
L Lxi Ly j Lzk M Mxi M y j Mzk
质点系对x轴的角动量定理
Mx
dLx dt
太原理工大学物理系
质点系的角动量守恒定律可以表示为三 个分量形式
解:小球的合外力矩为 0 ,故角动量守恒 。 有:
L = mvr = 恒量 即: m v1 r1 =m v2 r2
v2
r1v1 r2
太原理工大学物理系
五、质点系的角动量与角动量守恒
1.质点系对定点的角动量
P2
第i个质点对o点的角动量
r2
Li ri Pi
o
质点系对o点的角动量
ri fi 质点系受到的内力矩的矢量和
i
太原理工大学物理系
可以证明:内力 对定 点的力矩之和为零,即
ri fi 0
i
质点系内的重要结论之三
有 M
ri Fi
i
M外
dL dt
质点系的角动量定理:质点系对某定点的角动量的
时间变化率等于质点系对该点的合外力矩。
力矩在y轴方向的分量
M y zFx xFz
力矩在z轴方向的分量
M z xFy yFx
太原理工大学物理系
力矩在某一方向的分量称为力对该轴的力矩。
当质点在oxy平面内运动时,质点
z 所受的力也在该平面时,角动量和力
矩只有在z轴有分量。
Lx 0 Ly 0 Lz L
Mx 0 My 0 Mz M
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《大学物理》练习题 No 7 角动量守恒定律
班级__________学号 _________ 姓名 _________ 成绩 ________
一、选择题
1.刚体角动量守恒的充分必要条件是 [ B ] (A) 刚体不受外力矩的作用.
(B) 刚体所受合外力矩为零.
(C) 刚体所受的合外力和合外力矩均为零. (D) 刚体的转动惯量和角速度均保持不变
2.有一半径为R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动, 转动惯量为J , 开始时转台以匀角速度ω 0转动,此时有一质量为m 的人站在转台中心,随后人沿半径向外跑去,当人到达转台边缘时, 转台的角速度为 [ A ] (A) J ω 0/(J +mR 2
) .
(B) J ω 0/[(J +m )R 2].
(C) J ω 0/(mR 2) . (D) ω 0.
3.如图7.1所示,一静止的均匀细棒,长为L 、质量为M , 可绕通过棒的端点且垂直于棒长的光滑固定轴O 在水平面内转动, 转动惯量为ML 2/3.一质量为m 、速率为v 的子弹在水平面内沿与棒垂直的方向射入并穿出棒的自由端,设穿过棒后子弹的速率为v /2,则此时棒的角速度应为 [ B ] (A) mv/(ML ) .
(B) 3mv/(2ML ).
(C) 5mv/(3ML ). (D) 7mv/(4ML ).
二、填空题
1. 在XOY 平面内的三个质点,质量分别为m 1 = 1kg, m 2 = 2kg,和 m 3 = 3kg,位置坐标(以米为单位)分别为m 1 (-3,-2)、m 2 (-2,1)和m 3 (1,2),则这三个质点构成的质点组对Z 轴的转动惯量I z = 2
38m kg ⋅ .
2.质量均为70kg 的两滑冰运动员,以6.5s m /等速反向滑行,滑行路线的垂直距离为10m 。
当彼此交错时,各抓住10m 长绳子的两端,然后相对旋转。
则各自对中心的角动量=L
1
22275-⋅⋅s m kg ,当各自收绳到绳长为5m 时,各自速率为=v s m /13 。
3.一飞轮以角速度ω 0绕轴旋转, 飞轮对轴的转动惯量为J 1;另一静止飞轮突然被同轴地啮合
到转动的飞轮上,该飞轮对轴的转动惯量为前者的二倍,啮合后整个系统的角速度ω =
03
1ω.
v /2
图7.1
三、计算题
1. 如图7.2所示,有一飞轮,半径为r = 20cm,可绕水平轴转动,在轮上绕一根很长的轻绳,若在自由端系一质量m 1 = 20g 的物体,此物体匀速下降;若系m 2=50g 的物体,则此物体在10s 内由静止开始加速下降40cm .设摩擦阻力矩保持不变.求摩擦阻力矩、飞轮的转动惯量以及绳系重物m 2后的张力?
解: 摩擦阻力矩m N gr m M
f
⋅==04.01
系上m 2物体后, a m T g m 22=-
βJ M
Tr f
=-
N T 5.0≈
βr a = 2
49.1m kg J ⋅≈ 2
2t
S a =
2. 如图7.3所示,质量为M 的均匀细棒,长为L ,可绕过端点O 的水平光滑轴在竖直面内转动,当棒竖直静止下垂时,有一质量为m 的小球飞来,垂直击中棒的中点.由于碰撞,小球碰后以初速度为零自由下落,而细棒碰撞后的最大偏角为θ,求小球击中细棒前的速度值.
解:设小球碰撞前速度为v ω⋅=
-2
3
1)(ML a L mv
2
)
(3ML a L mv -=
ω
)cos 1(2
3
1212
2
θω-=⋅L
Mg ML
解出 3
)
c o s 1()
(θ--=
Lg a L m ML v
化简得到, 3
)
c o s 1(2θ-=Lg m
M v
图7.2
图7.3。
