3-3凹凸性和拐点
函数的凹凸性和拐点

函数的凹凸性和拐点
函数的凹凸性和拐点是微积分中的重要概念,用于研究函数图像的形态和性质。
下面
将分别对凹凸性和拐点进行详细介绍。
一、凹凸性
在数学中,一个函数在某一区间上的凹凸性是指函数图像在该区间上是向上凸或向下凸。
几何上,一个曲线在某点处向上凸表明曲线凹向上方,而向下凸则表明曲线凹向下方。
凹凸性的判断方法是通过函数的二阶导数来进行。
如果函数的二阶导数大于零,则函
数在该点处向上凸;反之,如果函数的二阶导数小于零,则函数在该点处向下凸。
函数的图像如果是向上凸的,则可以将其形容为“形如碗状”,反之则形容为“形如
山状”或“钩状”。
在具体的分析中,凹凸性可作为确定函数的最值和极值的重要参考。
二、拐点
拐点是指函数图像上的一点,该点处曲线的凹凸性发生变化。
在拐点之前,函数图像
呈现一种凹凸性,而在拐点之后,则呈现相反的凹凸性。
因此,拐点也被称为凹凸性变化点。
拐点的判断方法是通过函数的二阶导数进行判断。
如果函数在某一点处的二阶导数发
生了从正数变成负数,或从负数变成正数的变化,则该点即为拐点。
在实际分析中,拐点
可用于确定函数的折线形态,以及确定函数的最值和极值。
综上所述,函数的凹凸性和拐点是微积分中的重要概念,用于研究函数图像的性质和
形态。
凹凸性可以帮助我们更好地理解函数的最值和极值,而拐点则可以帮助我们确定函
数的折线形态,以及确定函数的最值和极值。
在实际运用中,我们应该结合具体问题进行
分析,寻找函数的凹凸性和拐点,以便更好地解决问题。
《曲线凹凸与拐点》课件

曲线凹凸的计算方法
定义法
通过定义凹凸性,利用二阶导数正负来判断。如果二阶导数大于0,则曲线在相 应区间内是凹的;如果二阶导数小于0,则曲线在相应区间内是凸的。
切线法
通过切线斜率判断。在某点处做切线,如果切线斜率在相邻两点之间由负变正, 则该点为拐点。
拐点的计算方法
定义法
根据拐点的定义,即函数在某点的左 右极限不相等,来确定拐点。
具体应用
在气候学中,通过研究气候数据的曲线凹凸性,可以更好地理解气候变化的规律和趋势 。在金融学中,通过研究股票价格的拐点,可以更好地把握股票市场的变化和趋势。
导数符号变化法
通过判断函数在某点附近左右两 侧导数的符号变化来确定是否为
拐点。
二阶导数测试法
通过判断二阶导数的符号变化来确 定是否为拐点。如果二阶导数在某 点处从正变为负或从负变为正,则 该点为拐点。
切线方向变化法
通过观察曲线在某点处的切线方向 是否发生变化来确定是否为拐点。 如果切线方向发生改变,则该点为 拐点。
导数法
通过求函数的二阶导数,并令其为0 ,解出相应的x值,再判断该点是否为 拐点。
曲线凹凸与拐点计算中的注意事项
初始判断
在计算前应先大致判断 函数的形态,以便选择
合适的计算方法。
精确度要求
对于实际应用,应考虑 计算结果的精确度,选 择合适的数学工具和算
法。
拐点判断
在确定拐点时,应同时 考虑左右极限,避免误
拐点是曲线上的一个点,在该点处曲线的切线方向发变符号
在拐点处,曲线的导数由正变负或由 负变正。
拐点处凹凸性改变
拐点处切线方向变化
在拐点处,曲线的切线方向发生变化 ,由上升变为下降或由下降变为上升 。
曲线的凹凸性与拐点

曲线的凹凸性与拐点在数学中,曲线的凹凸性以及拐点对于研究曲线的性质和变化具有重要的意义。
凹凸性可以帮助我们理解曲线的弯曲程度以及变化趋势,而拐点则是曲线上的一个特殊点,表示曲线在该处发生方向的变化。
本文将介绍曲线的凹凸性与拐点的概念,以及它们在数学和其他实际应用中的重要性。
一、凹凸性的定义与判断凹凸性是描述曲线在某一区间上的弯曲程度的性质。
我们有以下两个定义来判断曲线的凹凸性:1. 凹曲线:如果曲线上的任意两点连线的下方部分都在曲线上方,则称该曲线为凹曲线。
换句话说,如果对于曲线上的任意两点A和B,A和B连线的下方不与曲线相交,则该曲线为凹曲线。
2. 凸曲线:如果曲线上的任意两点连线的下方部分都在曲线下方,则称该曲线为凸曲线。
换句话说,如果对于曲线上的任意两点A和B,A和B连线的下方不与曲线相交,则该曲线为凸曲线。
凹凸性的判断可以通过曲线的二阶导数来进行。
如果曲线的二阶导数大于0,则曲线为凹曲线;如果二阶导数小于0,则曲线为凸曲线。
而当二阶导数恰好为0时,需要考虑其他方法。
二、拐点的定义与判断拐点是曲线上的一个特殊点,表示曲线在该点处方向发生改变。
我们有以下定义来判断曲线是否存在拐点:1. 拐点:如果曲线在某一点处既没有切线也没有二阶切线(即曲线在该点处没有明确的方向),则称该点为拐点。
判断曲线是否存在拐点可以通过曲线的三阶导数来进行。
如果曲线的三阶导数存在不连续的点,则该点即为拐点。
值得注意的是,如果曲线的三阶导数的符号在该点的左右两侧不同,也可以判断该点为拐点。
三、凹凸性与拐点的应用与意义凹凸性和拐点不仅仅在数学领域中有重要性,还被广泛应用于其他学科和实际问题中,如物理学、经济学等。
在物理学中,凹凸性可以帮助解释某一物体的形状和弯曲程度,例如在光学中,曲率半径越小的曲面会导致光线的弯曲程度越大。
因此,通过研究光线在曲面上的传播可以利用凹凸性来分析光的折射和反射现象。
在经济学中,凹凸性可以用来描述供需曲线的变化趋势。
函数的凹凸性与拐点的判定

函数的凹凸性与拐点的判定在微积分中,函数的凹凸性与拐点是非常重要的概念。
凹凸性描述了函数曲线的弯曲情况,而拐点则表示曲线的方向发生改变的点。
凹凸性和拐点的判定对于函数的研究和应用具有重要作用。
本文将介绍函数凹凸性和拐点的概念,并讨论如何判定和应用。
一、函数的凹凸性函数的凹凸性是指函数曲线的弯曲情况。
我们可以通过函数的二阶导数来判断函数的凹凸性。
1. 定义设函数f(x)在区间I上具有二阶导数,如果对于任意x1和x2∈I,有f''(x)>0,则函数f(x)在区间I上是凹函数;如果对于任意x1和x2∈I,有f''(x)<0,则函数f(x)在区间I上是凸函数。
2. 凹凸点根据函数的凹凸性质,我们可以定义凹凸点。
若对于函数f(x)的定义域I上的某一点x0,存在一个区间(x0-δ,x0+δ),在该区间内f(x)是凹函数,那么称点(x0,f(x0))是函数f(x)的一个凹点;若在区间(x0-δ,x0+δ)内f(x)是凸函数,则称点(x0,f(x0))是函数f(x)的一个凸点。
二、拐点的判定拐点表示函数曲线的方向发生改变的点。
我们可以通过函数的二阶导数来判断拐点。
1. 定义设函数f(x)在区间I上具有二阶导数。
如果在某一点x0∈I处,f''(x0)=0,并且f''(x0-)和f''(x0+)的符号相反,则称点(x0,f(x0))是函数f(x)的一个拐点。
2. 拐点的性质拐点具有以下性质:- 在拐点处,函数的凹凸性发生改变,由凸转为凹或由凹转为凸。
- 拐点不一定存在,只有当函数曲线的凹凸性发生改变时,才会有拐点。
- 如果函数曲线有k个拐点,那么至多有k+1个不同的凹凸区间。
三、判定和应用判定函数的凹凸性和拐点的方法可以通过以下步骤进行。
1. 求导数首先,求出函数f(x)的一阶和二阶导数f'(x)和f''(x)。
经济数学3.3曲线的凹向与拐点
ESC
二. 曲线凹凸与拐点的求法
例5 与拐点. 求曲线 y 2 ( x 4) 的凹凸区间
1 3
, 解 函数的连续区间为(, ) 2 5 1 2 ( x 4) 3 ( x 4) 3 y y 3 9 y 在 (,) 内恒不为零,但 x 4 时, y 不存在. x 在4的左侧邻近时, y 0 ; 在4的右 侧邻近时, y 0 .即 y在 x 4两侧异号,所 以 (4,2)是曲线的拐点. ESC
二. 曲线凹凸与拐点的求法
4) (, 曲线的凹区间是( , ,凸区间是 4 )
练习:
1、求曲线
y (x 1)31 的拐点。
2、 确定曲线
y x x 的凹凸区间与拐点.
3
ESC
内容小结
本节重点讲了: 一. 曲线凹凸与拐点的定义 二.曲线凹凸与拐点的求法 求拐点的一般步骤: ①求函数定义域; ②求函数的二阶导数 f (x) ; ③令 f ( x) 0,解出全部根,并求出所 有二阶导数不存在的点;
二. 曲线凹凸与拐点的求法
例2 (续)
结论: 在区间 (0, b)内,曲线凹; 2 在区间 ( b ,) 内, 曲线凸; 2 曲线的拐点是 ( b , Ae2).
设一消费品的需求 Q 是消费者的收入 x 的函数
Q Ae
b x
(A 0, b 0).
Q
试讨论该需求收入曲线的凹凸区间与拐点.
(3)判定:在各个部分区间内讨论导 数 (x) 的符号:设, b) I 的一个 是 f (a 部分区间,当 (a, b) 时,若(x) 0, x f (2)求二阶导数 (a (1)确定 f (x), 解方程 求其 则曲线在区间, b) 内凹;若 函数的 f (a 根.(x) 0, 其根将 (x) 0, 则曲线在区间, b) 内凸 f 连续区间; 又假设 I, 且有(x ) 0, 若在 x0 f 0 函数连续区间 分成 I 点 的左右邻近(x) 的符号相反, f 0 若干个部分区间; 则曲线上的点, f (x0)) 是曲线的拐 (x0 点; 若在点 的左右邻近(x) 的符 f 0 号相同,则在 处,曲线没有拐点. 0 ESC
曲线的凹凸性和拐点
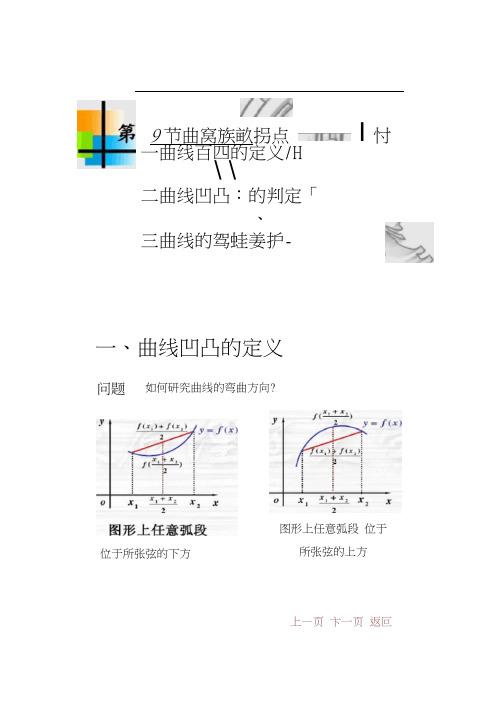
9节曲窝族畝拐点 I 忖一曲线百四的定义/H\ \二曲线凹凸:的判定「、三曲线的驾蛙姜护-一、曲线凹凸的定义如何研究曲线的弯曲方向?位于所张弦的下方问题图形上任意弧段位于所张弦的上方上—页卞一页返叵定义设/'(X)在(sZ>)内连续,如果对S上)内任意两点r严“恒2 2 那末称/(乂)在(6巧内的图形是凹的;如果恒有八巴上2)>八&)+八兀2)2那末称/(X)在@,巧内的图形是凸的。
上—页下—夷E?凹弧:曲线上任意一点切线都在曲线弧的下方。
凸弧:曲线上任意一点切线都在曲线弧的上方。
上—页下—夷I& E?曲线凹凸的判定X, +X,3畐eg __ ),2, ,X, +X, ―X. +X, — X,/(")-/(— )=广(刍)(兀- ')=厂(£)— -2 2 2X, +X.3^2 €( " 2 ),2X, +x\ X,十*. X, -X.定理1如果/•(*)在0上]上连续,在("0)内具有二阶导数,若在仗上)内(1)/"(x)>0,则八工)在|«,A1上的图形是凹的,(2)/^7x)<0,则八丄)在B上]上的图形是凸的。
上—页下—页证明:(1)分析:即证任取两点兀]宀(" < 兀2)要证八2 — 2X, + X予X. + X.————)1 >«2 2—X上—页下—页返叵/(©)-/(—)=厂©)(*2---—2 厂©)—-2 2 2上—页下页逅叵上—页 下—页 返叵两式相加为:X, X- + 七 X, —X, 1/(和-/( ~)]+[/(©)-[/烷)-/("】 ~-2 22即证;厂(务)一厂(£)>o V V 务)事实上:(冬一気)同理可证明(2)上—页.•・曲线在【U,y >)为凹的; 而 厂(G>0 ••・/'(§) 一厂(G>0(纟 <塩)例1判断曲线y = 的凹凸性解.•・• = 3厂,y" = 6x,当XV 0时,y"vO,・•・曲线在(-00,0]为凸的当x>0时,y">0,注意,点(0,0)是曲线由凸变凹的分界点。
三角函数的像凹凸性与拐点归纳
三角函数的像凹凸性与拐点归纳三角函数是数学中常见的一类函数,包括正弦函数、余弦函数和正切函数等。
而像凹凸性和拐点则是研究函数变化趋势的重要概念。
本文将对三角函数的像凹凸性与拐点进行归纳总结,以便更好地理解和应用。
一、正弦函数的凹凸性与拐点正弦函数是最基本的三角函数之一,表示为y = sin(x)。
我们首先来探讨正弦函数的凹凸性。
对于正弦函数,它的一阶导数是余弦函数,即y' = cos(x)。
通过求出一阶导数的二阶导数,可以得到正弦函数的二阶导数为负的余弦函数,即y'' = -sin(x)。
由此可见,正弦函数在整个定义域上都是凹的,没有凸的区间。
关于正弦函数的拐点,拐点是指函数曲线由凹转为凸或由凸转为凹的点。
通过求解二阶导数为零的点,可以找到正弦函数的拐点。
对于正弦函数来说,当x = (2n+1)π/2,其中n为整数,即π/2、3π/2、5π/2等,这些点即为正弦函数的拐点。
总结起来,正弦函数在整个定义域上是凹函数,没有凸的区间;拐点在x = (2n+1)π/2,其中n为整数。
二、余弦函数的凹凸性与拐点余弦函数是另一个常见的三角函数,表示为y = cos(x)。
同样地,我们来探讨余弦函数的凹凸性。
对于余弦函数,它的一阶导数是负的正弦函数,即y' = -sin(x)。
通过求一阶导数的二阶导数,可以得到余弦函数的二阶导数为负的余弦函数,即y'' = -cos(x)。
由此可见,余弦函数在整个定义域上都是凹的,没有凸的区间。
关于余弦函数的拐点,通过求解二阶导数为零的点,可以得到余弦函数的拐点。
对于余弦函数来说,当x = nπ,其中n为整数,即0、π、2π等,这些点即为余弦函数的拐点。
总结起来,余弦函数在整个定义域上是凹函数,没有凸的区间;拐点在x = nπ,其中n为整数。
三、正切函数的凹凸性与拐点正切函数是三角函数中的另一个重要函数,表示为y = tan(x)。
函数的凹凸性与拐点
函数的凹凸性与拐点函数的凹凸性以及拐点是微积分中重要的概念,它们能够帮助我们更好地理解函数的性质和行为。
在本文中,我们将详细探讨函数的凹凸性以及如何确定函数的拐点。
一、函数的凹凸性函数的凹凸性描述了函数曲线的弯曲程度。
具体而言,我们可以通过观察函数的二阶导数来确定函数是凹还是凸。
1. 凹函数:如果函数的二阶导数在定义域内恒小于等于零,则该函数被称为凹函数。
凹函数的图像呈现出一种向下的弯曲形状。
举例来说,考虑函数f(x),它在定义域内处处可导。
我们可以检查函数的二阶导数f''(x)是否小于等于零。
如果f''(x) <= 0对于所有x都成立,则函数f(x)是一个凹函数。
2. 凸函数:与凹函数相反,如果函数的二阶导数在定义域内恒大于等于零,则该函数被称为凸函数。
凸函数的图像呈现出一种向上的弯曲形状。
举例来说,考虑函数g(x),它在定义域内处处可导。
我们可以检查函数的二阶导数g''(x)是否大于等于零。
如果g''(x) >= 0对于所有x都成立,则函数g(x)是一个凸函数。
请注意,如果函数的二阶导数既不小于等于零也不大于等于零,那么该函数既不是凹函数也不是凸函数。
二、函数的拐点拐点是函数曲线上的一个特殊点,它代表了函数从凹转为凸或从凸转为凹的位置。
通过找到函数的拐点,我们可以进一步了解函数的曲线的形状。
1. 拐点的判定要确定函数的拐点,我们需要观察函数的二阶导数的变化情况。
首先,我们找到函数f(x)在定义域内的所有驻点,即一阶导数f'(x)等于零的点。
然后,我们计算这些驻点对应的二阶导数f''(x)的值。
- 如果二阶导数f''(x)在某个驻点x处由负转正,那么该点就是函数的拐点。
- 如果二阶导数f''(x)在某个驻点x处由正转负,那么该点也是函数的拐点。
需要注意的是,函数的拐点并不一定都存在。
函数凹凸性和拐点
xxxxxxxxxxx
2
目录
CONTENTS
1
函数的凹凸际应用
3
在数学和优化理论中,函数的凹凸性和 拐点是描述函数形态和变化的重要概念
这些特性对于理解函数的性质,以及寻 找最优解有着至关重要的作用
PART 1
函数的凹凸性
01
在二维平面上,一个函数如果是上凸的(或称为"凹"),那么 它的图形看起来像一个倒置的U型,或者像一个山丘。相反,
PART 3
实际应用
函数的凹凸性和拐点在很多实际应用中都有重要地位。例如,在经济学中,函数的凹凸性可以用来 描述一种商品的需求和价格之间的关系。如果需求对价格是凹的(即需求随着价格的上升而下降得越 来越快),那么我们可能会观察到价格和需求量之间有单向的关系。相反,如果需求对价格是凸的 (即需求随着价格的上升而下降的速度减慢),那么价格和需求量之间可能存在一种"非线性"的关系
此外,函数的凹凸性和拐点在图 形和图像处理中也有着广泛的应 用。例如,在计算机视觉中,图 像的边缘检测和特征提取就涉及 到函数的凹凸性和拐点。通过利 用这些特性,我们可以更好地理 解和描述图像的内容
在机器学习中,函数的凹凸性和 拐点也被广泛使用。例如,在神 经网络训练中,损失函数(或目 标函数)的凹凸性可以帮助我们 理解模型的学习过程。如果损失 函数是凸的,那么我们可以利用 这个特性来优化模型参数。如果 损失函数是凹的,那么我们可能 需要采用更复杂的优化策略,如 梯度下降结合线搜索等
01.
拐点是函数凹凸性发生改变的点。具体来说,如果一个函数在某一点的导数由正变为负, 或者由负变为正,那么这个点就是该函数的拐点。在数学上,我们通常用二阶导数的符 号变化来判断拐点的存在
4.3.3凹凸性与拐点
例4 求曲线 y 3 x 的拐点.
解
当x
0时,
y
1
x
2 3
,
y
4
5
x3
,
3
9
x 0是不可导点, y, y均不存在.
但在(,0)内, y 0, 曲线在(,0]上是凹的;
在(0,)内, y 0, 曲线在[0,)上是凸的.
点(0,0)是曲线 y 3 x的拐点.
例5
讨论两曲线f
(
x)
x,
x0
oa
bx
f ( x) 递增 y 0
f ( x) 递减 y 0
定理1 如果 f ( x) 在 [a, b] 上连续,在 (a, b) 内具有
一阶和二阶导数 ,若在 (a, b) 内
(1) f ( x) 0,则 f ( x) 在 [a, b] 上的图形是凹的 ;
(2) f ( x) 0,则 f ( x) 在 [a, b] 上的图形是凸的 .
例6 已知点(1,3)为曲线y x3 ax2 bx 14的拐点, 试求a、b的值。
解 y 3x2 2ax b,y=6x+2a.
因(1,3)为拐点,故知y(1)=0, 即6 1+2a=0, 得a= -3.
又因(1,3)在曲线上:y(1) 3,得 1+a b 14 3,故b 9
当 x 1 时,因y 0,所以曲线为凸的;
2h
当 x 1 时,因y 0,所以曲线为凹的.
2h
由拐点的定义,可知当x= 1 时,即h 1 时,
2h
2
概 率 曲 线 在x =处 有 拐 点.
思考题
设曲线y f ( x)与y g( x)在点x x0邻域内皆为凹的, 且f 、g存在, 则曲线y f ( x) g( x)与y f ( x)g( x)在该邻域内是否 也一定为凹的? 试加以说明或举反例说明之。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y 2 xe y 2e
令
x2
x2
4x e
2 x2
2(2 x 1)e
2
x2
y 0, 得x 0,
令y 0, 得x
1 . 2
列表如下:
x f (x )
f (x) f (x)
y b 是曲线 y
f (x) 的一条水平渐近线。
例2 确定 y arctan x 的渐近线。
解 因为
2
所以,y 如图
2
x
lim arctan x
, lim arctan x
x
2
,
及 y
2
y
是曲线的两条水平渐近线。
2
0
2
x
2、铅直渐近线 如果函数 y f (x) 有 lim f ( x) 或 lim f ( x) , 则称直线 x a是曲线 y f (x) 的一条铅直渐近线。
1 2
y
1
0
1 2
x
(1)函数定义域:(, ) (2)无对称性。 (3)单调性、极值、凹凸性及拐点:
f ( x) x 2 2 x, f ( x) 2 x 2
令 f ( x) 0 ,得驻点x1 0, x2 2 , 令 f ( x) 0, 得 x 1 , 列表
x
f (x )
定理 设函数 y f (x) 在区间[a,b]内具有二阶导 数, (1) 如果在区间[a, b]内 f ( x) 0 ,则曲线在 区间[a, b]内是凹的; (2) 如果在区间[a, b]内 f ( x) 0 ,则曲线在 区间[a, b]内是凸的; 定义2 连续曲线上凹弧和凸弧的分界点称为
y
M1
此时 f ( x) 0 ;
o
1 2
M2
x
y
从图可看出,凸的曲线 f (x) 的切线斜率 tan 随 x 的 f 增大而减小, (x )单调减小,
1
2
此时 f ( x) 0
o
x
因此,可以利用二阶导数的符号来判定曲线的凸凹 性。下面不加证明地给出曲线凸凹性判别法。
(,0)
0 0
(0,1)
f (x)
f (x)
极大值2
0
拐点(1, )
4 3
1
(1,2)
2
(2,)
极小值2 3
0
(4)无渐近线 (5) 与 y 轴交点(0,2) (6) 作图,如右图。
y
2
0
1
2
x
例5 作函数 y e
x2
的图形
( 解 (1)函数定义域: , )
定义1 如果在某区间内,曲线弧位于其上任意一 点的切线的下方,则称曲线在此区间内是凸的,此区 间成为凸区间;如果在某区间内,曲线弧位于其上任
意一点的切线的上方,则称曲线在此区间内是凹的,
此区间成为凹区间。 从图可看出,凹的曲线 f (x) 的切线斜率 tan 随x
f 的增大而增大, (x ) 单调增加,
(,
1 ) 2
1 2
(
1 ,0) 2
0 0
(0,
0
( 1 1 , ) 拐点 2 e
x2
1 ) 2
0
(
1 2
(
1 ,) 2
极大 值
1 1 , ) 拐点 2 e
lim (4)渐近线: e
x
0 ,所以 y 0
是一条水平渐近线。 (5)曲线与 y 轴相交于(0,1) (6)作图,如右图。
1 例3 求曲线 y 的水平和铅直渐近线。 x2
xa xa
解
因为
1 1 lim 0, lim x x 2 x 2 x 2
1 lim , x2 x 2
所以, y 0 是曲线的一条水平渐近线, x 2 是曲线 的一条铅直渐近线(如下图)。
y
0
2
x
三、函数作图
综合前面所讨论的函数的某些性态,得到函数 作图的步骤如下: (1)确定函数的定义域; (2) 确定曲线的对称性; (3)列表讨论函数的单调性和极值,曲线的 凹凸性与拐点; (4) 确定曲线的渐近线; (5) 计算一些特殊的点的坐标; (6) 作图。
例4 解
1 3 f ( x) x x 2 2 的图形。 作函数 3
曲线的拐点。 注意 (1)拐点是曲线上的点。
(2)拐点既然是凹凸分界点,则在拐点左右 邻近 f (x) 异号,因而在拐点处 f ( x) 0 或 f (x) 不存在。
y x3 6x 2 9x 的凹凸区间和拐点。 例1 求曲线 y 3 x 2 12x 9, y 6( x 2). 解 令 y 0, 得 x 2. 列表讨论函数的凹凸性与拐点。
第三节
函数的凹凸性与拐点 函数作图
一、曲线的凹凸性与拐点
二、曲线的渐近线
三、函数作图
一、曲线的凹凸性与拐点
如图,观察抛物线 y x2 , y x ,它们 在区间[0,1]上都是单调增加的,但弯曲的方向 y 不一样。 这说明,在研究函数的图形时, 仅知道他们的单调性是不够的, 还需要考察曲线的弯曲方向及 扭转弯曲方向的点。 1 o 1 x
x
y
y
(,2)
︵
2 0
(2,2) 拐点
(2,)
︶
曲线在区间(,2) 是凸的,在区间 ( 2,) 内是凹的,拐点 (2,2) ,如下图。
y
0
1 2
x
二、曲线的渐近线
定义3 曲线 y f (x)上的动点沿曲线无限远离 原点时,如果动点与定直线L的距离趋于零,则称 L为曲线的渐近线。 曲线的渐近线可分为水平、铅直和斜渐近线。 1、水平渐近线 如果函数 y f (x) 有xlim f ( x) b 或 xlim f ( x) b , 则称直线
