7.时程分析G
地震响应的反应谱法与时程分析比较 (1)

发电厂房墙体地震响应的反应谱法与时程分析比较1问题描述发电厂房墙体的基本模型如图1所示:图1 发电厂墙体几何模型基本要求:依据class 9_10.pdf的最后一页的作业建立ansys模型,考虑两个水平向地震波的共同作用(地震载荷按RG1.60标准谱缩放,谱值如下),主要计算底部跨中单宽上的剪力与弯矩最大值,及顶部水平位移。
要求详细的ansys反应谱法命令流与手算验证过程。
以时程法结果进行比较。
分析不同阻尼值(0.02,0.05,0.10)的影响。
RG1.60标准谱 (1g=9.81m/s2) (设计地震动值为0.1g)频率谱值(g)33 0.19 0.2612.5 0.3130.25 0.047与RG1.60标准谱对应的两条人工波见文件rg160x.txt与rg160y.txt2数值分析框图思路与理论简介2.1理论简介该问题主要牵涉到结构动力分析当中的时程分析和谱分析。
时程分析是用于确定承受任意随时间变化荷载的结构动力响应的一种方法。
谱分析是模态分析的扩展,是用模态分析结果与已知的谱联系起来计算模型的位移和应力的分析技术。
2.2 分析框架:时程分析:在X和Z两个水平方向地震波作用下,提取底部跨中单宽上的剪力、弯矩值和顶部水平位移,并求出最大响应。
谱分析:先做模态分析,再求谱解,由于X和Z两个方向的单点谱激励,因此需进行两次谱分析,分别记入不同的工况最后组合进行后处理得出结够顶部水平位移、底部单宽上剪力和弯矩的最大响应。
3有限元模型与荷载说明3.1 有限元模型考虑结构的几何特性建立有限元模型,首先建立平面几何模型,并将模型进行合理的切割,采用plane42单元,使用映射划分网格的方法生产平面单元(XOY平面)。
然后,采用solid45单元,设置拖拉方向的单元尺寸并清楚初始平面单元plane42,将平面单元进行拖拉,最后生成发电厂墙体的有限元立体几何模型。
单元总数为6060个,总节点数为8174个,有限元模型如图2所示:图2 发电厂墙体有限元模型3.2 荷载说明时程分析:首先计算结构的前两阶自振频率,分别为126.10008.2867f f ==,。
GFRP加固节点的钢筋混凝土框架结构的弹塑性时程分析

收稿日期:2021G10G11基金项目:国家自然科学基金项目(51879207)作者简介:金安杰(1995 ),男,硕士研究生,主要从事混凝土安全与耐久性研究.第36卷第4期徐州工程学院学报(自然科学版)2021年12月V o l .36N o .4J o u r n a lo f X u z h o uI n s t i t u t e o f T e c h n o l o g y (N a t u r a lS c i e n c e s E d i t i o n )D e c 2021G F R P 加固节点的钢筋混凝土框架结构的弹塑性时程分析金安杰a ,b ,杨莎莎a ,b ,刘㊀聪a ,b ,李㊀瑜a ,b(西京学院a .土木工程学院;b .陕西省混凝土结构安全与耐久性重点实验室,陕西西安㊀710123)㊀㊀摘要:针对我国抗震规范调整,使许多现有结构无法满足抗震规范要求,用G F R P 管对其节点进行加固从而增加其整体的抗震性能.采用P K P M 设计了4层两跨的框架结构,采用管厚为3㊁6㊁9m m 的G F R P 加固.用有限元软件A b a qu s ,建立了有限元模型,对加固前后的结构进行了弹塑性时程分析,比较了加固前后的结构顶点位移㊁层间最大位移㊁层间最大位移角及塑性铰区的变化.结果表明加固后的顶点位移㊁层间最大位移㊁层间最大位移角均明显小于加固前的顶点位移㊁层间最大位移㊁层间最大位移角,并满足规范要求,具有一定的安全性.关键词:钢筋混凝土框架结构;G F R P ;节点加固;有限元分析;塑性铰区中图分类号:T U 352.11㊀文献标志码:A㊀文章编号:1674G358X (2021)04G0077G09钢筋混凝土框架结构在地震作用下,容易出现梁铰机制㊁柱铰机制和混合铰机制,其中梁铰机制可使结构获得更大的塑性内力重分布和能量耗散能力,对结构抗震最有利.但在实际情况中,尤其在大震作用下,这种破坏机制无法得到很好的实现.许多钢筋混凝土结构在柱端出现严重的塑性铰区,严重影响整个结构的安全.对此,我国«建筑抗震设计规范»(G B50011 2010)6.2.2条在原规范的基础上,提高了柱端弯矩系数[1].许多现有建筑难以满足新规范抗震要求,可采取增大截面尺寸,粘贴外部钢板以及F R P 加固等技术对该类建筑进行加固.G F R P (g l a s s f i b e r r e i n f o r c e d p o l y m e r ),是复合纤维增强聚合物的一种,具有高强度㊁耐腐蚀和重量轻的特点.通过G F R P 包裹钢筋混凝土构件,可以增加构件的抗剪强度和侧向刚度.G F R P 材料的厚度及包裹层数决定了构件的抗剪强度和侧向刚度的改善效果.现有研究表明,F R P 复合材料不仅可以提高混凝土柱的承载能力,还可以改善柱子的变形能力,提高柱的耗能能力,抗震性能明显提高,非常适合用于结构的抗震设计[2G5].目前,国内外学者对F R P 管约束的混凝土技术在材料和构件层面以逐渐成熟.如L a m 等[6]在对大量F R P 约束混凝土圆柱轴压试验数据进行归纳与分析,提出了F R P 约束混凝土柱的混凝土应力G应变设计模型.S h a 等[7]对G F R P 管约束的钢筋混凝土柱进行研究,得出在G F R P 管约束混凝土柱内配置适量钢筋可有效改善其抗震性能,且配筋率对构件抗震性能影响较大.高献等[8]通过对比无约束钢筋混凝土圆柱与F R P 约束钢筋混凝土圆柱之间的抗震性能差异,得出F R P 能够有效改善钢筋混凝土柱抗震性能,同时明显提高其承载能力.王清翔等[9]通过试验,得出G F R P 管可以提高核心混凝土的强度和变形能力,且适当提高纵筋的配筋率可以提高短柱的延性.龙跃凌等[10]对不同尺寸的G F R P 管约束混凝土短柱进行研究,得出随着G F R P 管壁厚增加,G F R P 约束混凝土试件极限压应力和极限压应变均增加.K h a l e d 等[11]通过对不同加固形式的钢筋混凝土结构进行仿真模拟,得出F R P 加固的框架结构在加固其所有节点时,得到的抗震性能最佳.目前,虽然G F R P G钢筋混凝土组合结构技术在材料和构件层面已经逐渐成熟,但在结构层面的技术研究仍处在刚起步阶段,故而在结构层面对未加固的钢筋混凝土框架结构及G F R P 加固节点的钢筋混凝土结构,进行了8度地震作用下的仿真模拟,对其结果进行弹塑性时程分析.本文分析了其顶点位移时程曲线㊁层间最大位移角包络曲线㊁层间剪力时程曲线.771㊀模型建立1.1㊀结构为研究在经过G F R P 加固节点的原规范设计的结构,是否能满足现有规范的要求,故根据我国抗震规范[1],采用P K P M 设计了4层两跨的框架结构,其平面布置如图1所示,节点加固示意如图2所示.设计地震烈度为7度(0.15g ),地震分组为第二组,Ⅱ类场地.各层层高均为3.6m.结构所有钢筋均采用H R B 400级,框架梁㊁框架柱采用C 40混凝土,框架梁尺寸均为200m mˑ400m m ,框架柱尺寸均为400m mˑ400m m.G F R P 管的性能见表1.表1㊀G F R P 管的力学性能密度ρ/(gc m 2)弹性模量E /(M P a)抗拉强度f t k/(M P a ))泊松比v 2.547.3ˑ10434300.22图1㊀结构平面布置图(单位:m m)图2㊀节点加固示意图(单位:m m )1.2㊀材料本构模型1.2.1㊀G F R P 管本构模型对G F R P 管的弹性参数的设置,选用A b a qu s 材料属性的l a m i n a 进行模拟,需确定弹性常数:E 1,E 2,E 3,v 12,G 12,G 13,G 23,其中1为沿纤维方向,2为纤维切线方向,3为纤维法线方向.弹性常数由文献[12]提出的基于细观力学的预测公式确定.经大量的试验结果表明F R P 材料的基本失效模式为基体控制失效模式,根据H a s h i n [13]纤维控制失效模式基于失效模式的差异,提出了一种包含纤维拉伸断裂㊁纤维压缩屈服断裂㊁基本拉伸或压缩开裂的失效模式.该准则基于材料的参数退化准则,并考虑单层板的累计损伤,利用渐进失效分析方法判断材料的破坏状态,是目前区分失效模式中应用最广泛的判据之一,故选取H a s h i n 损伤模型,作为对G F R P 材料破坏的判断.1.2.2㊀混凝土本构模型采用A b a qu s 中的塑性损伤模型作为混凝土的本构关系,分析微裂缝和微空洞的扩展与演变,直至宏观破坏形成的过程.该模型是一个连续的基于塑性混凝土损伤模型,两个主要的假设破坏机理是混凝土材料的拉裂和压碎,屈服面是由两个硬化常数来控制,该模型可用于单向加载㊁循坏加载及低侧压下的动态加载等情况,其中损伤因子按文献[14]的方法计算.所设定的本构关系参考混凝土设计规范[15].87 徐州工程学院学报(自然科学版)㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀2021年第4期1.2.3㊀钢筋本构模型钢材采用A b a qu s 的等向弹塑性模型,满足V o n M i s e s 屈服准则.钢材的拉压应力G应变曲线假定为两折线模型,初始塑性应变为f y/E ,破坏应变取0.15,其中强化阶段为E ᶄ=0.01E .1.3㊀模态分析模态分析是研究结构动力特性的一种方法,本文采用兰索斯模态提取方法进行模态分析.不同G F R P管厚度的前六阶自振频率列于表2,前三阶振型见图3~5.表2㊀不同G F R P 管厚下框架结构的自振频率(ʎ)/s振型号自振频率G F R P 管厚0m mG F R P 管厚3m mG F R P 管厚6m mG F R P 管厚9m m一阶2.9913.1013.1913.268二阶3.1753.3043.4153.506三阶3.6213.7533.8613.951四阶6.8437.0997.2937.446五阶7.8178.1138.3358.507六阶9.92110.21310.45410.656图3㊀结构一阶振型图4㊀结构二阶振型图5㊀结构三阶振型1.4㊀阻尼计算阻尼的取值在结构的弹塑性时程分析时,对结构的动力反应幅值有着较大的影响.振型阻尼ξ在弹性分析中通常用来表示阻尼比,根据文献[1]规定,结构的振型阻尼ξ取0.05.采用瑞雷(R a y l e i g h )阻尼体系进行计算.其中阻尼分为质量阻尼α㊁刚度阻尼β.计算公式如下所示.ξ=α2ω+β2ω,(1)αβæèççöø÷÷=2ωi ωj ω2j -ω2i ωj-ωi-1ωj1ωiæèççççöø÷÷÷÷ξi ξj æèççöø÷÷,(2)式中:α=ξ2ωi ωjω2j +ω2i,β=ξ2ωi +ωj ,其中ωi 和ωj 为结构的圆频率.取不同G F R P 管厚的前两阶振型进行计算,计算结构如表3所示.表3㊀不同G F R P 管厚下结构阻尼计算G F R P 管厚/m m质量阻尼α/(N /(m /s))刚度阻尼β/(N /(m /s))00.9671650.00258331.0048420.00248561.0359200.00241191.0621500.00235197 金安杰,等:G F R P 加固节点的钢筋混凝土框架结构的弹塑性时程分析1.5㊀地震波选取仅考虑单向地震波输入,输入点为模型底部节点处.地震方向按模型第一模态变形方向加载即A B 轴方向,按8度进行加载.根据文献[1]规定,至少选取2条天然波和一条人工波,故选取E lC e n t r o 波(N GS )㊁T F A T (N GS )和一条人工波,其中人工波按文献[1]的要求进行选取.地震波调幅系数按式(3)进行计算,计算结果见表4.地震波加速度时程曲线见图6~8.a ᶄ(t)=A m a xA ᶄm a xa (t ),(3)式中:a ᶄ(t )为t 时刻调整前的地震加速度分值,a (t )为调整后加速度峰值,A ᶄm a x 为原纪录加速度值,A m a x 为调整后的地震加速度值.表4㊀地震波调幅系数计算地震波加速度峰值/(c m /s2)加速调幅系数E l C e n t r o 波341.71.17TF A T 波175.92.27人工波218.61.83图6㊀E l C e n t r o波加速度时程曲线图7㊀T A F T 波加速度时程曲线08 徐州工程学院学报(自然科学版)㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀2021年第4期图8㊀人工波加速度时程曲线2㊀结构抗震性能分析2.1㊀各层顶点位移时程分析各工况下结构顶点最大位移见表5.在E l C e n t r o 波和T A F T 波两条天然波的作用下,未加固的顶点位移明显大于加固后的顶点位移,且加固效果随玻璃纤维管的厚度增加而逐渐增加.这说明加固后的结构侧向刚度提高,地震作用下水平位移减小,且加固效果随厚度的增加而增加;在人工波的作用下结构的顶点最大位移,加固前与加固后有较大的区别,但由于人工波的整体加速度的整体频率过高,导致结构损伤逐渐累积,减弱了G F R P 管的加固效果.表5㊀各工况下结构顶点最大位移m m地震波顶点最大位移管厚0m m 管厚3m m 管厚6m m 管厚9m m E l C e n t r o 波27.0821.1720.7118.55T A F T 波29.8320.4220.2818.62人工波33.6924.3128.5625.312.2㊀各层层间位移时程分析表6列出了数值模拟所得各工况下楼层最大位移,可以看出各工况下加固后的结构的层间最大位移明显小于未加固的结构层间最大位移.表7列出了各工况下楼层最大位移角,根据文献[1]钢筋混凝土框架结构的层间位移角限值为1/550,可以看出在8度罕遇地震作用下未加固结构的位移角(不包含顶层)均大于限制,但经G F R P 管加固后位移角随管厚增加逐渐减小,虽然在管厚为3m m 和6m m 时仍有部分楼层不满足限值要求,但当管厚为9m m 时除人工波作用下的各层层间位移外,其余均满足限值.满足钢筋混凝土框架结构在地震作用下的位移角要求,具有一定的安全储备使结构满足现有规范要求.说明结构在G F R P 管加固后侧向刚度得到明显提升,G F R P 纤维管能有效提升结构的抗震性能.表6㊀各工况下结构各层最大层间位移m m地震波未加固管厚3m m 管厚6m m 管厚9m m E l C e n t r o 波一层7.254.193.983.30二层9.377.286.985.97三层7.886.185.765.28四层4.383.984.034.0018 金安杰,等:G F R P 加固节点的钢筋混凝土框架结构的弹塑性时程分析表6(续)地震波未加固管厚3m m 管厚6m m 管厚9m m T A F T 波一层8.834.224.193.98二层10.456.776.966.32三层9.056.465.705.52四层5.734.303.853.89人工波一层15.526.716.095.01二层10.788.399.508.42三层8.268.257.726.95四层5.266.125.254.96表7㊀各工况下结构各层最大层间位移角180ʎ/π地震波未加固管厚3m m 管厚6m m 管厚9m m E l C e n t r o 波一层1/4971/8591/9051/999二层1/3841/4951/5161/603三层1/4571/5821/6251/682四层1/8231/9031/8941/899T A F T 波一层1/4581/8531/8601/905二层1/3451/5321/5171/570三层1/3981/5571/6321/653四层1/6281/8381/9341/926人工波一层1/2321/5371/5911/719二层1/3341/4291/3791/428三层1/4361/4371/4671/518四层1/6851/5881/6861/725从图9~11可以看出,结构在E l C e n t r o 波和T A F T 波作用下的层间最大位移的变化相较于人工波的变化更加明显.同时,除管厚为3m m 与未加固的人工波作用下的工况外,其余各工况的最大层间位移均出现在第二层,说明G F R P 加固的框架结构在天然波的工况作用下,加固效果较为稳定,但对于高频率的人工波的加固由于逐渐累积损伤并不稳定.同时从图中可以看出,虽然G F R P 的加固效果与管厚成正比,但是其增加效果并不稳定.图9㊀E l C e n t r o波作用下结构楼层最大位移图10㊀T A F T 波作用下结构楼层最大位移28 徐州工程学院学报(自然科学版)㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀2021年第4期图11㊀人工波作用下结构楼层最大位移2.3㊀应力时程曲线变化结构在G F R P 材料加固下,应力时程曲线出现了明显的变化.由于各工况下,应力时程曲线的变化规律大致相同故选取E l C e n t r o 波作用下的未加固结构与壁厚为9m m 的G F R P 管加固的结构进行说明.图12为所选应力时程曲线的节点示意图,图13为未加固结构应力时程曲线图.图12㊀应力时程曲线所选节点示意图图13㊀E l C e n t r o 波作用下未加固结构应力时程曲线图14为经过壁厚为9m m 的G F R P 管加固的应力时程曲线图.其中未加固的结构的峰值应力出现在38 金安杰,等:G F R P 加固节点的钢筋混凝土框架结构的弹塑性时程分析徐州工程学院学报(自然科学版)㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀2021年第4期5.8s,其峰值应力为17634.9k P a;经G F R P管加固后的结构峰值应力出现在10.6s,其峰值应力为8657.1k P a.比较两者峰值应力出现时间与大小可以得出经G F R P加固后的结构的峰值应力出现时间具有一定的滞后性,同时经过G F R P加固后的结构的峰值应力明显小于未加固的结构.说明经G F R P加固节点后,节点处的刚度得到提升,同时经过G F R P加固后节点的位移具有一定的滞后性.图14㊀E l C e n t r o波作用下加固结构(管厚9m m)应力时程曲线3㊀结论1)加固后的结构的自振频率增大,自振周期减小.结构的质量阻尼增大,刚度阻尼略微减小.2)在地震作用下,各结构的顶点位移随着管厚的增加逐渐减小,说明加固提高了结构的侧向刚度,能保证结构在地震作用下不会产生过大的位移.3)在地震作用下,各层最大层间位移均发生第二层,且随着G F R P管厚的增加逐渐减小.加固后的层间位移均小于未加固的层间位移,并且加固后的层间位移角满足钢筋混凝土框架结构规范所要求的位移角限值,有一定的安全储备.4)与未加固结构相比,经G F R P结构加固后的应力值明显小于加固前的.同时,加固后结构节点处的峰值应力与加固前的峰值应力出现时间明显滞后.参考文献:[1]中华人民共和国建设部.建筑抗震设计规范:G B50011 2010[S].北京:中国建筑工业出版社,2010.[2]赵彤,谢剑.碳纤维布补强加固混凝土结构新技术[M].天津:天津大学出版社,2001.[3]于清.F R P约束混凝土柱力学性能研究[D].哈尔滨:哈尔滨工业大学,2002.[4]高献.F R P约束圆钢筋混凝土柱滞回性能研究[D].福州:福州大学,2005.[5]崔文涛.G F R P套管钢筋混凝土柱轴压力学性能研究[D].大连:大连理工大学,2007.[6]L AM L,T E N GJG.D e s i g nGo r i e n t e d s t r e s sGs t r a i nm o d e l f o r F R PGc o f i n e d c o n c r e t e[J].C o n s t r u c t i o n a n dB u i l d i n g M a t e r i a l s,2003,17(6/7):471G489.[7]S HA O Y,M I R M I R A N A.E x p e r i m e n t a l i n v e s t i g a t i o no f c y c l i cb e h a v i o ro f c o n c r e t eGf i l l e df i b e rr e i n f o r c e d p o l y m e r t u b e s [J].J o u r n a l o fC o m p o s i t e s f o rC o n s t r u c t i o n,2005,9(3):263G273.[8]高献,陶忠,杨有福,等.大轴压比下F R P约束混凝土柱滞回性能试验研究[J].工业建筑,2005,35(9):11G14.[9]王清湘,阮兵峰,崔文涛.G F R P套管钢筋混凝土短柱轴压力学性能试验研究[J].建筑结构学报,2009,30(6):122G127.[10]龙跃凌,蔡兆琼,黄启山,等.G F R P管约束混凝土短柱轴压性能和尺寸效应研究[J].混凝土,2015(9):47G49.[11]G A L A L K,E LGS O K K A R Y H.A n a l y t i c a l e v a l u a t i o no fs e i s m i c p e r f o r m a n c eo fR Cf r a m e sr e h a b i l i t a t e du s i n g F R Pf o ri n c r e a s e dd u c t i l i t y o fm e m b e r s[J].J o u r n a l o fP e r f o r m a n c e o fC o n s t r u c t e dF a c i l i t i e s,2008,22(5):276G288.[12]S AMA A N MS.A n a n a l y t i c a l a n d e x p e r i m e n t a l i n v e s t i g a t i o n o f c o n c r e t eGf i l l e d f i b e rGr e i n f o r c e d p l a s t i c s(F R P)t u b e s.[D].T e x a s:U n i v e r s i t y o fC e n t r a l F l o r i d a,1997.48金安杰,等:G F R P加固节点的钢筋混凝土框架结构的弹塑性时程分析[13]HA S H I NZ.F a i l u r e c r i t e r i a f o r u n i d i r e c t i o n a l f i b e r c o m p o s i t e s.JA p p lM e c h[J].1980,47(3):29G34.[14]白洁,黄长鑫.基于规范的A B A Q U S塑性损伤模型损伤因子的确定[J].城市建设理论研究(电子版),2015,5(13):506G508.[15]中华人民共和国建设部.混凝土结构设计规范:G B50010 2019[S].北京:中国建筑工业出版社,2019.(责任编辑㊀崔思荣) E l a s t oGp l a s t i cT i m eA n a l y s i s o fR e i n f o r c e dC o n c r e t eF r a m e S t r u c t u r e sw i t hG F R PR e i n f o r c e dN o d e sJ I N A n j i e a,b,Y A N GS h a s h a a,b,L I U C o n g a,b,L IY u a,b(a.S c h o o l o fC i v i l E n g i n e e r i n g;b.S h a n x i P r o v i n c i a lK e y L a b o r a t o r y o fC o n c r e t eS t r u c t u r eS a f e t y a n dD u r a b i l i t y,X i j i n g U n i v e r s i t y,X i'a n710123,C h i n a)㊀㊀A b s t r a c t:A c c o r d i n g t o t h ea d j u s t m e n to fC h i n a's s e i s m i c c o d e,m a n y e x i s t i n g s t r u c t u r e s c a n n o tm e e t t h e r e q u i r e m e n t so fs e i s m i cc o d e.T h e r e f o r e,t h i s p a p e r p r o p o s e dt h a t G F R P(G l a s s F i b e r R e i n f o r c e d P o l y m e r)p i p e s c a nb eu s e d t o r e i n f o r c e t h e i r j o i n t s s oa s t o i n c r e a s e t h e i ro v e r a l l s e i s m i c p e r f o r m a n c e.A f o u rGs t o r y t w oGs p a n f r a m e s t r u c t u r ew a s t h e n d e s i g n e d u s i n g P K P M,a n dG F R Pw i t h a t u b e t h i c k n e s s o f3,6,a n d9m m w a su s e df o r r e i n f o r c e m e n t.Af i n i t ee l e m e n tm o d e lw a se s t a b l i s h e d w i t ht h e f i n i t ee l e m e n t s o f t w a r eA b a q u s,a n dt h ee l a s t oGp l a s t i c t i m ea n a l y s i so f t h es t r u c t u r eb e f o r ea n da f t e r r e i n f o r c e m e n tw a s c a r r i e do u t.T h e v e r t e x d i s p l a c e m e n to ft h e s t r u c t u r e b e f o r e a n d a f t e rr e i n f o r c e m e n t,t h e m a x i m u m i n t e rGs t o r y d i s p l a c e m e n t,t h em a x i m u mi n t e rGs t o r y d i s p l a c e m e n t a n g l e a n d t h e c h a n g e s o f p l a s t i c h i n g e z o n e w e r e c o m p a r e d.T h e r e s u l t s s h o wt h a t t h e v e r t e xd i s p l a c e m e n t,t h em a x i m u mi n t e rGs t o r y d i s p l a c e m e n t,a n d t h em a x i m u mi n t e rGs t o r y d i s p l a c e m e n t a n g l e a f t e r r e i n f o r c e m e n t a r e s i g n i f i c a n t l y s m a l l e r t h a n t h o s e b e f o r e r e i n f o r c e m e n t,m e e t i n g t h e c o d e r e q u i r e m e n t sw i t hc e r t a i n s a f e t y r e s e r v e.K e y w o r d s:r e i n f o r c e dc o n c r e t ef r a m es t r u c t u r e;G F R P;j o i n tr e i n f o r c e m e n t;f i n i t ee l e m e n ta n a l y s i s; p l a s t i c h i n g e a r e a58。
反应谱与时程理论对比

反应谱是在给定的地震加速度作用期间内,单质点体系的最大位移反应、速度反应和加速度反应随质点自振周期变化的曲线。
用作计算在地震作用下结构的内力和变形.更直观的定义为:一组具有相同阻尼、不同自振周期的单质点体系,在某一地震动时程作用下的最大反应,为该地震动的反应谱.反应谱理论考虑了结构动力特性与地震动特性之间的动力关系,通过反应谱来计算由结构动力特性(自振周期、振型和阻尼)所产生的共振效应,但其计算公式仍保留了早期静力理论的形式.地震时结构所受的最大水平基底剪力,即总水平地震作用为:FEK= αG其中α为地震影响系数,即单质点弹性体系在地震时最大反应加速度。
另一方面地震影响系数也可视为作用在质点上的地震作用与结构重力荷载代表值之比。
目前,反应谱分析法比较成熟,一些主要国家的抗震规范均将它作为基本设计方法。
不过,它主要适合用于规则结构。
对于不规则结构以及高层建筑,各国规范多要求采用时程分析法进行补充计算。
地震作用反应谱分析本质上是一种拟动力分析,它首先使用动力法计算质点地震响应,并使用统计的方法形成反应谱曲线,然后使用静力法进行结构分析.但它并不是结构真实的动力响应分析,只是对于结构动力响应最大值进行估算的近似方法,在线弹性范围内,反应谱分析法被认为是高效而且合理的方法.反应谱分为加速度反应谱、速度反应谱和位移反应谱。
基于不同周期结构相应峰值的大小,我们可以绘制结构速度及加速度的反应谱曲线。
一般情况下,随着周期的延长,位移反应谱为上升曲线,速度反应谱为平直曲线,加速度反应谱为下降曲线,目前结构设计主要依据加速度反应谱。
加速度反应谱在短周期部分为快速上升曲线,并且在结构周期与场地特征周期接近时出现峰值,后面更大范围为逐渐下降阶段.峰值出现的时间与对应的结构周期和场地特征周期有关.一般来说结构自振周期的延长,地震作用将减小。
当结构自振周期接近场地特征周期时,地震作用最大。
反应谱分析方法需要先求解一个方向地震作用响应,再基于三个正交方向的分量考虑结构总响应,即基于振型组合求解一个方向的地震响应,再基于方向组合求解结构总响应。
水平地震影响系数

根据《抗规》GB50011-2001第5.1.2条的条文说明,多遇地震(小震)和罕遇地震(大震)的最大水平地震影响系数可将《抗规》表格5.1.2-2中所列有效峰值加速度数值乘以放大系数2.25得到。
同理,中震设计可按《抗规》表3.2.2中的设计基本加速度值乘以放大系数2.25得到。
下表是小震、中震、大震的最大水平地震影响系数。
midas中如何结合建筑抗震规范进行桥梁的地震时程分析?由于目前建筑抗震规范对于时程分析采用的最大加速度有了硬性的规定,因此首先就是要将时程的地震波比如简单的elcentro波进行系数调整,根据抗震规范5.1.2.2表中的规定,将. Elcentro的最大峰值与5.1.2.2规定的最大值进行比较得到修正系数,(需要注意的是midas时程函数定义里面的Elcentro给出的相对的值即多少倍的g,比如0.3559g,则系数为35/(0.3559*9.806*100)=0.1,注意选择的是无量刚加速度),填写到放大系数里面,点击生成地震反映谱,函数值就是所需要的一条曲线的a谱,不需要再除以g了(规范P232“其平均地震影响曲线与振型分解反应谱法所用的地震影响系数曲线相比,在各个周期点上相差不大于20%”这里的地震影响曲线就是将加速度谱转化得到的规范谱)。
按照规范需要两条实际一条人工模拟曲线,将得到的地震反映谱曲线(三条)进行数据拟和分析(可采用平均或者SRSS)与实际场地采用的规范规定的a谱进行比较,保证在各个周期点上相差不大于20%,人工波的选择一般是对于特大桥梁或者重要桥梁进行现场的试验后得到一定的模拟曲线,一般桥梁搞几条波就够了不要人工模拟。
开始错误的以为直接将地震波简单处理与a普比较,实际这里的地面运动的加速度波只是一个自由度体系的反应,而a谱则是多个自由度体系经过一系列的分析处理而得到的,因此必须将地震波进行转换,幸好有了midas的转换工具可以直接生成,不然要自己编写傅立叶转换程序了。
SAP2000一些应该注意的技巧,当你出错的时候,看看他

1、sap2000反应谱分析里有一个scale放大系数是怎么回事?应该怎么输入?答:(1)scale不仅调峰值,整个加速度时程都会乘以这个系数。
marry11(2)新的抗震规范,规定了不同地震烈度下,多遇和罕遇地震对应的地震加速度时程曲线的最大值,如8度地区对应的设计基本地震加速度为0.16g。
marry11(3)scale就是个放大系数,让最后得到的数值为程序需要,比如在反应谱分析中,如果输入的地震系数,那么scale就是g(要注意单位,如果采用m,就输入9.8,如果是mm,就输入9800),如果反应谱直接输入了谱加速度,那么scale就是1。
在时程分析中也同理。
Xfjiang说明:在“定义”-“反应谱函数”中选择chinese2002添加反应谱函数时,在此界面中的“加速度”栏中的各个数值代表不同时间的地震影响系数,而地震反应谱。
(4)楼上说得对,但是输入1时也要注意单位,因为sap本身要求这个地方输的不是简单的放大系数,而是与单位有关的一个加速度,因此要注意单位。
Ngmxf(5)我个人觉得是这样,这个系数有2个作用:一个是进行地震方向组合;还可以用来修正反应谱曲线中的数值,因为大多数人都是按照规范中的地震影响系数曲线公式去得到反应谱曲线的,这个曲线纵坐标是地震影响系数。
所以可以在反应谱分析选项中用这个scale factor去调整,即把scale factor设为重力加速度,单位一定要搞清楚。
sap的原意应该是进行地震方向组合用的。
如果当时在输反应谱曲线时就把纵坐标变为影响系数乘以重力加速度的话那第二个作用就不存在了。
Z625(6)g就是那个scale,还是同意这个,Scale还是取决于单位,比如国内通常取用9.8,因为大家用的都是m、N、s。
当用英制的时候就要注意单位的变换了,用Kip, ft,时scale是32.2。
用lb, in时,scale取386。
其实就是为了使用不同单位时的统一。
桥梁博士V4工程案例教程00 桥博V4抗震分析解决方案

桥梁博士V4 抗震分析解决方案➢前言➢第一章:抗震分析---计算功能➢第二章:抗震分析---分析示例➢第三章:抗震分析---规范验算➢结语➢我国是地震多发国家。
2008年汶川地震以来,全社会对建设工程地震安全性提出了更高的要求,抗震减灾工作日益受到重视。
➢桥梁工程作为交通网络的枢纽工程,其抗震性能关系到整个交通生命线的畅通与否,进而直接影响抗震救灾和灾后重建工作的大局。
➢研发成果:桥梁博士V4在研发时,针对抗震分析对国内各种的规范和理论进行了系统研究,并积极吸取国内近年来的工程实践成果,为桥梁的抗震分析和计算建立了一套系统的解决方案。
➢振幅➢频谱特性➢持时1.地震动的工程特性➢牛顿第二定律:F=ma➢结构周期:T=2πmk ;结构频率:f=1T➢达朗贝尔原理(D’Alembert):f I(t)+f D(t)+f S(t)=p(t) 2.基本物理公式桥梁抗震基本概论3.➢抗震设计思想:‘小震不坏、中震可修、大震不倒’。
➢抗震设防标准:两水准设防、两阶段设计。
(公路市政)共计5本:➢«CJJ 166-2011 城市桥梁抗震设计规范»➢«JTG/T B02-01-2008 公路桥梁抗震设计细则»➢«JTG B02-2013 公路工程抗震规范»➢«GB 50111-2006 铁路工程抗震设计规范»➢«GB 50909-2014 城市轨道交通结构抗震设计规范»4.抗震分析国内规范PS :本资料以城市及公路桥梁抗震设计规范为主进行介绍。
5.抗震分析方法分析方法适用范围说明静力法弹性静力法刚性结构仅对可视为刚体的结构有效,如桥台。
缺点:忽略结构动力反应。
*Pushover分析复杂桥梁设计一般不采用,多用于抗震性能评估,可计算非线性反应的需求和能力。
规范一般用于计算E2地震作用下桥墩墩顶容许位移以及求解能力保护构件设计内力(超强弯矩)的主要方法。
弹性动力时程分析地震波选取方法探讨

弹性动力时程分析地震波选取方法探讨摘要:本文根据珠海市某超限高层弹性动力时程分析结果,探讨了选波方法。
研究表明,采用小样本容量的地震波输入时,天然波输入数量的增加可以降低地震波的总体离散性,按规范推荐的比例输入三向地震波加速度是合理的。
关键词:结构设计;弹性动力时程分析;地震波Abstract: in this paper, according to the Zhuhai city high-rise overrun elastic dynamic time-history analysis results, discusses the selection of wave method. Studies show that, using the small sample size of earthquake input, natural wave input quantity increase can reduce the overall dispersion of seismic wave, according to the standard recommended proportional input three to seismic wave acceleration is reasonable.Key words: structural design; elastic time-history dynamic analysis; seismic wave近年来,随着我国社会经济的发展,各类高层建筑在全国各地日益增多。
它们新颖别致、多样化、复杂化和独特个性等特点给城市带来崭新面貌的同时也给高层建筑结构设计者带来了严峻的挑战。
《建筑抗震设计规范》[1]第5.1.2条和《高层建筑混凝土结构技术规程》[2]第4.3.4条规定了高层建筑应采用弹性时程分析法进行多遇地震下的补充验算的范围。
本文对珠海市某超限高层建筑进行弹性动力时程分析,探讨地震波的选取方法。
自振周期及地震作用计算讲义
n
i
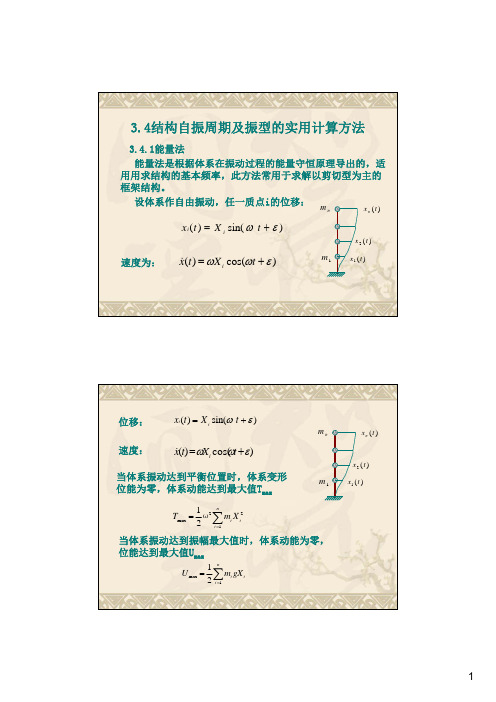
根据能量守恒原理:
g
m
i 1 n i
n
i
Xi
T1
2 i
2
m
i 1
X
1
2
m X
i i 1 n
n
2 i
g
m X
i i 1
2
i
G X
i
n
2 i
G X
i i 1
i 1 n
i
一般假定:将结构重力荷载当成水平荷载作用于质点上 所得的结构弹性曲线为结构的基本振型。
T 1 max 1 2
n
i 1
m i ( 1 x i )
2
mN
xn
M
eq
xm
单质点体系的最大动能为
T 2 max 1 M 2
eq
xm xn
m1 x1
( 1 x m ) 2
x m ---体系按第一振型振动时,相应于折算质点处的最大位移;
T1max
1 n mi (1xi )2 2 i1
ห้องสมุดไป่ตู้
竖向地震作用,烟囱上 抛后下落错位。
9
德阳利森水泥厂生料均化库,受到 竖向地震作用,塔筒上抛后下落。
底部框架底层为薄弱层, 底层墙体叠合塌落。 (9度 区)
10
底部框架结构底层框架叠合塌落(北川11度区)。
中间层叠合塌落(日本阪神大地震)。
11
中间层水平裂缝 中间层水平裂缝。
3.6.1高耸结构及高层建筑的竖向地震作用
台湾省漳化县富贵 名门大楼,16层钢筋混 凝土住宅楼,平面为C 型, 平面不规整,单排 柱框架,柱子间距太大, 数量偏少。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7、动力时程分析7.1结构的弹性动力时称分析(图01 )图01主界面图1 主菜单表5.1.2.1 采用时程分析法的房屋高度范围度、烈度、场地类别房屋高度范围8度Ⅰ、Ⅱ类和>1007`度8度Ⅲ、Ⅳ类>809度>601.1 结构的弹性动力时程分析(图1.1):位置:主菜单\结构的弹性动力时称分析图1 地震波选择操作说明及规范链接:○〈选择地震波〉:选用不少于二组的实际强震记录,一组人工模拟的加速度时程曲线。
见〈建筑抗震设计规范〉[GB50011-2001]第5.1.2条。
○〈地震波信息〉:纵坐标示〈加速度〉,横坐标示记录时间。
○〈峰值加速度值〉:最大值见〈建筑抗震设计规范〉[GB50011-2001]5.1.2条表5.1.2.-2 时程曲线最大值地震影响6度7度8度9度多遇地震18 35(55) 70(110) 140罕遇地震220(310) 4000(510) 620○方向:计算单向地震时,主分量峰值加速度赋正确值,其它赋0;计算双向地震时,主、次分量峰值加速度赋正确值,其它赋0;○楼层剪力、楼层弯矩不分塔统计:应勾选。
1.2分析参数(图1.2):位置:主菜单\分析参数图1.2 弹性动力时程分析参数操作说明及规范链接:○〈地震波主方向与X轴夹角〉:可用90。
○〈主分量峰值加速度〉:○〈次分量峰值加速度〉:○〈垂直分量峰值加速度〉:计算单向地震时,主分量峰值加速度赋正确值,其它赋0;计算双向地震时,主、次分量峰值加速度赋正确值,其它赋0;○〈结构阻尼比〉:钢筋混凝土结构:0.05;小于12层纲结构:0.03;大于12层纲结构:0.035。
○〈第一条地震波放大系数〉:可不放大。
○〈第二条地震波放大系数〉:可不放大。
○〈第三条地震波放大系数〉:可不放大。
2.1、时程分析结果图形显示(图2.1):位置:主菜单\时程分析结果图形显示图2.1.位置菜单2.1.1动力时程分析结果(WDYNA.OUT1):位置:位置菜单\动力时程分析结果WDYNA.OUTWDYNA.OUT动力时程分析结果2.1.2 最大楼层位移曲线(图2.1.2):位置:位置菜单\最大楼层位移曲线图2.1.2最大楼层位移曲线2.1.3 最大层间位移角曲线(图2.1.3):位置:位置菜单\最大层间位移角曲线图2.1.3最大层间位移角曲线2.1.4 最大楼层剪力曲线(图2.1.4):位置:位置菜单\最大楼层剪力曲线图2.1.4最大楼层剪力曲线2.1.5 最大楼层弯矩曲线(图2.1.5):位置:位置菜单\最大楼层弯矩曲线图2.1.5最大楼层弯矩曲线7.2EPDA/PUSH(图02 )图02主界面采用弹塑性静、动力分析范围1、甲类建筑及9度区的乙类建筑;2、7-9度区楼层屈服强度系数小于0.5的框架结构;3、高度大于150m的钢结构;4、采用隔震和消能减震设计的结构;5、9度及8度Ⅲ、Ⅳ类高大厂房的排架见〈建筑抗震设计规范〉[GB50011-2001]5.5.2条1、生成弹塑性静、动力分析数据(图1):位置:主界面\生成弹塑静、动力分析数据图1位置菜单1.1、接力SATWE或PMSAP生成三维弹塑性模型(图1.1.A-C):位置:位置菜单\接力SATWE或PMSAP生成三维弹塑性模型图1.1.A图1.1.B图1.1.C操作说明:○由图A选择单项。
○由图B选择程序。
○按图C提示操作。
1.2、修改构件实配钢筋(图1.2.A-B):位置:位置菜单\修改构件实配钢筋图1.2.A操作菜单图1.2.B操作简图操作说明:○按图A提示操作。
○在图B上修改。
○按图C提示操作。
1.3、EPDA最新更版说明:位置:位置菜单\ EPDA最新更版说明操作说明:○用于查看最新更版说明。
1.4、PUSH最新更版说明:位置:位置菜单\ PUSH最新更版说明操作说明:○用于查看最新更版说明。
2、弹塑性动力时程分析(图2.A-E):位置:主界面\弹塑性动力时程分析图2.A操作说明及规范链接:○〈地震波参数〉:1、选择地震波:见图2B。
2、地震波作用方向角:903、主分量峰值加速度:4、次分量峰值加速度:5、垂直分量峰值加速度:最大值见〈建筑抗震设计规范〉[GB50011-2001]5.1.2条表5.1.2.-2 时程曲线最大值地震影响6度7度8度9度多遇地震18 35(55) 70(110) 140罕遇地震220(310) 4000(510) 6206、地震波计算步长:见地震波记录。
7、地震波起始计算时刻:填0。
8、地震波终止计算时刻:填99。
○〈结构相关参数〉:1、结构阻尼比:钢筋混凝土结构:0.05;小于12层纲结构:0.03;大于12层纲结构:0.035。
2、阻尼计算对应第一周期:计算瑞利阻尼时需用到的第一周期。
3、阻尼计算对应第二周期:计算瑞利阻尼时需用到的第二周期。
○〈混凝土本构关系参数〉:1、混凝土本构考虑屈服面:2、混凝土本构关系类型:双线型、三线型2个选项。
3、初始刚度折减系数:据经验输入。
4、塑性刚度蜕化系数:混凝土受压阶段杨氏模量与初始阶段折后的弹性模量比值。
5、混凝土柏松比:输入弹性阶段和塑性阶段的平均值。
○〈钢材本构关系参数〉:1、钢材初始弹性模量:即弹性阶段的弹性模量。
2、钢材塑性刚度蜕化系数:输0为理想弹塑性模型。
○〈过程显示参数〉:1、结构模显示方式:“显示地震波进程”、“显示结构空间动画”、“显示搂层平均位移”三选一。
曾经出现过的塑性饺,以黄色表示;当前时间步的塑性饺,以红色表示;剪力墙的裂缝用小短线表示。
2、计算过程刷新屏幕:选是。
3、位移放大倍数:可输1000。
4、塑性饺判断方法:程序提供“弹性积分点比例”和“截面刚度退化比例”两种方法,二选一。
5、塑性饺判断参数:可输0.3。
?6、显示所有曾出县塑性饺位置:选是。
○〈计算参数选择〉:1、钢和混凝土材料选用:可选标准值。
2、结构始终保持弹性状态:选否。
3、竖向荷载折减系数:。
4、竖向荷载加载步数:可取1。
5、剪力墙刚度调整系数:。
6、剪力墙主筋折算为分布筋:选是。
7、考虑P-△影响:高、柔结构选是。
8、最大层间位移角限值:见〈建筑抗震设计规范〉[GB50011-2001]5.5.5条。
表5.5.5 弹塑性层间位移角限值结构类型[θp]单层钢筋混凝土排架1/30钢筋混凝土框架1/50底框框架-抗震墙1/100钢筋混凝土框架-抗震墙、板柱-抗震墙、框架-核心筒1/100钢筋混凝土抗震墙、筒中筒1/120多、高层钢结构1/509、线性方程组解法:“LDLT解法”、“PCG解法1”、“PCG解法2”可选后两种。
10、动力微分方程组解法:”Wilson-θ”、”Newmark-β”两重解法,二选一。
11、非线性方程组解法:”Raphson”、”Modifed Newton-Raphson”:。
混凝土结构选Newton-Raphson12、非线性迭代步数限值:10左右。
13、最佳收敛次数:0.01-0.001。
14、不收敛时步长缩减次数限值:5左右。
15、不收敛时步长缩减倍数:1/2。
16、步长自动判断指数:1/2-1/3。
图2.B操作说明及规范链接:○〈选择地震波〉:选用不少于二组的实际强震记录,一组人工模拟的加速度时程曲线。
见〈建筑抗震设计规范〉[GB50011-2001]第5.1.2条。
○〈地震波信息〉:纵坐标示〈加速度〉,横坐标示记录时间。
○〈峰值加速度值〉:最大值见〈建筑抗震设计规范〉[GB50011-2001]5.1.2条表5.1.2.-2 时程曲线最大值地震影响6度7度8度9度多遇地震18 35(55) 70(110) 140罕遇地震220(310) 4000(510) 620○方向:计算单向地震时,主分量峰值加速度赋正确值,其它赋0;计算双向地震时,主、次分量峰值加速度赋正确值,其它赋0;○楼层剪力、楼层弯矩不分塔统计:应勾选。
图2.C后处理参数选择操作说明及规范链接:○〈只进行文本文件输出〉:○〈内力文本文件输出〉:○〈图形输出参数〉:1、节点结果详细输出:2、判断塑性铰相关记录详细输出:○〈节点图形输出内容〉:1、节点位移时程:2、节点速度时程:3、节点加速度时程:4、节点惯性力时程:○〈层图形输出内容〉:1、层位移时程:2、层间位移角时程:3、层速度时程:4、层加速度时程:5、层反应力时程:6、层剪力时程:7、层弯矩时程:8、层最大反应力时程:图2.D删除提示图2.E计算进程显示3、查看弹塑性动力时程分析结果(图3):位置:主界面\看弹塑性动力时程分析结果图3位置菜单3.1、绘结构弹塑性计算模型图(图3.1):位置:位置菜单\绘结构弹塑性计算模型图图3.1弹塑性计算模型图3.2、绘楼层最大响应曲线(图3.2.A-B):位置:位置菜单\绘楼层最大响应曲线图3.2.A图3.2.B3.3、绘楼层平均时程响应曲线(图3.3.A-B):位置:位置菜单\绘楼层平均时程响应曲线图3.3.A图3.3.B3.4、绘节点时程响应曲线(图3.4):位置:位置菜单\绘节点时程响应曲线图3.43.5、绘结构弹塑性状态分布图(图3.5.A-C):位置:位置菜单\绘结构弹塑性状态分布图图3.5.A图3.5.B图3.5.C3.6、结构单元、节点编号图(图3.6):位置:位置菜单\结构单元、节点编号图图3.63.7、结构最大节点响应文本输出(图3.7):位置:位置菜单\结构最大节点响应文本输出图3.73.8、结构最大单元内力文本输出(图3.8):位置:位置菜单\结构最大单元内力文本输出图3.83.9、结构构件截面抗剪验算文本输出(图3.9):位置:位置菜单\结构构件截面抗剪验算文本输出图3.94、弹塑性静力分析(图4):位置:主界面\弹塑性静力分析图4弹塑性静力分析操作说明及规范链接:○〈从不同的角度使用本程序〉:1、验算结构是否能抵抗指定的恻向地震荷载。
2、求出结构的积限荷载,并了解结构弹塑反应的全过程。
需把基底剪力与总重量的比值设成一个狠大值,5;把X、Y向最大侧移限值设为很大数1/20。
以确保不停机。
○〈侧推荷载〉:1、荷载类型:可选倒三角形。
2、基底剪力与总重量的比值:见〈建筑抗震设计规范〉[GB50011-2001]表5.1.4-1。
表5.1.4.-1 水平地震影响系数最大值地震影响6度7度8度9度多遇地震0.04 0.08(0.12) 0.16(0.24) 0.32罕遇地震0.50(0.72) 0.90(1.200) 1.40注:7、8度时括号内数值分别用于设计基本地震加速度为0.15g和0.30g的地区。
3、荷载方向与X轴的夹角:可用90。
○〈竖向荷载〉:1、竖向荷载调整系数:可取0.65,见〈建筑抗震设计规范〉[GB50011-2001]表5.1.4-1。
